Transient analysis of a three-layer microbeam subjected to electric potential

ABSTRACT

In this paper, free vibration, wave propagation, and bending analyses of a sandwich microbeam integrated with piezoelectric face-sheets resting on Pasternak foundation under electric potential are presented based on the strain gradient theory and Euler–Bernoulli beam theory. The material properties of core are assumed variable along the thickness direction and piezoelectric face-sheets are assumed homogeneous piezoelectric materials. A two-dimensional electric potential distribution along the axial and transverse direction is applied on the face-sheets of microbeam. Hamilton principal is used to derive governing differential equations of motion. Three behaviors of sandwich microbeam including free vibration, wave propagation, and bending analyses are studied in this paper. Some numerical results are presented to capture the effect of important parameters of the problem such as in-homogeneous index, applied voltage, parameters of foundation, and material length scales. The numerical results indicate that the effect of electric potential along the axial direction is very small rather than one along the transverse direction where initial voltage is applied.

KEYWORDS:

• Euler–Bernoulli three-layer microbeam
• free vibration
• wave propagation
• electric potential
• applied voltage

1. Introduction

The scientists have found this fact that the behavior of materials in very small scales leads to important changes in fundamental governing equations and need more considerations. These changes for different analyses such as free vibration, wave propagation, bending, and other analyses present different behaviors. To capture the effect of various parameters in micro- and nanoscale, some new theories have been developed. Eringen’s nonlocal [1] and strain gradient [2] theories have been proposed to capture the effect of material length scale parameters in nano- and microscales, respectively. Studying the behavior of a three-layer microbeam can present important informations for researchers. A literature review on microscale problems can be presented as:

Backsto and Nilsson [3] used Bernoulli–Euler or Timoshenko beam theories to evaluate the responses of sandwich beams due to various types of boundary conditions. They verified the obtained results with literature for a sandwich beam with aluminium laminates and a plastic foam core. Structural analysis of Euler–Bernoulli laminated piezoelectric beam subjected to three-dimensional distributions of mechanical stresses and strains has been performed by Maurini et al. [4] based on mixed variational principle and Lagrange multiplier method. They evaluated efficiency of the present method by comparison with three-dimensional finite element approach. Aydogdu [5] presented axial vibration analysis of nanorods with clamped-clamped and clamped-free boundary conditions. He investigated that considering the nonlocal parameter leads to increase in natural frequencies of nanorods. The wave propagating in one-dimensional nanostructure with initial axial stress has been investigated by Song et al. [6]. They used a nonlocal elastic model incorporating with strain gradient theory. The governing equations for longitudinal and transverse waves in bars and beams have been derived using two scale parameters for introducing size effect. The phase and group velocities of wave propagation were analytically obtained. Buckling nonlocal analysis of a micro- or nanorods/tubes was studied by Ghannadpour and Mohammadi [7] using Eringen’s nonlocal elasticity theory based on the Timoshenko beam theory. They employed Chebyshev polynomial functions and method of minimum total potential energy to achieve the critical buckling loads. The obtained results have been compared to literatures and the effect of nonlocal parameters investigated.

Bending analysis of a microscale functionally graded (FG) Timoshenko beam was studied by Simsek et al. [8] based on the modified couple stress theory. They assumed that material properties are graded along the thickness direction based on the Mori–Tanaka homogenization technique and the classical rule of mixture. They studied the effect of micro-length scale parameter, aspect ratio, and volume fraction index on the bending results of microbeam. They concluded that employing the modified couple stress theory leads to a stiffer beam rather than old theories. Simsek and Reddy [9] presented bending and free vibration analyses of FG microbeams based on the modified couple stress theory and some higher-order beam theories. They used the couple stress theory to account the effect of material length scale parameters, different material compositions, and shear deformations on the responses of the system. Dynamic analysis of an Euler–Bernoulli microbeam due to a moving harmonic load made of functionally material that graded along the axial direction was studied by Simsek et al. [10]. They assumed that material properties such as elasticity modulus and mass density are varying along the axial direction. The effect of material distribution, velocity of the moving load, and excitation frequency on the dynamic response of the beam were investigated. Kien [11] analyzed large displacement response of tapered cantilever beams made of axially FG material using the finite element method.

Douville and Grognec [12] presented elastic buckling analyses of classical sandwich beam-columns. The core was considered as a two-dimensional continuous solid and two faces represented by Euler–Bernoulli beams. Akgöz and Civalek [13] used strain gradient theory to study longitudinal free vibration analysis of axially FG microbars. After derivation of the governing equations of motion, Rayleigh–Ritz solution technique was employed to obtain an approximate solution to the free longitudinal vibration problem of clamped-clamped and clamped-free boundary conditions. The effect of some important parameters such as material length scale parameters, material ratio, slenderness ratio, and ratio of Young’s modulus was studied in detail. Simsek and Reddy [14] used a unified higher-order beam theory for buckling analysis of a FG microbeam rest on Pasternak’s foundation using modified couple stress theory. They assumed that material properties were graded along the thickness direction based on the Mori–Tanaka homogenization technique and the classical rule of mixture. After derivation of the governing equations of motion, the Navier-type solution was developed for simply-supported boundary conditions. The effect of nonuniform geometry and non-homogeneity material properties on the vibration characteristics of Bernoulli–Euler microbeam was studied by Akgöz and Civalek [15] based on modified couple stress theory. Non-homogeneity was considered along the longitudinal direction.

Wave propagation analysis of nanorod-based nonlocal and surface elasticity was studied by Arefi [16,17]. Arefi and Zenkour [18] employed simplified shear and normal deformations nonlocal theory for bending analysis of FG piezomagnetic sandwich nanobeams. The nanobeam was subjected to thermal, mechanical, electrical, and magnetic loads. The nonlocal behavior of Kelvin–Voigt sandwich plate was studied by Arefi and Zenkour [19]. Arefi and Zenkour [20,21] presented transient analyses of sandwich nanoplates in thermal, electrical, and magnetic fields based on nonlocal elasticity theory and using classical and higher-order shear deformation plate theories. Zhou et al. [22] presented a review on mechanical behaviors of nano-laminates with carbon nanotubes (CNTs). They presented some important issues on the characteristics of CNTs and response of structures made of CNTs due to various loads. Ebrahimi and Barati [23] studied buckling results of FG nanoplate in magneto-electro-thermal environment. They studied the influence of thermal, electrical, and magnetic loads on the buckling behavior of nanoplate.

A comprehensive investigation on the literature indicates that although strain gradient theory has been developed for various structures and models, however combination of this subject with sandwich structures and piezoelectric materials leads to an important issue that has not been previously mentioned. This issue motivated authors to present this study. This study presents different analyses of a three-layer microbeam including a FG core and two piezoelectric face-sheets. The structure rests on Pasternak’s foundation and subjected to transverse loading and applied voltage. The strain gradient theory is developed for an Euler–Bernoulli beam model. Using Hamilton’s principal, the governing equations of motion were derived to capture the effect of some important parameters such as material length scale parameters, two parameters of Pasternak foundation, applied voltage on the phase velocities, natural frequencies, and deflection of microbeam.

2. Governing equations

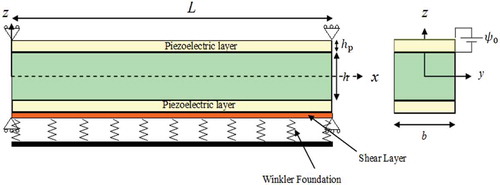
In this section, the basic relations of motion for a sandwich Euler–Bernoulli microbeam with simply-supported boundary conditions and subjected to applied electric potential are presented. The schematic figure of the problem is presented in Figure 1.

Figure 1. The schematic of a simply-supported three-layer Euler–Bernoulli microbeam.

Based on the Euler–Bernoulli beam model, the displacement field components are derived as

(1)

in which , , are displacement components along the Cartesian coordinate systems , , , respectively. Referring to assumed displacement field in Equation (1), only nonzero strain component is derived as:

(2)

Stress–strain relations for micro-core are derived as:

(3)

in which is modulus of elasticity and is stress of core. The constitutive relation for piezoelectric micro-face-sheets is derived as:

(4)

in which is piezoelectric constants, is electric field, and is stress of face-sheets. By considering the electric potential, we can complete required equations. A two-dimensional electric potential with an applied voltage is employed as following format [18–21]:

(5)

where is applied voltage at top of the plate and . For above electric potential, we have electric field as follows [18–21]:

(6)

Substitution of electric potential components from Equation (6) into stress equations, Equations (3) and (4), yields the following stress components for core and face-sheets as:

(7)

For an electromechanical system, electric displacement is defined as:

(8)

in which are dielectric coefficients. Substitution of electric potential components into electric displacement components leads to:

(9)

In this stage, the basic relations for strain gradient theory are expressed. The mentioned relations for this purpose are defined as [2]:

(10)

in which and are higher-order stress tensors, and are deviatoric stretch gradient tensor and symmetric gradient rotation tensor, and is dilatation gradient tensor. In addition, is the bulk shear modulus in which is the modulus of elasticity and is Poisson’s ratio, and , , and are micro-length scale parameters. In Equation (10), the deviator stretch gradient tensor, symmetric gradient rotation tensor, and corresponding dilatation are defined as [2]:

(11)

in which , , and is the permutation symbol. By using the displacement field defined in Equation (1), the nonzero higher-order strains and consequently can be derived as:

(12)

After derivation of higher-order strains, we will have (dilatation gradient tensor), (deviatoric stretch gradient tensor), and (symmetric gradient rotation tensor) as:

(13a)

(13b)

(13c)

After derivation of required terms for , , and the corresponding stress components , , and can be derived as:

(14a)

(14b)

(14c)

After derivation of the required expressions for stresses, electric displacements, and higher-order stresses corresponding to strain gradient theory, equations of motion are derived using Hamilton’s principle. Its variation form can be applied in which

(15)

where is kinetic energy of structure, is strain energy, and is the work performed by external works. In addition, and are spring and shear parameters of Winkler–Pasternak foundation. Substitution of variation forms of strain components , dilatation gradient tensor , deviatoric stretch gradient tensor , symmetric rotation gradient tensor , and electric field from Equation (13) and Equation (6) into variation form of energy equation and integration by part on the derived equation. In this stage and after completion of required terms of strain energy, kinetic energy, and energy due to external works, the final governing equations are obtained by separation of coefficients of , , and .

2.1. Equations of motion

(16a)

(16b)

(16c)

in which

(17)

and the integration constants are given by

(18)

In addition, the resultants components are expressed as

(19a)

(19b)

(19c)

(19d)

(19e)

(19f)

2.2. Boundary conditions

The extremum condition of Hamilton’s principle gives also the form of geometric (essential) and force (natural) boundary conditions:

(20a)

(20b)

(20c)

(20d)

(20e)

2.3. Constitutive equations

The constitutive equations will be derived from the extremum condition of Hamilton’s principle as follows:

(21a)

(21b)

(21c)

(21d)

(21e)

(21f)

(21g)

in which

(22)

and the integration constants are derived as:

(23)

3. Solution procedure

In this section, solution procedures for different analyses of Euler–Bernoulli microbeam are presented. These analyses are including wave propagation, free vibration, and bending results of microbeam. As a first case, wave propagation analysis is investigated.

3.1. Wave propagation

For wave propagation analysis [24], three unknown fields are assumed as in which is wave number, is phase velocity, and , , and are amplitudes of axial and transverse displacements and electric potential. Substitution of assumed solutions into governing equations of motion by ignoring the force terms lead to:

(24)

where

denotes

(25)

and the elements of matrix are given by

(26)

To arrive the phase velocity of wave propagation , the determinant of the matrix must be considered zero as .

3.2. Free vibration and bending analyses

For vibration and electro-elastic bending analysis of microbeam with two simply-supported ends and two short-circuited electric potential, the following solution may be supposed as:

(27)

in which is the natural frequency and . By substitution of two axial and transverse displacement components and electric field into equations of motion, the elements of stiffness, mass, damping, and force matrix are obtained as:

(28)

where the nonzero symmetric elements of stiffness , mass matrices, and force vector in this case can be obtained as:

(29)

4. Numerical results and discussions

The numerical results of the problem including the natural frequencies, phase velocities, and bending results may be presented as function of input parameters of the problem. To apply non-homogeneity on the material properties of micro-core, the variation of material properties are assumed to be graded along the thickness direction as:

(30)

in which , , and , , are modulus of elasticity, Poisson’s ratio and material density of top and bottom of core, respectively, and is non-homogeneity index. Before presentation of the numerical results, the material properties of core and piezoelectric face-sheets may be presented as ([8,18–21,25]):

Core:

(31)

Face-sheets:

(32)

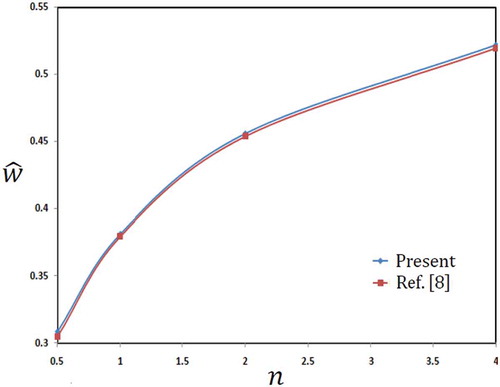
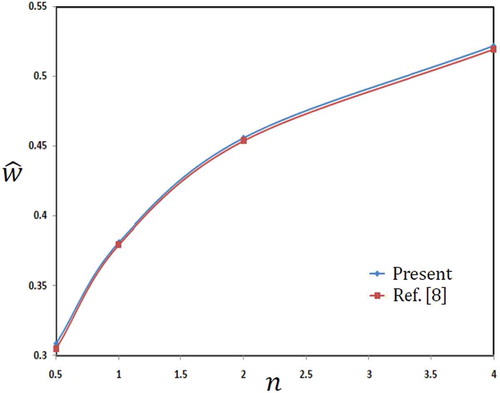
4.1. Comparison and verification

In this section, verification with published paper is performed. For verification, the work of Simsek et al. [8] is selected. Figures 2 and 3 present comparisons between current results and previous results of Ref [8]. The dimensionless deflection according to reference [8] is calculated as . Figures 2 and 3 show the dimensionless deflection in terms of non-homogeneity index, for , respectively. One can conclude that both comparisons presented in Figures 2 and 3 are in good agreement with reference [8].

Figure 2. Dimensionless deflection of a nanoplate in terms of non-homogeneity index for .

Figure 3. Dimensionless deflection of a nanoplate in terms of non-homogeneity index for .

4.2. Wave propagation responses

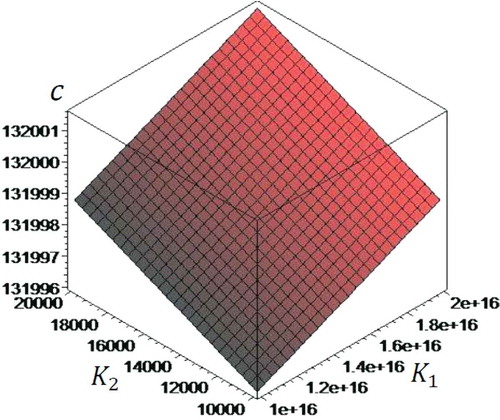
In this section, the numerical results corresponding to wave propagation responses are presented. Two-dimensional distribution of phase velocities in terms of two parameters of Pasternak’s foundation and for =0 are presented in Figure 4. It is observed that with increase of two parameters of Pasternak’s foundation and , the phase velocities are increased due to increase of stiffness of foundation.

Figure 4. Two-dimensional distribution of phase velocities in terms of two parameters of Pasternak’s foundation for .

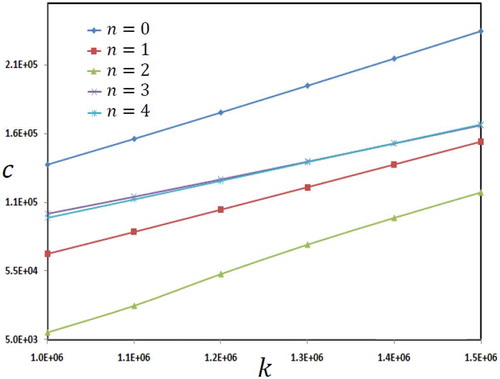
Figure 5 shows the variation of phase velocities in terms of wave number k for different values of non-homogeneity index . It can be concluded that for with increase of the non-homogeneity index , the phase velocities are decreased significantly. The minimum value of phase velocity is occurred for . For the phase velocities are decreased and finally tend to an asymptotic value. This is due to more decrease of the stiffness of microbeam rather than decrease of the mass of one. Furthermore, with increase of the wave number , the phase velocity is increased.

Figure 5. The phase velocities of three-layer nano/microbeam in terms of wave number and non-homogeneity index.

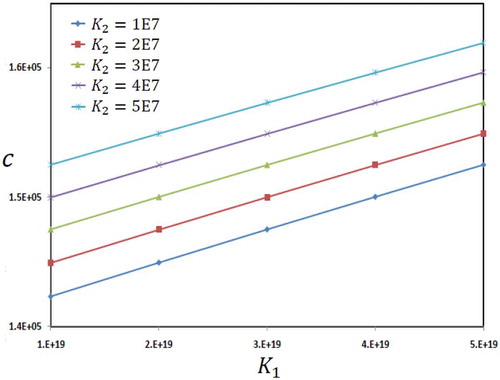
The effect of parameters of Pasternak’s foundation for homogeneous core can be investigated on the phase velocities of microbeam in Figure 6. This figure shows variation of phase velocity in terms of spring parameter of foundation for different values of shear parameter of foundation. One can conclude that phase velocities are increased with increase of both spring and shear parameters.

Figure 6. The phase velocities of microbeam in terms of two parameters of foundation and for .

4.3. Free vibration responses

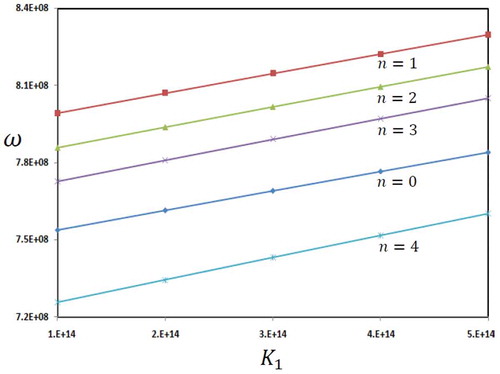
In this section the free vibration responses of the microbeam is presented. The results of remained sections are calculated for a microbeam with characteristics (, , ). Figure 7 shows the natural frequencies of microbeam in terms of first parameter of foundation (spring coefficient) for various values of non-homogeneity index. One can conclude that increase of spring parameter of foundation leads to stiffer structure and consequently increase natural frequencies. In addition, the influence of non-homogeneity index reflects the interesting results and conclusions. It can be observed that maximum natural frequencies are reached for . Increase of non-homogeneity index for decreases natural frequencies significantly. This decrease is due to more decrease of stiffness rather than decrease of mass of microbeam.

Figure 7. The natural frequencies of microbeam in terms of dimensionless microscale parameters and .

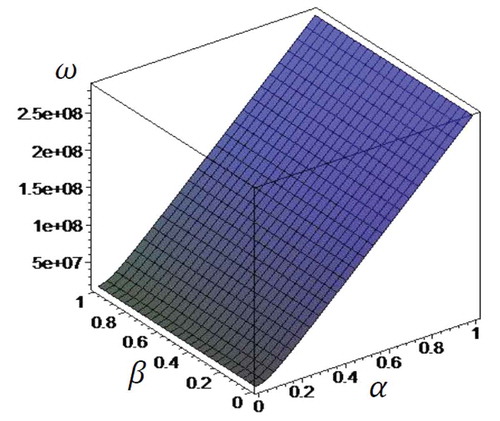
Two-dimensional distributions of the natural frequencies of microbeam in terms of dimensionless microscale parameters and are presented in Figure 8 for . It can be concluded that the effect of first dimensionless parameters of microscale is very greater than the second one . It can be concluded that increasing the first dimensionless parameters of microscale leads to a stiffer beam. Furthermore, it is revealed that the effect of second dimensionless parameters of microscale can be ignored on the natural frequencies of microbeam.

Figure 8. Two-dimensional distribution of the natural frequencies of microbeam in terms of dimensionless microscale parameters and for .

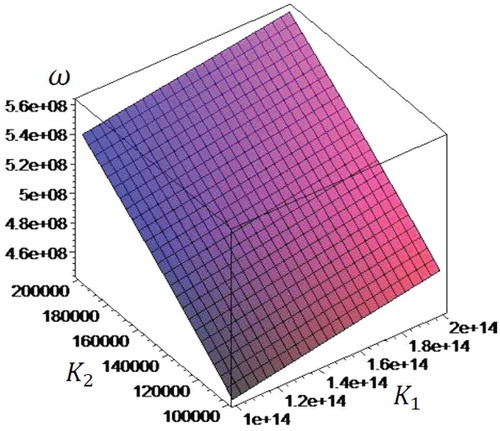
Two-dimensional distribution of natural frequencies of microbeam in terms of two parameters of Pasternak’s foundation can be presented in Figure 9. It can be concluded that with increase of the two parameters of foundation, the natural frequencies are increased considerably.

Figure 9. Two-dimensional distribution of the natural frequencies of microbeam in terms of two parameters of Pasternak’s foundation for .

4.4. Bending analysis results

The bending results of microbeam is presented in Figures 10–16 in terms of applied electric potential and parameters of foundation and material characteristics in microscale. Figure 10 shows the variation of dimensionless transverse displacement of microbeam in terms of two parameters of foundation and . The obtained results indicate that with increasing the two parameters of foundation and , the dimensionless deflection of microbeam is decreased due to increase of the stiffness of structure. The effect of applied voltage as well as shear parameter of foundation can be presented in Figure 11. It can be concluded that increasing the applied voltage slightly increases the transverse deflection of microbeam.

Figure 10. Dimensionless transverse displacement of microbeam in terms of two parameters of foundation and for .

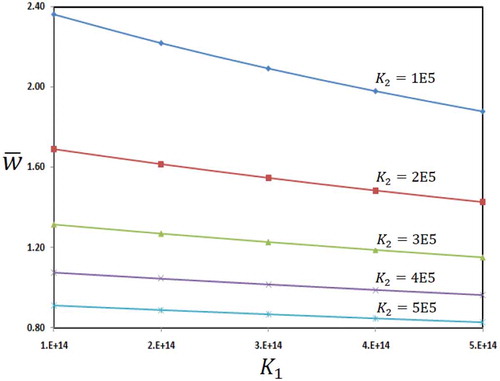
Figure 11. Dimensionless transverse displacement of microbeam in terms of applied voltage and shear parameter of foundation for .

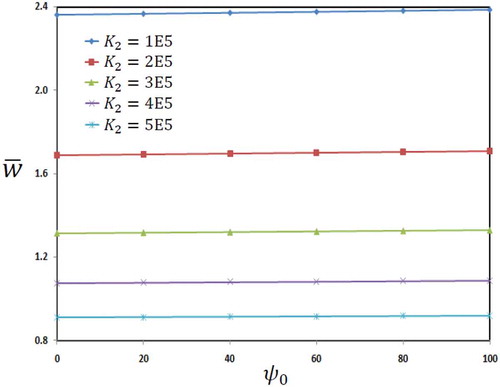
Figure 12. Two-dimensional dimensionless deflection of microbeam in terms of two parameters of foundation and for .

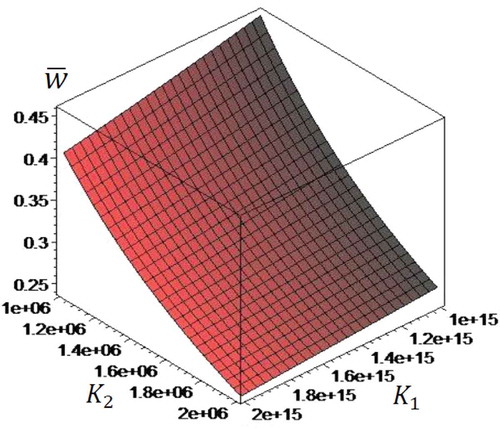
Figure 13. Dimensionless transverse displacement of microbeam in terms of non-homogeneity index and Winkler’s parameter of foundation .

Figure 14. Distribution of electric potential in terms of two parameters of foundation and for .

Figure 15. Two-dimensional distribution of electric potential in terms of two parameters of foundation and for .

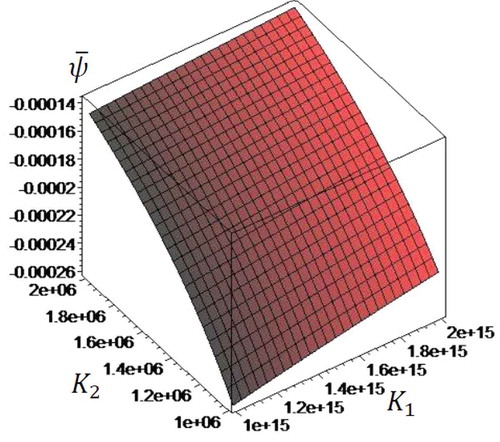
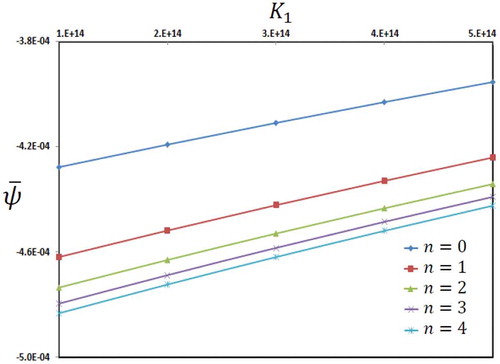
Figure 16. Distribution of electric potential of microbeam in terms of non-homogeneity index and Winkler’s parameter of foundation .

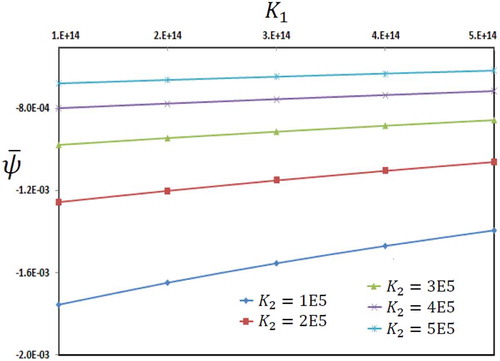
Two-dimensional distribution of deflection of microbeam in terms of two parameters of Pasternak’s foundation is presented in Figure 12. The effect of non-homogeneity index of core on the dimensionless deflection of microbeam is presented in Figure 13. It shows the variation of dimensionless deflection of microbeam in terms of spring parameter of foundation for various values of non-homogeneity index. It can be concluded that increase of non-homogeneity index leads to softer structure and consequently increases deflection.

Figure 14 shows the variation of electric potential of microbeam in terms of two parameters of foundation and . The obtained results indicate that with increase of the two parameters of foundation and , electric potential of microbeam is decreased. Two-dimensional distribution of electric potential of microbeam in terms of two parameters of Pasternak’s foundation and is presented in Figure 15.

Electric potential distribution in terms of spring parameter of foundation for various values of non-homogeneity index is presented in Figure 16. Similar to Figure 13, with increase of non-homogeneity index, the maximum electric potential is increased.

5. Conclusions

In this paper, the various analyses of a three-layer microbeam rest on Pasternak’s foundation were presented. The analyses were including wave propagation, free vibration, and bending. Euler–Bernoulli beam and strain gradient theories were used for analysis of the problem. Some important conclusions of this paper can be presented as:

• Phase velocities of microbeam are changed significantly with changing the important parameters of the problem such as non-homogeneity index, wave number, parameters of Pasternak’s foundation, and micro-length scale parameters. The numerical results indicate that the phase velocities are decreased with increase of the non-homogeneity index for and for greater values tend to an asymptotic value. Furthermore, increasing the two parameters of foundation leads to important increase of the phase velocities.

• Three micro-length scale parameters used in strain gradient theory have important effects on the natural frequencies of microbeam. The numerical results indicate that the second length scale parameter is very important rather than two other parameters and . In addition, increase of non-homogeneity index leads to increase of natural frequencies for and for greater values is decreased uniformly.

• The applied voltage can increase the transverse deflection of microbeam. Furthermore, increase of the two parameters of foundation leads to decrease of the transverse deflection. Electric potential distribution along the thickness direction indicates that the value of that is very small in face-sheets. In addition, increase of non-homogeneity index, increases deflection and electric potential due to decrease of stiffness of beam.

Acknowledgments

The research described in this paper was financially supported by the University of Kashan [grant number: 574613/027]. The first author would like to thank the Iranian Nanotechnology Development Committee for their financial support.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The research described in this paper was financially supported by the University of Kashan [grant number: 574613/027]. The first author would like to thank the Iranian Nanotechnology Development Committee for their financial support.

Notes on contributors

Mohammad Arefi

Mohammad Arefi is currently Assistant Professor of Mechanical Engineering at University of Kashan. He graduated from University of Kashan in 2006. He was awarded MSc and PhD degrees from Tarbiat Modares University in 2008 and 2012, respectively. He worked on piezoelectric and functionally graded materials in MSc and PhD thesis. He is currently working on nanostructures and microstructures in cooperation with MSc and PhD students. More than 65 scientific papers have been created by Mohammad Arefi. He reached to 350 citations and an H-Index=13 based on Scopus website.

Ashraf M. Zenkour

Ashraf M. Zenkour graduated from Mansoura University, Egypt, in Mathematics in 1985 and was awarded the MSc and PhD degrees from the same university in 1989 and 1995, respectively. He is Professor of Applied Mathematics at Kafrelsheikh University, Egypt, and he is currently Professor of Applied Mathematics at King Abdulaziz University, Saudi Arabia. His research interests are in the areas of structural stability, vibration, plated structures and shells. He is the author or co-author of over 220 scientific publications and received >2600 citations with 28 h-factor (ISI Web of Science). He is a reviewer of many international journals in Solid Mechanics and Applied Mathematics, and an editorial member of many journals. In addition, he delivered various lectures at national and international conferences. Professor Zenkour’s research papers have been cited in many articles and textbooks.