Abstract
A novel state-dependent control approach for continuous-time nonlinear systems with general performance criteria is presented in this paper. This controller is optimally robust for model uncertainties and resilient against control feedback gain perturbations in achieving general performance criteria to secure quadratic optimality with inherent asymptotic stability property together with quadratic dissipative type of disturbance reduction. For the system model, unstructured uncertainty description is assumed, which incorporates commonly used types of uncertainties, such as norm-bounded and positive real uncertainties as special cases. By solving a state-dependent linear matrix inequality at each time, sufficient condition for the control solution can be found which satisfies the general performance criteria. The results of this paper unify existing results on nonlinear quadratic regulator, H∞ and positive real control. The efficacy of the proposed technique is demonstrated by numerical simulations of the nonlinear control of the inverted pendulum on a cart system.
1. Introduction
Optimal control of nonlinear systems is traditionally characterized in terms of Hamilton Jacobi Equations (HJEs). The solution of the HJEs provides the necessary and sufficient optimal control condition for nonlinear systems. Furthermore, when the controlled system is linear time-invariant and the performance index is linear quadratic regulator (LQR), the HJEs reduced to Algebraic Riccati Equations (AREs). As for H∞ nonlinear control problem, the optimal control solution is equivalent to solving the corresponding Hamilton Jacobi Inequalities (HJIs) Basar andBernhard (1995). However, HJEs and HJIs, which are first-order partial differential equations and inequalities, cannot be solved for more than a few state variables. In the past few years, it has been shown that the problems of quadratic regulation and H∞ nonlinear control can be approached by the state-dependent Riccati equation (SDRE) and nonlinear matrix inequality (NLMI) techniques (Cloutier, 1997; Cloutier, D'Souza, & Mracek, 1996; Huang & Lu, 1996). The state-dependent linear matrix inequality (LMI) control of nonlinear systems, as pointed out in Wang and Yaz(2009), Wang, Yaz, and Jeong (2010), and Wang, Yaz, andYaz (2010, 2011) synthesizes a controller to achieve mixed nonlinear quadratic regulator (NLQR) and H∞ control objectives.
Dissipative control for linear systems has also received considerable attention over the past two decades. The concept of dissipative systems was first introduced by Willems(Citation1972a, 1972b), and further generalized by Hill and Moylan(1975, 1976, 1980), playing an important role in systems, circuits and controls. The theory of dissipative systems generalizes the basic tools including the passivity theorem, bounded real lemma, Kalman–Yakubovich lemma and circle criterion. Dissipativity performance includes H∞ performance, passivity, positive realness and sector-bounded constraint as special cases. Research addressing the problems of H∞ and positive real control systems can be found in Zhou and Khargonekar (Citation1988) Doyle, Glover,Khargonekar, and Francis (1989), Haddad and Bernstein(Citation1991), Sun, Khargonekar, and Shim (Citation1994), Safonov,Jonckheere, Verma, and Limebeer (1987) and Shim (Citation1996). Control of uncertain linear systems with L2 -bounded structured uncertainty satisfying H∞ and passivity criteria has been tackled in Khargonekar, Petersen, and Zhou (Citation1990) and Petersen (Citation1987). More recent development involving the quadratic dissipative control for linear systems problem has been tackled in Tan, Soh, and Xie (Citation2000) and Xie, Xie,and De Souza (1998).
In this paper, we further consider the problem of optimal, robust and resilient LMI control of continuous-time nonlinear systems with general performance criteria. The controller is robust for model uncertainties and resilient for control gain perturbations. As for uncertain nonlinear systems, we consider a general form of L2-bounded uncertainty description, without any standard structure, incorporating commonly used types of uncertainty, such as norm-bounded and positive real uncertainties as special cases. The purpose behind this novel approach is to convert a nonlinear system control problem into a convex optimization problem which is solved by state-dependent LMI. The recent development in convex optimization provides very efficient means for solving LMIs. If a solution can be expressed in a LMI form, then there exist optimization algorithms providing efficient global numerical solutions (Boyd, Ghaoui, Feron,& Balakrishnan, 1994). Therefore, if the LMI is feasible, the LMI control technique provides asymptotically stable solutions satisfying various general performance criteria. We further propose to employ general performance criteria to design the controller guaranteeing the quadratic sub-optimality with inherent stability property in combination with dissipativity type of disturbance attenuation. The general performance criteria are a generalization of the NLQR, H∞, positive realness and sector-bounded constraint; therefore, the results of the paper unify existing control results and provide a more general control design framework.
The paper is organized as follows. In Section 2, we present the general performance criteria including the performance of NLQR, H∞, positive realness and sector-bounded constraint. Section 3 presents the state-dependent LMI-based control for nonlinear systems achieving general performance criteria. Finally, the inverted pendulum on a cart is used for applying the algorithm to an under-actuated robot with nonlinear dynamics to examine the effectiveness and robustness of the new approach in Section 4.
2. System model and general performance criteria analysis
The following notation is used in this work: ℜ+ stands for the set of non-negative real numbers and ℜn stands for the n-dimensional Euclidean space. x∈ℜn denotes -dimensional real vector with norm
, where
indicates transpose.
is the set of n×m real matrices. In is the n×n identity matrix. A≥0 for a symmetric matrix denotes a positive semi-definite matrix. L2 is the space of finite dimensional vectors with finite energy:
. Let
be the extended space of L2 space defined by
where
is called the truncation function on ℜ+ with values in ℜn. The inner product in this space is defined as
, for u,
.
Consider the following nonlinear dynamical system equation and performance output equation
It is assumed that the state feedback is available and the state feedback control input is given by
definition 1
Given matrices ,
,
with Q, R symmetric, the system (1) and (2) with energy function (4) is said to be (Q, S, R) dissipative if for some real function
with β (0)=0. The physical meaning for
is the stored energy at the initial time, given by the initial condition x0.
Theorem 1
Consider the quadratic function , matrices
,
,
with Q, R symmetric,
, M>0,
, N>0 with M, N symmetric, the control of nonlinear system (1) and (2) will achieve mixed NLQR and dissipative performance if the following condition holds:
Proof By integrating Equation (7) from 0 to T, we have
Remark 1 Notice that both H∞ and passivity are special cases of (Q, S, R) dissipativity. The special cases are summarized as follows:
Case 1 Q=−I, S=0, R=γ2 I, the strict (Q, S, R) dissipativity reduces to H∞ design (Doyle et al.,Citation1989). The overall control design satisfies mixed NLQR–H∞ performance.
Q=0, S=I, R=0, the strict (Q, S, R) dissipativity reduces to strict positive realness (Sun et al.,Citation1994). The overall control design satisfies mixed NLQR–strict positive realness performance.
Q=−θ I,
, the strict (Q, S, R) dissipativity reduces to mixed H∞ and positive real performance design, when θ∈(0, 1). The overall control design satisfies mixed NLQR–H∞–positive real performance.
Q = −I,
,
, where K1 and K2 are constant matrices of appropriate dimensions, the strict (Q, S, R) dissipativity reduces to a sector-bounded constraint (Gupta & Joshi, 1994). The overall control design satisfies mixed NLQR–sector-bounded constraint performance.
Before introducing the main result of the paper, the following model of unstructured uncertainties is introduced.
Assumption 1 The following general form of L2-bounded unstructured uncertainties is considered:
3. State-dependent LMI control
lemma 1
This can be proven easily by considering
lemma 2
Denote X=P−1 for positive definite matrix P>0, then the following equality always holds:
Remark 2 Since in the presentation below, P will be used to describe the energy content, which needs to decrease due to the asymptotic stability requirement, X=P−1 matrix will be increasing in time. Therefore, we have .
The following theorem summarizes the main results of the paper:
Theorem 2
Given the system Equation (1), performance output Equation (2) and control Equation (3), if there exist matrices X=P−1>0 and Y for all t>0, such that the following state-dependent LMI holds:
Proof In the proof below, the time and state argument will be dropped for notational simplicity. By applying system and performance output Equations (1) and (2), and state feedback input Equation (3), the performance index can be formed as follows:
Remark 3 At this point, it is to be noted that other choices of positive constants are possible and can be tried if the value 1 for all these constants does not work.
4. Application to the inverted pendulum on a cart
The inverted pendulum on a cart problem (Wang & Yaz,2010) is used for testing the novel robust and resilient state-dependent LMI approach to compare the performance. Using the Euler–Lagrange equation technique, the complete equations of motion for the inverted pendulum on a cart can be reached as
Mixed NLQR–H∞ design (predominant NLQR)
Mixed NLQR–H∞ design (predominant H∞)
Mixed NLQR–H∞–positive real design (NLQR passivity)
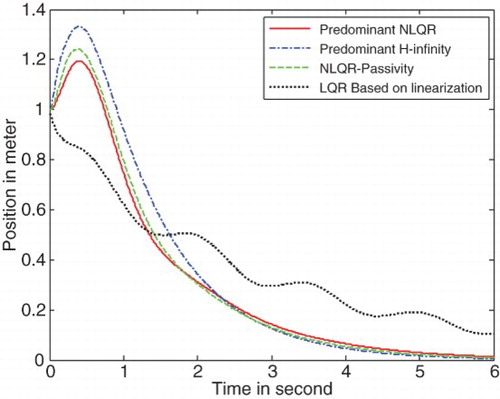
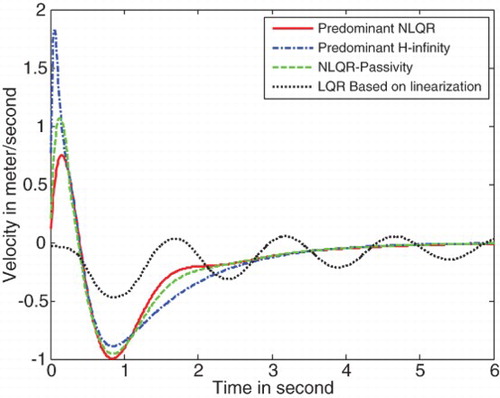
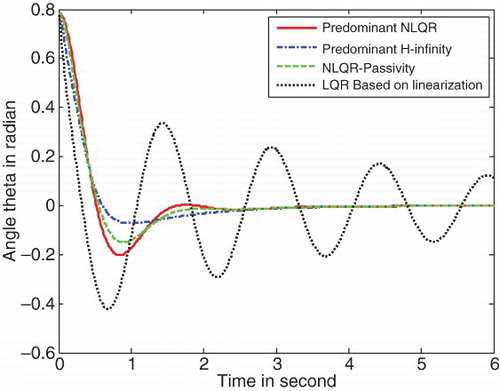
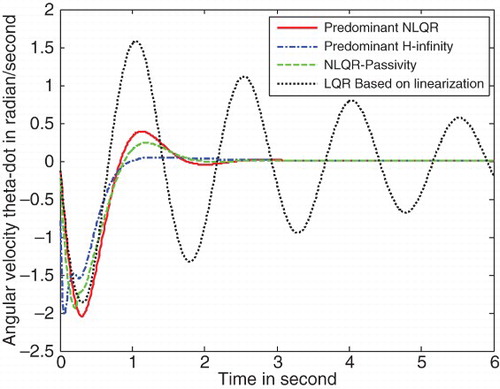
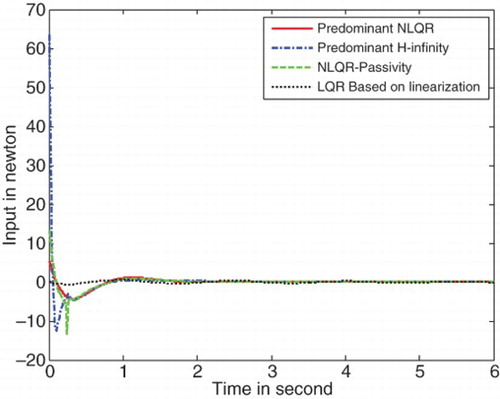
All of the above mixed criteria control performance results are shown in , in comparison with the traditional LQR technique based on linearization. From these figures, we find that the novel state-dependent LMI control has better performance compared with the traditional LQR technique based on linearization. Especially, and show that the traditional LQR technique loses control of the angle and angular velocities of the pendulum, respectively. shows that the highest magnitude of control is needed by the predominant H∞ control and the lowest control magnitude is needed by the linearization-based LQR technique.
5. Conclusions
This paper addresses nonlinear system control design with general NLQR and quadratic dissipative criteria to achieve asymptotic stability, quadratic optimality and strict quadratic dissipativeness. For systems with unstructured but bounded uncertainty, the LMI-based sufficient conditions are derived for the solution of general performance criteria control. Our results unify the existing results on SDRE control, robust H∞, positive real control and sector-bounded control. The relative weighting matrices of these criteria can be achieved by choosing different weighing coefficient matrices. The optimal control can be obtained by solving LMI at each time step. The inverted pendulum on a cart control, which is a benchmark under-actuated nonlinear control system, is used as an example to demonstrate its effectiveness and robustness of the proposed method. The simulation studies show that the proposed method provides a satisfactory alternative to the existing nonlinear control approaches.
We thank the reviewers for their remarks, which have improved the quality of the paper. This research has been financially supported by a grant from NITC (National Institute for Transportation and Communities), which is gratefully acknowledged.
REFERENCES
- Basar, T., & Bernhard, P. (1995). H-infinity optimal control and related minimax design problems – A dynamic game approach. (2nd ed.) Boston: Birkhauser.
- Boyd, S., Ghaoui, L. E., Feron, E., & Balakrishnan, V. (1994). Linear matrix inequalities in system and control theory, SIAM Studies in Applied Mathematics. Philadelphia, PA: SIAM.
- Cloutier, J. R. (1997). State-dependent Riccati equation techniques: An overview. Proceedings of the 1997 American Control Conference, pp. 932–936, Albuquerque, MN.
- Cloutier, J. R., D'Souza, C. N., & Mracek, C. P. (1996). Nonlinear regulation and nonlinear H-infinity control via the state-dependent Riccati equation technique: Part 1 theory, part 2 examples. Proceedings of 1st international conference on nonlinear problems in aviation and aerospace, pp. 117–141, Daytona Beach, FL.
- Doyle, J. C., Glover, K., Khargonekar, P. P., & Francis, B. A. (1989). State space solution to the standard H2 and H-infinity control problems. IEEE Transactions on Automatic Control 34, 831–847. doi: 10.1109/9.29425
- Gupta, S., & Joshi, S. M. (1994). Some properties and stability results for sector bounded LTI systems. Proceedings of 33rd IEEE conference on decision and control, pp. 2973–2978, Orlando, USA.
- Haddad, W. M., & Bernstein, D. S. (1991). Robust stabilization with positive real uncertainty, beyond the small gain theorem. Systems and Control Letters 17, 191–208. doi: 10.1016/0167-6911(91)90065-M
- Hill, D. J., & Moylan, P. J. (1975). Cyclo-dissipativeness, dissipativeness and losslessness for nonlinear dynamical systems (Technical Report EE7526). Department of Electrical and Computer Engineering, University of Newcastle, Australia.
- Hill, D. J., & Moylan, P. J. (1976). Stability of nonlinear dissipative systems. IEEE Transactions on Automatic Control, 21, 708–711. doi: 10.1109/TAC.1976.1101352
- Hill, D. J., & Moylan, P. J. (1980). Dissipative dynamical systems: Basic input-output and state properties. Journal of the Franklin Institute, 309 327–357. doi: 10.1016/0016-0032(80)90026-5
- Huang, Y., & Lu, W-M. (1996). Nonlinear optimal control: alternatives to Hamilton-Jacobi equation. Proceedings of 35th conference on decision and control, pp. 3942–3947, Kobe, Japan.
- Khargonekar, P. P., Petersen, I. R., & Zhou, K. (1990). Robust stabilization of uncertain linear systems: quadratic stabilizability and H-infinity control theory. IEEE Transactions on Automatic Control, 35, 356–361. doi: 10.1109/9.50357
- Mohseni, J., Yaz, E., & Olejniczak, K. (1998). State dependent LMI control of discrete-time nonlinear systems. Proceedings of the 37th IEEE conference on decision and control, pp. 4626–4627, Tampa, FL.
- Petersen, I. R. (1987). A stabilization algorithm for a class of uncertain systems. Systems and Control Letters, 8 181–188. doi: 10.1016/0167-6911(86)90077-0
- Safonov, M. G., Jonckheere, E. A., Verma, M., & Limebeer, D. J. N. (1987). Synthesis of positive real multivariable feedback systems. International Journal of Control, 45 817–842. doi: 10.1080/00207178708933772
- Shim, D. (1996). Equivalence between positive real and norm-bounded uncertainty. IEEE Transactions on Automatic Control, 41 1190–1193. doi: 10.1109/9.533682
- Sun, W., Khargonekar, P. P., & Shim, D. (1994). Solution to the positive real control problem for linear time-invariant systems. IEEE Transactions on Automatic Control, 39 2034–2046. doi: 10.1109/9.280776
- Tan, Z., Soh, Y. C., & Xie, L. (2000). Dissipative control of linear discrete-time systems with dissipative uncertainty. International Journal of Control , 73 (4), 317–328. doi: 10.1080/002071700219678
- Van der Shaft, A. J. (1993). Nonlinear state space H-infinity control theory. In dH. J. Trentelman & J. C. Willems (Eds.), Perspectives in control, pp. 153–190. Groningen: Birkhauser.
- Wang, X., & Yaz, E. E. (2009). The state dependent control of continuous time nonlinear systems with mixed performance criteria. Proceedings of IASTED international conference on identification and control applications, pp. 98–102, Honolulu, HI.
- Wang, X., Yaz, E. E., & Jeong, C. S. (2010). Robust nonlinear feedback control of discrete-time systems with mixed performance criteria. Proceedings of American control conference, pp. 6357–6362, Baltimore, MD.
- Wang, X., Yaz, E. E., & Yaz, Y. I. (2010). Robust and resilient state dependent control of continuous time nonlinear systems with general performance criteria. Proceedings of the 49th IEEE conference on decision and control, pp. 603–608, Atlanta, GA.
- Wang, X., Yaz, E. E., & Yaz, Y. I. (2011). Robust and resilient state dependent control of discrete time nonlinear systems with general performance criteria. Proceedings of the 18th IFAC congress, pp. 10904–10909, Milano, Italy.
- Willems, J. C. (1972a). Dissipative dynamical systems – Part 1: General theory. Archives for Rational Mechanics and Analysis , 45, 321–351. doi: 10.1007/BF00276493
- Willems, J. C. (1972b). Dissipative dynamical systems – Part 2: Linear systems with quadratic supply rates’. Archives for Rational Mechanics and Analysis, 45 352–393. doi: 10.1007/BF00276494
- Xie, S., Xie, L., & De Souza, C. E. (1998). Robust dissipative control for linear systems with dissipative uncertainty. International Journal of Control 70(2), 169–191. doi: 10.1080/002071798222352
- Zhou, K., & Khargonekar, P. P. (1988). An algebraic Riccati equation approach to H-infinity optimization. Systems and Control Letters, 11 85–91. doi: 10.1016/0167-6911(88)90080-1