Hopf bifurcation in a partial dependent predator–prey system with multiple delays

Abstract

In this paper, a partial dependent predator–prey system with multiple delays is investigated. By choosing τ₁, τ₂ and τ₃ as bifurcating parameters, we show that Hopf bifurcations occur. In addition, by using theory of functional differential equation and Hassard's method, explicit algorithms for determining the direction of the Hopf bifurcation and the stability of bifurcating periodic solutions are derived. Finally, numerical simulations are performed to support the analytical results, and the chaotic behaviors are observed.

Keywords:

• multiple delays
• Hopf bifurcation
• chaos
• predator–prey system

1. Introduction

Since the work of Volterra, the Lotka–Volterra system has been extensively investigated. A classical Lotka–Volterra system can be modeled by the following system:

where x and y can be interpreted as the population densities of prey and predator at time t, respectively (for example, Jin& Ma, 2002; Saito, 2002; Tang & Zhou, 2003). For a long time, it has been recognized that delays can have a very complicated impact on the dynamics of a system, which cannot only cause the loss of stability, but also induce various oscillations and periodic solutions (for example, Faria& Magalhaes, 1995; Song, Han, & Peng, 2004; Song, Peng,& Wei, 2008; Sun, Lin, & Han, 2006; Yan & Chu, 2006). Recently, Zhang, Jin, Yuan, & Sun (2009) investigated the competition system with a single delay:

Choosing the delay τ as the bifurcation parameter, they analyzed the stability of the interior positive equilibrium and the existence of the local Hopf bifurcation for system (2). Their results show that there exist critical values of the delay, as the delay passes through the first critical value, the positive equilibrium loses its stability and the Hopf bifurcation occurs. Further increasing the delay beyond the first critical value, the system goes into oscillations.

In the present paper, we devote our attention to the bifurcating phenomenons of the predator–prey system with three delays. So the system is not only more complicated, but also more close to the actuality. We described the system by

where r₁, r₂, a₁₁, a₁₂, a₂₁ and a₂₂ are all positive constants. r₂ is positive, which denotes that the food of the predator is partially dependent on the prey of the system. In this paper, assuming that the predator not only takes time to hunt prey, but also takes time to digest and the predator only feeds on the mature prey, then τ₁ denotes the time of the prey maturation, while τ₂ denotes the time taken for hunting of the maturation prey, called hunting delay, finally, τ₃ denotes the time predator use for digestion.

This paper is organized as follows: in Section 2, we investigate the effect of the time delays τ₁, τ₂ and τ₃ on the stability of the positive equilibrium of system (3). In Section 3, we derive the direction and stability of the Hopf bifurcation by using normal form and central manifold theory. Finally in Section 4, numerical simulations are carried out to illustrate the theoretical prediction and to explore the complex dynamics including chaos.

2. Stability analysis and Hopf bifurcation

It is easy to see that system (3) has a unique positive equilibrium provided that the following condition is satisfied: where Let , and still denote by , system (3) can be written as where We then obtain the linearized system The corresponding characteristic equation is

where

Case (a1) , Equation (4) becomes All roots have negative real parts if and only if

Theorem 2.1

For the interior equilibrium point E_* is locally asymptotically stable if conditions (H_*) and (5) hold.

Case (b1) .

Theorem 2.2

For assume that (H_*) and hold, the interior equilibrium point E_* is locally asymptotically stable for and it undergoes the Hopf bifurcation at given by

Proof On substituting , the characteristic equation (4) becomes

Let be a purely imaginary root of Equation (7), then it follows that Squaring both sides and adding them up, we get the following polynomial equation:

Equation (8) has unique positive root if The corresponding critical value of time delay is Let be the root of Equation (7), then the transversal condition can be obtained as Since we can obtain then we have

Case (b2) .

Theorem 2.3

For assume that (H_*) and hold, the interior equilibrium point E_* is locally asymptotically stable for and it undergoes the Hopf bifurcation at given by

where is a root of corresponding characteristic equation.

The proof is similar as in case (b1).

Case (b3) .

Theorem 2.4

For assume that (H_*) and hold, the interior equilibrium point E_* is locally asymptotically stable for and it undergoes the Hopf bifurcation at given by

where is a root of corresponding characteristic equation.

The proof is similar as in case (b1).

Case (c1) is fixed in the interval and τ₁>0.

Theorem 2.5

Let , τ₃=0 and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

Proof We know is in its stable interval and τ₁ is considered as a parameter. Let be a root of Equation (4). Separating real and imaginary parts leads to

It can give

where We assumed that then H(0)<0 and .

Without going into detailed analysis with Equation (13), it is assumed there exists at least one real positive root ω₁₂. Now Equation (12) can be written as

where Equations (14) are simplified to give and is purely imaginary root of Equation (4) for . Now verify the transversal condition of the Hopf bifurcation. Differentiating Equation (4) with respect to τ₁, we obtain the following: where then Noting that

Case (c2) is fixed in the interval and τ₂>0.

Theorem 2.6

Let and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

is a root of the corresponding characteristic equation and

The proof is similar as in case (c1).

Case (c3) is fixed in the interval and τ₁>0.

Theorem 2.7

Let and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

is a root of the corresponding characteristic equation and

The proof is similar as in case (c1).

Case (c4) is fixed in the interval and τ₃>0.

Theorem 2.8

Let and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

is a root of corresponding the characteristic equation and

The proof is similar as in case (c1).

Case (c5) is fixed in the interval and τ₂>0.

Theorem 2.9

Let and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

is a root of the corresponding characteristic equation and

The proof is similar as in case (c1).

Case (c6) is fixed in the interval and τ₃>0.

Theorem 2.10

Let , τ₁=0 and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

is a root of the corresponding characteristic equation and

The proof is similar as in case (c1).

Case (d1) τ₂ and τ₃ are fixed in the interval and , τ₁>0.

Theorem 2.11

Let , if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

Proof We know τ₂, τ₃ are in its stable interval and τ₁ is considered as a parameter. Let be a root of Equation (4). Separating real and imaginary parts leads to

It gives

where We have assumed that then H(0)<0 and .

Without going into detailed analysis with Equation (22), it is assumed there exists at least one real positive root ω₁₄. Now Equation (21) can be written as

where Equations (23) are simplified to give and are purely imaginary root of Equation (4) for . Now verify the transversal condition of the Hopf bifurcation, differentiating Equation (4) with respect to τ₁, it is obtained that where then Noting that

Case (d2) τ₁ and τ₃ are fixed in the interval , and τ₂>0.

Theorem 2.12

Let , and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes Hopf bifurcation at E_* when , where

is a root of the corresponding characteristic equation and

The proof is similar as in case (d1).

Case (d3) τ₁ and τ₂ are fixed in the interval , and τ₃>0.

Theorem 2.13

Let , and if (H_*) holds, then the equilibrium E_* is asymptotically stable for and system (3) undergoes the Hopf bifurcation at E_* when , where

is a root of the corresponding characteristic equation and

The proof is similar as in case (d1).

3. Direction and stability of the Hopf bifurcation

In this section, we show that system (3) undergoes a Hopf bifurcation for different combinations of τ₁, τ₂ and τ₃ satisfying sufficient conditions as described. By using the method based on the normal form theory and the center manifold theory introduced by Hassard, Kazarinoff, andWan (1981), we study the direction of bifurcations and the stability of bifurcating periodic solutions. Without loss of generality, these properties are studied for variable τ₂ as parameter and are fixed. Let , is described in Equation (18), then the Hopf bifurcation occurs at μ=0. Assume that where . Now we rescale the time by , for convenience, are still written as x(t), y(t), then system (3) can be written as where respectively, the nonlinear terms f₁ and f₂ are

The delayed system can be written in the functional form as By the Riesz representation theorem, there exists a matrix whose components are bounded variation functions such that where choosing For , define and where

Hence, Equation (3) can be rewritten as where and For define A(0)=A and the adjoint operator A* of A as where η^T is the transpose of the matrix η.

For and , in order to normalize the eigenvectors of operator A and adjoint operator A*, we define a bilinear inner product where .

Since are eigenvalues of A, they will also be the eigenvalues of A*. The eigenvectors of A and A* are calculated corresponding to the eigenvalues and .

lemma 3.1

is the eigenvector of A corresponding to ; is the eigenvector of A* corresponding to and where

Following the algorithms explained in Hassard,Kazarinoff, and Wan (1981), which is used to obtain the properties of Hopf bifurcation: where We know and are constant vectors.

Thus, we can compute the following quantities: These expressions give a description of the bifurcating periodic solutions in the center manifold of system (3) at critical values , whereas, which can be stated as follows:

• (i)  μ₂ gives the direction of the Hopf bifurcation: if , the Hopf bifurcation is supercritical (subcritical).

• (ii)  β₂ determines the stability of the bifurcating periodic solution, the periodic solution is stable (unstable) if .

• (iii)  T₂ denotes the period of bifurcating period solutions, if T₂>0 (T₂<0), the period increases (decrease).

4. Numerical simulations

To demonstrate the algorithm for determining the existence of the Hopf bifurcation in Section 2 and the direction and stability of the Hopf bifurcation in Section 3, we carry out numerical simulations on a particular case of Equation (3) in the following form.

where and a₂₂=17.5. It is easy to show that system (26) has a unique coexistence equilibrium . By calculation, when τ₂=0 and τ₃=0, the critical delay for τ₁ is obtained as , while when τ₁=0 and τ₃=0, whereas, if τ₁=0 and τ₂=0.

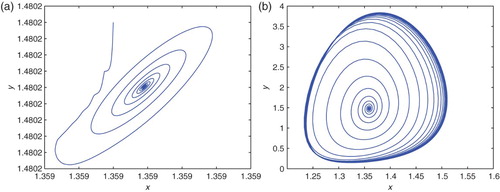
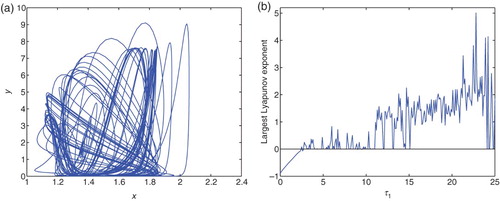
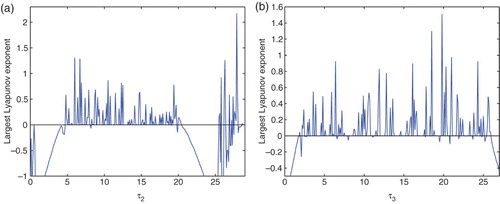
We can see from Figure 1(a) that E_* is asymptotically stable at and , while E_* loses its stability and the Hopf bifurcation occurs at and , see Figure 1(b). Then using the algorithm derived in Section 3, we obtain that , we know that the Hopf bifurcation is supercritical, the bifurcating periodic solution is stable and the period increases. Whereas, at and it loses stability and a chaotic solution occurs (see Figure 2(a)). In Figure 2(b), the largest Lyapunov exponent diagram is plotted for variable τ₁ when τ₂=5.0 and τ₃=2.1, it is easy to know when τ₁>2.6, the Lyapunov exponent is almost positive, then the chaotic solutions occur. From Figure 3(a), the largest Lyapunov exponent diagram is plotted for variable τ₂ when τ₁=2.7 and τ₃=2.1, it is easy to know when , the Lyapunov exponent is almost positive, then the chaotic solutions occur. Similarity, from Figure 3(b), the largest Lyapunov exponent diagram is plotted for variable τ₃ when τ₁=2.7 and τ₂=5.0, it is easy to know when the Lyapunov exponent is almost positive, then the chaotic solutions occur.

Figure 1. (a) E_* is asymptotically stable equilibrium at τ₁=1.3, τ₂=2.6 and τ₃=0.085; (b) E_* loses stability and Hopf bifurcation occurs at τ₁=2.1, τ₂=4.1 and τ₃=0.3.

Figure 2. (a) E_* loses stability and a chaotic solution occurs at τ₁=2.7, τ₂=5.0 and τ₃=2.1; (b) the largest Lyapunov exponent diagram of system (4.1) for variable τ₁ at τ₂=5.0 and τ₃=2.1.

Figure 3. (a) The largest Lyapunov exponent diagram of system (4.1) for variable τ₂ at τ₁=2.7 and τ₃=2.1; (b) for a variable τ₃ at τ₁=2.7 and τ₂=5.0.

5. Conclusions

In this paper, we investigate the effect of the time delays τ₁, τ₂ and τ₃ on the stability of the positive equilibrium of the system (3), and derive the direction and stability of the Hopf bifurcation. Numerical simulations are carried out to illustrate the theoretical prediction and to explore the complex dynamics including chaos.

Acknowledgements

We are grateful to the reviewers for their valuable comments and suggestions which have led to an improvement of this paper. This research is supported by the National Natural Science Foundation of China (No. 11061016).