Consensus control for multi-rate multi-agent systems with fading measurements: the dynamic event-triggered case

Abstract

This paper studies the distributed $H_{\mathrm{\infty }}$-consensus control problem for a class of multi-rate multi-agent systems with fading measurements. A multi-rate sampling strategy is adopted to be more in line with actual need and the channels between each agent and its sensor always fade non-identically. The multi-rate system is transformed into a single-rate system via the lifting technique. For the purpose of reducing the transmission burden, a dynamic event-triggered mechanism is utilized to determine whether the agent's information is allowed to transmit to its neighbours. This paper aims to design an observer-based event-triggered controller for each agent to achieve the $H_{\mathrm{\infty }}$-consensus control performance constraint. With the help of the Lyapuonv stability theory, sufficient conditions are obtained that can ensure the desired control performance for the resulting closed-loop systems, and then the desired gain matrices are calculated by solving the linear matrix inequality. Finally, a numerical simulation example is given to demonstrate the effectiveness of the distributed event-triggered consensus control scheme.

Keywords:

• Multi-agent systems
• multi-rate sampling
• dynamic event-triggered mechanism
• channel fading measurement
• $H_{\mathrm{\infty }}$-consensus control

1. Introduction

Over the past decades, the research interest in multi-agent systems (MASs) has surged owing mainly to their wide-ranging applications in various fields ranging from intelligent transportation, intelligent search and rescue, and geological exploration to maritime patrol and aerospace industries (Ma et al., 2017a, 2017b; Ming et al., 2016; Qin & Ma, 2016; L. Wang et al., 2019). One of the main research directions of MASs is the consensus control, the goal of which is to make the states of a team of agents achieve certain common features by designing a distributed consensus control scheme only using local neighbour information (Bao et al., 2022). The desired consensus generally depends on the states of all the agents with respect to the features (e.g. position, phase, velocity, attitude, etc.). Considering the existence of the external noises, model uncertainties and time delays, the corresponding distributed $H_{\mathrm{\infty }}$-consensus control algorithms have been investigated in J. Wang et al. (2015), W. Xu et al. (2017), Yu et al. (2012) and Z. Hu et al. (2021), especially for the observer-based controller design issues.

It is worth noting that in the complex practical systems, different components are typically sampled with different sampling rates according to their physical properties, system resource constraints and sensor constraints. In other words, most of the engineering systems are practically the multi-rate systems (Guan et al., 2010; Hua et al., 2015; Moarref & Rodrigues, 2014). As such, extensive attention has been focused on the research of the multi-rate systems owing to their significant advantages. For example, various fault detection schemes have been reported for the multi-rate systems in Geng et al. (2017), Geng et al. (2016) and Yong et al. (2016). Meanwhile, the distributed ${\mathcal{H}}_{\mathrm{\infty }}$-consensus control issues have been discussed for the multi-rate multi-agent systems in Han et al. (2021) based on an outlier-resistant observer. In addition, some new filtering methods have been developed for the case that there is a rational number proportional relationship between multiple sampling rates (L. Yan et al., 2016). Nevertheless, when considering the influence of the multi-rate samplings on the consensus control problem for the MASs, there have been very few corresponding results. Therefore, the first motivation of this paper is to explore the consensus control problem for a class of multi-rate MASs.

It is acknowledged that the information among neighbouring agents is transmitted via the communication channels and therefore some problems may occur induced by the imperfect channels (Ding et al., 2019; Mao et al., 2021). As a frequently encountered phenomenon, the channel fading, that are commonly caused by the refraction of vapour or the reflection of the buildings, has aroused tremendous research attention (L. Liu et al., 2021). The channel fading may lead to the signal distortion and further destroy the system performance. The Kalman filtering problem has been investigated over a wireless fading channel in Leong and Quevedo (2016), where the relay strategy is utilized to mitigate the adverse effect of the channel fading. Recent years have put much attention on the channel fading phenomenon (Liang et al., 2010; W. Liu & Shi, 2019; S. Wang, Wang, Dong, Chen, & Alsaadi, 2022; H. Yan et al., 2018). Recently, the consensus control problems of the MASs have been focused on under the influences of memory-free fading channels in L. Xu et al. (2016), L. Xu et al. (2018), J. Xu et al. (2021) and Gu et al. (2020). While up to now, it has not received adequate attention on achieving consensus tracking of multi-rate MASs affected by channel fading, which constitutes the second motivation of the current research.

In real applications, the communication resources and computing capabilities of the agents are usually subject to constraints (S. Liu et al., n.d.; Zou et al., 2021). To resolve the above problems, the event-triggered mechanism (ETM) is usually adopted with a predetermined triggering condition, whose purpose is to reduce the number of signal transmissions. More recently, many scholars have proposed the dynamic ETM, which not only depends on the available system information but also relies on an extra internal dynamic variable, thus making the triggering threshold adjust dynamically at different time instants. Owing to the non-negativity of the introduced extra internal dynamic variable, an event trigger can felicitously extend the average interactive time in most cases, and thereby leads to certain reductions of the consumption of limited communication resources (Du et al., 2018; He et al., 2019; W. Hu et al., 2020; Q. Li et al., 2020; Z. Li et al., 2021; D. Liu & Yang, 2020; S. Wang, Wang, Dong, & Chen, 2022; S. Wen et al., 2019; Yi et al., 2019; Yin et al., 2016, 2018). Although the ETMs have generated considerable research interest for MASs, while most existing literature has focused on the single-rate systems, which deserves further attention on the multi-rate systems.

Inspired by the above discussions, we strive to study the observer-based event-triggered consensus control problem for a class of multi-rate MASs with channel fading measurements. The desired goal of this paper is to design the observer and controller for each agent such that the resulting dynamics is asymptotically stable without the disturbances and achieves the $H_{\mathrm{\infty }}$-consensus performance under the zero-initial conditions. In doing so, the following problems need to be solved: How to consider the joint effect of the channel fading measurements and the dynamic ETM on the desired consensus control performance? How to implement the dynamic ETM in the consensus control scheme to save more resources? How to develop the sufficient conditions to guarantee the existence of the desired consensus controller? The above foreseeable problems are to be investigated in the current investigation.

The contributions of this paper are emphasized as follows:

1. The $H_{\mathrm{\infty }}$-consensus control problem is first investigated for a class of multi-rate MASs with channel fading measurements under the scheduling of the dynamic ETM.

2. A dynamic ETM is introduced to reduce the transmission burden among agents, where the event-triggering threshold is adjusted by an internal dynamic variable.

3. Sufficient condition is derived such that the resulting augmented system is asymptotically stable and satisfies the desired disturbance constraint performance.

The rest of this paper is arranged as follows. Section 2 introduces the discrete-time multi-rate MAS with channel fading measurements, the observer and the controller, the ETM and the desired performance. The sufficient conditions are presented and the gain matrices of the desired observer-based controller are designed in Section 3, respectively. Section 4 provides a simulation example to illustrate the effectiveness of the proposed control scheme. Section 5 concludes this paper and points out some future investigation directions.

Notation: ${\mathbb{R}}^n$ represents the n-dimensions Euclidean space and ${\mathbb{R}}^{n\times m}$ denotes the set of all n × m real matrices. $\mathrm{co}{\mathrm{l}}_1^{\mathrm{c}}\{x_l\}$ means the vector $[x_1^T{x}_2^T\dots x_c^T{]}^T$. $\mathrm{dia}{\mathrm{g}}_{\mathrm{c}}\{\cdots \}$ denotes a $c\times c$ block-diagonal matrix. $I_{bn}$ represents the identity matrix of $b\times n$ dimension (or compatible dimension). The notation ⊗ represents the Kronecker product.

2. Problem formulation

First, the communication topology among agents is modelled as a digraph $\mathcal{G}({\mathcal{V}}_{\mathrm{Q}},{\mathcal{S}}_{\mathrm{Q}},{\mathcal{A}}_{\mathrm{Q}})$, where ${\mathcal{V}}_Q=\{{\mathrm{v}}_1,{\mathrm{v}}_2,\dots ,{\mathrm{v}}_N\}$ is the set of N nodes, ${\mathcal{S}}_Q={\mathcal{V}}_Q\times {\mathcal{V}}_Q$ denotes the set of edges, and ${\mathcal{A}}_Q=[a_{ij}]\in {\mathbb{R}}^{N\times N}$ is the adjacency matrix. An edge is denoted by $e_{ij}=({\mathrm{v}}_i,{\mathrm{v}}_j)$ and $e_{ij}\in {\mathcal{S}}_Q$ means that agent j can send its information to agent i, where agent j is called a neighbour of agent i, and vice versa. Utilize ${\mathrm{N}}_i\triangleq \{{\mathrm{v}}_i\in {\mathcal{V}}_Q:e_{ij}\in {\mathcal{S}}_Q,j\ne i\}$ to represent the set of neighbouring agents. Define a matrix ${\mathcal{D}}_Q\triangleq \mathrm{diag}\{d_i\}\in {\mathbb{R}}^{N\times N}$ with $d_i\triangleq {\mathrm{\Sigma }}_{j\in {\mathrm{N}}_i}{a}_{ij}$ being the degree matrix and $L\triangleq {\mathcal{D}}_Q-{\mathcal{A}}_Q$ being the Laplacian matrix. This paper assumes that there exists at least a minimum spanning tree in the digraph $\mathcal{G}({\mathcal{V}}_{\mathrm{Q}},{\mathcal{S}}_{\mathrm{Q}},{\mathcal{A}}_{\mathrm{Q}})$.

Consider a kind of MASs including N agents, and the state-space model of agent i is described by (1) $\{\begin{array}{rl}{x}_i(T_{m+1})& =A{x}_i(T_m)+B{u}_i(T_m)+E{w}_i(T_m),\\ z_i(T_m)& =D{x}_i(T_m)\end{array}$(1) where $x_i(T_m)\in {\mathbb{R}}^{n_x}$, $u_i(T_m)\in {\mathbb{R}}^{n_u}$, and $z_i(T_m)\in {\mathbb{R}}^{n_z}$ represent the system state, the control input and the controlled output of the i-th agent, respectively. $w_i(T_m)\in l_2([0,\mathrm{\infty });{\mathbb{R}}^{n_w})$ is the process noise. $A\in {\mathbb{R}}^{n_x\times n_x}$, $B\in {\mathbb{R}}^{n_x\times n_u}$, $E\in {\mathbb{R}}^{n_x\times n_w}$, and $D\in {\mathbb{R}}^{n_z\times n_x}$ are constant matrices. B is a full-column rank matrix. $x_i(T_m)$ and $z_i(T_m)$ are updated at time instants $T_m(m\triangleq 0,1,2,\dots )$, where $T_{m+1}-T_m\triangleq g$.

The measurement model of the ith agent with the timescale $t_m$ is described by (2) $y_i(t_m)={\pi }_i(t_m)C{x}_i(t_m)+F{v}_i(t_m)$(2) where $y_i(t_m)\in {\mathbb{R}}^{n_y}$ is the measurement output. $v_i(t_m)\in l_2([0,\mathrm{\infty });{\mathbb{R}}^{n_v})$ is the measurement noise. $C\in {\mathbb{R}}^{n_y\times n_x}$ and $F\in {\mathbb{R}}^{n_y\times n_v}$ are known matrices. The fading channel is formulated by a set of random variables ${\pi }_i(t_m)\in \mathbb{R}$, which are independent and identically distributed with the mean $\mu \in (0,1]$ and variance ${\psi }^2$. $y_i(t_m)$ is sampled at time instant $t_m$, where $t_{m+1}-t_m\triangleq cg$ and c is a positive integer.

Defining ${\overline{u}}_i(t_m)\triangleq {\mathrm{col}}_1^c\{u_i(t_m+(f-1)g)\}$, ${\overline{w}}_i(t_m)\triangleq {\mathrm{col}}_1^c\{w_i(t_m+(f-1)g)\}$ and using the lifting technique, one derives the following system with timescale $t_m$: (3) $\begin{array}{rl}{x}_i(t_{m+1})& =A^c{x}_i(t_m)+{\overline{B}}_1{\overline{u}}_i(t_m)+{\overline{E}}_1{\overline{w}}_i(t_m),\\ x_i(t_{m+1}-g)& =A^{c-1}{x}_i(t_m)+{\overline{B}}_2{\overline{u}}_i(t_m)\\ & +{\overline{E}}_2{\overline{w}}_i(t_m),\\ ⋮\\ x_i(t_{m+1}-(c-1)g)& =A{x}_i(t_m)+{\overline{B}}_c{\overline{u}}_i(t_m)+{\overline{E}}_c{\overline{w}}_i(t_m)\end{array}$(3) where $\begin{array}{rl}{\overline{B}}_f& \triangleq [{\overline{B}}_{f1}\underset{f-1}{\underbrace{0\cdots 0}}],{\overline{B}}_{f1}\triangleq [\underset{c-f+1}{\underbrace{A^{c-f}B\cdots ABB}}],\\ {\overline{E}}_f& \triangleq [{\overline{E}}_{f1}\underset{f-1}{\underbrace{0\cdots 0}}],{\overline{E}}_{f1}\triangleq [\underset{c-f+1}{\underbrace{A^{c-f}E\cdots AEE}}],\\ f& \triangleq 1,2,3,\dots ,c.\end{array}$Furthermore, denoting $\begin{array}{rl}{\overline{x}}_i(t_m)& \triangleq {\mathrm{col}}_1^c\{x_i(t_m-(f-1)g)\},\\ {\overline{v}}_i(t_m)& \triangleq {\mathrm{col}}_1^c\{v_i(t_m+(f-1)g)\},\\ {\overline{z}}_i(t_m)& \triangleq {\mathrm{col}}_1^c\{z_i(t_m-(f-1)g)\},\end{array}$a new system with the unified timescale $t_m$ is obtained as follows: (4) $\{\begin{array}{rl}{\overline{x}}_i(t_{m+1})& =\hat{A}{\overline{x}}_i(t_m)+\hat{B}{\overline{u}}_i(t_m)+\hat{E}{\overline{w}}_i(t_m),\\ y_i(t_m)& ={\pi }_i(t_m)\overline{C}{\overline{x}}_i(t_m)+\overline{F}{\overline{v}}_i(t_m),\\ {\overline{z}}_i(t_m)& =\overline{D}{\overline{x}}_i(t_m)\end{array}$(4) where $\begin{array}{rl}\hat{A}& \triangleq [\overline{A}\underset{c-1}{\underbrace{0\cdots 0}}],\overline{A}\triangleq {\mathrm{col}}_c^1\{A^f\},\hat{B}\triangleq {\mathrm{col}}_1^c\{{\overline{B}}_f\},\\ \hat{E}& \triangleq {\mathrm{col}}_1^c\{{\overline{E}}_f\},\overline{C}\triangleq [C\underset{c-1}{\underbrace{0\cdots 0}}],\overline{F}\triangleq [F\underset{c-1}{\underbrace{0\cdots 0}}],\\ \overline{D}& \triangleq {\mathrm{diag}}_c\{D\}.\end{array}$Similar to P. Wen et al. (2021), in the following, an observer-based event-triggered control protocol is given for agent i: (5) $\{\begin{array}{rl}{\xi }_i(t_{m+1})& =\hat{A}{\xi }_i(t_m)+\hat{B}{\overline{u}}_i(t_m)+H(y_i(t_m)-\mu \overline{C}{\xi }_i(t_m)),\\ {\overline{u}}_i(t_m)& =K\sum _{j\in {\mathrm{N}}_i}{a}_{ij}({\xi }_j(t_m)-{\xi }_i(t_m))\end{array}$(5) where ${\xi }_i(t_m)$ is the estimate of ${\overline{x}}_i(t_m)$, and H and K are gain matrices to be determined later.

In order to save the communication resource, we introduce a dynamic ETM to schedule the information transmission among neighbouring agents. Denote ${t_m}_s^i$ and $\{{t_m}_s^i{\}}_{s\ge 0}$ as the s-th triggering instant and as the triggering-time sequence for agent i, respectively.

For $t_m\in [{t_m}_s^i,{t_m}_{s+1}^i)$, let ${\hat{\xi }}_i(t_m)\triangleq {\xi }_i({t_m}_s^i)$ and ${\hat{\xi }}_j(t_m)\triangleq {\xi }_j({t_m}_{s^{\prime }}^j)$ with ${t_m}_{s^{\prime }}^j\triangleq \underset{s}{max}\{{t_m}_s^j|{t_m}_s^j<t_m\}$. The triggering instant for agent i is determined by (6) $\begin{array}{rl}{t_m}_{s+1}^i& \triangleq inf\{t_m>{t_m}_s^i|\Vert e_i(t_m){\Vert }^2\ge {\sigma }_i\Vert {\xi }_i(t_m){\Vert }^2\phantom{\frac{1}{{\theta }_i}}\\ & +\frac{1}{{\theta }_i}{r}_i(t_m)\},\end{array}$(6) (7) $\begin{array}{rl}{r}_i(t_{m+1})& ={\lambda }_i{r}_i(t_m)+{\sigma }_i\Vert {\xi }_i(t_m){\Vert }^2-\Vert e_i(t_m){\Vert }^2\end{array}$(7) where ${\theta }_i>0$ and $0<{\lambda }_i<1$ are given positive scalars satisfying ${\theta }_i{\lambda }_i\ge 1$, ${\sigma }_i>0$ is a given positive scalar, $r_i(t_m)$ is an internal dynamical variable, and $e_i(t_m)\triangleq {\hat{\xi }}_i(t_m)-{\xi }_i(t_m)$. The initial values are set as $r_i(0)=0$ and ${t_m}_0^i=0$.

Remark 2.1

The main difference between the dynamic ETM and the static ETM lies in the introduction of the internal variable $r_i(t_m)$. If $r_i(t_m)\equiv 0$, then the dynamic ETM reduces to the static ETM. The advantage of the static ETM is simple design and easy to implement. Compared with the static ETM, the dynamic ETM can further decrease the times of information transmission because of $r_i(t_m)\ge 0$. Nevertheless, due to introduction of the internal variable, the dynamic ETM is more complicated than the static ETM.

As a result, under the schedule of dynamic ETM, (5(5) $\{\begin{array}{rl}{\xi }_i(t_{m+1})& =\hat{A}{\xi }_i(t_m)+\hat{B}{\overline{u}}_i(t_m)+H(y_i(t_m)-\mu \overline{C}{\xi }_i(t_m)),\\ {\overline{u}}_i(t_m)& =K\sum _{j\in {\mathrm{N}}_i}{a}_{ij}({\xi }_j(t_m)-{\xi }_i(t_m))\end{array}$(5) ) can be rewritten as (8) $\{\begin{array}{rl}{\xi }_i(t_{m+1})& =\hat{A}{\xi }_i(t_m)+\hat{B}{\overline{u}}_i(t_m)+H(y_i(t_m)-\mu \overline{C}{\xi }_i(t_m)),\\ {\overline{u}}_i(t_m)& =K\sum _{j\in {\mathrm{N}}_i}{a}_{ij}({\hat{\xi }}_j(t_m)-{\hat{\xi }}_i(t_m)).\end{array}$(8)

Remark 2.2

There exists a difference how to utilize the information through the event-triggering protocols between (8(8) $\{\begin{array}{rl}{\xi }_i(t_{m+1})& =\hat{A}{\xi }_i(t_m)+\hat{B}{\overline{u}}_i(t_m)+H(y_i(t_m)-\mu \overline{C}{\xi }_i(t_m)),\\ {\overline{u}}_i(t_m)& =K\sum _{j\in {\mathrm{N}}_i}{a}_{ij}({\hat{\xi }}_j(t_m)-{\hat{\xi }}_i(t_m)).\end{array}$(8) ) and that in the existing results. In Z. Wang et al. (2015), the distributed consensus controller is designed as ${\overline{u}}_i(t_m)=K\sum _{j\in {\mathrm{N}}_i}{a}_{ij}({\xi }_i({t_m}_s^i)-{\xi }_j({t_m}_s^i))$, where the estimates at the same triggering instant are utilized by agents i and j $(j\in {\mathrm{N}}_i)$. However, it is impossible that agent j does not know the accurate event-triggering time instant of agent i, because it takes a certain amount of time and communication resources for agent i to interact with agent j. Different from the above results, in this paper, agent j simply broadcasts its information to neighbouring agents at the triggering instant ${t_m}_s^j$, then agent i update its control signal with the latest message ${\xi }_i({t_m}_{s^{\prime }}^i)$. Therefore, such an idea is more aligned with the engineering practice.

The estimation error of observer is denoted as ${\delta }_i(t_m)\triangleq {\xi }_i(t_m)-{\overline{x}}_i(t_m)$. By denoting $\begin{array}{rl}\overline{x}(t_m)& \triangleq [{\overline{x}}_1^T(t_m){\overline{x}}_2^T(t_m)\cdots {\overline{x}}_N^T(t_m){]}^T,\\ \xi (t_m)& \triangleq [{\xi }_1^T(t_m){\xi }_2^T(t_m)\cdots {\xi }_N^T(t_m){]}^T,\\ \hat{\xi }(t_m)& \triangleq [{\hat{\xi }}_1^T(t_m){\hat{\xi }}_2^T(t_m)\cdots {\hat{\xi }}_N^T(t_m){]}^T,\\ e(t_m)& \triangleq [e_1^T(t_m)e_2^T(t_m)\cdots e_N^T(t_m){]}^T,\\ \overline{w}(t_m)& \triangleq [{\overline{w}}_1^T(t_m){\overline{w}}_2^T(t_m)\cdots {\overline{w}}_N^T(t_m){]}^T,\\ \overline{v}(t_m)& \triangleq [{\overline{v}}_1^T(t_m){\overline{v}}_2^T(t_m)\cdots {\overline{v}}_N^T(t_m){]}^T,\\ \delta (t_m)& \triangleq [{\delta }_1^T(t_m){\delta }_2^T(t_m)\cdots {\delta }_N^T(t_m){]}^T,\\ \overline{z}(t_m)& \triangleq [{\overline{z}}_1^T(t_m){\overline{z}}_2^T(t_m)\cdots {\overline{z}}_N^T(t_m){]}^T,\\ r(t_m)& \triangleq [r_1(t_m)r_2(t_m)\cdots r_N(t_m){]}^T,\\ \pi (t_m)& \triangleq \mathrm{diag}\{{\pi }_1(t_m),{\pi }_2(t_m),\dots ,{\pi }_N(t_m)\},\end{array}$one has (9) $\{\begin{array}{rl}\overline{x}(t_{m+1})& =(I_N\otimes \hat{A}-L\otimes (\hat{B}K))\overline{x}(t_m)-(L\otimes (\hat{B}K))e(t_m)\\ & -(L\otimes (\hat{B}K))\delta (t_m)+(I_N\otimes \hat{E})\overline{w}(t_m),\\ \delta (t_{m+1})& =(\pi (t_m)-\mu I_N)\otimes (H\overline{C})\overline{x}(t_m)\\ & +(I_N\otimes \hat{A}-\mu I_N\otimes (H\overline{C}))\delta (t_m)\\ & +(I_N\otimes (H\overline{F}))\overline{v}(t_m)-(I_N\otimes \hat{E})\overline{w}(t_m),\\ \overline{z}(t_m)& =(I_N\otimes \overline{D})\overline{x}(t_m).\end{array}$(9) Letting $\eta (t_m)\triangleq [{\overline{x}}^T(t_m){\delta }^T(t_m){]}^T$ and $\omega (t_m)\triangleq [{\overline{w}}^T(t_m){\overline{v}}^T(t_m){]}^T$, (9(9) $\{\begin{array}{rl}\overline{x}(t_{m+1})& =(I_N\otimes \hat{A}-L\otimes (\hat{B}K))\overline{x}(t_m)-(L\otimes (\hat{B}K))e(t_m)\\ & -(L\otimes (\hat{B}K))\delta (t_m)+(I_N\otimes \hat{E})\overline{w}(t_m),\\ \delta (t_{m+1})& =(\pi (t_m)-\mu I_N)\otimes (H\overline{C})\overline{x}(t_m)\\ & +(I_N\otimes \hat{A}-\mu I_N\otimes (H\overline{C}))\delta (t_m)\\ & +(I_N\otimes (H\overline{F}))\overline{v}(t_m)-(I_N\otimes \hat{E})\overline{w}(t_m),\\ \overline{z}(t_m)& =(I_N\otimes \overline{D})\overline{x}(t_m).\end{array}$(9) ) can be rewritten as (10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) where $\begin{array}{rl}\mathcal{A}& \triangleq \left[\begin{array}{cc}{I}_N\otimes \hat{A}-L\otimes (\hat{B}K)& -L\otimes (\hat{B}K)\\ -\mu I_N\otimes (H\overline{C})& I_N\otimes \hat{A}-\mu I_N\otimes (H\overline{C})\end{array}\right],\\ \overline{\mathcal{A}}& \triangleq \left[\begin{array}{cc}0& 0\\ I_N\otimes (H\overline{C})& 0\end{array}\right],\mathcal{B}\triangleq \left[\begin{array}{c}-L\otimes (\hat{B}K)\\ 0\end{array}\right],\\ \mathcal{E}& \triangleq \left[\begin{array}{cc}{I}_N\otimes \hat{E}& 0\\ -I_N\otimes \hat{E}& I_N\otimes (H\overline{F})\end{array}\right],\mathcal{D}\triangleq [I_N\otimes \overline{D}0].\end{array}$In view of the above notations, the event-triggered condition in (7(7) $\begin{array}{rl}{r}_i(t_{m+1})& ={\lambda }_i{r}_i(t_m)+{\sigma }_i\Vert {\xi }_i(t_m){\Vert }^2-\Vert e_i(t_m){\Vert }^2\end{array}$(7) ) becomes (11) $\{\begin{array}{rl}& e^T(t_m)e(t_m)<{\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m),\\ & \frac{\mathbf{1}}{\mathit{\theta }}r(t_{m+1})=\frac{\mathit{\lambda }}{\mathit{\theta }}r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)-e^T(t_m)Se(t_m)\end{array}$(11) where $\begin{array}{rl}M& \triangleq {\left[\begin{array}{cc}{I}_{bN{n}_x}& I_{bN{n}_x}\end{array}\right]}^T(\tilde{\sigma }\otimes I_{b{n}_x})\left[\begin{array}{cc}{I}_{bN{n}_x}& I_{bN{n}_x}\end{array}\right],\\ M_1& \triangleq {\left[\begin{array}{cc}{I}_{bN{n}_x}& I_{bN{n}_x}\end{array}\right]}^T(\hat{\sigma }\otimes I_{b{n}_x})\left[\begin{array}{cc}{I}_{bN{n}_x}& I_{bN{n}_x}\end{array}\right],\\ \tilde{\sigma }& \triangleq \mathrm{diag}\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_N\},\hat{\sigma }\triangleq \mathrm{diag}\{\frac{{\sigma }_1}{{\theta }_1},\frac{{\sigma }_2}{{\theta }_2},\dots ,\frac{{\sigma }_N}{{\theta }_N}\},\\ \frac{\mathbf{1}}{\mathit{\theta }}& \triangleq [\frac{1}{{\theta }_1}\frac{1}{{\theta }_2}\cdots \frac{1}{{\theta }_N}],\\ \frac{\mathit{\lambda }}{\mathit{\theta }}& \triangleq [\frac{{\lambda }_1}{{\theta }_1},\frac{{\lambda }_2}{{\theta }_2}\cdots \frac{{\lambda }_N}{{\theta }_N}],\\ S& \triangleq \mathrm{diag}\{\frac{1}{{\theta }_1},\frac{1}{{\theta }_2},\dots ,\frac{1}{{\theta }_N}\}\otimes I_{b{n}_x}.\end{array}$

Definition 2.1

For a given disturbance attenuation level $\tau >0$, the $H_{\mathrm{\infty }}$-consensus performance of the MAS (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) under the zero-initial condition is said to be achieved if the following inequality holds: (12) $\mathbb{E}\left\{\sum _{t_m=0}^{\mathrm{\infty }}\Vert \overline{z}(t_m)-\ell \overline{z}(t_m){\Vert }^2\right\}<{\tau }^2\sum _{t_m=0}^{\mathrm{\infty }}\Vert \omega (t_m){\Vert }^2$(12) where $\ell \triangleq (\frac{1}{N}{\mathbf{1}}_{N\times N})\otimes I_{b{n}_z}$.

The aim of this paper is to design appropriate parameters K and H for the proposed observer-based event-triggered control protocol (5(5) $\{\begin{array}{rl}{\xi }_i(t_{m+1})& =\hat{A}{\xi }_i(t_m)+\hat{B}{\overline{u}}_i(t_m)+H(y_i(t_m)-\mu \overline{C}{\xi }_i(t_m)),\\ {\overline{u}}_i(t_m)& =K\sum _{j\in {\mathrm{N}}_i}{a}_{ij}({\xi }_j(t_m)-{\xi }_i(t_m))\end{array}$(5) ) such that

• the augmented system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) with $\omega (t_m)\equiv 0$ is asymptotically stable;

• the augmented system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) under the zero-initial condition achieves the prescribed $H_{\mathrm{\infty }}$-consensus performance constraint (12(12) $\mathbb{E}\left\{\sum _{t_m=0}^{\mathrm{\infty }}\Vert \overline{z}(t_m)-\ell \overline{z}(t_m){\Vert }^2\right\}<{\tau }^2\sum _{t_m=0}^{\mathrm{\infty }}\Vert \omega (t_m){\Vert }^2$(12) ).

3. Main results

Before obtaining our main results, two important lemmas are first presented in the following.

For a full-column rank matrix $\mathcal{W}\in {\mathbb{R}}^{n_x\times n_u}$ ($n_x\ge n_u$) with $n_u$ nonzero singular values, i.e.${\zeta }_o(o=1,2,\dots ,n_u)$. Then, through the singular value decomposition process, one has two orthogonal matrices $\mathcal{Q}\in {\mathbb{R}}^{n_x\times n_x}$ and $\mathcal{V}\in {\mathbb{R}}^{n_u\times n_u}$ such that the following equation holds $\mathcal{W}=\mathcal{Q}\left[\begin{array}{c}\mathrm{\Xi }\\ 0\end{array}\right]{\mathcal{V}}^T=\left[\begin{array}{cc}{\mathcal{Q}}_1& {\mathcal{Q}}_2\end{array}\right]\left[\begin{array}{c}\mathrm{\Xi }\\ 0\end{array}\right]{\mathcal{V}}^T={\mathcal{Q}}_1\mathrm{\Xi }{\mathcal{V}}^T$where ${\mathcal{Q}}_1\in {\mathbb{R}}^{n_x\times n_u}$, ${\mathcal{Q}}_2\in {\mathbb{R}}^{n_x\times (n_x-n_u)}$, and $\mathrm{\Xi }\triangleq \mathrm{diag}\{{\zeta }_1,\dots ,{\zeta }_{{\mathrm{n}}_{\mathrm{u}}}\}$.

In light of the above formulations, one has the following lemma.

Lemma 3.1

Han et al., 2017

There is a nonsingular matrix $\tilde{\mathrm{\Re }}\in {\mathbb{R}}^{n_u\times n_u}$ such that $\mathcal{W}\tilde{\mathrm{\Re }}=\mathrm{\Re }\mathcal{W}$ holds, where $\tilde{\mathrm{\Re }}=\mathcal{V}{\mathrm{\Xi }}^{-1}{\mathrm{\Re }}_1\mathrm{\Xi }{\mathcal{V}}^T$ if the matrix $\mathrm{\Re }$ has the following structure: (13) $\begin{array}{rl}\mathrm{\Re }& =\left[\begin{array}{cc}{\mathcal{Q}}_1& {\mathcal{Q}}_2\end{array}\right]\mathrm{diag}\{{\mathrm{\Re }}_1,{\mathrm{\Re }}_2\}{\left[\begin{array}{cc}{\mathcal{Q}}_1& {\mathcal{Q}}_2\end{array}\right]}^T\\ & ={\mathcal{Q}}_1{\mathrm{\Re }}_1{\mathcal{Q}}_1^T+{\mathcal{Q}}_2{\mathrm{\Re }}_2{\mathcal{Q}}_2^T\end{array}$(13) where ${\mathrm{\Re }}_1\in {\mathbb{R}}^{n_u\times n_u}>0$, ${\mathrm{\Re }}_2\in {\mathbb{R}}^{(n_x-n_u)\times (n_x-n_u)}>0$, and $\mathrm{\Re }=\mathcal{V}{\mathrm{\Xi }}^{-1}{\mathrm{\Re }}_1\mathrm{\Xi }{\mathcal{V}}^T$.

Lemma 3.2

Ge et al., 2017

For given scalars ${\lambda }_i$ and ${\theta }_i$ satisfying ${\theta }_i>0$, ${\theta }_i{\lambda }_i\ge 1$, and $r_i(0)\ge 0$, the auxiliary variable $r_i(t_m)$ defined in (7(7) $\begin{array}{rl}{r}_i(t_{m+1})& ={\lambda }_i{r}_i(t_m)+{\sigma }_i\Vert {\xi }_i(t_m){\Vert }^2-\Vert e_i(t_m){\Vert }^2\end{array}$(7) ) satisfies $r_i(t_m)\ge 0$ for all $t_m\ge 0$.

Now, we are ready to obtain the main results by analysing the augmented system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ).

Theorem 3.1

Given the disturbance attenuation level $\tau >0$, gain matrices H and K, the system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) is asymptotically stable and meets the inequality constraint (12(12) $\mathbb{E}\left\{\sum _{t_m=0}^{\mathrm{\infty }}\Vert \overline{z}(t_m)-\ell \overline{z}(t_m){\Vert }^2\right\}<{\tau }^2\sum _{t_m=0}^{\mathrm{\infty }}\Vert \omega (t_m){\Vert }^2$(12) ) if there exists a symmetric positive-definite matrix P and a positive scalar ρ such that the following matrix inequality holds: (14) $\overline{\mathrm{\Omega }}\triangleq \left[\begin{array}{cccc}{\overline{\mathrm{\Omega }}}_{11}& \ast & \ast & \ast \\ {\overline{\mathrm{\Omega }}}_{21}& {\overline{\mathrm{\Omega }}}_{22}& \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast \\ {\overline{\mathrm{\Omega }}}_{41}& {\overline{\mathrm{\Omega }}}_{42}& 0& {\overline{\mathrm{\Omega }}}_{44}\end{array}\right]<0$(14) where $\begin{array}{rl}{\overline{\mathrm{\Omega }}}_{11}& \triangleq {\mathcal{A}}^{T}P\mathcal{A}+\overline{\mathcal{D}}-P+\rho M+M_1+2\mu {\overline{\mathcal{A}}}^{T}P\mathcal{A}\\ & +({\mu }^2+{\psi }^2){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}},\\ \overline{\mathcal{D}}& \triangleq (\mathcal{D}-\ell \mathcal{D}{)}^T(\mathcal{D}-\ell \mathcal{D}),{\overline{\mathrm{\Omega }}}_{21}\triangleq {\mathcal{B}}^{T}P\mathcal{A}+\mu {\mathcal{B}}^{T}P\overline{\mathcal{A}},\\ {\overline{\mathrm{\Omega }}}_{22}& \triangleq {\mathcal{B}}^{T}P\mathcal{B}-\rho I_{bN{n}_x}-S,{\overline{\mathrm{\Omega }}}_{41}\triangleq {\mathcal{E}}^{T}P\mathcal{A}+\mu {\mathcal{E}}^{T}P\overline{\mathcal{A}},\\ {\overline{\mathrm{\Omega }}}_{42}& \triangleq {\mathcal{E}}^{T}P\mathcal{B},{\overline{\mathrm{\Omega }}}_{44}\triangleq {\mathcal{E}}^{T}P\mathcal{E}-{\tau }^2{I}_{bN(n_w+n_v)},\\ {\overline{\mathrm{\Omega }}}_{33}& \triangleq \mathrm{diag}\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N\},{\alpha }_i\triangleq \frac{1}{{\theta }_i}({\lambda }_i+\rho -1).\end{array}$

Proof.

First, noticing that Lemma 3.2, $r(t_m)>0$ for all $t_m\ge 0$.

Next, choose the Lyapunov functions for system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) as follows: (15) $V(t_m)\triangleq V_1(t_m)+V_2(t_m)$(15) where $V_1(t_m)\triangleq {\eta }^T(t_m)P\eta (t_m),V_2(t_m)\triangleq \frac{\mathbf{1}}{\mathit{\theta }}r(t_m).$Then, calculate the mathematical expectation of the difference of $V_1(t_m)$ along the trajectory of system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) as follows: (16) $\begin{array}{rl}\mathbb{E}\{\mathrm{\Delta }{V}_1(t_m)\}& =\mathbb{E}\{V_1(t_{m+1})-V_1(t_m)\}\\ & =\mathbb{E}\{{\eta }^T(t_{m+1})P\eta (t_{m+1})-{\eta }^T(t_m)P\eta (t_m)\}\\ & =\mathbb{E}\{[(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)\\ & +{\mathcal{E}\omega (t_m)]}^{T}P[(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)\\ & +\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m)]\\ & -{\eta }^T(t_m)P\eta (t_m)\}\\ & ={\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)\\ & +{\omega }^T(t_m){\mathcal{E}}^{T}P\mathcal{E}\omega (t_m)\\ & +2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{E}\omega (t_m)\\ & +2e^T(t_m){\mathcal{B}}^{T}P\mathcal{E}\omega (t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{E}\omega (t_m).\end{array}$(16) Similarly, according to (11(11) $\{\begin{array}{rl}& e^T(t_m)e(t_m)<{\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m),\\ & \frac{\mathbf{1}}{\mathit{\theta }}r(t_{m+1})=\frac{\mathit{\lambda }}{\mathit{\theta }}r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)-e^T(t_m)Se(t_m)\end{array}$(11) ), we have (17) $\begin{array}{rl}\mathbb{E}\{\mathrm{\Delta }{V}_2(t_m)\}& =\mathbb{E}\{V_2(t_{m+1})-V_2(t_m)\}\\ & =\mathbb{E}\{\frac{\mathbf{1}}{\mathit{\theta }}r(t_{m+1})-\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)\}\\ & =(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & -e^T(t_m)Se(t_m).\end{array}$(17) Now we are ready to prove the asymptotic stability of (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) with $\omega (t_m)\equiv 0$. In light of (16(16) $\begin{array}{rl}\mathbb{E}\{\mathrm{\Delta }{V}_1(t_m)\}& =\mathbb{E}\{V_1(t_{m+1})-V_1(t_m)\}\\ & =\mathbb{E}\{{\eta }^T(t_{m+1})P\eta (t_{m+1})-{\eta }^T(t_m)P\eta (t_m)\}\\ & =\mathbb{E}\{[(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)\\ & +{\mathcal{E}\omega (t_m)]}^{T}P[(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)\\ & +\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m)]\\ & -{\eta }^T(t_m)P\eta (t_m)\}\\ & ={\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)\\ & +{\omega }^T(t_m){\mathcal{E}}^{T}P\mathcal{E}\omega (t_m)\\ & +2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{E}\omega (t_m)\\ & +2e^T(t_m){\mathcal{B}}^{T}P\mathcal{E}\omega (t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{E}\omega (t_m).\end{array}$(16) ) and (17(17) $\begin{array}{rl}\mathbb{E}\{\mathrm{\Delta }{V}_2(t_m)\}& =\mathbb{E}\{V_2(t_{m+1})-V_2(t_m)\}\\ & =\mathbb{E}\{\frac{\mathbf{1}}{\mathit{\theta }}r(t_{m+1})-\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)\}\\ & =(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & -e^T(t_m)Se(t_m).\end{array}$(17) ), we can obtain (18) $\begin{array}{rl}\mathbb{E}\left\{\mathrm{\Delta }V(t_m)\right\}& =\mathbb{E}\{V(t_{m+1})-V(t_m)\}\\ & =\mathbb{E}\{\mathrm{\Delta }{V}_1(t_m)\}+\mathbb{E}\{\mathrm{\Delta }{V}_2(t_m)\}\\ & <{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)\\ & +(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & -e^T(t_m)Se(t_m).\end{array}$(18) It follows from the positive scalar $\rho >0$ and (11(11) $\{\begin{array}{rl}& e^T(t_m)e(t_m)<{\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m),\\ & \frac{\mathbf{1}}{\mathit{\theta }}r(t_{m+1})=\frac{\mathit{\lambda }}{\mathit{\theta }}r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)-e^T(t_m)Se(t_m)\end{array}$(11) ) that (19) $\rho ({\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)-e^T(t_m)e(t_m))>0.$(19) We can further arrive at (20) $\begin{array}{rl}\mathbb{E}\left\{\mathrm{\Delta }V(t_m)\right\}& <{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)\\ & +(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & +\rho (\phantom{\frac{\mathbf{1}}{\mathit{\theta }}}{\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)-e^T(t_m)e(t_m))\\ & -e^T(t_m)Se(t_m)\\ & \triangleq {\overline{\eta }}^T(t_m)\mathrm{\Omega }\overline{\eta }(t_m)\end{array}$(20) where $\begin{array}{rl}\overline{\eta }(t_m)& \triangleq {\left[\begin{array}{ccc}{\eta }^T(t_m)& e^T(t_m)& {\overline{r}}^T(t_m)\end{array}\right]}^T,\\ \mathrm{\Omega }& \triangleq \left[\begin{array}{ccc}{\mathrm{\Omega }}_{11}& \ast & \ast \\ {\overline{\mathrm{\Omega }}}_{21}& {\overline{\mathrm{\Omega }}}_{22}& \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}\end{array}\right],\\ {\mathrm{\Omega }}_{11}& \triangleq {\mathcal{A}}^{T}P\mathcal{A}-P+\rho M+M_1+2\mu {\overline{\mathcal{A}}}^{T}P\mathcal{A}\\ & +({\mu }^2+{\psi }^2){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}},\\ \overline{r}(t_m)& \triangleq {\left[\begin{array}{cccc}\sqrt{r_1(t_m)}& \sqrt{r_2(t_m)}& \cdots & \sqrt{r_N(t_m)}\end{array}\right]}^T.\end{array}$As a result, the system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) with $\omega (t_m)=0$ is asymptotically stable owing to $\mathrm{\Omega }<0$ from (14(14) $\overline{\mathrm{\Omega }}\triangleq \left[\begin{array}{cccc}{\overline{\mathrm{\Omega }}}_{11}& \ast & \ast & \ast \\ {\overline{\mathrm{\Omega }}}_{21}& {\overline{\mathrm{\Omega }}}_{22}& \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast \\ {\overline{\mathrm{\Omega }}}_{41}& {\overline{\mathrm{\Omega }}}_{42}& 0& {\overline{\mathrm{\Omega }}}_{44}\end{array}\right]<0$(14) ).

Now, the remaining part is to prove that the system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) satisfies the inequality constraint (12(12) $\mathbb{E}\left\{\sum _{t_m=0}^{\mathrm{\infty }}\Vert \overline{z}(t_m)-\ell \overline{z}(t_m){\Vert }^2\right\}<{\tau }^2\sum _{t_m=0}^{\mathrm{\infty }}\Vert \omega (t_m){\Vert }^2$(12) ) under the case of $\omega (t_m)\ne 0$.

First, calculate the mathematical expectation of difference of $\mathrm{\Delta }\overline{V}(t_m)$ along the trajectories of system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) with $\omega (t_m)\ne 0$ as follows: (21) $\begin{array}{rl}\mathbb{E}\left\{\mathrm{\Delta }\overline{V}(t_m)\right\}& =\mathbb{E}\{\mathrm{\Delta }{V}_1(t_m)+\mathrm{\Delta }{V}_2(t_m)\}\\ & ={\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+{\omega }^T(t_m){\mathcal{E}}^{T}P\mathcal{E}\omega (t_m)\\ & +2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)\\ & +2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{E}\omega (t_m)\\ & +2e^T(t_m){\mathcal{B}}^{T}P\mathcal{E}\omega (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{E}\omega (t_m)\\ & +(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & -e^T(t_m)Se(t_m).\end{array}$(21) According to (19(19) $\rho ({\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)-e^T(t_m)e(t_m))>0.$(19) ), we can further arrive at (22) $\begin{array}{rl}& \mathbb{E}\left\{\mathrm{\Delta }\overline{V}(t_m)\right\}\\ <& {\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+{\omega }^T(t_m){\mathcal{E}}^{T}P\mathcal{E}\omega (t_m)\\ & +2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)\\ & +2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{E}\omega (t_m)\\ & +2e^T(t_m){\mathcal{B}}^{T}P\mathcal{E}\omega (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{E}\omega (t_m)\\ & +(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & -e^T(t_m)Se(t_m)\\ & +\rho ({\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)-e^T(t_m)e(t_m)).\end{array}$(22) It is noted that such an equality always holds: $(\overline{z}(t_m)-\ell \overline{z}(t_m){)}^T(\overline{z}(t_m)-\ell \overline{z}(t_m))={\eta }^T(t_m)\overline{\mathcal{D}}\eta (t_m).$Then, adding the term $(\overline{z}(t_m)-\ell \overline{z}(t_m){)}^T(\overline{z}(t_m)-\ell \overline{z}(t_m))-{\tau }^2{\omega }^T(t_m)\omega (t_m)$ to the both sides of (20(20) $\begin{array}{rl}\mathbb{E}\left\{\mathrm{\Delta }V(t_m)\right\}& <{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)\\ & +(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & +\rho (\phantom{\frac{\mathbf{1}}{\mathit{\theta }}}{\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)-e^T(t_m)e(t_m))\\ & -e^T(t_m)Se(t_m)\\ & \triangleq {\overline{\eta }}^T(t_m)\mathrm{\Omega }\overline{\eta }(t_m)\end{array}$(20) ) gives (23) $\begin{array}{rl}& \mathbb{E}\left\{\mathrm{\Delta }\overline{V}(t_m)\right\}+{\eta }^T(t_m)\overline{\mathcal{D}}\eta (t_m)-{\tau }^2{\omega }^T(t_m)\omega (t_m)\\ <& {\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{A}\eta (t_m)+e^T(t_m){\mathcal{B}}^{T}P\mathcal{B}e(t_m)\\ & -{\eta }^T(t_m)P\eta (t_m)+{\omega }^T(t_m){\mathcal{E}}^{T}P\mathcal{E}\omega (t_m)\\ & +2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{B}e(t_m)+2{\eta }^T(t_m){\mathcal{A}}^{T}P\mathcal{E}\omega (t_m)\\ & +2e^T(t_m){\mathcal{B}}^{T}P\mathcal{E}\omega (t_m)+2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{A}\eta (t_m)\\ & +({\mu }^2+{\psi }^2){\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\overline{\mathcal{A}}\eta (t_m)\\ & +2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{B}e(t_m)+2\mu {\eta }^T(t_m){\overline{\mathcal{A}}}^{T}P\mathcal{E}\omega (t_m)\\ & +(\frac{\mathit{\lambda }}{\mathit{\theta }}-\frac{\mathbf{1}}{\mathit{\theta }})r(t_m)+{\eta }^T(t_m)M_1\eta (t_m)\\ & +\rho [{\eta }^T(t_m)M\eta (t_m)+\frac{\mathbf{1}}{\mathit{\theta }}r(t_m)-e^T(t_m)e(t_m)]\\ & -e^T(t_m)Se(t_m)+{\eta }^T(t_m)\overline{\mathcal{D}}\eta (t_m)-{\tau }^2{\omega }^T(t_m)\omega (t_m)\\ \triangleq & {\tilde{\eta }}^T(t_m)\overline{\mathrm{\Omega }}\tilde{\eta }(t_m)\end{array}$(23) where $\tilde{\eta }(t_m)\triangleq [{\eta }^T(t_m)e^T(t_m){\overline{r}}^T(t_m){\omega }^T(t_m){]}^T$.

Recalling $\overline{\mathrm{\Omega }}<0$ from (14(14) $\overline{\mathrm{\Omega }}\triangleq \left[\begin{array}{cccc}{\overline{\mathrm{\Omega }}}_{11}& \ast & \ast & \ast \\ {\overline{\mathrm{\Omega }}}_{21}& {\overline{\mathrm{\Omega }}}_{22}& \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast \\ {\overline{\mathrm{\Omega }}}_{41}& {\overline{\mathrm{\Omega }}}_{42}& 0& {\overline{\mathrm{\Omega }}}_{44}\end{array}\right]<0$(14) ), we further have $\begin{array}{rl}& \mathbb{E}\left\{\mathrm{\Delta }\overline{V}(t_m)\right\}\\ <& {\tau }^2{\omega }^T(t_m)\omega (t_m)-{(\overline{z}(t_m)-\ell \overline{z}(t_m))}^T(\overline{z}(t_m)-\ell \overline{z}(t_m)).\end{array}$Then, one further derives (24) $\begin{array}{rl}& \mathbb{E}\left\{\sum _{t_m=0}^{\mathrm{\infty }}\mathrm{\Delta }\overline{V}(t_m)\right\}\\ & =\mathbb{E}\{{\eta }^T(\mathrm{\infty })P\eta (\mathrm{\infty })-{\eta }^T(0)P\eta (0)+\frac{\mathbf{1}}{\mathit{\theta }}r(\mathrm{\infty })-\frac{\mathbf{1}}{\mathit{\theta }}r(0)\}\\ & <-\sum _{t_m=0}^{\mathrm{\infty }}(\overline{z}(t_m)-\ell \overline{z}(t_m){)}^T(\overline{z}(t_m)-\ell \overline{z}(t_m))\\ & +\sum _{t_m=0}^{\mathrm{\infty }}{\tau }^2{\omega }^T(t_m)\omega (t_m).\end{array}$(24) By resorting to Lemma 3.2, one immediately has (25) $\mathbb{E}\left\{\sum _{t_m=0}^{\mathrm{\infty }}\Vert \overline{z}(t_m)-\ell \overline{z}(t_m){\Vert }^2\right\}<{\tau }^2\sum _{t_m=0}^{\mathrm{\infty }}\Vert \omega (t_m){\Vert }^2.$(25) The proof is therefore complete.

In the following, we will design gain matrices via Lemma 3.1 and Theorem 3.1.

Theorem 3.2

For a given positive scalar τ, the augmented system (10(10) $\{\begin{array}{rl}\eta (t_{m+1})& =(\mathcal{A}+\pi (t_m)\overline{\mathcal{A}})\eta (t_m)+\mathcal{B}e(t_m)+\mathcal{E}\omega (t_m),\\ \overline{z}(t_m)& =\mathcal{D}\eta (t_m)\end{array}$(10) ) is asymptotically stable and satisfies the $H_{\mathrm{\infty }}$ performance constraint (12(12) $\mathbb{E}\left\{\sum _{t_m=0}^{\mathrm{\infty }}\Vert \overline{z}(t_m)-\ell \overline{z}(t_m){\Vert }^2\right\}<{\tau }^2\sum _{t_m=0}^{\mathrm{\infty }}\Vert \omega (t_m){\Vert }^2$(12) ) if there exist matrices $\tilde{H}$ and $\tilde{K}$, and a symmetric positive-definite matrix $\overline{P}>0$ such that the following linear matrix inequality holds (26) $\left[\begin{array}{cccccc}{A}_{11}& \ast & \ast & \ast & \ast & \ast \\ 0& A_{22}& \ast & \ast & \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast & \ast & \ast \\ 0& 0& 0& A_{44}& \ast & \ast \\ A_{51}& A_{52}& 0& A_{54}& -P& \ast \\ A_{61}& 0& 0& 0& 0& -P\end{array}\right]<0$(26) where $\begin{array}{rl}{A}_{11}& \triangleq \overline{\mathcal{D}}-P+\rho M+M_1,P\triangleq \mathrm{diag}\{I_N\otimes \overline{P},I_N\otimes \overline{P}\},\\ A_{22}& \triangleq -\rho I_{bN{n}_x}-S,A_{44}\triangleq -{\tau }^2{I}_{bN(n_w+n_v)},\\ A_{51}& \triangleq \left[\begin{array}{cc}{I}_N\otimes (\overline{P}\hat{A})-L\otimes (\hat{B}\tilde{K})& -L\otimes (\hat{B}\tilde{K})\\ 0& I_N\otimes (\overline{P}\hat{A}-\mu \tilde{H}\overline{C})\end{array}\right],\\ A_{61}& \triangleq \left[\begin{array}{cc}0& 0\\ \psi I_N\otimes (\tilde{H}\overline{C})& 0\end{array}\right],A_{52}\triangleq \left[\begin{array}{c}-L\otimes (\hat{B}\tilde{K})\\ 0\end{array}\right],\\ A_{54}& \triangleq \left[\begin{array}{cc}{I}_N\otimes (\overline{P}\hat{E})& 0\\ -I_N\otimes (\overline{P}\hat{E})& I_N\otimes (\tilde{H}\overline{F})\end{array}\right].\end{array}$Furthermore, if (26(26) $\left[\begin{array}{cccccc}{A}_{11}& \ast & \ast & \ast & \ast & \ast \\ 0& A_{22}& \ast & \ast & \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast & \ast & \ast \\ 0& 0& 0& A_{44}& \ast & \ast \\ A_{51}& A_{52}& 0& A_{54}& -P& \ast \\ A_{61}& 0& 0& 0& 0& -P\end{array}\right]<0$(26) ) is feasible, the gain matrices H and K can be acquired by $H={\overline{P}}^{-1}\tilde{H},K={\tilde{P}}^{-1}\tilde{K}=V{\mathrm{\Xi }}^{-1}{\overline{P}}_1^{-1}\mathrm{\Xi }{V}^T\tilde{K}$where ${\overline{P}}_1$ is obtained by (13(13) $\begin{array}{rl}\mathrm{\Re }& =\left[\begin{array}{cc}{\mathcal{Q}}_1& {\mathcal{Q}}_2\end{array}\right]\mathrm{diag}\{{\mathrm{\Re }}_1,{\mathrm{\Re }}_2\}{\left[\begin{array}{cc}{\mathcal{Q}}_1& {\mathcal{Q}}_2\end{array}\right]}^T\\ & ={\mathcal{Q}}_1{\mathrm{\Re }}_1{\mathcal{Q}}_1^T+{\mathcal{Q}}_2{\mathrm{\Re }}_2{\mathcal{Q}}_2^T\end{array}$(13) ).

Proof.

According to Schur complement Lemma, (14(14) $\overline{\mathrm{\Omega }}\triangleq \left[\begin{array}{cccc}{\overline{\mathrm{\Omega }}}_{11}& \ast & \ast & \ast \\ {\overline{\mathrm{\Omega }}}_{21}& {\overline{\mathrm{\Omega }}}_{22}& \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast \\ {\overline{\mathrm{\Omega }}}_{41}& {\overline{\mathrm{\Omega }}}_{42}& 0& {\overline{\mathrm{\Omega }}}_{44}\end{array}\right]<0$(14) ) holds if and only if the following inequality holds (27) $\left[\begin{array}{cccccc}{A}_{11}& \ast & \ast & \ast & \ast & \ast \\ 0& A_{22}& \ast & \ast & \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast & \ast & \ast \\ 0& 0& 0& A_{44}& \ast & \ast \\ \mathcal{A}+\mu \overline{\mathcal{A}}& \mathcal{B}& 0& \mathcal{E}& -P^{-1}& \ast \\ \psi \overline{\mathcal{A}}& 0& 0& 0& 0& -P^{-1}\end{array}\right]<0.$(27) Next, performing the congruent transformation $\mathrm{diag}\{I,I,I,I,P,P\}$ to (27(27) $\left[\begin{array}{cccccc}{A}_{11}& \ast & \ast & \ast & \ast & \ast \\ 0& A_{22}& \ast & \ast & \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast & \ast & \ast \\ 0& 0& 0& A_{44}& \ast & \ast \\ \mathcal{A}+\mu \overline{\mathcal{A}}& \mathcal{B}& 0& \mathcal{E}& -P^{-1}& \ast \\ \psi \overline{\mathcal{A}}& 0& 0& 0& 0& -P^{-1}\end{array}\right]<0.$(27) ), one further has (28) $\left[\begin{array}{cccccc}{A}_{11}& \ast & \ast & \ast & \ast & \ast \\ 0& A_{22}& \ast & \ast & \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast & \ast & \ast \\ 0& 0& 0& A_{44}& \ast & \ast \\ P(\mathcal{A}+\mu \overline{\mathcal{A}})& P\mathcal{B}& 0& P\mathcal{E}& -P& \ast \\ \psi P\overline{\mathcal{A}}& 0& 0& 0& 0& -P\end{array}\right]<0.$(28) In consideration of the full-column rank matrix B, one has that $\hat{B}$ is also full-column. Noticing $P\triangleq \mathrm{diag}\{I_N\otimes \overline{P},I_N\otimes \overline{P}\}$ and Lemma 3.1, we have $\overline{P}\hat{B}=\hat{B}\tilde{P}$. Denoting $\tilde{K}=\tilde{P}K$ and $\tilde{H}=\overline{P}H$, one can obtain (26(26) $\left[\begin{array}{cccccc}{A}_{11}& \ast & \ast & \ast & \ast & \ast \\ 0& A_{22}& \ast & \ast & \ast & \ast \\ 0& 0& {\overline{\mathrm{\Omega }}}_{33}& \ast & \ast & \ast \\ 0& 0& 0& A_{44}& \ast & \ast \\ A_{51}& A_{52}& 0& A_{54}& -P& \ast \\ A_{61}& 0& 0& 0& 0& -P\end{array}\right]<0$(26) ), which ends the proof.

Remark 3.1

In this paper, the dynamic ETM-based $H_{\mathrm{\infty }}$-consensus control problem is studied for a class of multi-rate MASs with the channel fading measurements. The main results are summarized in Theorem 3.2, involving the system parameters, the occurring probability of fading channel, and the dynamic ETM parameters, whose combined impact is reflected in the performance constraint of the $H_{\mathrm{\infty }}$-consensus control. Compared with the existing results, our results stand out the three distinctive novelties: (1) compared to Q. Li et al. (2020), Ma et al. (2017b) and W. Xu et al. (2017), the problem solved in this paper is new under the background of the $H_{\mathrm{\infty }}$-consensus control for a type of multi-rate MAS with fading measurements; (2) compare to Han et al. (2021), Ma et al. (2017a) and Yin et al. (2016), the dynamic ETM is designed for each agent to determine the event-triggering time instants for further decreasing the number of information transmission; and (3) the sufficient conditions are derived that can guarantee the asymptotic stability and the $H_{\mathrm{\infty }}$-consensus control performance of the augmented system in the simultaneous presence of the channel fading measurements and the dynamic ETM.

4. A simulation example

In this section, an illustrative example is provided to verify the validity of the proposed consensus control scheme.

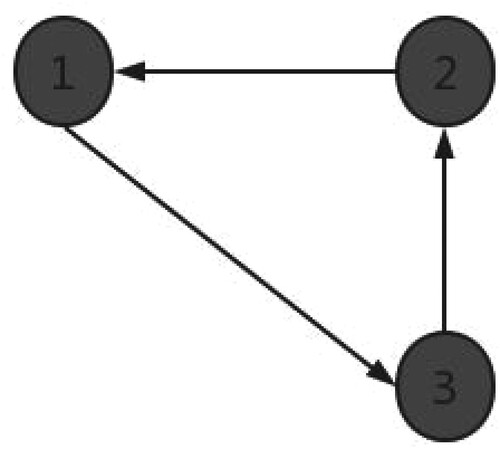
Consider an MASs composed of three agents whose communication topology is represented by a digraph $\mathcal{G}({\mathcal{V}}_Q,{\mathcal{S}}_Q,{\mathcal{A}}_Q)$ (i.e. Figure 1) where ${\mathcal{V}}_{\mathcal{Q}}=\{1,2,3\}$ and ${\mathcal{A}}_Q=\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right].$The parameters of the MAS are given as follows: $\begin{array}{rl}A& =\left[\begin{array}{cc}-0.0558& -0.9968\\ 0.598& -0.115\end{array}\right],B=\left[\begin{array}{c}0.0729\\ -0.475\end{array}\right],\\ E& =\left[\begin{array}{c}0.0991\\ 0.1023\end{array}\right],C=\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right],\\ D& =\left[\begin{array}{cc}0.5& 0.1\end{array}\right],F={\left[\begin{array}{cc}0.1& 0.1\end{array}\right]}^T.\end{array}$Set $T_m=m$ and $t_m=2m$. The initial values are given as $x_1(0)=[-1.52.7{]}^T$, $x_2(0)=[0.52.0{]}^T$, $x_3(0)=[-1.03.5{]}^T$, and the initial values of the observers are chosen as ${\xi }_i(0)=[00{]}^T$. Moreover, the other related parameters are $\mu =0.8$, ${\psi }^2=0.01$, $\tau =0.8$, $\rho =0.39$, ${\theta }_1=2$, ${\theta }_2=1.82$, ${\theta }_3=1.67$, ${\lambda }_1=0.5$, ${\lambda }_2=0.55$, ${\lambda }_3=0.6$, ${\sigma }_1=0.2$, ${\sigma }_2=0.3$, ${\sigma }_3=0.4$, ${\omega }_1(m)=e^{-m}\sin (m)$, ${\omega }_2(m)=e^{-0.1m}$, ${\omega }_3(m)=e^{-m}$, and $v_i(m)=e^{-0.1m}$. 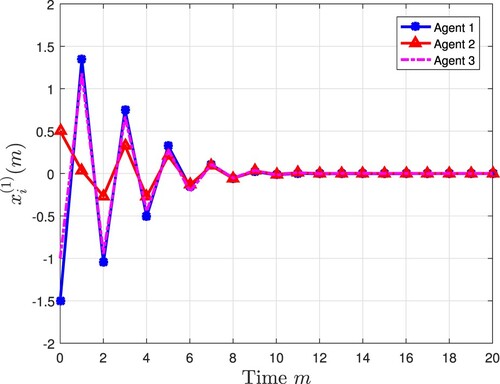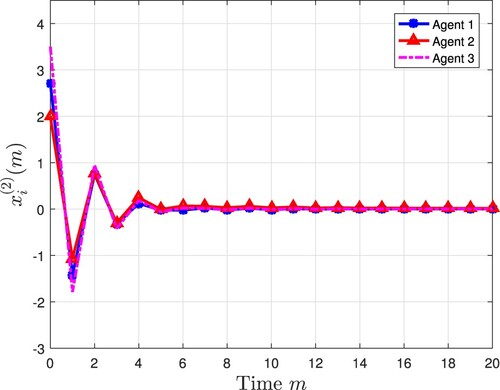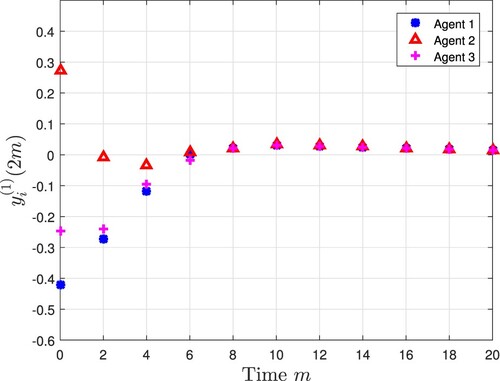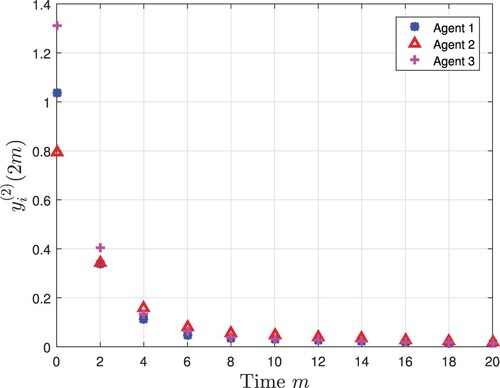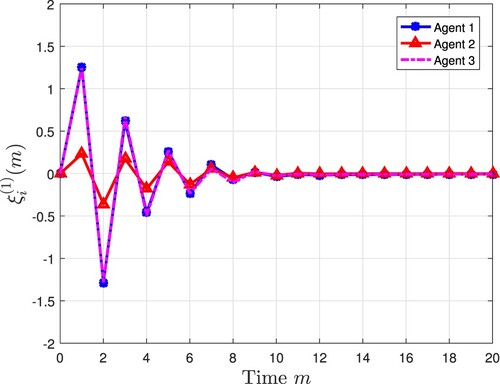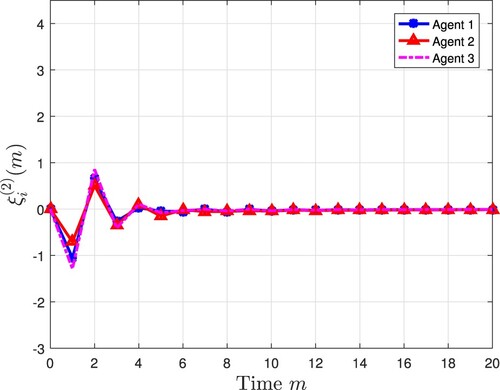By means of Theorem 3.2 and MATLAB toolbox, the gain matrices H and K are calculated as $\begin{array}{rl}H& ={\left[\begin{array}{cccc}-1.213& 0.1501& 0.4881& 1.1807\\ 0.7020& -0.9429& -1.6931& -0.6191\end{array}\right]}^T,\\ K& =\left[\begin{array}{cccc}-0.0838& 0.0105& 0.0083& 0.0162\\ -0.0015& 0.0984& 0.0252& 0.0012\end{array}\right].\end{array}$All the simulation results are exhibited in Figures 2 and 9. 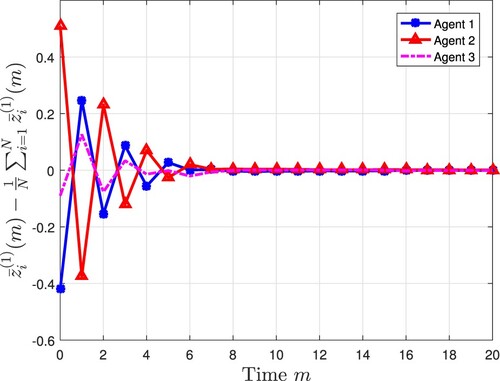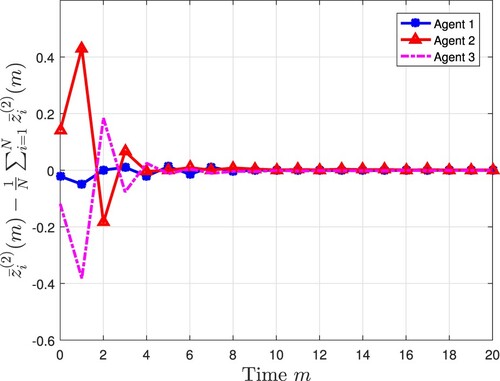Figures 2 and 3 plot three agents' state trajectory, where $x_i^{(\varsigma )}(t_m)$ denotes the ςth state ($\varsigma =1,2$) of the ith agent. Figures 4 and 5 depict the measurement output of three agents. Compared with Figures 1 and 2, the sampling rate of the measurement output is only half of that of the state, which reduces the consumption of communication resources while ensuring the stability of the system, thereby showing the advantage of the multi-rate strategy. Figures 6 and 7 depict state estimates from the designed observers. 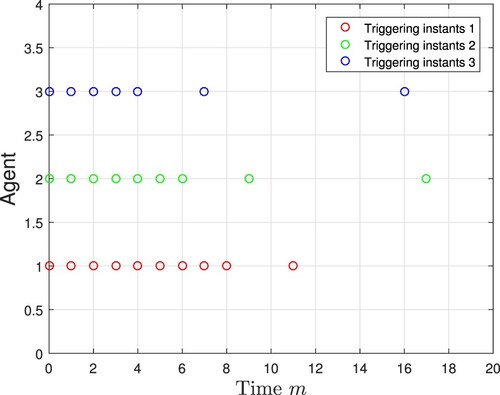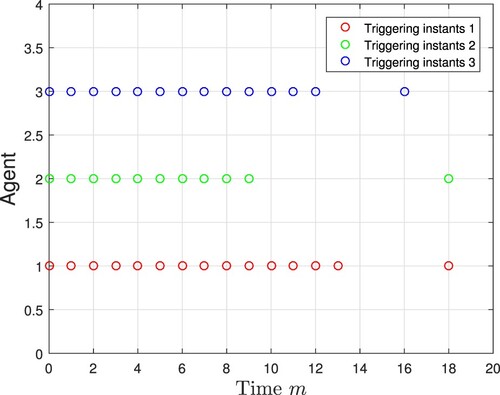Figures 8 and 9 show the consensus error ${\overline{z}}_i^{(\varsigma )}(t_m)-\frac{1}{N}\sum _{i=1}^N{\overline{z}}_i^{(\varsigma )}(t_m)$, which reveal that the desired $H_{\mathrm{\infty }}$-consensus control performance is achieved. Furthermore, Figures 10 and 11 depict the event-triggering instants under the cases of dynamic ETM and static ETM, respectively. Under the scheduling of dynamic ETM, the times of information transmissions and control protocol updates are reduced to a certain extent. It can be concluded that the distributed consensus control scheme proposed in this paper is indeed effective.

Figure 1. The digraph $\mathcal{G}$.

Figure 2. The state trajectory $x_i^{(1)}(m)$.

Figure 3. The state trajectory $x_i^{(2)}(m)$.

Figure 4. The measurements $y_i^{(1)}(2m)$.

Figure 5. The measurements $y_i^{(2)}(2m)$.

Figure 6. The state estimates ${\xi }_i^{(1)}(m)$.

Figure 7. The state estimates ${\xi }_i^{(2)}(m)$.

Figure 8. The consensus error ${\overline{z}}_i^{(1)}(m)-\frac{1}{N}\sum _{i=1}^N{\overline{z}}_i^{(1)}(m)$.

Figure 9. The consensus error ${\overline{z}}_i^{(2)}(m)-\frac{1}{N}\sum _{i=1}^N{\overline{z}}_i^{(2)}(m)$.

Figure 10. The triggering instants under the dynamic ETM.

Figure 11. The triggering instants under the static ETM.

5. Conclusion

This paper has designed the observer-based dynamic event-triggered distributed consensus controller for a class of multi-rate MASs subject to the fading measurements. The lifting technique has been utilized to unify the multi-rate MASs into a single-rate MASs. A set of random variables has been employed to characterize the occurrence of the channel fading measurements. The dynamic ETM has been formulated to schedule the information transformation among neighbouring agents. Using the Lyapunov stability theory, a distributed consensus control scheme has been proposed based on the adopted dynamic ETM to guarantee the desired performance constraint. Finally, a numerical example has been used to verify the effectiveness of the proposed consensus control scheme. The potential future research directions of this paper are put forward as follows: (1) find an effective method to deal with this computational burden problem caused by the lifting technique; and (2) study the consensus control problem via other ideas such as the sliding mode control (J. Hu et al., 2021), the ${\ell }_2$-${\ell }_{\mathrm{\infty }}$ output-feedback control (L. Wang, Liu, et al., 2022; Zhu et al., 2021), and the secure control (L. Wang, Tian, et al., 2022).

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported in part by the National Natural Science Foundation of China [grant number 62073070], [grant number U21A2019], [grant number 62203106], and [grant number 61933007], the China Postdoctoral Science Foundation [grant number 2017M621242], [grant number 2020T130092], and [grant number 2022M710660], the Natural Science Foundation of Heilongjiang Province of China [grant number LH2022324], the Key Laboratory for Metallurgical Equipment and Control of Ministry of Education in Wuhan University of Science and Technology [grant number MECOF2019B02], and the Hainan Province Science and Technology Special Fund of China [grant number ZDYF2022SHFZ105].