A computational study of suppression of sharp wave ripple complexes by controlling calcium and gap junctions in pyramidal cells

ABSTRACT

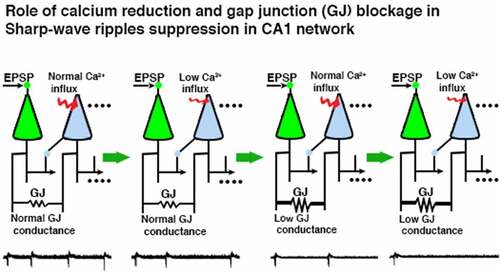
The hippocampus plays a key role in memory formation and learning. According to the concept of active systems memory consolidation, transiently stored memory traces are transferred from the hippocampus into the neocortex for permanent storage. This phenomenon relies on hippocampal network oscillations, particularly sharp wave ripples [SPW-Rs). In this process prior saved data in the hippocampus may be reactivated. Recent investigations reveal that several neurotransmitters and neuromodulators including norepinephrine, acetylcholine, serotonin, etc., suppress SPW-Rs activity in rodents’ hippocampal slices. This suppression of SPW-Rs may depend on various presynaptic and postsynaptic parameters including decrease in calcium influx, hyperpolarization/depolarization and alteration in gap junctions’ function in pyramidal cells. In this study, we demonstrate the impact of calcium influx and gap junctions on pyramidal cells for the modulation of SPW-Rs in a computational model of CA1.

We used,SPW-Rs model with some modifications. SPW-Rs are simulated with gradual reduction of calcium and with decreasing conductance through gap junctions in PCs. Both, with calcium reduction as well as with conductance reduction through gap junctions, SPW-Rs are suppressed. Both effects add up synergistically in combination.

Graphical abstract

KEYWORDS:

• Sharp wave ripples
• hippocampus
• calcium influx
• ca1
• oscillations

Introduction

The hippocampus exhibits a variety of neuronal network oscillations, which are associated with various mnemonic functions. These oscillations are mainly theta (θ; 4–10 Hz], gamma (γ; 30–90) and sharp wave ripples (SPW-Rs; 140–250 Hz). Theta and gamma oscillations appear during spatial searching, acquisition of learning and rapid eye movement (REM) sleep, while SPW-Rs emerge during slow-wave sleep (SWS), immobile state, during eating and drinking, and are essential for memory consolidation processes [2–4]. In rat hippocampus, SPW-Rs are the most consistent oscillatory rhythms having high local field potential amplitude (~1 mV) and high spatial coherence over 1 mm [2,5,6]. In CA1’s stratum radiatum, SPW-Rs are generated due to the synchronous excitatory input from the CA3 pyramidal cells through Schaffer collaterals [3]. These Schaffer collaterals initiate high-frequency oscillations (ripples; 140–250 Hz) in the CA1 region. The place cells, which fire during spatial searching or explorative behavior, exhibit reactivation during sleep, and in this reactivation period, cells have the same temporal firing pattern as it was during spatial searching [7–9]. Previously stored information reactivation is strongly observed during SPW-Rs in immobile state, slow-wave sleep [10,11] and rarely during searching [12,13]. This behavior-dependent switching of hippocampal network oscillations is an abrupt process.

Several investigations reveal that variations in cholinergic input to the hippocampus have been involved in these sudden transitions [14–16]. In addition to acetylcholine (ACh), other neuromodulators, such as norepinephrine (NE), serotonin (5-HT) also suppresses ripple activity in rodents [17–19]. These neuromodulators act via a variety of different receptors involving different signaling cascades and exert multiple effects on hippocampal neurons. NE and 5-HT cause mild to moderate hyperpolarizations of CA3 pyramidal neurons while ACh depolarizes them. Briefly, they modulate synaptic strength and efficacy, alter excitation and inhibition, interfere with transmitter release and reduce calcium influx [20–23]. In spite of having multimodal effects, these neuromodulators suppress SPW-Rs possibly by reducing calcium influx to axon collaterals [15,17,18] and altering conductance through gap junctions [24].

To validate these observations, we simulated a theoretical model of SPW-Rs in CA1 after [1] with small modifications. The majority of the SPW-Rs models are based on two elements: chemical synapses and gap junctions. Chemical synapses based SPW-Rs models with replay are based on strong synaptic connectivity in recurrent networks [25]. These models explain the encoding achieved by spike timing dependent plasticity with phase precession. According to Memmesheimer’s model [26], transient ripples can appear in a network of cells linked by excitatory synapses. Taxidis [27] suggested another SPW-Rs model, in which ripple-frequency rhythm in CA1 is generated only in interneurons, which are connected to each other by GABA_A synapses. Traub & Bibbig suggested a SPW-Rs model based on gap junctions. The axons of the pyramidal cells were stimulated by random spikes at low frequency, which generated high frequency (140 Hz or high) rhythms [28]. A later model of Traub [29] produced the axonal plexus driven SPW-Rs, where gap junctions were situated in axonal branches away from the soma. In another computational study for declarative memory formation [30], the SPW-Rs were studied in basket cells network with varying transient and noisy excitatory inputs. In recent studies [30], focused on disinhibition of the CA3 network and the role of interneurons during SPW-Rs activity.

In this study, we chose Vladimirov’s model (with small modifications) [1], which possibly provides a bridge between two presently opposite models of SPW-Rs, the first based on gap junctions and the other based on chemical synapses. In this proposed model of ripples, the occurrence of ripples and antidromic spikes are regulated by the input from dendrites of PCs. Slight alterations in somatic potential gate spike transmission from an axonal collateral to the main axon, so that EPSPs can turn on and IPSPs can turn off ripple-associated somatic spikes. Using the same mechanism, the replay in the ripple-associated PCs is demonstrated.

As mentioned above, modulation of calcium influx and electrical coupling play a pivotal role in the suppression of SPW-Rs in different experimental settings. Scientific literature reveals that there are several computational models for the generation of SPW-Rs, but there is not a single report describing the modulation of SPW-Rs based on calcium influx and electrical coupling in pyramidal cells. We evaluated the role of calcium influx and electric conductance through gap junctions on the generation of SPW-Rs. For these evaluations, after SPW-Rs generation, we gradually reduced calcium influx and decreased conductance through gap junctions in the pyramidal cells of our SPW-Rs model and examined the effects of these alterations on the generation of SPW-Rs.

Methods

CA1 pyramidal cells

The pyramidal cell model of Roger Traub and colleagues [31] was used for the computational simulation of a CA1 network model. In this cell model, six ionic currents were used: (1) fast sodium current, [Na (Fast)], (2) potassium after-hyper-polarization, K_(AHP)(3) potassium delayed-rectifier, K_(DR)(4) potassium transient current, K_(A), (5) high-threshold calcium current, Ca, and (6) calcium-dependent and voltage-dependent potassium current K_(Ca). For the soma-dendritic compartment k, the ionic current was computed by the equation:

For the axon-initial segment compartment k, the ionic current was computed by

$I_{\mathit{ionic},\mathit{k}}=g_{\mathit{L},\mathit{k}}{V}_k+{\bar{g}}_{\mathit{Na},\mathit{k}}{h}_k{m}_k^3\left(V_k-V_{\mathit{Na}}\right)+{\bar{g}}_{\mathit{K}\left(\mathit{DR}\right),\mathit{k}}{n}^4\left(V_k-V_K\right)+I_{\mathit{syn},\mathit{k}}-I_{\mathit{inj},\mathit{k}}\left(1.2\right)$

In the above equations, k denotes the compartment index and $\bar{g}$ represents the maximum conductance for a particular ion in compartment k (given in Table 1). V_k is the local membrane resting potential and g_L,k is the leak conductance. The resting potential of given ions is V_Na = 115 mV, V_K = −15 mV, V_Ca = 140 mV. For the axonal-initial segment (AIS) compartment, we have V_K = −25 mV. χ_k represents the Ca²⁺ in the submembrane shell in arbitrary units. m, h, n, s, a, b, q, and c are state variables having values between 0 and 1. The dynamics of these state variables is like follows: Let x_k represent a dimensionless state variable m, h, n, s, a or b and V_k represent the membrane potential in compartment k (if x_k represents q then V_k is χ_k). Then, these state variables follow the Hodgkin-Huxley [32] like equation:

(1.3) $\frac{d{x}_k}{\mathit{dt}}={\mathit{\alpha }}_x\left(V_k\right)\left(1-{\mathrm{x}}_k\right)-{\mathit{\beta }}_x\left(V_k\right){\mathrm{x}}_k$(1.3)

Table 1. Maximum conductance densities (S/cm²)

Level	Na^+	K(DR)	K(AHP)	K(A)	Ca^2+	K(Ca)
1	-	-	0.0008	-	0.001	0.004
2	-	-	0.0008	0.0005	0.001	0.004
3	0.001	0.015	0.0008	0.0005	0.001	0.008
4 (Soma)	0.070	0.170	0.0008	0.0005	0.001	0.02
5 (Shaft)	0.003	0.020	0.0008	0.0005	0.001	0.008
6	0.003	0.020	0.0008	0.0005	0.001	0.008
7	-	-	0.0008	-	0.002	0.004
8	-	-	0.0008	-	0.003	0.012
9	-	-	0.0008	-	0.003	0.012
10	-	-	0.0008	-	0.001	0.004
11	-	-	0.0008	-	0.001	0.004
AIS	0.300	0.400	-	-	-	-
Axon	0.300	0.400	-	-	-	-

where α_x and β_x are forward and backward rate functions, presented in Tables 2 and 3.

Table 2. Rate functions for soma-dendrite compartments

Function	Forward (α)	Backward (β)
gNa activation (m)	$\frac{0.32\left(13.1-\mathit{V}\right)}{\mathit{exp}\left(\frac{13.1-\mathit{V}}{4}\right)-1}$	$\frac{0.28\left(\mathit{V}-40.1\right)}{\mathit{exp}\left(\frac{\mathit{V}-40.1}{5}\right)-1}$
gNa inactivation (h)	$.128\mathit{exp}\left(\frac{17-\mathit{V}}{18}\right)$	$\frac{4}{1+\mathit{exp}\left(\frac{40-\mathit{V}}{5}\right)}$
gCa(s)	$\frac{1.6}{1+\exp \left(-0.072\left(\mathit{V}-65\right)\right)}$	$\frac{0.02\left(\mathit{V}-51.1\right)}{\mathit{exp}\left(\frac{\mathit{V}-51.1}{5}\right)-1}$
gK(DR) (n)	$\frac{0.016\left(35.1-\mathit{V}\right)}{\mathit{exp}\left(\frac{35.1-\mathit{V}}{5}\right)-1}$	$0.25\mathit{exp}\left(\frac{20-\mathit{V}}{40}\right)$
gK(AHP) (q)	$\min \left(0.2\times {10}^{-4}\mathit{\chi },0.01\right)$	$0.001$
gK(A) activation (a)	$\frac{0.02\left(13.1-\mathit{V}\right)}{\mathit{exp}\left(\frac{13.1-\mathit{V}}{10}\right)-1}$	$\frac{0.0175\left(\mathit{V}-40.1\right)}{\mathit{exp}\left(\frac{\mathit{V}-40.1}{10}\right)-1}$
gK(A) inactivation (b)	$0.0016\exp \left(\frac{-13-\mathit{V}}{18}\right)$	$\frac{0.05}{1+\mathit{exp}\left(\frac{10.1-\mathit{V}}{5}\right)}$
gK(Ca) (c) $\left[\mathit{V}\le 50\right]$	$\frac{\mathit{exp}\left[\left(\frac{\mathit{V}-10}{11}\right)-\left(\frac{\mathit{V}-6.5}{27}\right)\right]}{18.975}$	$2\times \mathit{exp}\left(-\frac{\mathit{V}-6.5}{27}\right)-{\propto }_c$
gK(Ca) (c) $\left[\mathit{V}\ge 50\right]$	$2\mathit{exp}\left(-\frac{\mathit{V}-6.5}{27}\right)$	$0$

Table 3. Rate functions for axon and axonal initial segment (AIS) compartments

Function	Forward (α)	Backward (β)
gNa activation (m)	$\frac{0.8\left(17.2-\mathit{V}\right)}{\mathit{exp}\left(\frac{17.2-\mathit{V}}{4}\right)-1}$	$\frac{0.7\left(\mathit{V}-42.2\right)}{\mathit{exp}\left(\frac{\mathit{V}-42.2}{5}\right)-1}$
gNa inactivation (h)	$0.32\mathit{exp}\left(\frac{42-\mathit{V}}{18}\right)$	$\frac{10}{1+\mathit{exp}\left(\frac{42-\mathit{V}}{5}\right)}$
gK(DR) (n)	$\frac{0.03\left(17.2-\mathit{V}\right)}{\mathit{exp}\left(\frac{17.2-\mathit{V}}{5}\right)-1}$	$0.45\mathit{exp}\left(\frac{12-\mathit{V}}{40}\right)$

Conductance densities of somato-dendrites were taken from the basic model [31] excluding the fast sodium in lower areas of the soma (0.070 S/cm²) to ensure that only a small number of spikes turn into soma spikes [33,34]. The densities of the ionic conductances were the same in all axonal compartments of the main axon, collaterals, and the axonal initial segment (AIS): Na (Fast) 0.3 S/cm² and potassium delayed-rectifier 0.4S/cm² (Table 1). The dimensions of the axonal compartments, i.e. AIS, main axon, collaterals, and the two collaterals branched out of the main axon (Figure 1a) were set according to Vladimirov’s model [1].

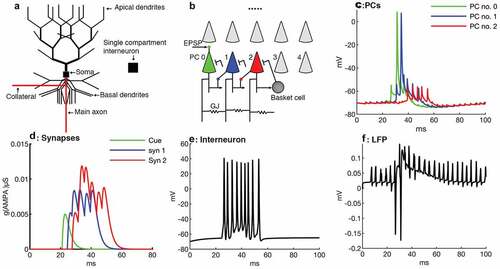
Figure 1. (Figure changes are made) Network design and simulation of CA1 SPW-Rs. (a) Schematic model of the pyramidal cell consisting of 64 compartments for soma and dendrites and the interneuron consisting of single compartment. (b) A network of 25 PCs (ten shown) and one interneuron. PC no. 0 receives an excitatory afferent (‘cue’) in its apical dendrites and starts replay sequentially in PC no. 1 and 2 which are synaptically connected. The distal collateral of PC (i) projects to the basal dendrite of PC (i + 1) (i = 0, 1) by an AMPA synapse (Arrows). Proximal collaterals of all PCs are randomly coupled via gap junctions and get random current stimulation. All PCs project to the interneuron by AMPA synapses (Arrows) and the interneuron targets back to the somas of all PCs by inhibitory synapses (blunt arrows). The complete cell connectivity is shown in PC no. 2. (c) PC no. 0 synaptically stimulates PC no. 1 which repeats the previous somatic spike generation cycle of PC no. 0 and generates a spike after ~4 ms following PC no. 0. (d) Excitatory synaptic inputs of the first three pyramidal cells. The first PC receives afferent input (cue) in its apical dendrite and starts to reactivate the synaptically connected cells’ sequence (i.e. PC no. 0, 1, 2). (e) Interneuron firing in the network, which receives an input from a PC and generates a spike. (f) Local field potential, which is temporally correlated to synaptic inputs of the first three PCs. The first deep negative spike occurs when PC no. 0 fires, and the ripple cycle occurs when PC no. 1 fires

All compartments had the same membrane capacitance of 0.75 μF/cm². The membrane resistance (R_m) for soma and dendrites was 5 × 10⁴ Ωcm² and for axonal compartments 10³ Ωcm². The cytoplasmic resistance of the soma and the dendritic compartments was 200 Ωcm and in axonal compartments 100 Ωcm. Leak current reversal potentials (E_rev) in all compartments were −65 mV. All compartments had 50 mV Na E_rev. Similarly, K reversal potential was −80 mV in compartments of soma-dendrites, and axonal compartments had −90 mV reversal potential [31]. The Reversal potential of AMPA was 0 mV. To suppress spike propagation into the main axon from proximal collaterals, AISs of all PCs except the first three PCs of the network were hyperpolarized by −0.107 nA during resting mode. According to [35], the place cells have a slide somatic depolarization compared to silent cells. In our model, the first three pyramidal cells played the place cell role and their AISs membrane potentials were set a bit more depolarized than the rest of the pyramidal cells. The AISs of the first three PCs were less hyperpolarized compared of other network cells (for instance, AIS of PC no. 0 was hyperpolarized by −.099 nA). The passive cable length constant $\mathit{\lambda }=\sqrt{\mathrm{aRm}}/2\mathrm{Ra}$ for the apical dendritic shaft was set to 2500 μm, for proximal basal dendrites to 1768 μm, for the main axonal trunk to 158 μm, and for the AIS to 223 μm.

Interneuron

A single compartmental model was used for the interneuron [36], which follows the current equation:

${\mathrm{C}}_{\mathrm{m}}\frac{\mathrm{dV}}{\mathrm{dt}}=-{\mathrm{I}}_{\mathrm{Na}}-{\mathrm{I}}_{\mathrm{K}}-{\mathrm{I}}_{\mathrm{L}}-{\mathrm{I}}_{\mathrm{syn}}+{\mathrm{I}}_{\mathrm{inj}}\mathit{\hspace{0.17em}}(2.1$

)

where C_m = 1 µF/cm² is membrane capacitance, I_syn is the synaptic current, I_inj the injected current, I_L the leak current (I_L = g_L(V-E_L) with leak conductance g_L = 0.1 mS/cm² and a reversal potential, E_L = −65 mV) and Na⁺ and K⁺ are spike generating voltage dependent ion currents. I_Na and I_K follow a Hodgkin and Huxley [32] kinetics. The sodium current is given by

I_Na = g_Na m³h(V-E_Na) (2.2)

with g_Na = 0.035 S/cm² and E_Na = 55 mV. m and h are again state variables. m is an activation variable substituted by the steady function m_∞ = α_m/(α_m+β_m) where α_m(V) = −0.1(V + 35)/(exp(−0.1(V + 35)) – 1) and β_m(V) = 4exp(-(V + 60)/18). The inactivation state variable h is calculated by a first order kinetics:

(2.3) $\frac{\mathit{dh}}{\mathit{dt}}=\mathit{\varphi }\left({\mathit{\alpha }}_h\left(1-\mathrm{h}\right)-{\mathit{\beta }}_h\mathrm{h}\right)$(2.3)

where α_h(V) = 0.07 exp(-(V + 58)/20) and β_h(V) = 1/(exp(−0.1(V + 28)) +1) and ϕ = 5.

The potassium delayed-rectifier current is described by:

I_K = g_Kn⁴(V-E_K) (2.4)

^{where gK = 0.009 S/cm2 and EK = −90mV. The activation variable n is also calculated by a first order kinetics:}

(2.5) $\frac{\mathit{dn}}{\mathit{dt}}=\mathit{\varphi }\left({\mathit{\alpha }}_n\left(1-\mathrm{n}\right)-{\mathit{\beta }}_n\mathrm{n}\right)$(2.5)

where α_n(V) = 0.01(V + 34)/(exp(−0.1(V + 34)) – 1) and β_n(V) = 0.125 exp(- (V + 44)/80).

The cell had the same diameter and length of 20 μm.

Synaptic connections in pyramidal cells

The conductance time course in AMPA synapses were chosen according to the alpha-function g = g_max(t/τ)exp(–(t–τ)/τ), which has the maximum conductance g_max at the time τ from start. AMPA targeted pyramidal to pyramidal cells (PC-PC) and pyramidal cells to the interneuron (PC-IN). The parameters of the AMPA synapses from PC-to-PC were g_max = 52 nS, τ = 2 ms, and from PCs-to-IN synapses g_max = 4 nS, τ = 0.8 ms. The excitatory afferent synaptic input ‘cue’ to the first PC was set to 5 nS, τ = 2 ms, and the Nernst potential was 0 mV. The PCs communicate to the targeted cells via the distal axonal collateral. The GABA_A synapses, which target to the PCs, are located in the middle of the PCs’ soma. The conductance time course for GABA_A synapses from IN to PCs was simulated by a double exponential function g = g_max(τ₂/τ₂–τ₁)(–exp(–t/τ₁)+exp(–t/τ₂)), which approaches g_max at time τ₁τ₂log(τ₁/τ₂)/(τ₁–τ₂) after the start. The values of the parameters were τ₁ = 2 ms, τ₂ = 5 ms, E_rev = −75 mV, and the maximum conductance was g_max = 40 nS [1].

Gap junction connections

In our network model, every PC had three gap junctions (GJ) situated in its proximal axonal collateral. These gap junctions were positioned in a random fashion in the range from 0.25 to 0.75 on the proximal collateral. Different collateral gap junctions were randomly interconnected in the network, with a connection probability independent of the cell distance. Cells were not allowed to make self-connections, but two cells were permitted to have double connections between each other. All pyramidal cells were electrically coupled and no cells were isolated.

Network architecture

The network model contained 25 pyramidal cells and one interneuron (Figure 1b). The first PC received an excitatory afferent input into its apical dendrites. We suppose that prior theta oscillations between PCs of CA1 formed some AMPA synapses via LTP [8]. Two AMPA synapses made contact between the first three PCs in a feed forward pattern. The first synapse is connected from PC no. 0 to 1, the second one from 1 to 2. Both synapses were set on PCs basal dendrites, 35 μm away from somas and played a gating role for antidromic spikes in targeted PCs and generated antidromic ripples in the CA1 network. All pyramidal cells of the network projected to the interneuron through AMPA synapses (3.5 nS). The interneuron also targeted back to the somas of all PCs through powerful GABA_A synapses (40 nS). The network model was implemented with the NEURON simulation environment [37].

Reduction of calcium influx and conductance through gap junction

A single pyramidal cell (Figure 1a) of our model had 11 soma-dendritic branching levels. The calcium conductance densities for the different branching levels was 1 mS cm⁻² for levels 1–6, 2 mS cm⁻² for level 7, 3 mS cm⁻² for level 8–9 and 1 mS cm⁻² for level 10–11. In the soma, the calcium conductance density was 1 mS cm⁻² [31]. The calcium conductance was gradually decreased in each dendritic level and in the soma with the same proportion to evaluate effects of presynaptic calcium influx on sharp wave ripples. Four simulation results were gathered with different calcium conductances in pyramidal cells: 0% g_ca, 30% g_ca, 50% g_ca, and 100% g_ca. Similarly, in order to investigate the role of gap junctions on the modulation of SPW-Rs, the conductance through gap junctions was decreased to half (partial reduction) and to complete blockage (full reduction). Calcium conductance was set to 50% and gap junction conductance to 1.6 nS (partial reduction) for obtaining synergistic effects of Ca and gap junctions on SPW-Rs modulation.

Results

In this study, we evaluate the effects of a reduction in calcium influx and electrical coupling on the generation of SPW-Rs in a computational model of these network oscillations. SPW-Rs are generated by a variant of the computational model proposed by Vladimirov and colleagues [1]. In a next step, calcium influx and gap junction conductances are gradually decreased during the simulation of SPW-Rs.

Simulation of SPW-Rs

In a first step, we simulated a network model with 26 cells, 25 multi compartment pyramidal cells and one interneuron having a single compartment (Figure 1a, 1b). In this network, proximal collaterals of pyramidal cells are coupled randomly through gap junctions, and these proximal collaterals are stimulated in a semi random fashion (NetStim.noise = 0.5 in the NEURON simulator) by current insertion via a distal tip (0.042 nA for 3 ms). As a proximal collateral of a single cell is stimulated, all proximal collaterals of the remaining cells participating in the network also generate action potentials synchronously within 0.5 to 1 ms with a frequency of ~250 Hz. All 25 pyramidal cells target to one interneuron and the interneuron targets back to all somas of the pyramidal cells. The first three pyramidal cells of the network are connected by two AMPA synapses. The distal collateral of pyramidal cell (i) targets to the basal dendrite of its next neighboring pyramidal cell (i + 1) by an excitatory synapse (Figure 1b). The somatic and axonal both inputs together reach the threshold and generate an action potential, which propagates in both directions: antidromic and orthodromic. In result of the antidromic propagation, the soma of PC no. 0 generates a spike. By this mechanism, one cell activates another cell by EPSP and, similarly, the other cell develops an EPSP in chain on replay basis (Figure 1c). According to Lee [35] place cells have a more somatic depolarization ‘hill’ compared to the silent cells. In our model, the somas and AISs of the first three PCs of the network had more depolarization than the other 22 pyramidal cells. When the AIS of PC no 0 gets strong input from proximal collaterals in combination with maximum gap junctions input, its reaches the threshold because of less hyperpolarization as compared to other cells, which leads to an action potential. This process produces second and so forth SPW-Rs (Figure 2d) (This is correct figure citation for 2^nd and so forth SPW-Rs).

Figure 2. Effects of suppression of calcium influx on SPW-Rs. (a) Calcium suppression effects on synapse no. 1, which makes a connection from PC no. 0 to PC. no. 1. Note that when calcium is decreased, the strength of the synapse is also decreased, which causes a delayed activation of the targeted PC or a suppression of spikes. (b) PC no. 1 firing behavior with different calcium quantities. With gradual calcium suppression it takes more time to produce a spike. Complete calcium suppression leads to spikelets (red). (c) Local field potentials for different calcium influxes showing less ripples in sharp waves. (d-g) Local field potentials (left) and spike raster of the first three PCs (right thick and dark ones are spikes and thin ones are spikelets) during different calcium influxes in pyramidal cells of the network. Note that gradual calcium suppression in PCs decreases the number of SPW-Rs

The first PC of the network receives an excitatory afferent input (cue) into its apical dendritic shaft, and it starts firing and delivers EPSPs to the next cell, which also starts firing after a short delay (~4 ms). Similarly, the third cell also fires but produces only spikelets (Figure 1c). Initially, only the first three synaptically connected PCs participate in the SPW-Rs generation (figure 1f). If any pyramidal cell fires it triggers the interneuron, which also fires following that pyramidal cell (Figure 1e). This is consistent with the experimental results that excitatory postsynaptic currents (EPSCs) and inhibitory postsynaptic currents (IPSCs) in pyramidal cells are phase-locked to the ripples, and IPSCs follow EPSCs [38]. The remaining 22 pyramidal cells are axonally linked to the other pyramidal cells via gap junctions. The proximal collaterals are stimulated by a current injection of 0.042 nA for 3 ms.

Suppression of calcium influx

Before proceeding with the results, we want to mention that in all simulation results, spikes or spikelets mean somatic spikes or spikelets (shown in Figures’ spike raster). Reduction in calcium influx weakens the strength of chemical synapses in pyramidal cells (Figure 2a). Due to these weaker synapses, the targeted cells fire with a time delay or cannot produce complete spikes (Figure 2b) at all. Reduction in calcium influx by 50% causes a 1.8 ms delay in the spike generation of PC no. 1 (Figure 2b). Consequently, the second SPW-R appears ~40 ms later than in the normal network (Figure 2d and 2e). A further decrease in calcium influx (30% of the normal calcium influx) results in an even longer delay in firing of PC no. 1, which now fires 3.86 ms later as compared to normal calcium influx. Similarly, there is a marked delay of ~420 ms in the appearance of the second SPW-Rs (Figure 2d and 2f). In the next step, calcium is completely suppressed, PC no. 1 does not produce any spike, however, spikelets are generated (Figure 2b & 2gspike raster) and PC no. 2 does not generate even any spikelet (Figure 2g spike raster). In addition, it decreases the amplitude and the number of ripples. The duration and the incidence of sharp waves are also decreased (Figure 2c). Moreover, in this paradigm, the network does not produce a second SPW-R (Figure 2g). The number of SPW-Rs in the network simulations is 4, 3, 2 and 1 at 100%, 50%, 30% and 0% calcium influx, respectively (Figure 2d-g also Figure 4c) in 650 ms.

Reduction in gap junction conductance

In another series of simulations, we studied effects of variations in gap junction conductance on network oscillations. As we mentioned earlier, when a proximal collateral is stimulated it generates an action potential in collateral. All other proximal collaterals of the network fire action potentials synchronously within 0.5 to 1 ms (Figure 3a). We observe that a reduction in electrical conductance through gap junctions reduces the synchronous activity of proximal collaterals of pyramidal cells (Figure 3b, 3c). Partial or full reduction in conductance through gap junction in proximal collaterals disturbs the temporal correlation among axonal and AIS inputs. Consequently, it weakens the strength of synapses (Figure 3d) because of inadequate proximal collateral input. This weakened synaptic strength during partial reduction causes 1.62 ms delay in PC no. 1 compared to a normal network with normal gap junction conductance (Figure 3e). PC no. 0 also generates a spike with a time delay of 1.1 ms with partial conductance (half blocked gap junction). Moreover, the number of spikelets also decreases in this scenario (Figure 3h, 3i spike raster). Consequently, the second SPW-Rs with partial conductance appears ~182 ms (Figure 3h) later than the respective SPW-Rs in a normal network (Figure 3g). PC no. 1 produces only one spikelet during complete gap junction blockage (Figure 3c, 3e), and PC no. 0 produces a spike with a delay of 2.3 ms and generates even fewer spikelets (one) than the normal GJ network (four spikelets) (Figure 3g and 3i raster plot). Proximal collaterals produce temporally unsynchronized action potentials during the complete gap junction blockage (Figure 3c). These sparse proximal collaterals’ spikes don’t make temporal coordination with somatic synaptic activities and, therefore, PC no. 1 cannot generate an action potential. These sparsely distributed proximal axonal action potentials decrease the amplitude of ripples and produce high frequency jittery pulses (figure 3f).

Figure 3. Effects of reduction in conductance through gap junctions (GJ) on SPW-Rs. (a) Proximal collaterals (green) of the first ten PCs with normal conductance generate synchronous action potentials, which are temporally coherent to AIS (blue) and somatic input (red) of PC no. 1. (b) Partial conductance through gap junctions leads to a decreased synchronous activity of the proximal collaterals, which also decreases the temporal correlation between somatic, AIS, and axonal inputs. Therefore, PC no. 1 produces only two spikelets after a spike (red), in contrast to four spikes with normal conductance. (c) Proximal collaterals exhibit a sparse firing activity with fully blocked gap junctions. AIS and axonal input do not correlate enough to reach the threshold, hence, the soma of PC no. 1 produce only one spikelet. (d) Synapse no. 1 looses its strength with gap junction blockage and causes a delay in the next SPW-Rs generation. (e) The firing behavior of PC no. 1 during normal conductance, partial and complete GJ blockage. The cell produces a spike with delay and only two post-spikelets with partial conductance, and it does not produce any spike but only one spikelet at all with complete GJ blockage. (f) The local field potentials (LFP) with partial and full GJ blockage exhibit ripples with small amplitude because of unsynchronized proximal collateral action potentials. (g-i) LFPs (left) and spike raster of first three PCs (right thick and dark ones are spikes and thin ones are spikelets) with normal, partial, and complete gap junction blockage in the pyramidal cells. Partial and complete GJ blockages also decrease the number of spikes and spikelets during SPW-Rs

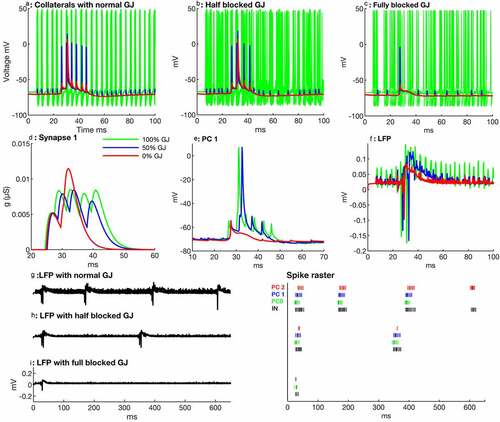
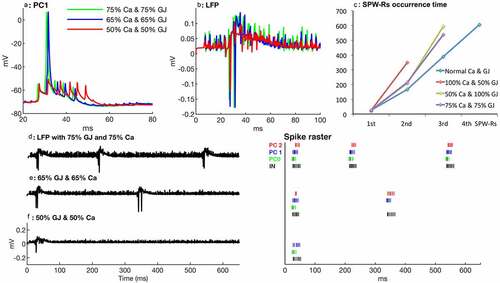
Figure 4. Synergistic effects of calcium and gap junction blockage. (a) PC no. 1 shows a spike delay with 65% calcium influx and 65% gap junction conductance (blue) as well as with 50% calcium and 50% gap junction blockage (red). (b) Partial blockage of gap junction conductance (50%) and calcium influx (50%) affects the number of ripples and their amplitude (red). (c) First, second, and so forth SPW-Rs occurrence time with different level of calcium and gap junction conductances. (d-f) LFPs (left) and spike raster (right) with 25% suppression of Ca and 25% blocked GJ (d) 35% suppression of Ca and 35% blocked GJ (e) and 50% blockage of both Ca and GJ (f). Note that during 650 ms, the network doesn’t generate a second SPW-R and PC no. 2 does not produce any spike or spikelet during a 50% simultaneous reduction of calcium influx and gap junctions’ conductance

Synergistic effects of reduction in calcium influx and gap junction conductance

According to the above results, the suppression of calcium influx or electrical conductance through gap junctions in pyramidal cells suppresses SPW-Rs. Calcium suppression decreases the strength of synapses, whereas the blockage of gap junctions decreases the synchronized activities of proximal collaterals. Weak coordination between proximal collaterals and AIS input also weakens the strength of synapses. In set of simulations, we investigated the combined effects of gradually reduced calcium influx and gap junction conductance on SPW-Rs. The simulation with 75% Ca and 75% GJ conductance shows approximately the same results as with 50% Ca suppression (Figs. 2E and Figs. 4d). Three SPW-Rs occur at time 27 ms, 216 ms, and 539 ms, respectively. In another simulation with simultaneous 65% Ca and GJ conductance, the network generates only two SPW-Rs (Figure 4e), the first at time 27 ms and 2^nd at 341 ms after the start of the simulation.

With simultaneous 50% suppression of Ca influx and gap junction blockage, PC no. 1 generates only spikelets and not, a spike, conversely it produces a complete spike in individual partial suppression of Ca (Figure 2b) or gap junction blockage (Figure 3e). Disturbance in synchronized proximal collateral activity and weakness in synaptic strength are further increased resulting in a marked delay in spiking and decrease in the number of spikelets of PC no. 0 and 1. PC no. 2 does not produce even any spikelet (figure 4f spike raster plot). However, amplitude and incidence of the ripples are similar to the partially blocked gap junction network because of sparse proximal collateral activities. The network does not generate a second SPW-Rs within 650 ms (figure 4f). Interestingly, we observed that 50% blockage of gap junctions together with 50% calcium suppression had a stronger effect on SPW-Rs suppression than the individual effects of 50% Ca influx or gap junction blockage.

Discussion

In this study we demonstrated the modulatory effects of calcium influx and gap junction activation during the expression of sharp-wave ripples in CA1. In our computational model we showed that the expression of SPW-Rs was a calcium dependent process. The number of SPW-Rs decreases with a reduction of calcium influx through pyramidal cells. Interestingly, similar results are obtained when the current is reduced through gap junctions. In another set of simulations, we demonstrated that a reduction in calcium influx and a decreased conductance through gap junctions had synergistic effects on the generation of SPW-Rs in our computational model of CA1.

Neurotransmitters like acetylcholine, norepinephrine, serotonin, etc. suppress SPW-Rs in experimental animals [15,17,18]. These neuromodulators are thought to reduce the calcium influx through presynaptic terminals in Schaffer collaterals [17,39]. This reduction in calcium influx in turn decreases the glutamate release in the synaptic cleft resulting in a decreased firing rate of neurons and eventually affects the network’s fast oscillations. Reduction in calcium influx into the PCs of CA3 and CA1 weakens the contact among neighboring cells by recurrent axonal collaterals [24]. This leads to less synchrony of postsynaptic cells and a suppression of SPW-Rs in CA3 and CA1.

In our model, we gradually reduced the calcium influx through axonal collaterals and dendrites assuming that this decline in calcium influx partially mimics the decrease in presynaptic calcium mediated by various neuromodulators in experimental settings. The decrease in calcium conductance weakens the strength of the synapses of the pyramidal cells. These weak synapses do not provide enough strength to targeted cells to fire in the network. Similarly, with low calcium conductance targeted cells depolarize slowly, which causes a delay in SPW-Rs generation. Furthermore, SPW-Rs disappeared when calcium influx was completely blocked in pyramidal cells in both models of ten cells (data not shown) and 26 cells except for the first sharp wave, which occurs during network stimulation time.

In our computational model we observed that SPW-Rs were also suppressed by reducing the conductance through gap junctions. Moreover, reducing both calcium influx and gap junction coupling had a synergistic effect on the suppression of SPW-Rs. As previously described, excitatory synaptic interaction and electrical signaling through gap junctions coordinate ripple activities [26,40]. Thus, these ripples are inhibited by blocking gap junctions [24,39]. Interestingly, monoamines like norepinephrine, serotonin and dopamine reduce the gap junction coupling mainly by two different signaling mechanisms, i.e. through the IP3/Ca²⁺/protein kinase C pathway and the adenylyl cyclase/cAMP/protein kinase A pathway [41–43]. In addition, cholinergic input also reduces gap junction coupling [44]. In a recent publication from Buzsaki’s lab, Fernández-Ruiz and colleagues showed that SPW-Rs were prolonged during learning processes, and these prolonged ripples recruit new neurons [45]. This finding opens a new window for a modulation of the temporal structure of SPW-Rs and its implication for learning, both experimentally and theoretically.

Conclusion

From these observations and findings we conclude that a sudden switching of behavioral dependent oscillatory patterns of the hippocampal neurons partially depends on the combined effects of decreased calcium influx and reduced gap junction coupling along with possible postsynaptic mechanisms like an imbalance of depolarization and hyperpolarization, mainly caused by increased cholinergic input.

Research highlights

• Sharp-wave ripples may occur by summation of electrical coupling among CA1 cells and synaptic inputs of place cells.

• Sharp-wave ripples may be suppressed by reduction in calcium influx.

• Weak electrical coupling between place cells may weaken SPW-Rs activities.

Combined reduction of calcium influx and electrical coupling has strong suppressive effect on SPW-Rs.

Disclosure of potential conflicts of interest

No potential conflict of interest was reported by the author(s).

Acknowledgements

The authors are grateful to Professor Dr. Uwe Heinemann (late) for his help in designing this project. This work was supported by the US-German Collaboration in Computational Neuroscience (NSF/BMBF grant 01GQ1706).

Additional information

Funding

This work was supported by the Bundesministerium für Bildung und Forschung under grant number [01GQ1706].