Multiple-stage strain hardening due to the deformation-induced martensitic transformation in additively manufactured high-entropy alloy

Abstract

This study investigates microstructural changes and the presence of multiple stages in strain hardening ratio (SHR) resulting from the sequential occurrence of deformation-induced martensitic transformation (DIMT) during the tensile deformation of an additively manufactured ferrous medium entropy alloy (AMed-FeMEA). The inherent microstructural heterogeneity in AMed-alloys contributes to distinctive deformation mechanisms and instantaneous hardening behavior at varying strain levels. To comprehensively address this phenomenon, a semi-empirical constitutive model is presented that associates multiple stages in SHR with the occurrence rate of DIMT. The model demonstrates its applicability by characterizing tensile deformation of AMed-FeMEA at both room temperature and liquid nitrogen temperature.

GRAPHICAL ABSTRACT

KEYWORDS:

• High/Medium entropy alloys
• additive manufacturing
• deformation-induced martensitic transformation
• multiple strain hardening behavior
• constitutive model

Introduction

A constitutive model describes the response of a specific material to applied loads, which arises from the internal constitution of the material [1,2]. This is essential as a material property for solving boundary value problems in solid mechanics and for achieving optimized part performance in the material design process. Among mechanical properties, plastic behavior can be represented as the stress—strain (σ-ε) relationship and strain hardening ratio (SHR, dσ/dε). In ductile materials, necking occurs when the stress equals the SHR so that an accurate prediction of this critical moment is necessary for their application as structural materials. However, describing SHR during straining is more challenging than the stress—strain relationship because it is highly sensitive to the instantaneous deformation mechanism and microstructure evolution.

In recent studies, numerous newly designed alloys demonstrating a remarkable combination of strength and ductility have been proposed [3–7]. These can be achieved by exhibiting multiple stages in SHR from the sequential occurrence of deformation mechanisms, primarily deformation-induced martensitic transformation (DIMT). Furthermore, additively manufactured (AMed) alloys have drawn significant attention due to the distinct deformation mechanisms and mechanical properties compared to conventional cast materials even with the same compositions [8–10]. These differences arise from the highly heterogeneous microstructures that originate from the complex thermal history during the additive manufacturing process [11–14]. However, this complexity and heterogeneity inherent in AMed alloys pose difficulty in precisely characterizing the physical characteristics of these promising structural materials using existing models. Therefore, an accurate and straightforward approach to describing the mechanical properties of these materials, particularly the complex interplay between the SHR, deformation mechanisms, and microstructural evolution is required.

This study aims to propose a semi-empirical constitutive model that comprehensively accounts for the multiple stages in SHR, particularly in the context of DIMT from face-centered cubic (FCC) to body-centered cubic (BCC) phases. The microstructural changes and mechanical behaviors of AMed-ferrous medium entropy alloy (FeMEA, Fe₆₅Ni₁₅Co₈Mn₈Ti₃Si (at%)) are investigated at different strain levels during tensile deformation at both room temperature (RT) and liquid nitrogen temperature (LNT, 77 K). Characterized by a highly heterogeneous microstructure, this alloy exhibits complex variability in SHR influenced by various deformation mechanisms, with DIMT as the predominant contributor. Consequently, the proposed modeling approach demonstrates its ability to simultaneously and accurately characterize the microstructural changes and the multiple stages in SHR observed in the AMed-FeMEA.

Materials and methods

The material stress σ is expressed using a composite-like model, as: (1) $\sigma =(1-f){\sigma }_{\text{FCC}}+f{\sigma }_{\text{BCC}},$(1) where σ_FCC, and σ_BCC are the local stresses of the FCC phase, and BCC phase, respectively, and f is the BCC phase fraction [15]. The flow stress of each constituent phase (FCC and BCC phases) deformed through dislocation glide [16–20] is described in detail in the Supplementary file—Section 1. The strain partitioning between two phases with different phase stresses is considered using the iso-work assumption [21], as: (2) ${\sigma }_{\text{FCC}}\text{d}{\epsilon }_{\text{FCC}}={\sigma }_{\text{BCC}}\text{d}{\epsilon }_{\text{BCC}},$(2) where dε_FCC and dε_BCC are the strain increments of each phase. This assumption allows both phases to undergo equal-work during deformation and different phase strain evolution according to the ratio of phase stresses. Thus, SHR (dσ/dε) can be expressed as: (3) $\begin{array}{rl}\frac{\text{d}\sigma }{\text{d}\epsilon }& =(1-f)\frac{\text{d}{\sigma }_{\text{FCC}}}{\text{d}{\epsilon }_{\text{FCC}}}\frac{\text{d}{\epsilon }_{\text{FCC}}}{\text{d}\epsilon }+f\frac{\text{d}{\sigma }_{\text{BCC}}}{\text{d}{\epsilon }_{\text{BCC}}}\frac{\text{d}{\epsilon }_{\text{BCC}}}{\mathrm{d\epsilon }}\\ & +\frac{\text{d}f}{\text{d}\epsilon }({\sigma }_{\text{BCC}}-{\sigma }_{\text{FCC}}).\end{array}$(3) The increase in SHR owing to DIMT can be determined from the third term of Equation (3), i.e. the rate of DIM evolution (df/dε) and the stress difference between the transformed and the parent phases (σ_BCC–σ_FCC). Assuming insignificant changes in the latter for short strain differences [22,23], the increase in SHR can be attributed to a rapid evolution of DIM. This high sensitivity of SHR to microstructural evolution elucidates the multiple stages in SHR due to instantaneous deformation mechanisms [24]. When df/dε is zero, the right-hand side of Equation (3) corresponds to the SHR for a single-phase material (f = 0 or 1) or dual-phase material (0 < f < 1) having phase fraction unchanged during deformation.

To represent the rate of DIM evolution (df/dε), this study employs the summation of one or more normal distribution functions, which can more flexibly represent the enhancement in SHR through morphological factors. The rate of DIM evolution can be expressed as follows: (4) $\begin{array}{r}{\left(\frac{\text{d}f}{\text{d}\overline{\epsilon }}\right)}_{\text{a}}=f_{\text{max}.\text{a}}\times \frac{1}{\sqrt{2\pi {\sigma }_{\text{dev}.\text{a}}^2}}\text{exp}\left(-\frac{{(\overline{\epsilon }-{\mu }_{\text{a}})}^2}{2{\sigma }_{\text{dev}.\text{a}}^2}\right),\end{array}$(4) where the subscript ‘a’ represents the number of each df/dε (a = 1, 2, 3, …), f_max is the maximum saturation value of DIM (less than one), $\overline{\epsilon }$ is the equivalent plastic strain, ${\sigma }_{\text{dev}}^2$ is the square of the standard deviation in df/dε, μ is $\overline{\epsilon }$ at the maximum df/dε, and f₀ is a thermally-induced martensitic fraction. Each ‘a’ can be considered with respect to the DIM phase nucleation sites (microstructural approach) or strain values (empirical approach) for the enhancement in SHR [3–7]. After considering the rate of DIM evolution of each ‘a’, the resultant DIM fraction can be represented as $f=\sum _{\text{a}}{f}_{\text{a}}$. When ‘a’ equals one, the DIM fraction follows a sigmoidal form cumulative distribution function, similar to the popular existing model, e.g. the Olson-Cohen model [25].

The proposed modeling method was applied to simulate the microstructural change and mechanical behavior of AMed-FeMEA, with a nominal composition of Fe₆₅Ni₁₅Co₈Mn₈Ti₃Si (at%) fabricated through a direct energy deposition process [26]. Initial sample microstructures were analyzed for phase distribution and elemental composition distribution using electron-backscattering diffraction (EBSD) analyzes and energy dispersive spectrometer (EDS) analyzes, respectively. Uniaxial tensile tests were performed at both RT and LNT, perpendicular to the building direction with a constant strain rate of 10⁻³ s⁻¹. All the numerical analyzes were performed using the commercial FEM software ABAQUS 2021. A fortran-based user subroutine (UMAT) was employed to calculate the stress and strain increments of each phase and the microstructural evolution of the modeled alloy. Detailed experimental procedures, including specimen processing, microstructural analysis, and numerical simulations can be found in the Supplementary file—Sections 2 and 3. The parameters used for the equations of DIM evolution are presented in Table 1.

Table 1. Numerical parameters used for the DIMT evolution for uniaxial tensile deformation under RT and LNT.

	${\sigma }_{\text{dev}.}^2$	μ	fmax
RT	0.0050	0.17	0.600
LNT1	0.0005	0.05	0.150
LNT2	0.0020	0.15	0.350
LNT3	0.0010	0.23	0.120

Results and discussion

Figure 1(a) represents the initial microstructure of the additively-manufactured ferrous-medium entropy alloy (AMed-FeMEA), as analyzed from the EBSD phase map. The average FCC grain size in this area, calculated using individual grain diameters and area fractions is 47.2 µm. The as-printed microstructure exhibits significant spatial heterogeneity, featuring regions characterized by fully FCC grains (Figure 1(b)) and regions with a mixture of FCC and BCC grains (Figure 1(c)). This heterogeneity arises from the complex thermal cycles during the layer-by-layer building process, leading to a heterogeneous distribution of thermally-induced martensitic transformation. Figure 1(b,c) show the elemental composition distributions of each region analyzed by EDS at higher magnification, alongside the EBSD phase maps. Both regions exhibit compositional differences within the nanoscale cellular structure due to the elemental segregation in AMed-alloys: the interior of the cellular structure has higher concentrations of Fe, a BCC stabilizer element reducing the free energy difference between the FCC and BCC phases (ΔG^FCC→BCC) [11,27]. Notably, Figure 1(c) demonstrates more pronounced elemental segregation than Figure 1(b), attributed to the diffusion process of solute elements during thermally-induced martensitic transformation [28]. The thermally-induced martensite (TIM) grains shown in Figure 1(c) exhibit equiaxed morphologies with an average grain size of 1.33 µm.

Figure 1. Initial microstructure of AMed-FeMEA with dual-type regions. (a) EBSD phase map, and (b,c) EBSD phase map and EDS analysis for elemental composition distribution in each region of interest; (b) FCC phase grain, and (c) a mixture of FCC and BCC phases.

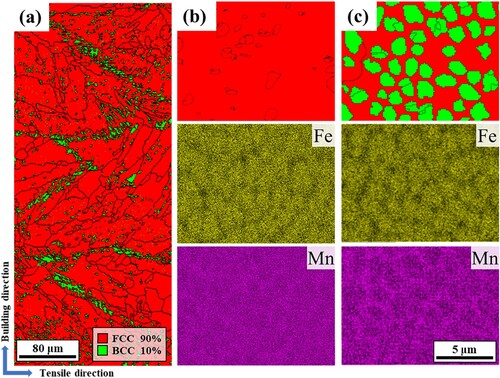
Figure 2 presents the EBSD phase maps and FCC grain inverse pole figure (IPF) maps of the deformed microstructure at local strains of 0.1 and 0.3 after tensile testing at room temperature (RT). In Figure 2(a,b), the BCC phases exhibit semi-equiaxial morphology with average grain sizes of 1.61 and 1.99 µm, respectively. A differentiated feature from homogeneous cast alloys is that grain boundaries or the intersection of shear bands are not favorable regions for deformation-induced martensitic transformation (DIMT) [25,29]. In this modeled alloy, most of the martensitic transformation predominantly occurs within the highly metastable interior of the cellular structures due to elemental segregation [8,11]. This preference is attributed to the higher Fe composition and significantly reduced ΔG^FCC→BCC. At high strain levels, the DIM phase nucleates at the phase boundary between the pre-existing BCC grains and the FCC matrix, eventually growing into the FCC matrix, as shown in Figure 2(b). Consequently, this AMed-FeMEA exhibits more pronounced DIMT with a BCC fraction exceeding 60% compared to the cast alloy deformed under the same conditions with a BCC fraction of 12% [30].

Figure 2. EBSD phase maps and FCC grain IPF maps of AMed-FeMEA at local strains of (a) 0.1 and (b) 0.3 after uniaxial tensile tests at RT.

Figure 3(a,b) show the EBSD phase maps corresponding to strains of 0.1 and 0.3, respectively, after tensile tests at liquid nitrogen temperature (LNT). Due to the lower phase metastability at cryogenic temperatures, the BCC fraction is higher than at the same strain level when deformed at RT. However, Figure 3(a,b) also demonstrate that the preferential nucleation sites of the DIM phase follow a pattern observed at RT. The elongated BCC grains indicated by the white arrow shown in Figure 3(a) originate from the morphological texture of cellular structures with columnar shapes growing in the thermal gradient direction [12]. Figure 3(c,d) show the grain orientation spread (GOS) value distribution graphs of BCC grains obtained from Figure 3(a,b), respectively. The GOS value indicates the average misorientation degree within a grain, where larger values represent severe lattice distortion (pre-existing grains) and lower values represent a more uniform strain distribution within the grain (newly formed DIM phases) [31]. Excluding the initial TIM fraction, which accounts for 10% of the total microstructure, a single normal distribution of GOS values is shown in Figure 3(c). Conversely, Figure 3(d) illustrates a bimodal distribution of GOS values, indicating the sequential occurrence of DIMT that actively nucleated at different strain levels, rather than a continuous process. The peaks delineating higher and lower GOS values correspond to the DIM grains emerged during the early strain levels (within the highly metastable region, i.e. the interior of cellular structures) and the later strain levels (along phase boundaries between existing BCC/FCC phases, advancing towards the FCC grain interior). The GOS map in a high magnification image for a more detailed strain level is highlighted in Figure S3.

Figure 3. EBSD phase maps of AMed-FeMEA at local strains of (a) 0.1 and (b) 0.3 after uniaxial tensile tests at LNT. (c,d) GOS value distribution of BCC grains shown in (a) and (b), respectively.

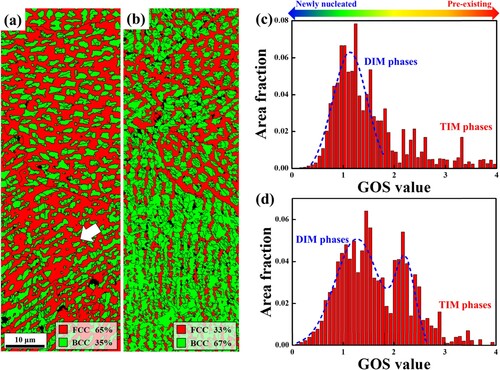
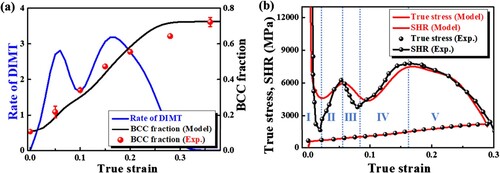
Figure 4 demonstrates good agreement between experimental and numerical results for microstructural evolution and mechanical behavior at RT. The equivalent plastic strain at the maximum DIMT rate (μ) is found to be 0.17, considering the influence of DIMT occurrence rate (df/dε) on the increase in strain hardening ratio (SHR). The normal distribution function allows for a direct adaptation of their increasing rate by associating the height, width, and location of the SHR curve increase with each parameter (f_max, ${\sigma }_{\text{dev}}^2$ and μ) of the DIMT rate for each origin. The multiple stages of SHR in Figure 4(b) can be divided into three stages: (I) a rapid drop, characteristic of elastoplastic materials, (II) a monotonic increase until strain about 0.17, and (III) a slow decrease until necking (dσ/dε = σ). Despite the highly heterogeneous initial microstructure, the DIMT occurrences in the macroscopic aspect at RT are rather simultaneous, superimposed, and monotonically increasing. This allows the DIMT evolution and associated mechanical behavior of the presented AMed-FeMEA at RT to be modeled using only a single-origin DIMT model, i.e. a = 1 at Equation (4).

Figure 4. Comparison in (a) martensitic fraction evolution and (b) true stress and SHR vs. true strain curves with experimental data during uniaxial tensile deformation at RT.

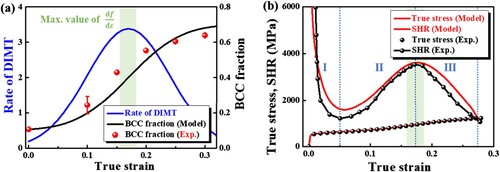
Figure 5 demonstrates that the proposed modeling approach can reasonably describe both the DIM fraction and mechanical properties under LNT, despite the complex variability. In contrast to RT, the rate of DIMT is determined to follow a bimodal distribution following the GOS values shown in Figure 3(c,d). The stages of SHR at LNT start with Stage (I) showing a drastic decrease, similar to RT. Around a strain level of 0.05, there is a rapid increase followed by a subsequent decrease in the SHR, corresponding to Stages (II-III). The Stage (II) is facilitated by the activation of DIMT within the highly metastable interior part of the cellular structure at the early strain levels, where the SHR and DIM fraction increase much faster at LNT compared to RT due to the severe conditions that further lower the phase stability. Meanwhile, the formation of DIM grains within the parent FCC matrix reduces the dislocation mean free math [32]. Additionally, the pre-existing high dislocation density from the cellular structure is further increased due to strain misfit during DIMT [33]. This reduced dislocation mobility slows down DIMT by requiring higher stress for further DIMT, resulting in the downward slope observed in Stage (III).

Figure 5. Comparison of (a) martensitic fraction evolution and (b) true stress and SHR vs. true strain curves with experimental data during uniaxial tensile deformation at LNT.

However, the entangled dislocation density in the DED-processed sample is not too high to strictly impede dislocation slip across the boundaries [34,35]. Moreover, because DIMT is a dislocation-mediated process, regions of high dislocation density around the existing BCC phases become preferential sites for DIMT as deformation progresses after Stage (III) [36]. Consequently, new DIM phases continuously nucleate at the phase boundaries between the previously formed BCC phase and the FCC matrix and grow towards the interior of the FCC grains during Stages (IV-V). Since the SHR at these stages has an asymmetric shape extending further towards the right side, the rate of DIMT occurrence can be represented by a superposition of two different origins, i.e. LNT₂ and LNT₃ shown in Table 1. At the end of Stage (V), the SHR quickly drops to negative after necking.

Despite the lower phase metastability at LNT, there is not a significant quantitative difference in DIM fraction at the same strain level between RT and LNT. However, the proposed modeling approach, which adapts the rate of DIMT based on the numerical expression of SHR and microstructural analysis, effectively captures the microstructural evolution and mechanical behavior at both RT and LNT. These findings confirm that it can provide a precise description of the multiple stages in SHR originating from the sequential and non-simultaneous occurrence of DIMT in a highly heterogeneous microstructure. A comparative table of previous constitutive modeling approaches for DIMT materials [15,25,37–43] can be found in Table S2.

Conclusion

In this study, a semi-empirical constitutive model for multiple stages of strain hardening ratio (SHR) is proposed in accordance with the rate of deformation-induced martensitic transformation (DIMT). The heterogeneity of microstructural metastability in additively manufactured ferrous-medium entropy alloy (AMed-FeMEA, Fe₆₅Ni₁₅Co₈Mn₈Ti₃Si (at%)) exhibits multiple stages in SHR, originating from the sequential occurrence of DIMT during tensile deformation. Comparisons between the model and experimental data for the mechanical properties and DIM fraction of AMed-FeMEA at both room temperature and liquid nitrogen temperature are in good agreement. It reveals that the proposed modeling approach is particularly capable of representing the complex variability of multiple-stage SHR through its close relationship with the microstructural change. Finally, it is expected to contribute to a material design strategy for designing the optimized heterogeneity of microstructural metastability to achieve target mechanical properties by controlling the rate of DIM evolution.

Data availability

The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.

Additional information

Funding

This study was financially supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIP) (NRF-2021R1A2C3006662). Dr. Farahnaz Haftlang is supported by Brain Pool Program through the NRF funded by the Ministry of Science and ICT (2020H1D3A1A04105882). Yeon Taek Choi was supported by the Basic Science Research Program ‘Fostering the Next Generation of Researcher’ through the NRF funded by the Ministry of Education (2022R1A6A3A13073824).