Defining Program Effects: A Distribution-Based Perspective

ABSTRACT

In an age of accountability, it is critical to define and estimate the effects of teacher education and professional development programs on student learning in ways that allow stakeholders to explore potential reasons for what is observed and to enhance program quality and fidelity. Across the suite of statistical models used for program evaluation, researchers consistently measure program effectiveness using the coefficients of fixed program effects. We propose that program effects are best characterized not as a single effect to be estimated, but as a distribution of teacher-specific effects. In this article, we first discuss this approach and then describe one way it could be used to define and estimate program effects within a value-added modeling context. Using an example dataset, we demonstrate how program effect estimates can be obtained using the proposed methodology and explain how distributions of these estimates provide additional information and insights about programs that are not apparent when only looking at average effects. By examining distributions of teacher-specific effects as proposed, researchers have the opportunity to more deeply investigate and understand the effects of programs on student success.

KEYWORDS:

• Education
• Professional development
• Student achievement
• Teacher effects

1. Introduction

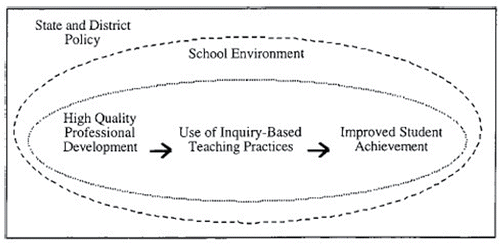
Ongoing policy, research, and funding initiatives continue to focus on improving the quality of education for grades K–12 students and beyond, thereby drawing attention to teacher education and professional development programs. A common goal of such programs is to improve student learning by providing teachers opportunities for learning, support, and advancement of content knowledge, instructional practices, and self-efficacy. The underlying assumption is that through teacher preparation and development, student learning outcomes will improve. This chain of logic, as depicted in Figure 1 and described by Supovitz and Turner (2000) suggests “high quality professional development will produce superior teaching in classrooms, which will, in turn, translate into higher levels of student achievement. School environments, as well as district and state policies, are powerful mediators of this sequence” (p. 965). However, to provide evidence for the extent to which professional development programs generate this chain to success, it is crucial to investigate and document the relationship between professional development and student achievement.

Figure 1. Model depicting theoretical relationship between professional development and student achievement. Reprinted from “The Effects of Professional Development on Science Teaching Practices and Classroom Culture,” by J. A. Supovitz and H. M. Turner, 2000, Journal of Research in Science Teaching, 37(9), p. 965. © 2000 John Wiley & Sons, Inc. Adapted with permission.

In this article, we focus on one component of this relationship: improved quality of teaching as measured by gains in student achievement test scores. We offer a new perspective for estimating the effects of professional development programs, also known as “program effects.” In particular, we address the following question: How are program effects understood, defined, and estimated? To date, the majority of studies assess the effects of professional development programs on student achievement by using standard hypothesis testing methodology to estimate fixed treatment effects and obtain p-values. However, we propose that program effects are best characterized not as a single effect to be estimated, but as a distribution of teacher-specific effects. This alternative characterization of program effects requires us to seek modeling approaches and statistical methodology that allow us to obtain such a distribution.

In the following sections, we first summarize current attempts to estimate program effects and then present an alternative approach. This approach can be used with any statistical model that allows the estimation of a distribution of teacher-specific effects. One possible strategy, and the one we demonstrate in this article, uses best linear unbiased prediction within the context of value-added modeling. Although the controversy associated with uses of value-added models (VAMs) has increased with their adoption (American Statistical Association 2014; American Educational Research Association 2015), the public controversy primarily concerns how these models are used for evaluation—especially high-stakes evaluation. Everson (2017) documented several statistical concerns associated with VAMs, but concluded, “The list of reasons not to use VA modeling may be long.… On the other hand, the list of reasons to use any of the alternatives to VA modeling … could well be longer” (p. 62). Therefore, in this article, we suggest that these models provide useful opportunities for exploring relationships between student achievement and instruction, especially within the context of a professional development program. In addition, we provide one example of how our proposed approach might be implemented, how its resulting interpretations of program effects differ from methods that only focus on a fixed treatment effect, and how it provides additional information and enables insights not otherwise available. Overall, the purpose of this demonstration is not to prescribe the design of professional development programs, but to describe in broad terms what information a distribution of changes in teacher effects can provide when investigating program effects. Finally, we conclude with a discussion of these results and propose future research to explore the behavior of program effect estimates when used in the manner described.

2. Estimating Program Effects: Existing and Proposed Methods

In an age of accountability, it is critical to define and estimate the effects of various educational factors on student learning in a manner that allows stakeholders to explore potential reasons for what is observed and to enhance program quality and fidelity (Tatto et al. 2016). When evaluating teacher training programs, Goldhaber (2013) suggested that such estimates should provide opportunities to answer more nuanced questions about the programs themselves and what features “quality” programs possess. This also applies to teacher education more broadly at both the preservice and the in-service level. In particular, research in teacher education and professional development should go beyond “answer[ing] ‘yes’ or ‘no’ regarding its value … [and] tease out the nature of programs and practices that matter most” (Sleeter 2014, p. 151).

In this section, we first provide a summary of research methods currently used to estimate program effects. Then we describe and provide justification for our proposed approach.

2.1. Existing Methods for Estimating Program Effects

Across the suite of statistical models used to estimate the effects of professional development programs on student achievement, researchers consistently measure program effectiveness using the coefficients of fixed program effects. In these studies, researchers often define a program effect as a single parameter or set of parameters. For instance, some researchers use classification or indicator variables to specify teachers’ (or schools’) participation or nonparticipation in a program (e.g., Dimitrov 2009; La Paz et al. 2011; Penuel, Gallagher, and Moorthy 2011; Barrett, Butler, and Toma 2012; Johnson and Fargo 2014), and some use covariates to account for the amount of time or number of activities a teacher has completed for professional development (e.g., Harris and Sass 2011; Foster, Toma, and Troske 2013).

In these cases, most researchers use measures of student achievement or gain to estimate program effects, but some use alternative responses, such as estimated teacher effects. For example, Goldhaber, Liddle, and Theobald (2013) estimated the fixed effects of teachers on student achievement in math and reading and then modeled those estimated teacher effects as a function of several factors, including teacher training program effects that were allowed to decay with teachers’ increased years of experience. Despite these differences, researchers primarily rely on fixed program effect coefficients to measure program effectiveness. In this way, they are using a single parameter to estimate the simple “average effects” of a program, assuming that professional development programs affect all teachers equally and ignoring additional information provided by the variability in program effects between teachers.

One exception is found in Biancarosa, Bryk, and Dexter’s (2010) longitudinal study to explore the effects of a literacy coaching program. In this study, the researchers collected grades K–2 student scores at the beginning and end of each school year for four years. Because the program was not implemented at the school level until the second year of the study, the first year of data served as a baseline. Modeling these data with a hierarchical, cross-classified value-added model, the researchers compared growth in student scores across time relative to the baseline year. Unlike in other studies, these researchers investigated the effects of the program using fixed program effect coefficients as well as random teacher- and school-level effects for each year of implementation. The fixed program effects allowed them to estimate the average changes in growth rates during each year of implementation relative to baseline growth rates, and the random teacher- and school-level effects for each year allowed them to investigate variation in growth rates among schools and teachers. The fixed effects, in conjunction with the distributions of empirical Bayes estimates for the teacher and school effects at each year of implementation, demonstrated that the effects of the program increased “over time in both size and variability within and between schools” (Biancarosa, Bryk, and Dexter 2010, p. 28). However, even with the additional information provided by the variability in growth rates among schools and teachers relative to the baseline year, the researchers were not able to control for outside initiatives that may have at least partially explained the observed changes in student growth.

Designing educational studies as randomized experiments with a control group helps researchers avoid this type of predicament. By randomly assigning experimental units (teachers, schools, districts, etc.) to treatment (programs) and control groups, researchers are able to make causal statements about the impact of professional development programs. Aligned with calls for the use of experimental and quasi-experimental designs to evaluate professional development (Wayne et al. 2008), more researchers are designing studies in this manner. However, even with the use of randomized control trial designs, most do not look beyond the fixed program effect estimates to determine program impact (e.g., Glazerman et al. 2010; Antoniou and Kyriakides 2011; Carlson, Borman, and Robinson 2011; Heller et al. 2012). Even in studies proposing guidelines for the design of multilevel experiments (Hedges and Borenstein 2014), program effects are measured via the coefficients of the corresponding fixed effects.

2.2. Proposed Method for Estimating Program Effects

Characterizing the distribution of changes in teachers’ effects on student achievement after participating in a professional development program is an alternative approach for estimating the effects of such a program. In this way, program effects are characterized not as a single effect to be estimated, but as a distribution of teacher-specific effects. Consequently, studies can explore program effects at the teacher level, allowing evaluators to ask deeper and more nuanced questions about why certain teachers appear to benefit from professional development and others do not.

Measuring teacher-specific program effects involves the characterization of changes in program participants’ effects on student achievement, as well as the characterization of changes in comparable, nonparticipating teachers’ effects. Therefore, programs need to be able to calculate estimates of teacher effectiveness before a program begins and after a program is in place or ends for both program participants and a comparable group of nonparticipating teachers. This enables programs to compare the changes in teacher-specific effect estimates for program participants to those for nonparticipants, thereby simultaneously accounting for the baseline effect of each participating teacher, as well as the natural year-to-year variability present in teacher effect estimates. Consequently, this approach allows each teacher to serve as his or her own control and helps address the complexities ignored by merely using a single fixed treatment effect to compare participating and nonparticipating teachers; instead of estimating a single value, this approach accounts for the reality that programs affect teachers differently and provides a distribution of program effects (estimated by the change in teacher-specific effect estimates) over teachers.

Approaches to obtaining teacher-specific effects can be characterized broadly into two groups: methods that assume fixed teacher effects, and methods that assume random teacher effects. If teacher effects are treated as fixed, conclusions apply only to teachers on whom data were collected, and no statistically legitimate conclusions may be drawn beyond teachers participating in the study. On the other hand, if the participating teachers comprise a sample of a larger population of teachers who could have participated in the program and the goal is to extend inference beyond the participating teachers, then teacher effects are regarded as random. For example, in professional development programs where the eventual intention is to scale up (e.g., from participants in the project to the entire district), the observed teachers are not the only teachers of interest, but instead represent a larger population of teachers. In those cases, specifying teacher effects as random allows one to indicate the observed teachers represent a sample from a population of teachers to which conclusions can be applied.

In this article, we illustrate the use of our proposed methodology for estimating program effects by presenting one possible approach that uses best linear unbiased prediction within the context of value-added modeling. We acknowledge there are other approaches, such as triple-goal estimation (Louis 1984; Shen and Louis 1998), which may be used to obtain teacher effect estimates. In addition, there is evidence that best linear unbiased prediction may result in “underestimation of the variation in the data, causing standard error estimates biased downward and intervals with undercoverage problems” (Morris 2002, p. 430). However, noting that best linear unbiased prediction is standard practice for inference with random effects in linear mixed model (LMM) theory (Robinson 1991; Raudenbush and Bryk 2002; Stroup 2013), we use it in this example.

3. Estimating Program Effects in a Value-Added Context

Examining program effects through the distribution of changes in teacher-specific effects requires a modeling approach capable of obtaining such a distribution. In addition, programs need longitudinal data on at least two cohorts of students, one before the program begins and a second one after the program is in place. Therefore, to estimate program effects in the manner proposed, researchers need to use statistical methodology that accounts for repeated measurements on multiple cohorts of students.

Even though any statistical model that defines teacher effects as random has the capacity to estimate program effects in the manner proposed, multivariate VAMs in particular provide opportunities to use longitudinal data to estimate the effects of educational factors, such as teachers, schools, or districts (and hence programs) on changes in student achievement (McCaffrey et al. 2003). These models provide flexible methodology and approaches for addressing complexities that arise when exploring relationships between student achievement and instruction over time. For example, multivariate VAMs can account for the complex, cross-classified structure of longitudinal student-level data. By using student scores over multiple years rather than at a single time, VAMs are able to model the dependence structure between student outcomes and control for student-level influences, such as student background or socioeconomic status, as a means of isolating the effects of teachers and other educational factors on changes in achievement (Ballou, Sanders, and Wright 2004). In particular, modeling this dependence structure has been shown to reduce bias associated with the inherent unmeasurable heterogeneity (e.g., nonrandom assignment of students to classrooms) commonly present in longitudinal education data (Lockwood and McCaffrey 2007). In addition, multivariate VAMs can account for variable contributions of both current teachers and past teachers to a student’s set of scores, that is, a student’s achievement at a given time can be linked to the current teacher as well as all previous teachers recorded (McCaffrey et al. 2003, 2004).

These features, among others, are useful when using trajectories of student achievement to estimate teacher effects. In particular, they enable researchers to investigate the effects of programs not only on “mean scores of students, but … also … on variances and robustness … [and explore w]hat methods work well even when they are not implemented under ideal conditions with experienced teachers” (Lohr 2015, p. 15). Therefore, we first provide an overview of VAMs and then present our proposed methodology for estimating program effects within this modeling framework.

3.1. Value-Added Model Overview

Although there are many variations on VAMs, the purpose of this section is to provide an overview of the main features of these models rather than an all-inclusive survey. To develop an initial definition of program effects within this context, we start with an idealized situation in which teachers are nested within a given grade level, students have a well-established baseline, test scores are on a single developmental scale, and there is no student or teacher attrition. Once the initial definitions are clear, these assumptions can be relaxed to accommodate more realistic scenarios.

We start with a version of a VAM that jointly models test scores for a single subject, such as math or reading, over a given time period for a single cohort of students. In this case, a student’s current score can be modeled as the sum of the effects of prior and current-year teachers, as well as the student baseline value indicating a student’s level of performance at the beginning of data collection. Many models include additional elements such as student covariates, but the inclusion of these terms does not change the definition of program effects as presented below.

As described, such VAMs may be specified as (1) $$\begin{array}{c}\hfill y_{ijt}=\eta +\beta X_i+a_j+\sum _{m=1}^t\sum _{s=1}^S{w}_{t-m}{\phi }_{ims}{c}_s+e_{it},\end{array}$$(1) where y_ijt denotes the test score for the ith student in the jth school at the tth time (i.e., the student’s year or grade level in school). Based on this model, the ith student’s score at time t depends on an overall intercept, η, a baseline covariate, a school effect, and the cumulative teacher effects through time t. The baseline covariate is denoted X_i, and β is its regression coefficient. The term a_j denotes the effect of the jth school. We use the model notation c_s to denote the effect of the sth teacher because “teacher effects” merely account for unexplained classroom-level heterogeneity (Lockwood et al. 2007), and it is arguably better to consider them as “classroom effects.” The term ${\phi }_{\text{ims}}$ is an indicator that equals 1 if the ith student was in the sth teacher’s class at time m and 0 otherwise. In this case, we assume each student has only one teacher each year, but ${\phi }_{\text{ims}}$ can be modified to account for a student having multiple teachers in a given year.

The term w_{t − m} is a weight, where t − m denotes the number of years in the past the student had teacher s with respect to the time measurement y_ijt was taken. This weight characterizes persistence: 0 ⩽ w_{t − m} ⩽ 1. A weight of zero indicates the situation where the teacher the student had t − m years ago has no remaining influence on the student’s current performance, whereas a weight of one means the past teacher’s influence on the student’s current performance is undiminished or the same as it was t − m years ago.

Summing over the products $w_{t-m}{\phi }_{\text{ims}}{c}_s$ provides the cumulative effects of all previous and current teachers student i had through time t. For example, when modeling a three-year sequence of scores (e.g., math scores through the 6th, 7th, and 8th grades) in which the ith student at school j had teacher 2 in year 1, teacher 5 in year 2, and teacher 7 in year 3, we obtain the following set of equations: (2) $$\begin{array}{c}\hfill \left[\begin{array}{c}{y}_{ij1}\\ y_{ij2}\\ y_{ij3}\end{array}\right]=\left[\begin{array}{c}\eta +\beta X_i+a_j+w_0{c}_2+e_{i1}\\ \eta +\beta X_i+a_j+w_1{c}_2+w_0{c}_5+e_{i2}\\ \eta +\beta X_i+a_j+w_2{c}_2+w_1{c}_5+w_0{c}_7+e_{i3}\end{array}\right].\end{array}$$(2) This weighting structure is reflective of the variable persistence (VP) model but could be modified to reflect the generalized persistence (GP) model by having teacher-specific weight terms, w_{(t − m)s} (Mariano, McCaffrey, and Lockwood 2010). One prominent value-added model, the SAS^® Educational Value Added Assessment System (EVAAS^®1) multivariate response teacher model (Sanders, Saxton, and Horn 1997; Wright et al. 2010), is a special case in which all w_{t − m} = 1.

Random teacher effects are assumed to be normally distributed with mean zero and cohort-specific variance, that is, c_s ∼ NI(0, σ²_c). In addition, teacher effects are assumed to be independent of the residual errors, e_it. The vector of random residuals for the ith student, denoted ${\mathbf{e}}_i^{\text{'}}=\left[\begin{array}{ccc}{e}_{i1}& e_{i2}& e_{i3}\end{array}\right]$, is assumed to be distributed multivariate normal with mean zero, that is, e_i ∼ NI(0, Σ), where Σ denotes the covariance structure among repeated measurements over time on each student. The residual vectors, e_i, are assumed to be mutually independent. In principle, any valid covariance model that adequately accounts for within student correlation can be used. Many VAMs, including the GP, VP, and EVAAS models, use an unstructured within-student covariance structure. Ballou, Sanders, and Wright (2004) justified using unstructured covariance because it accounts for variables affecting students’ levels of achievement more effectively than noninstructional student-level covariates.

3.2. Extension of a Value-Added Model to Estimate Program Effects

The use of a VAM with the features presented in Section 3.1 can be extended to estimate program effects as proposed in Section 2.2. Traditionally “program effect” refers only to the fixed effect of a program. What we suggest is an alternative understanding of the term “program effect” that is based on the distribution of estimates of the predictable functions defined later in this section. To measure program effectiveness in this way, we need at least two cohorts of students, one before the program begins and a second once the program is in place. This is a minimum requirement for estimation; in practice, studies measuring program effectiveness most likely take place over three or more cohorts. For simplicity, we first illustrate the model with two cohorts and then extend it to three cohorts.

The VAM discussed in Section 3.1, modified to allow the estimation of program effects, is as follows for the two-cohort case. Let y_ijklt denote the test score for the ith student in the jth school and kth cohort with lth program participation status (e.g., l = 0 if the student’s teacher has not been exposed to the professional development program at the time of the class; l = 1 if the student’s teacher has been exposed). As before, t denotes the student’s year or grade. Note that student i in one cohort is not the same as student i in a different cohort. The model is now (3) $$\begin{array}{c}\hfill y_{ijklt}=\eta +\beta X_{ik}+a_j+{\zeta }_k+{\tau }_l+\sum _{m=1}^t\sum _{s=1}^S{w}_{t-m}{\phi }_{ikms}{c}_{skl}+e_{ijkt},\end{array}$$(3) where X_ik is the baseline for the ith student in the kth cohort, a_j is the jth school effect, ζ_k is the cohort effect, τ_l is the fixed effect of program status l, and c_skl denotes the effect of teacher s for cohort k with program status l. As above, φ_ikms is an indicator that equals 1 if student i in cohort k had teacher s in year m and 0 otherwise, and w_{t − m} is a weight characterizing the persistence of past teacher effects on the student’s test score at time t. Unlike students, teacher s refers to the same teacher in both cohorts, but Equation (3(3) $$\begin{array}{c}\hfill y_{ijklt}=\eta +\beta X_{ik}+a_j+{\zeta }_k+{\tau }_l+\sum _{m=1}^t\sum _{s=1}^S{w}_{t-m}{\phi }_{ikms}{c}_{skl}+e_{ijkt},\end{array}$$(3) ) allows one to estimate a separate vector of teacher effects for each cohort and program status combination. In other words, ${\mathbf{c}}_{kl}^{\text{'}}=\left[\begin{array}{cccc}{c}_{1kl}& c_{2kl}& \dots & c_{kl}\end{array}\right]$ is the vector of S^(kl) teacher effects for the kth cohort and lth program status. We assume the vector of all teacher effects is distributed multivariate normal with mean zero and block-diagonal variance-covariance matrix, where multiple effects on the same teacher are allowed to covary, but effects across different teachers are assumed independent. For example, in the two-cohort case, $$\begin{array}{c}\hfill [\begin{array}{c}{c}_{s10}\\ c_{s20}\end{array}]\sim NI([\begin{array}{c}0\\ 0\end{array}],\left[\begin{array}{cc}{\sigma }_{10}^2& {\sigma }_{10,20}\\ {\sigma }_{10,20}& {\sigma }_{20}^2\end{array}\right])\end{array}$$and $$\begin{array}{c}\hfill [\begin{array}{c}{c}_{s10}\\ c_{s21}\end{array}]\sim NI\left([\begin{array}{c}0\\ 0\end{array}],[\begin{array}{cc}{\sigma }_{10}^2& {\sigma }_{10,21}\\ {\sigma }_{10,21}& {\sigma }_{21}^2\end{array}]\right)\end{array}$$for teachers who do not (l = 0) and do (l = 1), respectively, participate in the program for cohort k = 2, and who both do not participate in the program for cohort k = 1. In this case, σ²_kl denotes the variance among the teacher effects for the kth cohort and lth program status. In addition, the vector of residual terms ${\mathbf{e}}_{ij}^{\text{'}}=\left[\begin{array}{cccc}{e}_{ij1}& e_{ij2}& \dots & e_{ijT}\end{array}\right]$ is assumed to be distributed NI(0, Σ).

Based on Equation (3(3) $$\begin{array}{c}\hfill y_{ijklt}=\eta +\beta X_{ik}+a_j+{\zeta }_k+{\tau }_l+\sum _{m=1}^t\sum _{s=1}^S{w}_{t-m}{\phi }_{ikms}{c}_{skl}+e_{ijkt},\end{array}$$(3) ), a teacher’s change from one cohort to the next is defined by the difference between the teacher’s score in Cohort 2, $\eta +\beta {\bar{X}}_{..}+a_j+{\zeta }_2+{\tau }_l+c_{s2l}$, where the value of l depends on whether or not teacher s is a program participant, and the teacher’s score in Cohort 1, $\eta +\beta {\bar{X}}_{..}+a_j+{\zeta }_1+{\tau }_l+c_{s10}$. Thus, the change score for teachers participating in the professional development program is defined by (4) $$\begin{array}{c}\hfill {\zeta }_2-{\zeta }_1+{\tau }_1-{\tau }_0+c_{s21}-c_{s10},\end{array}$$(4) and the change score for nonparticipating teachers is defined by (5) $$\begin{array}{c}\hfill {\zeta }_2-{\zeta }_1+c_{s20}-c_{s10}.\end{array}$$(5) Note that each expression is a linear combination of fixed and random effects, that is, in LMM terminology, a predictable function.

These predictable functions allow us to estimate the change in teacher scores over cohorts, and the means and variances of these changes for participating and nonparticipating teachers can, in turn, be used to detect evidence of program influence on teacher effectiveness. For example, greater positive change among participating teachers relative to change among nonparticipating teachers would suggest the program is achieving positive results. However, focus should not be exclusively on the mean change over teachers; there is not a single program effect. It is also important to pay attention to the variability among teacher-specific change scores, that is, their distribution. This type of distribution allows us to account for the reality that programs affect teachers differently and enables us to investigate more nuanced questions about a program’s effectiveness.

The two-cohort model provides the minimum information needed to estimate teacher-specific change scores. However, the two-cohort case may only show an immediate short-term or temporary effect and little more. For this reason, implementation of professional development programs often takes place over several years and may take on many forms. For example, in one variation, a group of teachers begins participating in cohort 2 (or immediately before cohort 2 but after cohort 1, for example, a summer program between school years), another begins in cohort 3, and so forth. In another variation, all participating teachers begin participation in cohort 2, and then the participating teachers and the nonparticipating control group are followed through at least cohort 3. This then allows one to estimate the initial effect of the program (cohort 2 vs. cohort 1) and longer term effects (e.g., cohort 3 vs. cohort 1).

Regardless of how a program is implemented, we can extend the approach used in the two-cohort case to construct predictable functions to describe changes associated with the program when one^{Figure 2}has three or more cohorts. As in the two-cohort case, let y_ijklt denote the score for the ith student at the jth school in the kth cohort at grade t whose teacher at the time is in program group l. The corresponding model equation is similar to the two-cohort VAM (Equation (3(3) $$\begin{array}{c}\hfill y_{ijklt}=\eta +\beta X_{ik}+a_j+{\zeta }_k+{\tau }_l+\sum _{m=1}^t\sum _{s=1}^S{w}_{t-m}{\phi }_{ikms}{c}_{skl}+e_{ijkt},\end{array}$$(3) )), where the definition of all terms and all assumptions are as before. All cohort-specific teacher scores are also defined as they were in the two-cohort case. The difference is that we now have more teacher-specific change scores. In the two-cohort case, l was either 1 or 0 (in the program or not). However, with more than two cohorts, l may be 1 or 0, or it may have more levels. For example, l could be 0, 1, or 2, where 0 denotes “not participating,” 1 denotes “currently participating,” and 2 denotes “former participant.” Alternatively, 0 could denote “not participating,” 1 denotes “began participation in cohort 2,” and 2 denotes “began participation in cohort 3.” In general, there are several ways to define levels of l, but these levels should be defined in a manner that is consistent with how a program is implemented.

With three or more cohorts of students, one is able to calculate many different change scores. For instance, consider the case in which we specify three levels of l: 0 denotes “not participating,” 1 denotes “currently participating,” and 2 denotes “former participant.” In this situation, if one is interested in the immediate program effect, one subtracts each teacher’s cohort 1 score from the corresponding cohort 2 score. These are computed exactly as in the two-cohort case (Equations (4$$\begin{array}{c}\hfill [\begin{array}{c}{c}_{s10}\\ c_{s20}\end{array}]\sim NI([\begin{array}{c}0\\ 0\end{array}],\left[\begin{array}{cc}{\sigma }_{10}^2& {\sigma }_{10,20}\\ {\sigma }_{10,20}& {\sigma }_{20}^2\end{array}\right])\end{array}$$) and (5$$\begin{array}{c}\hfill [\begin{array}{c}{c}_{s10}\\ c_{s21}\end{array}]\sim NI\left([\begin{array}{c}0\\ 0\end{array}],[\begin{array}{cc}{\sigma }_{10}^2& {\sigma }_{10,21}\\ {\sigma }_{10,21}& {\sigma }_{21}^2\end{array}]\right)\end{array}$$)). On the other hand, if one wants to see if the change from cohort 1 to cohort 2 is maintained through cohort 3, one would subtract the cohort 2 score from the cohort 3 score. For participating teachers who began their participation in cohort 2 and completed before cohort 3, the corresponding teacher-specific change score would be (6) $$\begin{array}{c}\hfill {\zeta }_3-{\zeta }_2+{\tau }_2-{\tau }_1+c_{s32}-c_{s21}.\end{array}$$(6) For nonparticipating teachers, the change score would be (7) $$\begin{array}{c}\hfill {\zeta }_3-{\zeta }_2+c_{s30}-c_{s20}.\end{array}$$(7) For teachers who start the program in cohort 3, the change score for the initial effect of the program would be (8) $$\begin{array}{c}\hfill {\zeta }_3-{\zeta }_2+{\tau }_1-{\tau }_0+c_{s31}-c_{s20}.\end{array}$$(8)

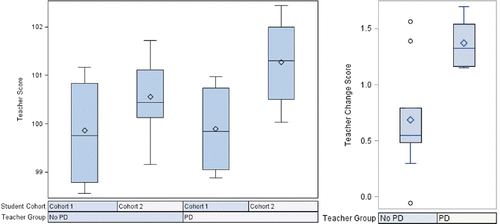
One could then track change scores over cohorts of students for each teacher or for each participant group to obtain a picture of how teacher effectiveness changes over time for participants in the program. An informative way to obtain such a picture is to use a side-by-side box-and-whisker plot to show each program group’s distribution of teacher-specific scores over cohorts. For example, in the two-cohort case, the plot may appear as illustrated in the left panel of Figure 2. One can see that for this example, the distributions of teacher-specific scores are essentially the same for the cohort of students preceding the professional development program, whereas for the cohort of students following the start of professional development, the distribution of teacher-specific scores for the participating teachers has moved well above that of the nonparticipating teachers. As illustrated in the right panel of Figure 2, these differences can also be visualized in a side-by-side box-and-whisker plot of each program group’s teacher-specific change scores. Both plots in Figure 2 suggest evidence of a positive program effect, which then can be followed by formal hypothesis testing or interval estimation. In the case of three or more cohorts, side-by-side plots could aid in visualizing what is happening over time and provide direction regarding what specific comparisons would be of greatest interest.

Figure 2. Hypothetical box-and-whisker plots of teacher-specific scores by student cohort and professional development (PD) teacher group (left) and changes in teacher-specific scores by professional development (PD) teacher group (right).

4. Demonstration

We demonstrate the proposed methodology with an example dataset. The purpose of this demonstration is to show how to implement the model and associated predictable functions of interest and to suggest ways in which this information might be used, not to draw conclusions about the study used in this example. In this section, we first describe the dataset and then highlight results of potential interest.

4.1. Example Dataset

We use middle-school mathematics achievement data from a single school district to demonstrate the proposed methodology with two levels of program status (noncompletion, completion) and three cohorts of students. The dataset, which is provided in the supplementary materials, meets the minimum requirements for estimating program effects. In particular, the dataset includes two essential features: (1) longitudinal data on a baseline cohort of students before teachers have been exposed to the professional development program, and (2) longitudinal data on a second cohort of students taught by the same teachers, a subset of whom have been exposed to the professional development program.

We implement our analysis on eight schools that had at least one teacher who participated in the professional development program. The dataset for these schools contains six consecutive years of grades 5 to 8 student achievement data in mathematics, as well as information linking students’ 6th, 7th, and 8th grade scores to their respective mathematics teachers; no teachers were linked to students’ 5th grade scores. During this time, 97 teachers taught 6th graders, 27 taught 7th graders, and 37 taught 8th graders in mathematics. Our analysis only includes students for which there were complete achievement records and teacher information for grades 6 to 8, as well as a 5th grade score, which was used as a baseline measurement. In cohorts 1, 2, and 3, 1071, 1254, and 1279 students, respectively, had complete records (see Figure 3). In any given cohort, a median number of 20 to 22 students were linked to each teacher.

Figure 3. Visual of how teachers and cohorts of students progressed through time in the example dataset. Each cohort is represented by a different shading, and the striped lines indicate the year when a subset of teachers at a given grade level completed the professional development program.

The dataset provides information about three cohorts of students as they progress through four grades. Figure 3 illustrates this progression through time, with each cohort represented by a different shading. The dataset also identifies which teachers during this span of time completed a professional development program in mathematics. For the first cohort of students, none of their teachers throughout the three years had completed the professional development program, and for the second cohort, seven of their 8th grade teachers had completed it. For the third cohort of students, 12 of their 7th and 8th grade teachers had completed the program. This structure is illustrated in Figure 3, with the striped lines representing the year when a subset of teachers at a given grade level had completed the professional development program. Within a cohort, a teacher’s program status was defined by either their completion or noncompletion of the program.

4.2. Results

The student data were analyzed using ^{Table 1}the value-added modeling approach presented in Section 3.2. The model given in Equation (3(3) $$\begin{array}{c}\hfill y_{ijklt}=\eta +\beta X_{ik}+a_j+{\zeta }_k+{\tau }_l+\sum _{m=1}^t\sum _{s=1}^S{w}_{t-m}{\phi }_{ikms}{c}_{skl}+e_{ijkt},\end{array}$$(3) ) was implemented using SAS HPMIXED to obtain the fixed effect estimates and the solutions to the random teacher effects. The latter were grouped by cohort and professional development (PD) program status, creating five groups: Cohort 1 (in which no teachers had completed any professional development); Cohort 2–no PD completion; Cohort 2–PD completion; Cohort 3–no PD completion; and Cohort 3–PD completion.

Teacher scores were then computed from the fixed effects estimates and random teacher effect solutions. Using the proposed modeling approach, we characterized program effects using predicted teacher-specific scores ($\widehat{\eta }+\widehat{\beta }{\bar{X}}_{..}+{\widehat{a}}_{.}+{\widehat{\zeta }}_k+{\widehat{\tau }}_l+{\widehat{c}}_{skl}$), as well as predicted teacher-specific change scores (e.g., predicted change scores from Cohort 1 to 2 are ${\widehat{\zeta }}_2-{\widehat{\zeta }}_1+{\widehat{\tau }}_1-{\widehat{\tau }}_0+{\widehat{c}}_{s21}-{\widehat{c}}_{s10}$ for teachers who completed the program and ${\widehat{\zeta }}_2-{\widehat{\zeta }}_1+{\widehat{c}}_{s20}-{\widehat{c}}_{s10}$ for teachers who had not). Notice that one can omit effects that are identical for all predictable functions of interest because they add no information relevant to characterizing distributions of scores among teachers. Fixed cohort and program status effects were included in the teacher scores because they do vary, and thus contribute essential information.

Table 1 provides^{Figure 4, Figure 5}estimates of various individual measures of overall program effectiveness, along with their standard errors. In this case, the estimated fixed effect of program status, ${\widehat{\tau }}_1$, is 0.021 with a standard error of 0.023, and the estimated differences between the mean teacher-specific change scores for those who had completed the program and those who had not (“avg pgm effect”) range from 0.020 to 0.044 across the cohort comparisons with relatively large standard errors. Although all of these estimates are positive, none provide statistically significant evidence of program influence on teacher effectiveness.

Table 1. Estimates, standard errors, and 95% intervals for different program effects.

Label	Estimate	SE	Lower	Upper
avg pgm effect, cohort 2 - cohort 1	0.020	0.067	−0.112	0.152
avg pgm effect, cohort 3 - cohort 2	0.044	0.033	−0.021	0.108
avg pgm effect, cohort 3 - cohort 1	0.040	0.042	−0.041	0.122
Fixed effect, τ1	0.021	0.023	−0.023	0.066

To provide additional insights about the program that are not apparent when only looking at average effects, the distributions of teachers’ predicted scores and their predicted change scores can be visualized across the different cohorts of students. For example, Figure 4 allows us to see how the distributions of teachers’ predicted scores compare across the two teacher groups for both the first cohort of students preceding the professional development program and the third cohort of students following the completion of the program. For Cohort 3, the predicted scores for participating teachers are considerably less variable than those for the nonparticipating teachers. Within a single teacher group, we can also see how the distributions of the teachers’ predicted scores change across the student cohorts. For instance, the variability of the participating teachers’ predicted scores decreases from Cohort 1 to Cohort 3. For these two distributions, the minimum predicted scores are similar, but there is a positive shift in the median score, with the median of teachers’ predicted scores after program completion being greater than their median predicted score prior to program completion. The distributions of the predicted change scores from Cohort 1 to Cohort 3 for both participating and nonparticipating teachers are displayed in the third panel in Figure 5.

Figure 4. Box-and-whisker plots of teacher-specific scores by cohort and professional development (PD) teacher group for cohorts 1 and 3.

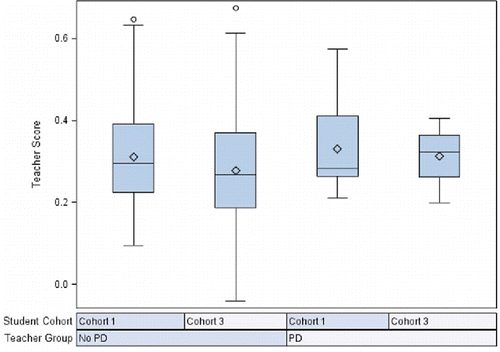
Figure 5. Box-and-whisker plots of teacher-specific change scores by professional development (PD) teacher group for the three comparisons across cohorts of students, from left to right: Cohort 2—Cohort 1 change score, Cohort 3—Cohort 2 change score, and Cohort 3—Cohort 1 change score.

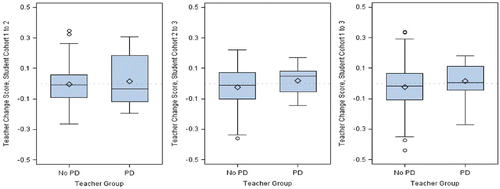
As illustrated by Figure 5, the plots of change scores allow us to visualize the variability in teachers’ predicted change scores, highlighting how programs can affect teachers differently. For example, the second panel in Figure 5 reveals that the predicted scores for at least 1/2 of the teachers who completed the program increased from Cohort 2 to Cohort 3, whereas at least 1/4 of the teachers who completed the program had predicted change scores that were negative. Taken together, these distributions provide an insight into the number of teachers who appear to be deriving some benefit from the program and the number who do not. In contrast, the median change score for teachers who had not completed the program was approximately 0, showing no noticeable shift in the distribution of their scores from Cohort 2 to Cohort 3.

These additional observations introduce a nuanced characterization of program effects that is unavailable when looking solely at average program effects. For instance, this alternative approach shifts focus from “mean program effect” to distribution of change associated with the program. Focusing in this way provides cautionary information not available otherwise: the distribution here appears to suggest that over half of the participant teachers derived some benefit, but not everybody benefited.

With this information, evaluators can examine additional questions to learn how to make the program more effective and/or why it should not be regarded as a one-size-fits-all program. Understanding program effects as a distribution rather than a single fixed effect, or even the difference between the average change for participating and nonparticipating teachers, provides valuable information unavailable when merely focusing on a mean. For example, one could look at covariates or predictors that might help explain variation in the degree to which teachers benefited from a program.

5. Summary and Conclusions

In this article, we propose a definition of program effects that focuses on the variability of such effects among teachers. More precisely, we provide a way of understanding program effects and demonstrate how to use a value-added model to define and estimate these effects. Characterizing the distribution of changes in teachers’ scores after participating in a professional development program allows each teacher to serve as his or her own control and helps address the complexities ignored by merely using fixed treatment effects to compare average gains in student achievement for participating and nonparticipating teachers.

For the purpose of developing an initial definition of program effects, we presented a clean data example that focused on a subset of schools within a district, only included students with complete achievement and teacher link records, defined two levels of program status (completed or not-completed), and used a single prior-grade achievement score as the student baseline. Because best linear unbiased prediction is standard practice for inference on random model effects in LMM theory and methodology (Robinson 1991; Raudenbush and Bryk 2002; Stroup 2013), we used this prediction method to estimate teachers’ scores. Best linear unbiased prediction can distort teaching rankings if class sizes vary across teachers (Tate 2004) and may underestimate the variation in the data (Morris 2002). Other approaches, such as triple-goal estimation (Louis 1984; Shen and Louis 1998) are also available. Future research should explore how variations in methodology, modeling decisions, and violations of model assumptions influence program effect estimates. In particular, studies should address issues related to establishing a “good” student baseline, identifying minimum data requirements, and selecting appropriate measures of student success. Additionally, the proposed methods should be extended for use with a multidimensional VAM (Broatch and Lohr 2012) to simultaneously estimate the effects of a program on student achievement test scores and “real-world” outcomes, such as college entry. By using the multidimensional model in this context, professional development programs would have methodology to more broadly define their effects on student success.

As current and future professional development programs and funding agencies continue to be concerned with program evaluation, it will become increasingly important to carefully consider the ways in which program effects are characterized to inform efforts to scale-up or continue support of successful programs. Statistical methodology provides a quantitative evaluation component; however, it is imperative to use this methodology in ways that connect research, policy, and practice. Estimates of program effects on student achievement should go beyond answering whether or not programs have an effect and provide opportunities to answer more nuanced questions about the programs themselves.

Supplementary Materials

PD demo student data:	Student achievement dataset used for the program effect demonstration discussed in Section 4. See.sas7bdat file.
PD demo teacher data:	Dataset containing teacher program groups used for the program effect demonstration discussed in Section 4. See.sas7bdat file.
SAS program for PD demo:	SAS program with code used to obtain results for the program effect demonstration discussed in Section 4. See.sas file.

Supplemental data for this article can be accessed on the publisher's website.

Acknowledgments

The authors gratefully acknowledge Erin E. Blankenship, Leslie Eastman, Stephen D. Kachman, Wendy M. Smith, and the reviewers of this article for their helpful comments and suggestions.

Additional information

Funding

This work is funded in part by grants from the National Science Foundation, DUE-1050667, DUE-0831835, and DGE-1336265. The findings expressed are those of the authors and not necessarily of NSF.

Notes

1 SAS and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in the USA and other countries. ® indicates USA registration.