Two-sided bounds on the mean vector and covariance matrix in linear stochastically excited vibration systems with application of the differential calculus of norms

Abstract

For a linear stochastic vibration model in state-space form, $\dot{x}(t)=Ax(t)+b(t),x(0)=x_0,$ with system matrix A and white noise excitation $b(t)$, under certain conditions, the solution $x(t)$ is a random vector that can be completely described by its mean vector, $m_x(t):=m_{x(t)}$, and its covariance matrix, $P_x(t):=P_{x(t)}$. If matrix $A$ is asymptotically stable, then $m_x(t)\to 0(t\to \infty )$ and $P_x(t)\to P(t\to \infty )$, where $P$ is a positive (semi-)definite matrix. As the main new points, in this paper, we derive two-sided bounds on $\Vert m_x{(t)\Vert }_2$ and $\Vert P_x{(t)-P\Vert }_2$ as well as formulas for the right norm derivatives $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$, and apply these results to the computation of the best constants in the two-sided bounds. The obtained results are of special interest to applied mathematicians and engineers.

Keywords:

• linear stochastic vibration system excited by white noise
• mean vector
• covariance matrix
• two-sided bounds
• differential calculus of norms

AMS Subject Classifications:

• 34D05
• 34F05
• 65L05

Public Interest Statement

In recent years, the author has developed a differential calculus for norms of vector and matrix functions. More precisely, differentiability properties of these quantities were derived for various vector and matrix norms, and formulas for the pertinent (right-hand, resp. left-hand) derivatives were obtained. These results have been applied to a number of linear and non-linear problems by computing the best constants in two-sided bounds on the solution of the pertinent initial value problems. In the present paper, the application area is extended to stochastically excited vibration systems. Specifically, new two-sided estimates on the mean vector and the co-variance matrix are derived, and the optimal constants in these bounds are computed in a numerical example employing the differential calculus of norms.

1. Introduction

In this paper, linear stochastic vibration models of the form $\dot{x}(t)=Ax(t)+b(t),x(0)=x_0,$ with real system matrix $A$ and white noise excitation $b(t)$ are investigated, in which the initial vector $x_0$ can be completely characterized by its mean vector $m_0$ and its covariance matrix $P_0$. Likewise, the solution $x(t)$, also called response, is a random vector that can be described by its mean vector $m_x(t):=m_{x(t)}$, and its covariance matrix, $P_x(t):=P_{x(t)}$. For asymptotically stable matrices $A$, it is known that $m_x(t)\to 0(t\to \infty )$ and $P_x(t)\to P(t\to \infty )$, where $P$ is a positive (semi-)definite matrix. This leads to the question of the asymptotic behavior of $m_x(t)$ and $P_x(t)-P$. As appropriate norms for the investigation of this problem, the Euclidean norm for $m_x(t)$ and the spectral norm for $P_x(t)-P$ is the respective natural choice; both norms are denoted by ${\Vert ·\Vert }_2$.

The main new points of the paper are

• the determination of two-sided bounds on $\Vert m_x{(t)\Vert }_2$ and $\Vert P_x{(t)-P\Vert }_2$,

• the derivation of formulas for the right norm derivatives $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$, and

• the application of these results to the computation of the best constants in the two-sided bounds.

The paper is structured as follows.

In Section 2, the linear stochastically excited vibration model in state-space form is presented. Then, in Section 3, new two-sided bounds on $\Vert m_x{(t)\Vert }_2$ are determined. In Section 4, preliminary work for two-sided bounds on $\Vert P_x{(t)-P\Vert }_2$ is made that is employed in Section 5 to derive new two-sided bounds on $\Vert P_x{(t)-P\Vert }_2$ itself. In Section 6, the local regularity of $\Vert P_x{(t)-P\Vert }_2$ is studied. In Section 7, as the new result, formulas for the right norm derivatives $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$ are obtained. In Section 8, for the specified data in the stochastically exited model, the differential calculus of norms is applied to compute the best constants in the new two-sided bounds on $\Vert m_x{(t)\Vert }_2$ and $\Vert P_x{(t)-P\Vert }_2$. In Section 9, conclusions are drawn. Finally, in Appendix 1 , more details on some items are given.

2. The linear stochastically excited vibration system

In order to make the paper as far as possible self-contained, we summarize the known facts on linear stochastically excited systems. In the presentation, we follow closely the line of Müller (1976, Sections 9.1 and 9.2).

So, let us depart from the deterministic model in state-space form(1) $$\begin{array}{c}\hfill \dot{x}(t)=Ax(t)+b(t),t\ge 0,x(0)=x_0\end{array}$$(1)

with system matrix $A\in {\mathbb{R}}^{n\times n}$, the state vector $x(t)\in {\mathbb{R}}^n$ and the excitation vector $b(t)\in {\mathbb{R}}^n,t\ge 0$.

Now, we replace the deterministic excitation $b(t)$ by a stochastic excitation in the form of white noise. Thus, $b(t)$ can be completely described by the mean vector $m_b(t)$ and the central correlation matrix $N_b(t,\mathit{\tau })$ with(2) $$\begin{array}{cc}\hfill m_b(t)& =0\hfill \\ \hfill N_b(t,\mathit{\tau })& =Q\mathit{\delta }(t-\mathit{\tau })\hfill \end{array}$$(2)

where $Q=Q_b$ is the $n\times n$intensity matrix of the excitation and $\mathit{\delta }(t-\mathit{\tau })$ the $\mathit{\delta }$-function (more precisely, the $\mathit{\delta }$-functional).

From the central correlation matrix, one obtains for $\mathit{\tau }=t$ the positive semi-definite covariance matrix(3) $$\begin{array}{c}\hfill P_b(t):=N_b(t,t)\end{array}$$(3)

At this point, we mention that the definition of a real positive semi-definite matrix includes its symmetry.

When the excitation is white noise, the deterministic initial value problem (1) can be formally maintained as the theory of linear stochastic differential equations shows. However, the initial state $x_0$ must be introduced as Gaussian random vector,(4) $$\begin{array}{c}\hfill x_0\sim (m_0,P_0)\end{array}$$(4)

which is to be independent of the excitation (2); here, the sign $\sim$ means that the initial state $x_0$ is completely described by its mean vector $m_0$ and its covariance matrix $P_0$. More precisely: $x_0$ is a Gaussian random vector whose density function is completely determined by $m_0$ and $P_0$ alone.

The stochastic response of the system (1) is formally given by(5) $$\begin{array}{c}\hfill x(t)=\mathrm{\Phi }(t)x_0+{\int }_0^t\mathrm{\Phi }(t-\mathit{\tau })b(\mathit{\tau })d\mathit{\tau }\end{array}$$(5)

where besides the fundamental matrix $\mathrm{\Phi }(t)=e^{At}$ and the initial vector $x_0$$-$ a stochastic integral occurs.

It can be shown that the stochastic response $x(t)$ is a non-stationary Gauss-Markov process that can be described by the mean vector $m_x(t):=m_{x(t)}$ and the correlation matrix $N_x(t,\mathit{\tau }):=N_{(x(t),x(\mathit{\tau }))}$. For $\mathit{\tau }=t$, we get the covariance matrix $P_x(t):=P_{x(t)}$.

If the system is asymptotically stable, the properties of first and second order for the stochastic response $x(t)$ we need are given by(6) $$\begin{array}{cc}\hfill m_x(t)& =\mathrm{\Phi }(t)m_0,\hfill \\ \hfill P_x(t)& =\mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)+P\hfill \end{array}$$(6)

where the positive semi-definite $n\times n$ matrix $P$ satisfies the Lyapunov matrix equation$$\begin{array}{c}\hfill AP+P{A}^T+Q=0\end{array}$$

This is a special case of the matrix equation $AX+XB=C$, whose solution can be obtained by a method of Ma (1966). For the special case of diagonalizable matrices $A$ and $B$, this is shortly described in Appendix A.1.

For asymptotically stable matrix $A$, one has ${lim}_{t\to \infty }\mathrm{\Phi }(t)=0$ and thus from (6),(7) $$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{m}_x(t)=0\end{array}$$(7)

and(8) $$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{P}_x(t)=P\end{array}$$(8)

Therefore, it is of interest to investigate the asymptotic behavior of $m_x(t)$ and $P_x(t)-P$. This investigation will be done in the next sections by giving two-sided bounds on both quantities in appropriate norms.

Even though the two-sided bounds on $m_x(t)$ can be obtained by just applying known estimates, they will be stated for the sake of completeness in Section 3.

As opposed to this, the determination of two-sided bounds on $P_x(t)-P$ leads to a new interesting problem and will be solved in two steps described in Sections 4 and 5.

3. Two-sided bounds on $m_x(t)$

According to Equation $(6_1)$, we have$$\begin{array}{c}\hfill m_x(t)=\mathrm{\Phi }(t)m_0,t\ge 0\end{array}$$

From Kohaupt (2006, Theorem 8), one obtains two-sided bounds on $m_x(t)$.

To see this, let $m_0\ne 0$ and ${\Vert ·\Vert }_2$ the Euclidean norm in ${\mathbb{R}}^n$. Then, there exists a constant $X_0>0$ and for every $\mathit{\epsilon }>0$ an constant $X_{1,\mathit{\epsilon }}>0$ such that(9) $$\begin{array}{c}\hfill X_0{e}^{{\mathit{\nu }}_{m_0}[A]t}\le {\Vert m_x(t)\Vert }_2\le X_{1,\mathit{\epsilon }}{e}^{({\mathit{\nu }}_{m_0}[A]+\mathit{\epsilon })t},t\ge 0\end{array}$$(9)

where ${\mathit{\nu }}_{m_0}[A]$ is the spectral abscissa of matrix $A$ with respect to the vector $m_0$ (see Kohaupt 2006, Section 7, p. 146). We mention that often ${\mathit{\nu }}_{m_0}[A]=\mathit{\nu }[A]$, cf. (Kohaupt, 2006, p. 154).

4. Preliminary work for two-sided bounds on $P_x(t)-P$

In this section, we derive two-sided bounds that are of general interest beyond their application in Section 5. Therefore, more general assumptions than needed there will be made. We obtain the following lemma.

Lemma 1

(Two-sided bounds on $\Vert {\mathrm{\Psi }}^{\ast }{C\mathrm{\Psi }\Vert }_2$)Let $C\in {\mathbb{C}}^{n\times n}$ with $C^{\ast }=C$, where $C^{\ast }$ is the adjoint of $C$. Further, let ${\Vert ·\Vert }_2$ be the spectral norm of a matrix.

Then, the two-sided bound(10) $$\begin{array}{c}\hfill c_0{\Vert \mathrm{\Psi }\Vert }_2^2\le \Vert {\mathrm{\Psi }}^{\ast }{C\mathrm{\Psi }\Vert }_2\le c_1{\Vert \mathrm{\Psi }\Vert }_2^2,\mathrm{\Psi }\in {\mathbb{C}}^{n\times m}\end{array}$$(10)

is valid where(11) $$\begin{array}{cc}\hfill c_0& =\underset{{\Vert v\Vert }_2=1}{inf}|(Cv,v)|\hfill \end{array}$$(11) (12) $$\begin{array}{cc}\hfill c_1& =\underset{{\Vert v\Vert }_2=1}{sup}|(Cv,v)|\hfill \end{array}$$(12)

Proof

(i) Decisive tool is the fact that for $A\in {\mathbb{C}}^{n\times n}$ with $A^{\ast }=A$ one has the two representations$$\begin{array}{c}\hfill {\Vert A\Vert }_2=\underset{{\Vert v\Vert }_2=1}{sup}{\Vert Av\Vert }_2=\underset{{\Vert v\Vert }_2=1}{sup}|(Av,v)|\end{array}$$

In the following, this will be applied to ${\mathrm{\Psi }}^{\ast }C\mathrm{\Psi }$.

(ii) Lower bound:

One has$$\begin{array}{cc}\hfill \Vert {\mathrm{\Psi }}^{\ast }{C\mathrm{\Psi }\Vert }_2& =\underset{{\Vert u\Vert }_2=1}{sup}|({\mathrm{\Psi }}^{\ast }C\mathrm{\Psi }u,u)|\hfill \\ \hfill & =\underset{{\Vert u\Vert }_2=1}{sup}|(C\mathrm{\Psi }u,\mathrm{\Psi }u)|\hfill \\ \hfill & =\underset{\genfrac{}{}{0pt}{}{{\Vert u\Vert }_2=1}{\mathrm{\Psi }u\ne 0}}{sup}|(C\frac{\mathrm{\Psi }u}{{\Vert \mathrm{\Psi }u\Vert }_2},\frac{\mathrm{\Psi }u}{{\Vert \mathrm{\Psi }u\Vert }_2}){|\Vert \mathrm{\Psi }u\Vert }_2^2\hfill \\ \hfill & \ge \hfill & \hfill \underset{\genfrac{}{}{0pt}{}{{\Vert u\Vert }_2=1}{\mathrm{\Psi }u\ne 0}}{sup}\underset{{\Vert v\Vert }_2=1}{inf}{|(Cv,v)|\Vert \mathrm{\Psi }u\Vert }_2^2\\ \hfill & =\underset{{\Vert v\Vert }_2=1}{inf}|(Cv,v)|\underset{{\Vert u\Vert }_2=1}{sup}{\Vert \mathrm{\Psi }u\Vert }_2^2\hfill \\ \hfill & =c_0{\Vert \mathrm{\Psi }\Vert }_2^2,\mathrm{\Psi }\ne 0\hfill \end{array}$$

For $\mathrm{\Psi }=0$, this upper bound remains valid.

(iii) Upper bound

Similarly, one obtains$$\begin{array}{c}\hfill \Vert {\mathrm{\Psi }}^{\ast }{C\mathrm{\Psi }\Vert }_2\le c_1{\Vert \mathrm{\Psi }\Vert }_2^2,\mathrm{\Psi }\ne 0\end{array}$$

For $\mathrm{\Psi }=0$, this lower bound remains valid.

Remark

In Lemma 1, it is known that(13) $$\begin{array}{c}\hfill c_1=\underset{{\Vert v\Vert }_2=1}{sup}|(Cv,v)|=\underset{v\ne 0}{sup}\frac{{\Vert Cv\Vert }_2}{{\Vert v\Vert }_2}=\underset{{\Vert v\Vert }_2=1}{sup}{\Vert Cv\Vert }_2={\Vert C\Vert }_2\end{array}$$(13)

where ${\Vert C\Vert }_2>0$ for $C\ne 0$.

Similarly, one can derive a chain of relations for $c_0={inf}_{{\Vert v\Vert }_2=1}|(Cv,v)|$, as the next lemma shows.

Lemma 2

(Chain of relations for $c_0={inf}_{{\Vert v\Vert }_2=1}|(Cv,v)|$)

Let $C\in {\mathbb{C}}^{n\times n}$ with $C^{\ast }=C$.

Then,(14) $$\begin{array}{c}\hfill c_0=\underset{{\Vert v\Vert }_2=1}{inf}|(Cv,v)|=\underset{v\ne 0}{inf}\frac{{\Vert Cv\Vert }_2}{{\Vert v\Vert }_2}=\underset{{\Vert v\Vert }_2=1}{inf}{\Vert Cv\Vert }_2\end{array}$$(14)

Now, let $C$ be additionally regular, let $\Vert ·\Vert$ denote any vector norm as well as the associated sub norm.

Then,(15) $$\begin{array}{c}\hfill {\displaystyle \underset{\Vert v\Vert =1}{inf}\Vert Cv\Vert =\frac{1}{\Vert C^{-1}\Vert }>0}\end{array}$$(15)

this is especially valid also for the spectral norm ${\Vert ·\Vert }_2$.

The proof will be given in Appendix A.2.

5. Two-sided bounds on $P_x(t)-P=\mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)$

In this section, the results of Section 4 are employed to estimate $\Vert P_x{(t)-P\Vert }_2$ above and below by ${\Vert \mathrm{\Phi }(t)\Vert }_2^2$ as well as by $e^{2(\mathit{\nu }[A]+\mathit{\epsilon })t}$ resp. $e^{2\mathit{\nu }[A]t}$ where $\mathit{\nu }[A]$ is the spectral abscissa of matrix $A$. New will be the quadratic asymptotic behavior of $\Vert P_x{(t)-P\Vert }_2$.

We show the following lemma.

Theorem 3

(Two-sided bounds on $P_x(t)-P=\mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)$ based on ${\Vert \mathrm{\Phi }(t)\Vert }_2^2$)

Let $A\in {\mathbb{R}}^{n\times n}$, let $\mathrm{\Phi }(t)=e^{At}$ be the associated fundamental matrix with $\mathrm{\Phi }(0)=E$ where $E$ is the identity matrix. Further, let $P_0,P\in {\mathbb{R}}^{n\times n}$ be the covariance matrices from Section 2.

Then,(16) $$\begin{array}{c}\hfill q_0{\Vert \mathrm{\Phi }(t)\Vert }_2^2\le \Vert P_x{(t)-P\Vert }_2\le q_1{\Vert \mathrm{\Phi }(t)\Vert }_2^2,t\ge 0\end{array}$$(16)

where(17) $$\begin{array}{c}\hfill q_0=\underset{{\Vert v\Vert }_2=1}{inf}|((P_0-P)v,v)|\end{array}$$(17)

and(18) $$\begin{array}{c}\hfill q_1=\underset{{\Vert v\Vert }_2=1}{sup}|((P_0-P)v,v)|=\Vert P_0{-P\Vert }_2\end{array}$$(18)

If $P_0\ne P$, then $q_1>0$. If $P_0-P$ is regular, then(19) $$\begin{array}{c}\hfill q_0=\Vert (P_0-P){{)}^{-1}\Vert }_2^{-1}>0\end{array}$$(19)

Proof

We obtain Theorem 3 by applying Lemmas 1 and 2 with $\mathrm{\Psi }={\mathrm{\Phi }}^{\ast }(t)={\mathrm{\Phi }}^T(t)=e^{A^{T}t}$, ${\mathrm{\Psi }}^{\ast }(t)=\mathrm{\Phi }(t)=e^{At}$ and $C=P_0-P$.

Further, two-sided bounds can be derived by using Kohaupt (2006, Theorem 8). Thus, there is a constant ${\mathit{\phi }}_0>0$ and for every $\mathit{\epsilon }>0$ a constant ${\mathit{\phi }}_{1,\mathit{\epsilon }}>0$ such that(20) $$\begin{array}{c}\hfill {\mathit{\phi }}_0{e}^{\mathit{\nu }[A]t}\le {\Vert \mathrm{\Phi }(t)\Vert }_2\le {\mathit{\phi }}_{1,\mathit{\epsilon }}{e}^{(\mathit{\nu }[A]+\mathit{\epsilon })t},t\ge 0\end{array}$$(20)

This leads to the following corollary.

Corollary 4

(Two-sided bounds on $P_x(t)-P=\mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)$ based on $\mathit{\nu }[A]$)

Let $A\in {\mathbb{R}}^{n\times n}$, let $\mathrm{\Phi }(t)=e^{At}$ be the associated fundamental matrix with $\mathrm{\Phi }(0)=E$ where $E$ is the identity matrix. Further, let $P_0,P\in {\mathbb{R}}^{n\times n}$ be the covariance matrices from Section 2.

Then, there exists a constant $p_0\ge 0$ and for every $\mathit{\epsilon }>0$ a constant $p_1(\mathit{\epsilon })\ge 0$ such that(21) $$\begin{array}{c}\hfill p_0{e}^{2\mathit{\nu }[A]t}\le {\Vert P_x(t)-P\Vert }_2\le p_1(\mathit{\epsilon })e^{2(\mathit{\nu }[A]+\mathit{\epsilon })t},t\ge 0.\end{array}$$(21)

If $P_0\ne P$, then $p_1(\mathit{\epsilon })>0$. If $P_0-P$ is regular, then also $p_0>0$.

Remark

Due to the equivalence of norms in finite-dimensional spaces, corresponding bounds as in Theorem 3 and Corollary 4 are valid also in all other (not necessarily multiplicative) matrix norms. Of course, besides the spectral norm ${\Vert ·\Vert }_2$, also the Frobenius norm ${\Vert ·\Vert }_F={|·|}_2$ (cf. Kohaupt, bib15) is of special interest in the context of stochastically excited systems.

6. Local regularity of the function $\Vert P_x{(t)-P\Vert }_2$

We have the following lemma which states $-$ loosely speaking $-$ that for every $t_0\ge 0$, the function $t\mapsto \Vert \mathrm{\Delta }{P}_x{(t)\Vert }_2:=\Vert P_x{(t)-P\Vert }_2:={\Vert \mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)\Vert }_2$ is real analytic in some right neighborhood $[t_0,t_0+\mathrm{\Delta }{t}_0]$.

Lemma 5

(Real analyticity of $t\mapsto \Vert P_x{(t)-P\Vert }_2$ on $[t_0,t_0+\mathrm{\Delta }{t}_0]$)

Let $t_0\in {\mathbb{R}}_0^{+}$. Then, there exists a number $\mathrm{\Delta }{t}_0>0$ and a function $t\mapsto \widehat{\mathrm{\Delta }{P}_x}(t)$, which is real analytic on $[t_0,t_0+\mathrm{\Delta }{t}_0]$ such that $\widehat{\mathrm{\Delta }{P}_x}(t)=\Vert \mathrm{\Delta }{P}_x{(t)\Vert }_2=\Vert P_x{(t)-P\Vert }_2={\Vert \mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)\Vert }_2,t\in [t_0,t_0+\mathrm{\Delta }{t}_0]$.

Proof

Based on $\Vert \mathrm{\Delta }{P}_x{(t)\Vert }_2=max\{|{\mathit{\lambda }}_{max}(\mathrm{\Delta }{P}_x(t))|,|{\mathit{\lambda }}_{min}(\mathrm{\Delta }{P}_x(t))\}|$, the proof is similar to that of Kohaupt (2001, Lemma 1). The details are left to the reader.

7. Formulas for the norm derivatives $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$

In this section, in a first step, for complex matrices $A$ and $C$ with $C^{\ast }=C$, we define a matrix function $\mathrm{\Psi }(t):=\mathrm{\Phi }(t)C{\mathrm{\Phi }}^{\ast }(t)$ and derive formulas for the right norm derivatives $D_{+}^k{\Vert \mathrm{\Psi }(t)\Vert }_2$ based on the representation ${\Vert \mathrm{\Psi }(t)\Vert }_2={sup}_{{\Vert u\Vert }_2=1}|(\mathrm{\Psi }u,u)|$ instead of ${\Vert \mathrm{\Psi }(t)\Vert }_2={sup}_{{\Vert u\Vert }_2=1}{\Vert \mathrm{\Psi }u\Vert }_2$. Even though the last one is also valid for $C^{\ast }\ne C$, the first one leads to simpler formulas. In a second step, the obtained formulas are employed for $C=P_0-P\in {\mathbb{R}}^{n\times n}$ and $A\in {\mathbb{R}}^{n\times n}$ to deliver the formulas for $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$.

Let $C\in {\mathbb{C}}^{n\times n}$ with $C^{\ast }=C$. Then, the eigenvalues ${\mathit{\lambda }}_j(C),j=1,\cdots ,n$ of $C$ are real, and for the spectral norm of $C$, one has the formula$${\Vert C\Vert }_2=\underset{{\Vert u\Vert }_2=1}{max}|(Cu,u)|=\underset{j=1,\cdots ,n}{max}|{\mathit{\lambda }}_j(C)|$$

and thus$${\Vert C\Vert }_2=max\{|{\mathit{\lambda }}_{max}(C)|,|{\mathit{\lambda }}_{min}(C)|\}$$

Now, let $A\in {\mathbb{C}}^{n\times n}$, $\mathrm{\Phi }(t)=e^{At}$ its fundamental matrix, and define$$\mathrm{\Psi }(t):=\mathrm{\Phi }(t)C{\mathrm{\Phi }}^{\ast }(t),t\ge 0$$

Then, $\mathrm{\Psi }(t)\in {\mathbb{C}}^{n\times n}$ with ${\mathrm{\Psi }}^{\ast }(t)=\mathrm{\Psi }(t)$ and thus$${\Vert \mathrm{\Psi }(t)\Vert }_2=max\{|{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t))|,|{\mathit{\lambda }}_{min}(\mathrm{\Psi }(t))|\},t\ge 0$$

cf. (Achieser & Glasman, 1968, Chapter II.2, p. 62) or (Kantorowitsch & Akilow, 1964, p. 255).

We mention that without $C^{\ast }=C$, one would have the formula$${\Vert \mathrm{\Psi }(t)\Vert }_2=\sqrt{{\mathit{\lambda }}_{max}({\mathrm{\Psi }}^{\ast }(t)\mathrm{\Psi }(t))},t\ge 0$$

Of course, this formula remains valid for $C^{\ast }=C$, but is more complicated and probably numerically less good than the first representation of ${\Vert \mathrm{\Psi }(t)\Vert }_2$. The computation of $D_{+}^k{\Vert \mathrm{\Psi }(t)\Vert }_2$ by the last formula would be similar as in Kohaupt (2001) for $D_{+}^k{\Vert \mathrm{\Phi }(t)\Vert }_2$.

In order to get a formula for $D_{+}^k{\Vert \mathrm{\Psi }(t)\Vert }_2$ in terms of the given matrices $A$ and $C$, at the beginning, we follow a similar line as in Kohaupt (2001, Section 3, pp. 6–7), however.

Starting point is the series expansion$${\displaystyle \mathrm{\Psi }(t):=\mathrm{\Phi }(t)C{\mathrm{\Phi }}^{\ast }(t)=\sum _{j=0}^{\infty }\mathrm{\Phi }(t_0)B_j{\mathrm{\Phi }}^{\ast }(t_0)\frac{{(t-t_0)}^j}{j!}}$$

with$${\displaystyle B_j=\sum _{k=0}^j\left(\genfrac{}{}{0pt}{}{j}{k}\right){A^{\ast }}^{j-k}C{A}^k,}$$$j=0,1,2,\cdots$. Thus, e.g.$$\begin{array}{cc}\hfill B_0& =C\hfill \\ \hfill B_1& =AC+C{A}^{\ast }\hfill \\ \hfill B_2& =A^{2}C+2AC{A}^{\ast }+C{A^{\ast }}^2\hfill \end{array}$$

Consequently,$$\mathrm{\Psi }(t)=T^{(0)}+T^{(1)}(t-t_0)+T^{(2)}{(t-t_0)}^2+\cdots$$

with$$\begin{array}{cc}\hfill T^{(0)}& =\mathrm{\Phi }(t_0)B_0{\mathrm{\Phi }}^{\ast }(t_0)\hfill \\ \hfill T^{(1)}& =\mathrm{\Phi }(t_0)B_1{\mathrm{\Phi }}^{\ast }(t_0)\hfill \\ \hfill T^{(2)}& =\mathrm{\Phi }(t_0)(\frac{1}{2}{B}_2){\mathrm{\Phi }}^{\ast }(t_0)\hfill \end{array}$$

Then, due to Kato (1966, Theorem 5.11, Chapter II, pp. 115–116) and Kohaupt (1999, Lemma 2.1),$${\mathit{\lambda }}_{max}(\mathrm{\Psi }(t))={\mathit{\nu }}_{0,max}+{\mathit{\nu }}_{1,max}(t-t_0)+{\mathit{\nu }}_{2,max}{(t-t_0)}^2+\cdots ,t_0\le t\le t_0+\mathrm{\Delta }{t}_0$$

where the quantities ${\mathit{\nu }}_{j,max},j=0,1,2$ are given by the formulas for ${\mathit{\nu }}_j,j=0,1,2$ in Kohaupt (2001, pp. 6–7) with the operators $T^{(0)},T^{(1)},T^{(2)}$ defined above. This is shortly recapitulated in Appendix A.3.

The series expansion$${\mathit{\lambda }}_{min}(\mathrm{\Psi }(t))={\mathit{\nu }}_{0,min}+{\mathit{\nu }}_{1,min}(t-t_0)+{\mathit{\nu }}_{2,min}{(t-t_0)}^2+\cdots ,t_0\le t\le t_0+\mathrm{\Delta }{t}_0$$

is obtained via the formula$${\mathit{\lambda }}_{min}(\mathrm{\Psi }(t))=-{\mathit{\lambda }}_{max}(-\mathrm{\Psi }(t))$$

Now, define$$s(t):=\left[\begin{array}{c}{s}_1(t)\\ s_2(t)\end{array}\right]:=\left[\begin{array}{c}{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t))\\ {\mathit{\lambda }}_{min}(\mathrm{\Psi }(t))\end{array}\right]$$

Then,$$s(t)=s(t_0)+Ds(t_0)(t-t_0)+D^{2}s(t_0)\frac{{(t-t_0)}^2}{2}+\cdots ,t_0\le t\le t_0+\mathrm{\Delta }{t}_0$$

with$$\begin{array}{cc}s(t_0)& :=\left[\begin{array}{c}{\mathit{\nu }}_{0,max}\\ {\mathit{\nu }}_{0,min}\end{array}\right]\\ \\ Ds(t_0)& :=\left[\begin{array}{c}{\mathit{\nu }}_{1,max}\\ {\mathit{\nu }}_{1,min}\end{array}\right]\\ \\ D^{2}s(t_0)& :=\left[\begin{array}{c}2{\mathit{\nu }}_{2,max}\\ 2{\mathit{\nu }}_{2,min}\end{array}\right]\end{array}$$

and$$\Vert \mathrm{\Psi }(t_0){\Vert }_2={\Vert s(t_0)\Vert }_{\infty }$$

Hence, for fixed $t_0\in {\mathbb{R}}_0^{+}$,$$D_{+}^k\Vert \mathrm{\Psi }(t_0){\Vert }_2=D_{+}^k{\Vert s(t_0)\Vert }_{\infty },k=0,1,2$$

where the norm derivatives $D_{+}^k{\Vert s(t_0)\Vert }_{\infty },k=0,1,2$ are obtained by the formulas of Kohaupt (2002, Theorem 6). This is shortly recapitulated in Appendix A.4.

If one replaces $t_0$ by $t$, then one gets the functions $t\mapsto D_{+}^k{\Vert \mathrm{\Psi }(t)\Vert }_2=D_{+}^k{\Vert s(t)\Vert }_{\infty },k=0,1,2$.

The norm derivatives $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$ are obtained as the special case $C\in {\mathbb{R}}^{n\times n}$ with $C=P_0-P$ and $A\in {\mathbb{R}}^{n\times n}$.

These formulas are needed in Section 8.

8. Applications

In this section, we apply the new two-sided bounds on $\Vert P_x{(t)-P\Vert }_2$ obtained in Section 5 as well as the differential calculus of norms developed in Sections 6 and 7 to a linear stochastic vibration model with asymptotically stable system matrix and white noise excitation vector.

In Section 8.1, the stochastic vibration model as well as its state-space form is given, and in Section 8.2 the data are chosen. In Section 8.3, computations with the specified data are carried out, such as the computation of $P$ and $P_0-P$ as well as the computation of the curves $y=D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$ and of the curve $y=\Vert P_x{(t)-P\Vert }_2$ along with its best upper and lower bounds. In Section 8.4, computational aspects are shortly discussed.

8.1. The stochastic vibration model and its state-space form

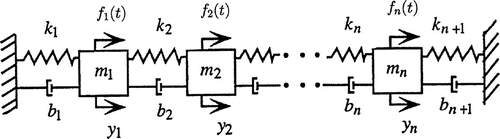
Consider the multi-mass vibration model in Figure 1.

Figure 1. Multi-mass vibration model.

The associated initial-value problem is given by$$M\ddot{y}+B\dot{y}+Ky=f(t),y(0)=y_0,\dot{y}(0)={\dot{y}}_0$$

where $y={[y_1,\cdots ,y_n]}^T$ and $f(t)={[f_1(t),\cdots ,f_n(t)]}^T$ as well as$$M=\left[\begin{array}{cccc}{m}_1& & & \\ & m_2& & \\ & & m_3& & \\ & & \ddots \\ & & & m_n\end{array}\right]$$$$B=\left[\begin{array}{cccc}{b}_1+b_2& -b_2& & \\ -b_2& b_2+b_3& -b_3& & \\ & -b_3& b_3+b_4& -b_4& \\ & \ddots & \ddots & \ddots & \\ & & -b_{n-1}& b_{n-1}+b_n& -b_n\\ & & -b_n& b_n+b_{n+1}\end{array}\right]$$$$K=\left[\begin{array}{cccc}{k}_1+k_2& -k_2& & \\ -k_2& k_2+k_3& -k_3& & \\ & -k_3& k_3+k_4& -k_4& \\ & \ddots & \ddots & \ddots & \\ & & -k_{n-1}& k_{n-1}+k_n& -k_n\\ & & -k_n& k_n+k_{n+1}\end{array}\right]$$

Here, $y$ is the displacement vector, $f(t)$ the applied force, and $M$, $B$, and $K$ are the mass, damping, and stiffness matrices, as the case may be. Matrix $M$ is regular.

In the state-space description, one obtains$$\dot{x}(t)=Ax(t)+b(t),x(0)=x_0$$

with $x={[y^T,z^T]}^T,z=\dot{y}$, and $x_0={[y_0^T,z_0^T]}^T,z_0={\dot{y}}_0$,

where the initial vector $x_0={[y_0^T,z_0^T]}^T$ is characterized by the mean vector $m_0$ and the covariance matrix $P_0$.

The system matrix $A$ and the excitation vector $b(t)$ are given by respectively. The vector $x(t)$ is called state vector.

The (symmetric positive semi-definite) intensity matrix $Q=Q_b$ is obtained from the (symmetric positive semi-definite) intensity matrix $Q_f$ by (see Müller, 1976, Formulas (9.65)) and the derivation of this relation in Appendix A.5 .

8.2. Data for the model

As of now, we specify the values as$$\begin{array}{ccc}& m_j& =1,j=1,\cdots ,n\\ & k_j& =1,j=1,\cdots ,n+1\\ \mathrm{and}& & \\ & b_j& =\left\{\begin{array}{c}1/2,jeven\hfill \\ 1/4,jodd\hfill \end{array}\right.\end{array}$$

Then,$$M=E$$$$B=\left[\begin{array}{cccc}\frac{3}{4}\hfill & -\frac{1}{2}\hfill & \hfill & \\ -\frac{1}{2}\hfill & \frac{3}{4}\hfill & -\frac{1}{4}\hfill & \hfill & \\ \hfill & -\frac{1}{4}\hfill & \frac{3}{4}\hfill & -\frac{1}{2}\hfill & \\ \hfill & \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill \\ \hfill & \hfill & -\frac{1}{4}\hfill & \frac{3}{4}\hfill & -\frac{1}{2}\hfill \\ \hfill & \hfill & -\frac{1}{2}\hfill & \frac{3}{4}\hfill \end{array}\right]$$(if $n$ is even), and$$K=\left[\begin{array}{cccc}2\hfill & -1\hfill & \hfill & \\ -1\hfill & 2\hfill & -1\hfill & \hfill & \\ \hfill & -1\hfill & 2\hfill & -1\hfill & \\ \hfill & \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill \\ \hfill & \hfill & -1\hfill & 2\hfill & -1\hfill \\ \hfill & \hfill & -1\hfill & 2\hfill \end{array}\right]$$

We choose n=5 in this paper so that the state-space vector $x(t)$ has the dimension $m=2n=10$.

Remark

In Sections 2–7, we have denoted the dimension of $x(t)$ by $n$. From the context, the actual dimension should be clear.

For $m_0$, we take$$m_0={[m_{y_0}^T,m_{z_0}^T]}^T$$

with$$m_{y_0}={[-1,1,-1,1,-1]}^T$$

and$$m_{z_0}=\left\{\begin{array}{cc}{\left[0,0,0,0,0,0\right]}^T\hfill & (\mathrm{Case}\mathrm{I})\hfill \\ {\left[-1,-1,-1,-1,-1\right]}^T\hfill & (\mathrm{Case}\mathrm{II})\hfill \end{array}\right.$$

similarly as in Kohaupt (2002) for $y_0$ and ${\dot{y}}_0$. For the $10\times 10$ matrix $P_0$, we choose$$P_0=0.01E$$

The white-noise force vector $f(t)$ is specified as$$f(t)={\left[0,\cdots ,0;f_n(t)\right]}^T$$

so that its intensity matrix $Q_f\in {\mathbb{R}}^{n\times n}$ with $q_{f,nn}=:q$ has the form We choose$$q=0.01$$

With $M=E$, this leads to (see Appendix A.5) In the Lyapunov equation $BX+XA=C$ of Section 2, we employ the replacements$$B\to A,A\to A^T,C\to -Q$$

to obtain the limiting covariance matrix $X=P={lim}_{t\to \infty }{P}_x(t)$.

8.3. Computations with the specified data

(i) Bounds on $y=\mathrm{\Phi }(t)m_0$ in the vector norm ${\Vert ·\Vert }_2$

Upper bounds on $y=\mathrm{\Phi }(t)m_0$ in the vector norm ${\Vert ·\Vert }_2$ for the two cases (I) and (II) of $m_0$ are already given in Kohaupt (2002, Figures 2 and 3). There, we had a deterministic problem with $f(t)=0$ and the solution vector $x(t)=\mathrm{\Phi }(t)x_0$, where $x_0$ there had the same data as $m_0$ here. We mention that for the specified data, ${\mathit{\nu }}_{m_0}[A]=\mathit{\nu }[A]$ in both cases (cf. Kohaupt, 2006, p. 154) for a method to prove this. For the sake of brevity, we do not compute or plot the lower bounds and thus the two-sided bounds, but leave this to the reader.

(ii) Computation of $P$ and $P_0-P$ as well as of their associated eigenproblems

With the data of Section 2, we obtain$$P=\left[\begin{array}{cccccccccc}\hfill 0.1624& \hfill 0.2497& \hfill 0.2347& \hfill 0.1645& \hfill 0.0809& \hfill -0.0000& \hfill -0.0084& \hfill -0.0249& \hfill -0.0312& \hfill -0.0058\\ \hfill 0.2497& \hfill 0.4034& \hfill 0.4129& \hfill 0.3134& \hfill 0.1525& \hfill 0.0084& \hfill -0.0000& \hfill -0.0421& \hfill -0.0701& \hfill -0.0260\\ \hfill 0.2347& \hfill 0.4129& \hfill 0.4977& \hfill 0.4453& \hfill 0.2305& \hfill 0.0249& \hfill 0.0421& \hfill 0.0000& \hfill -0.0706& \hfill -0.0821\\ \hfill 0.1645& \hfill 0.3134& \hfill 0.4453& \hfill 0.4826& \hfill 0.3205& \hfill 0.0312& \hfill 0.0701& \hfill 0.0706& \hfill -0.0000& \hfill -0.1426\\ \hfill 0.0809& \hfill 0.1525& \hfill 0.2305& \hfill 0.3205& \hfill 0.4249& \hfill 0.0058& \hfill 0.0260& \hfill 0.0821& \hfill 0.1426& \hfill -0.0000\\ \hfill 0.0000& \hfill 0.0084& \hfill 0.0249& \hfill 0.0312& \hfill 0.0058& \hfill 0.0793& \hfill 0.1023& \hfill 0.0541& \hfill 0.0040& \hfill 0.0007\\ \hfill -0.0084& \hfill 0.0000& \hfill 0.0421& \hfill 0.0701& \hfill 0.0260& \hfill 0.1023& \hfill 0.1506& \hfill 0.1124& \hfill 0.0363& \hfill -0.0103\\ \hfill -0.0249& \hfill -0.0421& \hfill -0.0000& \hfill 0.0706& \hfill 0.0821& \hfill 0.0541& \hfill 0.1124& \hfill 0.1621& \hfill 0.1300& \hfill -0.0282\\ \hfill -0.0312& \hfill -0.0701& \hfill -0.0706& \hfill -0.0000& \hfill 0.1426& \hfill 0.0040& \hfill 0.0363& \hfill 0.1300& \hfill 0.1998& \hfill 0.0514\\ \hfill -0.0058& \hfill -0.0260& \hfill -0.0821& \hfill -0.1426& \hfill 0.0000& \hfill 0.0007& \hfill -0.0103& \hfill -0.0282& \hfill 0.0514& \hfill 0.4937\end{array}\right]$$The column vector of eigenvalues ${\mathrm{\Lambda }}_P$ and the modal matrix $X_P$, that is, the matrix whose columns are made up of the eigenvectors, are computed as$${\mathrm{\Lambda }}_P=\left[\begin{array}{c}1.54687260865985\hfill \\ 0.55390744777884\hfill \\ 0.50669339270302\hfill \\ 0.26282228387153\hfill \\ 0.12187876942246\hfill \\ 0.05658235034695\hfill \\ 0.00625573952218\hfill \\ 0.00160497361429\hfill \\ 0.00001727972012\hfill \\ 0.00002903815291\hfill \end{array}\right]$$and$$X_P=\left[\begin{array}{cccccccccc}\hfill -0.2584& \hfill -0.1685& \hfill -0.1691& \hfill -0.0346& \hfill -0.4563& \hfill 0.1911& \hfill -0.4245& \hfill 0.1102& \hfill 0.6068& \hfill 0.2642\\ \hfill -0.4509& \hfill -0.2648& \hfill -0.2304& \hfill -0.0776& \hfill -0.3978& \hfill 0.2037& \hfill 0.0009& \hfill 0.0373& \hfill -0.6809& \hfill -0.0524\\ \hfill -0.5517& \hfill -0.1522& \hfill -0.0849& \hfill -0.1348& \hfill 0.0842& \hfill -0.2420& \hfill 0.4392& \hfill -0.4102& \hfill 0.3492& \hfill -0.3135\\ \hfill -0.5321& \hfill 0.1348& \hfill 0.1400& \hfill -0.0065& \hfill 0.3553& \hfill -0.3934& \hfill -0.1093& \hfill 0.5373& \hfill -0.0662& \hfill 0.3050\\ \hfill -0.3465& \hfill 0.5405& \hfill -0.0388& \hfill 0.4707& \hfill 0.2111& \hfill 0.4732& \hfill -0.1727& \hfill -0.2410& \hfill -0.0095& \hfill -0.0904\\ \hfill -0.0295& \hfill 0.1043& \hfill 0.0511& \hfill -0.4547& \hfill 0.1232& \hfill 0.4945& \hfill 0.1521& \hfill 0.5148& \hfill 0.1529& \hfill -0.4557\\ \hfill -0.0537& \hfill 0.2292& \hfill 0.1198& \hfill -0.6320& \hfill 0.1107& \hfill 0.2326& \hfill 0.0712& \hfill -0.3678& \hfill -0.0806& \hfill 0.5636\\ \hfill -0.0354& \hfill 0.4144& \hfill 0.1863& \hfill -0.3279& \hfill -0.2773& \hfill -0.3810& \hfill -0.5002& \hfill -0.1605& \hfill -0.0923& \hfill -0.4223\\ \hfill 0.0217& \hfill 0.5263& \hfill 0.0116& \hfill 0.1227& \hfill -0.5647& \hfill -0.1168& \hfill 0.5517& \hfill 0.2068& \hfill 0.0581& \hfill 0.1558\\ \hfill 0.1301& \hfill 0.2364& \hfill -0.9155& \hfill -0.1559& \hfill 0.1798& \hfill -0.1653& \hfill -0.0489& \hfill 0.0513& \hfill -0.0029& \hfill 0.0083\end{array}\right]$$showing that $P$ is positive definite. Correspondingly,$${\mathrm{\Lambda }}_{P_0-P}=\left[\begin{array}{c}\hfill -0.54687260865985\\ \hfill 0.44609255222115\\ \hfill 0.49330660729698\\ \hfill 0.73717771612847\\ \hfill 0.87812123057754\\ \hfill 0.94341764965305\\ \hfill 0.99374426047782\\ \hfill 0.99839502638571\\ \hfill 0.99998272027988\\ \hfill 0.99997096184709\end{array}\right]$$and$$X_{P_0-P}=\left[\begin{array}{cccccccccc}\hfill 0.2584& \hfill 0.1685& \hfill 0.1691& \hfill 0.0346& \hfill 0.4563& \hfill -0.1911& \hfill 0.4245& \hfill 0.1102& \hfill -0.6068& \hfill 0.2642\\ \hfill 0.4509& \hfill 0.2648& \hfill 0.2304& \hfill 0.0776& \hfill 0.3978& \hfill -0.2037& \hfill -0.0009& \hfill 0.0373& \hfill 0.6809& \hfill -0.0524\\ \hfill 0.5517& \hfill 0.1522& \hfill 0.0849& \hfill 0.1348& \hfill -0.0842& \hfill 0.2420& \hfill -0.4392& \hfill -0.4102& \hfill -0.3492& \hfill -0.3135\\ \hfill 0.5321& \hfill -0.1348& \hfill -0.1400& \hfill 0.0065& \hfill -0.3553& \hfill 0.3934& \hfill 0.1093& \hfill 0.5373& \hfill 0.0662& \hfill 0.3050\\ \hfill 0.3465& \hfill -0.5405& \hfill 0.0388& \hfill -0.4707& \hfill -0.2111& \hfill -0.4732& \hfill 0.1727& \hfill -0.2410& \hfill 0.0095& \hfill -0.0904\\ \hfill 0.0295& \hfill -0.1043& \hfill -0.0511& \hfill 0.4547& \hfill -0.1232& \hfill -0.4945& \hfill -0.1521& \hfill 0.5148& \hfill -0.1529& \hfill -0.4557\\ \hfill 0.0537& \hfill -0.2292& \hfill -0.1198& \hfill 0.6320& \hfill -0.1107& \hfill -0.2326& \hfill -0.0712& \hfill -0.3678& \hfill 0.0806& \hfill 0.5636\\ \hfill 0.0354& \hfill -0.4144& \hfill -0.1863& \hfill 0.3279& \hfill 0.2773& \hfill 0.3810& \hfill 0.5002& \hfill -0.1605& \hfill 0.0923& \hfill -0.4223\\ \hfill -0.0217& \hfill -0.5263& \hfill -0.0116& \hfill -0.1227& \hfill 0.5647& \hfill 0.1168& \hfill -0.5517& \hfill 0.2068& \hfill -0.0581& \hfill 0.1558\\ \hfill -0.1301& \hfill -0.2364& \hfill 0.9155& \hfill 0.1559& \hfill -0.1798& \hfill 0.1653& \hfill 0.0489& \hfill 0.0513& \hfill 0.0029& \hfill 0.0083\end{array}\right]$$showing that $P_0-P$ is symmetric and regular (but not positive definite). Matrix $P_0-P$ is needed to compute the curve $y=\Vert P_x{(t)-P\Vert }_2={\Vert \mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)\Vert }_2$.

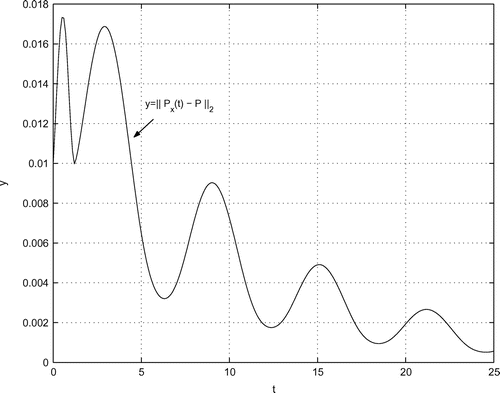
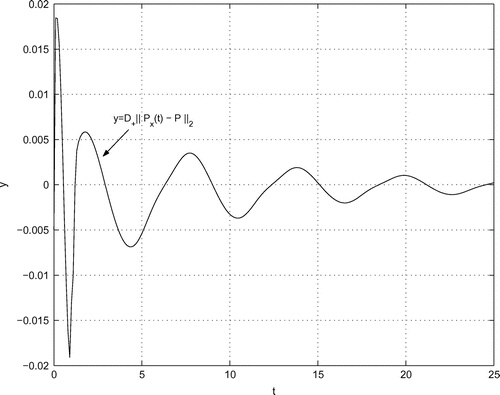
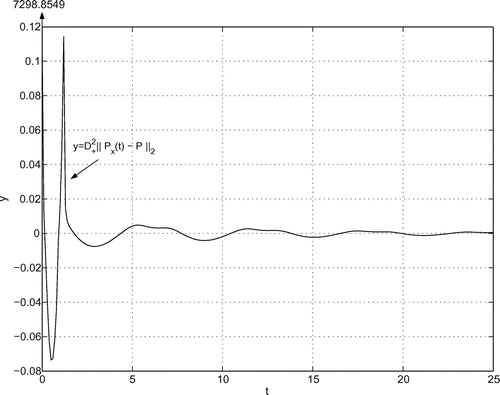
(iii) Computation of the curves $y=D_{+}^k\Vert P_x{(t)-P\Vert }_2=D_{+}^k{\Vert \mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)\Vert }_2$, $k=0,1,2$

The computation of $y=D_{+}^k{\Vert P_x(t)-P\Vert }_2$, $k=0,1,2$ for the given data is done according to Section 7 with $C=P_0-P$. The pertinent curves are illustrated in Figures 2–4. By inspection, there are no kinks (like in the curve $y=\sqrt{t}$ at $t=0$) so that $D_{+}^k\Vert P_x{(t)-P\Vert }_2=D^k\Vert P_x{(t)-P\Vert }_2=\frac{d^k}{d{t}^k}{\Vert P_x(t)-P\Vert }_2$, $k=0,1,2$. For some details on the computation of $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=1,2$, see Appendix A.6

We have checked the results numerically by difference quotients. More precisely, setting$$\mathrm{\Delta }{P}_x(t):=P_x(t)-P,t>0$$

and$$g(t):=\Vert \mathrm{\Delta }{P}_x{(t)\Vert }_2={\Vert P_x(t)-P\Vert }_2,t>0$$

we have investigated the approximations$${\mathit{\delta }}_{h}g(t):=\frac{g(t+h)-g(t-h)}{2h}\approx Dg(t),t-h\ge 0$$

and$${\mathit{\delta }}_{\frac{h}{2}}^{2}g(t):={\mathit{\delta }}_{\frac{h}{2}}({\mathit{\delta }}_{\frac{h}{2}}g(t))=\frac{g(t+h)-2g(t)+g(t-h)}{h^2}\approx D^{2}g(t),t-h\ge 0$$

as well as$${\mathit{\delta }}_{h}Dg(t):=\frac{Dg(t+h)-Dg(t-h)}{2h}\approx D^{2}g(t),t-h\ge 0$$

For$$\begin{array}{cc}t\hfill & =2.5\\ h\hfill & ={10}^{-5}\end{array}$$

we obtain$$\begin{array}{ccc}Dg(t)\hfill & =D\Vert P_x{(t)-P\Vert }_2& =0.00304667381090\\ {\mathit{\delta }}_{h}g(t)\hfill & ={\mathit{\delta }}_h{\Vert P_x(t)-P\Vert }_2& =0.00304667381375\end{array}$$

as well as$$\begin{array}{ccc}\hfill D^{2}g(t)& =D^2{\Vert P_x(t)-P\Vert }_2& =-0.00667087489483\\ \hfill {\mathit{\delta }}_{\frac{h}{2}}^{2}g(t)& ={\mathit{\delta }}_{\frac{h}{2}}^2{\Vert P_x(t)-P\Vert }_2& =-0.00667393224019\end{array}$$

and$$\begin{array}{ccc}{D}^{2}g(t)\hfill & =D^2{\Vert P_x(t)-P\Vert }_2& =-0.00667087489483\\ {\mathit{\delta }}_{h}Dg(t)\hfill & ={\mathit{\delta }}_{h}D{\Vert P_x(t)-P\Vert }_2& =-0.00667087489555\end{array}$$

so that the computational results for $y=D_{+}^k\Vert P_x{(t)-P\Vert }_2=D^k\Vert P_x{(t)-P\Vert }_2=\frac{d^k}{d{t}^k}{\Vert P_x(t)-P\Vert }_2$, $k=0,1,2$ with $t=2.5$ are well underpinned by the difference quotients. As we see, the approximation of $D^{2}g(t)=D^2{\Vert P_x(t)-P\Vert }_2$ by ${\mathit{\delta }}_{h}Dg(t)$ is much better than by ${\mathit{\delta }}_{\frac{h}{2}}^{2}g(t)$, which was to be expected, of course.

Figure 2. Curve $y=\Vert P_x{(t)-P\Vert }_2,0\le t\le 25,\mathrm{\Delta }t=0.1$.

Figure 3. Right norm derivative $y=D_{+}{\Vert P_x(t)-P\Vert }_2,0\le t\le 25,\mathrm{\Delta }t=0.1$.

Figure 4. Second right norm derivative $y=D_{+}^2{\Vert P_x(t)-P\Vert }_2,0\le t\le 25,\mathrm{\Delta }t=0.1$.

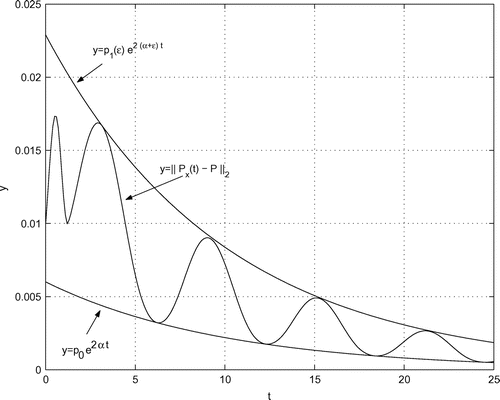
(iv) Bounds on $y=P_x(t)-P=\mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)$ in the spectral norm ${\Vert ·\Vert }_2$

Let $\mathit{\alpha }:=\mathit{\nu }[A]$ be the spectral abscissa of the system matrix $A$. With the given data, we obtain$$\mathit{\alpha }:=\mathit{\nu }[A]=-0.05023936121946$$

so that the system matrix $A$ is asymptotically stable.

The upper bound on $y=\Vert P_x{(t)-P\Vert }_2={\Vert \mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^T(t)\Vert }_2$ is given by $y=p_1(\mathit{\epsilon })e^{2(\mathit{\alpha }+\mathit{\epsilon })t}$, $t\ge 0$. Here, $\mathit{\epsilon }=0$ can be chosen since matrix $A$ is diagonalizable. But, in the programs, we have chosen the machine precision $\mathit{\epsilon }=eps=2^{-52}\doteq 2.2204\times {10}^{-16}$ of MATLAB in order not to be bothered by this question.

With ${\mathit{\phi }}_{1,\mathit{\epsilon }}(t):=p_1(\mathit{\epsilon })e^{2(\mathit{\alpha }+\mathit{\epsilon })t},t\ge 0$, the optimal constant $p_1(\mathit{\epsilon })$ in the upper bound is obtained by the two conditions$$\begin{array}{cc}\hfill \Vert P_x(t_c){-P\Vert }_2& ={\mathit{\phi }}_{1,\mathit{\epsilon }}(t_c)=p_1(\mathit{\epsilon })e^{2(\mathit{\alpha }+\mathit{\epsilon })t_c}\hfill \\ \hfill D_{+}{\Vert P_x(t_c)-P\Vert }_2& ={\mathit{\phi }}_{1,\mathit{\epsilon }}^{\prime }(t_c)=2(\mathit{\alpha }+\mathit{\epsilon }){\mathit{\phi }}_{1,\mathit{\epsilon }}(t_c)\hfill \end{array}$$

where $t_c$ is the place of contact between the curves.

This is a system of two non-linear equations in the two unknowns $t_c$ and $p_1(\mathit{\epsilon })$. By eliminating ${\mathit{\phi }}_{1,\mathit{\epsilon }}(t_c)$, this system is reduced to the determination of the zero of$$D_{+}\Vert P_x(t_c){-P\Vert }_2-2(\mathit{\alpha }+\mathit{\epsilon }){\Vert P_x(t_c)-P\Vert }_2=0$$

which is a single non-linear equation in the single unknown $t_c$. For this, MATLAB routine fsolve was used.

After $t_c$ has been computed from the above equation, the best constant $p_1(\mathit{\epsilon })$ is obtained from$$p_1(\mathit{\epsilon })={\Vert P_x(t_c)-P\Vert }_2{e}^{-2(\mathit{\alpha }+\mathit{\epsilon })t_c}$$

From the initial guess $t_{c,0}=3.0$, the computations deliver the values$$\begin{array}{cc}{t}_c\hfill & =3.14231573176783\\ p_1(\mathit{\epsilon })\hfill & =0.02288922631729\end{array}$$

In a similar way, in the lower bound $y=p_0{e}^{2\mathit{\alpha }t}$, we compute the best constant $p_0$ and the place of contact $t_s$. For the initial guess $t_{s,0}=6.0$, the results are$$\begin{array}{cc}{t}_s\hfill & =6.20977038583445\\ p_0\hfill & =0.00600530767800\end{array}$$

The curve $y=\Vert P_x(t_c){-P\Vert }_2$ along with the best upper and lower bounds is illustrated in Figure 5.

Figure 5. $y=\Vert P_x{(t)-P\Vert }_2$ along with the best upper and lower bounds.

(v) Applicability of the second norm derivative $D_{+}^2{\Vert P_x(t)-P\Vert }_2$

The first norm derivative $D_{+}{\Vert P_x(t)-P\Vert }_2$ was employed in Point (iv). Apart from this, it can be applied to determine the relative extrema of the curve $y=\Vert P_x(t_c){-P\Vert }_2$.

The second norm derivative $D_{+}^2{\Vert P_x(t)-P\Vert }_2$ can be used to compute the inflexion points. The details are left to the reader.

8.4. Computational aspects

In this subsection, we say something about the computer equipment and the computation time for some operations.

(i) As to the computer equipment, the following hardware was available: an Intel Pentium D(3.20 GHz, 800 MHz Front-Side-Bus, 2x2MB DDR2-SDRAM with 533 MHz high-speed memories). As software package, we used MATLAB, Version 6.5.

(ii) The computation time $t$ of an operation was determined by the command sequence $t_i=clock;operation;t=etime(clock,t_i)$; it is put out in seconds rounded to two decimal places by Matlab. For the computation of the eigenvalues of matrix $A$, we used the command $[XA,DA]=eig(A)$; the pertinent computation time is less than $0.01s$. To determine $\mathrm{\Phi }(t)=e^{At}$, we employed Matlab routine $expm$. For the computation of the $251$ values $t,y,yu,yl$ in Figure 5, it took $t($Table for Figure 5)$=0.83$ s. Here, $t$ stands for the time value running from $t_0=0$ to $t_e=25$ with stepsize $\mathrm{\Delta }t=0.1$; $y$ stands for the value of $\Vert P_x{(t)-P\Vert }_2$, $yu$ for the value of the best upper bound $p_1(\mathit{\epsilon })e^{2(\mathit{\alpha }+\mathit{\epsilon })t}$ and $yl$ for the value of the best lower bound $p_0{e}^{2\mathit{\alpha }t}$.

9. Conclusion

In the present paper, linear stochastic vibration systems of the form $\dot{x}(t)=Ax(t)+b(t),x(0)=x_0,$ are investigated driven by white noise $b(t)$. If the system matrix $A$ is asymptotically stable, then the mean vector $m_x(t)$ and the covariance matrix $P_x(t)$ both converge with $m_x(t)\to 0(t\to \infty )$ and $P_x(t)\to P(t\to \infty )$ for some symmetric positive (semi-)definite matrix $P$. This raises the question of the asymptotic behavior of both quantities. The pertinent investigations are made in the Euclidean norm ${\Vert ·\Vert }_2$ for $m_x(t)$ and in the spectral norm, also denoted by ${\Vert ·\Vert }_2$, for $P_x(t)-P$. The main new points are the derivation of two-sided bounds on both quantities, the derivation of the right norm derivatives $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$ and, as application, the computation of the best constants in the bounds. Since we have used a new way to determine the norm derivatives $D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$, we have checked the obtained formulas by various difference quotients. They underpin the correctness of the numerical values for the specified data.

It is reminded that the original system consists of a multi-mass vibration model with damping and white noise force excitation. By a standard method, it is cast into state-space form.

As illustration of the results, the curves $y=D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=0,1,2$ are plotted as well as the curve $y=\Vert P_x{(t)-P\Vert }_2$ together with the best two-sided bounds.

The computation time to generate the last figure with a $10\times 10$ matrix $A$ is less than a second. Of course, in engineering practice, much larger models occur. As in earlier papers, we mention that in this case engineers usually employ a method called condensation to reduce the size of the matrices.

We have added an Appendix to exhibit more details on some items in order to make the paper easier to comprehend.

The numerical values were given in order that the reader can check the results.

Altogether, the results of the paper should be of interest to applied mathematicians and particularly to engineers.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Ludwig Kohaupt

Ludwig Kohaupt received the equivalent to the Master Degree (Diplom-Mathematiker) in Mathematics in 1971 and the equivalent to the PhD (Dr phil nat) in 1973 from the University of Frankfurt/Main.

From 1974 until 1979, he was a teacher in Mathematics and Physics at a Secondary School. During that time (from 1977 until 1979), he was also an auditor at the Technical University of Darmstadt in Engineering Subjects, such as Mechanics, and especially Dynamics.

From 1979 until 1990, he joined the Mercedes-Benz car company in Stuttgart as a Computational Engineer, where he worked in areas such as Dynamics (vibration of car models), Cam Design, Gearing, and Engine Design. Some of the results were published in scientific journals (on the whole, 12 papers and 1 monograph).

Then, in 1990, he combined his preceding experiences by taking over a professorship at the Beuth University of Technology Berlin. He retired on 01 April 2014.

Appendix 1

In this Appendix, we show more details on some items in order to make this paper more easily understandable especially for engineers and generally for a broader readership.

Solution of the Lyapunov matrix equation $BX+XA=C$ by a method of Ma

In this section, we restrict ourselves to the case of diagonalizable matrices $B$ and $A$ since we need only this case in Section 8. The treatment of the general case can be found in Ma (1966).

Let $A\in {\mathbb{C}}^{n\times n}$, $B\in {\mathbb{C}}^{m\times m}$, and $C\in {\mathbb{C}}^{m\times n}$. The problem is to find the solution matrix $X\in {\mathbb{C}}^{m\times n}$ such that$$BX+XA=C$$

We suppose that matrices $A$ and $B$ both be diagonalizable and that the eigenvalues ${\mathit{\lambda }}_i(A),i=1,\cdots ,n$ and ${\mathit{\mu }}_j(B),j=1,\cdots ,m$satisfy the condition$${\mathit{\mu }}_j(B)+{\mathit{\lambda }}_k(A)\ne 0;k=1,\cdots ,n;j=1,\cdots ,m$$

Then, the solution of the equation $BX+XA=C$ can be obtained as follows.

Since $A$ and $B$ are diagonalizable, there exist regular matrices $U\in {\mathbb{C}}^{n\times n}$ and $V\in {\mathbb{C}}^{m\times m}$ such that$$\tilde{A}=U^{-1}AU,\tilde{B}=V^{-1}BV$$

where$$\tilde{A}=diag{({\mathit{\lambda }}_k(A))}_{k=1,\cdots ,n},\tilde{B}=diag{({\mathit{\mu }}_j(B))}_{j=1,\cdots ,m}$$

Define$$\tilde{X}=V^{-1}XU,\tilde{C}=V^{-1}CU$$

Then, $BX+XA=C$ can be written as$$(V^{-1}BV)(V^{-1}XU)+(V^{-1}XU)(U^{-1}AU)=V^{-1}CU$$

or$$\tilde{B}\tilde{X}+\tilde{X}\tilde{B}=\tilde{C}$$

Its solution $\tilde{X}=({\tilde{X}}_{jk})$ is given by$${\tilde{X}}_{jk}=\frac{{\tilde{C}}_{jk}}{{\mathit{\mu }}_j+{\mathit{\lambda }}_k},j=1,\cdots ,m;k=1,\cdots ,n$$

From this, we obtain the solution of the original matrix equation $BX+XA=C$ by the relation$$X=V\tilde{X}{U}^{-1}$$

Remarks

(i)	The solution $X$ could depend on the transformation matrices $U$ and $V$. But, it is actually independent of these matrices since the mapping $L(X):=BX+XA:{\mathbb{C}}^{m\times n}\mapsto {\mathbb{C}}^{m\times n}$ is injective. Therefore, the solution $X$ is uniquely determined.
(ii)	If $B=A^{\ast }$ and $C=C^{\ast }$, then $X=X^{\ast }$ and $X$ is even positive semi-definite. The proof is left to the reader.
(iii)	If $A\in {\mathbb{R}}^{n\times n}$ and $B=A^T$ as well as $C\in {\mathbb{R}}^{n\times n}$ with $C=C^T$, then $X=X^T$ and $X$ is positive semi-definite.

Proof of Lemma 2

In this section, we follow closely the line of Heuser to carry over the proof of ${sup}_{{\Vert v\Vert }_2=1}|(Cv,v)|={sup}_{{\Vert v\Vert }_2=1}{\Vert Cv\Vert }_2={\Vert C\Vert }_2$ to derive a corresponding relation for ${inf}_{{\Vert v\Vert }_2=1}{|(Cv,v)|\Vert }_2$ for $C\in {\mathbb{C}}^{n\times n}$ with $C=C^{\ast }$ (see Heuser, 1975, pp. 277–278 resp. Theorem 6.8.5).

So, let $\Vert ·\Vert ={\Vert ·\Vert }_2$ be the common vector norm resp. the spectral matrix norm.

Let $\mathit{\lambda }>0$ be chosen arbitrarily. Then,$${4\Vert Cx\Vert }_2^2=(C(\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}x),\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}x)-(C(\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x),\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x),x\in {\mathbb{C}}^n$$

which is proven by simplifying the right member of the equation. This entails$$\begin{array}{cc}{4\Vert Cx\Vert }^2\hfill & \le |(C(\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx),\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx)|+|(C(\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx),\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx)|\\ \hfill \\ \hfill & {\displaystyle =\frac{|(C(\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx),\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx)|}{\Vert \mathit{\lambda }x+\frac{1}{\mathit{\lambda }}{Cx\Vert }^2}{\Vert \mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx\Vert }^2}\\ \hfill \\ \hfill & & {\displaystyle +\frac{|(C(\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx),\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx)|}{\Vert \mathit{\lambda }x-\frac{1}{\mathit{\lambda }}{Cx\Vert }^2}{\Vert \mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx\Vert }^2}\hfill \end{array}$$

if $\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}x\ne 0$ and $\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x\ne 0$, $\Vert x\Vert =1$. Thus,$${\displaystyle 4\underset{\Vert x\Vert =1}{inf}{\Vert Cx\Vert }^2\le \frac{|(Cy,y)|}{(y,y)}\Vert \mathit{\lambda }x+\frac{1}{\mathit{\lambda }}{x\Vert }^2+\frac{|(Cz,z)|}{(z,z)}{\Vert \mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x\Vert }^2}$$

with $y=\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}x$ and $z=\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x$, if $y\ne 0$ and $z\ne 0$.

Using the parallelogram identity, we obtain$$\begin{array}{cc}{\displaystyle 4{inf}_{\Vert x\Vert =1}{\Vert Cx\Vert }^2}\hfill & {\displaystyle \le {inf}_{\Vert y\Vert =1}\frac{|(Cy,y)|}{(y,y)}\Vert \mathit{\lambda }x+\frac{1}{\mathit{\lambda }}{Cx\Vert }^2+{inf}_{\Vert z\Vert =1}\frac{|(Cz,z)|}{(z,z)}{\Vert \mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx\Vert }^2}\\ \hfill \\ \hfill & {\displaystyle ={inf}_{\Vert y\Vert =1}\frac{|(Cy,y)|}{(y,y)}\left(\Vert \mathit{\lambda }x+\frac{1}{\mathit{\lambda }}{Cx\Vert }^2+{\Vert \mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx\Vert }^2\right)}\\ \hfill \\ \hfill & {\displaystyle ={inf}_{\Vert y\Vert =1}\frac{|(Cy,y)|}{(y,y)}\left({2\Vert \mathit{\lambda }Cx\Vert }^2+2{\Vert \frac{1}{\mathit{\lambda }}Cx\Vert }^2\right)}\\ \hfill \\ \hfill & {\displaystyle ={inf}_{\Vert y\Vert =1}\frac{|(Cy,y)|}{(y,y)}\left(2{\mathit{\lambda }}^2{\Vert x\Vert }^2+2\frac{{\Vert Cx\Vert }^2}{{\mathit{\lambda }}^2}\right)}\end{array}$$

Let ${\mathit{\lambda }}^2=\frac{\Vert Cx\Vert }{\Vert x\Vert }=\Vert Cx\Vert$ and $\Vert x\Vert =1$. Then,$${\displaystyle 4\underset{\Vert x\Vert =1}{inf}{\Vert Cx\Vert }^2\le \underset{\Vert y\Vert =1}{inf}\frac{|(Cy,y)|}{(y,y)}\left(2\Vert Cx\Vert +2\Vert Cx\Vert \right)}$$

or$${\displaystyle \underset{\Vert x\Vert =1}{inf}{\Vert Cx\Vert }^2\le \underset{\Vert y\Vert =1}{inf}\frac{|(Cy,y)|}{(y,y)}\underset{\Vert x\Vert =1}{inf}\Vert Cx\Vert }$$

Now,$${\displaystyle \underset{\Vert x\Vert =1}{inf}{\Vert Cx\Vert }^2=[\underset{\Vert x\Vert =1}{inf}{\Vert Cx\Vert ]}^2}$$

This leads to if $\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}x\ne 0$ and $\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x\ne 0$, $\Vert x\Vert =1$.

Special cases (S1)–(S3):

(S1) This implies $-\frac{1}{\mathit{\lambda }}Cx=\mathit{\lambda }x$. Therefore,$$\begin{array}{cc}{4\Vert Cx\Vert }^2\hfill & \le \underset{=0}{\underbrace{|(C(\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}x),\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx)|}}+|(C(\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x),\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx)|\\ \hfill \\ \hfill & =|(C(\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}x),\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx)|\\ \hfill \\ \hfill & =|(C(2\mathit{\lambda }x),2\mathit{\lambda }x)|=4{\mathit{\lambda }}^2|(Cx,x)|,\Vert x\Vert =1\end{array}$$

Let$${\mathit{\lambda }}^2=\frac{\Vert Cx\Vert }{\Vert x\Vert }=\Vert Cx\Vert ,\Vert x\Vert =1$$

Then,$${4\Vert Cx\Vert }^2\le 4\Vert Cx\Vert |(Cx,x)|$$

and therefore$$\Vert Cx\Vert \le |(Cx,x)|,\Vert x\Vert =1$$

Thus,$${\displaystyle \underset{\Vert y\Vert =1}{inf}\Vert Cy\Vert \le |(Cx,x)|,\Vert x\Vert =1}$$

so that$${\displaystyle \underset{\Vert y\Vert =1}{inf}\Vert Cy\Vert \le \underset{\Vert x\Vert =1}{inf}|(Cx,x)|=\underset{x\ne 0}{inf}\frac{|(Cx,x)|}{{\Vert x\Vert }^2}}$$

Thus, relation $(22)$ is also proven in the special case (S1).

(S2) This case is treated similarly as (S1).

(S3) This leads to$${4\Vert Cx\Vert }_2^2=(C(\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx),\mathit{\lambda }x+\frac{1}{\mathit{\lambda }}Cx)-(C(\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx),\mathit{\lambda }x-\frac{1}{\mathit{\lambda }}Cx)=0$$

for an $x$ with $\Vert x\Vert =1$. Therefore, ${\displaystyle \underset{\Vert x\Vert =1}{inf}\Vert Cx\Vert =0}$ so that inequality (22) is also valid in the special case (S3).

Relation (22) with $\le$ instead of $\ge$ is trivial. On the whole, the chain of Equation (14) is proven.

Now, let $C\in {\mathbb{C}}^{n\times n}$be regular, let $\Vert ·\Vert$ denote any vector norm and the associated sub matrix norm. Because for the range of $C$ one has $R(C)={\mathbb{C}}^n$, then$$\begin{array}{c}{\displaystyle {inf}_{x\ne 0}\frac{\Vert Cx\Vert }{\Vert x\Vert }={inf}_{x\ne 0}\frac{\Vert Cx\Vert }{\Vert C^{-1}Cx\Vert }={inf}_{x\ne 0}\frac{1}{\frac{\Vert C^{-1}Cx\Vert }{\Vert Cx\Vert }}=\frac{1}{{\displaystyle {sup}_{x\ne 0}\frac{\Vert C^{-1}Cx\Vert }{\Vert Cx\Vert }}}=\frac{1}{{\displaystyle {sup}_{y\ne 0}\frac{\Vert C^{-1}y\Vert }{\Vert y\Vert }}}=\frac{1}{\Vert C^{-1}\Vert }}\hfill \end{array}$$

thus showing relation (15). On the whole, the proof of Lemma 2 is completed.

Remark

We have seen that the method described by Heuser (1975) to derive the relation$${\displaystyle \underset{\Vert x\Vert =1}{sup}|(Cx,x)|=\underset{\Vert x\Vert =1}{sup}\Vert Cx\Vert }$$

for $C\in {\mathbb{C}}^{n\times n}$ with $C=C^{\ast }$ can be carried over to prove the relation$${\displaystyle \underset{\Vert x\Vert =1}{inf}|(Cx,x)|=\underset{\Vert x\Vert =1}{inf}\Vert Cx\Vert }$$

As opposed to this, using Taylor’s method in Taylor (1958, pp. 322–323), it seems to be impossible to prove the inf relations in a similar way as the sup relations.

Since Heuser’s book is written in German, we think that it is worthwhile to make Heuser’s proof idea accessible to a broad readership. Of course, the author cannot rule out that the above inf formulas have been derived before. But, he has not found such a derivation in literature.

Series expansion of ${\mathit{\lambda }}_{max}(\mathrm{\Psi }(t)),t_0\le t\le t_0+\mathrm{\Delta }{t}_0$

We determine the coefficients ${\mathit{\nu }}_j,j=0,1,2$ in the series expansion of Section 7, where we have set ${\mathit{\nu }}_j:={\mathit{\nu }}_{j,max},j=0,1,2$. The derivation follows a line similar to that of Kohaupt (2001, pp. 6–7). We note that the operators $\mathrm{\Psi }(t)$ and $T^{(0)}$, $T^{(1)}$, $T^{(2)}$ are defined in a way different from that in Kohaupt (2001), however. This is the first difference.

Let ${\mathit{\lambda }}_{max}(\mathrm{\Psi }(t))$ be the largest eigenvalue of $\mathrm{\Psi }(t)$. Then, due to

Kato (1966, Theorem 5.11, Chapter II, pp. 115–116] and Kohaupt (1999, Lemma 2.1)$${\mathit{\lambda }}_{max}(\mathrm{\Psi }(t))={\mathit{\nu }}_0+{\mathit{\nu }}_1(t-t_0)+{\mathit{\nu }}_2{(t-t_0)}^2+\cdots ,t_0\le t\le t_0+\mathrm{\Delta }{t}_0$$

where the quantities ${\mathit{\nu }}_0$, ${\mathit{\nu }}_1$, and ${\mathit{\nu }}_2$ are derived now.

Let $n_{-1}:=n$ and ${\mathit{\nu }}_k^{(0)}[T^{(0)}],k=1,\cdots ,n_{-1}$ be the eigenvalues of $T^{(0)}$. Then,$${\displaystyle {\mathit{\nu }}_0=\underset{k=1,\cdots ,n_{-1}}{max}{\mathit{\nu }}_k^{(0)}[T^{(0)}]}$$

Further, define$$M_{-1}:=X:={\mathbb{C}}^n$$

Let$$V_0:=[v_1^{({\mathit{\nu }}_0)},\cdots ,v_{n_0}^{({\mathit{\nu }}_0)}]$$

be the matrix formed by the orthonormal set of eigenvectors $v_k^{({\mathit{\nu }}_0)},k=1,\cdots ,n_0$ associated with ${\mathit{\nu }}_0$, and let $P_{{\mathit{\nu }}_0}$ be the orthogonal projection on the algebraic eigenspace$$M_0:=\mathrm{span}\{v_1^{({\mathit{\nu }}_0)},\cdots ,v_{n_0}^{({\mathit{\nu }}_0)}\}$$(which is here identical with the geometric eigenspace). Then, $M_0=P_{{\mathit{\nu }}_0}X$ with $dim{M}_0=n_0$. Further, $P_{{\mathit{\nu }}_0}$ can be calculated by$$P_{{\mathit{\nu }}_0}=V_0{V}_0^{\ast }$$(cf. Niemeyer & Wermuth, 1987, pp. 234–238). Let$${\tilde{T}}^{(1)}:=P_{{\mathit{\nu }}_0}{T}^{(1)}{P}_{{\mathit{\nu }}_0}$$

and$${\mathit{\nu }}_k^{(1)}[{\tilde{T}}^{(1)}],k=1,\cdots ,n_0$$

be the eigenvalues of ${\tilde{T}}^{(1)}$. Then,$${\displaystyle {\mathit{\nu }}_1:=\underset{k=1,\cdots ,n_0}{max}\{{\mathit{\nu }}_k^{(1)}[{\tilde{T}}^{(1)}]|theassociatedeigenvectorliesin{M}_0\}}$$

Let$$V_1:=[v_1^{({\mathit{\nu }}_1)},\cdots ,v_{n_1}^{({\mathit{\nu }}_1)}]$$

be the matrix formed by the orthonormal set of eigenvectors $v_k^{({\mathit{\nu }}_1)},k=1,\cdots ,n_1$ associated with ${\mathit{\nu }}_1$, and let $P_{{\mathit{\nu }}_1}$ be the orthogonal projection on the algebraic eigenspace$$M_1:=\mathrm{span}\{v_1^{({\mathit{\nu }}_1)},\cdots ,v_{n_1}^{({\mathit{\nu }}_1)}\}$$

Then, $M_1=P_{{\mathit{\nu }}_1}X$ with $dim{M}_1=n_1$. As above, $P_{{\mathit{\nu }}_1}$ can be calculated by$$P_{{\mathit{\nu }}_1}=V_1{V}_1^{\ast }$$

Let$${\widehat{T}}^{(2)}:=P_{{\mathit{\nu }}_1}{\tilde{T}}^{(2)}{P}_{{\mathit{\nu }}_1}:=P_{{\mathit{\nu }}_1}(T^{(2)}-T^{(1)}{S}_{{\mathit{\nu }}_0}{T}^{(1)})P_{{\mathit{\nu }}_1}$$

with$${\displaystyle S_{{\mathit{\nu }}_0}:=\sum _{{\mathit{\nu }}_k^{(0)}\ne {\mathit{\nu }}_0}\frac{1}{{\mathit{\nu }}_k^{(0)}-{\mathit{\nu }}_0}{P}_{{\mathit{\nu }}_k^{(0)}}}$$(for $S_{{\mathit{\nu }}_0}$ cf. Kato, 1966, p. 40, Problem 5.10, Formula (5.32)) and for ${\tilde{T}}^{(2)}$ (cf. Kato, 1966, p. 116). Let$${\mathit{\nu }}_k^{(2)}[{\widehat{T}}^{(2)}],k=1,\cdots ,n_1$$

be the eigenvalues of ${\widehat{T}}^{(2)}$. Then,$${\displaystyle {\mathit{\nu }}_2:=\underset{k=1,\cdots ,n_1}{max}\{{\mathit{\nu }}_k^{(2)}[{\widehat{T}}^{(2)}]|theassociatedeigenvectorliesin{M}_1\}}$$

Remark

In the formula for ${\mathit{\nu }}_1$, exactly those eigenvectors $v^{(1)}$ lie in $M_0$ for which $rank{P}_{{\mathit{\nu }}_0}=rank[P_{{\mathit{\nu }}_0},v^{(1)}]$. (In Kohaupt (2001, p. 7, Remark), instead of $P_{{\mathit{\nu }}_0}$ it reads $P_{{\mathit{\nu }}_1}$ there, which is a typo.) Similarly one proceeds in the formula for ${\mathit{\nu }}_2$.

The second difference to Kohaupt (2001) is that the formulas of Kohaupt (2001, Theorem 4) are not applied. Instead, one may use the relations $D_{+}^k\Vert \mathrm{\Psi }(t_0){\Vert }_2=D_{+}^k{\Vert s(t_0)\Vert }_{\infty },k=0,1,2$.

Formulas for $D_{+}^k{\Vert s(t_0)\Vert }_{\infty },k=0,1,2$

For these formulas, we refer to Kohaupt (2002, pp. 433–434). Let $s\in C^m({\mathbb{R}}_0^{+},{\mathbb{R}}^n)$ and $s(t)={[s_1(t),\cdots ,s_n(t)]}^T$, and define the following sign functionals for $i\in \{1,\cdots ,n\}$:$$\begin{array}{cc}& s_i^{(0)}:=\mathrm{sgn}[s_i(t_0)]\hfill \\ \hfill \\ \hfill & s_i^{(1)}:=\left\{\begin{array}{cc}\mathrm{sgn}[s_i(t_0)],\hfill & s_i(t_0)\ne 0\hfill \\ \hfill \\ \mathrm{sgn}[D{s}_i(t_0)],\hfill & s_i(t_0)=0\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill & ⋮\hfill \\ \hfill \\ \hfill & s_i^{(m)}:=\left\{\begin{array}{cc}\mathrm{sgn}[s_i(t_0)],\hfill & s_i(t_0)\ne 0\hfill \\ \hfill \\ \mathrm{sgn}[D{s}_i(t_0)],\hfill & s_i(t_0)=0,D{s}_i(t_0)\ne 0\hfill \\ ⋮\hfill & \\ \mathrm{sgn}[D^m{s}_i(t_0)],\hfill & D^k{s}_i(t_0)=0,k=0,1,\cdots ,m-1\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill \mathrm{or}\mathrm{briefly},& \\ \hfill \\ \hfill & s_i^{(k)}=\left\{\begin{array}{cc}{s}_i^{(k-1)},\hfill & s_i^{(k-1)}\ne 0\hfill \\ \hfill \\ \mathrm{sgn}[D^k{s}_i(t_0)],\hfill & s_i^{(k-1)}=0\hfill \end{array}\right.\hfill \end{array}$$$i=1,\cdots ,n$; $k=1,\cdots ,m$. With these sign functionals, define the further functionals(A1) $$\begin{array}{c}\hfill S_i^{(k)}:=s_i^{(k)}·D^k{s}_i(t_0),i=1,\cdots ,n;k=0,1,\cdots ,m\end{array}$$(A1)

Then, the right derivatives for real vector functions read as follows.

Theorem 6

($p=\infty$, real vector function) Let $s:{\mathbb{R}}_0^{+}\to {\mathbb{R}}^n$ be an n-dimensional real-valued vector function that is m times continuously differentiable, and let $t_0\in {\mathbb{R}}_0^{+}$. Suppose additionally that each two components of $s$ are either identical or intersect each other at most finitely often near $t_0$. Further, let $I_{-1}=\{1,\cdots ,n\}$ and $I_k$ be the set of all indices $i_k\in I_{k-1}$ where $S_i^{(k)}$ from (23) attains its maximum, i.e.$$I_k:=\left\{{\displaystyle i_k\in I_{k-1}|S_{i_k}^{(k)}=\underset{i\in I_{k-1}}{max}{S}_i^{(k)}}\right\}$$$k=1,\cdots ,m$. Then, the right derivatives of $t\mapsto {\Vert s(t)\Vert }_{\infty }$ at $t=t_0\ge 0$ are given by$${\displaystyle D_{+}^k{\Vert s(t_0)\Vert }_{\infty }=\underset{i\in I_{k-1}}{max}{S}_i^{(k)},k=1,\cdots ,m}$$

Remark

In our case, in Section 7, one has $n=2$ and $m=2$. Further, $s(t),t_0\le t\le t_0+\mathrm{\Delta }{t}_0$ is analytic so that the additional condition is automatically fulfilled.

Determination of symmetric positive semi-definite intensity matrix $Q=$$Q_b$ from $Q_f$

Since with one obtains, using $M^T=M$, the relation $B^T=B$ and thus$$b(t)b^T(\mathit{\tau })=Bw(t)w^T(\mathit{\tau })B^T=Bw(t)w^T(\mathit{\tau })B$$

Thus, according to Müller (1976, Formula (9.7)) with $m_b(t)=0$, one has$$N_b(t,\mathit{\tau })=E\{b(t)b^T(\mathit{\tau })\}=BE\{w(t)w^T(\mathit{\tau })\}B$$

Now, Since $f(t)$ is white noise, one has $N_f(t,\mathit{\tau })=E\{f(t)f^T(\mathit{\tau })\}=Q_f\mathit{\delta }(t-\mathit{\tau })$, leading to This implies giving with

Some details on the computation of $y=D_{+}^k{\Vert P_x(t)-P\Vert }_2,k=1,2$

According to Section 7 and Appendix A.3, the computation of $y=D_{+}^k\Vert P_x{(t)-P\Vert }_2=D_{+}^k{\Vert \mathrm{\Psi }(t)\Vert }_2=D_{+}^k\Vert \mathrm{\Phi }(t)C{\mathrm{\Phi }}^{\ast }{(t)\Vert }_2=D_{+}^k{\Vert \mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^{\ast }(t)\Vert }_2,k=1,2$ is based on$${\displaystyle {\mathit{\nu }}_{1,max}:=\underset{k=1,\cdots ,n_0}{max}\{{\mathit{\nu }}_k^{(1)}[{\tilde{T}}^{(1)}]|\mathrm{the}\mathrm{associated}\mathrm{eigenvector}\mathrm{lies}\mathrm{in}{M}_0\}}$$

and$${\displaystyle {\mathit{\nu }}_{1,min}:=-\underset{k=1,\cdots ,n_0}{max}\{{\mathit{\nu }}_k^{(1)}[-{\tilde{T}}^{(1)}]|\mathrm{the}\mathrm{associated}\mathrm{eigenvector}\mathrm{lies}\mathrm{in}{M}_0\}}$$

as well as$${\displaystyle {\mathit{\nu }}_{2,max}:=\underset{k=1,\cdots ,n_1}{max}\{{\mathit{\nu }}_k^{(2)}[{\widehat{T}}^{(2)}]|\mathrm{the}\mathrm{associated}\mathrm{eigenvector}\mathrm{lies}\mathrm{in}{M}_1\}}$$

and$${\displaystyle {\mathit{\nu }}_{2,min}:=-\underset{k=1,\cdots ,n_1}{max}\{{\mathit{\nu }}_k^{(2)}[-{\widehat{T}}^{(2)}]|\mathrm{the}\mathrm{associated}\mathrm{eigenvector}\mathrm{lies}\mathrm{in}{M}_1\}}$$

where the quantities ${\tilde{T}}^{(1)}$ and ${\widehat{T}}^{(2)}$ depend on $t_0$.

For all $t_0=0(\mathrm{\Delta }t)t_e=0(0.1)25$, the constraint “$theassociatedeigenvectorliesin{M}_0$" resp. “$theassociatedeigenvectorliesin{M}_1$" was fulfilled with the only exception of that for ${\mathit{\nu }}_{1,min}$ and ${\mathit{\nu }}_{2,min}$ with $t_0=3.4$. The reason for this could not be clarified, however. In this exceptional case, we have set the quantities equal to zero. Since for $t_0=3.4$ we have $\Vert \mathrm{\Psi }(t_0){\Vert }_2=max\{|{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0))|,|{\mathit{\lambda }}_{min}(\mathrm{\Psi }(t_0))|\}=|{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0))|={\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0))$, the norm derivatives are given by $D_{+}{\Vert \mathrm{\Psi }(t_0)\Vert }_2={\mathit{\nu }}_{1,max}$ and $D_{+}^2{\Vert \mathrm{\Psi }(t_0)\Vert }_2=2{\mathit{\nu }}_{2,max}$, and thus do not depend on ${\mathit{\nu }}_{1,min}$ or ${\mathit{\nu }}_{2,min}$ for $t_0=3.4$, however.

Remark

It is interesting to note that for all $t_0=0(0.1)25$ without exception, only one of the eigenvalues ${\mathit{\nu }}_k^{(1)}[{\tilde{T}}^{(1)}],{\mathit{\nu }}_k^{(1)}[-{\tilde{T}}^{(1)}],k=1,\cdots ,n_0$ and ${\mathit{\nu }}_k^{(2)}[{\widehat{T}}^{(2)}],{\mathit{\nu }}_k^{(2)}[-{\widehat{T}}^{(2)}],k=1,\cdots ,n_1$ was different from zero, and further that the above-mentioned constraints can be dropped for the given data without changing the results.

Remark

Finally, we want to remind the reader that, since the operator $\mathrm{\Psi }(t)=\mathrm{\Phi }(t)(P_0-P){\mathrm{\Phi }}^{\ast }(t),t\ge 0,$ is different from zero as well as finite dimensional, it is self-adjoint and completely continuous. Therefore, according to Achieser and Glasman (1968, no. 60, p. 158) or Kantorowitsch and Akilow (1964, Chapter IX, §4.3, p. 255), $\mathrm{\Psi }(t)$ has at least one eigenvalue different from zero for all $t\ge 0$.

Simplification of the computation of $D_{+}^k\Vert \mathrm{\Psi }(t_0){\Vert }_2=D_{+}^k{\Vert P_x(t_0)-P\Vert }_2,k=1,2$

In the case of $|{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0))|\ne |{\mathit{\lambda }}_{min}(\mathrm{\Psi }(t_0))|$, one can simplify the computation as follows. Let$$\mathit{\lambda }(\mathrm{\Psi }(t_0))):=\left\{\begin{array}{cc}{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0)),\hfill & |{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0))|>|{\mathit{\lambda }}_{min}(\mathrm{\Psi }(t_0))|\hfill \\ \hfill \\ {\mathit{\lambda }}_{min}(\mathrm{\Psi }(t_0)),\hfill & |{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0))|<|{\mathit{\lambda }}_{min}(\mathrm{\Psi }(t_0))|\hfill \end{array}\right.$$

Then,$$\Vert \mathrm{\Psi }(t_0){\Vert }_2=|\mathit{\lambda }(\mathrm{\Psi }(t_0))|=:|s(t_0)|$$

Further, according to the last Remark above, $\mathrm{\Psi }(t_0)\ne 0$ and therefore $s(t_0)\ne 0$, so that in Appendix A.4 with $n=1$ and $s_1(t_0)=s(t_0)$, we obtain the signs$$s^{(0)}=s^{(1)}=s^{(2)}=\cdots =s^{(m)}=sgn(s(t_0))=sgn((\mathrm{\Psi }(t_0)))$$

Thus, from Appendix A.3, we get$$\begin{array}{cc}\Vert \mathrm{\Psi }(t_0){\Vert }_2\hfill & =s^{(0)}{\mathit{\nu }}_0\\ \hfill \\ D_{+}{\Vert \mathrm{\Psi }(t_0)\Vert }_2\hfill & =s^{(0)}{\mathit{\nu }}_1\\ \hfill \\ D_{+}^2{\Vert \mathrm{\Psi }(t_0)\Vert }_2\hfill & =s^{(0)}2{\mathit{\nu }}_2\end{array}$$

With the given data in Section 8, we had $|{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t_0))|>|{\mathit{\lambda }}_{min}(\mathrm{\Psi }(t_0))|$ and $s^{(0)}=1$ for all $t_0=0(0.1)25$. This means ${\Vert \mathrm{\Psi }(t)\Vert }_2=|{\mathit{\lambda }}_{max}(\mathrm{\Psi }(t))|={\mathit{\lambda }}_{max}(\mathrm{\Psi }(t)),t=0(0.1)25$.