An asymptotic analysis for an integrable variant of the Lotka–Volterra prey–predator model via a determinant expansion technique

Abstract

The Hankel determinant appears in representations of solutions to several integrable systems. An asymptotic expansion of the Hankel determinant thus plays a key role in the investigation of asymptotic analysis of such integrable systems. This paper presents an asymptotic expansion formula of a certain Casorati determinant as an extension of the Hankel case. This Casorati determinant is then shown to be associated with the solution to the discrete hungry Lotka–Volterra (dhLV) system, which is an integrable variant of the famous prey–predator model in mathematical biology. Finally, the asymptotic behavior of the dhLV system is clarified using the expansion formula for the Casorati determinant.

Keywords:

• Casorati determinant
• discrete hungry Lotka–Volterra system
• asymptotic expansion

AMS Subject Classifications:

• 39A12
• 34E05
• 15A15

Public Interest Statement

In this paper, we present a powerful new technique for an asymptotic expansion of the Casorati determinant. The Casorati determinant is associated with several difference equations appearing in mathematical physics, and plays a role similar to the Wronskian in the theory of differential equations. Our technique will be useful for asymptotically analyzing not only the discrete hungry Lotka–Volterra system, but also other dynamical systems associated with the Casorati determinant.

1. Introduction

Integrable systems are often classified as nonlinear dynamical systems whose solutions can be explicitly expressed. Such an integrable system is the Toda equation which describes the current–voltage function in an electric circuit. A time discretization, called the discrete Toda equation (Hirota, 1981), is simply equal to the recursion formula of the qd algorithm for computing eigenvalues of a symmetric tridiagonal matrix (Henrici, 1988; Rutishauser, 1990) and singular values of a bidiagonal matrix (Parlett, 1995).

Another commonly investigated integrable system is the integrable Lotka–Volterra (LV) system, which is a prey–predator model in mathematical biology (Yamazaki, 1987). The discrete LV (dLV) system was shown in Iwasaki and Nakamura (2002) to be applicable to computing for bidiagonal singular values. The hungry Lotka–Volterra (hLV) system is a variant that captures a more complicated prey–predator relationship in comparison with the original LV system (Bogoyavlensky, 1988; Itoh, 1987). Time discretization of this system leads to the discrete hungry Lotka–Volterra (dhLV) system. It was shown in Fukuda, Ishiwata, Iwasaki, and Nakamura (2009), Fukuda, Ishiwata, Yamamoto, Iwasaki, and Nakamura (2013), Yamamoto, Fukuda, Iwasaki, Ishiwata, and Nakamura (2010) that the dhLV system can generate $LR$ matrix transformations for computing eigenvalues of a banded totally nonnegative (TN) matrix whose minors are all nonnegative.

The determinant solutions to both the discrete Toda equation and the dLV system can be expressed using the Hankel determinant,(1.1) $$\begin{array}{c}\hfill H_0^{(n)}:=1,H_j^{(n)}:=\left|\begin{array}{cccc}{a}^{(n)}& a^{(n+1)}& \cdots & a^{(n+j-1)}\\ a^{(n+1)}& a^{(n+2)}& \cdots & a^{(n+j)}\\ ⋮& ⋮& \ddots & ⋮\\ a^{(n+j-1)}& a^{(n+j)}& \cdots & a^{(n+2j-2)}\end{array}\right|,j=1,2,\cdots \end{array}$$(1.1)

where $j$ and $n$ correspond to the discrete spatial and discrete time variables, respectively (Tsujimoto, 2001). Here, the formal power series $f(z)={\sum }_{n=0}^{\infty }{a}^{(n)}{z}^n$ associated with $H_j^{(n)}$ is assumed to be analytic at $z=0$ and meromorphic in the disk $D=\{z\mid |z|<\mathit{\zeta }\}$. The finite or infinite types of poles $u_1^{-1},u_2^{-1},\cdots$ of $f(z)$ are ordered such that $0<|u_1^{-1}|<|u_2^{-1}|<\cdots <\mathit{\zeta }$. Then, there exists a nonzero constant $c_j$ independent of $n$ such that, for some $\mathit{\varrho }$ satisfying $|u_j|>\mathit{\varrho }>|u_{j+1}|$,(1.2) $$\begin{array}{c}\hfill H_j^{(n)}=c_j{(u_1{u}_2\cdots u_j)}^n\left(1+O\left({\left(\frac{\mathit{\varrho }}{|u_j|}\right)}^n\right)\right)\end{array}$$(1.2)

as $n\to \infty$ (Henrici, 1988). The asymptotic expansion (1.2) as $n\to \infty$ enables the asymptotic analysis of the discrete Toda equation and the dLV system as in Henrici (1988), Rutishauser (1990) and in Iwasaki and Nakamura (2002), respectively.

A generalization of the Hankel determinant $H_j^{(n)}$ is given in the below determinant of a nonsymmetric square matrix of order $j$,(1.3) $$\begin{array}{c}\hfill C_{i,0}^{(n)}:=1,C_{i,j}^{(n)}:=\left|\begin{array}{cccc}{a}_i^{(n)}& a_{i+1}^{(n)}& \cdots & a_{i+j-1}^{(n)}\\ a_i^{(n+1)}& a_{i+1}^{(n+1)}& \cdots & a_{i+j-1}^{(n+1)}\\ ⋮& ⋮& \ddots & ⋮\\ a_i^{(n+j-1)}& a_{i+1}^{(n+j-1)}& \cdots & a_{i+j-1}^{(n+j-1)}\end{array}\right|,i=0,1,\cdots ,j=1,2,\cdots \end{array}$$(1.3)

which is called the Casorati determinant or Casoratian. The Casorati determinant is useful in the theory of difference equations, particularly in mathematical physics, and plays a role similar to the Wronskian in the theory of differential equations (Vein & Dale, 1999). No one wonder here that the formal power series $f_i(z)={\sum }_{n=0}^{\infty }{a}_i^{(n)}{z}^n$ is associated with the Casorati determinant $C_{i,j}^{(n)}$ for each $i$. The formal power series $f_i(z)$ differs from $f(z)$ in that not only the superscript, but also the subscript, appears in the coefficients.

To the best of our knowledge, from the viewpoint of the formal power series $f_i(z)$, the asymptotic analysis for the Casorati determinant $C_{i,j}^{(n)}$ has not yet been discussed in the literature. The first purpose of this paper is to present an asymptotic expansion of the Casorati determinant $C_{i,j}^{(n)}$ as $n\to \infty$. The asymptotic behavior of the dhLV system was discussed in Fukuda et al. (2009, 2013) in the case where the discretization parameter ${\mathit{\delta }}^{(n)}$ is restricted to be positive. However, it was suggested in Yamamoto et al. (2010) that the choice ${\mathit{\delta }}^{(n)}<0$ in the dhLV system yields a convergence acceleration of the $LR$ transformations. The discrete time evolution in the dhLV system with ${\mathit{\delta }}^{(n)}<0$ corresponds to a reverse of the continuous-time evolution in the hLV system. It is interesting to note that such artificial dynamics are useful for computing eigenvalues of a TN matrix. The second purpose of this paper is to provide an asymptotic analysis for the dhLV system without being limited by the sign of ${\mathit{\delta }}^{(n)}$.

The remainder of this paper is organized as follows. In Section 2, we first observe that the entries in $C_{i,j}^{(n)}$ can be expressed using poles of $f_i(z)$. We then give an asymptotic expansion of the Casorati determinant in terms of the poles of $f_i(z)$ as $n\to \infty$ by expanding the theorem analyticity for the Hankel determinant given in Henrici (1988). In Section 3, we find the determinant solution to the dhLV system through relating the dhLV system to a three-term recursion formula. With the help of the resulting theorem for the Casorati determinant $C_{i,j}^{(n)}$, we explain in Section 4 that the determinant solution to the dhLV system can be rewritten using the Casorati determinant $C_{i,j}^{(n)}$, and we clarify the asymptotic behavior of the solution to the dhLV system. Finally, we give concluding remarks in Section 5.

2. An asymptotic expansion of the Casorati determinant

In this section, we first give an expression of the entries of the Casorati determinant $C_{i,j}^{(n)}$ in terms of poles of the formal power series $f_i(z)$ associated with $C_{i,j}^{(n)}$. Referring to the theorem on analyticity for the Hankel determinant given in Henrici (1988), we present an asymptotic expansion of the Casorati determinant $C_{i,j}^{(n)}$ as $n\to \infty$ using the poles of $f_i(z)$. We also describe the case where some restriction is imposed on the poles of $f_i(z)$.

Let $f_i(z)={\sum }_{n=0}^{\infty }{a}_i^{(n)}{z}^n$, which is the formal power series associated with $C_{i,j}^{(n)}$ for $i=0,1,\cdots ,$ be analytic at $z=0$ and meromorphic in the disk $D=\{z\mid |z|<\mathit{\zeta }\}$. Moreover, let $r_{i,1}^{-1},r_{i,2}^{-1},\cdots ,$ denote the poles of $f_i(z)$ such that $|r_{i,1}^{-1}|<|r_{i,2}^{-1}|<\cdots <\mathit{\zeta }$. By extracting the principal parts in $f_i(z)$, we derive(2.1) $$\begin{array}{cc}\hfill f_i(z)& =\frac{{\mathit{\alpha }}_{i,1}}{r_{i,1}^{-1}-z}+\frac{{\mathit{\alpha }}_{i,2}}{r_{i,2}^{-1}-z}+\cdots +\frac{{\mathit{\alpha }}_{i,p}}{r_{i,p}^{-1}-z}+\sum _{n=0}^{\infty }{b}_i^{(n)}{z}^n\hfill \end{array}$$(2.1)

where $p$ is an arbitrary positive integer, ${\mathit{\alpha }}_{i,1},{\mathit{\alpha }}_{i,2},\cdots ,{\mathit{\alpha }}_{i,p}$ are some nonzero constants, and $b_i^{(n)}$, which contains the terms with respect to $r_{i,p+1}^{-1},r_{i,p+2}^{-1},\cdots$, satisfies(2.2) $$\begin{array}{c}\hfill |b_i^{(n)}|\le {\mathit{\mu }}_i{\mathit{\rho }}_i^n\end{array}$$(2.2)

for some nonzero positive constants ${\mathit{\mu }}_i$ and ${\mathit{\rho }}_i$ with $|r_{i,p+1}|<{\mathit{\rho }}_i<|r_{i,p}|$. The proof of (2.2) is given in Henrici (1988) utilizing the Cauchy coefficient estimate. We now give a lemma for an expression of $a_i^{(n)}$ appearing in $f_i(z)={\sum }_{n=0}^{\infty }{a}_i^{(n)}{z}^n$.

Lemma 2.1

Let us assume that the poles $r_{i,1}^{-1},r_{i,2}^{-1},\cdots ,r_{i,p}^{-1}$ of $f_i(z)$ are not multiple. Then, $a_i^{(n)}$ can be expressed using $r_{i,1},r_{i,2},\cdots ,r_{i,p}$ as(2.3) $$\begin{array}{c}\hfill a_i^{(n)}=\sum _{\ell =1}^p{c}_{i,\ell }{r}_{i,\ell }^n+b_i^{(n)}\end{array}$$(2.3)

where $c_{i,1},c_{i,2},\cdots ,c_{i,p}$ are some nonzero constants.

Proof

The crucial element is the replacement ${\mathit{\alpha }}_{i,1}=c_{i,1}{r}_{i,1}^{-1},{\mathit{\alpha }}_{i,2}=c_{i,2}{r}_{i,2}^{-1},\cdots ,{\mathit{\alpha }}_{i,p}=c_{i,p}{r}_{i,p}^{-1}$ in (2.1), namely,(2.4) $$\begin{array}{cc}\hfill f_i(z)& =\frac{c_{i,1}{r}_{i,1}^{-1}}{r_{i,1}^{-1}-z}+\frac{c_{i,2}{r}_{i,2}^{-1}}{r_{i,2}^{-1}-z}+\cdots +\frac{c_{i,p}{r}_{i,p}^{-1}}{r_{i,p}^{-1}-z}+\sum _{n=0}^{\infty }{b}_i^{(n)}{z}^n\hfill \end{array}$$(2.4)

Since each $c_{i,\ell }{r}_{i,\ell }^{-1}/(r_{i,\ell }^{-1}-z)$ in (2.4) can be regarded as the summation of a geometric series, we obtain$$\begin{array}{cc}\hfill f_i(z)& =\sum _{n=0}^{\infty }{c}_{i,1}{r}_{i,1}^n{z}^n+\sum _{n=0}^{\infty }{c}_{i,2}{r}_{i,2}^n{z}^n+\cdots +\sum _{n=0}^{\infty }{c}_{i,p}{r}_{i,p}^n{z}^n+\sum _{n=0}^{\infty }{b}_i^{(n)}{z}^n\hfill \\ \hfill & =\sum _{n=0}^{\infty }\left[\left(\sum _{\ell =1}^p{c}_{i,\ell }{r}_{i,\ell }^n\right)+b_i^{(n)}\right]z^n\hfill \end{array}$$

which implies (2.3).

Similarly to the asymptotic expansion as $n\to \infty$ of the Hankel determinant $H_j^{(n)}$ given in Henrici (1988), we have the following theorem for the Casorati determinant $C_{i,j}^{(n)}$.

Theorem 2.2

Let us assume that the poles $r_{i,1}^{-1},r_{i,2}^{-1},\cdots ,r_{i,p}^{-1}$ of $f_i(z)$ are not multiple. Then there exists some constant $c_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}$ independently of $n$ such that, as $n\to \infty$,(2.5) $$\begin{array}{c}\hfill C_{i,j}^{(n)}=\sum _{\mathit{\sigma }}[c_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}(r_{i,{\mathit{\kappa }}_1}{r}_{i+1,{\mathit{\kappa }}_2}\cdots r_{i+j-1,{\mathit{\kappa }}_j}{)}^n(1+\sum _{\ell =1}^{j}O((\frac{{\mathit{\rho }}_{i+\ell -1}}{|r_{i+\ell -1,{\mathit{\kappa }}_{\ell }}|}{)}^n))]\end{array}$$(2.5)

where $\mathit{\sigma }$ denotes the mapping from $\{{\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j\}$ to $\{1,2,\cdots ,p\}$ and ${\mathit{\rho }}_{i+\ell -1}$ is some constant such that $|r_{i+\ell -1,p+1}|<{\mathit{\rho }}_{i+\ell -1}<|r_{i+\ell -1,p}|$.

Proof

By applying Lemma 2.1 and the addition formula of determinants to the Casorati determinant $C_{i,j}^{(n)}$, we derive(2.6) $$\begin{array}{c}\hfill C_{i,j}^{(n)}=\sum _{\mathit{\sigma }}{D}_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}^{(n)}+\sum _{\mathit{\sigma }}{\widehat{D}}_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}^{(n)}\end{array}$$(2.6)

where in the first summation$$\begin{array}{c}\hfill D_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}^{(n)}:=\left|\begin{array}{cccc}{c}_{i,{\mathit{\kappa }}_1}{r}_{i,{\mathit{\kappa }}_1}^n& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}^n& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}^n\\ c_{i,{\mathit{\kappa }}_1}{r}_{i,{\mathit{\kappa }}_1}^{n+1}& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}^{n+1}& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}^{n+1}\\ ⋮& ⋮& \ddots & ⋮\\ c_{i,{\mathit{\kappa }}_1}{r}_{i,{\mathit{\kappa }}_1}^{n+j-1}& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}^{n+j-1}& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}^{n+j-1}\end{array}\right|\end{array}$$

and ${\widehat{D}}_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}^{(n)}$ in the second summation denotes a determinant of the same form as $D_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}^{(n)}$ except that the $\ell$th column is replaced with ${\mathbf{b}}_{\ell }:={(b_{i+\ell -1}^{(n)},b_{i+\ell -1}^{(n+1)},\cdots ,b_{i+\ell -1}^{(n+j-1)})}^{\top }$ for at least one of $\ell$. Evaluating the first summation in (2.6), we obtain(2.7) $$\begin{array}{c}\hfill \sum _{\mathit{\sigma }}{D}_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}^{(n)}=\sum _{\mathit{\sigma }}{c}_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}{\left(r_{i,{\mathit{\kappa }}_1}{r}_{i+1,{\mathit{\kappa }}_2}\cdots r_{i+j-1,{\mathit{\kappa }}_j}\right)}^n\end{array}$$(2.7)

where(2.8) $$\begin{array}{c}\hfill c_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}:=\left|\begin{array}{cccc}{c}_{i,{\mathit{\kappa }}_1}& c_{i+1,{\mathit{\kappa }}_2}& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}\\ c_{i,{\mathit{\kappa }}_1}{r}_{i,{\mathit{\kappa }}_1}& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}\\ ⋮& ⋮& \ddots & ⋮\\ c_{i,{\mathit{\kappa }}_1}{r}_{i,{\mathit{\kappa }}_1}^{j-1}& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}^{j-1}& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}^{j-1}\end{array}\right|\end{array}$$(2.8)

To estimate the second summation in (2.6), for example, we consider the case where the $1$st column is replaced with ${\mathbf{b}}_1$. It immediately follows from (2.2) that$$\begin{array}{c}\hfill \left|\begin{array}{cccc}{b}_i^{(n)}& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}^n& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}^n\\ b_i^{(n+1)}& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}^{n+1}& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}^{n+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_i^{(n+j-1)}& c_{i+1,{\mathit{\kappa }}_2}{r}_{i+1,{\mathit{\kappa }}_2}^{n+j-1}& \cdots & c_{i+j-1,{\mathit{\kappa }}_j}{r}_{i+j-1,{\mathit{\kappa }}_j}^{n+j-1}\end{array}\right|=O({\left({\mathit{\rho }}_i{r}_{i+1,{\mathit{\kappa }}_2}\cdots r_{i+j-1,{\mathit{\kappa }}_j}\right)}^n)\end{array}$$

It is also easy to check $O({(r_{i,{\mathit{\kappa }}_1}{r}_{i+1,{\mathit{\kappa }}_2}\cdots r_{i+\ell -2,{\mathit{\kappa }}_{\ell -1}}{\mathit{\rho }}_{i+\ell -1}{r}_{i+\ell ,{\mathit{\kappa }}_{\ell +1}}\cdots r_{i+j-1,{\mathit{\kappa }}_j})}^n)$ if the $\ell$th column is replaced with ${\mathbf{b}}_{\ell }$. Similarly, by examining the case where some columns are replaced with some of ${\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_j$, we can see that(2.9) $$\begin{array}{c}\hfill \sum _{\mathit{\sigma }}{\widehat{D}}_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}=\sum _{\mathit{\sigma }}{c}_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}{(r_{i,{\mathit{\kappa }}_1}{r}_{i+1,{\mathit{\kappa }}_2}\cdots r_{i+j-1,{\mathit{\kappa }}_j})}^n\sum _{\ell =1}^{j}O\left({\left(\frac{{\mathit{\rho }}_{i+\ell -1}}{|r_{i+\ell -1,{\mathit{\kappa }}_{\ell }}|}\right)}^n\right)\end{array}$$(2.9)

Thus, from (2.7)–(2.9), we obtain (2.5).

Now, let us consider the restriction $r_{i,1}=r_1,r_{i,2}=r_2,\cdots ,r_{i,j}=r_j$ in $f_i(z)$. Then, by replacing $r_{i,\ell }$ with $r_{\ell }$ in (2.3), we easily obtain(2.10) $$\begin{array}{c}\hfill a_i^{(n)}=\sum _{\ell =1}^p{c}_{i,\ell }{r}_{\ell }^n+b_i^{(n)}\end{array}$$(2.10)

As a specialization of Theorem 2.2, we derive the following theorem for an asymptotic expansion of the Casorati determinant $C_{i,j}^{(n)}$ with restricted $a_i^{(n)}$ as $n\to \infty$.

Theorem 2.3

Let us assume that the poles $r_1^{-1},r_2^{-1},\cdots ,r_j^{-1}$ of $f_i(z)$ are not multiple. Then there exists some constant $c_{i,j}\ne 0$ independently of $n$ such that, for $|r_{j+1}|<{\mathit{\rho }}_i<|r_j|$, as $n\to \infty$,(2.11) $$\begin{array}{c}\hfill C_{i,j}^{(n)}=c_{i,j}{\left(r_1{r}_2\cdots r_j\right)}^n\left(1+\sum _{\ell =1}^{j}O\left({\left(\frac{{\mathit{\rho }}_{i+\ell -1}}{|r_j|}\right)}^n\right)\right)\end{array}$$(2.11)

Proof

Replacing $r_{i,1}=r_1,r_{i,2}=r_2,\cdots ,r_{i,p}=r_p$ in (2.8) gives(2.12) $$\begin{array}{c}\hfill c_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}=c_{i,{\mathit{\kappa }}_1}{c}_{i+1,{\mathit{\kappa }}_2}\cdots c_{i+j-1,{\mathit{\kappa }}_j}\left|\begin{array}{cccc}1& 1& \cdots & 1\\ r_{{\mathit{\kappa }}_1}& r_{{\mathit{\kappa }}_2}& \cdots & r_{{\mathit{\kappa }}_j}\\ ⋮& ⋮& \ddots & ⋮\\ r_{{\mathit{\kappa }}_1}^{j-1}& r_{{\mathit{\kappa }}_2}^{j-1}& \cdots & r_{{\mathit{\kappa }}_j}^{j-1}\end{array}\right|\end{array}$$(2.12)

Thus, by taking into account that $c_{\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}\ne 0$ only in the case where ${\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j$ are distinct to each other, we can simplify (2.7) as(2.13) $$\begin{array}{c}\hfill \sum _{\mathit{\pi }}{D}_{i,\mathit{\pi }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}^{(n)}={(r_1{r}_2\cdots r_j)}^n\sum _{\mathit{\pi }}{c}_{i,{\mathit{\kappa }}_1}{c}_{i+1,{\mathit{\kappa }}_2}\cdots c_{i+j-1,{\mathit{\kappa }}_j}\left|\begin{array}{cccc}1& 1& \cdots & 1\\ r_{{\mathit{\kappa }}_1}& r_{{\mathit{\kappa }}_2}& \cdots & r_{{\mathit{\kappa }}_j}\\ ⋮& ⋮& \ddots & ⋮\\ r_{{\mathit{\kappa }}_1}^{j-1}& r_{{\mathit{\kappa }}_2}^{j-1}& \cdots & r_{{\mathit{\kappa }}_j}^{j-1}\end{array}\right|\end{array}$$(2.13)

where $\mathit{\pi }$ denotes the bijection from $\{{\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j\}$ to $\{1,2,\cdots ,j\}$. It is noted here that the bijection $\mathit{\pi }$ is equal to the mapping $\mathit{\sigma }$ with $p=j$. Moreover, there exists a constant ${\mathit{\rho }}_i$, which is not equal to one in Theorem 2.2, such that $|r_{j+1}|<{\mathit{\rho }}_i<|r_j|$. This is because ${\mathit{\rho }}_i$ and ${\mathit{\rho }}_{i+1}$ do not always satisfy ${\mathit{\rho }}_i={\mathit{\rho }}_{i+1}$ even if $r_{i,1}=r_1,r_{i,2}=r_2,\cdots ,r_{i,j}=r_j$ in Theorem 2.2. Thus, (2.9) becomes(2.14) $$\begin{array}{c}\hfill \sum _{\ell =1}^{j}O\left({\left(r_1{r}_2\cdots r_{j-1}{\mathit{\rho }}_{i+\ell -1}\right)}^n\right)\end{array}$$(2.14)

Therefore, from (2.13) and (2.14), we obtain (2.11).

Theorem 2.3 covers an asymptotic expansion of the Hankel determinant $H_j^{(n)}$. Theorems 2.2 and 2.3 should be useful for the asymptotic analysis of dynamical systems with solutions expressed in terms of the Casorati determinant $C_{i,j}^{(n)}$.

3. The dhLV system and its determinant solution

In this section, similarly to work in Tsujimoto and Kondo (2000), Spiridonov and Zhedanov (1997), we derive the dhLV system from a three-term recursion formula, and then clarify the determinant expression of an auxiliary variable in the solution to the dhLV system through investigating the three-term recursion formula.

Let us consider a three-term recursion formula with respect to the polynomials $T_0^{(n)}(x),T_1^{(n)}(x),$$\cdots$ at the discrete time $n$,(3.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{T}_{k+1}^{(n)}(x)=x{T}_k^{(n)}(x)-v_k^{(n)}{T}_{k-M}^{(n)}(x),k=M,M+1,\cdots ,\hfill \\ T_0^{(n)}(x):=1,T_1^{(n)}(x):=x,\cdots ,T_M^{(n)}(x):=x^M\hfill \end{array}\right.\end{array}$$(3.1)

where $M$ is a positive integer and $v_M^{(n)},v_{M+1}^{(n)},\cdots$ do not depend on $x$. Accordingly, $T_0^{(n)}(x),T_1^{(n)}(x),\cdots ,$ are all monic. Moreover, let us prepare a time evolution from $n$ to $n+1$,(3.2) $$\begin{array}{c}\hfill T_k^{(n+1)}(x)=\frac{1}{x^{M+1}-{\left({\mathit{\delta }}^{(n)}\right)}^{M+1}}(T_{k+M+1}^{(n)}(x)-V_k^{(n)}{T}_k^{(n)}(x))\end{array}$$(3.2)

where $V_k^{(n)}:=T_{k+M+1}^{(n)}({\mathit{\delta }}^{(n)})/T_k^{(n)}({\mathit{\delta }}^{(n)})$. Then, by replacing $n$ with $n+1$ in (3.1) and using (3.2), we obtain(3.3) $$\begin{array}{c}\hfill T_{k+M+2}^{(n)}(x)-V_{k+1}^{(n)}{T}_{k+1}^{(n)}(x)=x\left(T_{k+M+1}^{(n)}(x)-V_k^{(n)}{T}_k^{(n)}(x)\right)-v_k^{(n+1)}\left(T_{k+1}^{(n)}(x)-V_{k-M}^{(n)}{T}_{k-M}^{(n)}(x)\right)\end{array}$$(3.3)

By using (3.1) again for deleting except for terms with respect to $T_{k+1}^{(n)}(x)$ and $T_{k-M}^{(n)}(x)$ in (3.3), we derive$$\begin{array}{c}\hfill \left(V_k^{(n)}+v_k^{(n+1)}-v_{k+M+1}^{(n)}-V_{k+1}^{(n)}\right)T_{k+1}^{(n)}(x)=\left(V_k^{(n)}{v}_k^{(n)}-v_k^{(n+1)}{V}_{k-M}^{(n)}\right)T_{k-M}^{(n)}(x)\end{array}$$

Thus, it is observed that(3.4) $$\begin{array}{cc}& V_k^{(n)}+v_k^{(n+1)}=v_{k+M+1}^{(n)}+V_{k+1}^{(n)}\hfill \end{array}$$(3.4) (3.5) $$\begin{array}{cc}& v_k^{(n)}{V}_k^{(n)}=v_k^{(n+1)}{V}_{k-M}^{(n)}\hfill \end{array}$$(3.5)

Let us introduce a new variable $u_k^{(n)}$ such that(3.6) $$\begin{array}{cc}& v_k^{(n)}=u_{k-M}^{(n)}\prod _{j=1}^M\left({\mathit{\delta }}^{(n)}+u_{k-j-M}^{(n)}\right)\hfill \end{array}$$(3.6) (3.7) $$\begin{array}{cc}& V_k^{(n)}=-\prod _{j=0}^M\left({\mathit{\delta }}^{(n)}+u_{k-j}^{(n)}\right)\hfill \end{array}$$(3.7)

Then, it follows from (3.5)–(3.7) that(3.8) $$\begin{array}{c}\hfill v_k^{(n+1)}=u_{k-M}^{(n)}\prod _{j=1}^M\left({\mathit{\delta }}^{(n)}+u_{k-j+1}^{(n)}\right)\end{array}$$(3.8)

Moreover, from (3.6) and (3.8), we see that(3.9) $$\begin{array}{c}\hfill v_k^{(n+1)}-v_{k+M+1}^{(n)}=\prod _{j=0}^M\left({\mathit{\delta }}^{(n)}+u_{k-j}^{(n)}\right)-\prod _{j=0}^M\left({\mathit{\delta }}^{(n)}+u_{k-j+1}^{(n)}\right)\end{array}$$(3.9)

It is obvious from (3.7) that the right-hand side of (3.9) is equal to $V_{k+1}^{(n)}-V_k^{(n)}$. This implies that $v_k^{(n+1)}$ in (3.8) also satisfies (3.4). Consequently, by combining (3.6) and (3.8), noting that ${\prod }_{j=1}^M\left({\mathit{\delta }}^{(n)}+u_{k+1-j}^{(n)}\right)={\prod }_{j=1}^M\left({\mathit{\delta }}^{(n)}+u_{k-M+j}^{(n)}\right)$ and replacing $k-M$ with $k$, we have the discrete system(3.10) $$\begin{array}{c}\hfill u_k^{(n+1)}\prod _{j=1}^M\left({\mathit{\delta }}^{(n+1)}+u_{k-j}^{(n+1)}\right)=u_k^{(n)}\prod _{j=1}^M\left({\mathit{\delta }}^{(n)}+u_{k+j}^{(n)}\right)\end{array}$$(3.10)

Equation (3.10) can be regarded as a discretization of the hLV system which differs from the simple LV system in that more than one food exists for each species. Thus, (3.10) is the dhLV system and $M$ corresponds to the number of the species of foods for each species. Clearly, from the definition, (3.10) with $M=1$ is simply equal to the dLV system. The dhLV system (3.10) is essentially equal to the dhLV system in Fukuda et al. (2009),(3.11) $$\begin{array}{c}\hfill u_k^{(n+1)}\prod _{j=1}^M\left(1+{\mathit{\delta }}^{(n+1)}{u}_{k-j}^{(n+1)}\right)=u_k^{(n)}\prod _{j=1}^M\left(1+{\mathit{\delta }}^{(n)}{u}_{k+j}^{(n)}\right)\end{array}$$(3.11)

This is because (3.11) is derived by replacing $u_k^{(n)}$ with $\left[1/{({\mathit{\delta }}^{(n)})}^M\right]u_k^{(n)}$ and $1/{({\mathit{\delta }}^{(n)})}^{M+1}$ with ${\mathit{\delta }}^{(n)}$ for $n=0,1,\cdots$ in (3.10).

Let ${\tilde{T}}_0^{(n)},{\tilde{T}}_1^{(n)},\cdots$ be polynomials satisfying a three-term recursion formula,(3.12) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\tilde{T}}_{k+1}^{(n)}(x)=x^M{\tilde{T}}_{k-M+1}^{(n)}(x)-w_k^{(n)}{\tilde{T}}_{k-M}^{(n)}(x),k=M,M+1,\cdots ,\hfill \\ {\tilde{T}}_0^{(n)}(x):=1,{\tilde{T}}_1^{(n)}(x):=x,\cdots ,{\tilde{T}}_M^{(n)}(x):=x^M\hfill \end{array}\right.\end{array}$$(3.12)

where $w_M^{(n)},w_{M+1}^{(n)},\cdots ,$ do not depend on $x$. It is obvious from (3.12) that ${\tilde{T}}_M^{(n)}(x)$, ${\tilde{T}}_{M+1}^{(n)}(x)$, $\cdots$ are also all monic. Moreover, let us introduce a linear functional (form) ${\mathcal{L}}^{(n)}$,(3.13) $$\begin{array}{cc}\hfill {\mathcal{L}}^{(n)}[T_k^{(n)}(x^M){\tilde{T}}_{\ell }^{(n)}(x)]& :={\int }_{\mathbb{R}}{T}_k^{(n)}(x^M){\tilde{T}}_{\ell }^{(n)}(x){\mathit{\omega }}^{(n)}(x)dx\hfill \\ \hfill & =\left\{\begin{array}{cc}{h}_k^{(n)}\hfill & (k=\ell )\hfill \\ 0\hfill & (k\ne \ell )\hfill \end{array}\right.\hfill \end{array}$$(3.13)

where ${\mathit{\omega }}^{(n)}(x)$ is a weight function. The linear functional ${\mathcal{L}}^{(n)}$ with $M=1$ is equivalent to that in Chihara (1978). Further, ${\mathcal{L}}^{(n)}$ with arbitrary $M$ is a specialization of a linear function appearing in Maeda, Miki, and Tsujimoto (2013). Since it follows from (3.1), (3.12), and (3.13) that $\mathcal{L}[T_k^{(n)}(x^M)$$x^M{\tilde{T}}_{k-M}^{(n)}(x)]=h_k^{(n)}$ and $\mathcal{L}\left[x^M{T}_k^{(n)}(x^M){\tilde{T}}_{k-M}^{(n)}(x)\right]=v_k^{(n)}{h}_{k-M}^{(n)}$, we easily derive(3.14) $$\begin{array}{c}\hfill v_k^{(n)}=\frac{h_k^{(n)}}{h_{k-M}^{(n)}}\end{array}$$(3.14)

Let ${\mathit{\mu }}_k^{(n)}:={\mathcal{L}}^{(n)}[x^k]$ for $k=0,1,\cdots$. From (3.12), it turns out that ${\tilde{T}}_k^{(n)}(x)$ is expressed as ${\tilde{T}}_k^{(n)}(x)=s_{k,0}^{(n)}+\cdots +s_{k,k-1}^{(n)}{x}^{k-1}+x^k$ where $s_{k,0}^{(n)},\cdots ,s_{k,k-1}^{(n)}$ are some constants at each $k$ and each $n$. Since it is clear from (3.1) that $T_{\ell }^{(n)}(x)$ can be given as the summation of $x^{\ell }$ and the linear combination of $T_0^{(n)}(x)$, $T_1^{(n)}(x)$, $\cdots$, $T_{\ell -1}^{(n)}(x)$, we see from (3.13) that ${\mathcal{L}}^{(n)}[T_{\ell }^{(n)}(x^M){\tilde{T}}_k^{(n)}(x)]={\mathcal{L}}^{(n)}[x^{\ell M}{\tilde{T}}_k^{(n)}(x)]$. Thus, it follows that$$\begin{array}{cc}& {\mathcal{L}}^{(n)}[T_0^{(n)}(x^M){\tilde{T}}_k^{(n)}(x)]=s_{k,0}^{(n)}{\mathit{\mu }}_0^{(n)}+\cdots +s_{k,k-1}^{(n)}{\mathit{\mu }}_{k-1}^{(n)}+{\mathit{\mu }}_k^{(n)}\hfill \\ \hfill & ⋮\hfill \\ \hfill & {\mathcal{L}}^{(n)}[T_{k-1}^{(n)}(x^M){\tilde{T}}_k^{(n)}(x)]=s_{k,0}^{(n)}{\mathit{\mu }}_{(k-1)M}^{(n)}+\cdots +s_{k,k-1}^{(n)}{\mathit{\mu }}_{(k-1)(M+1)}^{(n)}+{\mathit{\mu }}_{(k-1)M+k}^{(n)}\hfill \\ \hfill & {\mathcal{L}}^{(n)}[T_k^{(n)}(x^M){\tilde{T}}_k^{(n)}(x)]=s_{k,0}^{(n)}{\mathit{\mu }}_{kM}^{(n)}+\cdots +s_{k,k-1}^{(n)}{\mathit{\mu }}_{k(M+1)-1}^{(n)}+{\mathit{\mu }}_{k(M+1)}^{(n)}\hfill \end{array}$$

By combining the above with (3.13), we derive a system of linear equations(3.15) $$\begin{array}{c}\hfill \left(\begin{array}{cccc}{\mathit{\mu }}_0^{(n)}& \cdots & {\mathit{\mu }}_{k-1}^{(n)}& {\mathit{\mu }}_k^{(n)}\\ ⋮& \ddots & ⋮& ⋮\\ {\mathit{\mu }}_{(k-1)M}^{(n)}& \cdots & {\mathit{\mu }}_{(k-1)(M+1)}^{(n)}& {\mathit{\mu }}_{(k-1)M+k}^{(n)}\\ {\mathit{\mu }}_{kM}^{(n)}& \cdots & {\mathit{\mu }}_{k(M+1)-1}^{(n)}& {\mathit{\mu }}_{k(M+1)}^{(n)}\end{array}\right)\left(\begin{array}{c}{s}_{k,0}^{(n)}\\ ⋮\\ s_{k,k-1}^{(n)}\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ ⋮\\ 0\\ h_k^{(n)}\end{array}\right).\end{array}$$(3.15)

Since $s_{k,0}^{(n)},\cdots ,s_{k,k-1}^{(n)}$ are uniquely determined, the coefficient matrix in (3.15) is nonsingular. This suggests that (3.15) can be transformed into(3.16) $$\begin{array}{c}\hfill \left(\begin{array}{c}{s}_{k,0}^{(n)}\\ ⋮\\ s_{k,k-1}^{(n)}\\ 1\end{array}\right)=\frac{1}{{\mathit{\tau }}_{k+1}^{(n)}}\left(\begin{array}{cccc}{\widehat{\mathit{\mu }}}_0^{(n)}& \cdots & {\widehat{\mathit{\mu }}}_{k-1}^{(n)}& {\widehat{\mathit{\mu }}}_k^{(n)}\\ ⋮& \ddots & ⋮& ⋮\\ {\widehat{\mathit{\mu }}}_{(k-1)M}^{(n)}& \cdots & {\widehat{\mathit{\mu }}}_{(k-1)(M+1)}^{(n)}& {\widehat{\mathit{\mu }}}_{(k-1)M+k}^{(n)}\\ {\widehat{\mathit{\mu }}}_{kM}^{(n)}& \cdots & {\widehat{\mathit{\mu }}}_{k(M+1)-1}^{(n)}& {\widehat{\mathit{\mu }}}_{k(M+1)}^{(n)}\end{array}\right)\left(\begin{array}{c}0\\ ⋮\\ 0\\ h_k^{(n)}\end{array}\right),\end{array}$$(3.16)

where the hat denotes cofactors of the coefficient matrix in (3.15) and(3.17) $$\begin{array}{c}\hfill {\mathit{\tau }}_{k+1}^{(n)}:=\left|\begin{array}{cccc}{\mathit{\mu }}_0^{(n)}& \cdots & {\mathit{\mu }}_{k-1}^{(n)}& {\mathit{\mu }}_k^{(n)}\\ ⋮& \ddots & ⋮& ⋮\\ {\mathit{\mu }}_{(k-1)M}^{(n)}& \cdots & {\mathit{\mu }}_{(k-1)(M+1)}^{(n)}& {\mathit{\mu }}_{(k-1)M+k}^{(n)}\\ {\mathit{\mu }}_{kM}^{(n)}& \cdots & {\mathit{\mu }}_{k(M+1)-1}^{(n)}& {\mathit{\mu }}_{k(M+1)}^{(n)}\end{array}\right|\end{array}$$(3.17)

It is of significance to note that ${\widehat{\mathit{\mu }}}_{k(M+1)}^{(n)}={\mathit{\tau }}_k^{(n)}$. Thus, by examining the last row for both sides of (3.16), we find(3.18) $$\begin{array}{c}\hfill h_k^{(n)}=\frac{{\mathit{\tau }}_{k+1}^{(n)}}{{\mathit{\tau }}_k^{(n)}}\end{array}$$(3.18)

Equations (3.14) and (3.18) therefore lead to(3.19) $$\begin{array}{c}\hfill v_k^{(n)}=\frac{{\mathit{\tau }}_{k+1}^{(n)}{\mathit{\tau }}_{k-M}^{(n)}}{{\mathit{\tau }}_k^{(n)}{\mathit{\tau }}_{k-M+1}^{(n)}}\end{array}$$(3.19)

Since we can easily obtain the solution to the dhLV system (3.10), by combining (3.6) with (3.19), the determinant expression of $v_k^{(n)}$ is important for the asymptotic analysis of the dhLV system (3.10) in the next section.

Let us define the time evolution of the linear functional from ${\mathcal{L}}^{(n)}$ to ${\mathcal{L}}^{(n+1)}$ by(3.20) $$\begin{array}{c}\hfill {\mathcal{L}}^{(n+1)}[P(x)]={\mathcal{L}}^{(n)}\left[{\left(x^{M(M+1)}-({\mathit{\delta }}^{(n)}\right)}^{M+1})P(x)\right]\end{array}$$(3.20)

where $P(x)$ is an arbitrary polynomial. Then, it is easy to check that $T_k^{(n+1)}(x^M)$ and ${\tilde{T}}_{\ell }^{(n)}(x)$ are orthogonal to each other with respect to ${\mathcal{L}}^{(n+1)}$. Equation (3.20) yields a time evolution with respect to $\mathit{\mu }$’s,(3.21) $$\begin{array}{c}\hfill {\mathit{\mu }}_k^{(n+1)}={\mathit{\mu }}_{k+M(M+1)}^{(n)}-{({\mathit{\delta }}^{(n)})}^{M+1}{\mathit{\mu }}_k^{(n)}\end{array}$$(3.21)

Noting (3.1) and (3.12), we find that ${\mathcal{L}}^{(n)}[T_k^{(n)}(x^M){\tilde{T}}_{\ell }^{(n)}(x)]$ with $k=\ell$ can be expressed as the linear combination of ${\mathit{\mu }}_0^{(n)}$, ${\mathit{\mu }}_{(M+1)}^{(n)}$, $\cdots$, ${\mathit{\mu }}_{k(M+1)}^{(n)}$. Thus, by combining it with (3.13), we derive(3.22) $$\begin{array}{c}\hfill {\mathit{\mu }}_{j(M+1)}^{(n)}\ne 0,j=0,1,\cdots ,k\end{array}$$(3.22)

Similarly, in the case where ${\mathcal{L}}^{(n)}\left[T_k^{(n)}(x^M){\tilde{T}}_{\ell }^{(n)}(x)\right]$ with $k\ne \ell$, we have(3.23) $$\begin{array}{c}\hfill {\mathit{\mu }}_{i+j(M+1)}^{(n)}=0,i=1,2,\cdots ,M,j=0,1,\cdots ,k\end{array}$$(3.23)

Taking into account that the sequence ${\{{\mathit{\mu }}_{j(M+1)}^{(n)}\}}_{n=0,1,\cdots }$ with (3.21) is a specialization of the sequence ${\left\{a_j^{(n)}\right\}}_{n=0,1,\cdots }$ appearing in the previous section, we may replace ${\mathit{\mu }}_{j(M+1)}^{(n)}$ with $a_j^{(n)}$ in the following discussion. Thus, we can rewrite ${\mathit{\tau }}_k^{(n)}$ as$$\begin{array}{cc}& {\mathit{\tau }}_0^{(n)}:=1,{\mathit{\tau }}_{j(M+1)}^{(n)}:=\left|\begin{array}{cccc}{\mathit{\tau }}_{0,M}^{(n)}& {\mathit{\tau }}_{1,M}^{(n)}& \cdots & {\mathit{\tau }}_{j-1,M}^{(n)}\\ {\mathit{\tau }}_{M,M}^{(n)}& {\mathit{\tau }}_{M+1,M}^{(n)}& \cdots & {\mathit{\tau }}_{M+j-1,M}^{(n)}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{\tau }}_{(j-1)M,M}^{(n)}& {\mathit{\tau }}_{(j-1)M+1,M}^{(n)}& \cdots & {\mathit{\tau }}_{(j-1)(M+1)-1,M}^{(n)}\end{array}\right|\hfill \\ \hfill & {\mathit{\tau }}_{i+j(M+1)}^{(n)}:=\left|\begin{array}{ccccc}{\mathit{\tau }}_{0,M}^{(n)}& {\mathit{\tau }}_{1,M}^{(n)}& \cdots & {\mathit{\tau }}_{j-1,M}^{(n)}& {\mathit{\tau }}_{j,i-1}^{(n)}\\ {\mathit{\tau }}_{M,M}^{(n)}& {\mathit{\tau }}_{M+1,M}^{(n)}& \cdots & {\mathit{\tau }}_{M+j-1,M}^{(n)}& {\mathit{\tau }}_{M+j,i-1}^{(n)}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ {\mathit{\tau }}_{(j-1)M,M}^{(n)}& {\mathit{\tau }}_{(j-1)M+1,M}^{(n)}& \cdots & {\mathit{\tau }}_{(j-1)(M+1)-1,M}^{(n)}& {\mathit{\tau }}_{(j-1)(M+1),i-1}^{(n)}\\ {\mathit{\tau }}_{jM,i-1}^{(n)}& {\mathit{\tau }}_{jM+1,i-1}^{(n)}& \cdots & {\mathit{\tau }}_{j(M+1)-1,i-1}^{(n)}& {\mathit{\tau }}_{j(M+1),i-1}^{(n)}\end{array}\right|,i=1,2,\cdots ,M\hfill \end{array}$$

where ${\mathit{\tau }}_{s,t}^{(n)}:=\mathrm{diag}(a_s^{(n)},a_{s+1}^{(n)},\cdots ,a_{s+t}^{(n)})$ is an $(t+1)$-by-$(t+1)$ diagonal matrix with the relationship concerning the evolution from $n$ to $n+1$,(3.24) $$\begin{array}{c}\hfill a_k^{(n+1)}=a_{k+M}^{(n)}-{({\mathit{\delta }}^{(n)})}^{M+1}{a}_k^{(n)}\end{array}$$(3.24)

4. Asymptotic analysis of the dhLV system

This section begins by explaining that the auxiliary variable in the dhLV system can be rewritten in terms of the Casorati determinant. By using Theorem 2.2, we clarify the asymptotic behavior of the dhLV variables as $n\to \infty$.

The $1$st, $2$nd, $\cdots$, $(j-1)$th row and column blocks in ${\mathit{\tau }}_{i+j(M+1)}^{(n)}$ are $M$-by-$M$ matrices, but the $j$th row and column blocks are $(i-1)$-by-$(i-1)$ matrices. The following lemma gives the representation of $v_k^{(n)}$ in terms of the $C_{i,j}^{(n)}$ appearing in Section 1.

Lemma 4.1

The auxiliary variable $v_k^{(n)}$ is expressed as(4.1) $$\begin{array}{cc}& v_{i+j(M+1)}^{(n)}=\frac{{\displaystyle C_{i,j+1}^{(n)}{C}_{i+1,j-1}^{(n)}}}{{\displaystyle C_{i,j}^{(n)}{C}_{i+1,j}^{(n)}}},i=0,1,\cdots ,M-1,j=1,2,\cdots ,m-1\hfill \end{array}$$(4.1) (4.2) $$\begin{array}{cc}& v_{M+j(M+1)}^{(n)}=\frac{{\displaystyle C_{M,j+1}^{(n)}{C}_{0,j}^{(n)}}}{{\displaystyle C_{M,j}^{(n)}{C}_{0,j+1}^{(n)}}},j=0,1,\cdots ,m-1\hfill \end{array}$$(4.2)

Proof

Let us introduce a new determinant of a square matrix of order $j$,(4.3) $$\begin{array}{c}\hfill G_{i,0}^{(n)}:=1,G_{i,j}^{(n)}:=\left|\begin{array}{cccc}{a}_i^{(n)}& a_{i+1}^{(n)}& \cdots & a_{i+j-1}^{(n)}\\ a_{i+M}^{(n)}& a_{i+M+1}^{(n)}& \cdots & a_{i+M+j-1}^{(n)}\\ ⋮& ⋮& \ddots & ⋮\\ a_{i+M(j-1)}^{(n)}& a_{i+M(j-1)+1}^{(n)}& \cdots & a_{i+(M+1)(j-1)}^{(n)}\end{array}\right|,j=1,2,\cdots \end{array}$$(4.3)

We begin by showing that ${\mathit{\tau }}_{j(M+1)}^{(n)}$ can be transformed into a block diagonal determinant with respect to $G_{0,j}^{(n)},G_{1,j}^{(n)},\cdots ,G_{M,j}^{(n)}$. By interchanging the $2$nd, $3$rd, $\cdots$$j$th rows and columns with the $[1+(M+1)]$th, $[1+2(M+1)]$th, $\cdots$, $[1+(j-1)(M+1)]$th rows and columns in ${\mathit{\tau }}_{j(M+1)}^{(n)}$, we observe that the same form of $G_{0,j}^{(n)}$ appears in the $1$st diagonal block of ${\mathit{\tau }}_{j(M+1)}^{(n)}$. The entries in the $1$st, $2$nd, $\cdots$, $j$th rows and columns in ${\mathit{\tau }}_{j(M+1)}^{(n)}$ are simultaneously all $0$, except for those in the diagonal block section. Permutations similar to the above provide the forms of $G_{1,j}^{(n)},G_{2,j}^{(n)},\cdots ,G_{M,j}^{(n)}$ as the $2$nd, $3$rd, $\cdots$, $(M+1)$th blocks in ${\mathit{\tau }}_{j(M+1)}^{(n)}$. Thus, ${\mathit{\tau }}_{j(M+1)}^{(n)}$ can be expressed in terms of $G_{0,j}^{(n)},G_{1,j}^{(n)},\cdots ,G_{M,j}^{(n)}$ as(4.4) $$\begin{array}{c}\hfill {\mathit{\tau }}_{j(M+1)}^{(n)}=\prod _{\ell =0}^M{G}_{\ell ,j}^{(n)}\end{array}$$(4.4)

Similarly, ${\mathit{\tau }}_{i+j(M+1)}^{(n)}$ can be transformed into the determinant of a block diagonal matrix whose $M+1$ blocks are $G_{0,j+1}^{(n)},G_{1,j+1}^{(n)},\cdots ,G_{i-1,j+1}^{(n)}$ and $G_{i,j}^{(n)},G_{i+1,j}^{(n)},\cdots ,G_{M,j}^{(n)}$. Thus, it follows that(4.5) $$\begin{array}{c}\hfill {\mathit{\tau }}_{i+j(M+1)}^{(n)}=\left(\prod _{\ell =0}^{i-1}{G}_{\ell ,j+1}^{(n)}\right)\left(\prod _{\ell =i}^M{G}_{\ell ,j}^{(n)}\right)\end{array}$$(4.5)

The cases where $k=i+j(M+1)$ and $k=M+j(M+1)$ in (3.19) become$$\begin{array}{cc}& v_{i+j(M+1)}^{(n)}=\frac{{\mathit{\tau }}_{i+j(M+1)+1}^{(n)}{\mathit{\tau }}_{i+(j-1)(M+1)+1}^{(n)}}{{\mathit{\tau }}_{i+j(M+1)}^{(n)}{\mathit{\tau }}_{i+(j-1)(M+1)+2}^{(n)}}\hfill \end{array}$$(4.6) $$\begin{array}{cc}& v_{M+j(M+1)}^{(n)}=\frac{{\mathit{\tau }}_{(j+1)(M+1)}^{(n)}{\mathit{\tau }}_{j(M+1)}^{(n)}}{{\mathit{\tau }}_{M+j(M+1)}^{(n)}{\mathit{\tau }}_{j(M+1)+1}^{(n)}}\hfill \end{array}$$(4.6)

By combining them with (4.4) and (4.5), we obtain(4.7) $$\begin{array}{cc}& v_{i+j(M+1)}^{(n)}=\frac{{\displaystyle G_{i,j+1}^{(n)}{G}_{i+1,j-1}^{(n)}}}{{\displaystyle G_{i,j}^{(n)}{G}_{i+1,j}^{(n)}}},i=0,1,\cdots ,M-1\hfill \\ \hfill & v_{M+j(M+1)}^{(n)}=\frac{{\displaystyle G_{M,j+1}^{(n)}{G}_{0,j}^{(n)}}}{{\displaystyle G_{M,j}^{(n)}{G}_{0,j+1}^{(n)}}}\hfill \end{array}$$(4.7)

The entries in the $j$th row of $G_{i,j}^{(n)}$ are given by the linear combination $a_{i+M(j-1)+\ell }^{(n)}=a_{i+M(j-2)+\ell }^{(n+1)}+{({\mathit{\delta }}^{(n)})}^{M+1}{a}_{i+M(j-2)+\ell }^{(n)}$ for $\ell =0,1,\cdots ,j-1$. By multiplying the $(j-1)$th row by $-{({\mathit{\delta }}^{(n)})}^{M+1}$ and then adding it to the $j$th, we get row $(a_{i+M(j-2)}^{(n+1)},a_{i+M(j-2)+1}^{(n+1)},\cdots ,a_{i+(M+1)(j-2)+1}^{(n+1)})$ as the new $j$th row. Similarly, for the $(j-1)$th, $(j-2)$th, $\cdots$, $2$nd rows, it follows that$$\begin{array}{c}\hfill G_{i,j}^{(n)}=\left|\begin{array}{cccc}{a}_i^{(n)}& a_{i+1}^{(n)}& \cdots & a_{i+j-1}^{(n)}\\ a_i^{(n+1)}& a_{i+1}^{(n+1)}& \cdots & a_{i+j-1}^{(n+1)}\\ ⋮& ⋮& \ddots & ⋮\\ a_{i+M(j-2)}^{(n+1)}& a_{i+M(j-2)+1}^{(n+1)}& \cdots & a_{i+(M+1)(j-2)+1}^{(n+1)}\end{array}\right|\end{array}$$

It is worth noting here that the subscript $M$ can be regarded as be transformed into the superscript $1$. Thus, $G_{i,j}^{(n)}$ in (4.3) is equal to the Casorati determinant $C_{i,j}^{(n)}$ in (1.3). Then, by accounting for it in (4.6) and (4.7), we have (4.1) and (4.2).

Lemma 4.1 with Theorem 2.2 leads to the following theorem for asymptotic behavior of $v_{M+j(M+1)}^{(n)}$ as $n\to \infty$.

Theorem 4.2

The auxiliary variable $v_{M+j(M+1)}^{(n)}$ converges to some constant ${\widehat{c}}_j$ as $n\to \infty$.

Proof

Let ${\mathit{\sigma }}^{\ast }$ be the mapping from $\{{\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j\}$ to $\{{\mathit{\kappa }}_1^{\ast },{\mathit{\kappa }}_2^{\ast },\cdots ,{\mathit{\kappa }}_j^{\ast }\}$ where ${\mathit{\kappa }}_1^{\ast },{\mathit{\kappa }}_2^{\ast },\cdots ,{\mathit{\kappa }}_j^{\ast }$ are positive integers such that $r_{i,{\mathit{\kappa }}_1^{\ast }}{r}_{i+1,{\mathit{\kappa }}_2^{\ast }}\cdots r_{i+j-1,{\mathit{\kappa }}_j^{\ast }}={\displaystyle \underset{\mathit{\sigma }}{max}}(r_{i,{\mathit{\kappa }}_1}{r}_{i+1,{\mathit{\kappa }}_2}\cdots r_{i+j-1,{\mathit{\kappa }}_j})$. Then, it follows from Theorem 2.2 that(4.8) $$\begin{array}{cc}& \underset{n\to \infty }{lim}\frac{C_{i,j}^{(n)}}{{\left(r_{i,{\mathit{\kappa }}_1^{\ast }}{r}_{i+1,{\mathit{\kappa }}_2^{\ast }}\cdots r_{i+j-1,{\mathit{\kappa }}_j^{\ast }}\right)}^n}\hfill \\ \hfill & =\underset{n\to \infty }{lim}\{c_{i,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}(1+\sum _{\ell =1}^{j}O((\frac{{\mathit{\rho }}_{i+\ell -1}}{|r_{i+\ell -1,{\mathit{\kappa }}_{\ell }^{\ast }}|}{)}^n))\hfill \\ \hfill & +\sum _{\mathit{\sigma }\backslash {\mathit{\sigma }}^{\ast }}[c_{i,\mathit{\sigma }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}(\frac{r_{i,{\mathit{\kappa }}_1}{r}_{i+1,{\mathit{\kappa }}_2}\cdots r_{i+j-1,{\mathit{\kappa }}_j}}{r_{i,{\mathit{\kappa }}_1^{\ast }}{r}_{i+1,{\mathit{\kappa }}_2^{\ast }}\cdots r_{i+j-1,{\mathit{\kappa }}_j^{\ast }}}{)}^n(1+\sum _{\ell =1}^{j}O((\frac{{\mathit{\rho }}_{i+\ell -1}}{|r_{i+\ell -1,{\mathit{\kappa }}_{\ell }}|}{)}^n))]\}\hfill \\ \hfill & =c_{i,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}\hfill \end{array}$$(4.8)

It is of significance to note the relationship between $f_i(z)$ and $f_{i+M}(z)$ is derived from (3.24),(4.9) $$\begin{array}{cc}\hfill f_{i+M}(z)& =\frac{\left[1+{({\mathit{\delta }}^{(n)})}^{M+1}z\right]f_i(z)-a_i^{(0)}}{z}\hfill \end{array}$$(4.9)

Equation (4.9) implies that the poles of $f_i(z)$ and $f_{i+M}(z)$ are equal to each other, namely, $r_{i,1}=r_{i+M,1}$, $r_{i,2}=r_{i+M,2}$, $\cdots$. Thus, by combining them with Theorem 2.2, we derive(4.10) $$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\frac{C_{i+M,j}^{(n)}}{{\left(r_{i,{\mathit{\kappa }}_1^{\ast }}{r}_{i+1,{\mathit{\kappa }}_2^{\ast }}\cdots r_{i+j-1,{\mathit{\kappa }}_j^{\ast }}\right)}^n}& =\underset{n\to \infty }{lim}\frac{C_{i+M,j}^{(n)}}{{\left(r_{i+M,{\mathit{\kappa }}_1^{\ast }}{r}_{i+M+1,{\mathit{\kappa }}_2^{\ast }}\cdots r_{i+M+j-1,{\mathit{\kappa }}_j^{\ast }}\right)}^n}\hfill \\ \hfill & =c_{i+M,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}\hfill \end{array}$$(4.10)

Since (4.8) and (4.10) imply that $C_{0,j}^{(n)}/C_{M,j}^{(n)}\to c_{0,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}/c_{M,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}$ as $n\to \infty$, we can conclude that $v_{M+j(M+1)}^{(n)}\to {\widehat{c}}_j=(c_{0,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}{c}_{M,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_{j+1})})/(c_{M,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_j)}{c}_{0,{\mathit{\sigma }}^{\ast }({\mathit{\kappa }}_1,{\mathit{\kappa }}_2,\cdots ,{\mathit{\kappa }}_{j+1})})$ as $n\to \infty$.

By considering the positivity of $v_{j(M+1)}^{(n)}$, $v_{1+j(M+1)}^{(n)}$, $\cdots$, $v_{M-1+j(M+1)}^{(n)}$, we derive the following theorem for the asymptotic behavior of $v_{j(M+1)}^{(n)}$, $v_{1+j(M+1)}^{(n)}$, $\cdots$, $v_{M-1+j(M+1)}^{(n)}$ as $n\to \infty$.

Theorem 4.3

Let us assume that $v_{j(M+1)}^{(n)}>0$, $v_{1+j(M+1)}^{(n)}>0$, $\cdots$, $v_{M-1+j(M+1)}^{(n)}>0$ for $n=0,1,\cdots$. Then $v_{j(M+1)}^{(n)}$, $v_{1+j(M+1)}^{(n)}$, $\cdots$, $v_{M-1+j(M+1)}^{(n)}$ converge to $0$ as $n\to \infty$.

Proof

From the Jacobi determinant identity (Hirota, 2003), it follows that(4.11) $$\begin{array}{c}\hfill C_{i,j+1}^{(n)}{C}_{i+1,j-1}^{(n+1)}=C_{i,j}^{(n)}{C}_{i+1,j}^{(n+1)}-C_{i,j}^{(n+1)}{C}_{i+1,j}^{(n)}\end{array}$$(4.11)

Equation (4.11) allows us to simplify ${\sum }_{i=0}^{M-1}{v}_{i+j(M+1)}^{(n)}$ as(4.12) $$\begin{array}{cc}\hfill \sum _{i=0}^{M-1}{v}_{i+j(M+1)}^{(n)}& =\sum _{i=0}^{M-1}(\frac{C_{i+1,j}^{(n+1)}}{C_{i+1,j}^{(n)}}-\frac{C_{i,j}^{(n+1)}}{C_{i,j}^{(n)}})\hfill \\ \hfill & =\frac{C_{M,j}^{(n+1)}}{C_{M,j}^{(n)}}-\frac{C_{0,j}^{(n+1)}}{C_{0,j}^{(n)}}\hfill \end{array}$$(4.12)

From (4.8), we derive(4.13) $$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\frac{C_{i,j}^{(n+1)}}{C_{i,j}^{(n)}}=r_{i,{\mathit{\kappa }}_1^{\ast }}{r}_{i+1,{\mathit{\kappa }}_2^{\ast }}\cdots r_{i+j-1,{\mathit{\kappa }}_j^{\ast }}\end{array}$$(4.13)

Thus, by combining (4.13) and $r_{M,{\mathit{\kappa }}_1^{\ast }}=r_{0,{\mathit{\kappa }}_1^{\ast }}$, $r_{M+1,{\mathit{\kappa }}_2^{\ast }}=r_{1,{\mathit{\kappa }}_2^{\ast }}$, $\cdots$, $r_{M+j-1,{\mathit{\kappa }}_j^{\ast }}=r_{j-1,{\mathit{\kappa }}_j^{\ast }}$ with (4.12), we have(4.14) $$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\sum _{i=0}^{M-1}{v}_{i+j(M+1)}^{(n)}& =0\hfill \end{array}$$(4.14)

Therefore, by taking into account that $v_{j(M+1)}^{(n)}>0$, $v_{1+j(M+1)}^{(n)}>0$, $\cdots$, $v_{M-1+j(M+1)}^{(n)}>0$ in (4.14), we find that $v_{j(M+1)}^{(n)}\to 0$, $v_{1+j(M+1)}^{(n)}\to 0$, $\cdots$, $v_{M-1+j(M+1)}^{(n)}\to 0$ as $n\to \infty$.

By recalling the relationship of the dhLV variable $u_k^{(n)}$ to the auxiliary variable $v_k^{(n)}$ in (3.6), we have the following theorem concerning an asymptotic convergence of $u_k^{(n)}$ as $n\to \infty$.

Theorem 4.4

As $n\to \infty$, the dhLV variable $u_{j(M+1)}^{(n)}$ converges to some nonzero constant ${\overline{c}}_j$, and $u_{1+j(M+1)-M}^{(n)}$, $u_{2+j(M+1)-M}^{(n)}$, $\cdots$, $u_{M+j(M+1)}^{(n)}$ go to $0$, provided that ${\mathit{\delta }}^{(n)}$ satisfy $u_{k-M}^{(n)}{\prod }_{j=1}^M({\mathit{\delta }}^{(n)}+u_{k-M-j}^{(n)})>0$ for $n=0,1,\cdots$ and the limit of ${\mathit{\delta }}^{(n)}$ as $n\to \infty$ exists.

Proof

The proof is given by induction for $j$. Without loss of generality, let us assume that ${lim}_{n\to \infty }{\mathit{\delta }}^{(n)}=\mathit{\delta }$ where $\mathit{\delta }$ denotes some constant. From (3.6), it holds that(4.15) $$\begin{array}{c}\hfill u_k^{(n)}=\frac{v_{k+M}^{(n)}}{{\displaystyle \prod _{\ell =1}^M\left({\mathit{\delta }}^{(n)}+u_{k-\ell }^{(n)}\right)}}\end{array}$$(4.15)

By taking the limit as $n\to \infty$ of both sides of (4.15) with $k=0$ and using $v_M^{(n)}\to {\widehat{c}}_0$ as $n\to \infty$, we obtain(4.16) $$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{u}_0^{(n)}& ={\overline{c}}_0\hfill \end{array}$$(4.16)

where ${\overline{c}}_0={\widehat{c}}_0/{\mathit{\delta }}^M$. By considering Theorem 4.2 with (4.16) in the case where $k=1,2,\cdots ,M$ in (4.15), we successively check that $u_1^{(n)}\to 0,u_2^{(n)}\to 0,\cdots ,u_M^{(n)}\to 0$ as $n\to \infty$.

Let us assume that $u_{j(M+1)}^{(n)}\to {\overline{c}}_j$ and $u_{1+j(M+1)}^{(n)}\to 0,u_{2+j(M+1)}^{(n)}\to 0,\cdots ,u_{M+j(M+1)}^{(n)}\to 0$ as $n\to \infty$. Equation (4.15) with $k=(j+1)(M+1)$ becomes(4.17) $$\begin{array}{cc}\hfill u_{(j+1)(M+1)}^{(n)}& =\frac{v_{M+(j+1)(M+1)}^{(n)}}{{\displaystyle \prod _{\ell =1}^M\left({\mathit{\delta }}^{(n)}+u_{(j+1)(M+1)-\ell }^{(n)}\right)}}\hfill \end{array}$$(4.17)

It is clear that the denominator on the right-hand side of (4.17) converges to ${\mathit{\delta }}^M$ as $n\to \infty$ under this assumption. By combining it with $v_{M+(j+1)(M+1)}^{(n)}\to {\widehat{c}}_{j+1}$ as $n\to \infty$, we observe that $u_{(j+1)(M+1)}^{(n)}\to {\overline{c}}_{j+1}={\widehat{c}}_{j+1}/{\mathit{\delta }}^M$ as $n\to \infty$. Moreover, it follows that(4.18) $$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{u}_{i+(j+1)(M+1)+1}^{(n)}=\underset{n\to \infty }{lim}\frac{v_{i+(j+2)(M+1)}^{(n)}}{{\displaystyle \prod _{\ell =1}^M\left({\mathit{\delta }}^{(n)}+u_{i+(j+1)(M+1)+1-\ell }^{(n)}\right)}}=0,i=0,1,\cdots ,M-1\end{array}$$(4.18)

since ${\prod }_{\ell =1}^M\left({\mathit{\delta }}^{(n)}+u_{i+(j+1)(M+1)+1-\ell }^{(n)}\right)\to {\mathit{\delta }}^{M-1}\left(\mathit{\delta }+{\overline{c}}_{j+1}\right)$ and $v_{i+(j+2)(M+1)}^{(n)}\to 0$ as $n\to \infty$.

The convergence theorem concerning the dhLV system (3.10) in Fukuda et al. (2009) is restricted to the case where the dhLV variable $u_k^{(n)}$ is positive and the discretization parameter ${\mathit{\delta }}^{(n)}$ is fixed positive for every $n$. Theorem 4.4 claims that the $[j(M+1)]$th species survives and the $[1+j(M+1)]$th, $[2+j(M+1)]$th,..., $[M+j(M+1)]$th species vanish as $n\to \infty$ even in the case where ${\mathit{\delta }}^{(n)}$ is a changeable negative for each $n$. Although the case of negative $u_k^{(n)}$ is not longer recognized as a valid biological model, we note that the convergence is not different from the positive case if the values of ${\mathit{\delta }}^{(n)}$ are suitable for $n=0,1,\cdots$.

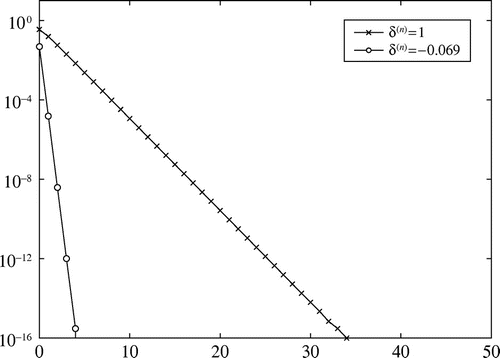
To observe the asymptotic convergence numerically, we consider two cases where ${\mathit{\delta }}^{(n)}=1$ and ${\mathit{\delta }}^{(n)}=-0.069$ in the dhLV system (3.10). The initial values are set as $u_k^{(0)}={({\mathit{\delta }}^{(n)})}^M/{\prod }_{\ell =1}^M({\mathit{\delta }}^{(n)}+u_{k-\ell }^{(0)})$ for $k=0,1,\cdots ,8$ in the dhLV system (3.10) with $M=3$ and $m=3$. Figure 1 shows the behavior of $u_7^{(n)}$ for $n=0,1,\cdots ,50$ in the case where ${\mathit{\delta }}^{(n)}=1$ and ${\mathit{\delta }}^{(n)}=-0.069$. This figure demonstrates that $u_7^{(n)}$ tends to $0$ as $n$ grows larger even if ${\mathit{\delta }}^{(n)}<0$. We also see that the case where ${\mathit{\delta }}^{(n)}=-0.069$ has a superior convergence speed in comparison with the case where ${\mathit{\delta }}^{(n)}=1$. Similarly, the asymptotic behavior of $u_0^{(n)},u_1^{(n)},\cdots ,u_8^{(n)}$ can be seen to follow Theorem 4.4.

Figure 1. A graph of the discrete time $n$ ($x$-axis) and the value of $|u_7^{(n)}|$ ($y$-axis) in the dhLV system (3.10) with $M=3$ and $m=3$. Cross : ${\mathit{\delta }}^{(n)}=1$, Circle : ${\mathit{\delta }}^{(n)}=-0.069$.

5. Concluding remarks

In this paper, we associated a formal power series $f_i(z)={\sum }_{n=0}^{\infty }{a}_i^{(n)}{z}^n$ with the Casorati determinant $C_{i,j}^{(n)}$, and gave asymptotic expansions of the Casorati determinants as $n\to \infty$ in Theorems 2.2 and 2.3. By making use of Theorem 2.2, we then clarified the asymptotic behavior of the dhLV variables as $\to \infty$ in Theorem 4.4.

Theorems 2.2 and 2.3 may contribute to asymptotic analysis for other discrete integrable systems. One possible application is the discrete hungry Toda (dhToda) equation derived from the numbered box and ball system through inverse ultra-discretization (Tokihiro, Nagai, & Satsuma, 1999). The dhToda equation has a relationship of variables to the dhLV system whose solution is given in the Casorati determinant (Fukuda, Yamamoto, Iwasaki, Ishiwata, & Nakamura, 2011). The Casorati determinant directly appears in, for example, the solution to the discrete Darboux–Pöschl–Teller equation which is a discretization of a dynamical system concerning a special class of potentials for the $1$-dimensional Schrödinger equation (Gaillard & Matveev, 2009).

It was proved in Fukuda et al. (2013) that the dhLV system (3.10) with a fixed positive ${\mathit{\delta }}^{(n)}$ is associated with the $LR$ transformation for a TN matrix. The paper (Yamamoto et al., 2010) also suggested that the dhLV system (3.10) with changeable negative ${\mathit{\delta }}^{(n)}$ generates the shifted $LR$ transformation for a TN matrix. Eigenvalues of an $m$-by-$m$ TN matrix correspond to the constants ${\widehat{c}}_1={\mathit{\delta }}^M{\overline{c}}_1$, ${\widehat{c}}_2={\mathit{\delta }}^M{\overline{c}}_2$, $\cdots$, ${\widehat{c}}_m={\mathit{\delta }}^M{\overline{c}}_m$ in Theorem 4.4. Theorems 4.2–4.4 will be useful for investigating the convergence of the sequence of the shifted $LR$ transformations based on the dhLV system (3.10) in the changeable negative case of ${\mathit{\delta }}^{(n)}$.

Acknowledgements

The authors would like to thank Prof. S. Tsujimoto for helpful discussions on the determinant expression. The authors also thank the reviewers for their careful reading and insightful suggestions.

Additional information

Funding

This work is supported by the Grant-in-Aid for Scientific Research (C) [grant number 26400208] from the Japan Society for the Promotion of Science.

Notes on contributors

Masato Shinjo

Masato Shinjo is a doctoral student in the Department of Applied Mathematics and Physics, Graduate School of Informatics, Kyoto University. He studies asymptotic analysis of nonlinear dynamical systems known as integrable systems.