Kernel techniques for generalized audio crossfades

Abstract

This paper explores a variety of density and kernel-based techniques that can smoothly connect (crossfade or “morph” between) two functions. When the functions represent audio spectra, this provides a concrete way of adjusting the partials of a sound while smoothly interpolating between existing sounds. The approach can be applied to both interpolation crossfades (where the crossfade connects two different sounds over a specified duration) and to repetitive crossfades (where a series of sounds are generated, each containing progressively more features of one sound and fewer of the other). The interpolation surface can be thought of as the two dimensions (time and frequency) of a spectrogram, and the kernels can be chosen so as to constrain the surface in a number of desirable ways. When successful, the timbre of the sounds is changed dynamically in a plausible way. A series of sound examples demonstrate the strengths and weaknesses of the approach.

Keywords:

• audio crossfade
• morphing
• kernel techniques
• Poisson process
• interpolation

Public Interest Statement

A common cinematic effect is the morphing of one image to another: a person transforms smoothly into a werewolf or the features of one person change fluidly into those of another. The analogous effect in audition is sometimes called a crossfade, and this paper examines two kinds of generalized crossfades that allow one sound to smoothly transform into another. Using ideas from differential equations and probability theory, the “kernel” of the crossfade is defined, and its structure helps to determine the behavior of the resulting sound in terms of audible ridges. A number of sound examples present the uses and limitations of the method.

1. Introduction

Crossfading between two sounds can be simple: one sound decreases in volume as the second sound increases in volume. More interesting crossfades may attempt to maintain common aspects of the sounds while smoothly changing dissimilar aspects. For example, it may be desirable to gradually transform one sound into another while requiring that nearby partials sweep between nearby partials or it may be advantageous to require that the sound retains its harmonic integrity over the duration of the crossfade. Sometimes called audio morphing, such generalized crossfades are an area of investigation in the computer music field (Hatch, 2004; Slaney, Covell, & Lassiter, 1996; Tellman, Haken, & Holloway, 1995) and the techniques may also find use in speech synthesis, where smoothly connecting speech sounds is not a trivial operation (Farnetani & Recasens, 2010).

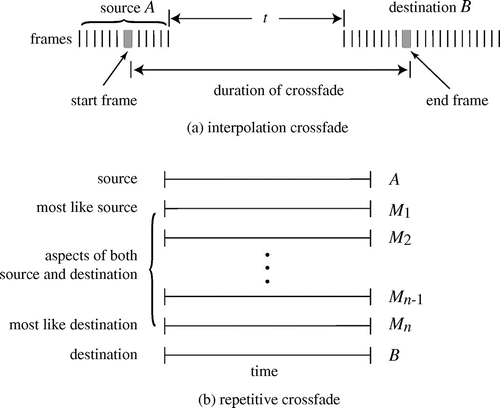
Two kinds of crossfades may be distinguished based on the information used and the desired time over which the fade is to be conducted. In interpolation crossfades, two sounds A and B are separated in time by some interval t. The goal of the fade is to smoothly and continuously change from A (the source) to B (the destination) over the time t. The fade “fills in” the time between a single (starting) frame in A and a single (ending) frame in B. Figure 1(a) shows this schematically. In a repetitive crossfade, the goal is to create a series of intermediate sounds $M_i,i=1,2,\dots ,n$ each of which exhibits progressively more aspects of B and fewer aspects of A, as shown in Figure 1(b). Observe that repetitive crossfading is formally analogous to image morphing since it creates a series of intermediaries between the specified start and end points. Interpolation crossfades, by filling in a silence between two sounds, can be thought of as a time-stretching procedure where the start and end sounds may be chosen arbitrarily. In both cases, kernel-based techniques can be used to place constraints on and guide the crossfade.

Figure 1. Audio crossfades generate sounds that change smoothly between a source and a destination sound. Notes: In interpolation crossfades (a), the sound begins as A and over time smoothly becomes like B. The total duration of the output sound is independent of the duration of A and B and the cross only depends on the sound in the starting and ending frames. The overall effect is one of stretching time under the constraint that the sound must emerge continuously from A and merge continuously into B. In repetitive crossfades (b), a series of intermediate sounds $M_i$ merge aspects of A and B, analogous to the intermediary photographs of an image morph that merges various aspects of the starting and ending photographs. The duration of each output sound $M_i$ is equal to the common duration of A and B. Thus, interpolation crosses begin as one sound and end as another, while in a repetitive cross, each $M_i$ contains features of both of the original sounds. For instance, an interpolation crossfade might start with the attack portion of a cymbal and end with the final moments of a lion’s roar. The interpolation crossfade is the transition that occurs over a user specified time. In contrast, each intermediate sound in a repetitive crossfade merges aspects of both the complete lion sound (from start to end) with those of the complete cymbal (from attack to decay).

Perhaps the most common strategy for creating audio morphings is to:

(1)	derive sets of features $f_A$ and $f_B$,
(2)	create a correspondence where features in sound A are assigned to features in sound B,
(3)	interpolate between the corresponding features over the specified time of the morph, and
(4)	synthesize the morphed sound from the interpolated features.

Most current approaches to morphing follow the general plan (1–4). For example, Boccardi and Drioli (2001) model the sound as a Gaussian Mixture which is trained on notes from the same instrument played with different intensities or on notes from different instruments. Other approaches exploit the sinusoidal plus noise decomposition of Serra (1994) or use the bandwidth-enhanced sinusoidal approach (Fitz, Haken, Lefvert, & O’Donnell, 2002) to allow for the more faithful reproduction of nonsinusoidal elements in the sound. A variety of spectral manipulations including audio morphings are suggested by Erbe (1994) and Polansky and McKinney (1991). Our previous work (Sethares, Milne, Tiedje , Prechtl, & Plamondon, 2009) separated the noise part of the sound from the tonal part using a median filter, then morphed the two parts independently. Most such methods incorporate peak-finding routines [as may be familiar from McAulay and Quatieri’s tracking method (1986)] in the choice of features and use some kind of ad hoc assignment method for creating the correspondences. Tellman et al. (1995) describes some of the issues that arise when carrying out complex assignments.

This paper suggests an alternative procedure for the construction of smooth audio connections that generalizes to any sensible kernel function. An advantage of this method is that two of the common problems in the general scheme (1–4) are avoided. First, no choice of specific features is made and there is no need to locate significant partials or features in the sound. Hence, there can be no mistakes made in identifying such features. Second, since the crossfade is defined by a PDE or, in a probabilistic sense, as a density or kernel function, no correspondence of features is required, and hence there is no possibility of error in the assignment of such correspondences.

Section 2 presents the conceptual and analytical foundations of the method, which reside in the specification of a pair of density-like functions $f_{z|L}$ and $f_{z|R}$ that describe how the left and right spectra of the sound are propagated and a pair of mixing functions $G_L$ and $G_R$ that describe how the spectra are combined. Section 3 presents a number of crossfades between sinusoids that are simple enough to approach analytically, and the idea of a ridge able to connect nearby partials is introduced and analyzed. Section 4 then presents several sound examples that demonstrate the basic functioning of the generalized crossfading process and a selection of examples are conducted between both instrumental and environmental sounds, including a set of fades between clarinet multiphonics. Section 4.2 then provides details on the repetitive crossfades along with corresponding sound demonstrations.

2. Crossfading, potentials, and probability theory

Given two functions of a real variable, $S_0(y)$ and $S_d(y)$, the solution to the mathematical crossfade problem may be defined to be a real-valued function of two real variables $S(x,y)$ with domain $D=\{(x,y)\in {\mathfrak{R}}^2:0\le x\le d,y\in (-\infty ,\infty )\}$ and such that $S(0,y)=S_0(y)$ and $S(d,y)=S_d(y)$. The domain D is an infinite strip of width $d$ in the ${\mathfrak{R}}^2$ plane, with the strip extending from $x=0$ to $x=d$ and extending infinitely in the positive and negative y directions. The two functions $S_0$ and $S_d$ act as boundary conditions on the left and right margins (respectively) of the infinite strip. A solution to the crossfade problem is then any real-valued function over the strip that when restricted to the left (right) margin is $S_0$ ($S_d$). We often impose additional conditions in order to avoid useless and/or trivial answers. For example, in this paper, we always require that $S(x,y)$ have some sort of smoothness or differentiability on the interior of D to ensure that the surface $S(x,y)$ is smooth.

This is analogous in many ways to the Dirichlet problem which consists of finding a solution to Laplace’s equation on some domain D where the solution on the boundary of D is equal to a given function. Perhaps the simplest field equation is Laplace’s equation, which is the linear, second-order, steady-state elliptic PDE(1) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}u=0\end{array}$$(1)

where ${\mathrm{\nabla }}^2$ is the Laplacian operator. For 2-D rectangular coordinates,(2) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^2\equiv \frac{{\mathit{\partial }}^2}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^2}{\mathit{\partial }{y}^2}.\end{array}$$(2)

Problems of great physical diversity can be studied using this equation. For example, in the thermal case, the field potential function $u(x,y)$ represents the temperature; in gravitational problems, it is the gravitational potential; in hydrodynamics, it is the velocity potential; and in electrostatics, it is the voltage.

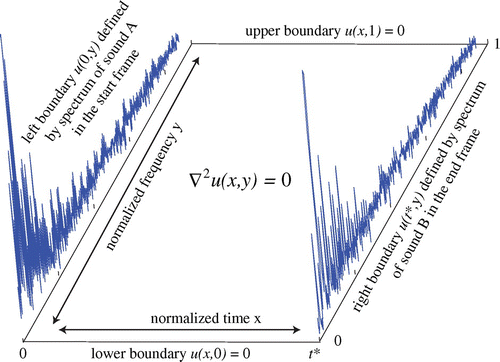
Laplace’s equation is the condition required from a variational analysis for minimizing the field energy of a surface “stretched across” the boundaries (Gustafson, 1980). Imagine a rectangular wire frame where the contour of the left-hand side is specified by the spectrum of the sound A (given by the function $S_0(y)$), the contour of the right-hand side is given by the spectrum of the sound B (given by $S_d(y)$), and where the top and bottom are set to zero as depicted in Figure 2. This is tantamount to an assumption that there is no sound energy at DC and none at high frequencies, for instance, those outside the normal range of hearing. If this wire frame is dipped into a pool of soapy water and carefully retracted, a smooth sheet forms that is characterized as the surface that minimizes the surface energy where the height of the sheet at each point is $u(x,y)$. Mathematically, this can be stated as the PDE (1) with the specified boundary conditions. Reinterpreting the contour of the soap film (i.e. the field values) as sound provides the audio output, which can be heard to smoothly interpolate from the left-hand spectrum to the right-hand spectrum. This views the crossfade function as the solution to a boundary value problem over a two-dimensional domain defined by the spectrum of the sound in the y dimension and the duration of the crossfade in the x direction. The soapy film is, in essence, reinterpreted as a spectrogram.

Figure 2. A crossfade surface can be defined by Laplace’s equation ${\mathrm{\nabla }}^{2}u(x,y)=0$ with boundary conditions given by the spectra of two sounds A and B. Notes: The x-axis (representing time) proceeds from time 0 to time $t^{\ast }$, while the y-axis (representing frequency) covers the range from DC (at 0) to the Nyquist rate (at 1). The surface is formally analogous to a spectrogram and can be inverted back into the time domain using a variety of standard techniques.

Close connections exist between potential theory and the theory of Markov processes (Doob, 1984); most famously, the solution to the Dirichlet problem can be expressed as a functional of the mean hitting time of a standard Brownian motion. Suppose that $B_z$ is a standard two-dimensional Brownian motion whose value at time zero is $z=(x_z,y_z)\in D$. Let $E_z[·]$ denote the expectation operator with respect to this Brownian motion and let ${\mathit{\tau }}_{\mathit{\partial }D}$ denote the time that the Brownian motion first hits the boundary of the strip $\mathit{\partial }D$ = $\{x=0\}\cup \{x=d\}$. The value of $B_z$ at this time is $B_z({\mathit{\tau }}_{\mathit{\partial }D})$. Defining the “initial condition” function over $\mathit{\partial }D$ as $S_{\mathit{\partial }D}(x,y)=1_{\{x=0\}}{S}_0(y)+1_{\{x=d\}}{S}_d(y)$, the solution to the Dirichlet problem can be rewritten$$S(z)=E_z[S_{\mathit{\partial }D}(B_z({\mathit{\tau }}_{\mathit{\partial }D}))].$$

A Brownian motion that begins at the point z in the interior of D wanders about in D until (with probability one) it hits either the left $\{x=0\}$ or the right $\{x=d\}$ boundary. It is true (and intuitive) that areas on the boundary closer to z have a greater chance of being hit than areas further away, and the probability distribution of the points hit on the boundary (the so-called hitting distribution) is(3) $$\begin{array}{c}\hfill f_z(x,y)=\frac{1}{2d}\left(K\left(\frac{x_z\mathit{\pi }}{d},\frac{(y-y_z)\mathit{\pi }}{d}\right)1_{\{x=0\}}+K\left(\mathit{\pi }-\frac{x_z\mathit{\pi }}{d},\frac{(y-y_z)\mathit{\pi }}{d}\right)1_{\{x=d\}}\right),\end{array}$$(3)

where $K(x,y)$ is called the kernel. Making the specific choice of the Poisson kernel(4) $$\begin{array}{c}\hfill K(x,y)=P(x,y)=\frac{sin(x)}{cosh(y)-cos(x)}\end{array}$$(4)

allows a complete analogy with the heat equation. The indicator functions keep track of the hitting distributions on the left and right boundaries. $1_A=1$ if A is true and is zero if A is false. Since$${\int }_{-\infty }^{\infty }P(x,y)dy=2(\mathit{\pi }-x),$$

it can be shown that starting from the point $z=(x_z,y_z)$, the Brownian motion will hit the left boundary with a probability $1-x_z/d$ and the right boundary with a probability $x_z/d$. Thus, the hitting distribution conditioned on the event that the left boundary is hit first is(5) $$\begin{array}{c}\hfill f_{z|L}(y)=\frac{1}{2(d-x_z)}K\left(\frac{x_z\mathit{\pi }}{d},\frac{(y-y_z)\mathit{\pi }}{d}\right)\end{array}$$(5)

and the hitting distribution conditioned on the event that the right boundary is hit first is(6) $$\begin{array}{c}\hfill f_{z|R}(y)=\frac{1}{2x_z}K\left(\mathit{\pi }-\frac{x_z\mathit{\pi }}{d},\frac{(y-y_z)\mathit{\pi }}{d}\right).\end{array}$$(6)

Observe that $f_{z|L}(y)$ converges to the Dirac delta function $\mathit{\delta }(y-y_z)$ as $x_z$ approaches zero and $f_{z|R}(y)$ converges to $\mathit{\delta }(y-y_z)$ as $x_z$ approaches $d$. Thus, the Dirichlet problem can be restated as(7) $$\begin{array}{c}\hfill S(z)=G_L(x_z){\int }_{-\infty }^{\infty }{f}_{z|L}(y)S_0(y)dy+G_R(x_z){\int }_{-\infty }^{\infty }{f}_{z|R}(y)S_d(y)dy.\end{array}$$(7)

We call the functions $G_L$ and $G_R$crossover functions because they control the relative hitting probabilities in the x direction. Making the specific choice that $G_L(x_z)=1-G(x_z)$ and $G_R(x_z)=G(x_z)$ where(8) $$\begin{array}{c}\hfill G(x_z)=\frac{x_z}{d}\end{array}$$(8)

allows a complete analogy with the heat equation, that is, $S(z)=S(x_z,y_z)$ is equal to the field potential function $u(x_z,y_z)$ given by the heat Equation (2).

In the crossfade setting, there is no compelling reason that the kernel function $K(x,y)$ must have exactly the form of the Poisson kernel (4) or that the crossover function $G(z)$ must have the form (8). The essence of the audio morphing design problem is encapsulated in (7), which exists independently of the heat equation or reference to Brownian motions. The crucial factors (for audio morphing) are that $f_{z|L}(y)$ converges to $\mathit{\delta }(y-y_z)$, $G_L(x_z)\to 1$, and $G_R(x_z)\to 0$ as $x_z$ converges to zero, and similarly that $f_{z|R}(y)$ converges to $\mathit{\delta }(y-y_z)$, $G_R(x_z)\to 1$, and $G_L(x_z)\to 0$ as $x_z$ converges to $d$. Together, these allow $S(z)$ to converge to the desired boundary conditions (as z approaches the boundaries), and to smoothly connect the left-hand initial condition with the right-hand initial condition. Thus, the role of the hitting distributions may be played by any kernel that smoothly connects the boundaries, which, in the audio morphing application, are given by the spectra of the starting and ending sounds. By choosing kernel and crossover functions judiciously, fades with a variety of different (audible) properties may be selected.

Example 1

(Simple Linear Crossfade) Let $G(x)=x/d$, $f_{z|L}(y)=\mathit{\delta }(y-y_z)$, and $f_{z|R}(y)=\mathit{\delta }(y-y_z)$. Then, $S(z)=(1-x_z/d)S_0(y_z)+(x_z/d)S_d(y_z)$.

This crossfade is the standard audio crossfade in which the volume of the first sound is lowered proportionally as the volume of the second is raised. Fortunately, there are more interesting forms of crossfades.

Example 2

(Heat Equation) With $f_{z|L}(y)$ and $f_{z|R}(y)$ chosen as in (5) and (6) with kernel (4) and with $G(x)=x/d$, this is the standard heat equation corresponding to the solution given by (Equation 2) (and the intuition of Figure 2).

The heat equation formulation is used in several of the sound examples as it gives a smooth fade that connects nearby partials at the two endpoints. For instance, a frequency $f$ at the left boundary sweeps smoothly upwards to meet another frequency $g$ at the right boundary. By its nature, the heat equation diffuses energy as it moves away from the boundaries, and this can sometimes be heard as a lowering of the volume of the sound toward the middle of the crossfade surface.

Example 3

(Harmonic Integrity) Since the human auditory apparatus perceives pitches (roughly) on a log scale, it makes sense to allow the hitting distribution to scale so that it is wider at higher frequencies. Let $f(z)$ be an arbitrary probability density function and choose a reference frequency $y_0$. For a point $z=(x_z,y_z)$, define the left hitting density$$f_{z|L}(y)=\frac{1}{x_z}\frac{y_z}{y_0}f\left((y-y_z)\frac{y_z}{x_z{y}_0}\right)$$

and the right hitting density$$f_{z|R}(y)=\frac{1}{d-x_z}\frac{y_z}{y_0}f\left((y-y_z)\frac{y_z}{(d-x_z)y_0}\right).$$

Note that as $x_z$ approaches either zero or $d$, these hitting distributions collapse to the required boundary Dirac delta functions. This strategy tends to maintain the perceptual integrity of a harmonic collection. A number of other choices for the functional forms of $G_L(x)$, $f_{z|L}(y)$, $G_R(x)$, and $f_{z|R}(y)$ are investigated in the following sections.

3. Crossfades between sinusoids

The simplest setting is where the starting and ending sounds both consist of a small number of sinusoids. In the first example, a pair of sinusoids with normalized frequencies ${\mathit{\omega }}_{L_1}=5$ and ${\mathit{\omega }}_{L_2}=12$ at the left boundary are crossed with a pair of sinusoids with normalized frequencies ${\mathit{\omega }}_{R_1}=6$ and ${\mathit{\omega }}_{R_2}=11$ at the right boundary. Accordingly, the left boundary function is the (one-sided) Fourier transform $S_0(y)=\mathit{\delta }(y-{\mathit{\omega }}_{L_1})+\mathit{\delta }(y-{\mathit{\omega }}_{L_2})$ and the right boundary function is $S_{\mathit{\pi }}(y)=\mathit{\delta }(y-{\mathit{\omega }}_{R_1})+\mathit{\delta }(y-{\mathit{\omega }}_{R_2})$. For simplicity, the duration of the crossfade is scaled to be $d=\mathit{\pi }$ and the two boundary functions only consider positive frequencies (the negative frequencies proceed analogously). Because the boundary functions have a simple form (as a sum of $\mathit{\delta }()$ functions), the crossfade surface (7) can be integrated exactly as$$\begin{array}{cc}\hfill S(x,y)& =\frac{1}{2\mathit{\pi }}\left(\frac{xsin(x)}{cos(x)+cosh({\mathit{\omega }}_{R_2}-y)}+\frac{xsin(x)}{cos(x)+cosh({\mathit{\omega }}_{R_1}-y)},\dots \right.\hfill \\ \hfill & \left.+\frac{(\mathit{\pi }-x)sin(x)}{cosh({\mathit{\omega }}_{L_2}-y)-cos(x)}+\frac{(\mathit{\pi }-x)sin(x)}{cosh({\mathit{\omega }}_{L_1}-y)-cos(x)}\right)\hfill \end{array}$$

when the kernels are chosen to mimic the heat equation as in Example 2 (with $K(x,y)$ given by (4) and $G(x)$ by (8)).

This is plotted in Figure 3(a). The boundaries at the left and right show the two sinusoids (as delta functions at their respective frequencies) while the surface gradually descends to the middle where they meet. Observe that there are two shapes that connect the nearby frequencies, ${\mathit{\omega }}_{L_1}$ to ${\mathit{\omega }}_{R_1}$ and ${\mathit{\omega }}_{L_2}$ to ${\mathit{\omega }}_{R_2}$. These are local maxima (in the y direction) which form a connected set as x varies over its range; call these ridges. Observe that there is a significant loss of height in the ridges of Figure 3(a). Since the magnitude of the surface corresponds to the amplitude of the spectral components, this may be perceptible as a drop in the volume toward the middle of the crossfade region.

Figure 3. Sinusoids of frequencies ${\mathit{\omega }}_{L_1}=5$ and ${\mathit{\omega }}_{L_2}=12$ are crossed with frequencies ${\mathit{\omega }}_{R_1}=6$ and ${\mathit{\omega }}_{R_2}=11$ using the Poisson kernel and three different crossover functions (see text for details). Notes: Though the ridges connecting the nearby frequencies appear in all three figures, the drop in (a) is likely to be heard as a drop in volume over the course of the first half of the crossfade.

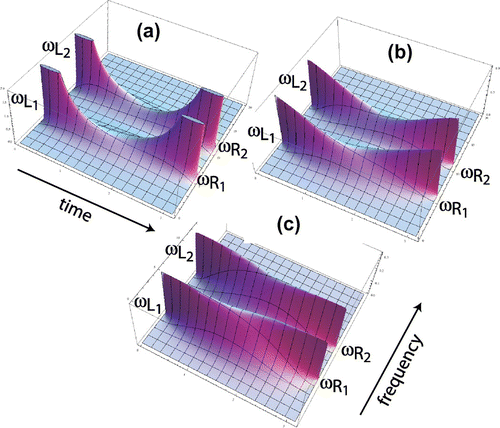
Figure 3(b) also uses the Poisson kernel (4) but chooses crossover functions $G_L(x)=(\mathit{\pi }-x)sin(x)$ and $G_R(x)=xsin(x)$. This tends to increase the total mass in the middle of the crossfade, and the ridge sags less than in (a). Figure 3(c) shows the results when using crossover functions(9) $$\begin{array}{c}\hfill G_L(x)=G_R(x)=sin(x).\end{array}$$(9)

This boosts the ridge to a (near) constant height as it spans the duration to connect the sinusoidal pairs on the two boundaries. Observe that in all three cases, the sinusoids sweep smoothly from their starting to ending frequencies. In contrast, a linear combination of the two sounds (as in the crossfade of Example 1) has no ridges: the amplitudes of the two starting frequencies die away to zero over the duration of the fade while the amplitudes of the two ending frequencies slowly increase.

The kernels used in Figure 3 have the same width at all frequencies y, which may not be desirable when attempting to cross more complex sounds. Consider a source sound with partials at (relative) frequencies 8, 16, 32, and 64 and a destination sound with partials at 9, 18, 36, and 72. If these sounds are to be spectrally crossed, it is desirable to have $8\to 9$, $16\to 18$, $32\to 36$, and $64\to 72$. With an equal width between all pairs, this is impossible since the distance between 9 and 16 (two partials which should not be connected by a ridge) is less than 8, while the distance between 64 and 72 (two partials which should be connected by a ridge) is 8. This is shown in the left side of Figure 4. While the lower ridges appear as expected, the upper two pairs are not joined together by a ridge. Once again, the freedom to modify the kernels allows a solution. The right-hand side of Figure 4 shows a kernel, as suggested by Example 3, that is narrow at lower frequencies and wider at higher frequencies, allowing ridges to form for all the pairs. The specific kernel used is(10) $$\begin{array}{c}\hfill K(x,y)=\frac{sin(x)}{cosh\left(\frac{y-y_0}{c{y}_0}\right)-cos(x)}.\end{array}$$(10)

With $c<1$, the $K(x,y)$ values stretch more for larger y, mimicking the sensitivity of the auditory system. In subsequent examples, $c=0.12$ is chosen as a compromise. If c is chosen much larger, the desired ridges fail to exist; if chosen much smaller, the ridges in the low frequencies tend to merge together.

Figure 4. The ridges in the crossfade surface on the left are equally wide, irrespective of the absolute frequency. In some situations, it may be advantageous to allow the width of the ridges to become wider at higher frequencies, as shown on the right. This can be accomplished by defining the kernels as in (10).

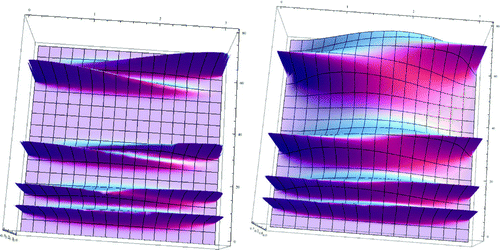
The above discussion emphasizes the importance of the ridges, and it is crucial to be able to make good choices of kernels that lead to desirable ridges. While it is difficult to prove in general when ridges will occur and how wide they are, in the simple case where the kernel is a rectangle function, the existence and behavior of ridges can be described analytically. Viewing the smooth kernels as having a support that can be approximated by an appropriate set of rectangle functions suggests that insights gained from studying the rectangle kernels may be useful in more general situations.

The rectangle function $\text{rect}(x)$ is defined as one for $x\in (-1/2,1/2)$ and zero otherwise. For $a>0$, let $f(x)=a\text{rect}(ax)$ and define the kernel as in Example 3. The support of the left boundary hitting density is $\left[y-\frac{xy}{a{y}_0},y+\frac{xy}{a{y}_0}\right]$ and the support of the right boundary hitting density is $\left[y-\frac{(d-x)y}{a{y}_0},y+\frac{(d-x)xy}{a{y}_0}\right]$. The support of the left density varies linearly in x (if y is held constant) from zero at $x=0$ to a maximum of $2dy/y_{0}a$ at $x=d$ (and similarly for the support of the right density). Consider the crossfade between a pure frequency ${\mathit{\omega }}_L$ on the left boundary to a pure frequency ${\mathit{\omega }}_R$ on the right boundary. Thus, $S_0(y)=\mathit{\delta }(y-{\mathit{\omega }}_L)$ and $S_d(y)=\mathit{\delta }(y-{\mathit{\omega }}_R)$. The crossfade surface is$$\begin{array}{cc}\hfill S(z)& =(1-G(x))f_{z|L}({\mathit{\omega }}_L)+G(x)f_{z|R}({\mathit{\omega }}_R)\hfill \\ \hfill & =(1-G(x))\frac{a}{x}\frac{y_0}{y}\text{rect}\left(a({\mathit{\omega }}_L-y)\frac{y_0}{xy}\right)\hfill \\ \hfill & +G(x)\frac{a}{d-x}\frac{y_0}{y}\text{rect}\left(a({\mathit{\omega }}_R-y)\frac{y_0}{(d-x)y}\right)\hfill \end{array}$$

A ridge is said to exist whenever there is a trajectory $T=\{(x,y(x)):\forall x\in [0,1]$ such that both terms in the above expression are nonzero }.

Theorem 1

(The Ridge Theorem) Suppose that ${\mathit{\omega }}_R>{\mathit{\omega }}_L$ and that $d<2a{y}_0$. A ridge exists if and only if(11) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}_R}{{\mathit{\omega }}_L}<1+\frac{d}{2a{y}_0}.\end{array}$$(11)

A proof is given in Appendix A.1.

4. Audio crossfades

This section presents a series of experiments that carry out generalized crossfades between a variety of sounds, including sinusoids, instrumental, and environmental sounds. The experiments demonstrate the ridge theorem concretely by showing the interaction between the width of the kernel and the frequencies joined by the ridges. To be practical, it is desirable to have ridges that connect partials of the starting and ending sounds when the frequencies are close and to not have ridges when the frequencies of the partials are distant.

In order to implement the crossfade procedure, it is necessary to discretize the two dimensions, to choose the size $n$ of the FFTs that will be used to specify the boundary spectra, and to select a window that will extract the $n$ samples from the sound waveforms. These choices are familiar from short-time Fourier transform (STFT) modeling (Oppenheim & Schafer, 2009), and the same trade-offs apply. In addition, $n$ must be equal to the number of points in the vertical y direction. We have found $n=2^{10}$, $2^{11}$, and $2^{12}$ to be convenient and have used a standard Hann window. In the horizontal x direction, we have typically used between $m=200$ and $m=500$ points.

The inversion of the two-dimensional surface $S(x,y)$ of (7) into a sound waveform can be accomplished using any of the techniques that would invert an STFT image into sound. The sound examples of this section implement a “phase vocoder” strategy that is well known in applications such as time scaling and pitch transposition (Dolson, 1986; Laroche & Dolson, 1999; Sethares, 2007). This method synthesizes phase values for a given set of magnitude values, effectively choosing phase values that guarantee continuity across successive frames. To be explicit, suppose that the frequency $f_i$ is to be mapped to some value $g$. Let $k$ be the closest frequency bin in the FFT vector, i.e. the integer $k$ that minimizes $\left|k\frac{sr}{n}-g\right|$ where $sr$ is the sampling rate. Then, the $k$th bin of the output spectrum at time index $j+1$ has magnitude equal to the magnitude of the $i$th bin of the input spectrum with corresponding phase(12) $$\begin{array}{c}\hfill {\mathit{\theta }}_k^{j+1}={\mathit{\theta }}_k^j+2\mathit{\pi }dtg\end{array}$$(12)

where $dt$ is the time separation between consecutive frames. The phase values in (12) guarantee that the resynthesized partials are continuous across frame boundaries, reducing the likelihood of discontinuities and clicks. An advantage of this approach is that it allows the duration of the fade to be freely chosen after the solution to the crossfade surface has been obtained. Thus, the relationship between $t^{\ast }$ in Figure 2 and real time can be freely adjusted even after the calculation of the surface $S(x,y)$.

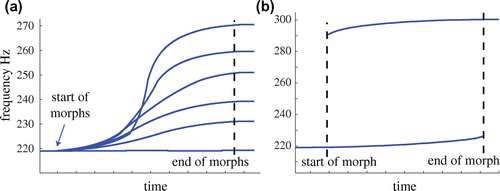
A series of generalized crossfades demonstrate that the ridges of Figures 3 and 4 are perceived as pitch glides. Sound examples 220to230.wav, 220to240.wav, through 220to270.wav are available at the website (http://sethares.engr.wisc.edu/papers/audioMorph.html, date last viewed 27 September 2015, as are all other sound files discussed throughout the paper). All examples use the kernel $K(x,y)$ in (10) and the crossover function $G(x)$ of (9). In each case, the crossfade starts at the pitch corresponding to the first frequency and rises smoothly to the pitch corresponding to the second frequency, as shown graphically in Figure 5(a). The frequency values are calculated from the output of the phase vocoder using an analysis that interpolates three frequency bins in each FFT frame. In these graphs, the method is accurate to about 2 Hz (far better than the $\frac{44100}{2048}\approx 22$ Hz resolution of the FFT bins).

When the frequencies of the sinusoids at the start and end are far apart, there is less interaction. The sound example in 220to300.wav begins as a sine wave at 220 Hz and ends as a sine wave at 300 Hz. What happens is that the starting sinusoid decreases in amplitude and the ending sinusoid increases in amplitude throughout the process. Essentially, the kernel is no longer wide enough to form ridges and the connecting sound has become a simple crossfade. The instantaneous frequencies of the two sines are shown in Figure 5(b), which show that both sines are individually identifiable throughout the process. The pitches are not completely fixed at 220 and 300, but bend slightly toward each other. The final sinusoidal example shows how superposition applies to the crossfade process when the sine waves are far apart in frequency. In the example 220to260+440to400.wav, a sine at 220 glides smoothly to 260, while a sine at 440 glides smoothly to 400. The two are effectively independent. Indeed, the output to the two crossfaded pairs is (almost exactly) the sum of outputs to the two pairs crossfaded separately. Observe that the goal of this method is not to connect every frequency with every other but to gain control over the spreading of the kernel. Indeed, this is exactly what the ridge theorem quantifies: how to trade off the spreading of the energy to nearby frequencies vs. the continuity over the course of the crossfade.

Figure 5. (a) Six different crossfades begin at 220 Hz and proceed to 220, 230, 240, 250, 260, and 270 Hz. Each sounds like a single sine wave that slowly increases in pitch up to the specified frequency. (b) A sinusoid at 220 Hz is crossfaded with a sinusoid at 300 Hz. Because the pitches only bend slightly, the process is almost indistinguishable from a simple amplitude crossfade.

4.1. Instrumental and environmental crossfades

The crossfades in this section are conducted as interpolation crossfades, which stretch time proportional to the x-width of the surface $S(x,y)$. Again, the kernel used is $K(x,y)$ of (10) and the crossover function $G(x)$ is (9). The first two examples cross between single-tone instrumental sounds. In morph-PianoClarinet.wav, an $A2$ attack on the piano changes slowly into a sustained $A2$ on the clarinet. Similarly, in morph-ViolinTrumpet.wav, both instruments play a $C4$ as the attack of the violin crossfades into the sustained portion of the trumpet. Two spectrally rich sounds, a chinese gong and a low C on a minimoog synth, are crossed in morph-GongMinimoog.wav. Several nonobvious effects can be heard including the rising and falling pitch contours, and the slow swelling of the low C toward the end. Then, in morph-GongLion.wav, the same gong recording is crossed with the roar of a lion. Spectrally rich sounds seem to crossfade particularly well.

Multiphonics occur in wind instruments when the coupling between the driver (the reed or lips) and the resonant tube evokes more than a single fundamental pitch. The sounds tend to be inharmonic and spectrally rich; the timbres range from soft and mellow to noisy and harsh. We recorded Paris-based instrumentalist Carol Robinson playing a large number (about 80) of multiphonics. These ranged in duration from brief (a few hundred milliseconds) to fully sustained (several seconds). The timbres ranged from soft and mellow to noisy and harsh. For the present application, a number of these were selected, and sustained crossfades were calculated between a variety of starting and ending multiphonics. These are

                        morph-MultiXMultiY.wav

where (X,Y) take on values (13, 23), (29, 66), (32, 14), (39, 28), (48, 64), and (74, 53). All of these can be heard (along with the original recordings of the multiphonics) on the website for the paper (http://sethares.engr.wisc.edu/papers/audioMorph.html, date last viewed 27 September 2015). Despite the variety of starting and ending timbres, the crossfades connect smoothly. There are partials that move in frequency (as suggested by the experiments of Section 3) and the basic level of noisiness in some of the samples also changes smoothly throughout the process.

4.2. Repetitive crossfades

Interpolation crossfades tend to change the timbre of the sounds in proportion to the amount time is stretched. Repetitive crossfades more closely parallel visual morphing since the output is a collection of sounds that are each the same duration as the sounds A and B. In this case, the sounds are not partitioned into frames and the boundaries of the crossfade surface are the complete spectra of the sounds. Each column of the solution $S(x,y)$ represents the spectrum of a different intermediate sound.

This distinction has several implications. First, the sounds cannot be too long since they must be analyzed (and inverted) all at once; at the normal CD sampling rate, this limits the duration to a few seconds. Second, the horizontal axis needs only as many points as the desired number of output (intermediate) sounds (recall that for the interpolation crossfades, there needs to be as many mesh points as there are frames in the duration t). Thus, while the frequency y dimension is significantly larger, the time dimension x is significantly smaller. It is possible to be clever. Appendix A.2 shows how, when using the Poisson kernel (4), it is possible to calculate the crossed signal at the midpoint $d/2$ without calculating the complete surface, that is, to calculate $S(d/2,y)$ in isolation. This can reduce the numerical complexity significantly. The method of the Appendix can also be iterated to yield the solutions for $S(d/4,y)$, $S(3d/4,y)$, etc.

Perhaps the greatest difference is in the reinterpretation of the $S(x,y)$ into sound. In the interpolation crossfade, it is necessary to reconstruct the phases of the spectra in some way (for instance, using the phase vocoder strategy as in (12)). In the repetitive crossfade, it is possible to use the complete complex-valued spectra as the boundary conditions; the surface $S(x,y)$ becomes complex valued and each column represents the complete spectrum of the sound.

The first two examples of the repetitive crossfade are between single-tone instrumental sounds. In repmorph-PianoClarinet.wav, an $A2$ attack on the piano is crossed with an $A2$ on the clarinet. Each of the sounds was truncated to about 2.5 seconds, and nine different intermediate sounds were generated. In the soundfile, each of the nine sounds is separated by about 0.25 seconds of silence. The first sound is the trumpet (sound A), the last is the clarinet (sound B), and the others are the intermediaries. Similarly, in repmorph-TrumpetViolin.wav, both instruments play a $C4$ as the attack of the trumpet is crossed into the violin.

Two spectrally rich sounds, a chinese gong and a low C on a minimoog synth, are crossed in repmorph-MinimoogGong.wav. The first 2.5-second sound is the minimoog note, and the next several slowly incorporate increasing amount of gong noise. The final segment is the pure gong sound. Observe that this is quite a different set of effects from the interpolation crossfades of the same sounds. In repmorph-Gong1Gong2.wav, two different gong sounds are faded together, creating a variety of “new” intermediate gong-like sounds. Finally, in repmorph-LionGong.wav, the same gong recording is crossed with the roar of a lion. Spectrally rich sounds cross easily, and the middle sounds are plausible hybrids.

5. Conclusion

By formalizing the idea of a crossfade function as one which smoothly connects two signals, this paper provides a basis for studying processes that underlie sound transitions. The use of a variety of kernels is key, as this specification connects a family of uninteresting transitions (such as simple crossfades) with more interesting transitions (such as spectral crossfades). The ridge theorem delineates in a simple setting when spectral peaks in one signal connect to those in another. The methodology (of regarding the spectrogram as a surface defined by hitting points of a stochastic process) provides some hope that similar questions can also be handled analytically. The mathematics is applied concretely to the problems of interpolation and repetitive crossfades, and each is demonstrated in a handful of sound examples where the strengths and weaknesses of the approach become apparent. In many of the examples, it is possible to clearly hear the ridges, indicating that these plausibly correspond (in an audio sense) to the smooth ridges that appear in Figures 3 and 4. Using this setup, interpolation crossfades appear to be more convincing (as spectrally rich audio morphs) than the repetitive crossfades, which tend to sound more like simple amplitude crossfades. There are two competing factors in the choice of the kernels and the crossover functions: the desire to have a level ridge and the desire to not have the energy spread out in the middle. We suspect it may be possible to find better functions using some kind of optimization procedure that trades off these two features, but we have been unable to formulate and solve this in a concrete way.

Acknowledgements

The authors would like to thank Howard Sharpe for extensive discussions during the early phases of this project.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

William A. Sethares

William A Sethares and James A Bucklew are both with the Department of Electrical and Computer Engineering at the University of Wisconsin-Madison. Their research interests include signal processing as applied to audio, images, and telecommunications.

Appendix 1

Proof of the Ridge Theorem

Fix a value of x in the interval $[0,d]$. There is a nonzero contribution from both terms as long as the upper part of the rectangle for the first term extends further than the lower part of the rectangle for the second term. The y value for where the upper part of the rectangle for the first term terminates satisfies$$\begin{array}{cc}\hfill (y-{\mathit{\omega }}_L)\frac{a{y}_0}{xy}=& \frac{1}{2}\hfill \\ \hfill y=& \frac{{\mathit{\omega }}_L}{1-\frac{x}{2a{y}_0}}.\hfill \end{array}$$

Similarly, the y value for where the lower part of the rectangle for the second term terminates satisfies$$\begin{array}{cc}\hfill (y-{\mathit{\omega }}_R)\frac{a{y}_0}{((d-x)y}=& -\frac{1}{2}\hfill \\ \hfill y=& \frac{{\mathit{\omega }}_R}{1-\frac{d-x}{2a{y}_0}}.\hfill \end{array}$$

Thus, the condition for overlap is$$\begin{array}{cc}\hfill \frac{{\mathit{\omega }}_L}{1-\frac{x}{2a{y}_0}}>& \frac{{\mathit{\omega }}_R}{1-\frac{d-x}{2a{y}_0}}\hfill \\ \hfill \frac{{\mathit{\omega }}_R}{{\mathit{\omega }}_L}<& \frac{2a{y}_0+(d-x)}{2a{y}_0-x}\hfill \end{array}$$

It is easy to verify that the right-hand side of the above inequality is increasing in x and thus takes on its minimum value at $x=0$. This gives the theorem statement. $\square$

A computational simplification

Let $P(x,y)$ be the Poisson kernel (4(4) $$\begin{array}{c}\hfill K(x,y)=P(x,y)=\frac{sin(x)}{cosh(y)-cos(x)}\end{array}$$(4) ). The line where $x=d/2=\mathit{\pi }/2$ represents the center strip of the crossfade surface. A Brownian motion started on this center strip has the hitting distribution$$\begin{array}{cc}\hfill f_{\mathit{\pi }/2}(y)=& \frac{1}{2\mathit{\pi }}(P(\mathit{\pi }/2,y)1_L+P(\mathit{\pi }-\mathit{\pi }/2,y)1_R)\hfill \\ \hfill =& \frac{1}{2\mathit{\pi }}(\frac{1}{cosh(y)}{1}_L+\frac{1}{cosh(y)}{1}_R)\hfill \\ \hfill =& \frac{1}{2\mathit{\pi }}(\frac{2exp(|y|)}{exp(2|y|)+1})(1_L+1_R).\hfill \end{array}$$

To find the characteristic function or Fourier transform of this probability density,$$\begin{array}{cc}\hfill z_x(y)=& \frac{P(x,y)}{2(\mathit{\pi }-x)}\hfill \\ \hfill =& \frac{1}{2(\mathit{\pi }-x)}\frac{sin(x)}{cosh(y)-cos(x)}.\hfill \end{array}$$

The following transform pair can be found in Oberhettinger (1973), Table 1A, Even Functions, # 201:$$\begin{array}{cc}\hfill f(x)⟺& g(y)\hfill \\ \hfill \frac{1}{2N}\frac{1}{cosh(ax)+cos(b)}⟺& \frac{1}{N}\frac{1}{a}\mathit{\pi }csc(b)\frac{sinh(\frac{by}{a})}{sinh(\frac{\mathit{\pi }y}{a})}\hfill \end{array}$$

where $N=\frac{b}{a}csc(b)b<\mathit{\pi }$. Letting $a=1$, $b=\mathit{\pi }-t$, and $N=(\mathit{\pi }-t)csc(\mathit{\pi }-t)$ gives the transform relation$$\frac{1}{cosh(x)-cos(t)}⟺\frac{2\mathit{\pi }}{sin(\mathit{\pi }-t)}\frac{sinh[(\mathit{\pi }-t)y]}{sinh[\mathit{\pi }y]}$$

Hence,$$\begin{array}{cc}\hfill z_x(y)& =\frac{1}{2(\mathit{\pi }-x)}\frac{sin(x)}{cosh(y)-cos(x)}\hfill \\ \hfill & ⟺\frac{\mathit{\pi }}{(\mathit{\pi }-x)}\frac{sin(x)}{sin(\mathit{\pi }-x)}\frac{sinh[(\mathit{\pi }-x)\mathit{\omega }]}{sinh[\mathit{\pi }\mathit{\omega }]}\hfill \\ \hfill & =\frac{\mathit{\pi }}{(\mathit{\pi }-x)}\frac{sinh[(\mathit{\pi }-x)\mathit{\omega }]}{sinh[\mathit{\pi }\mathit{\omega }]}\hfill \\ \hfill & =Z_x(\mathit{\omega })\hfill \end{array}$$

where $Z_x(\mathit{\omega })$ is the characteristic function (and Fourier transform since we are dealing with even functions) of $z_x(y)$.