Super edge-magic sequence of maximal outer planer graph and its characteristics

Abstract

In this paper, we study specific striped maximal outer planar graph (MOP) in the view of super edge-magic sequences (SEMS). Also, we derive a formula for the Wiener index (WI) of above MOP graph which is having SEMS. We analyze graphical properties like independence number, chromatic number, dominance number, and matching number of specific striped MOP graph through SEMS.

Keywords:

• maximal outer planar
• super edge-magic sequence
• Wiener index

Public Interest Statement

The number of triangulations of regular polygon with n + 2 sides is the nth Catalan number, which is a famous number in Combinatorics. Guanhang provides closed formulas involving the Catalan numbers for the number of both labeled and unlabeled MOPs of a fixed order. It is interesting to note that the direct relation is between the number of internal triangles and the number of vertices of degree 2 in a maximal outer plane graph.

In this direction, we scan the maximal outer planar graphs (MOP) and its characteristics through our novel tool of super edge-magic sequences. We detect the specific graphs, which will influence the graphical characteristics like chromatic number, matching number, dominance number, and independence number. We formulate specific critical issues, which can yield the solutions of several queries in computer science, communication engineering, and also in chemistry.

1. Introduction

We have considered all the graphs which are simple and finite. Kotzig and Rosa (1970) introduced the concepts of magic valuation. Ringle and Laldo called this type of valuation as edge-magic labeling (Ringel & Llado, 1996; Wallis, Baskoro, Miller, & Slamin, 2000). The concept of super edge-magic was introduced by Enomoto, Llado, Nakamigawa, and Ringel (1998) and Chen (2001).

A (p, q) graph G is called edge-magic if there exists a bijective function f: V(G)UE(G) → {1, 2, 3, … , p + q} such that f(u) + f(v) + f(uv) = k is a magic constant for any edge uv ∊ E(G). Moreover, G is said to be super edge-magic if f (V(G)) → {1, 2, 3, … , p}.

The concept of super edge-magic sequence was introduced in Vijayabarathi and Anjaneyulu (2013a). More about the super edge-magic graphs like fabrication of new super edge-magic sequences (SEMS) and their properties can be found in the same paper (Vijayabarathi & Anjaneyulu, 2013a). As an application of SEMG and SEMS, the study on the Wiener index (WI) of the molecular graph to analyze the structure of organic molecules like Cyclo alkane, Alkane-n-amine, and Alkane-n, n′-domain through this SEMS has been presented in Vijayabarathi and Anjaneyulu (2013b). We are giving the basic definition of SEMS, which was published in Vijayabarathi and Anjaneyulu (2013a) for smooth understanding and convenience of the readers as follows:

“Let G be a super edge-magic graph with p vertices and q edges. Here, we introduce a new term, i.e. a constant of super edge-magic sequence and is denoted by α*. A sequence < x_i > is said to be super edge-magic sequence if$$\underset{1\le i\le q}{max}\left\{2x_i+i\right\}<\mathit{\alpha }\ast +q\le p+\underset{1\le i\le q}{min}\left\{x_i+i\right\}$$

where x_i is always the lower end vertex of the edge label p + i, 1 ≤ i ≤ q i.e. x_i = min{f(x), f(y)/xy ∊ E(G)} and α* = min(S), where S = {f(x) + f(y)/xy ∊ E(G)}”. More details can be seen with fine illustrations in our paper (Vijayabarathi & Anjaneyulu, 2013a).

2. Maximal outer planar graph

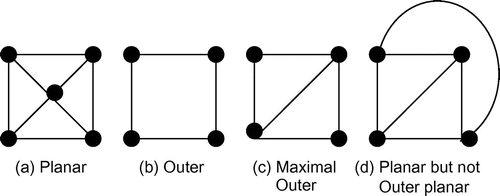
A planar graph which can be drawn without edge crossing. A graph is outer planar if there exists a planar embedding of G in which all the vertices lie on the unbounded face. The edges on the boundary of an outer planar graph are called outer edges and the other edges are called inner edges or chords.

An outer planar graph is said to be maximal if it has the maximum possible number of edges for the given number of vertices. A maximal outer planar graph (MOP) can be viewed as a triangulation of a convex polygon. Figure 1(a–d) presents the difference between planar, outer planar, maximal outer planar, and planar but not outer planar.

Figure 1. Difference between planar, outer planar, and maximal outer planar.

Let f be an inner face of a MOP G. If f is adjacent to the outer face, then we say that f is a marginal triangle. Otherwise we say that f is an internal triangle. A maximal outer plane graph G without internal triangle is called striped. It is well known that every maximal outer planar is 2-connected. Moreover, each maximal outer planar has a unique Hamiltonian cycle, which is the boundary of the exterior region while every interior region is a triangle. Because each interior region of G is a triangle, it follows that the two vertices incident to chord of G have exactly two common neighbors, while two vertices incident to an outer edge of G have exactly one common neighbor. The number of edges and regions in a maximal outer planar can be determined from the order of the maximal outer planar. We present some significant results in MOP. More results can be seen in Campos and Wakabayashi (2013).

Lemma 2.1

Let G be a MOP with n vertices n ≥ 3. Then we have the following (i) there are 2n − 3 edges, of which there are n − 3 chords (ii) there are n − 2 inner faces and each inner face is a triangle (iii) there are at least two vertices with degree 2.

Proposition 2.1

If G is a MOP, then there is an embedding of G in the plane such that the boundary of the outer face is a Hamiltonian cycle and each inner face is a triangle.

Proposition 2.2

Let G be a MOP of order n ≥ 4. If G has k internal triangles, then G has k + 2 vertices of degree 2.

3. Motivation and proposed work

Lee, Kitagaki, Young, and Kocay (2006), proved Edge graceful and Edge-magic graphs are MOP. In this paper, we would like to study and analyze specific striped MOP in the direction of SEMS. Then we investigate “independence number, chromatic number, dominance number and matching number for Specific Striped MOP through SEMS”.

4. Striped MOP

4.1. Algorithm for super edge-magic labeling

Step 1: Let G be a striped MOP of order n ≥ 4.

Let V = (x₁, x₂, … , x_n) be the vertex set of G.

Step 2: The vertices x₁, x₂, … , x_n lie on the boundary of its outer face.

Step 3: From Proposition 2.2, we know that G has exactly two vertices of degree 2. Without loss of generality, we may assume that x₁ and x_n are the two vertices of degree 2 in G.

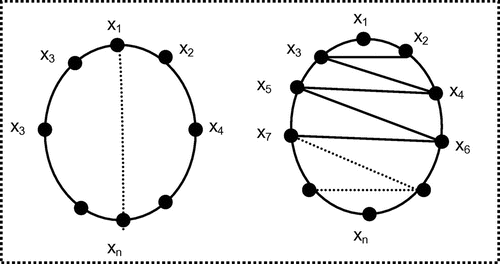
Step 4: The removal of the vertices x₁ and x_n breaks the cycle into two paths:

P₁ = (x₂, x_4, …) and P₂ = (x₃, x₅, …).

Step 5: The paths P₁ and P₂ are joined by an edge from x_i to x_i + 1, for i = 2, 3, … , n − 2 which can be depicted in Figure 2. Also we call this type of labeling assignment as a consecutive vertex labeling.

Figure 2. Construction of consecutive vertex labeling.

Step 6: Now G is always super edge-magic.

Step 7: As we discussed in Kotzig and Rosa (1970), SEMG has SEMS and is of the form (n − 1, n − 2, n − 2, n − 3, n − 3, … , 2, 2, 1, 1) where n is the number of vertices of G.

For illustration, if n = 6, SEMS: (5, 4, 4, 3, 3, 2, 2, 1, 1) (Figure

Figure 3. SEMG for MOP–SEMS.

3).

Remark 4.1.1

The above consecutive vertex labeling is super edge-magic. Then by SEM labeling property sum of edge label is: S = {f(x) + f(y)/ for each xy ∊ E(G)}, where f(x) denotes label of the vertex x and vice versa which contains q(=2n − 3) consecutive integers. Each integer value is a sign of an edge of a graph. Therefore:$$q=n+(n-3)$$$$q=\text{edges on Hamiltonian circuit (boundary)}+\text{Chords}$$

Since the edge sum of the chords are always odd, because of the consecutive vertex labeling. According to the odd sum, the order of the chord is:

Sum 3 = (x₁, x₂) fixed on the boundary.

Sum 5 = (x₁, x₄)/(x₂, x₃)

Sum 7 = (x₁, x₆)/(x₂, x₅)/(x₃, x₄)   Chord

………

………

Sum 2n − 1 = (x₁, x_2n − 2)/(x₂, x_2n − 3)/ … /(x_n − 1, x_n) fixed on the boundary.

The above sum provides the total number of possibilities, according to that we can choose a chord for a given graph of n vertices. The graph will vary only the choice of the chord. In this procedure, we attain all super edge-magic graphs but not all maximal outer planar. Some of them may be non-planar also. Now the total number super edge-magic graphs can be computed by the following theorem.

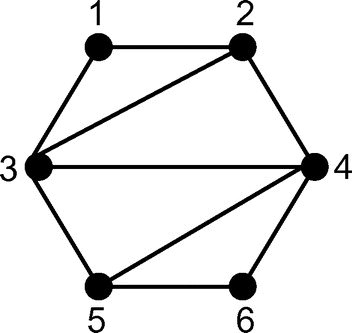
Figure 4. Total SEMG for n = 5.

Notes: Total super edge-magic graphs = 4; Maximal outer planar graphs = 2; non-planar graphs = 2.

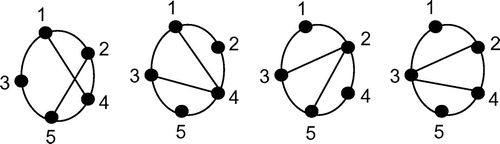
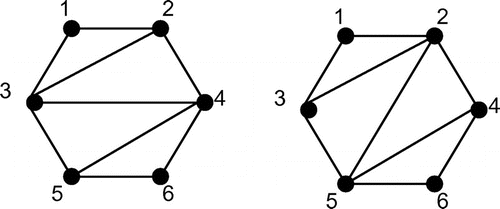
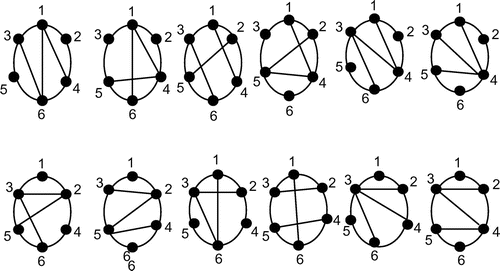
Figure 5. SEMG for n = 6.

Notes: Total super edge-magic graphs = 12; Maximal outer planar graphs = 6; non-planar graphs = 6.

Theorem 4.1.1

Let G be a graph with n vertices and 2n − 3 edges. Then the number of super edge-magic graphs is equal to: $\left\{\begin{array}{cc}\left(\frac{n}{2}\right)!\left(\frac{n}{2}-1\right)!\hfill & \text{when}n\text{is}\text{even}\hfill \\ {\left(\left(\frac{n-1}{2}\right)!\right)}^2\hfill & \text{when}n\text{is}\text{odd}\hfill \end{array}\right.$

Proof

The theorem is proved by mathematical induction on the order of graph. According to the Remark 4.1.1, the total number of possible super edge-magic graphs are:

for n = 4

sum 3 = (x₁, x₂) fixed on the boundary.

sum 5 = (x₁, x₄)/(x₂, x₃) Chord

sum 7 = (x₃, x₄) fixed on the boundary

Therefore, total SEMG = 1 × 2 × 1 = 2! × 1! = 2.

for n = 5:

Sum 3 = (x₁, x₂) fixed on the boundary.

Sum 5 = (x₁, x₄)/(x₂, x₃)

Sum 7 = (x₁, x₆)/(x₂, x₅)/(x₃, x₄)

Sum 9 = (x₁, x₈)/(x₂, x₇)/(x₃, x₆)/(x₄, x₅)

Total SEMG = 1 × 2 × 2 × 1 = (2!)² = 4.

and for n = 6:

sum 3 = (x₁, x₂) fixed on the boundary.

sum 5 = (x₁, x₄)/(x₂, x₃)   chords

sum 7 = (x₁, x₆)/(x₂, x₅)/(x₃, x₄)

sum 9 = (x₁, x₈)/(x₂, x₇)/(x₃, x₆)/(x₄, x₅)

sum 11 = (x₁, x₁₀)/(x₂, x₉)/(x₃, x₈)/(x₄, x₇)/(x₅, x₆) fixed on the boundary.

Total SEMG = 1 × 2 × 3 × 2 × 1 = 3! × 2! = 12.

Similarly, For n = 7: 1 × 2 × 3 × 3 × 2 × 1 = (3!)² = 36.

For n = 8: 1 × 2 × 3 × 4 × 3 × 2 × 1 = 4! × 3! = 144.

Now the theorem is true for the case, when n = 4, 5, 6, 7, 8.

Assume that the theorem holds true for all the graphs with fewer vertices, i.e. n = m vertices. To prove the theorem is true for n = m + 2, we have the cases either m is even or odd.

For the case, when n = m is even, we know that,$$1\times 2\times 3\times \dots \times \left(\frac{m}{2}\right)\times \left(\frac{m}{2}-1\right)\times \left(\frac{m}{2}-2\right)\dots \times 2\times 1=\left(\frac{m}{2}\right)!\times \left(\frac{m}{2}-1\right)!$$

Now for n = m + 2 and it is also even:$$\therefore ,1\times 2\times 3\times \dots \times \left(\frac{m}{2}\right)\times \left(\frac{m+2}{2}\right)\times \left(\frac{m+2}{2}-1\right)\times \left(\frac{m}{2}-1\right)\times \left(\frac{m}{2}-2\right)\dots \times 2\times 1=\left(\frac{m+2}{2}\right)!\left(\frac{m+2}{2}-1\right)!$$

This proves the result for the case, when n is even.

For the case, when n = m is odd, we know that,$$1\times 2\times 3\times \dots \times \left(\frac{m}{2}\right)\times \left(\frac{m}{2}\right)\times \left(\frac{m}{2}-1\right)\dots \times 2\times 1={\left(\left(\frac{m-1}{2}\right)!\right)}^{2}a$$

Now for n = m + 2 and it is also odd:$$\therefore 1\times 2\times 3\times \dots \times \left(\frac{m}{2}\right)\times \left(\frac{m+2}{2}\right)\times \left(\frac{m+2}{2}\right)\times \left(\frac{m+2}{2}-1\right)\times \left(\frac{m+2}{2}-2\right)\dots \times 2\times 1={\left(\left(\frac{m+2-1}{2}\right)!\right)}^2$$

This also proves the result for the case, when n is odd. Hence, the theorem is true for all values of n by mathematical induction. □

4.2. Significant observations

•	In the above theorem, all the graphs are not maximal outer planar. Some of them are non-planar. From this we conclude that$$\mathbf{Number}\mathbf{of}\mathbf{MOP}\mathbf{graphs}=\mathbf{Total}\mathbf{SEM}\mathbf{graphs}-\mathbf{Non}\mathbf{planar}\mathbf{graphs}.$$ We can verify this equation by the following for n = 5, n = 6 and in other cases also (Figures 4 and 5).
•	The planar graphs which were depicted in Theorem 4.1.1 are always maximal outer planar without internal triangles. These are also called simply striped graphs.
•	A MOP without internal triangles is super edge-magic, but the converse need not be true.
•	All MOPs with four vertices are super edge-magic.

5. Properties of specific striped MOP

Definition 5.1

Consecutive Striped MOP

Let G be a super edge-magic MOP which has consecutive vertex labeling. Then super edge-magic sequence this for specific striped MOP is: (n − 1, n − 2, n − 2, n − 3, n − 3, … , 2, 2, 1, 1), where n is the number of vertices of G with α* = 3. We call this type of graph as consecutive striped MOP.

Calculation of Wiener Index

Let G be specific striped super edge-magic MOP with n vertices. Calculation of WI for the above MOP graph is pursued by the method described in the paper (Vijayabarathi & Anjaneyulu, 2013b). We formulate this in the following theorem. More about WI discussed in the papers Mohar and Pisanski (1988), Wiener (1947a), and Mihalić et al. (1992), Wiener (1947b).

Theorem 5.1

The WI of the consecutive striped MOP W(G_n), n be the number of vertices is, given by$$W(Gn)=\left\{\begin{array}{cc}W\left(G_{n-1}\right)+{\left(\frac{n}{2}\right)}^2\hfill & \text{if}n\text{is}\text{even}\hfill \\ W\left(G_{n-1}\right)+\left(\frac{n^2-1}{4}\right)\hfill & \text{if}n\text{is}\text{odd}\hfill \end{array}\right.$$

where G_n − 1 is also a consecutive striped MOP on (n − 1) vertices.

Proof

The theorem is proved by mathematical induction on number of vertices using bond matrix.

When n = 3, the bond matrix of the corresponding MOP is: $\left[\begin{array}{cccc}& 1\hfill & 2\hfill & 3\hfill \\ 1\hfill & 0\hfill & 1\hfill & 1\hfill \\ 2\hfill & & 0\hfill & 1\hfill \\ 3\hfill & & & 0\hfill \end{array}\right]$

W(G₃) = 1 + 2 = 3

When n = 4, the bond matrix of the corresponding MOP is: $\left[\begin{array}{ccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill \\ 1\hfill & \mathbf{0}\hfill & \mathbf{1}\hfill & \mathbf{1}\hfill & 2\hfill \\ 2\hfill & & \mathbf{0}\hfill & \mathbf{1}\hfill & 1\hfill \\ 3\hfill & & & \mathbf{0}\hfill & 1\hfill \\ 4\hfill & & & & 0\hfill \end{array}\right]$

W(G₄) = 1 + 2 + 4 $\left[={\left(\frac{n}{2}\right)}^2\right]$ = W(G₃) + 4 = 7

In the above matrix, bolded element indicates that the entries and the corresponding sum of the values of W(G₃).

When n = 5, the bond matrix MOP is: $\left[\begin{array}{cccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill & 5\hfill \\ 1\hfill & \mathbf{0}\hfill & \mathbf{1}\hfill & \mathbf{1}\hfill & \mathbf{2}\hfill & 2\hfill \\ 2\hfill & & \mathbf{0}\hfill & \mathbf{1}\hfill & \mathbf{1}\hfill & 2\hfill \\ 3\hfill & & & \mathbf{0}\hfill & \mathbf{1}\hfill & 1\hfill \\ 4\hfill & & & & \mathbf{0}\hfill & 1\hfill \\ 5\hfill & & & & & 0\hfill \end{array}\right]$

Sum = 1 + 2 + 4 + 6$\left[=\left(\frac{n-1}{2}\right)\times \left(\frac{n+1}{2}\right)\right]$ = W(G₄) + 6 = 13

The theorem is true for n = 3, 4, 5.

Assume that the theorem is true for n = m, and m is either even or odd

Let m be an odd.

Then the corresponding bond matrix is: $\left[\begin{array}{ccccccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill & .\hfill & .\hfill & .\hfill & m\hfill \\ 1\hfill & 0\hfill & 1\hfill & 1\hfill & 2\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]\hfill \\ 2\hfill & & 0\hfill & 1\hfill & 1\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]\hfill \\ 3\hfill & & & 0\hfill & 1\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]-1\hfill \\ 4\hfill & & & & 0\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]-1\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & 1\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & 1\hfill \\ m\hfill & & & & & .\hfill & .\hfill & .\hfill & 0\hfill \end{array}\right]$

Since the division takes only integral part alone.

Sum = 1 + 2 + 4 + 6 + … + $\left(\frac{m-1}{2}\right)\times \left(\frac{m+1}{2}\right)$ = W(G_m − 1) + $\left(\frac{m-1}{2}\right)\times \left(\frac{m+1}{2}\right)$ = W(G_m).

Since the length of the mth column is even so each term is repeated twice.

If n = m is even: then $\left[\begin{array}{ccccccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill & .\hfill & .\hfill & .\hfill & m\hfill \\ 1\hfill & 0\hfill & 1\hfill & 1\hfill & 2\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]\hfill \\ 2\hfill & & 0\hfill & 1\hfill & 1\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]-1\hfill \\ 3\hfill & & & 0\hfill & 1\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]-1\hfill \\ 4\hfill & & & & 0\hfill & .\hfill & .\hfill & .\hfill & \left[\frac{m}{2}\right]-2\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & 1\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & 1\hfill \\ m\hfill & & & & & .\hfill & .\hfill & .\hfill & 0\hfill \end{array}\right]$

Sum = 1 + 2 + 4 + 6 + … + ${\left(\frac{m}{2}\right)}^{{}^2}$ = W(G_m − 1) + ${\left(\frac{m}{2}\right)}^2$.

Here the length of the mth column is odd, so except the first term, remaining is repeated twice.

We have to prove for n = m + 1,

If m is even, Then m + 1 is odd, the length of the (m + 1)th column will be even.

Which is: $\begin{array}{ccccccccc}\left(\frac{m+1}{2}\right)\hfill & \left(\frac{m+1}{2}\right)\hfill & \left(\frac{m+1}{2}\right)-1\hfill & \left(\frac{m+1}{2}\right)-1\hfill & .\hfill & .\hfill & .\hfill & 1\hfill & 1\hfill \end{array}$$$\left[\begin{array}{ccccccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill & .\hfill & .\hfill & m\hfill & m+1\hfill \\ 1\hfill & \mathbf{0}\hfill & \mathbf{1}\hfill & \mathbf{1}\hfill & \mathbf{2}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]\hfill & \left[\frac{m+1}{2}\right]\hfill \\ 2\hfill & & \mathbf{0}\hfill & \mathbf{1}\hfill & \mathbf{1}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]-\mathbf{1}\hfill & \left[\frac{m+1}{2}\right]\hfill \\ 3\hfill & & & \mathbf{0}\hfill & \mathbf{1}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]-\mathbf{1}\hfill & \left[\frac{m+1}{2}\right]-1\hfill \\ 4\hfill & & & & \mathbf{0}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]-\mathbf{2}\hfill & \left[\frac{m+1}{2}\right]-1\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & \mathbf{1}\hfill & 1\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & \mathbf{0}\hfill & 1\hfill \\ m\hfill & & & & & .\hfill & & & 0\hfill \end{array}\right]$$

Sum = W(G_m) + $\left(\frac{m}{2}\right)\times \left(\frac{m+2}{2}\right)$ = W(G_m + 1)

If m is odd, then n = m + 1 is even, $\left[\begin{array}{ccccccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill & .\hfill & .\hfill & m\hfill & m+1\hfill \\ 1\hfill & \mathbf{0}\hfill & \mathbf{1}\hfill & \mathbf{1}\hfill & \mathbf{2}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]\hfill & \left[\frac{m+1}{2}\right]\hfill \\ 2\hfill & & \mathbf{0}\hfill & \mathbf{1}\hfill & \mathbf{1}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]\hfill & \left[\frac{m+1}{2}\right]-1\hfill \\ 3\hfill & & & \mathbf{0}\hfill & \mathbf{1}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]-\mathbf{1}\hfill & \left[\frac{m+1}{2}\right]-1\hfill \\ 4\hfill & & & & \mathbf{0}\hfill & .\hfill & .\hfill & \left[\frac{\mathit{m}}{\mathbf{2}}\right]-\mathbf{1}\hfill & \left[\frac{m+1}{2}\right]-2\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & \mathbf{1}\hfill & 1\hfill \\ .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & .\hfill & \mathbf{0}\hfill & 1\hfill \\ m\hfill & & & & & .\hfill & .\hfill & .\hfill & 0\hfill \end{array}\right]$

Sum = W(G_m) + ${\left(\frac{m+1}{2}\right)}^{{}^2}$ = W(G_m + 1)

Thus, the theorem is true for the case n = m + 1 also. Hence, by induction hypothesis, the theorem is true for all n.

Therefore, $W(G_n)=\left\{\begin{array}{cc}W(G_{n-1})+\left(\frac{n-1}{2}\right)\times \left(\frac{n+1}{2}\right)\hfill & \text{if}n\text{is}\text{odd}\hfill \\ W(G_{n-1})+{\left(\frac{n}{2}\right)}^2\hfill & \text{if}n\text{is}\text{even}\hfill \end{array}\right.$. □

Corollary 5.1

If G is consecutive striped MOP then the independence number of G is $\left[\frac{n-a}{{\mathit{\alpha }}^{\ast }}\right]+1$ where [x] denote the integral part and “a” is first number in any largest maximal independent set.

Proof

In each row of the bond matrix, the distance more than 1 indicates that the corresponding vertices are paired, which generate independent set.

Size of the independent set is increased, when any two of the independent sets have a common element in which the distance between each pair of elements must have more than 1. Now the extended independent set is called maximal independent set. Largest among all maximal independent sets in size is called independence number.

Consecutive striped MOP graph has so many maximal independent sets of different sizes with additional property that each maximal independent set is in the form of arithmetic progression with common difference α*. By using property of arithmetic progression, the independence number of any largest maximal independent set is: $\left[\frac{n-a}{{\mathit{\alpha }}^{\ast }}\right]+1$ where [x]-denote integral part only and a is first number in any largest maximal independent set. This completes the proof. □

Concrete Example: The following is the bond matrix of consecutive striped MOP for the case n = 8:$$\left[\begin{array}{ccccccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill & 5\hfill & 6\hfill & 7\hfill & 8\hfill \\ 1\hfill & 0\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill & 3\hfill & 3\hfill & 4\hfill \\ 2\hfill & & 0\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill & 3\hfill & 3\hfill \\ 3\hfill & & & 0\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill & 3\hfill \\ 4\hfill & & & & 0\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill \\ 5\hfill & & & & & 0\hfill & 1\hfill & 1\hfill & 2\hfill \\ 6\hfill & & & & & & 0\hfill & 1\hfill & 1\hfill \\ 7\hfill & & & & & & & 0\hfill & 1\hfill \\ 8\hfill & & & & & & & & 0\hfill \end{array}\right]$$

Figure 6. Isomorphic consecutive striped MOP.

Independent sets Row 1: {1, 4}, {1, 5}, {1, 6},{1, 7}, {1, 8}

Row 2: {2, 5}, {2, 6}, {2, 7}, {2, 8}

Row 3: {3, 6}, {3, 7},{3, 8}

Row 4: {4, 7}, {4, 8}

Row 5: {5, 8}

Bolded sets form a Maximal Independent sets: {1, 4, 7}, {2, 5, 8}, {3, 6}

According to the corollary,

Table 1. Dominance number of consecutive striped MOP

Consecutive striped MOP on n vertices	3	4	5	6	7	8	9	10	11	12	13	14	15
Dominance number	1	1	1	2	2	2	2	2	3	3	3	3	3

Independence Number is 3.

Corollary 5.2

If G is a consecutive striped MOP then chromatic number of G is 3.

Proof

By the property of the planarity, size of the maximum clique is equal to the chromatic number of a graph. Maximum clique for this consecutive striped MOP graph is triangle. By the above corollary, we group all maximal independent sets, since maximal independent sets are disjoint and are arithmetic progression with common difference 3(α*). So this graph has only three chromatic partitions which are:

{1, 1 + α*, 1 + 2 α*, …}

{2, 2 + α*, 2 + 2 α*, …}

{3, 3 + α*, 3 + 2 α*, …}

Each partition has one color, so chromatic partition of consecutive striped MOP is 3.

This completes the proof. □

Remark 5.1

A Perfect Matching is a matching which matches all the vertices of the graph and A near Perfect Matching is one in which exactly one vertex is unmatched. This can only occur when the graph has an odd number of vertices; such a matching must be maximum. If there is a perfect matching, then both the matching number and the edge cover number are $\frac{n}{2}$, where n is the number of vertices of a graph. This result is true for consecutive striped MOP which is calculated from the bond matrix.

$$\left[\begin{array}{ccccccc}& 1\hfill & 2\hfill & 3\hfill & 4\hfill & 5\hfill & 6\hfill \\ 1\hfill & 0\hfill & \boxed{1}\hfill & 1\hfill & 2\hfill & 2\hfill & 3\hfill \\ 2\hfill & & 0\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill \\ 3\hfill & & & 0\hfill & \boxed{1}\hfill & 1\hfill & 2\hfill \\ 4\hfill & & & & 0\hfill & 1\hfill & 1\hfill \\ 5\hfill & & & & & 0\hfill & \boxed{1}\hfill \\ 6\hfill & & & & & & 0\hfill \end{array}\right]$$

In the above matrix “1” indicates a direct edge between the vertices. Select “1” in the first row and then leave that corresponding row and column. Choose the next row and select “1” likewise. Finally, that marked “1” shows the perfect matching, sum of the entries are marked equals to matching number. For this table, matching Number of G₆ is 3.

Remark 5.2

Each striped MOP is super edge-magic, it has SEM sequence. So it easy to calculate the WI for those graphs and that number is not unique. But the graphs that are isomorphic to consecutive striped MOP have same WI as well as independence number, matching number, and chromatic number. Figure 6 exhibits the above properties.

Remark 5.3

Every maximal independent set is a dominating set. A minimal dominating set is a dominating set from which no vertex can be removed without destroying its dominance property. A graph having many minimal dominating sets with different size, smallest in size is called dominance number. Table 1 gives the analysis of dominance number for consecutive striped MOP.

By comparing independence number proved in corollary 5.1 and dominance number listed in Table 1, we can observe that, dominance number is less than the independence number. In addition, the equality is attained only when n = 3 and n = 6.

6. Conclusion

In this paper, the total number of super edge-magic graphs with n vertices and 2n − 3 edges are calculated. Also, we derived formula for WI of consecutive striped MOP. From this, we investigated the properties: independence number, chromatic number, matching number, and dominance number for this consecutive striped MOP through SEMS.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

G.S.G.N. Anjaneyulu

G.S.G.N. Anjaneyulu received MPhil in “Theory of Semirings” in 2004 and PhD in “Digital Signatures using Semiring Structures” from S.V. University, Tirupati, India in 2008. He has 18 years of teaching experience in graduate, postgraduate, and Engineering Mathematics. He published 25 research papers in international journals and presented papers in conferences. He is currently working as a professor, Division of Applied Algebra, SAS, VIT University, Vellore, India. His current research interest includes “Cryptography, Network Security, Image Processing, Data Mining, Algebra and Graph Theory”.

A. Vijayabarathi

A. Vijayabarathi received MPhil in 2001 and PhD in “Super Edge-magic Sequences of Graphs and Applications” from VIT University, Vellore, India in 2014. She has nine years of teaching experience in graduate and postgraduate Mathematics. She published eight research papers in national and international journals and presented papers in conferences. She is currently working as an assistant professor of Mathematics, College of Arts and Sciences, Thiruvalluvar University, Tittagudi, India.