A detection for patent infringement suit via nanotopology induced by graph

Abstract

The aim of this paper was to generate nanotopological structure on the power set of vertices of simple digraphs using new definition neighbourhood of vertices on out linked of digraphs. Based on the neighbourhood we define the approximations of the subgraphs of a graph. A new nanotopological graph reduction to symbolic circuit analysis is developed in this paper. By means of structural equivalence on nanotopology induced by graph we have framed an algorithm for detecting patent infringement suit.

Keywords:

• graph
• neighbourhood
• isomorphism
• homeomorphism
• electrical circuits

2010 AMS Subject classifications:

• 54B05
• 54C05

Public Interest Statement

Lellis Thivagar introduced nanotopological space with respect to a subset X of an universe which is defined in terms of lower and upper approximations of X. The elements of a nanotopological space are called the nano-open sets. But certain nanoterms are satisfied simply to mean “very small”. It originates from the Greek word “Nanos” which means “Dwarf” in its modern scientific sense, an order to magnititude—one billionth of something. Nanocar is an example. The topology recommended here is named so because of its size, since it has atmost five elements in it. The purpose of the present work was to put a starting point for the nanotopological graph theory. We hope these new results will further assist to comprehend the concept of nanotopological space in various applied fields.

1. Introduction

The theory of nanotopology proposed by Lellis Thivagar and Richard (2013a, b), is an extension of set theory for the study of intelligent systems characterized by in sufficient and incomplete information. The purpose of the present work was to put a starting point for the nanotopological graph theory. Most real-life situations need some sort of approximation to fit mathematical models. The beauty of using nanotopology in approximation is achieved via approximation for qualitative subgraphs without coding or using assumption. We believe that nanotopological graph structure will be an important base for modification of knowledge extraction of processing. In this section, we define graphical isomorphism (Diestel, Diestel (2010); Jensen & Shen, 2007) is a related task for deciding when two graphs with different specifications are structurally equivalent, that is whether they have the same pattern of connections. Nanohomeomorphism (Bonikowski, Bryniarski, & Wybraniec, 1998) between two nanotopological spaces are said to be topologically equivalent. Here, we are formalizing the structural equivalence of basic circuit of the chips from the graphs and their corresponding nanotopologies generated by them.

2. Preliminaries

This section represents a review of some fundamental notions related to nanotopology and graph theory.

Definition 2.1

   (Lellis Thivagar & Richard, 2013a, b) Let $\mathcal{U}$ be an universe. $\mathcal{R}$ be an equivalence relation on $\mathcal{U}$ and ${\mathit{\tau }}_R(X)=\{\mathcal{U},\mathrm{\varnothing },L_R(X),U_R(X),B_R(X)\}$ where $X\subseteq \mathcal{U}$. ${\mathit{\tau }}_R(X)$ satisfies the following axioms:

(i)	$\mathcal{U}$ and $\mathrm{\varnothing }\in {\mathit{\tau }}_R(X)$.
(ii)	The union of elements of any sub collection of ${\mathit{\tau }}_R(X)$ is in ${\mathit{\tau }}_R(X)$.
(iii)	The intersection of the elements of any finite sub collection of ${\mathit{\tau }}_R(X)$ is in ${\mathit{\tau }}_R(X)$. That is, ${\mathit{\tau }}_R(X)$ forms a topology on $\mathcal{U}$ the nanotopology on $\mathcal{U}$ with respect to X. We call $(\mathcal{U},{\mathit{\tau }}_R(X))$ as the nanotopological space. The elements of ${\mathit{\tau }}_R(X)$ are called nano-open sets.

Definition 2.2

(Bonikowski et al., 1998; Diestel, Diestel (2010)) A graph G is an ordered pair of disjoint sets (V, E), where V is nonempty and E is a subset of unordered pairs of V. The vertices and edges of a graph G are the elements of V=V(G) and E=E(G), respectively. We say that a graph G is finite (resp. infinite) if the set V(G) is finite (resp.finite). The degree of a vertex $u\in V(G)$ is the number of edge in a graph contains a vertex u, then u is called an isolated point and so the degree of u is zero (Lellis Thivagar & Richard, 2013a, b). An edge which has the same vertex to ends is called a loop and the edge with distinct ends is called a link (Jensen & Shen, 2007).

Definition 2.3

(Bonikowski et al., 1998; Diestel, Diestel (2010)) A graph is simple if it has no loops and no two of its links join the same pair of vertices. A graph which has no edge called a null graph. A graph which has no vertices is called a empty graph (Jensen & Shen, 2007; Lellis Thivagar & Richard, 2013a, b).

Definition 2.4

(Deseor & Kuh, 2009; Diestel, Diestel (2010)) If G[V, E] is a directed graph and $u,v\in V$, then:

(i)	u is invertex of v if $\overrightarrow{uv}\in E(G)$.
(ii)	u is outvertex of v if $\overrightarrow{vu}\in E(G)$.
(iii)	The indegree of a vertex ’v’ is the number of vertices ’u’ such that $\overrightarrow{uv}\in E(G)$.
(iv)	The outdegree of a vertex ’v’ is the number of vertices ’u’ such that $\overrightarrow{vu}\in E(G)$.

Throughout this paper the word graph means direct simple graph.

3. Approximations via neighbourhood

In this section, we will define lower and upper approximation of subgraph H of a graph G[V, E]. Some properties of these concepts are studied.

Definition 3.1

Let G(V,E) be a graph, $v\in V(G)$. Then we define the neighbourhood of ’v’ as follows, $N(v)=\{v\}\bigcup \{u\in V(G):\overrightarrow{vu}\in E(G)\}$.

Definition 3.2

Let G(V,E) be a graph, H is a subgraph of G and N(v) be neighbourhood of v in V. Then we define

(i)	The lower approximation operation as follows: $L:P[V(G)]\to P[V(G)]$ such that, $L_N[V(H)]=\bigcup _{v\in V(G)}\{v|N(v)\subseteq V(H)\}$
(ii)	The upper approximation operation as follows: $U:P[V(G)]\to P[V(G)]$ such that, $U_N[V(H)]=\{N(v):v\in V(H)\}$
(iii)	The boundary region is defined as $B_N[V(H)]=U_N[V(H)]-L_N[V(H)]$

Definition 3.3

Let G be a graph, N(v) be neighbourhood of v in V and H be a subgraph of G, ${\mathit{\tau }}_N[V(H)]=\{V(G),\mathrm{\varnothing },L_N[V(H)],U_N[V(H)],B_N[V(H)]\}$ forms a topolgy on V(G) called the nanotopology on V(G) with respect to V(H). We call $[V(G),{\mathit{\tau }}_N[V(H)]]$ as the nanotopological space induced by a graph.

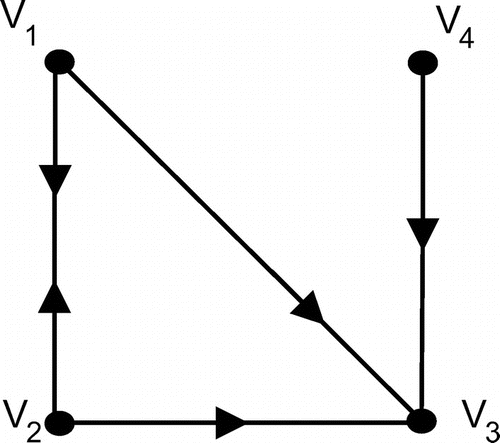
Example 3.4

Consider Figure 1.

Then $V(G)=\{V_1,V_2,V_3,V_4\}$ and $N(v_1)=\{V_1,V_2,V_3\},N(v_2)=\{v_1,v_2,v_3\},N(v_3)=\{v_3\},N(v_4)=\{v_3,v_4\}$ and H be a subgraph of G, where $V(H)=\{V_2,V_3,V_4\}$, then $L_N[V(H)]=\{V_3,V_4\},U_N[V(H)]=V(G),B_N[V(H)]=\{V_1,V_2\}$. Therefore, the nanotopology induced by the graph is ${\mathit{\tau }}_N[V(H)]=\{V(G),\mathrm{\varnothing },\{V_3,V_4\},\{V_1,V_2\}\}$ and let H be a subgraph of G, where $V(H)=\{V_1,V_2\}$ then $L_N[V(H)]=\{V_3\},U_N[V(H)]=\{V_1,V_2,V_3\},B_N[V(H)]=\{V_1,V_2\}$. Therefore, the nanotopology induced by the graph is ${\mathit{\tau }}_N[V(H)]=\{V(G),\mathrm{\varnothing },\{V_3\},\{V_1,V_2,V_3\},\{V_1,V_2\}\}$

Figure 1. Graph for Example 3.4.

Theorem 3.5

Let G[V, E] be a graph, H is a subgraph of G, then:

(i)	$L_N[V(H)]\subseteq V(H)\subseteq U_N[V(H)]$
(ii)	$L_N[V(G)]=V(G)=U_N[V(G)]$
(iii)	$L_N[\mathrm{\varnothing }]=U_N[\mathrm{\varnothing }]=\mathrm{\varnothing }$.

Theorem 3.6

Let G[V, E] be a graph, H and K are two subgraphs of a graph G, then

(a)	If $V(H)\subseteq V(K)$ then $L_N[V(H)]\subseteq L_N[V(K)]$ and $U_N[V(H)]\subseteq U_N[V(K)]$
(b)	$L_N[V(H)]\cup L_N[V(K)]\subseteq L_N[V(H)\cup V(K)]$
(c)	$L_N[V(H)\cap V(K)]=L_N[V(H)]\cap L_N[V(K)]$
(d)	$U_N[V(H)\cup V(K)]=U_N[V(H)]\cup U_N[V(K)]$
(e)	$U_N[V(H)\cap V(K)]\subseteq U_N[V(H)]\cap U_N[V(K)]$

Proof

 

(a)	Let $v\in L_N[V(H)]$. By definition of $L_N[V(H)]$, $N(v)\subseteq V(H)$, but $V(H)\subseteq V(K)\Rightarrow N(v)\subseteq V(H)\subseteq V(K)$ and hence $v\in L_N[V(K)]$. Since $v\in L_N[V(H)]\Rightarrow v\in L_N[V(K)]$. Therefore $L_N[V(H)]\subseteq L_N[V(K)]$. In a similar manner we can also prove that $U_N[V(H)]\subseteq U_N[V(K)]$.
(b)	Since $V[H]\subseteq V(H)\cup V(K),V[K]\subseteq V(H)\cup V(K),L_N[V(H)]\subseteq L_N[V(H)\cup V(K)],and{L}_N[V(K)]\subseteq L_N[V(H)\cup V(K)]$. Therefore $L_N[V(H)]\cup L_N[V(K)]\subseteq L_N[V(H)\cup V(K)]$.
(c)	Since $V(H)\cap V(K)\subseteq V(H),V(H)\cap V(K)\subseteq V(K),L_N[V(H)\cap V(K)]\subseteq L_N[V(H)]$ and $L_N[V(H)\cap V(K)]\subseteq L_N[V(K)]$. Therefore $L_N[V(H)\cap V(K)]\subseteq L_N[V(H)]\cap L_N[V(K)]$. Let $v\in L_N[V(H)]\cap L_N[V(K)]\Rightarrow v\in L_N[V(H)]andv\in L_N[V(K)]$. Hence by definition $N(v)\subseteq V(H)$ and $N(v)\subseteq V(K)\Rightarrow N(v)\subseteq V(H)\cap V(K)$. This means that $v\in L_N[V(H)\cap V(K)].$ Therefore $L_N[V(H)]\cup L_N[V(K)]\subseteq L_N[V(H)\cap V(K)]$. Hence, we conclude that $L_N[V(H)]\cap L_N[V(K)]=L_N[V(H)\cap V(K)].$
(d)	Since $V(H)\subseteq V(H)\cup V(K),V(K)\subseteq V(H)\cup V(K),U_N[V(H)]\subseteq U_N[V(H)\cup V(K)]$ and $U_N[V(K)]\subseteq U_N[V(H)\cup V(K)]$. Therefore $U_N[V(H)]\cup U_N[V(K)]\subseteq U_N[V(H)\cup V(K)]$. Let $v\in U_N[V(H)\cap V(K)]$, then by definition $x\in \bigcup \{N(v):v\in [V(H)\cup V(K)]\}\Rightarrow x\in \bigcup \{N(v):v\in V(H)\}orx\in \bigcup \{N(v):v\in V(K)\Rightarrow x\in U_N[V(H)]orx\in U_N[V(K)]\Rightarrow x\in U_N[V(H)]\cup U_N[V(K)]$. Therefore $U_N[V(H)\cup V(K)]\subseteq U_N[V(H)]\cup U_N[V(K)]$. Hence, we conclude that $U_N[V(H)\cup V(K)]=U_N[V(H)]\cup U_N[V(K)]$.
(e)	Since $V(H)\cap V(K)\subseteq V(H),V(H)\cap V(K)\subseteq V(K),U_N[V(H)\cap V(K)]\subseteq U_N[V(H)]$ and $U_N[V(H)\cap V(K)]\subseteq U_N[V(K)]$. Therefore $U_N[V(H)\cap V(K)]\subseteq U_N[V(H)]\cap U_N[V(K)]$.

$\square$

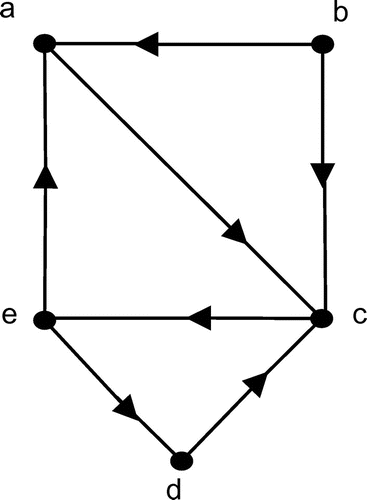
Example 3.7

Consider Figure 2

Then $V(G)=\{a,b,c,d,e\}$ and $N(a)=\{a,c\},N(b)=\{a,b,c\},N(c)=\{c,e\},N(d)=\{a,d,e\}$. Table 1 shows the nanotopology of any subgraph H of a subgraph of G.

Figure 2. Graph for Example 3.7 and Remark 3.8.

Table 1. Nanotopology for the possible subgraphs of G

V(H)	$L_N[V(H)]$	$U_N[V(H)]$	$B_N[V(H)]$	$T_N[V(H)]$
$\{a\}$	$\mathrm{\varnothing }$	$\{a,c\}$	$\{a,c\}$	$\{V(G),\mathrm{\varnothing },\{a,c\}\}$
$\{b\}$	$\mathrm{\varnothing }$	$\{a,b,c\}$	$\{a,b,c\}$	$\{V(G),\mathrm{\varnothing },\{a,b,c\}\}$
$\{c\}$	$\mathrm{\varnothing }$	$\{c,e\}$	$\{c,e\}$	$\{V(G),\mathrm{\varnothing },\{c,e\}\}$
$\{d\}$	$\mathrm{\varnothing }$	$\{c,d\}$	$\{c,d\}$	$\{V(G),\mathrm{\varnothing },\{c,d\}\}$
$\{e\}$	$\mathrm{\varnothing }$	$\{a,d,e\}$	$\{a,d,e\}$	$\{V(G),\mathrm{\varnothing },\{a,d,e\}\}$
$\{a,b\}$	$\mathrm{\varnothing }$	$\{a,b,c\}$	$\{a,b,c\}$	$\{V(G),\mathrm{\varnothing },\{a,b,c\}\}$
$\{a,c\}$	$\{a\}$	$\{a,c,e\}$	$\{c,e\}$	$\{V(G),\mathrm{\varnothing },\{a\},\{a,c,e\},\{c,e\}\}$
$\{a,d\}$	$\mathrm{\varnothing }$	$\{a,c,d\}$	$\{a,c,d\}$	$\{V(G),\mathrm{\varnothing },\{a,c,d\}\}$
$\{a,e\}$	$\mathrm{\varnothing }$	$\{a,c,d,e\}$	$\{a,c,d,e\}$	$\{V(G),\mathrm{\varnothing },\{a,c,d,e\}\}$
$\{b,c\}$	$\mathrm{\varnothing }$	$\{a,b,c,e\}$	$\{a,b,c,e\}$	$\{V(G),\mathrm{\varnothing },\{a,b,c,e\}\}$
$\{b,d\}$	$\mathrm{\varnothing }$	$\{a,b,c,d\}$	$\{a,b,c,d\}$	$\{V(G),\mathrm{\varnothing },\{a,b,c,d\}\}$
$\{b,e\}$	$\mathrm{\varnothing }$	V(G)	V(G)	$\{V(G),\mathrm{\varnothing }\}$
$\{c,d\}$	$\{d\}$	$\{c,d,e\}$	$\{c,e\}$	$\{V(G),\mathrm{\varnothing },\{d\},\{c,d,e\},\{c,e\}\}$
$\{c,e\}$	$\{c\}$	$\{a,c,d,e\}$	$\{a,d,e\}$	$\{V(G),\mathrm{\varnothing },\{c\},\{a,c,d,e\},\{a,d,e\}\}$
$\{d,e\}$	$\mathrm{\varnothing }$	$\{a,c,d,e\}$	$\{a,c,d,e\}$	$\{V(G),\mathrm{\varnothing },\{a,c,d,e\}\}$
$\{a,b,c\}$	$\{a,b\}$	$\{a,b,c,e\}$	$\{c,e\}$	$\{V(G),\mathrm{\varnothing },\{a,b\},\{a,b,c,e\},\{c,e\}\}$
$\{a,b,d\}$	$\mathrm{\varnothing }$	$\{a,b,c,d\}$	$\{a,b,c,d\}$	$\{V(G),\mathrm{\varnothing },\{a,b,c,d\}\}$
$\{a,b,e\}$	$\mathrm{\varnothing }$	V(G)	V(G)	$\{V(G),\mathrm{\varnothing }\}$
$\{a,c,d\}$	$\{a,d\}$	$\{a,c,d,e\}$	$\{c,e\}$	$\{V(G),\mathrm{\varnothing },\{a,d\},\{a,c,d,e\},\{c,e\}\}$
$\{a,c,e\}$	$\{a,c\}$	$\{a,c,d,e\}$	$\{d,e\}$	$\{V(G),\mathrm{\varnothing },\{a,c\},\{a,c,d,e\},\{d,e\}\}$
$\{a,d,e\}$	$\{e\}$	$\{a,c,d,e\}$	$\{a,c,d\}$	$\{V(G),\mathrm{\varnothing },\{e\},\{a,c,d,e\},\{a,c,d\}\}$
$\{b,c,d\}$	$\{d\}$	V(G)	$\{a,b,c,e\}$	$\{V(G),\mathrm{\varnothing },\{d\},\{a,b,c,e\}\}$
$\{b,c,e\}$	$\{c\}$	V(G)	$\{a,d,e,d\}$	$\{V(G),\mathrm{\varnothing },\{c\},\{a,b,d,e\}\}$
$\{b,d,e\}$	$\mathrm{\varnothing }$	V(G)	V(G)	$\{V(G),\mathrm{\varnothing }\}$
$\{c,d,e\}$	$\{c,d\}$	$\{a,c,d,e\}$	$\{a,e\}$	$\{V(G),\mathrm{\varnothing },\{c,d\},\{a,c,d,e\},\{a,e\}\}$
$\{a,b,c,d\}$	$\{a,b,d\}$	V(G)	$\{c,e\}$	$\{V(G),\mathrm{\varnothing },\{a,b,d\},\{c,e\}\}$
$\{a,b,c,e\}$	$\{a,b,c\}$	V(G)	$\{d,e\}$	$\{V(G),\mathrm{\varnothing },\{a,b,c\},\{d,e\}\}$
$\{a,b,d,e\}$	$\{e\}$	V(G)	$\{a,b,c,e\}$	$\{V(G),\mathrm{\varnothing },\{e\},\{a,b,c,e\}\}$
$\{a,c,d,e\}$	$\{a,c,d,e\}$	$\{a,c,d,e\}$	$\mathrm{\varnothing }$	$\{V(G),\mathrm{\varnothing },\{a,c,d,e\}\}$
$\{b,c,d,e\}$	$\{c,d\}$	V(G)	$\{a,b,e\}$	$\{V(G),\mathrm{\varnothing },\{c,d\},\{a,b,e\}\}$
V(G)	V(G)	V(G)	$\mathrm{\varnothing }$	$\{V(G),\mathrm{\varnothing }\}$
$\mathrm{\varnothing }$	$\mathrm{\varnothing }$	$\mathrm{\varnothing }$	$\mathrm{\varnothing }$	$\{V(G),\mathrm{\varnothing }\}$

Remark 3.8

Let G[V, E] be a graph, H and K are two subgraphs of G. Then from the examples 3.7 we can see some perception as follows:

(i)	$L[V(H)\cup V(K)]⊈L[V(H)]\cup L[V(K)],$ take $V(H)=\{a,b\}andV(K)=\{c\}$
(ii)	$U[V(H)]\cap U[V(K)]⊈U[V(H)\cap V(K)],$ take $V(H)=\{a,d\}andV(K)=\{a,e\}$
(iii)	$L{[V(H)]}^c\ne {[U[V(H)]]}^c,$ take $V(H)=\{a\}$
(iv)	$U{[V(H)]}^c\ne {[L[V(H)]]}^c,$ take $V(H)=\{a,b\}$
(v)	$U[U[V(H)]]⊈[U[V(H)]],$ take $V(H)=\{a\}$
(vi)	$U[V(H)]⊈L[U[V(H)]],$ take $V(H)=\{a,c\}$
(vii)	$L[U[V(H)]]⊈V(H),$ take $V(H)=\{b\}$
(viii)	$V(H)⊈U[L[V(H)]],$ take $V(H)=\{a\}$
(ix)	$U[L[V(H)]]⊈L[V(H)],$ take $V(H)=\{a,c\}$
(x)	$L[V(H)]⊈L[L[V(H)]],$ take $V(H)=\{a,c\}.$

Theorem 3.9

Let G[V,E], H is a subgraph of G, then $U[L[V(H)]]\subseteq V(H)\subseteq L[U[V(H)]].$

Proof

Let $x\in U[L[V(H)]]\Rightarrow$ there exists a $v\in L[V(H)]$ such that $\overrightarrow{vx}\in E[G],$ therefore $x\in N(v)\subseteq V(H).$

Now, since $x\in V(H)$, then $N(x)\subseteq U[V(H)]$ implies, $x\in L[U[V(H)]].$$\square$

Theorem 3.10

Let G[V,E], H is a subgraph of G, then

(i)	$L[U[L[V(H)]]]=L[V(H)].$
(ii)	$U[L[U[V(H)]]]=U[V(H)].$

Proof

 

(i)	Let $x\in L[V(H)]\Rightarrow$$N(x)\subseteq U[L[V(H)]]$. So $x\in L[U[L[V(H)]]]$ we know that $U[L[V(H)]]\subseteq V(H),$ implies $L[U[L[V(H)]]]=L[V(H)]$.
(ii)	we know that $U[L[V(H)]]\subseteq V(H)$ implies $U[L[U[V(H)]]]\subseteq U[V(H)]$ we know that $V(H)\subseteq L[U[[V(H)]]$ implies $U[L[U[V(H)]]]=U[V(H)]$.

$\square$

4. Formalizing structural equivalence

Here we are formalizing the structural equivalence for the graphs and their corresponding nanotopologies generated by them.

Remark 4.1

In this section we define graphical isomorphism is a related task for deciding when two graphs with different specifications are structurally equivalent, that is whether they have the same pattern of connections. Nanohomeomorphism between two nanotopological spaces are said to be topologically equivalent. Here we are formalizing the structural equivalence for the graphs and their corresponding nanotopologies generated by them.

Definition 4.2

(Hsu & Lin, 2008) Two digraphs G and H are isomorphic if there is an isomorphism f between their underlying graphs that preserves the direction of each edge. That is, e is directed from u to v if and only if f(e) is directed from f(u) to f(v).

Definition 4.3

(Hsu & Lin, 2008) Two digraphs Cand D are isomorphic if D can be obtained by relabelling the vertices of C, that is, if there is a bijection between the vertices of C and those of D, such that the arcs joining each pair of vertices in C agree in both number and direction with the arcs joining the corresponding pair of vertices in D.

Definition 4.4

Let $(\mathcal{U},{\mathit{\tau }}_R(X))$ and $(\mathcal{V},{\mathit{\tau }}_{R^{\prime }}(Y))$ be nanotopological spaces, then the mapping $f:(\mathcal{U},{\mathit{\tau }}_R(X))\to (\mathcal{V},{\mathit{\tau }}_R(Y))$ is said to be a nanocontinuous on $\mathcal{U}$ if the inverse image of every nano-open set in $\mathcal{V}$ is nano-open in $\mathcal{U}$.

Definition 4.5

Let $(\mathcal{U},{\mathit{\tau }}_R(X))$ and $(\mathcal{V},{\mathit{\tau }}_{R^{\prime }}(Y))$ be a nanotopological spaces, then the mapping $f:(\mathcal{U},{\mathit{\tau }}_R(X))\to (\mathcal{V},{\mathit{\tau }}_R(Y))$ is said to be a nanohomeomorphism if

(i)	f is 1–1 and onto
(ii)	f is nanocontinuous
(iii)	f is nano-open

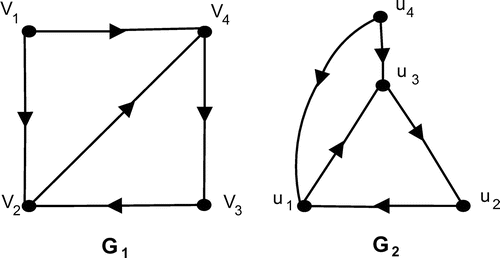
Example 4.6

Let G = [V,E] and G’= [V’,E’] be two isomorphic graphs, where V= $\{v_1,v_2,v_3,v_4\}$, E = $\{(v_1,v_2),(v_1,v_4),(v_2,v_4),(v_4,v_3),(v_3,v_2)\}$, V’ = $\{u_1,u_2,u_3,u_4\}$ and E’ = $\{(u_1,u_3),(u_2,u_1),(u_3,u_2),(u_4,u_1),(u_4,u_3)\}$.

Then there exists a function $f:V\to V^{\prime }$ such that $f(v_1)=u_4,f(v_2)=u_1,f(v_3)=u_2,f(v_4)=u_3$. Let H be any subgraph of G and V(H) = $\{v_2,v_3\}$. Then the nanotopology generated by vertices of V(H) and V(f(H)) are ${\mathit{\tau }}_N[V(H)]=\{V(G),\mathrm{\varnothing },\{v_3\},\{v_2,v_3,v_4\},\{v_2,v_4\}\}$ and ${\mathit{\tau }}_N[f(V(H))]=\{V(G^{\prime }),\mathrm{\varnothing },\{u_2\},\{u_1,u_2,u_3\},\{u_1,u_3\}\}$. Then the function $\mathit{\varphi }:[V(G),{\mathit{\tau }}_N(V(H))]\to [V(G^{\prime }),{\mathit{\tau }}_N(f(V(H))]$ is a homeomorphism (Figure 3).

Figure 3. Isomorphic graphs.

Theorem 4.7

Let G = [V,E] and G’ = [V’,E’] be any two isomorphic graphs then there exists a homeomorphism $\mathit{\varphi }:[V(G),{\mathit{\tau }}_N(V(H))]\to [V(G^{\prime }),{\mathit{\tau }}_N(f(V(H))]$ for every subgraph H of G.

Proof

Since G and G’ are isomorphic by defn. there is an isomorphism $f:V[G]\to V[G^{\prime }]$ between their uderlying graphs that preserves the direction of each edge and also N(x) = N(f(x)) $\forall x\in V(G)$. Suppose $[V(G),{\mathit{\tau }}_N(V(H))]$ and $[V(G^{\prime }),{\mathit{\tau }}_N(f(V(H))]$ be the nanotopological space generated by V(H) and f(V(H)). Since f is a bijection clearly, it follows that $\mathit{\varphi }$ is 1–1 and onto.

(i)	To prove that $\mathit{\varphi }$ is an open map. Let A be any nano-open set in ${\mathit{\tau }}_N(V(H))$, then $\mathit{\varphi }(A)$ is nano-open since N(x) = N(f(x)) $\forall x\in A$.
(ii)	To prove that $\mathit{\varphi }$ is continuous. Let B be any nano-open set in ${\mathit{\tau }}_N(f(V(H))$, then ${\mathit{\varphi }}^{-1}[B]$ is nano-open in ${\mathit{\tau }}_N[V(H)]$.

Thus $\mathit{\varphi }$ is a homeomorphism.

$\square$

5. Computer chip intellectual property rights

Based on the structural equivalence of graphs and the corresponding nanotopology induced by them, we have made an attempt to check whether the chip produced by a company have striking operational similarity produced by the another company.

Suppose that not long after Corporation $\mathcal{X}$ develops and markets a computer chip, it happens that the Corporation $\mathcal{Y}$ markets a chip with striking operational similarities. If Corporation $\mathcal{X}$ could prove that Corporation $\mathcal{Y}$’s circuit is merely a rearrangement of the Corporation$\mathcal{X}$ circuitry that is the circuitries are isomorphic], they might have the basis for a patent infringement suit.

Algorithm to detect patent infringement suit: Step1: Given the electrical circuit of the chips manufactured by two companies. An electrical network is an interconnection of electrical network elements such as resistances, capacitances, inductances, voltage and current sources, etc., We also assign reference direction by a directed edge results in the directed graph representing the network.

Step2: Convert the electrical circuits $C_1$ and $C_2$ into graphs $G_1$ and $G_2$.

Step3: Check whether $G_1$ and $G_2$ are isomorphic, and their corresponding nanotopologies induced from their vertices are homeomorphic.

Step4: If $G_1\approxeq G_2$ and $[V(G),{\mathit{\tau }}_N(V(H))]\approx [V(G^{\prime }),{\mathit{\tau }}_N(f(V(H))]$ then the corresponding circuitries have striking operational similarities, and the company $\mathcal{X}$ can claim on the basis for a patent infringement suit.

Step5: Otherwise, we can conclude that both the chip produced are entirely different.

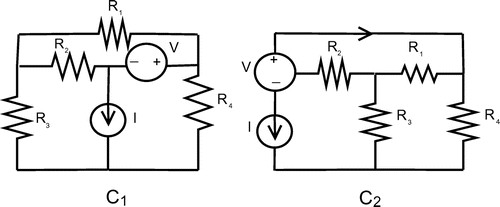
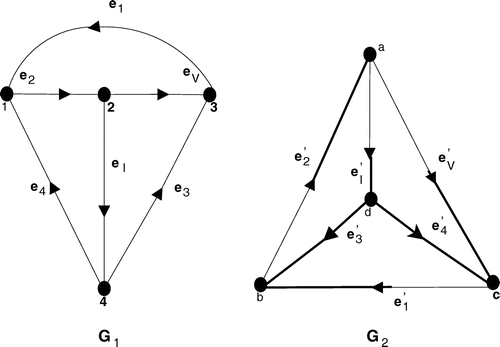
Step1: Consider the following basic circuit of the chip manufactured by two companies Corporation $\mathcal{X}$ and Corporation $\mathcal{Y}$. Using the above algorithm we can prove whether these two circuits have functional similarities via nanotopology induced by the vertices of its subgraphs (Figure ).

Figure 4. Electrical circuit of chips produced by X and Y.

Step2: The graphs are good pictorial representations of circuits and capture all their structural characteristics. Transform the basic circuit $C_1$ and $C_2$ of the chip produced by Corporation $\mathcal{X}$ and Corporation $\mathcal{Y}$ into graphs $G_1=[V_1,E_1]$ and $G_2=[V_2,E_2]$, respectively (Figure 5).

Figure 5. Graphs for circuit $C_1$ and circuit $C_2$.

Step3: From the following graph we define a function $f:V_1\to V_2$ such that f(1) = b, f(2) = a, f(3) = c, f(4) = d and clearly f is an isomorphism. Since $G_2$ can be obtained by relabelling the vertices of $G_1$, that is, f is a bijection between the vertices of $G_1$ and those of $G_2$, such that the arcs joining each pair of vertices in $G_1$ agree in both number and direction with the arcs joining the corresponding pair of vertices in $G_2$.

Then we also have to check $\mathit{\varphi }:[V(G),{\mathit{\tau }}_N(V(H))]\to [V(G^{\prime }),{\mathit{\tau }}_N(f(V(H))]$ is a homeomorphism for every subgraph H of G.

Since f is a bijection clearly, it follows that $\mathit{\varphi }$ is 1–1 and onto.

(i)	To prove that $\mathit{\varphi }$ is an open map.

Then the nanotopology generated by vertices of V(H) = $\{1,3\}$ and $V(f(H))=\{b,c\}$ are ${\mathit{\tau }}_N[V(H)]=\{V(G_1),\mathrm{\varnothing },\{3\},\{1,2,3\},\{1,2\}\}$ and ${\mathit{\tau }}_N[f(V(H))]=\{V(G_2),\mathrm{\varnothing },\{c\},\{a,b,c\},\{a,b\}\}$.

Then the function $\mathit{\varphi }:[V(G_1),{\mathit{\tau }}_N(V(H))]\to [V(G_2),{\mathit{\tau }}_N(f(V(H))]$ is a homeomorphism. This holds for every subgraph H of $G_1$ (Table 2).

Table 2. Nanotopolgy for V(H) and f(V(H))

V(H)	${\mathit{\tau }}_N[V(H)]$	f[V(H)]	${\mathit{\tau }}_N[f[V(H)]]$
$\{1\}$	$\{V(G_1),\mathrm{\varnothing },\{1,2\}\}$	$\{b\}$	$\{V(G_2),\mathrm{\varnothing },\{a,b\}\}$
$\{2\}$	$\{V(G_1),\mathrm{\varnothing },\{2,3,4\}\}$	$\{a\}$	$\{V(G_2),\mathrm{\varnothing },\{a,c,d\}\}$
$\{3\}$	$\{V(G_1),\mathrm{\varnothing },\{1,3\}\}$	$\{c\}$	$\{V(G_2),\mathrm{\varnothing },\{b,c\}\}$
$\{4\}$	$\{V(G_1),\mathrm{\varnothing },\{1,3,4\}\}$	$\{d\}$	$\{V(G_2),\mathrm{\varnothing },\{b,c,d\}\}$
$\{1,2\}\}$	$\{V(G_1),\mathrm{\varnothing },\{1\},\{2,3,4\}\}$	$\{a,b\}$	$\{V(G_2),\mathrm{\varnothing },\{b\},\{a,c,d\}$
$\{1,3\}$	$\{V(G_1),\mathrm{\varnothing },\{3\},\{1,2,3\},\{1,2\}\}$	$\{b,c\}$	$\{V(G_2),\mathrm{\varnothing },\{c\},\{a,b,c\},\{a,b\}\}$
$\{1,4\}$	$\{V(G_1),\mathrm{\varnothing }\}$	$\{b,d\}$	$\{V(G_2),\mathrm{\varnothing }\}$
$\{2,3\}$	$\{V(G_1),\mathrm{\varnothing }\}$	$\{a,c\}$	$\{V(G_2),\mathrm{\varnothing }\}$
$\{2,4\}$	$\{V(G_1),\mathrm{\varnothing }\}$	$\{a,d\}$	$\{V(G_2),\mathrm{\varnothing }\}$
$\{3,4\}$	$\{V(G_1),\mathrm{\varnothing },\{1,3,4\}\}$	$\{c,d\}$	$\{V(G_2),\mathrm{\varnothing },\{b,c,d\}\}$
$\{1,2,3\}$	$\{V(G_1),\mathrm{\varnothing },\{1,3\},\{2,4\}\}$	$\{a,b,c\}$	$\{V(G_2),\mathrm{\varnothing },\{b,c\},\{a,d\}\}$
$\{2,3,4\}$	$\{V(G_1),\mathrm{\varnothing },\{2\},\{1,3,4\}\}$	$\{a,c,d\}$	$\{V(G_2),\mathrm{\varnothing },\{a\},\{b,c,d\}\}$
$\{1,3,4\}$	$\{V(G_1),\mathrm{\varnothing },\{3,4\},\{1,2\}\}$	$\{b,c,d\}$	$\{V(G_2),\mathrm{\varnothing },\{c,d\},\{a,b\},\{a,b\}\}$
$\{4,1,2\}$	$\{V(G_1),\mathrm{\varnothing },\{1\},\{2,3,4\}\}$	$\{a,b,d\}$	$\{V(G_2),\mathrm{\varnothing },\{b\},\{a,c,d\}\}$
$V(G_1)$	$\{V(G_1),\mathrm{\varnothing }\}$	$V(G_2)$	$\{V(G_2),\mathrm{\varnothing }\}$
$\mathrm{\varnothing }$	$\{V(G_1),\mathrm{\varnothing }\}$	$\mathrm{\varnothing }$	$\{V(G_2),\mathrm{\varnothing }\}$

Step4: From the above process, we can conclude that the graph of the circuits and their corresponding nanotopologies generated by the vertices of the subgraphs are homeomorphic.

Step5: Thus we can characterize that the chips manufactured by Corporation $\mathcal{Y}$ is just a rearrangement of Corporation$\mathcal{X}$ and also they have striking operational similarities and Corporation$\mathcal{X}$ can also claim for his patent infringement suit.

Observation: Using the above structural equivalence technique we can check whether two circuits are equivalent and we can also extend our theory in many industrial products for patent infringement suit.

6. Conclusion

The purpose of the present work was to put a starting point for the application of nanotopology via graph theory. We believe that nanotopological graph structure will be an important base for modification of knowledge extraction and processing.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

M. Lellis Thivagar

M. Lellis Thivagar has published 210 research publications both in National and International journals to his credit. In his collaborative work, he has joined hands with intellectuals of high reputed persons internationally. He serves as a referee for 12 peer-reviewed international journals. At present he is the professor & chair person, School Of Mathematics, Madurai Kamaraj University.

Paul Manuel

Paul Manuel has published 114 research publications both in National and International journals to his credit. He is expertise in Graph Algorithms, Combinatorial chemistry and Grid computing and also reviewer of many prestigious professional bodies. Currently he is an Professor, Department of Information sciences, Kuwait University, Kuwait.

V. Sutha Devi

V. Sutha Devi is a research scholar of Mathematics under the guidance of M. Lellis Thivagar at the School of Mathematics, Madurai Kamaraj University, Madurai. She had 9 years of working experience as Assistant Professor of Mathematics. She has attended and presented two papers in international conferences. Four of her research papers are published/accepted in the reputed international peer-reviewed journals.