?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
A graph with either positive or negative labels on the edge becomes a signed graph. Given a signed graph , a subset D of V is said to be a double dominating set for
, if it satisfies the following conditions: (i) every vertex u of
is either in D and u has at least one neighbour in D or whenever
,
(ii)
is balanced where N(u) denotes the open neighbourhood of a vertex u and
is the subgraph of the
induced by the edges between the vertices in D and
. In this paper, we initiate the discussion on the double domination in signed graphs.
Keywords:
Public Interest Statement
Domination in graphs is one of the major research areas in graph theory. Currently, many interesting and important researches are taking place in this area. Double domination is a particular type of domination and the double domination in graphs is relative new research area and hence there is a wide scope for studies in this particular area of domination theory. Well-known mathematicians F. Harary and T. Haynes initiated the studies in the double domination in graph theory. Later, B. D. Acharya extended the domination theory to different types of signed graphs. Being a relatively new research area, double domination in graphs offers much further investigations. Domination theory has proved to have many applications in many theoretical as well as practical real-life problems like optimization problems, communication problems, network problems, etc.
1. Introduction
Graphs used in this article, unless otherwise mentioned, will be undirected, simple and finite. For all definitions in (unsigned) graph theory, one can refer to Harary (Citation1972) and for the terminology and definitions in the theory of dominations for simple graphs, we refer the reader to Chartrand and Zang (Citation2009), Haynes, Hedetneimi, and Slater (Citation1998a,Citation1998b). Signed graphs (also called sigraphs) are graphs with positive or negative labels on the edges. Formally, a signed graph is an ordered pair where
is a graph called the underlying graph of
and
called a signing, is a function (also called a signature) from the edge set E of G into the set
. For more details on theory and applications of signed graphs, one may refer to Germina and Shahul Hameed (Citation2010), Germina, Shahul Hameed, and Zaslavsky (Citation2011), Harary (Citation1953), Zaslavsky (Citation1982, Citation1998).
A signed graph is all-positive (respectively, all-negative) if all of its edges are positive (negative); further, it is said to be homogeneous if it is either all-positive or all-negative and heterogeneous otherwise. denotes an all-positive graph and
an all-positive complete graph. Similarly,
represents an all-negative complete graph. Note that a graph can be considered to be a homogeneous signed graph. A signed graph
is said to be balanced or cycle balanced if all of its cycles are positive, where the sign of a cycle is the product of the signs of its edges. We use N(u) to denote the open neighbourhood of a vertex u in a graph.
We denote by where
, signed paths of order n and size
with r negative edges . Also
for
denotes signed cycles with r negative edges. If
is a function , called a switching function, then switching of the signed graph
by
means changing
to
defined by
(1)
(1)
The switched graph, denoted by , is the signed graph
. We call two signed graphs
and
switching equivalent, if there exists a switching function
such that
.
The following important result will be used very often in signed graph theory.
Lemma 1.1
(Zaslavsky, Citation1982) A signed graph is balanced if and only if it can be switched to an all-positive signed graph.
2. Double domination in signed graphs
Domination theory for unsigned graphs is a well-developed area of knowledge with plenty of real-life applications where the hectic research is still on, a survey of which can be found in Haynes et al. (Citation1998a,Citation1998b). Acharya (Citation2013) initiated the discussion of domination theory for signed graphs by giving the following definition.
Definition 2.1
(Acharya, Citation2013) Let be a signed graph. A subset
of vertices of
is a dominating set of
, if there exists a marking
of
such that every vertex u of
is either in D or whenever
,
and
for every
.
Ashraf and Germina (Citation2015) gave a simple characterization of dominating sets of a signed graph in terms of balance as follows.
We use to denote the subgraph of a signed graph
induced by the edges between D and
when
.
Theorem 2.2
(Ashraf & Germina, Citation2015) If D is a dominating set of G, then it is a dominating set for the signed graph if and only if
is balanced.
Double domination theory for unsigned graph, initiated by Harary and Haynes in their seminal paper (Citation2000), is now a hot area of research in graph theory. Based on the characterization in Theorem 2.2, we now define the double domination in signed graph as follows.
Definition 2.3
Let be a signed graph where
. A subset
of vertices of
is a double dominating set of
, if it satisfies the following conditions: (i) every vertex u of
is either in D and u has at least one neighbour in D or whenever
,
(ii)
is balanced.
A dominating set (respectively, a double dominating set) D of is called a minimal dominating set (respectively, a double dominating set) if no proper subset of D becomes a dominating set (respectively, a double dominating set). A minimum dominating set is a minimal dominating set with least cardinality. This least number is called domination number of
and is denoted by
. We use
to denote the double domination number of
.
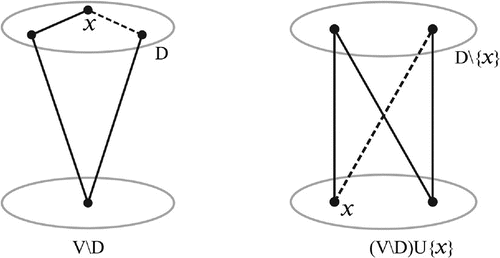
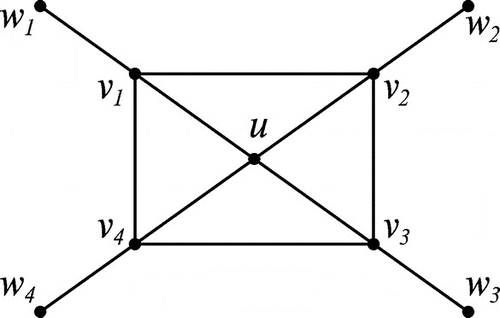
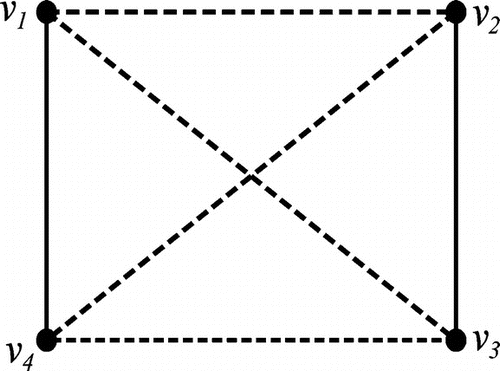
Now we exhibit some of the major distinctions between the double domination in unsigned graphs and that of signed graphs. In the case of unsigned graphs, if S is a double dominating set for G, then dominates G which is not true in the case of signed graphs. To see this, we have provided an example in Figure .
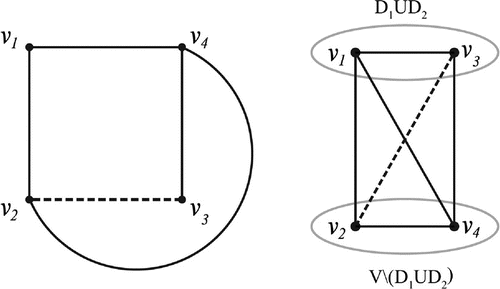
Also, if and
are disjoint dominating sets for the unsigned graph G with no isolated vertices, then it is given in Harary and Haynes (Citation2000) that their union
will be a double dominating set for G. But the failure of this result in the case of signed graphs is illustrated in Figure . See that the sets
and
are disjoint dominating sets. But their union is not a double dominating set for
.
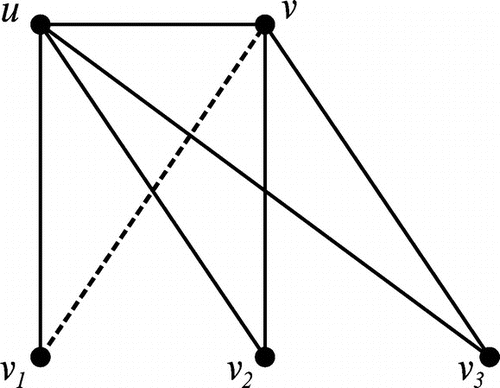
One more interesting distinction is that vertices of maximal independent set of edges in the case of unsigned graphs do form a double dominating set for it. But this result also fails in the case of signed graphs as given in Figure . Here, is a maximal independent set. But the set of end vertices of these edges, namely,
is not a double dominating set.
Moreover, in the case of unsigned graphs, super sets of a double dominating set will be again a double dominating set. But this fails for signed graphs for which the following Figure is a counter example.
More details on the domination theory for signed graphs can be found in Ashraf and Germina (Citation2015) , Germina and Ashraf (Citation2013), Ashraf and Germina (Citation2014). Before we proceed, we note that the following is an important result in Acharya (Citation2013) which will be used in the sequel.
Theorem 2.4
(Acharya, Citation2013) Domination is invariant under switching.
It is worthy to note that every double dominating set is a dominating set. That is, if we denote the set of all double dominating sets for a signed graph by
and set of all dominating sets by
, then
(2)
(2)
In light of Equation 2, it is evident that(3)
(3)
The inequality in Equation 3 is strict. To see this, take the case of signed cycle where
and
. Now we provide a list of important observations regarding double domination of signed graphs.
Observation 2.5
Any double dominating set for a signed graph should include all its end vertices and their neighbours.
Observation 2.6
Double domination is not possible in the case of a signed graph with isolated vertices.
Theorem 2.7
Double domination is invariant under switching.
Proof
Let D be a double dominating set for the signed graph which is switched to
.
is balanced. Subgraphs of switching equivalent graphs being switching equivalent,
is balanced. Hence, D is a double dominating set for
. Converse follows from the fact that
Corollary 2.8
Proof
Proof follows from Theorem 2.7.
In Germina and Ashraf (Citation2013), it is defined that a set is an open dominating set (also called total dominating set) of the signed graph
, if every vertex of
is adjacent to at least one vertex of D and if there exists a marking
such that
for every adjacent
and
. Also the minimum cardinality of an open dominating set is defined as the open domination number of
denoted by
. An open dominating set of cardinality
is a minimum open dominating set for
More details on the open domination for signed graphs can be had from Germina and Ashraf (Citation2013).
Observation 2.9
Every double dominating set is an open dominating set.
Thus, we have(4)
(4)
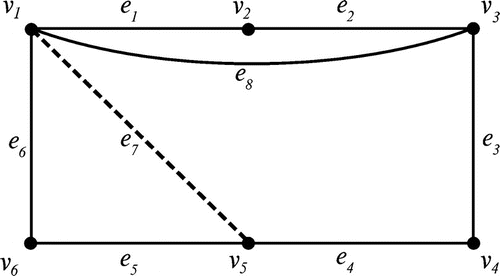
To see if the inequality in (Equation 4) can become strict, we provide the following example. Consider the signed graph built on the underlying graph in Figure where
and
.
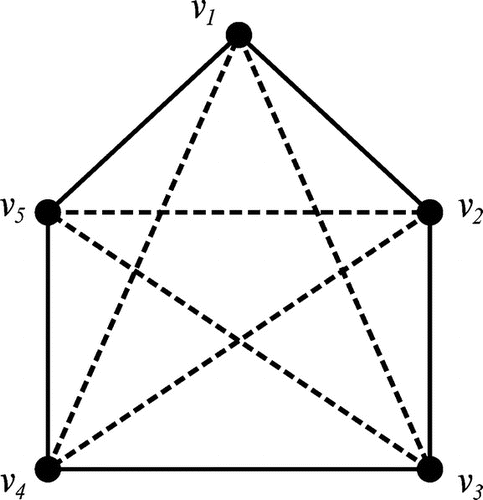
The second value is computed based on the observation made above that all end vertices and their neighbours belong to the double dominating set. To illustrate the case when the two become equal, consider the signed graph in Figure built on the complete graph
where
.
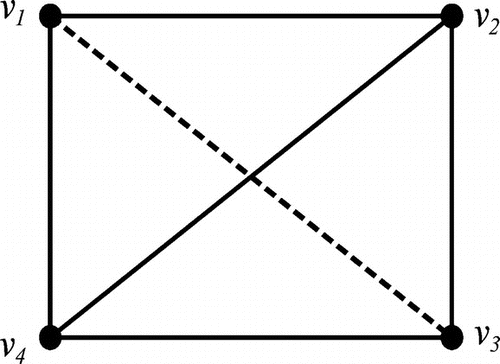
Note that every double dominating set for the signed graph is a double dominating set for its underlying graph, but not conversely. This is illustrated in Figure where is a double dominating set for G but not for
.
Thus, in general,(5)
(5)
when is a signed graph and
is a minimum double dominating set for the underlying graph
and
is balanced, then
(6)
(6)
Using Equation (6), the following identities are obtained: the double domination in the case of corresponding underlying graphs are taken from Blidia, Chellali, Haynes, and Henning (Citation2006) and Harary and Haynes (Citation2000).
| (i) | In the case of signed Petersen graph | ||||
| (ii) | In the case of signed cycle | ||||
| (iii) | In the case of signed paths, | ||||
Definition 2.10
(Ashraf & Germina, Citation2015) Let of a signed graph
and
. The private neighbourhood of u relative to S in
, denoted by
is the set of vertices which is in the closed neighbourhood of u but not in the closed neighbourhood of any vertex in
. That is,
Note that if and only if u is an isolated vertex of
in
. A vertex
is called a private neighbour of u with respect to S.
Definition 2.11
(Ashraf & Germina, Citation2015) An is called an irredundant set if
for every
.
In this regard, the following theorem found in Ashraf and Germina (Citation2015) is significant.
Theorem 2.12
(Ashraf & Germina, Citation2015) If D is a minimum dominating set for , then it is irredundant.
But, in the case of double domination of signed graphs, we have
Observation 2.13
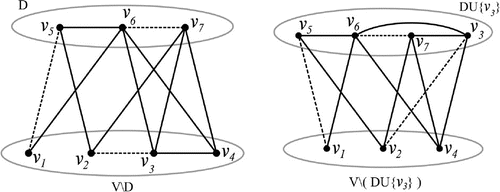
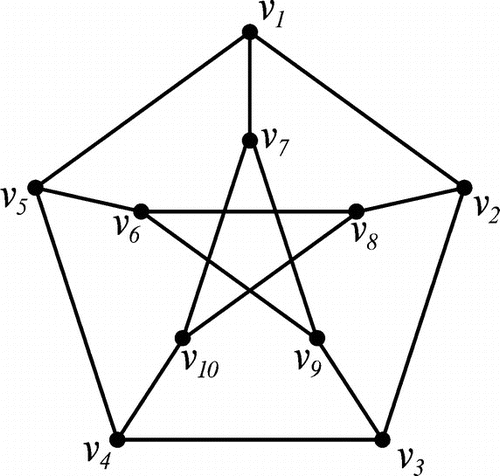
If D is a minimum double dominating set for , then it need not be irredundant. For example, the signed graph built on Petersen graph given in Figure ,
is a minimum double dominating set but it is not irredundant since
.
3. Double domination number
Theorem 3.1
Every signed graph with no isolated vertices has a double dominating set and hence has a double domination number.
Proof
Without loss of generality, let the underlying graph of the signed graph
be connected. Then, the vertex set V itself is a double dominating set, for, as each vertex v dominates itself and G is connected without isolate vertices, there is a vertex u adjacent to v. Thus, both u and v dominate v. The remaining part with regard to the balance of
is trivial. Thus, the existence of double dominating set for
is established. To prove the existence of a minimal double dominating set for
, we adopt the procedure that a vertex
is removed from V by verifying the conditions that the remaining subset
is still a double dominating set for the underlying graph and
is balanced. This removal procedure is continued till no more vertex may be moved to D satisfying the above criteria. This stage will give a minimal double dominating set. Among all the minimal double dominating sets, each of the smallest sets has cardinality
.
Theorem 3.2
for any signed graph
without isolated vertices and these bounds are sharp.
Proof
In order to find the lower bound, it is noted that for a vertex to be a member of any double dominating set, it must be adjacent to a vertex in that set. For the upper bound, we remarked that V itself is a double dominating set for a signed graph without isolated vertices. For the lower bound see Figure and for the upper bound see the signed star .
Now we provide a bound for the double domination number in the case of signed graphs built on complete bipartite graphs which we denote by
.
Theorem 3.3
if
.
Proof
For the lower bound, we use the inequality (Equation 5) and a result from Harary and Haynes (Citation2000) that if
. To obtain the upper bound, select one vertex one partite and keep it in the set D and other vertex from the next partite and keep in
in such a way that
and
. This will make
balanced and D becomes a double dominating set. Therefore,
The sharpness of the upper bound is still open to explore. The lower bound is attained by the all-positive signed graph found in Harary and Haynes (Citation2000).
In addition to the distinctions between the double domination in unsigned graphs and that of signed graphs listed initially one more, regarding the lower bound in Theorem 3.2, it is given in Harary and Haynes (Citation2000 ) that in the case of unsigned graphs G, if and only if G has vertices u and v such that
. But this result fails generally in the case of a signed graph as illustrated in Figure .
Theorem 3.4
A signed graph has V as its unique double dominating set if and only if for each
there is a vertex with degree 1 in N[v].
Proof
If there is a vertex of degree 1 in N[v] for every , then as any double dominating set for a signed graph should include all its end vertices and their neigbhours, V is the unique double dominating set. Conversely, suppose
has V as its unique double dominating set. If there exists a vertex
such that
and for all
,
, then
becomes a double dominating set since
is balanced. This leads to a contradiction and the proof is complete.
Corollary 3.5
If there exists such that
for all
, then
.
Proof
Proof follows from Theorem 3.4.
4. Multiple domination
Generalizing the double domination, we now define k-tuple domination in signed graphs as follows.
Definition 4.1
Let be a signed graph where
. A subset
of vertices of
is a k-tuple dominating set of
, if it satisfies the following conditions: (i) every vertex u of
is either in D and u has at least
neighbours in D or whenever
,
(ii)
is balanced.
Also, the k-tuple dominating number of a signed graph , denoted by
, is the smallest number of vertices in a k-tuple dominating set. In particular, we have
.
Many of the results valid for double domination in signed graphs hold good in the case of multiple domination also. The proofs of these results are nothing but simple generalizations of those in the case of double domination which are discussed in this paper. For completeness, we list these results without proof.
Theorem 4.2
k-tuple domination is invariant under switching.
Corollary 4.3
In general,(7)
(7)
Theorem 4.4
Every signed graph with
has a k-tuple dominating set and hence has a k-tuple domination number.
Regarding the bound, we have
Theorem 4.5
for any signed graph
and these bounds are sharp.
Indeed, the upper bound and the lower bound are attained for the signed graph built on the complete graph .
Theorem 4.6
If a vertex v has degree , then N[v] must be a subset of every k-tuple dominating set.
Additional information
Funding
Notes on contributors
P.K. Ashraf
P.K. Ashraf is presently working as an assistant professor in the Department of Mathematics, Government Arts and Science College, Kondotty, Kerala, India. He has more than 4 years of research experience and 10 years of teaching experience. He has published his research findings in many recognized international journals.
K.A. Germina
K.A. Germina is currently a professor in Mathematics in University Botswana, Gaborone, Botswana. She has more than two decades of teaching experience and 15 years of research experience. She has more than a hundred research publications and she is the reviewer and editor for many journals and premiere reviewing services.
References
- Acharya, B. D. (2013). Domination and absorbance in signed graphs and digraphs, I: Foundations. Journal of Combinatorial Mathematics and Combinatorial Computing, 84, 5–20.
- Ashraf, P. K., & Germina, K. A. (2014). Neighbourhood balanced domination in signed graphs. International Journal of Mathematical Sciences and Engineering Applications, 8, 193–203.
- Ashraf, P. K., & Germina, K. A. (2015). On minimal dominating sets for signed graphs. Advances and Applications in Discrete Mathematics, 15, 101–112.
- Blidia, M., Chellali, M., Haynes, T. W., & Henning, M. (2006). Independent and double domination in trees. Utilitas Mathematica, 70, 159–173.
- Chartrand, G., & Zang, P. (2009). Introduction to graph theory. New Delhi: Tata McGraw-Hill.
- Germina, K. A., & Ashraf, P. K. (2013). On open domination and domination in signed graphs. International Mathematical Forum, 8, 1863–1872.
- Germina, K. A., & Shahul Hameed, K. (2010). On signed paths, signed cycles and their energies. Applied Mathematical Science, 4, 3455–3466.
- Germina, K. A., Shahul Hameed, K., & Zaslavsky, T. (2011). On product and line graphs of signed graphs, their eigenvalues and energy. Linear Algebra and its Applications, 435, 2432–2450.
- Harary, F. (1972). Graph theory. Reading, MA: Addison Wesley.
- Harary, F. (1953). On the notion of balance of a signed graph. Michigan Mathematical Journal, 2, 143–146.
- Harary, F., & Haynes, T. (2000). Double domination in graphs. Ars Combinatoria, 55, 201–213.
- Haynes, T., Hedetneimi, S. T., & Slater, P. J. (1998a). Fundamentals of domination in graphs. New York, NY: Marcel Dekker.
- Haynes, T., Hedetniemi, S. T., & Slater, P. J. (1998b). Domination in graphs: Advanced topics. New York, NY: Marcel Dekker.
- Zaslavsky, T. (1982). Signed graphs. Discrete Applied Mathematics, 4, 47–74 ( 1983, Erratum, Discrete Applied Mathematics, 5, 248).
- Zaslavsky, T. (1998). A mathematical bibliography of signed and gain graphs and allied areas. Electronic Journal of Combinatorics, 8, DS8.