Regular product vague graphs and product vague line graphs

Abstract

Vague graph is a generalized structure of fuzzy graph which gives more precision, flexibility, and compatibility to a system when compared with systems that are designed using fuzzy graphs. In this paper, we introduced the notion of regular, totally regular product vague graphs, and product vague line graph. We proved that under some conditions regular and totally regular product vague graph becomes equivalent. Some properties of product vague line graph are investigated. We showed that a product vague graph is isomorphic to its corresponding product vague line graph under some conditions.

Keywords:

• vague sets
• product vague graphs
• regular product vague graphs
• totally regular product vague graphs
• product vague line graphs

AMS subject classifications:

• 05C72
• 05C76

Public Interest Statement

The theoretical concepts of graphs are highly utilized by computer science applications, especially in research areas of computer science such as data mining, image segmentation, clustering, image capturing, and networking. The vague graphs are more flexible and compatible than fuzzy graphs due to the fact that they have many applications in networks. In this paper, the concept of vague sets is applied to define and study many important properties of regular, totally regular product vague graphs and product vague line graphs.

1. Introduction

Now a days, most mathematical models are developed using fuzzy sets to handle various types of systems containing elements of uncertainty. In 1993, Gau and Buehrer (1993), introduced the notion of vague set theory as a generalization of Zadeh fuzzy set theory (1965). Vague sets are higher order fuzzy sets. Application of higher order fuzzy sets makes the solution-procedure more complex, but if the complexity on computation-time, computation-volume, or memory-space are not matters of concern, then we can achieve better results. In a fuzzy set, each element is associated with a point-value selected from the unit interval [0, 1], which is termed as the grade of membership in the set. Instead of using point-based membership as in fuzzy sets, interval-based membership is used in a vague set. The interval-based membership in vague sets is more expressive in capturing vagueness of data. There are some interesting features for handling vague data that are unique to vague sets. For example, vague sets allow for a more intuitive graphical representation of vague data, which facilitates significantly better analysis in data relationships, incompleteness, and similarity measures.

Considering the fuzzy relations between fuzzy sets, Rosenfeld (1975) first introduced the concept of fuzzy graphs in 1975 and developed the structure of fuzzy graphs, obtaining analogous of several graph concepts. Ramakrishna (2009) introduced the concept of vague graphs. Akram et al. studied some properties of vague graphs (Akram, Chen, & Shum, 2013), vague hypergraphs (Akram, Gani, & Saeid, 2014), regularity in vague intersection graphs (Akram, Dudek, & Yousaf, 2014), irregular and highly irregular vague graphs (Akram, Feng, Sarwar, & Jun, 2014), and vague cycles and vague trees (Akram, Feng, Sarwar, & Jun, 2015). Talebi, Rashmanlou, and Mehdipoor (2013), Talebi, Mehdipoor, and Rashmanlou (2014) studied isomorphism and operations on vague graphs. Borzooei and Rashmanlou (2015a, b, c, 2016), Rashmanlou and Borzooei (2015, 2016, 2015) introduced manynew concepts of vague graphs. Samanta et al. introduced fuzzy competition graphs (Samanta, Akram, & Pal, 2013; Samanta & Pal, 2015), fuzzy planar graphs (Samanta & Pal, 2015), bipolar fuzzy intersection graphs (Samanta & Pal, 2014), and strength of vague graphs (Samanta, Pal, Rashmanlou, & Borzooei, 2016). Later on, Ghorai and Pal studied some properties of generalized m-polar fuzzy graphs (2016a), defined operations and density of m-polar fuzzy graphs (2015), introduced m-polar fuzzy planar graphs (2016b), and defined faces and dual of m-polar fuzzy planar graphs (2016c). In this paper, the concept of regular, totally regular product vague graphs, and product vague line graphs are introduced. Necessary and sufficient condition is established under which regular and totally regular product vague graph becomes equivalent and a product vague graph is isomorphic to its corresponding product vague line graph.

2. Preliminaries

In this section, we point out some basic definitions of graphs. The readers are encouraged to see these references (Balakrishnan, 1997; Harary, 1972; Mordeson & Nair, 2000) for further study.

Definition 2.1

   Harary (1972) A graph is an ordered pair $G^{\ast }=(V,E)$, where V is the set of vertices of $G^{\ast }$ and E is the set of all edges of $G^{\ast }$. Two vertices x and y in an undirected graph $G^{\ast }$ are said to be adjacent in $G^{\ast }$ if xy is an edge of $G^{\ast }$. A simple graph is an undirected graph that has no loops and not more than one edge between any two different vertices.

A subgraph of a graph $G^{\ast }=(V,E)$ is a graph $H=(W,F)$, where $W\subseteq V$ and $F\subseteq E$.

We write $xy\in E$ to mean $(x,y)\in E$, and if $e=xy\in E$, we say x and y are adjacent. Formally, given a graph $G^{\ast }=(V,E)$, two vertices $x,y\in V$ are said to be neighbors or adjacent nodes, if $xy\in E$. The neighborhood of a vertex v in a graph $G^{\ast }$ is the induced subgraph of $G^{\ast }$ consisting of all vertices adjacent to v and all edges connecting two such vertices. The neighborhood of v is often denoted by N(v). The degree $\text{deg}(v)$ of vertex v is the number of edges incident on v. The open neighborhood for a vertex v in a graph $G^{\ast }$ consists of all vertices adjacent to v but not including v, i.e. $N(v)=\{u\in V:uv\in E\}$. If v is included in N(v), then it is called closed neighborhood for v and is denoted by N[v], i.e. $N[v]=N(v)\cup \{v\}$. A regular graph is a graph where each vertex has the same open neighborhood degree. A complete graph is a simple graph in which every pair of distinct vertices has an edge.

An isomorphism $\mathit{\varphi }$ of the graphs $G_1^{\ast }$ and $G_2^{\ast }$ is a bijection between the vertex sets of $G_1^{\ast }$ and $G_2^{\ast }$ such that any two vertices $v_1$ and $v_2$ of $G_1^{\ast }$ are adjacent in $G_1^{\ast }$ if and only if $\mathit{\varphi }(v_1)$ and $\mathit{\varphi }(v_2)$ are adjacent in $G_2^{\ast }$. If $G_1^{\ast }$ and $G_2^{\ast }$ are isomorphic, then we denote it by $G_1^{\ast }\cong G_2^{\ast }$.

The line graph $L(G^{\ast })$ of a simple graph $G^{\ast }$ is a graph which represents the adjacentness between edges of $G^{\ast }$. For a graph $G^{\ast }$, its line graph $L(G^{\ast })$ is a graph such that:

(i)	Each vertex of $L(G^{\ast })$ represents an edge of $G^{\ast }$, and
(ii)	Two vertices of $L(G^{\ast })$ are adjacent if and only if their corresponding edges have a common end point in $G^{\ast }$.

Let $G^{\ast }=(V,E)$ be a graph where $V=\{v_1,v_2,\dots ,v_n\}$. Let $S_i=\{v_i,x_{i1},\dots ,x_{i{q}_i}\}$ where $x_{ij}\in E$ and $x_{ij}$ has $v_i$ as a vertex, $j=1,2,\dots ,q_i$; $i=1,2,\dots ,n$. Let $S=\{S_1,S_2,\dots ,S_n\}$. Let $T=\{S_i{S}_j:S_i,S_j\in S,S_i\cap S_j\ne \mathrm{\varnothing },i\ne j\}$. Then $P(S)=(S,T)$ is an intersection graph and $P(S)=G^{\ast }$. The line graph $L(G^{\ast })$ of $G^{\ast }$, is by definition the intersection graph P(E). That is, $L(G^{\ast })=(Z,W)$ where $Z=\{\{x\}\cup \{u_x,v_x\}:x\in E,u_x,v_x\in V,x=u_x{v}_x\}$ and $W=\{S_x{S}_y:S_x\cap S_y\ne \mathrm{\varnothing },x,y\in E,x\ne y\}$ and $S_x=\{x\}\cup \{u_x,v_x\}$, $x\in E$.

Definition 2.2

   Gau and Buehrer (1993)   A vague set on a non-empty set X is a pair $(t_A,f_A)$, where $t_A:X\to [0,1]$, $f_A:X\to [0,1]$ are true and false membership functions, respectively, such that $t_A(x)+f_A(x)\le 1$ for all $x\in X$.

In the above definition, $t_A(x)$ is considered as the lower bound for degree of membership of x in A (based on evidence for), and $f_A(x)$ is the lower bound for negation of membership of x in A (based on evidence against). Therefore, the degree of membership of x in the vague set A is characterized by the interval $[t_A(x),1-f_A(x)]$. So, a vague set is a special case of interval-valued sets studied by many mathematicians and applied in many branches of mathematics. Vague sets also have many applications. The interval $[t_A(x),1-f_A(x)]$ is called the vague value of x in A and is denoted by $V_A(x)$. We denote zero vague and unit vague value by $\mathbf{0}=[0,0]$ and $\mathbf{1}=[1,1]$, respectively.

It is worth to mention here that interval-valued fuzzy sets are not vague sets. In interval-valued fuzzy sets, an interval-valued membership value is assigned to each element of the universe considering the “evidence for x” only, without considering “evidence against x”. In vague sets both are independently proposed by the decision-maker. This makes a major difference in the judgment about the grade of membership.

A vague relation is a further generalization of a fuzzy relation.

Definition 2.3

Ramakrishna (2009)   Let X and Y be ordinary finite non-empty sets. We call a vague relation a vague subset of $X\times Y$, that is an expression R defined by $R=\{<(x,y),t_R(x,y),f_R(x,y)>:x\in X,y\in Y\}$, where $t_R:X\times Y\to [0,1]$ and $f_R:X\times Y\to [0,1]$, which satisfies the condition $0\le t_R(x,y)+f_R(x,y)\le 1$, for all $(x,y)\in X\times Y$.

Definition 2.4

Ramakrishna (2009)    A vague relation B on a set V is a vague relation from V to V. If A is a vague set on a set V, then a vague relation B on A is a vague relation which satisfies $t_B(x,y)\le \text{min}\{t_A(x),t_A(y)\}$ and $f_B(x,y)\ge \text{max}\{t_B(x),t_B(y)\}$ for all $x,y\in V$.

Definition 2.5

Ramakrishna (2009)   Let $G^{\ast }=(V,E)$ be a crisp graph. A pair $G=(V,A,B)$ is called a vague graph of $G^{\ast }$, where $A=(t_A,f_A)$ is a vague set on V and $B=(t_B,f_B)$ is a vague set on $E\subseteq V\times V$ such that $t_B(x,y)\le \text{min}\{t_A(x),t_A(y)\}$ and $f_B(x,y)\ge \text{max}\{t_B(x),t_B(y)\}$ for each $(x,y)\in E$.

We call A the vague vertex set of G and B as the vague edge set of G, respectively.

A vague graph G is said to be strong if $t_B(u,v)=\text{min}\{t_A(u),t_A(v)\}$ and $f_B(u,v)=\text{max}\{f_A(u),f_A(v)\}$ for all $(u,v)\in E$.

A vague graph G is said to be complete if $t_B(u,v)=\text{min}\{t_A(u),t_A(v)\}$ and $f_B(u,v)=\text{max}\{f_A(u),f_A(v)\}$ for all $u,v\in V$.

3. Regular and totally regular product vague graphs

Throughout the paper, $G^{\ast }$ represents a crisp graph and G is a product vague graph of $G^{\ast }$. Rashmanlou and Borzooei (2015) defined the product vague graphs as follows.

Here after we use $xy\in E$ to denote $(x,y)\in E$ throughout the paper.

Definition 3.1

A product vague graph of a graph $G^{\ast }=(V,E)$ is a pair $G=(V,A,B)$ where $A=(t_A,f_A)$ is an vague set in V and $B=(t_B,f_B)$ is a vague set on $V^2$ such that $t_B(xy)\le t_A(x)\times t_A(y)$ and $f_B(xy)\ge f_A(x)\times f_A(y)$ for all $x,y\in V$.

Note that, every product vague graph is also a vague graph.

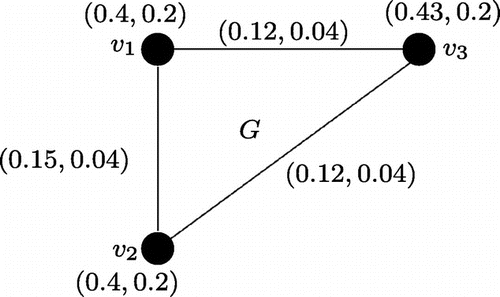
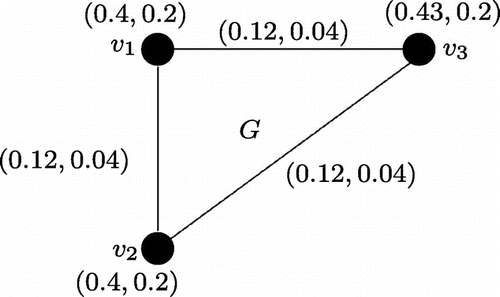
Example 3.2

Let us consider the graph $G^{\ast }=(V,E)$ where $V=\{v_1,v_2,v_3,v_4\}$ and $E=\{v_1{v}_4,v_2{v}_3\}$. A product vague graph G of $G^{\ast }$ is shown in Figure 1.

Definition 3.3

A product vague graph $G=(V,A,B)$ of $G^{\ast }=(V,E)$ is said to be strong if $t_B(xy)=t_A(x)\times t_A(y)$ and $f_B(xy)=f_A(x)\times f_A(y)$ for all $xy\in E$.

The product vague graph G of Figure 1 is not strong.

Definition 3.4

Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }=(V,E)$. The open neighborhood degree of a vertex v in G is defined by $\text{deg}(v)=({\text{deg}}^t(v),{\text{deg}}^f(v))$, where ${\text{deg}}^t(v)=\sum _{\begin{array}{c}u\ne v\\ uv\in E\end{array}}{t}_B(uv)$ and ${\text{deg}}^f(v)=\sum _{\begin{array}{c}u\ne v\\ uv\in E\end{array}}{f}_B(uv)$. If all the vertices of G have the same open neighborhood degree $(r_1,r_2)$, then G is called $(r_1,r_2)$-regular product vague graph.

Definition 3.5

Let $G=(V,A,B)$ be a regular product vague graph of $G^{\ast }=(V,E)$. The order of G is defined as $O(G)=(O^t(G),O^f(G))$ where $O^t(G)=\sum _{v\in V}{t}_A(v)$ and $O^f(G)=\sum _{v\in V}{f}_A(v)$. The size of G is defined as $S(G)=(S^t(G),S^f(G))$ where $S^t(G)=\sum _{uv\in E}{t}_B(uv)$ and $S^f(G)=\sum _{uv\in E}{f}_B(uv)$.

Definition 3.6

Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }=(V,E)$. The closed neighborhood degree of a vertex v is defined by $\text{deg}[v]=({\text{deg}}^t[v],{\text{deg}}^f[v])$, where ${\text{deg}}^t[v]={\text{deg}}^t(v)+t_A(v)$ and ${\text{deg}}^f[v]={\text{deg}}^f(v)+f_A(v)$. If each vertex of G has the same closed neighborhood degree $(g_1,g_2)$, then G is called $(g_1,g_2)$-totally regular product vague graph.

Now, we give some examples which show that product vague graphs may be both regular and totally regular, neither totally regular nor regular and totally regular but not regular. In other words, there is no relation between regular and totally regular product vague graphs.

First we give an example of a product vague graph which is both regular and totally regular (see Figure 2).

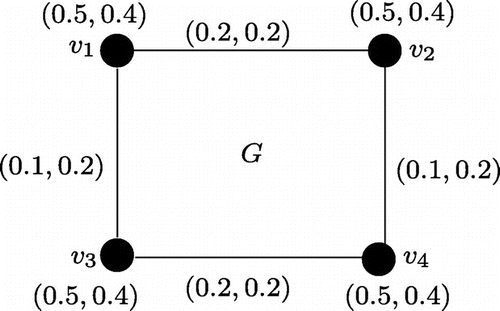
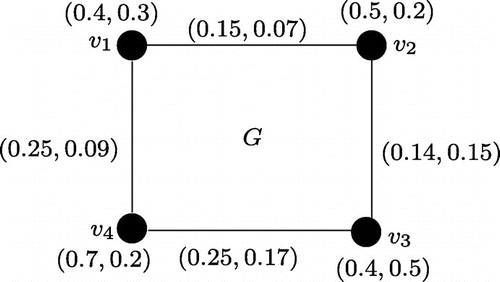
Example 3.7

Let us consider the graph $G^{\ast }=(V,E)$ where $V=\{v_1,v_2,v_3,v_4\}$ and $E=\{v_1{v}_2,v_2{v}_4,v_3{v}_4,v_1{v}_3\}$ and consider the product vague graph $G=(V,A,B)$ of $G^{\ast }$ (see Figure 2). Here, $\text{deg}(v_1)=\text{deg}(v_2)=\text{deg}(v_3)=\text{deg}(v_4)=(0.3,0.4)$ and $\text{deg}[v_1]=\text{deg}[v_2]=\text{deg}[v_3]=\text{deg}[v_4]=(0.8,0.8)$. Hence, G is both (0.3,0.4)-regular and (0.8,0.8)-totally regular product vague graph.

Now, we give an example of a product vague graph which is neither regular nor totally regular (see Figure 3).

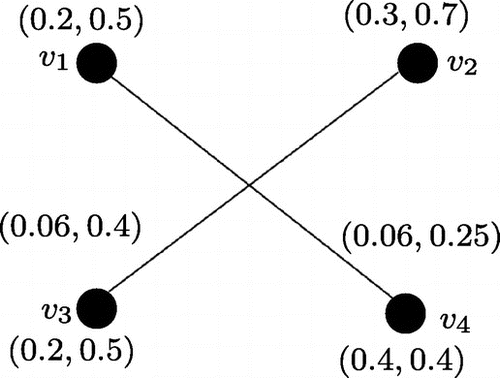
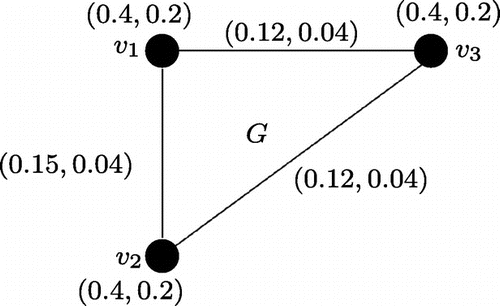
Example 3.8

Let us consider a product vague graph $G=(V,A,B)$ of $G^{\ast }=(V,E)$ where $V=\{v_1,v_2,v_3\}$ and $E=\{v_1{v}_2,v_1{v}_3\}$ (see Figure 3). We have, $\text{deg}(v_1)=(0.4,0.45),\text{deg}(v_2)=(0.2,0.2),\text{deg}(v_3)=(0.2,0.25)$ and $\text{deg}[v_1]=(0.8,0.95),\text{deg}[v_2]=(0.7,0.6),\text{deg}[v_3]=(0.8,0.65)$. Hence, G is neither regular nor totally regular product vague graph.

The following example shows that a product vague graph may be totally regular but not regular (see Figure 4).

Example 3.9

Consider the product vague graph G given in Figure 4. Since $\text{deg}(v_1)=\text{deg}(v_2)=(0.27,0.08)\ne \text{deg}(v_3)=(0.24,0.08)$ and $\text{deg}[v_1]=\text{deg}[v_2]=\text{deg}[v_3]=(0.67,0.28)$, therefore G is (0.67, 0.28)-totally regular and but not regular product vague graph.

Similarly, we can give example of a product vague graph which is regular but not totally regular (see Figure 5).

We now state the following propositions without proof.

Proposition 3.10

Let $G=(V,A,B)$ be a $(r_1,r_2)$-regular product vague graph of $G^{\ast }=(V,E)$. Then $S(G)=\frac{n}{2}(r_1,r_2)$ where $|V|=n$.

Proposition 3.11

Let $G=(V,A,B)$ be a $(g_1,g_2)$-totally regular product vague graph of $G^{\ast }=(V,E)$. Then $2S(G)+O(G)=n(g_1,g_2)$ where $|V|=n$.

Proposition 3.12

Let $G=(V,A,B)$ be a $(r_1,r_2)$-regular and $(g_1,g_2)$-totally regular product vague graph of $G^{\ast }=(V,E)$. Then $O(G)=n(g_1-r_1,g_2-r_2)$ where $|V|=n$.

Theorem 3.13

Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }=(V,E)$. Then $A=(t_A,f_A)$ is constant function if and only if the following are equivalent:

(i)	G is $(r_1,r_2)$-regular vague graph,
(ii)	G is $(g_1,g_2)$-totally regular vague graph.

Proof

Let us assume that $A=(t_A,f_A)$ is constant function. Therefore, let $t_A(v)=a_1$ and $f_A(v)=a_2$ for all $v\in V$, where $a_1,a_2\in [0,1]$.

We will now show that the statements (i) and (ii) are equivalent.

(i)$\Rightarrow$(ii): Let G be a $(r_1,r_2)$-regular product vague graph. Therefore, $\text{deg}(v)=({\text{deg}}^t(v),{\text{deg}}^f(v))=(r_1,r_2)$ for all $v\in V$.

Now, $\text{deg}[v]=({\text{deg}}^t[v],{\text{deg}}^f[v])=({\text{deg}}^t(v)+t_A(v),{\text{deg}}^f(v)+f_A(v))=(r_1+a_1,r_2+a_2)$ for all $v\in V$. Hence, G is $(r_1+a_1,r_2+a_2)$-totally regular product vague graph.

(ii)$\Rightarrow$(i): Let G be a $(g_1,g_2)$- totally regular product vague graph.

Then $\text{deg}[v]=({\text{deg}}^t[v],{\text{deg}}^f[v])=(g_1,g_2)$ for all $v\in V$.

That is, ${\text{deg}}^t(v)+t_A(v)=g_1$ and ${\text{deg}}^f(v)+f_A(v)=g_2$ for all $v\in V$, or ${\text{deg}}^t(v)=g_1-a_1$ and ${\text{deg}}^f(v)=g_2-a_2$ for all $v\in V$. Hence, G is $(g_1-a_1,g_2-a_2)$-regular product vague graph.

Conversely, let (i) and (ii) are equivalent. Suppose A is not constant function. This means there exist at least two vertices $u,v\in V$ such that $t_A(u)\ne t_A(v)$ and $f_A(u)\ne f_A(v)$.

Let G be a $(r_1,r_2)$-regular product vague graph. Then, $\text{deg}[u]=({\text{deg}}^t(u)+t_A(u),{\text{deg}}^f(u)+f_A(u))=(r_1+t_A(u),r_2+f_A(u))$ and $\text{deg}[v]=({\text{deg}}^t(v)+t_A(v),{\text{deg}}^f(v)+f_A(v))=(r_1+t_A(v),r_2+f_A(v))$.

This shows that $\text{deg}[u]\ne \text{deg}[v]$ since $t_A(u)\ne t_A(v)$ and $f_A(u)\ne f_A(v)$. Hence, G is not totally regular which is a contradiction to the assumption that (i) and (ii) are equivalent. Therefore, A must be constant.

In a similar way, we can show that if A is not constant function, then G totally regular does not imply G is regular. $\square$

Proposition 3.14

Let $G=(V,A,B)$ be a product vague graph which is both regular and totally regular. Then $A=(t_A,f_A)$ is constant.

Proof

Let G be a $(r_1,r_2)$-regular and $(g_1,g_2)$-totally regular product vague graph. Now, ${\text{deg}}^t[v]={\text{deg}}^t(v)+t_A(v)=r_1+t_A(v)=g_1$ and ${\text{deg}}^f[v]={\text{deg}}^f(v)+f_A(v)=r_2+f_A(v)=g_2$ for all $v\in V$. Hence, $t_A(v)=g_1-r_1$ and $f_A(v)=g_2-r_2$ for all $v\in V$. This shows that $A(v)=(t_A(v),f_A(v))=(g_1-r_1,g_2-r_2)$ for all $v\in V$, i.e. A is constant. $\square$

Remark 3.15

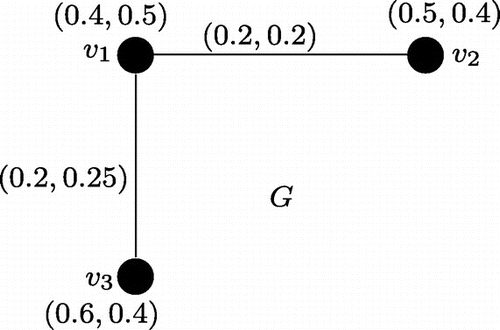
The converse of the Proposition 3.14 is not true always. For example, consider the product vague graph $G=(V,A,B)$ of $G^{\ast }=(V,E)$ where $V=\{v_1,v_2,v_3\}$ and $E=\{v_1{v}_2,v_2{v}_3,v_3{v}_1\}$ (see Figure 6). Here, $A(v)=(t_A(v),f_A(v))=(0.4,0.2)$ for all $v\in V$, i.e. A is constant but G is neither regular nor totally regular.

Theorem 3.16

Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }=(V,E)$ where $G^{\ast }$ is an odd cycle. Then G is regular product vague graph of $G^{\ast }$ if and only if $B=(t_B,f_B)$ is constant.

Proof

Let G be a $(r_1,r_2)$-regular product vague graph. Let $e_1,e_2,\dots ,e_{2n+1}$ be the edges of $G^{\ast }$ such that $e_i=v_{i-1}{v}_i\in E$, $v_0,v_i\in V$, $i=1,2,\dots ,2n+1$ and $v_0=v_{2n+1}$. Let $t_B(e_1)=k_1$ and $f_B(e_1)=k_2$ where $k_1,k_2\in [0,1]$.

G is $(r_1,r_2)$-regular implies that ${\text{deg}}^t(v_1)=r_1$ and ${\text{deg}}^f(v_1)=r_2$.

This means, ${\text{deg}}^t(v_1)=t_B(e_1)+t_B(e_2)=r_1$ and ${\text{deg}}^f(v_1)=f_B(e_1)+f_B(e_2)=r_2$.

i.e. $k_1+t_B(e_2)=r_1$ and $k_2+f_B(e_2)=r_2$,

i.e. $t_B(e_2)=r_1-k_1$ and $f_B(e_2)=r_2-k_2$.

Again, ${\text{deg}}^t(v_2)=t_B(e_2)+t_B(e_3)=r_1$ and ${\text{deg}}^f(v_2)=f_B(e_2)+f_B(e_3)=r_2$.

This implies, $t_B(e_3)=r_1-(r_1-k_1)=k_1$ and $f_B(e_3)=r_2-(r_2-k_2)=k_2$, and so on.

Therefore, $t_B(e_i)=\left\{\begin{array}{cc}{k}_1& \text{if}i\text{is}\text{odd}\\ (r_1-k_1)& \text{if}i\text{is}\text{even}\end{array}\right.$ and $f_B(e_i)=\left\{\begin{array}{cc}{k}_2& \text{if}i\text{is}\text{odd}\\ (r_2-k_2)& \text{if}i\text{is}\text{even}\end{array}\right.$

Therefore, $t_B(e_1)=t_B(e_{2n+1})=k_1$ and $f_B(e_1)=f_B(e_{2n+1})=k_2$.

Since $e_1$ and $e_{2n+1}$ are incident on the vertex $v_0$, and $\text{deg}(v_0)=(r_1,r_2)$, we have, $t_B(e_1)+t_B(e_{2n+1})=r_1$ and $f_B(e_1)+f_B(e_{2n+1})=r_2$.

i.e. $2k_1=r_1$ and $2k_2=r_2$, i.e. $k_1=\frac{r_1}{2}$ and $k_2=\frac{r_2}{2}$.

Therefore, $t_B(e_i)=\frac{r_1}{2}$ and $f_B(e_i)=\frac{r_2}{2}$ for all $i=1,2,\dots ,2n+1$. Hence B is constant.

Conversely, let B be a constant function. Let $B(uv)=(t_B(uv),f_B(uv))=(k_1,k_2)$ for all $uv\in E$, where $k_1,k_2\in [0,1]$.

Then $\text{deg}(v)=({\text{deg}}^t(v),{\text{deg}}^f(v))=(\sum _{\begin{array}{c}u\ne v\\ uv\in E\end{array}}{t}_B(uv),\sum _{\begin{array}{c}u\ne v\\ uv\in E\end{array}}{t}_B(uv))=(2k_1,2k_2)$ for all $v\in V$.

Consequently, G is $(2k_1,2k_2)$-regular product vague graph. $\square$

4. Product vague line graphs

In this section, we first define a product vague intersection graph of a product vague graph. Finally we define the product vague line graphs.

Definition 4.1

Let $P(S)=(S,T)$ be an intersection graph of a simple graph $G^{\ast }=(V,E)$. Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }$. We define a product vague intersection graph $P(G)=(A_1,B_1)$ of P(S) as follows:

(i)	$A_1$ and $B_1$ are vague subsets of S and T, respectively,
(ii)	$t_{A_1}(S_i)=t_A(v_i)$, $f_{A_1}(S_i)=f_A(v_i)$,
(iii)	$t_{B_1}(S_i{S}_j)=t_B(v_i{v}_j)$, $f_{B_1}(S_i{S}_j)=f_B(v_i{v}_j)$ for all $S_i,S_j\in S$, $S_i{S}_j\in T$. In other words, any product vague graph of P(S) is called a product vague intersection graph.

The following proposition is immediate.

Proposition 4.2

Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }=(V,E)$ and $P(G)=(A_1,B_1)$ be a product vague intersection graph of P(S). Then the following holds:

(a)	P(G) is a product vague graph of P(S),
(b)	$G\cong P(G)$.

Proof

 

(a)

Since $G=(V,A,B)$ is a product vague graph we have by Definition 4.1, $t_{B_1}(S_i{S}_j)=t_B(v_i{v}_j)\le t_A(v_i)\times t_A(v_j)=t_{A_1}(S_i)\times t_{A_1}(S_j)$ and $f_{B_1}(S_i{S}_j)=f_B(v_i{v}_j)\ge f_A(v_i)\times f_A(v_j)=f_{A_1}(S_i)\times f_{A_1}(S_j)$. Hence, P(G) is a product vague graph.

(b)

Let us define a mapping $\mathit{\varphi }:V\to S$ by $\mathit{\varphi }(v_i)=S_i$ for$i=1,2,\dots ,n$. Then clearly $\mathit{\varphi }$ is one to one mapping of V onto S. Now $v_i{v}_j\in E$ if and only if $S_i{S}_j\in T$ and $T=\{\mathit{\varphi }(v_i)\mathit{\varphi }(v_j):v_i{v}_j\in E\}$. Also, $t_A(v_i)=t_{A_1}(S_i)=t_{A_1}(\mathit{\varphi }(v_i))$ and $f_A(v_i)=f_{A_1}(S_i)=f_{A_1}(\mathit{\varphi }(v_i))$ for all $v_i\in V$, $t_B(v_i{v}_j)=t_{B_1}(S_i{S}_j)=t_B(\mathit{\varphi }(v_i)\mathit{\varphi }(v_j))$ and $f_B(v_i{v}_j)=f_{B_1}(S_i{S}_j)=f_B(\mathit{\varphi }(v_i)\mathit{\varphi }(v_j))$ for all $v_i{v}_j\in E$. Hence, $\mathit{\varphi }$ is an isomorphism of G onto P(G), i.e. $G\cong P(G)$.

$\square$

This proposition shows that any product vague graph is isomorphic to a product vague intersection graph. The product vague line graph of a product vague graph is defined as below.

Definition 4.3

Let $L(G^{\ast })=(Z,W)$ be a line graph of a simple graph $G^{\ast }=(V,E)$. Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }$. Then a product vague line graph $L(G)=(A_1,B_1)$ of G is defined as follows:

(i)	$A_1$ and $B_1$ are vague subsets of Z and W, respectively,
(ii)	$t_{A_1}(S_x)=t_B(x)=t_B(u_x{v}_x)$,
(iii)	$f_{A_1}(S_x)=f_B(x)=f_B(u_x{v}_x)$,
(iv)	$t_{B_1}(S_x{S}_y)=t_B(x)\times t_B(y)=t_B(u_x{v}_x)\times t_B(u_y{v}_y)$,
(v)	$f_{B_1}(S_x{S}_y)=f_B(x)\times f_B(y)=f_B(u_x{v}_x)\times f_B(u_y{v}_y)$ for all $S_x,S_y\in Z$ and $S_x{S}_y\in W$.

Example 4.4

Consider now a graph $G^{\ast }=(V,E)$ where $V=\{v_1,v_2,v_3,v_4\}$ and $E=\{x_1=v_1{v}_2,x_2=v_2{v}_3,x_3=v_3{v}_4,x_4=v_4{v}_1\}$. Let $G=(V,A,B)$ be a product vague graph of $G^{\ast }$ (see Figure 7).

Now, consider a line graph $L(G^{\ast })=(Z,W)$ such that $Z=\{S_{x_1},S_{x_2},S_{x_3},S_{x_4}\}$ and $W=\{S_{x_1}{S}_{x_2},S_{x_2}{S}_{x_3},S_{x_3}{S}_{x_4},S_{x_4}{S}_{x_1}\}$.

Let $A_1$ and $B_1$ be vague subsets of Z and W, respectively. Then we have$$\begin{array}{cc}\hfill t_{A_1}(S_{x_1})& =t_B(x_1)=0.15,t_{A_1}(S_{x_2})=t_B(x_2)=0.14,\hfill \\ \hfill t_{A_1}(S_{x_3})& =t_B(x_3)=0.25,t_{A_1}(S_{x_4})=t_B(x_4)=0.25,\hfill \\ \hfill f_{A_1}(S_{x_1})& =f_B(x_1)=0.07,f_{A_1}(S_{x_2})=f_B(x_2)=0.15,\hfill \\ \hfill f_{A_1}(S_{x_3})& =f_B(x_3)=0.17,f_{A_1}(S_{x_4})=f_B(x_4)=0.09,\hfill \\ \hfill t_{B_1}(S_{x_1}{S}_{x_2})& =t_B(x_1)\times t_B(x_2)=0.15\times 0.14=0.021,\hfill \\ \hfill t_{B_1}(S_{x_2}{S}_{x_3})& =t_B(x_2)\times t_B(x_3)=0.14\times 0.25=0.035,\hfill \\ \hfill t_{B_1}(S_{x_3}{S}_{x_4})& =t_B(x_3)\times t_B(x_4)=0.25\times 0.25=0.0625,\hfill \\ \hfill t_{B_1}(S_{x_4}{S}_{x_1})& =t_B(x_4)\times t_B(x_1)=0.25\times 0.15=0.0375,\hfill \\ \hfill f_{B_1}(S_{x_1}{S}_{x_2})& =f_B(x_1)\times f_B(x_2)=0.07\times 0.15=0.0105,\hfill \\ \hfill f_{B_1}(S_{x_2}{S}_{x_3})& =f_B(x_2)\times f_B(x_3)=0.15\times 0.17=0.0255,\hfill \\ \hfill f_{B_1}(S_{x_3}{S}_{x_4})& =f_B(x_3)\times f_B(x_4)=0.17\times 0.09=0.0153,\hfill \\ \hfill f_{B_1}(S_{x_4}{S}_{x_1})& =f_B(x_4)\times f_B(x_1)=0.07\times 0.09=0.0063.\hfill \\ \hfill \end{array}$$

Hence, $L(G)=(A_1,B_1)$ is the product vague line graph of G. We see that L(G) is neither regular nor totally regular product vague line graph.

Proposition 4.5

A product vague line graph is a strong product vague graph.

Proof

Follows from the definition of product vague line graph. $\square$

Proposition 4.6

If L(G) is a product vague line graph of the product vague graph G, then $L(G^{\ast })$ is the line graph of $G^{\ast }$.

Proof

Since $G=(V,A,B)$ is a product vague graph and $L(G)=(A_1,B_1)$ is a product vague line graph, therefore $t_{A_1}(S_x)=t_B(x)$ and $f_{A_1}(S_x)=f_B(x)$ for all $x\in E$ and so $S_x\in Z$$\iff x\in E$.

Also, $t_{B_1}(S_x{S}_y)=t_B(x)\times t_B(y)$ and $f_{B_1}(S_x{S}_y)=f_B(x)\times f_B(y)$ for all $S_x,S_y\in Z$, and so $W=\{S_x{S}_y:S_x\cap S_y\ne \mathrm{\varnothing },x,y\in E,x\ne y\}$. This completes the proof. $\square$

Proposition 4.7

$L(G)=(A_1,B_1)$ is a product vague line graph of some product vague graph $G=(V,A,B)$ if and only if $t_{B_1}(S_x{S}_y)=t_{A_1}(S_x)\times t_{A_1}(S_y))$ and $f_{B_1}(S_x{S}_y)=f_{A_1}(S_x)\times f_{A_1}(S_y)$ for all $S_x{S}_y\in W$.

Proof

Suppose that $t_{B_1}(S_x{S}_y)=t_{A_1}(S_x)\times t_{A_1}(S_y)$ and $f_{B_1}(S_x{S}_y)=f_{A_1}(S_x)\times f_{A_1}(S_y)$ for all $S_x{S}_y\in W$. Let us now define $t_A(x)=t_{A_1}(S_x)$ and $f_A(x)=f_{A_1}(S_x)$ for all $x\in E$. Then, $t_{B_1}(S_x{S}_y)=t_{A_1}(S_x)\times t_{A_1}(S_y))=t_A(x)\times t_A(y))$ and $f_{B_1}(S_x{S}_y)=f_{A_1}(S_x)\times f_{A_1}(S_y)=f_A(x)\times f_A(y)$. A vague set $A=(t_A,f_A)$ that yields that the property $t_B(xy)\le t_A(x)\times t_A(y)$ and $f_B(xy)\ge f_A(x)\times f_A(y)$ will suffice. The converse part follows from the Definition 4.3. $\square$

Proposition 4.8

$L(G)=(A_1,B_1)$ is a product vague line graph of some product vague graph if and only if $L(G^{\ast })=(Z,W)$ is a line graph satisfying $t_{B_1}(uv)=t_{A_1}(u)\times t_{A_1}(v)$ and $f_{B_1}(uv)=f_{A_1}(u)\times f_{A_1}(v)$ for all $uv\in W$.

Proof

Follows from the Propositions 4.6 and 4.7. $\square$

Definition 4.9

Let $G_1=(V_1,A_1,B_1)$ and $G_2=(V_2,A_2,B_2)\dots$ be two product vague graphs of the graphs $G_1^{\ast }=(V_1,E_1)$ and $G_2^{\ast }=(V_2,E_2)$, respectively. A homomorphism between $G_1$ and $G_2$ is a mapping $\mathit{\varphi }:V_1\to V_2$ such that

(i)	$t_{A_1}(x)\le t_{A_2}(\mathit{\varphi }(x))$ and $f_{A_1}(x)\ge f_{A_2}(\mathit{\varphi }(x))$ for all $x\in V_1$,
(ii)	$t_{B_1}(xy)\le t_{B_2}(\mathit{\varphi }(x)\mathit{\varphi }(y))$ and $f_{B_1}(xy)\ge f_{B_2}(\mathit{\varphi }(x)\mathit{\varphi }(y))$ for all $xy\in V_1^2$.

A bijective homomorphism with the property that $t_{A_1}(x)=t_{A_2}(\mathit{\varphi }(x))$ and $f_{A_1}(x)=f_{A_2}(\mathit{\varphi }(x))$ for all $x\in V_1$ is called a (weak) vertex-isomorphism.

A bijective homomorphism with the property that $t_{B_1}(xy)=t_{B_2}(\mathit{\varphi }(x)\mathit{\varphi }(y))$ and $f_{B_1}(xy)=f_{B_2}(\mathit{\varphi }(x)\mathit{\varphi }(y))$ for all $xy\in V_1^2$, is called a (weak) line-isomorphism.

If $\mathit{\varphi }$ is both (weak) vertex isomorphism and (weak) line-isomorphism, then $\mathit{\varphi }$ is called a (weak) isomorphism of $G_1$ onto $G_2$. If $G_1$ is isomorphic to $G_2$, then we write $G_1\cong G_2$.

Proposition 4.10

Let $G_1=(A_1,B_1)$ and $G_2=(A_2,B_2)$ be two product vague graphs of the graphs $G_1^{\ast }=(V_1,E_1)$ and $G_2^{\ast }=(V_2,E_2)$, respectively. If $\mathit{\varphi }$ is a weak isomorphism of $G_1$ onto $G_2$, then $\mathit{\varphi }$ is an isomorphism of $G_1^{\ast }$ onto $G_2^{\ast }$.

Proof

Obvious. $\square$

Proposition 4.11

Let $L(G)=(A_1,B_1)$ be the product vague line graph corresponding to the product vague graph $G=(V,A,B)$ of $G^{\ast }=(V,E)$. Suppose that $G^{\ast }$ is connected. Then the following hold:

(i)	There exists a weak isomorphism of G onto L(G) if and only if $G^{\ast }$ is a cycle and for all $v\in V$, $x\in E$, $t_A(v)=t_B(x)$, $f_A(v)=f_B(x)$, i.e. $A=(t_A,f_A)$ and $B=(t_B,f_B)$ are constant functions on V and E, respectively, taking on the same value.
(ii)	If $\mathit{\varphi }$ is a weak isomorphism of G onto L(G), then $\mathit{\varphi }$ is an isomorphism.

Proof

Suppose that $\mathit{\varphi }$ is a weak isomorphism of G onto L(G). By Proposition 4.10, $\mathit{\varphi }$ is an isomorphism of $G^{\ast }$ onto $L(G^{\ast })$. By Proposition 4.6, $G^{\ast }$ is a cycle, (by Harary, 1972), Theorem 8.2).

Let $V=\{v_1,v_2,\dots ,v_n\}$ and $E=\{x_1=v_1{v}_2,x_2=v_2{v}_3,\dots ,x_n=v_n{v}_1\}$, where $v_1{v}_2\dots v_n{v}_1$ is a cycle. Let us define the vague sets $t_A(v_i)=s_i$, $f_A(v_i)=\acute{s_i}$ and $t_B(v_i{v}_{i+1})=t_i$, $f_B(v_i{v}_{i+1})=\acute{t_i}$, $i=1,2,\dots ,n$, $v_{n+1}=v_1$, $s_i,t_i,\acute{s_i},\acute{t_i}\in [0,1]$.

Then for $s_{n+1}=s_1$, ${\acute{s}}_{n+1}=\acute{s_1}$,(1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{t}_i\le s_i\times s_{i+1}\\ \acute{t_i}\ge \acute{s_i}\times {\acute{s}}_{i+1},i=1,2,\dots ,n.\end{array}\right.\end{array}$$(1)

Now, $Z=\{S_{x_1},S_{x_2},\dots ,S_{x_n}\}$ and $W=\{S_{x_1}{S}_{x_2}{S}_{x_2}{S}_{x_3},\dots ,S_{x_n}{S}_{x_1}\}$.

Also for $t_{n+1}=t_1$ and ${\acute{t}}_{n+1}=\acute{t_1}$, $t_{A_1}(S_{x_i})=t_B(x_i)=t_B(v_i{v}_{i+1})=t_i$, $f_{A_1}(S_{x_i})=f_B(x_i)=f_B(v_i{v}_{i+1})=\acute{t_i}$ and

$t_{B_1}(S_{x_i}{S}_{x_{i+1}})=t_B(x_i)\times t_B(x_{i+1})=t_i\times t_{i+1}$, $f_{B_1}(S_{x_i}{S}_{x_{i+1}})=f_B(x_i)\times f_B(x_{i+1})=\acute{t_i}\times {\acute{t}}_{i+1}$, $i=1,2,\dots ,n$, where $v_{n+1}=v_1,v_{n+2}=v_2$.

Since $\mathit{\varphi }$ is an isomorphism of $G^{\ast }$ onto $L(G^{\ast })$, $\mathit{\varphi }$ maps V one-to-one onto Z. Also $\mathit{\varphi }$ preserves adjacency. Hence, $\mathit{\varphi }$ induces a permutation $\mathit{\pi }$ of $\{1,2,\dots ,n\}$ such that $\mathit{\varphi }(v_i)=S_{x_{\mathit{\pi }(i)}}=S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}}$ and $x_i=v_i{v}_{i+1}\to \mathit{\varphi }(v_i)\mathit{\varphi }(v_{i+1})=S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}}{S}_{v_{\mathit{\pi }(i+1)}{v}_{\mathit{\pi }(i+2)}}$, $i=1,2,\dots ,(n-1)$.

Now,$$\begin{array}{c}\hfill s_i=t_A(v_i)\le t_{A_1}(\mathit{\varphi }(v_i))=t_{A_1}(S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}})=t_{\mathit{\pi }(i)},\end{array}$$$$\begin{array}{c}\hfill \acute{s_i}=f_A(v_i)\ge f_{A_1}(\mathit{\varphi }(v_i))=f_{A_1}(S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}})={\acute{t}}_{\mathit{\pi }(i)},\end{array}$$$$\begin{array}{cc}\hfill t_i& =t_B(v_i{v}_{i+1})\le t_{B_1}(\mathit{\varphi }(v_i)\mathit{\varphi }(v_{i+1}))=t_{B_1}(S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}}{S}_{v_{\mathit{\pi }(i+1)}{v}_{\mathit{\pi }(i+2)}})\hfill \\ \hfill & =t_{B_1}(S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}})\times t_{B_1}(S_{v_{\mathit{\pi }(i+1)}{v}_{\mathit{\pi }(i+2)}})=t_{\mathit{\pi }(i)}\times t_{\mathit{\pi }(i+1)},\hfill \end{array}$$$$\begin{array}{cc}\hfill \acute{t_i}& =f_B(v_i{v}_{i+1})\ge f_{B_1}(\mathit{\varphi }(v_i)\mathit{\varphi }(v_{i+1}))=f_{B_1}(S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}}{S}_{v_{\mathit{\pi }(i+1)}{v}_{\mathit{\pi }(i+2)}})\hfill \\ \hfill & =f_{B_1}(S_{v_{\mathit{\pi }(i)}{v}_{\mathit{\pi }(i+1)}})\times f_{B_1}(S_{v_{\mathit{\pi }(i+1)}{v}_{\mathit{\pi }(i+2)}})={\acute{t}}_{\mathit{\pi }(i)}\times {\acute{t}}_{\mathit{\pi }(i+1)}\hfill \end{array}$$

for $i=1,2,\dots ,n$. That is, $s_i\le t_{\mathit{\pi }(i)}$, $\acute{s_i}\ge {\acute{t}}_{\mathit{\pi }(i)}$ and(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{t}_i\le t_{\mathit{\pi }(i)}\times t_{\mathit{\pi }(i+1)}\hfill \\ \acute{t_i}\ge {\acute{t}}_{\mathit{\pi }(i)}\times {\acute{t}}_{\mathit{\pi }(i+1)},i=1,2,\dots ,n.\hfill \end{array}\right.\end{array}$$(2)

By (2), we have $t_i\le t_{\mathit{\pi }(i)}$, $\acute{t_i}\ge {\acute{t}}_{\mathit{\pi }(i)}$ for $i=1,2,\dots ,n$ and so $t_{\mathit{\pi }(i)}\le t_{\mathit{\pi }(\mathit{\pi }(i))}$, ${\acute{t}}_{\mathit{\pi }(i)}\ge {\acute{t}}_{\mathit{\pi }(\mathit{\pi }(i))}$ for $i=1,2,\dots ,n$. Continuing, we have$$\begin{array}{c}\hfill t_i\le t_{\mathit{\pi }(i)}\le \dots \le t_{{\mathit{\pi }}^j(i)}\le t_i,\acute{t_i}\ge {\acute{t}}_{\mathit{\pi }(i)}\ge \dots \ge {\acute{t}}_{{\mathit{\pi }}^j(i)}\ge \acute{t_i}\end{array}$$

and so $t_i=t_{\mathit{\pi }(i)}$, $\acute{t_i}={\acute{t}}_{\mathit{\pi }(i)}$, $i=1,2,\dots ,n$ where ${\mathit{\pi }}^{j+1}$ is the identity map. Again by (2), we have $t_i\le t_{\mathit{\pi }(i+1)}=t_{i+1}$, $\acute{t_i}\ge {\acute{t}}_{\mathit{\pi }(i+1)}={\acute{t}}_{(i+1)}$, $i=1,2,\dots ,n$ where $t_{n+1}=t_n$, ${\acute{t}}_{n+1}={\acute{t}}_n$.

Hence by (1) and (2), we have $t_1=\dots =t_n=s_1=\cdots s_n$, $\acute{t_1}=\cdots =\acute{t_n}=\acute{s_1}=\cdots =\acute{s_n}$.

Thus we have not only proved the conclusion about A and B being constant functions, but also we have shown that (ii) holds.

Conversely, suppose that $G^{\ast }$ is a cycle and for all $v\in V$, $x\in E$, $t_A(v)=t_B(x)$, $f_A(v)=f_B(x)$. By Proposition 4.6, $L(G^{\ast })$ is the line graph of $G^{\ast }$. Since $G^{\ast }$ is a cycle, $G^{\ast }\cong L(G^{\ast })$ by (Harary (Harary (1972)), Theorem 8.2). This isomorphism induces an isomorphism of G onto L(G) since $t_A(v)=t_B(x)$, $f_A(v)=f_B(x)$ for all $v\in V$, $x\in E$ and so $A=B=A_1=B_1$ on their respective domains. $\square$

Proposition 4.12

Let $G_1=(V_1,A_1,B_1)$ and $G_2=(V_2,A_2,B_2)$ be two product vague graphs of the graphs $G_1^{\ast }=(V_1,E_1)$ and $G_2^{\ast }=(V_2,E_2)$, respectively, such that $G_1^{\ast }$ and $G_2^{\ast }$ is connected. Let $L(G_1)=(A_3,B_3)$ and $L(G_2)=(A_4,B_4)$ be the product vague line graphs corresponding to $G_1$ and $G_2$, respectively. Suppose that it is not the case that one of $G_1^{\ast }$ and $G_2^{\ast }$ is complete graph $K_3$ and other is bipartite complete graph $K_{1,3}$. If $L(G_1)\cong L(G_2)$, then $G_1$ and $G_2$ are line isomorphic.

Proof

Since $L(G_1)\cong L(G_2)$, therefore by Proposition 4.10, $L(G_1^{\ast })\cong L(G_2^{\ast })$. Since $L(G_1^{\ast })$ and $L(G_2^{\ast })$ are the line graphs of $G_1^{\ast }$ and $G_2^{\ast }$, respectively, by Proposition 4.6, we have that $G_1^{\ast }\cong G_2^{\ast }$ by (Harary (1972), Theorem 8.3).

Let $\mathit{\psi }$ be the isomorphism of $L(G_1)$ onto $L(G_2)$ and $\mathit{\varphi }$ be the isomorphism of $G_1^{\ast }$ onto $G_2^{\ast }$. Then $t_{A_3}(S_x)=t_{A_4}(\mathit{\psi }(S_x))=t_{A_4}(S_{\mathit{\varphi }(x)})$, $f_{A_3}(S_x)=f_{A_4}(\mathit{\psi }(S_x))=f_{A_4}(S_{\mathit{\varphi }(x)})$, where the latter equalities holds by the proof of (Harary (1972), Theorem 8.3) and so $t_{B_1}(x)=t_{B_2}(\mathit{\varphi }(x))$, $f_{B_1}(x)=f_{B_2}(\mathit{\varphi }(x))$. Hence $G_1$ and $G_2$ are line isomorphic. $\square$

Figure 1. G is a product vague graph of $G^{\ast }$.

Figure 2. G is (0.3,0.4)-regular and (0.8,0.8)-totally regular product vague graph.

Figure 3. G is neither regular nor totally regular product vague graph.

Figure 4. G is (0.67,0.28)-totally regular but not regular product vague graph.

Figure 5. G is (0.24,0.08)-regular but not totally regular product vague graph.

Figure 6. A is constant but G is neither regular nor totally regular.

Figure 7. G is a product vague graph.

Figure 8. The product vague line graph L(G) of G.

5. Conclusions

Graph theory has several interesting applications in system analysis, operations research, computer applications, and economics. Since most of the time the aspects of graph problems are uncertain, it is nice to deal with these aspects via the methods of fuzzy systems. It is known that fuzzy graph theory has numerous applications in modern sciences and technology, especially in the fields of neural networks, artificial intelligence, and decision-making. In this paper, we defined the notions of regular, totally regular product vague graphs, and product vague line graphs. We investigated some properties of them. In our future work we will focus on categorical properties on product vague graphs, edge regular, and irregular product vague graph product vague competition graph.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Ganesh Ghorai

Ganesh Ghorai is an assistant professor in the Department of Applied Mathematics, Vidyasagar University, India. His research interests include fuzzy sets, fuzzy graphs, and graph theory.

Madhumangal Pal

Madhumangal Pal is a professor of Applied Mathematics, Vidyasagar University, India. He received jointly with G. P. Bhattacherjee the “Computer Division Medal” from the Institute of Engineers (India) in 1996 for best research work. He received the Bharat Jyoti Award from International Friendship Society, New Delhi, in 2012. He has published more than 250 articles in international and national journals and 31 articles in edited books and in conference proceedings. His specializations include computational graph theory, genetic algorithms and parallel algorithms, fuzzy correlation and regression, fuzzy game theory, fuzzy matrices and fuzzy algebra. He is the editor-in-chief of Journal of Physical Sciences and Annals of Pure and Applied Mathematics, and a member of the editorial boards of several other journals.