A review on graceful and sequential integer additive set-labeled graphs

Abstract

Let ${\mathbb{N}}_0$ be the set of all non-negative integers and $\mathcal{P}$ be its power set. Then, an integer additive set-labeling (IASL) of a graph G is an injective function $f:V(G)\to \mathcal{P}({\mathbb{N}}_0)$, such that the induced function $f^{+}:E(G)\to \mathcal{P}({\mathbb{N}}_0)$ defined by $f^{+}(uv)=f(u)+f(v)$ and an integer additive set-indexer (IASI) is an integer additive set-labeling such that the induced function $f^{+}:E(G)\to \mathcal{P}({\mathbb{N}}_0)$ is also injective. An integer additive set-labeling (or an integer additive set-indexer) is said to be a graceful integer additive set-labeling (or graceful integer additive set-indexer) if $f^{+}(E(G))=\mathcal{P}(X)-\{\mathrm{\varnothing },\{0\}\}$ and an integer additive set-labeling (or an integer additive set-indexer) is said to be a sequential integer additive set-labeling (or sequential integer additive set-indexer) if $f(V(G))\cup f^{+}(E(G))=\mathcal{P}(X)-\{\mathrm{\varnothing }\}$. In this write-up, we creatively and critically review certain studies made on graceful integer additive set-labeling and sequential integer additive set-labeling of given graphs and certain properties and characteristics of the graphs which satisfy this type of set-labelings.

Keywords:

• integer additive set-labeled graphs
• integer additive set-graceful graphs
• integer additive set-sequential graphs

AMS Subject Classifications:

• 05C78

Public Interest Statement

Graph Labeling problems have numerous applications in various fields. Various graph labeling types are the result of many practical considerations. Different types of labeled graphs have become highly useful in modeling a wide range of applications such as routing, transportation, communication networks, Optimization, and social interactions. Different types of set-labeling problems mainly originated as an effective method to model social relations and interactions. Graceful and sequential labeling are some types of optimal set-assignments to elements of a graph subject to some specific predefined conditions. So these types of set-labelings have significant applications in optimization and distribution networks.

1. Introduction

For all terms and definitions, not defined specifically in this paper, we refer to Bondy and Murty (2008), Brandstädt, Le, and Spinrad (1999), Harary (1969), West (2001). For more about graph labeling, we refer to Gallian (2014). Unless mentioned otherwise, all graphs we consider here are simple, finite and have no isolated vertices.

The preliminary concepts of graph labeling was introduced in Rosa (1967) and researches on various graph labeling problems and their applications, both theoretical and practical, have been done extensively since then. The notion of $\mathit{\beta }$-valuation of graphs, introduced in Rosa (1967), has popularly been known as graceful labeling of graphs in later studies.

Analogous to the number valuations of graphs, the concepts of set-labelings and set-indexers of graphs are introduced in Acharya (1983) as follows.

Definition 1.1

Acharya (1983)    Let X be a non-empty set and $\mathcal{P}(X)$ be its power set. A set-labeling of a graph G with respect to the set X is an injective set-valued function $f:V(G)\to \mathcal{P}(X)$ with the induced edge function $f^{\oplus }(E(G))\to \mathcal{P}(X)$ defined by $f^{\oplus }(uv)=f(u)\oplus f(v)$ for all $uv\in E(G)$, where $\oplus$ is the symmetric difference of sets. A graph which admits a set-labeling is called a set-labeled graph.

Definition 1.2

A set-labeling $f:V(G)\to \mathcal{P}(X)$ of G is said to be a set-indexer of G if the induced edge function $f^{\oplus }:(E(G))\to \mathcal{P}(X)$, defined by $f^{\oplus }(uv)=f(u)\oplus f(v)$, is also injective. A graph which admits a a set-indexer is called a set-indexed graph.

Modeling different problems on social interactions among people were the main cause and motivation for the introduction of set-labeling of graphs. Several studies on set-valuations of graphs have also been taken place in recent research. It is proved in Acharya (1983) that every graph has a set-indexer.

In later studies, different types of set-labelings of graphs have been introduced and the properties and characteristics of different set-labeled graphs have been studied. Graceful set-labelings and sequential set-labelings are the two major types of set-valuations defined for given graphs and discussed in different studies.

The notion of a graceful set-indexer has been introduced in Acharya (2001), as given below.

Definition 1.3

A set-indexer $f:V(G)\to \mathcal{P}(X)$ of a given graph G is said to be a set-graceful labeling of G if $f^{\oplus }(E(G))=\mathcal{P}(X)-\{\mathrm{\varnothing }\}$. A graph G which admits a set-graceful labeling is called a set-graceful graph.

The notion of set-sequential labeling of a graph has been introduced in Acharya and Hegde (1985) and studied in Acharya and Hegde (1985), Acharya, Germina, Abhishek, and Slater (2012), Acharya, Germina, Princy, and Rao (2008). The notion is as follows.

Definition 1.4

A set-indexer $f:V(G)\to \mathcal{P}(X)$ of a given graph G is said to be a set-sequential labeling of G if $f(V(G))\cup f^{\oplus }(E(G))=\mathcal{P}(X)-\{\mathrm{\varnothing }\}$. A graph G which admits a set-sequential labeling is called a set-sequential graph.

We have some other set-valuations in which some binary operation of sets, other than their symmetric difference, is used to construct the set-labels of edges of G. Integer additive set-labeling of graphs is one of such set-valuations in which the edges are labeled by the sumset of the set-labels of their end vertices.

1.1. Integer additive set-labeling of graphs

The sumset (see Nathanson, 1996a) of two non-empty sets A and B, denoted by $A+B$, is the set defined by $A+B=\{a+b:a\in A,b\in B\}$. Here the sets A and B are said to be the summands of the set $C=A+B$. If either A or B is countably infinite, then their sumset $A+B$ is also countably infinite. Hence, all sets we consider here are non-empty finite sets.

Note that $A+\{0\}=A$ for any subset A of X. Here, the sets $\{0\}$ and A are said to be the trivial summands of A. If $C=A+B$, where $A\ne \{0\}$ and $B\ne \{0\}$, then A and B are said to be the non-trivial summands of the set C and C is said to be a non-trivial sumset of A and B.

Using the concepts of sumsets, the notion of integer additive set-labeling of a given graph G is defined as follows.

Definition 1.5

Germina and Sudev (2013), Sudev and Germina (2014)    Let ${\mathbb{N}}_0$ be the set of all non-negative integers. Let $X\subseteq {\mathbb{N}}_0$ and $\mathcal{P}(X)$ be its power set. An integer additive set-labeling (IASL, in short) of a graph G is an injective function $f:V(G)\to \mathcal{P}(X)$ whose associated function $f^{+}:E(G)\to \mathcal{P}(X)$ is defined by $f^{+}(uv)=f(u)+f(v),uv\in E(G)$. A graph G which admits an integer additive set-labeling is called an integer additive set-labeled graph (IASL-graph).

An integer additive set-indexer of a graph is a special type of integer additive set-labeling which is defined as follows.

Definition 1.6

Germina and Sudev (2013), Sudev and Germina (2014)    An integer additive set-labeling f is said to be an integer additive set-indexer (IASI, in short) if the induced edge function $f^{+}:E(G)\to \mathcal{P}(X)$ defined by $f^{+}(uv)=f(u)+f(v)$ is also injective. A graph G which admits an integer additive set-indexer is called an integer additive set-indexed graph (IASI-graph).

The cardinality of the set-label of an element (a vertex or an edge) of a graph G is called the set-indexing number of that element. An IASL (or an IASI) is said to be a k-uniform IASL (or k-uniform IASI) if $|f^{+}(e)|=k\forall e\in E(G)$, where k is a positive integer. The vertex set V(G) is called l-uniformly set-indexed, if all the vertices of G have the set-indexing number l.

With respect to an integer additive set-labeling (or integer additive set-indexer) of a graph G, the vertices of G have non-empty set-labels and the set-labels of every edge of G is the sumsets of the set-labels of its end vertices and hence no element of a given graph can have $\mathrm{\varnothing }$ as its set-labeling. Hence, we need to consider only non-empty subsets of X for set-labeling the elements of G. Hence, all sets we mention in this paper are finite sets of non-negative integers. We denote the cardinality of a set A by |A|.

We denote by X the finite ground set of non-negative integers that is used for set-labeling the elements of G and cardinality of X by n.

Analogous to the set-graceful labeling of graphs, the notion of an integer additive set-graceful labeling of a graph G has been introduced in Sudev and Germina (2016) and the properties and structural characteristics of the graphs which admit this type of set-labeling studied.

Note that the range sets of an integer additive set-graceful labeling and integer additive set-sequential labeling of graphs are the maximum possible subsets of the power set of the ground set. It can be observed that all graphs need not admit these types of set-labelings. The procedure for labeling the vertices of the graph under consideration is important in this context. Moreover, the graphs admitting these types of set-labelings hold certain common or similar structural properties and characteristics. The main motivation of this article is to enable researchers to analyze and compare the studies done in this direction. We also try to suggest some new directions for future studies in this area.

In the following section, we review the main results on the graphs admitting graceful IASL.

2. Integer additive set-graceful graphs

Certain studies on set-graceful graphs have been conducted in Acharya (1983,2001), Acharya and Hegde (1985), Acharya, Germina, Princy et al. (2008), Acharya, Germina, Abhishek et al. (2012). Motivated by these studies we have introduced the notion of a graceful integer additive set-labeling of a given graph G, in Sudev and Germina (2016) as given below.

Definition 2.1

Sudev and Germina (2016)    Let G be a graph and let X be a non-empty set of non-negative integers. An integer additive set-indexer $f:V(G)\to \mathcal{P}(X)-\{\mathrm{\varnothing }\}$ is said to be an integer additive set-graceful labeling (graceful IASL) or a graceful integer additive set-indexer of G if $f^{+}(E(G))=\mathcal{P}(X)-\{\mathrm{\varnothing },\{0\}\}$. A graph G which admits an integer additive set-graceful labeling is called an integer additive set-graceful graph (in short, graceful IASL-graph).

As all graphs do not admit graceful IASLs in general, studies on the structural properties of graceful IASL-graphs arouse much interest. The choice of set-labels of the elements of G and the corresponding ground set is very important to define a graceful IASI for a given graph.

The following result is an obvious, but an important property of integer additive set-graceful graphs.

Proposition 2.2

Sudev and Germina (2016)    If $f:V(G)\to \mathcal{P}(X)-\{\mathrm{\varnothing }\}$ is an integer additive set-graceful labeling on a given graph G, then $\{0\}$ must be a set-label of one vertex of G.

This property can be viewed as an immediate consequence of the fact that $(X+\{a\})\supset X$ for any $0\ne a\in X$. Invoking the above proposition of graceful IASL-graphs, it can be noted that if an IASL $f:V(G)\to \mathcal{P}(X)-\{\mathrm{\varnothing }\}$ of a given graph G is an integer additive set-graceful labeling on G, then the ground set X must contain the element 0 and $\{0\}\in f(V(G))$.

Since f is a graceful IASL of G, $\mathrm{\varnothing }\ne A_i\subseteq X$ must be the set-label of some edge of G, which is possible only when $A_i$ is the set-label of some vertex $v_i$ that is adjacent to the vertex v whose set-label is $\{0\}$. Hence, the following is a trivial but an important property of the vertex set-labels of a graceful IASL-graph G.

Proposition 2.3

Sudev and Germina (2016)   Let $f:V(G)\to \mathcal{P}(X)-\{\mathrm{\varnothing }\}$ be an integer additive set-graceful labeling on a given graph G. Then, the vertices of G, whose set-labels are not the non-trivial sumsets of any two subsets of X, must be adjacent to the vertex v that has the set-label $\{0\}$.

For any element $x_i\in X$, that is not the sum of any two elements in X, $\{x_i\}$ must be the set-label of one edge, which is possible only when one end vertex of e has the set-label $\{0\}$ and the other end vertex has the set-label $\{x_i\}$. In view of this argument, the following result is also a simple, but important property of the vertex set-labels of a graceful IASL-graph G.

Proposition 2.4

Sudev and Germina (2016)   Let $x_i$ be a non-zero element of X, which is not the sum of two elements in X. Then, the vertex with the set-label $\{x_i\}$ must be adjacent to the vertex having the set-label $\{0\}$.

In view of the above two propositions, we can observe the following result as a straightforward result.

Corollary 2.5

Sudev and Germina (2016)   Let $f:V(G)\to \mathcal{P}(X)-\{\mathrm{\varnothing }\}$ be an integer additive set-graceful labeling on a given graph G and let $x_1$ and $x_2$ be the minimal and second minimal non-zero elements of X. Then, the vertices of G that have the set-labels $\{x_1\}$ and $\{x_2\}$, must be adjacent to the vertex v that has the set-label $\{0\}$.

If the vertex $v_i$ of G, whose set-label contains $x_n$, is adjacent to a vertex v whose set-label contains a non-zero element $x_l$, then $f^{+}(uv)$ contains the element $x_n+x_l$ which is not an element of X. Hence we have the following result.

Proposition 2.6

Sudev and Germina (2016)   Let $f:V(G)\to \mathcal{P}(X)-\{\mathrm{\varnothing }\}$ be an integer additive set-graceful labeling on a given graph G and let $x_n$ be the maximal element of X. Then, $x_n$ is an element of the set-label of a vertex $v_i$ of G if $v_i$ is a pendant vertex that is adjacent to the vertex labeled by $\{0\}$.

As a direct consequence of the above proposition, we note a condition for two subsets of the ground set X to be the set-labels of two adjacent vertices of a graceful IASL-graph.

Proposition 2.7

Sudev and Germina (2016)   Let $A_i$ and $A_j$ be two distinct subsets of the ground set X and let $x_i$ and $x_j$ be the maximal elements of $A_i$ and $A_j$, respectively. Then, $A_i$ and $A_j$ are the set-labels of two adjacent vertices of a graceful IASL-graph G if $x_i+x_j\le x_n$, the maximal element of X.

Invoking the of the results mentioned above, we can observe the following result.

Corollary 2.8

Sudev and Germina (2016)   If G is a graph without pendant vertices, then no vertex of G can have a set-label consisting of the maximal element of the ground set X.

We have $f^{+}(E)=\mathcal{P}(X)-\{\mathrm{\varnothing },\{0\}\}$. Therefore, $|E(G)|=|\mathcal{P}(X)|-2=2^{|X|}-2=2(2^{|X|-1}-1)$ and hence we have

Theorem 2.9

Sudev and Germina (2016)   If a graph G admits an integer additive set-graceful labeling, then it has even number of edges.

In every study of different types of set-labeling of graphs, the cardinality, especially the minimum required cardinality of the ground set X has attracted much interest and has become a major parameter for further studies. In this context, the following results establish the relation between the size of a graceful IASL-graph and the cardinality of its ground set.

Theorem 2.10

Sudev and Germina (2016)    Let G be a graceful IASL-graph, with an integer additive set-graceful labeling f. Then, the cardinality of the ground set X is ${log}_2[|E(G)|+2]$.

The result follows obviously from the fact that for a graceful IASL-graph G, $|E(G)|=2^{|X|}-2$.

What we have discussed so far are the fundamental structural characteristics of a graceful IASL-graph in terms of their vertex set-labels. The following few results discuss necessary and sufficient conditions for certain graphs and graph classes to admit integer additive set-graceful labelings.

Theorem 2.11

Sudev and Germina (2016)   A star graph $K_{1,m}$ admits an integer additive set-graceful labeling if and only if $m=2^n-2$ for any integer $n>1$.

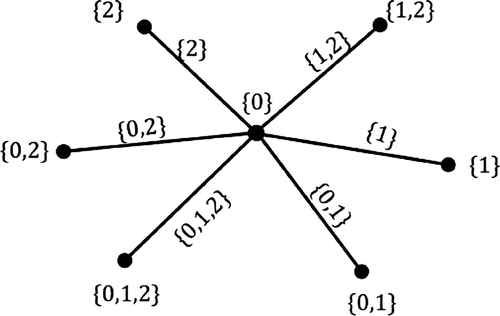
Figure 1 illustrates the admissibility of the star graph $K_{1,m}$, where m is an integer of the form $2^m-2$.

Figure 1. A star graph with a graceful integer additive set-labeling.

In view of the fact that for a tree G, $|E(G)|=|V(G)|-1$, the following proposition establishes the structural characteristic of a tree that admits a graceful IASL.

Proposition 2.12

Sudev and Germina (2016)   If a tree on n vertices admits an integer additive set-graceful labeling, then $1+n=2^r$, for some positive integer $r>1$.

In view of the above proposition, the following result describes the minimum required cardinality of the ground set X so that a given tree admits a graceful IASL.

Corollary 2.13

Sudev and Germina (2016)   Let G be a tree on n vertices. For a ground set X, let $f:V(G)\to \mathcal{P}(X)$ be be an integer additive set-graceful labeling on G. Then, $|X|={log}_2(n+1)$.

Invoking the above results, a necessary and sufficient condition for tree to admit a graceful IASL has been established in Sudev and Germina (2016) as follows.

Theorem 2.14

Sudev and Germina (2016)    A tree G is a graceful IASL-graph if and only if it is isomorphic to a star $K_{1,2^n-2}$, for some positive integer n.

The following proposition discussed the admissibility of integer additive set-graceful labeling by paths.

Proposition 2.15

Sudev and Germina (2016)   Except for $n=3$, no path $P_n$ admits an integer additive set-graceful labeling.

The proof of this proposition immediately follows from the fact no path other than $P_2$ and $P_3$ is a star graph. For $P_2$, the number of edges is 1, which is not equal to $2^m-2$ for any integer value of m.

As a result, we have the following theorem.

Theorem 2.16

A path $P_n$ on n vertices admits a graceful IASL if and only if $n=3$.

Note that the set-labels of the vertices of $C_n$ can not contain the maximal element of the ground set X and hence the number of vertices m is less than or equal to $2^{n-1}-1$, which contradicts the fact that $n=2^r-2$ for some positive integer n. Hence, we have

Proposition 2.17

Sudev and Germina (2016)   No cycle $C_n$ admits an integer additive set-graceful labeling.

Invoking the conditions on number of vertices and edges of a graph which admits a graceful IASL, mentioned above, the following theorem has ruled out the admissibility of graceful IASLs by complete graphs.

Theorem 2.18

Sudev and Germina (2016)   No complete graph $K_m$ admits an integer additive set-indexer.

We have already seen that $\{0\}$ must be the set-label of some vertex of a graceful IASL-graph G. We observe that in $\mathcal{P}(X)$, there will be some elements which are not non-trivial sumsets of any other elements of $\mathcal{P}(X)$. Hence, we have

Theorem 2.19

Sudev and Germina (2016)   Let G be a graceful IASL-graph. Then, the minimum number of vertices of G that are adjacent to the vertex having the set-label $\{0\}$ is the number of subsets of X which are not the non-trivial sumsets of any subsets of X.

In a similar way, we also observe that in $\mathcal{P}(X)$, there will be some elements which are not non-trivial summands of any other element of $\mathcal{P}(X)$. As a result of this fact, we have the following result.

Theorem 2.20

Sudev and Germina (2016)   If a graph G admits a graceful IASL f with respect to a finite ground set X, then the vertices of G, which have the set-labels which are not non-trivial summands of any subset of X, are the pendant vertices of G.

We can combine the above two results so that we get the number of pendant vertices which are attached to a particular vertex of the graceful IASL as described in the following theorem.

Theorem 2.21

Sudev and Germina (2016)   If G is a graceful IASL-graph, then at least k pendant vertices must be adjacent to a single vertex of G, where k is the number of subsets of X which are neither the non-trivial sumsets of subsets of X nor the non-trivial summands of any subset of X.

In view of the above theorem, a lower bound for the number of pendant vertices in a graceful IASL-graph has been determined in the following theorem.

Theorem 2.22

Sudev and Germina (2016)   Let G be a graceful IASL-graph which admits a graceful IASL f with respect to a finite non-empty set X. Then, G must have at least $|X|-1$ pendant vertices.

The questions about the existence of a graph G such that the function $f:V(G)\to \mathcal{P}(X)$ is a graceful IASI on G, corresponding to a given ground set X have been settled in the following theorem.

Theorem 2.23

Sudev and Germina (2016)   Let X be a non-empty finite set of non-negative integers. Then, there exists a graph G which admits a graceful IASL with respect to the set X.

The above theorem leads us to introduce the following notion.

Definition 2.24

Sudev and Germina (2016)   Let X be a non-empty finite set of non-negative integers. A graph G which admits a graceful IASI with respect to the set X is said to be a graceful graph-realization of the set X with respect the IASL f.

Hence, we can restate the above theorem as follows.

Theorem 2.25

Sudev and Germina (2016)   There exist a graceful graph-realization for any non-empty finite set of non-negative integers X with three or more elements.

Invoking all the results mentioned above, a necessary and sufficient condition for a graph G to admit a graceful IASI with respect to a given ground set X has been summarized in Sudev and Germina (2016) as in the following theorem.

Theorem 2.26

Sudev and Germina (2016)   Let X be a non-empty finite set of non-negative integers. Then, a graph G admits a graceful IASI if and only if the following conditions hold.

(a)	$0\in X$ and $\{0\}$ be a set-label of some vertex, say v, of G
(b)	the minimum number of pendant vertices in G is the number of subsets of X which are not the non-trivial summands of any subsets of X.
(c)	the minimum degree of the vertex v is equal to the number of subsets of X which are not the sumsets of any two subsets of X or not non-trivial summands of any other subsets of X.
(d)	the minimum number of pendant vertices that are adjacent to a given vertex of G is the number of subsets of X which are neither the non-trivial sumsets of any two subsets of X nor the non-trivial summands of any subsets of X.

The necessary part of the theorem follows together from Proposition 2.3, Theorems 2.19, 2.20 and 2.21 and the converse of the theorem follows from Theorem 2.23.

3. Integer additive set-sequential graphs

Let f be an integer additive set-indexer of a given graph G. Define a set-valued function $f^{\ast }:V(G)\cup E(G)\to \mathcal{P}(X)-\{\mathrm{\varnothing }\}$ as follows.(3.0.1) $$\begin{array}{c}\hfill f^{\ast }(x)=\left\{\begin{array}{cc}f(x)\hfill & \text{if}x\in V(G)\hfill \\ f^{+}(x)\hfill & \text{if}x\in E(G)\hfill \end{array}\right.\end{array}$$(3.0.1)

Clearly, $f^{\ast }[V(G)\cup E(G)]=f(V(G))\cup f^{+}(E(G))$. By the notation, $f^{\ast }(G)$, we mean $f^{\ast }[V(G)\cup E(G)]$. Then, $f^{\ast }$ is an extension of both f and $f^{+}$ of G. Throughout our discussions in this section, the function $f^{\ast }$ is as per the definition in Equation (3.0.1).

Using the definition of the newly defined function $f^{\ast }$ of f, the following notion has been introduced in Sudev and Germina (2015b) as the sumset analogue of set-sequential graphs.

Definition 3.1

Sudev and Germina (2015b)    An IASI f of G is said to be an integer additive set-sequential labeling (sequential IASL) (or sequential IASL) if the induced function $f^{\ast }(G)=f(V(G))\cup f^{+}E(G))=\mathcal{P}(X)-\{\mathrm{\varnothing }\}$. A graph G which admits a sequential IASL may be called an integer additive set-sequential graph (sequential IASL-graph).

In a similar way, an integer additive set-sequential indexer has been defined in Sudev and Germina (2015b) as follows.

Definition 3.2

Sudev and Germina (2015b)   An integer additive set-sequential labeling f of a given graph G is said to be an integer additive set-sequential indexer (IASSI) if the induced function $f^{\ast }$ is also injective. A graph G which admits an IASSI may be called an integer additive set-sequential indexed graph (or sequential IASI-graph).

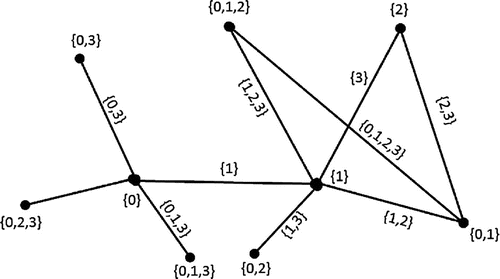
Figure 2 illustrates an integer additive set-labeling of a graph G.

Figure 2. An illustration to a graceful integer additive set-labeled graph.

In view of the fact that $f^{+}(E(G))\subseteq f^{\ast }(G)$, a relation between a graceful IASL and a sequential IASL of a given graph G has been established in following theorem.

Theorem 3.3

Sudev and Germina (2015b)   Every integer additive set-graceful labeling of a graph G is also an integer additive set-sequential labeling of G.

The following is an obvious but important result on the set-labels of the vertices of sequential IASL-graphs.

Proposition 3.4

Sudev and Germina (2015b)   Let G be a graph without isolated vertices. If the function $f^{\ast }$ is an injective function, then no vertex of G can have a set-label $\{0\}$.

As $f^{\ast }$ need not be injective for a sequential IASL-graph G, it can be noted that some edges may possess the same same set-label of some vertices in G.

If $f^{\ast }$ is injective, then the following observations are the direct consequences of Proposition 3.4.

Remark 3.5

Sudev and Germina (2015b)   Suppose that the function $f^{\ast }$ defined in (3.0.1) is injective. Then, if one vertex v of G has the set label $\{0\}$, then v is an isolated vertex of G.

Remark 3.6

Sudev and Germina (2015b)   If the function $f^{\ast }$ defined in (3.0.1) is injective, then no edge of G can also have the set label $\{0\}$.

We know the result that $|A\cup B|=|A|+|B|-|A\cap B|$. Invoking this result, namely the addition theorem on the cardinality of sets, the result given below has been proved in Sudev and Germina (2015b). This result provides a relation connecting the size and order of a given sequential IASL-graph G and the cardinality of its ground set X.

Proposition 3.7

Sudev and Germina (2015b)   Let G be a graph on n vertices and m edges. If f is a sequential IASL of a graph G with respect to a ground set X, then $m+n=2^{|X|}-(1+\mathit{\kappa })$, where $\mathit{\kappa }$ is the number of subsets of X which is the set-label of both a vertex and an edge.

Two sets A and B are said to have same parity if their cardinalities are simultaneously odd or simultaneously even. Then, the following theorem describes the parity of the vertex set and the edge set of a sequential IASL-graph G.

Proposition 3.8

Sudev and Germina (2015b)   Let f be a sequential IASL of a given graph G, with respect to a ground set X. Then, if V(G) and E(G) are of same parity, then $\mathit{\kappa }$ is an odd integer and if V(G) and E(G) are of different parity, then $\mathit{\kappa }$ is an even integer, where $\mathit{\kappa }$ is the number of subsets of X which are the set-labels of both vertices and edges.

Let f be a graceful IASL defined on a given graph G. Then, we know that $\{0\}\in f(V(G))$ and $|f^{+}(E(G))|=\mathcal{P}(X)-\{\mathrm{\varnothing },\{0\}\}$. Therefore, $\{0\}\in f^{\ast }(G)$ and hence $f^{\ast }(G)$ contains all non-empty subsets of X. Therefore, we have the following theorem.

Theorem 3.9

Sudev and Germina (2015b)   Every integer additive set-graceful labeling of a graph G is also an integer additive set-sequential labeling of G.

The structural properties of sequential IASL-graphs have been studied in Sudev and Germina (2015b). In the coming results, we discuss the major results on the structural properties of sequential IASL-graphs. The following result determines the minimum number of vertices in a graph that admits a sequential IASL with respect to a finite non-empty set X.

Theorem 3.10

Sudev and Germina (2015b)   Let X be a non-empty finite set of non-negative integers. Then, a graph G that admits a sequential IASL with respect to X has at least $\mathit{\rho }$ vertices, where $\mathit{\rho }$ is the number of elements in $\mathcal{P}(X)$ which are not the sumsets of any two elements of $\mathcal{P}(X)$.

In the example of sequential IASL-graphs, given in Figure 3, the graph G has some pendant vertices. The minimum number of pendant vertices required in a given sequential IASL-graph, satisfying certain conditions, has been determined in the following Theorem.

Theorem 3.11

Sudev and Germina (2015b)   Let G admit a sequential IASL with respect to a ground set X and let $\mathcal{B}$ be the collection of subsets of X which are neither the sumsets of any two subsets of X nor their sumsets are subsets of X. If $\mathcal{B}$ is non-empty, then

(1)	$\{0\}$ is the set-label of a vertex in G,
(2)	the minimum number pendant vertices in G is the cardinality of $\mathcal{B}$.

Since the ground set X of a sequential IASL-graph must contain the element 0, every subset $A_i$ of X is the sumset of $\{0\}$ and $A_i$ itself. In this sense, each subset $A_i$ may be considered as a trivial sumset of two subsets of X. In the coming discussions, by a sumset of subsets of X, we mean the non-trivial sumsets of subsets of X.

Let f be a sequential IASL of G with respect to a ground set X. Also, let $\mathcal{B}$ be the collection of subsets of X which are neither the sumsets of any two subsets of X nor their sumsets are subsets of X. Let $A\subset X$ be an element of $\mathcal{B}$. then A must be the set-label of a vertex of G. Since $A\in \mathcal{B}$, the only set that can be adjacent to A is $\{0\}$. Therefore, since G is a connected graph, $\{0\}$ must be the set-label of a vertex of G. Moreover, since A is an arbitrary vertex in $\mathcal{B}$, the minimum number of pendant vertices in G is $|\mathcal{B}|$.

The following result thus established the existence of pendant vertices in a sequential IASL-graph.

Theorem 3.12

Sudev and Germina (2015b)   Every graph that admits a sequential IASL, with respect to a non-empty finite ground set X, has at least one pendant vertex.

Remark 3.13

Sudev and Germina (2015b)   In view of the above results, we can make the following observations.

(1)	No cycle $C_n$ can have a sequential IASL.
(2)	For $n\ge 2$, no complete graph $K_n$ admits a sequential IASL.
(3)	No complete bipartite graph $K_{m,n}$ admits an IASL.

The following result establishes the existence of a graph that admits a sequential IASL with respect to a given ground set X.

Theorem 3.14

Sudev and Germina (2015b)   For any non-empty finite set X of non-negative integers containing 0, there exists a graph G which admits a sequential IASL with respect to X.

Analogous to the corresponding definition of graceful graph-realization, the notion of the sequential graph-realization of a given ground set X has been defined as a graph which admits a sequential IASL with respect to X. Hence, the above theorem establishes the existence of a sequential graph-realization for any given non-empty, finite set X. It is also to be noted that the sequential graph realization need not be unique for a given ground set X.

We note that, for a given graph G, the choice of a ground set X is also very important to have an integer additive set-sequential labeling. There are certain other restrictions in assigning set-labels to the elements of G.

The properties of a graph G that admits a sequential IASL with respect to a given ground set X are discussed in the following results. If Since $x_1$ and $x_2$ are the minimal non-zero elements of X, then they are not the non-trivial sumsets of any other sets in $\mathcal{P}(X)$. Then, we have

Proposition 3.15

Sudev and Germina (2015b)   Let G be a connected integer additive set-sequential graph with respect to a ground set X. Let $x_1$ and $x_2$ be the two minimal non-zero elements of X. Then, no edges of G can have the set-labels $\{x_1\}$ and $\{x_2\}$.

The following theorem discusses the condition for a set A in $\mathcal{P}(X)$ containing the maximal the maximal element $x_n$ of the ground set X to the set-label of a vertex in a sequential IASL-graph G.

Proposition 3.16

Sudev and Germina (2015b)   Let G be a connected integer additive set-sequential graph with respect to a ground set X. Then, any subset A of X that contains the maximal element of X can be the set-label of a vertex v of G if and only if v is a pendant vertex that is adjacent to the vertex u having the set-label $\{0\}$.

Now, we look at the conditions for some graph classes to admit sequential IASL. For any tree, we have $|V(G)|+|E(G)|=n+n-1=2n-1$. Invoking this condition, the following theorem discussed whether trees admit integer additive set-sequential labeling, with respect to a given ground set X.

Theorem 3.17

Sudev and Germina (2015b)   If a tree G admits a sequential IASL f with respect to a finite ground set X, then G has $2^{|X|-1}$ vertices.

By Proposition 3.4, if the induced function $f^{\ast }$ is injective, then $\{0\}$ can not be the set-label of any element of G. But, by Proposition 3.15 and 3.16, every connected sequential IASL-graph has a vertex with the set-label $\{0\}$. Hence, we have

Theorem 3.18

Sudev and Germina (2015b)   No connected graph G admits an integer additive set-sequential indexer.

By Theorem 3.11, $\{0\}$ must be the set-label of one vertex v in G and the vertices of G with set-labels from $\mathcal{B}$ can be adjacent only to the vertex v. By Remark , v must be an isolated vertex in G. In view of these results, the following theorem discussed a characterization of (disconnected) graphs which admit integer additive set-indexer.

Theorem 3.19

Sudev and Germina (2015b)   A graph G admits an integer additive set-sequential indexer f with respect to a ground set X if and only if G has ${\mathit{\rho }}^{\prime }$ isolated vertices, where ${\mathit{\rho }}^{\prime }$ is the number of subsets of X which are neither sumsets of any two subsets of X nor the summands of any subsets of X.

Analogous to Theorem 3.14, we can also establish the existence of a sequential IASI-graph with respect to a given non-empty ground set X.

Theorem 3.20

Sudev and Germina (2015b)   For any non-empty finite set X of non-negative integers, there exists a graph G which admits an IASSI with respect to X.

Figure 3. An illustration to a sequential IASI-group.

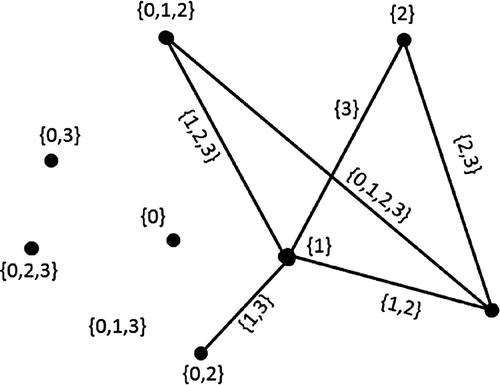
Figure 3 illustrates the existence of a sequential IASL for a given graph with isolated vertices.

4. Conclusion

In this paper, we have reviewed the studies taken place so far on graceful and sequential IASL-graphs and the properties and characteristics of the graphs that admit these types of IASLs. Certain problems regarding the complete characterization of graceful and sequential integer additive set-indexed graphs are still open.

We note that the admissibility of graceful and sequential integer additive set-labelings by the graphs depends upon the nature of elements in the ground set X and hence the choice of a ground set is very important in the discussions related to the admissibility of graceful and sequential IASL-graphs and graceful and sequential IASL-graphs. Let us define the graceful set-labeling number (and sequential set-labeling number) as the minimum cardinality required for the ground set X so that the given graph G admits a graceful IASL (or sequential IASL) with respect to the ground set X. Determining graceful set-labeling number and sequential set-labeling number is an area which seems to be promising for further research.

There are several other problems in this area which are promising for further studies. We are yet to establish a necessary and sufficient condition for the admissibility of sequential IASLs by many graph classes.

Characterization of different graph classes which admit integer additive set-graceful labelings or integer additive set-sequential labelings and verification of the existence of integer additive set-graceful labelings and integer additive set-sequential labelings for different graph operations, graph products and graph products are some of the promising problems which seem to be promising.

The integer additive set-indexers under which the vertices of a given graph are labeled by different standard sequences of non-negative integers, are also worth studying. All these facts highlight the wide scope for further studies in this area.

Acknowledgements

The authors would like to dedicate this work to the bright memory of the great Indian mathematician Prof (Dr) Belamannu Devadas Acharya, who introduced the concept set-indexers of graphs.The authors gratefully acknowledge the critical and creative comments made by the anonymous referee(s), which helped a lot in improving the style of presentation of the paper.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

N.K. Sudev

N.K. Sudev is a Professor (Associate) in the Department of Mathematics, Vidya Academy of Science and Technology, Thrissur, India., for the last fifteen years. His primary research areas are Graph Theory and Combinatorics. He has forty-five research papers in International Journals. He is a referee for many journals and premiere reviewing services.

K.P. Chithra

K.P. Chithra is an independent researcher in Mathematics. Her primary research area is also Graph Theory. She Possess twelve international publications in Graph Theory and related areas.

K.A. Germina

K.A. Germina is currently a Professor in Mathematics in University Botswana, Gaborone, Botswana. She has more than two decades of teaching experience and fifteen years of research experience. She has more than hundred research publications and she is the reviewer and editor for many journals and premiere reviewing services.