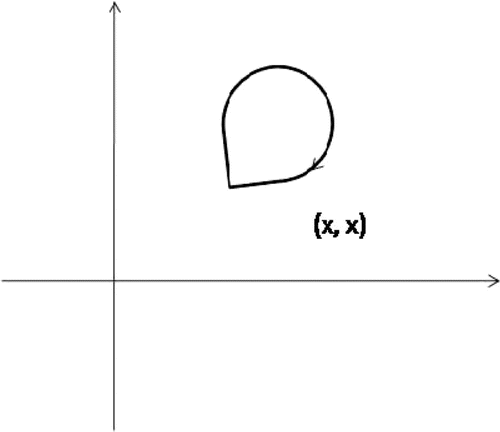Best proximity results for proximal contractions in metric spaces endowed with a graph

Abstract

In this paper we define a generalized proximal G-contraction on a metric space having the additional structure of a directed graph. We obtain a best proximity point result for such contractions which is with a view to obtaining minimum distance between the domain and range sets. An example illustrating the main theorem is also discussed. The work is in the line of research on mathematical analysis as well as optimization in metric spaces with a graph.

Keywords:

• metric space
• graph
• best proximity point
• rational proximal contraction
• optimal approximate solution
• minimum distance

Mathematics subject classifications:

• 47H10
• 54H10
• 54H25

Public Interest Statement

In this paper some results of mathematical analysis are established. It is a core area of mathematics on which stands a large part of the theoretical development of mathematics as well as many applications of mathematics. Particularly the results are in the domain of fixed point theory which is an extensive branch of mathematics having overlapping with various branches of pure and applied mathematics. The theory has also important implications in computer science. Although the present results are theoretical, there are potential applications of similar results in the literature. A noticeable aspect of the present work is the development of algorithm.

1. Introduction and mathematical preliminaries

The purpose of this paper is to establish a best proximity point theorem for generalized rational proximal contractions. It is a study on metric spaces with the additional structure of a graph on it. We begin with the following technical details which are necessary for the discussion in the paper.

Throughout the paper $(X,d)$ denotes a metric space and $A,B\subseteq X$. We use the following notations.$$\begin{array}{cc}\hfill d(A,B)& =\text{inf}\{d(a,b):a\in A\text{and}b\in B\},\hfill \\ \hfill A_0& =\{a\in A:d(a,b)=d(A,B)\text{for some}b\in B\},\hfill \\ \hfill B_0& =\{b\in B:d(a,b)=d(A,B)\text{for some}a\in A\}.\hfill \end{array}$$

It is to be noted that if $(A,B)$ is a nonempty, weakly compact and convex pair in a Banach space X, then $A_0$ and $B_0$ are nonempty (Basha & Veeramani, 2000; Gabeleh, 2015).

Definition 1.1

   [P-property (Sankar Raj, 2011)] Let A and B be two nonempty subsets of a metric space $(X,d)$ with $A_0\ne \mathrm{\varnothing }$. Then the pair $(A,B)$ is said to have the P-property if for any $x_1,x_2\in A_0$ and $y_1,y_2\in B_0$,$$\begin{array}{c}\hfill \left.\begin{array}{c}d(x_1,y_1)=d(A,B)\hfill \\ d(x_2,y_2)=d(A,B)\hfill \end{array}\right\}\Rightarrow d(x_1,x_2)=d(y_1,y_2).\end{array}$$

Abkar and Gabeleh (2012) have shown that every nonempty, bounded, closed and convex pair of subsets of a uniformly convex Banach space has the P-property. Some nontrivial examples of nonempty pairs of subsets which satisfy the P-property are given in Abkar and Gabeleh (2012).

Lemma 1.1

   (Gabeleh, 2013) Let $(A,B)$ be a pair of nonempty closed subsets of a complete metric space $(X,d)$ such that $A_0$ is nonempty and $(A,B)$ has the P-property. Then $(A_0,B_0)$ is a closed pair of subsets of X.

Definition 1.2

An element $x\in A$ is said to be a best proximity point the mapping $S:A⟶B$ if $d(x,Sx)=d(A,B)$.

Let $\mathrm{\Delta }:=\{(x,x):x\in X\}$. Let $G=G(V(G),E(G))$ be a directed graph such that its vertex set V(G) coincides with X, that is, $V(G)=X$ and the edge set E(G) contains all loops, that is, $\mathrm{\Delta }\subseteq E(G)$. Assume that G has no parallel edges. By $G^{-1}$ we denote the conversion of a graph G, that is, the graph obtained from G by reversing the directions of the edges. Thus we have$$\begin{array}{c}\hfill V(G^{-1})=V(G)\text{and}E(G^{-1})=\{(x,y)\in X\times X:(y,x)\in E(G)\}.\end{array}$$

Let $\tilde{G}$ denote the undirected graph obtained from G by ignoring the directions of edges. Actually, it is convenient for us to treat $\tilde{G}$ as a directed graph for which the set of its edges is symmetric. Under this convention,$$\begin{array}{c}\hfill V(\tilde{G})=V(G)\text{and}E(\tilde{G})=E(G)\cup E(G^{-1}).\end{array}$$

A graph $S(V(S),E(S))$ is called a subgraph of the graph $G(V(G),E(G))$ if $V(S)\subseteq V(G)$ and $E(S)\subseteq E(G)$. If $H\subseteq X$, then $G_H(V(G_H),E(G_H))$ denotes the subgraph of graph G, where $V(G_H)=H$.

Definition 1.3

If x and y are vertices in a graph G, then a path in G from x to y of length $m(m\in \mathbb{N})$ is a sequence ${(x_i)}_{i=0}^m$ of $m+1$ vertices such that $x_0=x,x_m=y$ and $(x_{i-1},x_i)\in E(G)$ for $i=1,...,m$.

A graph G is connected if there is a path between any two vertices. G is weakly connected if $\tilde{G}$ is connected.

Let G be such that E(G) is symmetric and x is a vertex in G, then the subgraph $G_x$ consisting of all edges and vertices which are contained in some path beginning at x is called the component of G containing x. In this case $V(G_x)={[x]}_G$, where ${[x]}_G$ is the equivalence class of the relation R defined on V(G) by the rule: yRz whenever there is a path in G from y to z.

We say a metric space $(X,d)$ is endowed with a directed graph G, if G is a directed graph such that $V(G)=X$ and $\mathrm{\Delta }\subseteq E(G)$. We suppose that $(X,d)$ is metric space endowed with a directed graph G.

Definition 1.4

Let $S:A⟶B$ be a mapping. Then $\text{Prox}(S)$ and $X_S(G_{A_0})$ are defined as follows:$$\begin{array}{cc}& \text{Prox}(S):=\{x\in A:d(x,Sx)=d(A,B)\},\hfill \\ \hfill & X_S(G_{A_0}):=\{x\in A_0:\exists y\in A_0\text{for which}d(y,Sx)=d(A,B)\text{and}(x,y)\in E(G)\}.\hfill \end{array}$$

Definition 1.5

A mapping $S:A⟶B$ is a Banach type proximal G- contraction if for all $x,y,u,v\in A$ with $(x,y)\in E(G),d(u,Sx)=d(A,B)$ and $d(v,Sy)=d(A,B)$, the followings are satisfied.

(i)	$(u,v)\in E(G)$ and
(ii)	$d(u,v)\le kd(x,y)$, where $k\in (0,1)$.

Definition 1.6

A mapping $S:A⟶B$ is a generalized proximal G- contraction if for all $x,y,u,v\in A$ with $(x,y)\in E(G),d(u,Sx)=d(A,B)$ and $d(v,Sy)=d(A,B)$ the followings are satisfied.

(i)	$(u,v)\in E(G)$ and
(ii)	$d(u,v)\le kM(x,y,u,v)$, where $k\in (0,1)$ and $$\begin{array}{cc}\hfill M(x,y,u,v)& =max\{d(x,y),{\displaystyle \frac{d(y,v)[1+d(x,u)]}{1+d(x,y)}},{\displaystyle \frac{d(y,u)[1+d(x,v)]}{1+d(x,y)}},\hfill \\ \hfill & {\displaystyle \frac{d(x,y)[1+d(x,u)+d(y,u)]}{1+d(x,y)}}\}.\hfill \end{array}$$

Definition 1.7

A mapping $S:A⟶B$ is a generalized proximal G- contraction on $A_0$ if for all $x,y,u,v\in A_0$ with $(x,y)\in E(G),d(u,Sx)=d(A,B)\text{and}d(v,Sy)=d(A,B)$ the followings are satisfied.

(i)	$(u,v)\in E(G)$ and
(ii)	$d(u,v)\le kM(x,y,u,v)$, where $k\in (0,1)$ and $M(x,y,u,v)$ is as in Definition 1.6.

Definition 1.8

The triple $(X,d,G)$ is said to be regular if

(i)	For any sequence $\{x_n\}$ in X with $x_n⟶x$ and $(x_n,x_{n+1})\in E(G)$ for all $n\in \mathbb{N}$, then $(x_n,x)\in E(G)$ for all $n\in \mathbb{N}$,
(ii)	For any sequence $\{x_n\}$ in X with $x_n⟶x$ and $(x_{n+1},x_n)\in E(G)$ for all $n\in \mathbb{N}$, then $(x,x_n)\in E(G)$ for all $n\in \mathbb{N}$.

As stated earlier, our purpose is to establish best proximity point results. Best proximity points are associated with non-self maps defined from one subset of a metric space to another. They are studied for the purpose of obtaining minimum distance between two sets. There are two aspects of this problem. Primarily, it is a global minimization problem where the quantity $d(x,Sx)$ is minimized over $x\in A$ subject to the condition that the minimum value is $d(A,B)$. When this global minimum is attained at a point z, then we have a best proximity point for which $d(z,Sz)=d(A,B)$. Another aspect is that it is an extension of the idea of fixed point to which it reduces in the cases where $A\cap B$ is nonempty. This is illustrated through the following. Let $A=(-\infty ,0]$ and $B=[1,\infty )$ be two subsets of $X=\mathbb{R}$ with the usual metric $d(x,y)=|x-y|$. Let $S:A⟶B$ be a mapping such that $S(x)=1-{\displaystyle \frac{x}{2}}$. Then $d(0,S(0))=1=d(A,B)$. So that 0 is a best proximity point of the mapping S. This is not a fixed point of S. In fact fixed point of the non-self map S does not exist.

On the contrary if $C=[0,\infty )$, then the mapping $T:A⟶C$ given by $Tx=-{\displaystyle \frac{x}{2}}$ has a best proximity point which is also a fixed point.

In fact fixed points are best proximity points, but the converse is not true. The above is the reason for which fixed point methodologies are applicable to this category of problems. More elaborately, the problem can be treated as that of finding a global optimal approximate solution of the fixed point equation $x=Sx$ even when the exact solution is nonexistent for $A\cap B=\mathrm{\varnothing }$ which is the case of interest here. We adopt the later approach in this paper.

Metric spaces with the structure of graph have been considered in recent times especially in the context of fixed point theory of contractive type mappings. The line of research was originated in the work of Jachymski (2008) and was further pursued in Abbas, Nazir, Lampert, and Radenović (2016), Beg, Butt, and Radojević (2010), Bojor (2012), Eshi, Das, and Debnath (2016), Kumam, Salimi, and Vetro (2014), Tiammee and Suantai (2014), Shukla (2014). The essential feature of these works is that the metric inequality for the purpose of ensuring the fixed point need only be satisfied on certain pairs of points which are, in this case, connected by the edges of the graph. It is a further extension of metric spaces with a partial order structure on it.

In this paper, against the above background, we establish a best proximity point theorem in a metric space having a structure of graph defined on it by using generalized proximal G-contractions. In the last section we discuss an illustrative example.

2. Main results

Theorem 2.1

Let $(X,d)$ be a complete metric space endowed with a directed graph G. Let $(A,B)$ be a pair of nonempty and closed subsets of X such that $A_0$ is nonempty and closed. Let $S:A⟶B$ be a mapping with the properties that $S(A_0)\subseteq B_0$ and S is generalized proximal G- contraction on $A_0$. Suppose that (a) S is continuous or (b) the triple $(X,d,G)$ is regular. Then the the following statements hold:

(1)	For any $x\in X_S(G_{A_0})$, S has a best proximity point in ${[x]}_{\widetilde{G_{A_0}}}$.
(2)	If $X_S(G_{A_0})\ne \mathrm{\varnothing }$ and $G_{A_0}$ is weakly connected, then S has a best proximity point in $A_0$.
(3)	If $X^{\ast }:=\cup \{{[x]}_{\widetilde{G_{A_0}}}:x\in X_S(G_{A_0})\}$, then S has best proximity point in $X^{\ast }$.
(4)	$\text{Prox}(S)\ne \mathrm{\varnothing }$ if and only if $X_S(G_{A_0})\ne \mathrm{\varnothing }$.

Proof

 

(1)

It follows from the definition of $A_0$ and $B_0$ that for every $x\in A_0$ there exists $y\in B_0$ such that $d(x,y)=d(A,B)$ and conversely, for every $y^{\prime }\in B_0$ there exists $x^{\prime }\in A_0$ such that $d(x^{\prime },y^{\prime })=d(A,B)$. Since $S(A_0)\subseteq B_0$, for every $x\in A_0$ there exists a $y\in A_0$ such that $d(y,Sx)=d(A,B)$.

Let $x_0\in X_S(G_{A_0})$. By the definition of $X_S(G_{A_0})$, there exists $x_1\in A_0$ such that $(x_0,x_1)\in E(G)$ and $d(x_1,S{x}_0)=d(A,B)$. Now $x_1\in A_0$ and $S(A_0)\subseteq B_0$ imply the existence of a point $x_2\in A_0$ such that $d(x_2,S{x}_1)=d(A,B)$. As S is generalized proximal G- contraction on $A_0$, we get $(x_1,x_2)\in E(G)$. In this way we obtain a sequence $\{x_n\}$ in $A_0$ such that for all $n\ge 0$,(2.1) $$\begin{array}{c}\hfill (x_n,x_{n+1})\in E(G)\end{array}$$(2.1)

and(2.2) $$\begin{array}{c}\hfill d(x_{n+1},S{x}_n)=d(A,B).\end{array}$$(2.2)

Now, for all $n\ge 0$ we have $x_n\in A_0$, $(x_n,x_{n+1})\in E(G),d(x_{n+1},S{x}_n)=d(A,B)$ and $d(x_{n+2},S{x}_{n+1})=d(A,B)$. Since S is generalized proximal G- contraction on $A_0$, we have(2.3) $$\begin{array}{c}\hfill d(x_{n+1},x_{n+2})\le kM(x_n,x_{n+1},x_{n+1},x_{n+2}),\end{array}$$(2.3)

where$$\begin{array}{cc}\hfill M(x_n,x_{n+1},x_{n+1},x_{n+2})& =max\{d(x_n,x_{n+1}),{\displaystyle \frac{d(x_{n+1},x_{n+2})[1+d(x_n,x_{n+1})]}{1+d(x_n,x_{n+1})}},\hfill \\ \hfill & {\displaystyle \frac{d(x_{n+1},x_{n+1})[1+d(x_n,x_{n+2})]}{1+d(x_n,x_{n+1})}},\hfill \\ \hfill & {\displaystyle \frac{d(x_n,x_{n+1})[1+d(x_n,x_{n+1})+d(x_{n+1},x_{n+1})]}{1+d(x_n,x_{n+1})}}\}\hfill \\ \hfill & =max\{d(x_n,x_{n+1}),d(x_{n+1},x_{n+2})\}.\hfill \end{array}$$

Suppose that $d(x_n,x_{n+1})<d(x_{n+1},x_{n+2})$, for some positive integer n. Then $d(x_{n+1},x_{n+2})>0$. Then it follows from (2.3) that$$\begin{array}{c}\hfill 0<d(x_{n+1},x_{n+2})<kd(x_{n+1},x_{n+2}),\end{array}$$

which is a contradiction. Therefore,(2.4) $$\begin{array}{c}\hfill d(x_{n+1},x_{n+2})\le d(x_n,x_{n+1}),\text{for all}n\ge 0.\end{array}$$(2.4)

Hence we have from (2.3) and (2.4) that(2.5) $$\begin{array}{c}\hfill d(x_{n+1},x_{n+2})\le kd(x_n,x_{n+1}),\text{for all}n\ge 0.\end{array}$$(2.5)

By repeated application of (2.5), we have(2.6) $$\begin{array}{c}\hfill d(x_{n+1},x_{n+2})\le k^{n+1}d(x_0,x_1).\end{array}$$(2.6)

For arbitrary $m,n\in \mathbb{N}$ with $m>n$,$$\begin{array}{cc}\hfill d(x_m,x_n)& \le d(x_n,x_{n+1})+d(x_{n+1},x_{n+2})+...+d(x_{m-1},x_m)\hfill \\ \hfill & \le [k^n+k^{n+1}+k^{n+2}+...+k^{m-1}]d(x_0,x_1)\hfill \\ \hfill & \le {\displaystyle \frac{k^n}{1-k}}d(x_0,x_1)⟶0\text{as}n⟶\infty .\hfill \end{array}$$

Therefore, $\{x_n\}$ is a Cauchy sequence in $A_0$. Since $A_0$ is a closed subset of complete metric space $(X,d)$, there exists $z\in A_0$ such that(2.7) $$\begin{array}{c}\hfill x_n⟶z\text{as}n⟶\infty .\end{array}$$(2.7)

• Suppose that S is continuous. Taking $n⟶\infty$ in (2.2) and using the continuity of S, we have $d(z,Sz)=d(A,B)$; that is, z is a best proximity point of S.

• Next we suppose that the triple $(X,d,G)$ is regular. By (2.1) and (2.7), we have (2.8) $$\begin{array}{c}\hfill (x_n,z)\in E(G)\text{for all}n\ge 0.\end{array}$$(2.8) Now $z\in A_0$ and $S(A_0)\subseteq B_0$ imply the existence of a point $p\in A_0$ for which (2.9) $$\begin{array}{c}\hfill d(p,Sz)=d(A,B).\end{array}$$(2.9)

By (2.2), (2.8) and (2.9), we have for all $n\ge 0$$$\begin{array}{c}\hfill (x_n,z)\in E(G),d(x_{n+1},S{x}_n)=d(A,B)\text{and}d(p,Sz)=d(A,B),\text{where}{x}_n,z,x_{n+1},p\in A_0.\end{array}$$

Since S is generalized proximal G- contraction on $A_0$, we have(2.10) $$\begin{array}{c}\hfill d(x_{n+1},p)\le kM(x_n,z,x_{n+1},p),\end{array}$$(2.10)

where$$\begin{array}{cc}\hfill M(x_n,z,x_{n+1},p)& =max\{d(x_n,z),{\displaystyle \frac{d(z,p)[1+d(x_n,x_{n+1})]}{1+d(x_n,z)}},{\displaystyle \frac{d(z,x_{n+1})[1+d(x_n,p)]}{1+d(x_n,z)}},\hfill \\ \hfill & {\displaystyle \frac{d(x_n,z)[1+d(x_n,x_{n+1})+d(z,x_{n+1})]}{1+d(x_n,z)}}\}.\hfill \end{array}$$

Using (2.7), we have(2.11) $$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}M(x_n,z,x_{n+1},p)=d(z,p).}\end{array}$$(2.11)

Taking the limit as $n⟶\infty$ in (2.10), using (2.7) and (2.11), we have $d(z,p)\le kd(z,p)$, which is a contradiction unless $d(z,p)=0$; that is, $p=z$. Then by (2.9) we have that $d(z,Sz)=d(A,B)$; that is, z is a best proximity point of S. By (2.8), it is obvious that $(x_0,z)\in E(G_{A_0})$ and so $z\in {[x_0]}_{\widetilde{G_{A_0}}}$. Hence S has best proximity point in ${[x_0]}_{\widetilde{G_{A_0}}}$.

(2)	Let $X_S(G_{A_0})\ne \mathrm{\varnothing }$ and $G_{A_0}$ is weakly connected. Since $G_{A_0}$ is weakly connected, ${[x]}_{\widetilde{G_{A_0}}}=A_0$ for every $x\in A_0$. Since $X_S(G_{A_0})\ne \mathrm{\varnothing }$, there exists an $x_0\in X_S(G_{A_0})$. Then ${[x_0]}_{\widetilde{G_{A_0}}}=A_0$. So by (1), S has best proximity point in $A_0$.
(3)	Let $X^{\ast }:=\cup \{{[x]}_{\widetilde{G_{A_0}}}:x\in X_S(G_{A_0})\}$. By (1) and (2), S has a best proximity point in $X^{\ast }$.
(4)	Let $\text{Prox}(S)\ne \mathrm{\varnothing }$. Then there exists atleast one element $x\in \text{Prox}(S)$. Now $x\in \text{Prox}(S)$ means $d(x,Sx)=d(A,B)$. So, $x\in A_0$. Now $\mathrm{\Delta }\subseteq E(G)$ implies that $(x,x)\in E(G)$. Therefore, we have $x\in A_0$ such that $d(x,Sx)=d(A,B)$ and $(x,x)\in E(G)$, which implies that $x\in X_S(G_{A_0})$. Hence $X_S(G_{A_0})\ne \mathrm{\varnothing }$. Conversely suppose that $X_S(G_{A_0})\ne \mathrm{\varnothing }$. Then by (1), $\text{Prox}(S)\ne \mathrm{\varnothing }$.

$\square$

With the help of P - property we have the following theorem which is obtained by an application of Theorem 2.1.

Figure 1. $(x,x)\in \mathrm{\Delta }\forall x\in X$.

Figure 2. $(p,q)\in E_1$ where $p=(x1,y_1)$, $q=(u_1,v_1)\in S_1$ with $x_1\ge u_1$ and $y_1\ge v_1$.

Figure 3. $(s,t)\in E_2$ where $s=(x_2,y_2)$, $t=(u_2,v_2)\in S_2$ with $x_2\le u_2$ and $y_2\le v_2$.

Theorem 2.2

Let $(X,d)$ be a complete metric space endowed with a directed graph G. Let $(A,B)$ be a pair of nonempty and closed subsets of X such that $A_0$ is nonempty and $(A,B)$ satisfies the P-property. Let $S:A⟶B$ be a mapping with $S(A_0)\subseteq B_0$. Suppose that for all $x,y,u,v\in A_0$ with $(x,y)\in E(G),d(u,Sx)=d(A,B)\text{and}d(v,Sy)=d(A,B)$ the followings are satisfied.

(i)	$(u,v)\in E(G)$ and
(ii)	$d(Sx,Sy)\le kM(x,y,u,v)$, where $k\in (0,1)$ and $$\begin{array}{cc}\hfill M(x,y,u,v)& =max\{d(x,y),{\displaystyle \frac{d(y,v)[1+d(x,u)]}{1+d(x,y)}},{\displaystyle \frac{d(y,u)[1+d(x,v)]}{1+d(x,y)}},\hfill \\ \hfill & {\displaystyle \frac{d(x,y)[1+d(x,u)+d(y,u)]}{1+d(x,y)}}\}.\hfill \end{array}$$

Also, suppose that (a) S is continuous or (b) the triple $(X,d,G)$ is regular. Then the following statements hold :

(1)	For any $x\in X_S(G_{A_0})$, S has a best proximity point in ${[x]}_{\widetilde{G_{A_0}}}$.
(2)	If $X_S(G_{A_0})\ne \mathrm{\varnothing }$ and $G_{A_0}$ is weakly connected, then S has a best proximity point in $A_0$.
(3)	If $X^{\ast }:=\cup \{{[x]}_{\widetilde{G_{A_0}}}:x\in X_S(G_{A_0})\}$, then S has best proximity point in $X^{\ast }$.
(4)	$\text{Prox}(S)\ne \mathrm{\varnothing }$ if and only if $X_S(G_{A_0})\ne \mathrm{\varnothing }$.

Proof

By Lemma 1.1, $A_0$ is nonempty and closed. Since $(A,B)$ satisfies P-property, $d(u,Sx)=d(A,B)$ and $d(v,Sy)=d(A,B)$ imply that $d(u,v)=d(Sx,Sy)$. Then condition (ii) of the theorem reduces to the following inequality $d(u,v)\le kM(x,y,u,v)$, where $k\in (0,1)$ and$$\begin{array}{cc}\hfill M(x,y,u,v)& =max\{d(x,y),{\displaystyle \frac{d(y,v)[1+d(x,u)]}{1+d(x,y)}},{\displaystyle \frac{d(y,u)[1+d(x,v)]}{1+d(x,y)}},\hfill \\ \hfill & {\displaystyle \frac{d(x,y)[1+d(x,u)+d(y,u)]}{1+d(x,y)}}\}.\hfill \end{array}$$

Hence S is generalized proximal G-contraction on $A_0$. Therefore, we have the required proof from that of Theorem 2.1. $\square$

3. Example

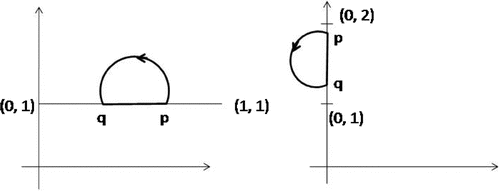
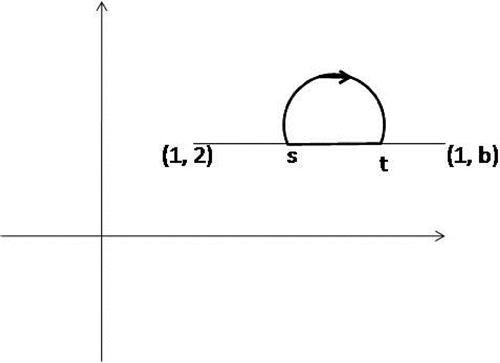
Example 3.1

Let $X=R^2$ (R denotes the set of real numbers) and d be a metric on X defined as $d(x,y)=\mid x_1-x_2\mid +\mid y_1-y_2\mid ,\text{for}x=(x_1,y_1),y=(x_2,y_2)\in X$. Let $A=S_1\bigcup S_2$ and $B=H_1\bigcup H_2$, where $S_1=\{(x,1):0\le x\le 1\}\bigcup \{(0,y):1\le y\le 2\}$, $S_2=\{(x,1):2\le x\le b\}$, $H_1=\{(x,-1):0\le x\le 1\}\bigcup \{(0,y):-2\le y\le -1\}$ and $H_2=\{(x,-1):2\le x\le b\}$. Let G be a directed graph with $V(G)=X$ and $E(G)=\mathrm{\Delta }\bigcup E_1\bigcup E_2,$ where$$\begin{array}{cc}\hfill \mathrm{\Delta }& :=\{(x,x):x\in X\},\hfill \\ \hfill E_1& :=\{(p,q):p=(x_1,y_1),q=(u_1,v_1)\in S_1\text{with}{x}_1\ge u_1\text{and}{y}_1\ge v_1\}\hfill \end{array}$$

and$$\begin{array}{c}\hfill E_2:=\{(s,t):s=(x_2,y_2),t=(u_2,v_2)\in S_2\text{with}{x}_2\le u_2\text{and}{y}_2\le v_2\}.\end{array}$$

Let$$A_0=\{(x,1):0\le x\le 1\}\bigcup \{(x,1):2\le x\le b\}\subseteq A$$

and$$B_0=\{(x,-1):0\le x\le 1\}\bigcup \{(x,-1):2\le x\le b\}\subseteq B.$$

Let $S:A\to B$ be defined as$$\begin{array}{c}\hfill S(t)=\left\{\begin{array}{cc}({\displaystyle \frac{x}{2}},-1),\hfill & \text{if}t=(x,1)\text{where}0\le x\le 1,\hfill \\ (0,-y),\hfill & \text{if}t=(0,y)\text{where}1\le y\le 2,\hfill \\ (x+{\displaystyle \frac{1}{x}}-{\displaystyle \frac{1}{b}},-1),\hfill & \text{if}t=(x,1)\text{where}2\le x\le b.\hfill \end{array}\right.\end{array}$$

Let $k\in (0,1)$ be such that $1-{\displaystyle \frac{1}{b^2}}\le k<1$. The function S satisfies all the postulates of Theorems 2.1. The set of best proximity points of the mapping S, that is, Prox (S) is nonempty. Here $\text{Prox}(S)=\{(0,1),(b,1)\}\subseteq A_0$ (Figures 1–3).

Additional information

Funding

Author Binayak S. Choudhury gratefully acknowledges the support of DST, W.B., India under Scheme Sanction No 624(Sanc.)/ST/P/S & T/Misc-5/2012.

Notes on contributors

Binayak S. Choudhury

Binayak S. Choudhury is Professor of Mathematics in IIEST, Shibpur, Howrah, 711103, West Bengal, India, since 2003. He has supervised several PhD students in different areas of pure and applied mathematics and theoretical physics and has published a good number of research articles in international journals. Particularly he has published more than 100 research articles in metric space related studies. He has served his institute in several administrative capacities.

Nikhilesh Metiya

Nikhilesh Metiya is an assistant professor in the Department of Mathematics, Sovarani Memorial College, Jagatballavpur, Howrah-711408, West Bengal, India. He got his PhD from IIEST (Formerly BESUS), Shibpur, Howrah, 711103, West Bengal, India, in 2013. He has 32 international publications in fixed point theory and allied subjects. His research interests include with mathematical analysis, nonlinear analysis and optimization.