Lanczos bidiagonalization-based inverse solution methods applied to electrical imaging of the heart by using reduced lead-sets: A simulation study

Abstract

In inverse problem of electrocardiography (ECG), electrical activity of the heart is estimated from body surface potential measurements. This electrical activity provides useful information about the state of the heart, thus it may help clinicians diagnose and treat heart diseases before they cause serious health problems. For practical application of the method, having fewer number of electrodes for data acquisition is an advantage. Additionally, inverse problem of ECG is ill-posed due to attenuation and smoothing within the body. Therefore, the solution of ECG inverse problem has to be regularized. In this study, we constrain ourselves to two Lanczos-bidiagonalization-based inverse solution methods, namely, Lanczos least-squares QR (L-LSQR) factorization and Lanczos truncated total least-squares (L-TTLS). Tikhonov regularization is also implemented as a base for comparison for these methods. We use body surface measurements simulated using epicardial potentials measured from the surface of canine hearts. In these experiments, the hearts are stimulated from the ventricles at various sites, mimicking ectopic beats. Torso potentials are obtained from these epicardial measurements by multiplying them with the forward transfer matrix and adding Gaussian distributed noise. We solve the inverse problem using different number of leads on the body surface (771, 192, 64, and 32 leads), and assess the performances of these regularization methods for the reduced lead-sets. These reduced lead-sets are selected from the primary 771-lead configuration by using two main approaches. The first approach is manually selecting appropriate leads, and the second one uses the inverse problem approach to select leads sequentially. The results show that the L-TTLS method is more successful in reconstructing epicardial potentials than the L-LSQR method. The L-TTLS method is faster than the Tikhonov regularization, since it benefits from bidiagonal form of the forward matrix. Reducing the number of electrodes to 64 has a small effect on the solutions, but with 32 leads, inverse solutions get less precise, and the difference between the results of Tikhonov regularization and L-TTLS method becomes less significant.

Keywords:

• inverse problem of electrocardiography
• Tikhonov regularization
• lead reduction
• Lanczos least-squares QR (L-LSQR)
• Lanczos truncated total least-squares (L-TTLS)

Public Interest Statement

In modern society there are increasing number of people suffering from heart diseases. The diagnosis of the heart problems in early stages is a very important step toward quick recovery. One way to achieve this is to understand the electrical activity of the heart by measuring the heart potentials reflected onto the body surface. Then, estimating the source of these potentials, which is the ultimate goal of inverse problem of electrocardiography, gives an idea about the electrical activity of the heart. Apparently, the more the electrodes to detect the electrical signals, the better the quality of the signal is. However, there are limitations for the locations and the number of electrodes to be used for this purpose. Here, the aim is to find an electrode configuration which uses a smaller number of electrodes and results in nearly the same signal quality measured by a large number of electrodes and to solve the inverse problem of electrocardiography faster and more precise.

1. Introduction

According to a World Health Organization (WHO) report, an estimated 17 million people die of cardiovascular diseases such as heart attack and stroke, around the world every year (WHO, 2014). Yearly growing number of patients around the world has motivated researchers to seek clinically practical non-invasive methods to attain detailed and precise information about the electrical activity of the heart. Although several cardiac abnormalities are diagnosable by the standard 12-lead ECG, many others are not detectable by this fixed lead configuration. Furthermore, 12-lead ECG suffers from sparse sampling in space. Alternatively, body surface potential mapping (BSPM) approach has been proposed, in which ECG signals are acquired from large number of electrodes densely placed on the torso surface. But still, these measurements also suffer from attenuation and smoothing that occur inside the body. One way to recover lost details on the body surface is to obtain actual electrical sources within the heart that generate the body surface measurements by solving the inverse ECG problem. This technique is also called as electrical imaging of the heart. The solution of the inverse ECG problem can help physicians diagnose various heart diseases and treat them properly before they turn into life threatening health issues. However, inverse ECG problem is ill-posed because of attenuation and smoothing of cardiac signals inside the body (Gulrajani, 1998; Ramanathan, Ghanem, Jia, Ryu, & Rudy, 2004). Thus, even small perturbations in the measurements or errors in the mathematical model relating the sources to the measurements can cause unbounded errors in the solution. To overcome this ill-posed nature of the problem and to obtain reasonable and meaningful cardiac electrical images, the solution has to be regularized.

Researchers have proposed several regularization and statistical estimation methods to overcome the ill-posedness of the inverse ECG problem. Tikhonov regularization (Tikhonov & Arsenin, 1977) and truncated singular value decomposition (TSVD) (Shou, Xia, & Jiang, 2007) are the most well-known methods for regularization. A modified version of Tikhonov regularization, which is called as the “Twomey” regularization, has not been as practical as Tikhonov regularization, since it needs prior information about the desired solution (Twomey, 1963). Truncated total least-squares (TTLS) is another method that has been shown to be effective, especially in the presence of geometric noise (Shou et al., 2008). However, as with TSVD, computation of singular values for a large matrix is time consuming. Alternatively, Lanczos-bidiagonalization-based TTLS method (L-TTLS) has been proposed in (Güçlü, 2013) to reduce the computational complexity and the run time. Another Lanczos-bidiagonalization-based method is Lanczos least-squares QR factorization (L-LSQR); Jiang, Xia, Shou, and Tang (2007) compared the performances of conventional regularization methods, Tikhonov regularization and TSVD, with L-LSQR method. Most of the regularization methods employ L₂-norm (Euclidian norm)-based approaches, both in the data and penalty terms to deal with the ill-posed nature of the inverse problem. L₁-norm based solutions have also been proposed to overcome over-smoothing effects present in the L₂-norm based solutions (Ghosh & Rudy, 2009; Shou, Xia, Liu, Jiang, & Crozier, 2011; Wang, Qin, Wong, & Heng, 2011). Bayesian Maximum a posteriori (MAP) estimation (Serinagaoglu, Brooks, & MacLeod, 2006; van Oosterom, 1999), Kalman filters and smoothers (Aydin & Dogrusoz, 2011; Ghodrati, Brooks, Tadmor, & MacLeod, 2006) are some of the statistical approaches that incorporate prior information on the solutions in the form of a prior probability density function.

For cardiac electrical imaging to be practical in clinical applications, it is important to use small number of electrodes (Ghodrati, Brooks, & MacLeod, 2007). But at the same time, data acquired via these electrodes should have effective coverage of the changes in the electrical potentials that are reflected onto the body surface. Another point to keep in mind is that smaller number of electrodes usually result in an under-determined system. In that case, much of the burden of reconstructing cardiac electrical image is on the regularization algorithms.

In this paper, our main goal is to study the effects of employing a smaller number of leads (electrodes) for recording the body surface potentials, on the inverse ECG solutions. We propose a simple lead-set reduction algorithm based on inverse solutions, and we compare the performances of these reduced lead-sets with the performances of the manually selected lead-sets and the complete lead-set. We have applied Lanczos-bidiagonalization-based methods, L-TTLS and L-LSQR in this study to take advantage of their reduced computational complexity and fast computation. L-LSQR has been applied previously to solve the inverse ECG problem (Jiang et al., 2007), and L-TTLS has been proposed in an earlier study by one of our research group (Güçlü, 2013) to reduce the computational complexity and the run time. However, to the best of our knowledge, neither method has been assessed elsewhere in terms of their performances with reduced lead-sets. Here we compare performances of these methods in reconstructing real heart potentials with Tikhonov regularization. Results are quantitatively compared by calculating correlation coefficient (CC) and relative difference measurement star (RDMS). Qualitative comparisons are also carried out by plotting the heart surface potential distributions using MAP3D visualization software, which provides an interactive display of both geometry and data assigned to elements of that geometry.

2. Problem definition

In cardiac electrical imaging, electrical sources in the heart may be represented in various equivalent sources. In this study, we use epicardial potentials, which are the potentials on the outer surface of the heart. Epicardial potentials are related to body surface potentials by the following linear system:

(1) $$B=AX+N,$$(1)

where $B\in {\mathbb{R}}^{m\times p}$ and $X\in {\mathbb{R}}^{n\times p}$ are the matrices that contain body surface potentials and epicardial potentials, respectively. The matrix $A\in {\mathbb{R}}^{m\times n}$ is the forward transfer matrix, which is the result of the solution of the forward problem of ECG, and the matrix $N\in {\mathbb{R}}^{m\times p}$ is used to model measurement errors. For vector notation we can redefine the above equation as:(2) $$b\left(t\right)=Ax\left(t\right)+n\left(t\right)(t=1,2,\dots ,p),$$(2)

where t represents each time instant, and b(t), x(t), and n(t) correspond to the tth column of matrices B, X, and N, respectively. The solution to Equation (2) is found separately for every t. For simplicity, we drop the time index from the equations in the following sections.

3. Regularization methods

3.1. Tikhonov regularization

Tikhonov regularization method is one of the most well-known and popular regularization methods to deal with the ill-posed nature of the inverse ECG problem (Golub & van Loan, 1980). In this method, a cost function consisting of the residual norm and the constraint norm is defined, and the solution is chosen to minimize this cost function (Aster, Borcher, & Thurber, 2005):(3) $$x_{\mathit{\lambda }}={\text{argmin}}_x{\Vert Ax-b\Vert }_2^2+{\mathit{\lambda }}^2{\Vert Rx\Vert }_2^2,$$(3)

where $\mathit{\lambda }$ is the regularization parameter, $x_{\mathit{\lambda }}$ is the solution for a specific $\mathit{\lambda }$ value, and R is the regularization matrix representing the constraints to be used for regularization. Here, ${\Vert .\Vert }_2$ stands for the Euclidean norm, and we use $R=I$ (identity matrix, i.e. zeroth-order regularization), because it is more suitable for inverse problem of ECG (Franzone, Guerri, Taccardi, & Viganotti, 1985).

Two alternative representations of Tikhonov regularization are presented below:(4) $$\left(A^{T}A+{\mathit{\lambda }}^2{R}^{T}R\right)x=A^{T}b,$$(4) (5) $$\text{min}{∥\left(\begin{array}{c}A\\ \mathit{\lambda }R\end{array}\right)x-\left(\begin{array}{c}b\\ 0\end{array}\right)∥}_2$$(5)

Considering the above two equations, it can be inferred that if the null space of A intersects with the null space of R (i.e. $N\left(A\right)\cap N\left(R\right)=\{0\}$), then there would be a unique solution, x_est, then the coefficient matrix, $\left(A^{T}A+{\mathit{\lambda }}^2{R}^{T}R\right)$, has full rank, and the solution is calculated as:(6) $$x_{est}=A_{\mathit{\lambda }}b,$$(6)

where(7) $$A_{\mathit{\lambda }}={(A^{T}A+{\mathit{\lambda }}^2{R}^{T}R)}^{-1}{A}^T$$(7)

is the Tikhonov regularized inverse of matrix A. As in many regularization methods, large singular values are more effective than smaller ones; therefore, the determination of the regularization parameter λ is important.

3.2. Lanczos least-squares QR (L-LSQR)

Lanczos least-squares QR factorization (L-LSQR) is an iterative method to solve linear systems. When the coefficient matrix is large, iterative methods are more preferable than direct solutions. L-LSQR method iteratively produces solution matrices. After k iterations, the solution will approach an optimal solution. However, this method suffers from a phenomenon called as “semi-convergence”. If the number of iterations is not limited, the solution may converge to a worse solution with higher relative error (Jiang et al., 2007).

L-LSQR method starts with finding the sequence of Lanczos vectors using Lanczos-bidiagonalization method. Lanczos-bidiagonalization computes $u_j\in {\mathbb{R}}^m$, $v_j\in {\mathbb{R}}^n$ and scalars α_j and β_j such that B_k = U^TAV is met. Here, B_k is a lower bidiagonal matrix, with 0 representing triangular 0-matrices:(8) $$B_k=\left[\begin{array}{ccccc}{\mathit{\alpha }}_1\hfill & & & & 0\hfill \\ {\mathit{\beta }}_1\hfill & {\mathit{\alpha }}_2\hfill & & & \\ \hfill & {\mathit{\beta }}_2\hfill & & \ddots \hfill & \\ \hfill & & & \ddots \hfill & {\mathit{\alpha }}_k\hfill \\ 0\hfill & & & & {\mathit{\beta }}_{k+1}\hfill \end{array}\right].$$(8)

Lanczos vectors are orthonormal such that:$$U_{k+1}=(u_1,u_2,\dots ,u_{k+1})\in {\mathbb{R}}^{m\times (k+1)},U_{k+1}^T{U}_{k+1}=I_{k+1},$$

and$$V_k=(v_1,v_2,\dots ,v_k)\in {\mathbb{R}}^{m\times k},V_k^T{V}_k=I_k.$$

3.2.1. Lanczos-bidiagonalization

1.	Choose a starting vector $b\in {\mathbb{R}}^m$ and ${\mathit{\beta }}_1={\Vert b\Vert }_2$, $u_1=\frac{b}{{\mathit{\beta }}_1}$, v0 = 0 and α1.
2.	For $i=1,2,\dots ,k$ do a. $r_i=A^T{u}_i-{\mathit{\beta }}_i{v}_{i-1}$ b. ${\mathit{\alpha }}_i={\Vert r_i\Vert }_2$ c. $v_i=\frac{r_i}{{\mathit{\alpha }}_i}$ d. $P_i=A{v}_i-{\mathit{\alpha }}_i{u}_i$ e. ${\mathit{\beta }}_{i+1}={\Vert P_i\Vert }_2$ f. $u_{i+1}=\frac{P_i}{{\mathit{\beta }}_{i+1}}$ End

After k iterations, three matrices will have been computed, a lower bidiagonal matrix B_k and two matrices U_k+1 and V_k. These matrices are related by the following relationships:(9) $$\begin{array}{c}b={\mathit{\beta }}_1{u}_1={\mathit{\beta }}_1{U}_{k+1}{e}_1,\hfill \\ A{V}_k=U_{k+1}{B}_k,\hfill \\ A^T{U}_{k+1}=V_k{B}_k^T+{\mathit{\alpha }}_{k+1}{v}_{k+1}{e}_{k+1}^T\hfill \end{array}$$(9)

where $e_i$ represents the ith unit vector. Now, the calculated quantities by Lanczos-bidiagonalization algorithm can be used to solve the least-squares problem:(10) $${\text{min}\Vert Ax-b\Vert }_2.$$(10)

Here, the solution has the form:(11) $$x^{(k)}=v_k{y}^{(k)},$$(11)

where the length of the vector y^(k) is k. Then, r^(k) = b − Ax is defined and by substitution we have:(12) $$r^{(k)}={\mathit{\beta }}_1{u}_1-A{V}_k{y}^{\left(k\right)}=U_{k+1}\left({\mathit{\beta }}_1{e}_1-B_k{y}^{\left(k\right)}\right).$$(12)

Let us define $t_{k+1}={\mathit{\beta }}_1{u}_1-B_k{y}^{(k)}$. Since $U_{k+1}$ has orthonormal columns, it can be concluded that $y^{\left(k\right)}$ should be chosen so that it minimizes $\Vert t_{k+1}{\Vert }_2$. Thus, the least-squares problem changes to:(13) $$\text{min}\Vert {\mathit{\beta }}_1{e}_1-B_k{y}^{(k)}{\Vert }_2.$$(13)

By standard QR factorization of Equation (13) we have:(14) $$Q_k\left[B_k{\mathit{\beta }}_1{e}_1\right]=\left[\begin{array}{cc}{R}_k\hfill & f_k\hfill \\ g_k^T\hfill & {\tilde{\mathit{\phi }}}_{k+1}\hfill \end{array}\right]=\left[\begin{array}{ccccccc}{\mathit{\rho }}_1\hfill & {\mathit{\theta }}_2\hfill & & & & & {\mathit{\phi }}_1\hfill \\ & {\mathit{\rho }}_2\hfill & {\mathit{\theta }}_3\hfill & & 0\hfill & & {\mathit{\phi }}_2\hfill \\ & & \ddots \hfill & \ddots \hfill & & & ⋮\hfill \\ & & & \ddots \hfill & \ddots \hfill & & ⋮\hfill \\ & 0\hfill & & & {\mathit{\rho }}_{k-1}\hfill & {\mathit{\theta }}_k\hfill & {\mathit{\phi }}_{k-1}\hfill \\ & & & & & {\mathit{\rho }}_k\hfill & {\mathit{\phi }}_k\hfill \\ g_{k1}\hfill & g_{k2}\hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill & g_{kk}\hfill & {\mathit{\phi }}_{k+1}\hfill \end{array}\right].$$(14)

Then, y^(k) and $t_{k+1}$ can be calculated as:(15) $$f_k=R_k{y}^{(k)},t_{k+1}=Q_k^T\left[\begin{array}{c}0\\ {\tilde{\mathit{\phi }}}_{k+1}\end{array}\right].$$(15)

Finally, by combining Equations (13) and (15) we have:(16) $$x^{(k)}=v_k{R}_k^{-1}{f}_k=D_k{f}_k.$$(16)

As it was stated before, L-LSQR is a semi-convergence method, which by further iteration may diverge from optimal solution. Therefore, defining the bound for k appropriately is an important issue.

3.3. Lanczos truncated total least-squares (L-TTLS)

When Lanczos-bidiagonalization method is combined and used along with TTLS, we call it as the Lanczos TTLS (L-TTLS) method. In L-TTLS algorithm (Morigi & Sgallari, 2001), starting with an initial vector, $u_1=b/{\Vert b\Vert }_2$, two sets of matrices V_k and $U_k$, and the $(k+1)\times k$ bidiagonal matrix, B_k, are produced after k iterations such that:

V_k = {v₁, v₂, …, v_k}, and U_k = {u₁, u₂, …, u_k+1}.

These matrices are related to each other by the subsequent equations:(17) $$A{V}_k=U_k{B}_k\text{and}b={\mathit{\beta }}_1{u}_1$$(17)

After k iterations, if k is large enough to include all singular values of the matrix A, the TLS problem can be projected into subspaces spanned by V_k and U_k.

The final form of the problem will be:(18) $$\text{min}\Vert B_k,{\mathit{\beta }}_1{e}_1-{\widehat{B}}_k,{\widehat{e}}_{(k)}{\Vert }_F,\text{subject}\text{to}{\widehat{B}}_{k}y={\widehat{e}}_{(k)},$$(18)

where ${\Vert .\Vert }_F$ denotes the Frobenius norm. Then TLS method is applied on a small sized matrix, which is the result of Lanczos-bidiagonalization process, in order to create the truncated TLS solution, namely, the TTLS solution. To calculate TTLS solution, SVD is applied on the matrix $(B_k={\mathit{\beta }}_1{u}_1)$:

(19) $$(B_k{\mathit{\beta }}_1{u}_1)={\overline{\overline{U}}}^{\left(k\right)}{\overline{\overline{\mathrm{\Sigma }}}}^{\left(k\right)}{\left({\overline{\overline{V}}}^{\left(k\right)}\right)}^T.$$(19)

The matrix ${\overline{\overline{V}}}^{(k)}$ is partitioned as noted below:(20) $$\overline{\overline{V}}=\left(\begin{array}{cc}{\overline{\overline{V}}}_{11}& {\overline{\overline{V}}}_{12}\\ {\overline{\overline{V}}}_{21}& {\overline{\overline{V}}}_{22}\end{array}\right),$$(20)

where ${\overline{\overline{V}}}_{11}\in {\mathbb{R}}^{(k-1)\times (k-1)}$, ${\overline{\overline{V}}}_{12}\in {\mathbb{R}}^{(k-1)\times 1}$, ${\overline{\overline{V}}}_{21}\in {\mathbb{R}}^{1\times (k-1)}$, and ${\overline{\overline{V}}}_{22}\in {\mathbb{R}}^{1\times 1}$.

Then the standard TLS solution can be defined as:(21) $${\overline{y}}_k=-{\overline{\overline{V}}}_{12}^{\left(k\right)}{\left({\overline{\overline{v}}}_{22}^{(k)}\right)}^{-1}.$$(21)

Finally, the solution is calculated as:(22) $$\tilde{x}=V_k{\overline{\overline{V}}}_{12}^{\left(k\right)}{\left({\overline{\overline{v}}}_{22}^{(k)}\right)}^{-1}.$$(22)

3.4. Regularization parameter selection method

The regularization parameters in this study are the λ parameter in Tikhonov regularization method and the truncation number k in L-LSQR and L-TTLS methods. In this study, Maximum Correlation Coefficient (MCC) method is used as a regularization parameter selection method, in which the corresponding parameter is selected so that the CC of the solution with the true potentials is maximized.

4. Lead reduction for body surface potential mapping (BSPM)

Inverse ECG has the potential to be a strong tool for clinical diagnosis of various heart diseases. However, for practical purposes, the number of attached electrodes on the body surface should be as small as possible considering their optimal configuration to acquire information as much as possible. Toward this end, numerous studies are conducted under “Lead Reduction” topic, each of which aims to reduce the number of attached electrodes to the body surface in a way that informative potential distribution on the torso surface would still be accurately detectable (Barr, Spach, & Herman-Giddens, 1971; Donnelly, Finlay, Nugent, & Black, 2008; Finlay et al., 2006; Lux, Smith, Wyatt, & Abildskov, 1978; Lux et al., 1979). The common aim in all these studies is to use a smaller number of electrodes than the nodes in the associated geometry model.

Beside the desired number of leads, the location of them on the surface of the body is of a great importance. For instance, the electrical activity of the heart is more detectable in the frontal region of the torso (Lux et al., 1978). Several lead-sets are used in this study, and the effects of reducing the number of leads are evaluated.

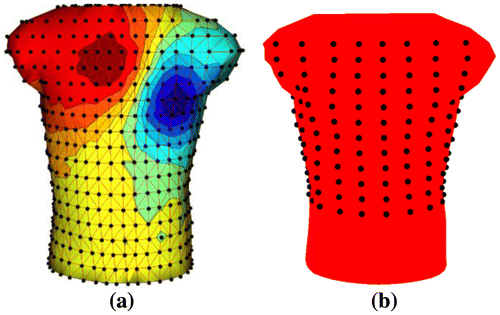
We start with a complete lead-set consisting of 771 electrodes (Figure 1(a)), then we reduce these leads to 192 leads as presented in (Lux et al., 1978) (Figure 1(b)). These 192 leads are from equally spaced electrodes (a 12 × 16 1electrode array) that cover the upper part of the body.

Figure 1. (a) 771 complete lead-set and (b) 192 lead-set.

To relate the reduced lead-set problems to the original problem in Equation (1), there should be a row-removal process which can be done by pre-multiplication of the forward matrix, A, by a selection matrix, S, which contains “1” in each row at the column number corresponding to the desired row of matrix A that will be selected, and zero elsewhere:(23) $$A_s=SA.$$(23)

Therefore, the corresponding 192, 64, and 32 rows of selected configurations are extracted from the original forward matrix, $A_{771\times 490}$, by removing the undesired rows. The same process should be applied to the data matrix, B, to obtain a reduced data matrix corresponding to the new reduced forward matrix (Ghodrati et al., 2007):(24) $$B_s=SB.$$(24)

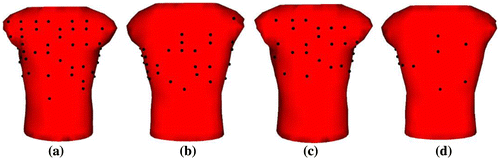
In this study, two approaches are considered to select 64 and 32 electrodes out of a larger number of electrodes. In the first approach, the desired number and the locations of the reduced-leads are manually selected from a larger lead set. We have two major selection criteria in this approach: the first one is to select electrodes only from the frontal region of the torso. The second, and the fundamental one is to select electrodes more densely between potential extrema on the torso (blue and red regions in Figure 1(a)), since this region contains significant information about the electrical activity of the heart and better represents the waveform pattern compared to other regions. The resulting lead-sets are shown in Figure 2, and referred to as 64 lead-set-I and 32-lead-set-I, respectively.

Figure 2. (a) 64-lead-set-I and (b) 32-lead-set-I.

Note: In this approach, reduced leads are manually selected from the frontal surface of the body.

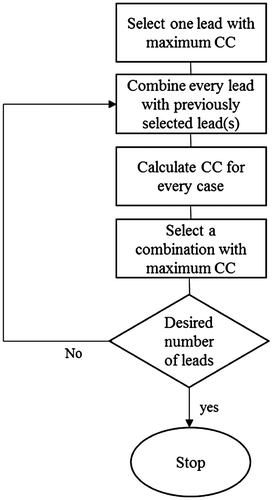
The second way for selecting reduced lead-sets employs an inverse problem solution approach, which results in 64 lead-set-II and 32 lead-set-II. In this approach, instead of the 771 complete lead-set, 192 lead-set configuration proposed by Lux et al. (1978) is considered as the primary lead-set, out of which we select 64 and 32 leads automatically. Thus, we start with a forward transfer matrix, A, of size 192 × 490, and a data matrix B of size 192 × 109, which contains the torso surface measurements. The process of selecting the optimal 64 or 32 leads out of these 192 leads is based on selecting only one optimal lead per iteration. In each iteration, the lead whose acquired signal gives the best inverse solution to the whole system is selected. To solve the related inverse problem, Tikhonov regularization along with maximum CC as regularization parameter selection method is used. In other words, in this method the lead selection process is addressed as a criterion of how well each individual electrode is able to reconstruct the epicardial potentials.

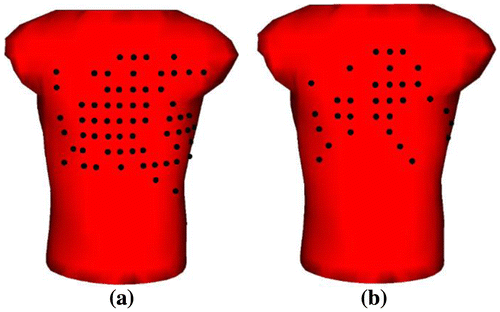
A flowchart for the reduced lead set selection steps is presented in Figure 3. At the first iteration step, the inverse problem is solved for each body surface potential measurement separately. The lead that yields the maximum CC in the inverse solution is then selected as the first lead for the reduced lead-set. At the second iteration step, each body surface lead (except the one that was already selected) is appended to the previously selected lead in sequence, and the combination leads (consisting of 2 leads) that yield the maximum CC in the solution compose the first two leads for the reduced lead-set. This iteration of appending one lead next to the previously selected leads and solving the inverse problem for maximum CC value is repeated until the desired number of leads are achieved. These reduced lead-sets are referred to as 64-lead-set-II and 32-lead-set-II, and their configurations are shown in Figure 4. Note that this is an automatic lead selection algorithm, which may yield frontal and back lead distributions.

Figure 3. Main steps of lead-selection approach.

Figure 4. (a) 64-lead-set-II front view, (b) 64-lead-set-II back view, (c) 32-lead-set-II front view, and (d) 32-lead-set-II back view.

5. Results

The epicardial potentials used for this study were measured at University of Utah Nora Eccles Harrison Cardiovascular Research and Training Institute (CVRTI) (MacLeod, Lux, & Taccardi, 1998). These epicardial measurements were taken from 490 points over the heart surface (epicardial surface) with a sampling rate of 1,000 samples per second and the forward transfer matrix is used to simulate 771 body surface potentials from epicardial potential measurements. We simulated the body surface potentials at 30 dB Signal to Noise Ratio (SNR). For this study, data from a single animal are included.

The goal here can be summarized in two parts:

(1)	We know from literature that reduced lead-sets also yield high-quality inverse solutions compared to larger data-sets, if an appropriate lead number and a suitable distribution can be selected. Here, we aim to study and compare the performances of two reduced lead-set selection algorithms, with each other and with the solutions that are based on the complete lead-set.
(2)	There are various regularization algorithms in literature used for solving the inverse ECG problem. Here we aim to compare two Lanczos bidiagonalization-based methods in terms of their performances when reduced lead-sets are used.

Correlation Coefficient (CC) and Relative Difference Measurement Star (RDMS) metrics are used as two quantitative criteria to compare the results of the three regularization algorithms with the true (experimentally obtained) epicardial potentials. Smaller values of RDMS indicate a higher quality of the answer, i.e. the regularized solution is closer to the real solution.

Here, the inverse problem is solved at all time instants using the three regularization methods for each lead-set combination, including the case where we include all 771 leads. Then, CC and RDMS values are calculated by comparing the true epicardial potentials with the reconstructed ones over the heart surface at each time instant. Table 1 includes averages and standard deviations over time of the calculated CC and RDMS values for different regularization methods and lead-set selections. It can be inferred that the L-TTLS method is able to reconstruct epicardial potentials better than the L-LSQR method. As the number of leads decreases, considering the average and standard deviation values of CC, the difference between the results of Tikhonov regularization and L-TTLS method becomes smaller. This indicates that by reducing the number of measurement sites on the torso, L-TTLS method acts more robust than the L-LSQR method. Clearly, 64 lead-set-II and 32-lead-set-II perform better than 64 lead-set-I and 32-lead-set-I, respectively. This is due to the process of selecting leads for 64 lead-set-II and 32-lead-set-II which is significantly more accurate than the manual selection scheme used for 64-lead-set-I and 32-lead-set-I cases. Similarly, by considering the values in the last column of Table 1, the average and standard deviation values of RDMS values for different regularization methods, it can be concluded that although the amount of RDMS values increase by reducing the number of measuring sites, there is no drastic change in these values. Therefore, it can be concluded that to reconstruct epicardial potentials, a large number of electrodes is unnecessary and similar results can be obtained using a small number of leads in an optimal configuration.

Table 1. Average and standard deviation values of CC and RDMS of different regularization methods for different lead-sets

Leads	Method	Avg ± std (CC)	Avg ± std (RDMS)
771	Tikhonov	0.7946 ± 0.1995	0.5488 ± 0.2333
	L-LSQR	0.7166 ± 0.2042	0.6840 ± 0.2432
	L-TTLS	0.7609 ± 0.2126	0.6069 ± 0.2623
192	Tikhonov	0.7793 ± 0.2006	0.5809 ± 0.2428
	L-LSQR	0.7296 ± 0.2032	0.6644 ± 0.2440
	L-TTLS	0.7614 ± 0.2100	0.6088 ± 0.2586
64-I	Tikhonov	0.7393 ± 0.2080	0.6435 ± 0.2359
	L-LSQR	0.7068 ± 0.2050	0.7026 ± 0.2390
	L-TTLS	0.7312 ± 0.2109	0.6602 ± 0.2512
64-II	Tikhonov	0.7406 ± 0.2233	0.6308 ± 0.2617
	L-LSQR	0.7036 ± 0.2195	0.6928 ± 0.2548
	L-TTLS	0.7317 ± 0.2270	0.6472 ± 0.2697
32-I	Tikhonov	0.7119 ± 0.2049	0.6911 ± 0.2299
	L-LSQR	0.6887 ± 0.1995	0.7332 ± 0.2302
	L-TTLS	0.7081 ± 0.2024	0.6991 ± 0.2369
32-II	Tikhonov	0.7329 ± 0.2232	0.6453 ± 0.2600
	L-LSQR	0.7104 ± 0.2200	0.6833 ± 0.2557
	L-TTLS	0.7294 ± 0.2231	0.6524 ± 0.2604

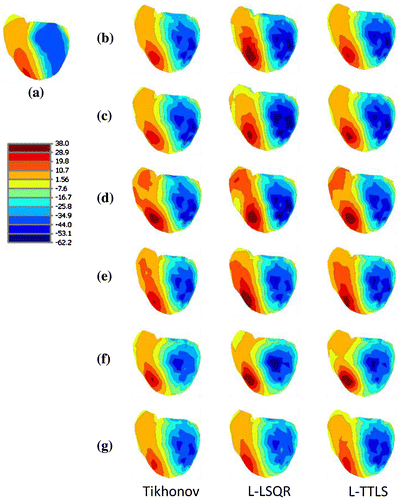
In order to assess the quality of the inverse solutions using reduced lead sets, we also plot the epicardial potential distributions (iso-potential maps) over the heart surface at a single time instant using the MAP3D visualization software (CIBC, 2016), represented in Figure 5. In this figure, the top row shows the true potential distribution at a single time instant and the remaining plots show solutions obtained by different methods and lead-sets. In these maps, the blue regions are the depolarized parts of the heart and the red regions correspond to tissue at rest. This figure shows that, the contours of the real epicardial potentials and 64 lead-set-II and 32-lead-set-II are very similar, indicating that the quality of the solutions of this reduced lead-set are significantly high. By looking at the wave-front form, again it can be concluded that the regularization results of 64 lead-set-II and 32-lead-set-II, especially for the L-TTLS method, have a higher quality than 64 lead-set-I and 32-lead-set-I. This validates that optimally selected 64 lead-set-II and 32-lead-set-II have the ability to reconstruct epicardial potentials better than 64 lead-set-I and 32-lead-set-I.

Figure 5. MAP3D results at t = 53 ms for Tikhonov regularization, L-LSQR, and L-TTLS methods. Panel (a) show true epicardial potential distribution. The remaining panels (in groups of 3 images) correspond to solutions with (b) 771 complete lead-set, (c) 192 lead-set, (d) 64 lead-set-I, (e) 64 lead-set-II, (f) 32 lead-set-I, and (g) 32 lead-set-II.

6. Conclusion

In this study, three regularization methods, namely, Tikhonov regularization, L-LSQR and L-TTLS, are employed to reconstruct potential distributions on the epicardial surface by solving the inverse problem of ECG. These regularization methods are applied to data corresponding to complete and reduced lead-sets. To compare the results of these regularization methods, average and standard deviation values of correlation coefficient (CC) and relative difference measurement star (RDMS) are calculated. Our results show that L-TTLS method performs better than L-LSQR. By assuming the results of Tikhonov regularization as a baseline, it can be concluded that as the number of measurement leads decreases, the difference between the reconstructed potentials using Tikhonov regularization and L-TTLS reduces. So it can be inferred that L-TTLS method is more robust and accurate than Tikhonov regularization method when the number of measurement sites is reduced. In fact, it would be beneficial to use methods that employ Lanczos-bidiagonalization as part of the regularization process to speed up the execution time. The short runtime is an important issue when dealing with big data matrices to solve ECG inverse problems (for example, inverse problems in terms of transmembrane potentials).

In many studies, in order to obtain electrical activity of the heart, a large number of leads are used. However, according to the results obtained in this study, there is no need to use a large number of leads to acquire signals on the surface of the body, and a small number of leads optimally located on the surface of the torso will be enough to estimate the potential distribution on the surface of the heart. Therefore, by employing a small number of measurement leads, electrical sources on the heart surface and correspondingly pathologies of the heart can be diagnosed and treated, since the inverse solution of ECG provides spatial and temporal information about the electrical activity of the heart.

As future work, we will apply the proposed lead-selection method in this study on a wider range of data with varying pacing sites on the epicardial surface. In this way, it would be possible to understand how the reduced lead-sets are affected from different propagation patterns of potentials on the heart, and to develop and introduce a generalized lead-set that produces good solutions for these different data.

Funding

This project (i.e. MAP3D) was supported by the National Institute of General Medical Sciences of the National Institutes of Health [grant number P41 GM103545-18].

Acknowledgments

The authors would like to thank Dr Robert S. Macleod from University of Utah (CVRTI and SCI Institute) for the data used in this study. This work was made possible in part by the MAP3D software.

Additional information

Notes on contributors

Fourough Gharbalchi

Yesim Serinagaoglu Dogrusoz is an associate professor of Electrical and Electronics Engineering at Middle East Technical University, and an affiliated member of the Institute of Applied Mathematics and Biomedical Engineering Graduate Program. Her research interests include forward/inverse problems in electrocardiography, cardiac electrical modeling, and electrocardiography signal processing.

Yesim Serinagaoglu Dogrusoz

Fourough Gharbalchi is currently a PhD student in biomedical engineering in the Middle East Technical University, Ankara, Turkey. Her research interests are statistical signal processing with particular focus on biomedical applications, forward and inverse problems of electrocardiography, modeling the electrical activity of the heart, video and image processing using Deep-Learning approach, and open-source software systems for these applications.

Gerhard Wilhelm Weber

Gerhard Wilhelm Weber is a professor at IAM, METU, Ankara, with research on OR, finance, optimization, data-mining, life-sciences. He received Diploma/Doctorate at RWTH Aachen, Habilitation at TU Darmstadt and held short professorships in Cologne/Chemnitz, and is “EURO conference-advisor” and chair of IFORS OR for Developing-Countries online-resources.