Trigonometric symmetric boundary value method for oscillating solutions including the sine-Gordon and Poisson equations

Abstract

We construct a continuous linear multistep method with trigonometric coefficients from which a symmetric main method as well as additional methods are reproduced. The main and additional methods whose coefficients depend on the frequency and step length are then applied as a trigonometric symmetric boundary value method (SBVM) to solve systems of second-order initial and boundary value problems of the form ${\mathbf{y}}^{″}=f(x,y)$ without first reducing the ordinary differential equation into an equivalent first-order system. Moreover, the method is successfully applied to solve hyperbolic and elliptic partial differential equations, such as the sine-Gordon and the Poisson equations. The stability property of the SBVM is discussed and numerical experiments are performed to show the accuracy of the method.

Keywords:

• symmetric boundary value methods
• trigonometric basis
• oscillating solutions
• hyperbolic and elliptic equations

AMS Subject Classifications:

• 65L05
• 65L06
• 65L12

Public Interest Statement

Traditionally, linear multistep methods are used to solve initial value problems in a step-by-step fashion in predictor-corrector mode since they are restricted by initial conditions. In this paper, a self-starting linear multistep method with trigonometric coefficients is presented and applied as a boundary value method to solve systems of second-order initial and boundary value problems as well as hyperbolic and elliptic partial differential equations, such as the sine-Gordon and the Poisson equations.

1. Introduction

In this paper, we consider the given system of second-order initial value problem (IVP)(1) $$\begin{array}{c}\hfill y^{″}=f(x,y),y(x_0)=y_0,y^{\prime }(x_0)=y_0^{\prime },x_0\le x\le x_N,\end{array}$$(1)

where $f:\mathfrak{R}\times {\mathfrak{R}}^d\to {\mathfrak{R}}^d$, $N>0$ is an integer, and d is the dimension of the system. We propose a symmetric boundary value method (SBVM) in which on the sequence of points $\{x_n\}$, defined by $x_n=x_0+nh,h>0$,  $n=0,1,\dots ,N$, the 4-step $[x_n,y_n]\mapsto [x_{n+4}=x_n+4h,y_{n+4}]$ is given by the main method(2) $$\begin{array}{c}\hfill y_{n+4}+{\mathit{\alpha }}_0{y}_n+{\mathit{\alpha }}_1{y}_{n+1}+{\mathit{\alpha }}_2{y}_{n+2}+{\mathit{\alpha }}_3{y}_{n+3}=h^2({\mathit{\beta }}_0{f}_n+{\mathit{\beta }}_1{f}_{n+1}+{\mathit{\beta }}_2{f}_{n+2}+{\mathit{\beta }}_3{f}_{n+3}+{\mathit{\beta }}_4{f}_{n+4}),\end{array}$$(2) $n=0,1,\cdots ,N-4,$ which is used together with two additional initial methods $(n=0)$ given by(3) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{y}_3={\widehat{\mathit{\alpha }}}_0{y}_0+{\widehat{\mathit{\alpha }}}_1{y}_1+{\widehat{\mathit{\alpha }}}_2{y}_2+h^2({\widehat{\mathit{\beta }}}_0{f}_0+{\widehat{\mathit{\beta }}}_1{f}_1+{\widehat{\mathit{\beta }}}_2{f}_2+{\widehat{\mathit{\beta }}}_3{f}_3+{\widehat{\mathit{\beta }}}_4{f}_4),\hfill \\ h{y}_0^{\prime }={\overline{\mathit{\alpha }}}_0{y}_0+{\overline{\mathit{\alpha }}}_1{y}_1+{\overline{\mathit{\alpha }}}_2{y}_2+h^2({\overline{\mathit{\beta }}}_0{f}_0+{\overline{\mathit{\beta }}}_1{f}_1+{\overline{\mathit{\beta }}}_2{f}_2+{\overline{\mathit{\beta }}}_3{f}_3+{\overline{\mathit{\beta }}}_4{f}_4),\hfill \end{array}\right.\end{array}$$(3)

and one additional boundary method given as(4) $$\begin{array}{c}\hfill y_{N-3}={\widehat{\mathit{\alpha }}}_0{y}_N+{\widehat{\mathit{\alpha }}}_1{y}_{N-1}+{\widehat{\mathit{\alpha }}}_2{y}_{N-2}+h^2({\widehat{\mathit{\beta }}}_0{f}_N+{\widehat{\mathit{\beta }}}_1{f}_{N-1}+{\widehat{\mathit{\beta }}}_2{f}_{N-2}+{\widehat{\mathit{\beta }}}_3{f}_{N-3}+{\widehat{\mathit{\beta }}}_4{f}_{N-4}),\end{array}$$(4)

where ${\mathit{\alpha }}_j,{\widehat{\mathit{\alpha }}}_j,{\overline{\mathit{\alpha }}}_j$, ${\mathit{\beta }}_j,{\widehat{\mathit{\beta }}}_j,{\overline{\mathit{\beta }}}_j$, $j=0,1,\dots ,4$ are coefficients that depend on the step length h and frequency w. The coefficients of the SBVM are chosen so that the method integrates the IVP (1) exactly where the solutions are members of the linear space $⟨1,x,x^2,x^3,x^4,x^5,sin(wx),cos(wx)⟩$.

The methods (2), (3), and (4) are combined and applied as boundary value methods (BVM) which discretize (1) and simultaneously solve the resulting system as given in Amodio, Golik, and Mazzia (1995), Amodio and Mazzia (1995), Brugnano and Trigiante (1998), and Ghelardoni and Marzulli (1995). However, these methods are applied to solve higher order IVPs by first reducing the problem into an equivalent first-order system. Nevertheless, it has been shown that solving (1) directly is preferable since about half of the storage space can be saved (see Coleman & Duxbury, 2000; D’Ambrosio, Ferro, & Paternoster, 2009; Franco, 2002; Hairer, 1982; Hairer, Nörsett, & Wanner, 1993; Ixaru & Berghe, 2004; Simos, 2002; Sommeijer, 1993; Tsitouras, 2006; Twizell & Khaliq, 1984).

It is well known that the solution of (1) has special properties and a reasonable amount of attention has been focused on developing methods that take advantage of these special properties of the solution that may be known in advance (see Coleman & Ixaru, 1996; Fang et al., 2009; Franco & Gomez, 2014; Nguyen, Sidje, & Cong, 2007; Ozawa, 2005; Simos, 1998; Vanden, Ixaru, & van Daele, 2001; Vigo-Aguiar & Ramos, 2003; Wua & Tian, 2014). Nevertheless, most of these methods are implemented in a step-by-step fashion.

Table 1. Results, with $\mathit{\omega }=5$, for Example 4.1

	SBVM	Wang (2005)
h	Err	Err
$\frac{\mathit{\pi }}{4}$	$2.4\times {10}^{-4}$	$1.8\times {10}^{-1}$
$\frac{\mathit{\pi }}{8}$	$2.2\times {10}^{-5}$	$9.0\times {10}^{-4}$
$\frac{\mathit{\pi }}{12}$	$9.9\times {10}^{-7}$	$5.0\times {10}^{-5}$
$\frac{\mathit{\pi }}{16}$	$1.4\times {10}^{-7}$	$8.0\times {10}^{-6}$

We remark that Amodio and Iavernaro (2006) proposed symmetric BVMs based on polynomial basis functions for special second-order ODEs of the Hamiltonian type. In this paper, we propose a trigonometric SBVM whose coefficients depend on the frequency and step length. The SBVM is applied to solve systems of second-order initial and boundary value problems of the form ${\mathbf{y}}^{″}=f(x,y)$ without first reducing the ordinary differential equation (ODE) into an equivalent first-order system. We also note that the trigonometric SBVM takes advantage of the special properties of the solution of (1) that may be known in advance.

The paper is organized as follows. In Section 2, the trigonometric SBVM is derived and its stability properties discussed. The computational aspects are given in Section 3 and numerical experiments are performed in Section 4. Finally, the conclusion of the paper is discussed in Section 5.

2. Derivation of the SBVM

We derive a continuous representation of (2) on the interval $[x_n,x_n+4h]$ by approximating the exact solution y(x) by the interpolating function(5) $$\begin{array}{c}\hfill Y(x)=\sum _{j=0}^7{\mathit{\eta }}_j{\mathrm{\Phi }}_j(x),\end{array}$$(5)

where ${\mathrm{\Phi }}_j(x)$ are members of the linear space $⟨1,x,x^2,x^3,x^4,x^5,sin(wx),cos(wx)⟩$ and ${\mathit{\eta }}_j,j=0,1,\dots ,7$ are coefficients which are determined by imposing the following conditions:(6) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}Y(x_{n+i})=y_{n+i},\hfill & i=0,1,2,\hfill \\ Y^{″}(x_{n+i})=f_{n+i},\hfill & i=0,1,\dots ,4.\hfill \end{array}\right.\end{array}$$(6)

Thus, Equation (6) leads to a system of eight equations which is solved to obtain ${\mathit{\eta }}_j$. The continuous approximation is then constructed by substituting the values of ${\mathit{\eta }}_j$ into Equation (5) to yield(7) $$\begin{array}{c}\hfill Y(x)=\sum _{j=0}^3{\mathit{\alpha }}_j(x)y_{n+j}+h^2\sum _{j=0}^4{\mathit{\beta }}_j(x)f_{n+j},\end{array}$$(7)

whose first derivative is given by(8) $$\begin{array}{c}\hfill Y^{\prime }(x)=\frac{\text{d}}{\text{d}x}\left(\sum _{j=0}^3{\mathit{\alpha }}_j(x)y_{n+j}+h^2\sum _{j=0}^4{\mathit{\beta }}_j(x)f_{n+j}\right),\end{array}$$(8)

where ${\mathit{\alpha }}_j(x)$ and ${\mathit{\beta }}_j(x)$ are continuous coefficients. We assume that $y_{n+j}=Y(x_n+jh)$ is the numerical approximation to the analytical solution $y(x_{n+j})$, $y_n^{\prime }=Y^{\prime }(x_n)$ is an approximation to $y^{\prime }(x_n)$, and $f_{n+j}=Y^{″}(x_n+jh)$ is an approximation to $y^{″}(x_{n+j})$.

We specify the coefficients of the main method (2) and the first member of (3) by evaluating (7) at $x=x_{n+4}$ and $x=x_{n+3}$, respectively, whereas the coefficients of the second member of (3) are specified by evaluating (8) $x=x_n$. We note that the method (4) is the additional boundary method obtained from (3) by obvious notational modifications. In particular, $y_{n+4}=Y(x_n+4h)$, $y_{n+3}=Y(x_n+3h)$, and $y_n^{\prime }=Y^{\prime }(x_n)$ yield methods (2), (3), and (4) whose coefficients and their corresponding Taylor series equivalence are given as follows:(9) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathit{\alpha }}_0\hfill & =1,{\mathit{\alpha }}_1=0,{\mathit{\alpha }}_2=-2,{\mathit{\alpha }}_3=0,{\mathit{\alpha }}_4=1,\hfill \\ {\mathit{\beta }}_0\hfill & =-\frac{(-3+2u^2+4u^{2}cos(u)+3cos(2u))csc{(u/2)}^4}{24u^2},\hfill \\ \hfill & =\frac{1}{15}+\frac{2u^2}{945}+\frac{u^4}{56700}-\frac{u^6}{415800}-\frac{167u^8}{833976000}-\frac{2633u^{10}}{245188944000},\hfill \\ {\mathit{\beta }}_1\hfill & =\frac{(-3+5u^2+(3+u^2)cos(2u))csc{(u/2)}^4)}{6u^2},\hfill \\ \hfill & =\frac{16}{15}-\frac{8u^2}{945}-\frac{u^4}{14175}+\frac{u^6}{103950}+\frac{167u^8}{208494000}+\frac{2633u^{10}}{61297236000},\hfill \\ {\mathit{\beta }}_2\hfill & =\frac{(9-20u^{2}cos(u)+(-9+2u^2)cos(2u))csc{(u/2)}^4}{12u^2},\hfill \\ \hfill & =\frac{26}{15}+\frac{4u^2}{315}+\frac{u^4}{9450}-\frac{u^6}{69300}-\frac{167u^8}{138996000}-\frac{2633u^{10}}{40864824000},\hfill \\ {\mathit{\beta }}_3\hfill & =\frac{(-3+5u^2+(3+u^2)cos(2u))csc{(u/2)}^4}{6u^2},\hfill \\ \hfill & =\frac{16}{15}-\frac{8u^2}{945}-\frac{u^4}{14175}+\frac{u^6}{103950}+\frac{167u^8}{208494000}+\frac{2633u^{10}}{61297236000},\hfill \\ {\mathit{\beta }}_4\hfill & =-\frac{(-3+2u^2+4u^{2}cos(u)+3cos(2u))csc{(u/2)}^4}{24u^2},\hfill \\ \hfill & =\frac{1}{15}+\frac{2u^2}{945}+\frac{u^4}{56700}-\frac{u^6}{415800}-\frac{167u^8}{833976000}-\frac{2633u^{10}}{245188944000}).\hfill \end{array}\right.\end{array}$$(9)  (10) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\widehat{\mathit{\alpha }}}_0\hfill & =0,{\widehat{\mathit{\alpha }}}_1=-1,{\widehat{\mathit{\alpha }}}_2=2,\hfill \\ {\widehat{\mathit{\beta }}}_0\hfill & =-\frac{(-12+5u^2+(12+u^2)cos(u))csc{(u/2)}^4}{96u^2},\hfill \\ \hfill & =-\frac{1}{240}-\frac{31u^2}{60480}-\frac{67u^4}{1814400}-\frac{109u^6}{53222400}-\frac{18127u^8}{186810624000}-\frac{64931u^{10}}{15692092416000},\hfill \\ {\widehat{\mathit{\beta }}}_1\hfill & =\frac{(-48+23u^2+48cos(u)+u^{2}cos(2u))csc{(u/2)}^4}{96u^2},\hfill \\ \hfill & =\frac{1}{10}+\frac{31u^2}{15120}+\frac{67u^4}{453600}+\frac{109u^6}{13305600}+\frac{18127u^8}{46702656000}+\frac{64931u^{10}}{3923023104000},\hfill \\ {\widehat{\mathit{\beta }}}_2\hfill & =\frac{(36-(36+23u^2)cos(u)+5u^{2}cos(2u))csc{(u/2)}^4}{48u^2},\hfill \\ \hfill & =\frac{97}{120}-\frac{31u^2}{10080}-\frac{67u^4}{302400}-\frac{109u^6}{8870400}-\frac{18127u^8}{31135104000}-\frac{64931u^{10}}{2615348736000},\hfill \\ {\widehat{\mathit{\beta }}}_3\hfill & =\frac{(-48+23u^2+48cos(u)+u^{2}cos(2u))csc{(u/2)}^4}{96u^2},\hfill \\ \hfill & =\frac{1}{10}+\frac{31u^2}{15120}+\frac{67h^2{u}^4}{453600}+\frac{109u^6}{13305600}+\frac{18127u^8}{46702656000}+\frac{64931u^{10}}{3923023104000},\hfill \\ {\widehat{\mathit{\beta }}}_4\hfill & =-\frac{(-12+5u^2+(12+u^2)cos(u))csc{(u/2)}^4}{96u^2},\hfill \\ \hfill & =-\frac{1}{240}-\frac{31u^2}{60480}-\frac{67u^4}{1814400}-\frac{109u^6}{53222400}-\frac{18127u^8}{186810624000}-\frac{64931u^{10}}{15692092416000}.\hfill \end{array}\right.\end{array}$$(10)  (11) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\overline{\mathit{\alpha }}}_0\hfill & =\frac{-180+203u^2+127u^{2}cos(u)+180ucos(2u)csc(u)}{30(-12+5u^2+(12+u^2)cos(u))},\hfill \\ \hfill & =-\frac{149}{42}-\frac{16u^2}{245}-\frac{1324u^4}{169785}-\frac{559246u^6}{695269575}-\frac{14310311u^8}{175207932900}-\frac{170868550903u^{10}}{20641246574949000},\hfill \\ {\overline{\mathit{\alpha }}}_1\hfill & =\frac{4((-45+28u^2)cos(u)+u(32u+45cos(2u)csc(u)))}{15(-12+5u^2+(12+u^2)cos(u))},\hfill \\ \hfill & =\frac{128}{21}+\frac{32u^2}{245}+\frac{2648u^4}{169785}+\frac{1118492u^6}{695269575}+\frac{14310311u^8}{87603966450}+\frac{170868550903u^{10}}{10320623287474500},\hfill \\ {\overline{\mathit{\alpha }}}_2\hfill & =\frac{-180-53u^2+(360-97u^2)cos(u)-180ucos(2u)csc(u)}{30(-12+5u^2+(12+u^2)cos(u))},\hfill \\ \hfill & =-\frac{107}{42}-\frac{16u^2}{245}-\frac{1324u^4}{169785}-\frac{559246u^6}{695269575}-\frac{14310311u^8}{175207932900}-\frac{170868550903u^{10}}{20641246574949000},\hfill \\ {\overline{\mathit{\beta }}}_0\hfill & {=-(csc(u/2)}^{5}sec(u/2)(1080u+180u(-12+7u^2)cos(u)-90u(-12+5u^2)cos(2u)\hfill \\ \hfill & +360u^{3}cos(3u)-90u^{3}cos(4u)+2160sin(u)-6624u^{2}sin(u)+1418u^{4}sin(u)-1080sin(2u)\hfill \\ \hfill & +5340u^{2}sin(2u)-850u^{4}sin(2u)-2220u^{2}sin(3u)+214u^{4}sin(3u)\hfill \\ \hfill & +381u^{2}sin(4u)))/(5760u^2(-12+5u^2+(12+u^2)cos(u))),\hfill \\ \hfill & =-\frac{67}{1260}+\frac{1241u^2}{198450}+\frac{277961u^4}{366735600}+\frac{26460409u^6}{333729396000}+\frac{1363374533u^8}{168199615584000}+\frac{16323847966961u^{10}}{19815596711951040000},\hfill \\ {\overline{\mathit{\beta }}}_1\hfill & {=(csc(u/2)}^{5}sec(u/2)(2160u+630u^3-4320ucos(u)+720u(3+4u^2)cos(2u)\hfill \\ \hfill & -1800u^{3}cos(3u)+450u^{3}cos(4u)+4320sin(u)+2964u^{2}sin(u)+198u^{4}sin(u)-2160sin(2u)\hfill \\ \hfill & -6162u^{2}sin(2u)+710u^{4}sin(2u)+3228u^{2}sin(3u)-442u^{4}sin(3u)-621u^{2}sin(4u)\hfill \\ \hfill & +107u^{4}sin(4u)))/(2880u^2(-12+5u^2+(12+u^2)cos(u))),\hfill \\ \hfill & =\frac{188}{105}+\frac{5078u^2}{99225}+\frac{556159u^4}{91683900}+\frac{51834031u^6}{83432349000}+\frac{67782373u^8}{1078202664000}+\frac{1854079193287u^{10}}{291405833999280000},\hfill \\ {\overline{\mathit{\beta }}}_2\hfill & {=-(csc(u/2)}^{5}sec(u/2)(6480u+450u^3+1440u(-9+4u^2)cos(u)+6480ucos(2u)\hfill \\ \hfill & +360u^{3}cos(3u)-90u^{3}cos(4u)+12960sin(u)-9612u^{2}sin(u)+1544u^{4}sin(u)-6480sin(2u)\hfill \\ \hfill & +1458u^{2}sin(2u)+376u^{4}sin(2u)+108u^{2}sin(3u)-27u^{2}sin(4u)\hfill \\ \hfill & -34u^{4}sin(4u)))/(5760u^2(-12+5u^2+(12+u^2)cos(u))),\hfill \\ \hfill & =\frac{31}{90}+\frac{341u^2}{33075}+\frac{79361u^4}{61122600}+\frac{23456627u^6}{166864698000}+\frac{1228061399u^8}{84099807792000}+\frac{14797833720283u^{10}}{9907798355975520000},\hfill \\ {\overline{\mathit{\beta }}}_3\hfill & =-\frac{(90-31u^2+u^{2}cos(2u)-90ucot(u))csc{(u/2)}^4}{360u^2},\hfill \\ \hfill & =-\frac{4}{105}-\frac{46u^2}{14175}-\frac{809u^4}{1871100}-\frac{27827u^6}{567567000}-\frac{637171u^8}{122594472000}-\frac{33500737u^{10}}{62523180720000},\hfill \\ {\overline{\mathit{\beta }}}_4\hfill & =\frac{(45-17u^2+2u^{2}cos[u]-45ucot[u])csc{[u/2]}^4}{720u^2},\hfill \\ \hfill & =\frac{1}{252}+\frac{23u^2}{28350}+\frac{809u^4}{7484400}+\frac{27827u^6}{2270268000}+\frac{637171u^8}{490377888000}+\frac{33500737u^{10}}{250092722880000}.\hfill \end{array}\right.\end{array}$$(11)

Definition 2.1

The method (2) is said to be symmetric if ${\mathit{\alpha }}_j={\mathit{\alpha }}_{k-j},{\mathit{\beta }}_j={\mathit{\beta }}_{k-j},j=0,1,\dots ,k$ (see Lambert & Watson, 1976).

2.1. Order and local truncation error

The algebraic order of each method is given by the integer $p=6$.

We define the local truncation errors (LTEs) of (2) and (3) specified by the coefficients (5), (6), and (7) as(12) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathit{\phi }}_1[y(x_n);h]\hfill & =y(x_n+4h)+{\mathit{\alpha }}_{0}y(x_n+{\mathit{\alpha }}_{1}y(x_n+h)+{\mathit{\alpha }}_{2}y(x_n+2h)+{\mathit{\alpha }}_{3}y(x_n+3h)\hfill \\ \hfill & -h^2({\mathit{\beta }}_0{y}^{″}(x_n+{\mathit{\beta }}_1{y}^{″}(x_n+h)+{\mathit{\beta }}_2{y}^{″}(x_n+2h)+{\mathit{\beta }}_3{y}^{″}(x_n+3h)+{\mathit{\beta }}_4{y}^{″}(x_n+4h)),\hfill \\ {\mathit{\phi }}_2[y(x_n);h]\hfill & =y(x_n+3h)-({\widehat{\mathit{\alpha }}}_{0}y(x_n+{\widehat{\mathit{\alpha }}}_{1}y(x_n+h)+{\widehat{\mathit{\alpha }}}_{2}y(x_n+2h)+h^2({\widehat{\mathit{\beta }}}_0{y}^{″}(x_n\hfill \\ \hfill & +{\widehat{\mathit{\beta }}}_1{y}^{″}(x_n+h)+{\widehat{\mathit{\beta }}}_2{y}^{″}(x_n+2h)+{\widehat{\mathit{\beta }}}_3{y}^{″}(x_n+3h)+{\widehat{\mathit{\beta }}}_4{y}^{″}(x_n+4h))),\hfill \\ {\mathit{\phi }}_3[y(x_n);h]\hfill & =h{y}^{\prime }(x_n)-({\overline{\mathit{\alpha }}}_{0}y(x_n+{\overline{\mathit{\alpha }}}_{1}y(x_n+h)+{\overline{\mathit{\alpha }}}_{2}y(x_n+2h)+h^2({\overline{\mathit{\beta }}}_0{y}^{″}(x_n+{\overline{\mathit{\beta }}}_1{y}^{″}(x_n+h)\hfill \\ \hfill & +{\overline{\mathit{\beta }}}_2{y}^{″}(x_n+2h)+{\overline{\mathit{\beta }}}_3{y}^{″}(x_n+3h)+{\overline{\mathit{\beta }}}_4{y}^{″}(x_n+4h))).\hfill \end{array}\right.\end{array}$$(12)

Assuming that y(x) is sufficiently differentiable, we can expand the terms in ${\mathit{\phi }}_1$, ${\mathit{\phi }}_2$, and ${\mathit{\phi }}_3$ as a Taylor series about the point $x_n$ to obtain the expressions for the LTEs as$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathit{\phi }}_1[y(x_n);h]\hfill & =-\frac{2h^8}{945}(w^2{y}^{(6)}(x_n)+y^{(8)}(x_n))+O(h^9),\hfill \\ {\mathit{\phi }}_2[y(x_n);h]\hfill & =\frac{31h^8}{60480}(w^2{y}^{(6)}(x_n)+y^{(8)}(x_n))+O(h^9),\hfill \\ {\mathit{\phi }}_3[y(x_n);h]\hfill & =-\frac{43h^8}{39690}(w^2{y}^{(6)}(x_n)+y^{(8)}(x_n))+O(h^9).\hfill \end{array}\right.\end{array}$$

Remark 2.2

We note that for small values of u, the trigonometric coefficients are vulnerable and subject to heavy cancelation; hence, the Taylor series coefficients must be used (see Simos, 2002). Moreover, the main method is symmetric and reduces to the sixth-order conventional LMM as $u\to 0$.

2.2. Stability

The linear stability of the SBVM is discussed by applying the method to the test equation $y^{″}=-{\mathit{\lambda }}^{2}y$, where $\mathit{\lambda }$ is real. Letting $\mathrm{{\rm Y}}=\mathit{\lambda }h$, it is easily shown that the application of the symmetric method (2) specified by (9) to the test equation yields the characteristic equation which is simplified and solved to obtain the roots as follows:(13) $$\begin{array}{cc}\hfill ({\mathrm{{\rm Y}}}^2{\mathit{\beta }}_0+1)+{\mathrm{{\rm Y}}}^2{\mathit{\beta }}_{1}r+{\mathrm{{\rm Y}}}^2{\mathit{\beta }}_2-2r^2+{\mathrm{{\rm Y}}}^2{\mathit{\beta }}_3{r}^3+({\mathrm{{\rm Y}}}^2{\mathit{\beta }}_4+1)r^4)& =0,\hfill \\ \hfill 1+\frac{{\mathit{\beta }}_1}{{\mathit{\beta }}_4+1}r+(\frac{{\mathrm{{\rm Y}}}^2{\mathit{\beta }}_2-2}{{\mathit{\beta }}_4+1})r^2+\frac{{\mathit{\beta }}_1}{{\mathit{\beta }}_4+1}{r}^3+r^4& =0,\hfill \\ \hfill 1+Ar+B{r}^2+A{r}^3+r^4& =0,\hfill \end{array}$$(13)

where $A=\frac{{\mathit{\beta }}_1}{{\mathit{\beta }}_4+1}$, $B=\frac{{\mathrm{{\rm Y}}}^2{\mathit{\beta }}_2-2}{{\mathit{\beta }}_4+1}.$

In the spirit of Dai, Wang, and Wu (DWW) (2006), letting $Z=1/r+r$, (13) becomes$$\begin{array}{c}\hfill Z^2+AZ+B-2=0,\end{array}$$

which is solved to give the roots $r_1,r_2$, where for $\mathrm{\Theta }=(-A-\sqrt{8+A^2-4B})/4$, $r_1=\mathrm{\Theta }+i\sqrt{1-{\mathrm{\Theta }}^2}$ and $r_1=\mathrm{\Theta }-i\sqrt{1-{\mathrm{\Theta }}^2}$.

Definition 2.3

The SBVM is said to have an interval of periodicity $(0,{\mathrm{{\rm Y}}}_0^2)$ if the roots $r_1$ and $r_2$ are distinct and lie on the unit circle for all ${\mathrm{{\rm Y}}}^2\mathit{ϵ}(0,{\mathrm{{\rm Y}}}_0^2)$ (see Coleman & Ixaru, 1996).

Remark 2.4

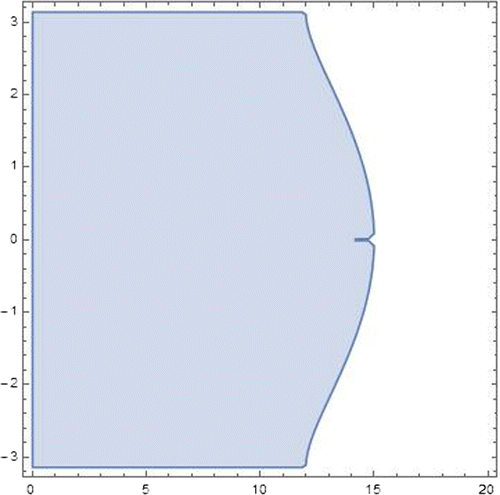
The periodicity condition is met by imposing that $|\mathrm{\Theta }|\le 1$ and it is observed that in the ${\mathrm{{\rm Y}}}^2-u$ plane, the SBVM has an interval of periodicity ${\mathrm{{\rm Y}}}^2\mathit{ϵ}(0,15)$ for $u\mathit{ϵ}[-\mathit{\pi },\mathit{\pi }]$ (see Figure 1).

Figure 1. The stability region for the SBVM plotted in the (${\mathrm{{\rm Y}}}^2$, u)-plane.

3. Computational aspects

In this section, we implement the SBVM in the sense of Amodio and Iavernaro (2006), Amodio et al. (1995), Amodio and Mazzia (1995), and Brugnano and Trigiante (1998). The methods (2), (3), and (4) are applied as a BVM which discretizes the problem using the SBVM and simultaneously solves the resulting system. Specifically, the discretization of (1) using$$\begin{array}{c}\hfill y_{n+4}+{\mathit{\alpha }}_0{y}_n+{\mathit{\alpha }}_1{y}_{n+1}+{\mathit{\alpha }}_2{y}_{n+2}+{\mathit{\alpha }}_3{y}_{n+3}=h^2({\mathit{\beta }}_0{f}_n+{\mathit{\beta }}_1{f}_{n+1}+{\mathit{\beta }}_2{f}_{n+2}+{\mathit{\beta }}_3{f}_{n+3}+{\mathit{\beta }}_4{f}_{n+4}),\end{array}$$$n=0,1,\dots ,N-4$, leads to $N-3$ equations and N unknowns, which give an indeterminate system. This situation is fixed using the main method together with the following two additional initial methods $(n=0)$ given by(14) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{y}_3\hfill & ={\widehat{\mathit{\alpha }}}_0{y}_0+{\widehat{\mathit{\alpha }}}_1{y}_1+{\widehat{\mathit{\alpha }}}_2{y}_2+h^2({\widehat{\mathit{\beta }}}_0{f}_0+{\widehat{\mathit{\beta }}}_1{f}_1+{\widehat{\mathit{\beta }}}_2{f}_2+{\widehat{\mathit{\beta }}}_3{f}_3+{\widehat{\mathit{\beta }}}_4{f}_4),\hfill \\ h{y}_0^{\prime }\hfill & ={\overline{\mathit{\alpha }}}_0{y}_0+{\overline{\mathit{\alpha }}}_1{y}_1+{\overline{\mathit{\alpha }}}_2{y}_2+h^2({\overline{\mathit{\beta }}}_0{f}_0+{\overline{\mathit{\beta }}}_1{f}_1+{\overline{\mathit{\beta }}}_2{f}_2+{\overline{\mathit{\beta }}}_3{f}_3+{\overline{\mathit{\beta }}}_4{f}_4),\hfill \end{array}\right.\end{array}$$(14)

and one additional boundary method given as$$\begin{array}{c}\hfill y_{N-3}={\widehat{\mathit{\alpha }}}_0{y}_N+{\widehat{\mathit{\alpha }}}_1{y}_{N-1}+{\widehat{\mathit{\alpha }}}_2{y}_{N-2}+h^2({\widehat{\mathit{\beta }}}_0{f}_N+{\widehat{\mathit{\beta }}}_1{f}_{N-1}+{\widehat{\mathit{\beta }}}_2{f}_{N-2}+{\widehat{\mathit{\beta }}}_3{f}_{N-3}+{\widehat{\mathit{\beta }}}_4{f}_{N-4}),\end{array}$$

where the coefficients are specified by (9), (10), and (11). The resulting system is then simultaneously solved using the SBVM to provide the values of the solution generated by the sequences $\{y_n\},n=0,\dots ,N$, where the system of equations is solved while adjusting for boundary conditions. The SBVM was implemented using a code written in Mathematica 10.0 enhanced by the feature $NSolve[]$ for linear problems, while nonlinear problems were solved by the Newton’s method enhanced by the feature $FindRoot[]$.

3.1. Estimating the frequency

A classical procedure for estimating the frequency is not available; however, some techniques for estimating the frequency are given in Ramos and Vigo-Aguiar (2010), Ixaru, Vanden Berghe, and De Meyer (2002). A preliminary testing indicates that a good estimate of the frequency can be obtained by demanding that ${\mathit{\phi }}_1=0$, and solving for the frequency. In particular, solve for $\mathit{\omega }$ given that$$\begin{array}{c}\hfill -\frac{2h^8}{945}(w^2{y}^{(6)}(x_n)+y^{(8)}(x_n))=0,\end{array}$$

where $y^{(j)}=\frac{{\text{d}}^{j}y}{\text{d}{x}^j},j=6,8$ are jth derivative, $D=\frac{\text{d}}{\text{d}x}$ is a differential operator, and w is assumed to be a constant. We estimate the frequency by imposing that(15) $$\begin{array}{c}\hfill (w^2+D^2)y=0,\end{array}$$(15)

and solving for w at $x=x_n$. We implemented this procedure on Example 4.5 and obtained $w=10$ which is in agreement with the known frequency. Nevertheless, the subject needs further investigation and will be the subject of our future research.

4. Numerical examples

In this section, we have tested the SBVM on some numerical examples using a constant step size to illustrate its accuracy and efficiency. We have calculated the error of the approximate solution as $\text{Err}=\text{Max}|y(x_n)-y_n|$. It is worth noting that the number of function evaluations (NFEs) per step involved in implementing the SBVM is one since the method avoids the predictor-corrector mode implementation which requires two function evaluations per step due to the introduction of a predictor.

Example 4.1

We consider the following IVP by Wang (2005).$$\begin{array}{c}\hfill y^{″}+{\mathit{\omega }}^{2}y=12cos(x),y(0)=1,y^{\prime }(0)=0,\mathit{\omega }=5,x\in [0,500\mathit{\pi }]\end{array}$$

where the analytic solution is given by$$\begin{array}{c}\hfill \text{Exact}:y(x)=(cos(5x)+cos(x))/2.\end{array}$$

The exponentially fitted method in Wang (2005) is of order six and hence comparable to the sixth-order SBVM. It is obvious from Table 1 that SBVM is more accurate than the method in Wang (2005).

Example 4.2

We consider the nonlinear Duffing equation which was also solved by Simos (1998) and Ixaru and Berghe (2004).$$\begin{array}{c}\hfill y^{″}+y+y^3=Bcos(\mathrm{\Omega }x),y(0)=C_0,y^{\prime }(0)=0.\end{array}$$

The analytic solution is given by$$\begin{array}{c}\hfill \text{Exact}:y(x)=C_{1}cos(\mathrm{\Omega }x)+C_{2}cos(3\mathrm{\Omega }x)+C_{3}cos(5\mathrm{\Omega }x)+C_{4}cos(7\mathrm{\Omega }x),\end{array}$$

where $\mathrm{\Omega }=1.01,B=0.002,C_0=0.200426728069,C_1=0.200179477536,C_2=0.246946143\times {10}^{-3},C_3=0.304016\times {10}^{-6},C_4=0.374\times {10}^{-9}.$ We choose $\mathit{\omega }=1.01$

 

Table 2. Results, with $\mathit{\omega }=1.01$, for Example 4.2

SBVM		Simos		Ixaru et al.
N	Err	N	Err	N	Err
50	$2.2\times {10}^{-4}$	300	$1.7\times {10}^{-3}$	300	$1.1\times {10}^{-3}$
100	$5.2\times {10}^{-7}$	600	$1.9\times {10}^{-4}$	600	$5.4\times {10}^{-5}$
200	$9.3\times {10}^{-9}$	1,200	$1.4\times {10}^{-5}$	1,200	$1.9\times {10}^{-6}$
400	$1.1\times {10}^{-10}$	2,400	$8.7\times {10}^{-7}$	2,400	$6.2\times {10}^{-8}$

In Table 2, we show that the SBVM uses fewer NFEs and is more accurate than the methods in Simos (1998) and Ixaru et al. (2004).

Example 4.3

We consider the nonlinear system of second-order IVP (see Nguyen et al., 2007)$$\begin{array}{c}\hfill y_1^{″}={(y_1-y_2)}^3+6368y_1-6384y_2+42cos(10x),y_1(0)=0.5,y_1^{\prime }(0)=0,\\ \hfill y_1^{″}& =-{(y_1-y_2)}^3+12768y_1-12784y_2+42cos(10x),y_2(0)=0.5,y_2^{\prime }(0)=0,x\mathit{ϵ}[0,10],\hfill \end{array}$$

with exact solution $y_1(x)=y_2(x)=cos(4x)-cos(4x)/2$.

 

Table 3. Results, with $\mathit{\omega }=4$, for Example 4.3

TIRK3		RADAU5		EFRK43		SBVM
NFEs	Err	NFEs	Err	NFEs	Err	NFEs	Err
907	$2.5\times {10}^{-4}$	853	$2.2\times {10}^{-4}$	2,057	$3.7\times {10}^{-4}$	801	$2.6\times {10}^{-7}$
1,288	$6.6\times {10}^{-6}$	1,208	$4.4\times {10}^{-4}$	1,715	$3.0\times {10}^{-4}$	1,201	$1.6\times {10}^{-8}$
1,682	$7.0\times {10}^{-6}$	1,639	$6.0\times {10}^{-6}$	3,079	$2.7\times {10}^{-5}$	1,601	$2.8\times {10}^{-9}$

This problem was chosen to demonstrate the performance of the SBVM on a nonlinear system. It is seen from Table 3 that SBVM performs better than those in Nguyen et al. (2007) in terms of accuracy and efficiency.

Example 4.4

We consider the stiff second-order IVP (see Nguyen et al., 2007)$$\begin{array}{cc}\hfill y_1^{″}& =(\mathit{\epsilon }-2)y_1+(2\mathit{\epsilon }-2)y_2,y_2^{″}=(1-\mathit{\epsilon })y_1+(1-2\mathit{\epsilon })y_2,\hfill \\ \hfill y_1(0)& =2,y_1^{\prime }(0)=0,y_2(0)=-1,y_2^{\prime }(0)=0,\mathit{\epsilon }=2500,x\mathit{ϵ}[0,100].\hfill \end{array}$$$y_1(x)=2cosx,y_2(x)=-cosx$, where $\mathit{\epsilon }$ is an arbitrary parameter and $w=1$.

This problem was chosen to demonstrate the performance of the SBVM on a linear stiff system. It is seen from Table 4 that SBVM performs better than those in Nguyen et al. (2007) in terms of accuracy and efficiency.

Table 4. Results, with $\mathit{\omega }=1$, for Example 4.4

SBVM			TIRK3
N	Err	NFEs	N	Err	NFEs
10	$1.4\times {10}^{-12}$	22	73	$3.3\times {10}^{-12}$	327
20	$3.2\times {10}^{-12}$	42	142	$9.0\times {10}^{-12}$	707
40	$8.0\times {10}^{-12}$	82	170	$3.7\times {10}^{-12}$	811

Example 4.5

We consider the following IVP by Dai et al. (2006).$$\begin{array}{c}\hfill y^{″}+{\mathit{\omega }}^{2}y=0,y(0)=1,y^{\prime }(0)=0,x\in [0,10\mathit{\pi }],\end{array}$$

where the analytic solution is given by$$\begin{array}{c}\hfill \text{Exact}:y(x)=cos(\mathit{\omega }x).\end{array}$$

 

Table 5. Results, with $\mathit{\omega }=10$, for Example 4.5

	SBVM	Dai et al. (2006)
x	$\text{Err}(h=\mathit{\pi }/4)$	$\text{Err}(h=\mathit{\pi }/12)$
$\mathit{\pi }$	$5.55\times {10}^{-16}$	$2.22\times {10}^{-15}$
$2\mathit{\pi }$	$9.99\times {10}^{-16}$	$1.78\times {10}^{-15}$
$4\mathit{\pi }$	$6.66\times {10}^{-16}$	$7.55\times {10}^{-15}$
$6\mathit{\pi }$	$7.77\times {10}^{-16}$	$8.88\times {10}^{-15}$
$8\mathit{\pi }$	$8.88\times {10}^{-16}$	$9.77\times {10}^{-15}$
$10\mathit{\pi }$	$2.22\times {10}^{-16}$	$4.44\times {10}^{-16}$

It is shown in Table 5 that the SBVM is more accurate than the exponentially fitted method in Wang (2005) which is also of order six.

Example 4.6

Consider the singularly perturbed BVP that was also solved in El-Gamel (2012)(16) $$\begin{array}{cc}& \left\{\begin{array}{cc}\mathit{ϵ}{y}_1^{″}+x^2{y}_1-2x{y}_2\hfill & =-2\mathit{ϵ}+4x^3(1-x)-2xsin(\mathit{\pi }x),y_1(0)=0,y_1(1)=0,\hfill \\ \mathit{ϵ}{y}_2^{″}+x^2{y}_2+x^2{y}_1\hfill & =-\mathit{ϵ}{\mathit{\pi }}^{2}sin(\mathit{\pi }x)+x^{2}sin(\mathit{\pi }x)+4x^3(1-x),y_2(0)=0,y_2(1)=0,\hfill \end{array}\right.\hfill \\ \hfill & \text{Exact}:y_1(x)=x-x^2,y_2(x)=sin(\mathit{\pi }x).\hfill \end{array}$$(16)

 

Table 6. Absolute errors for $y_1$-components, with $N=40,\mathit{\omega }=1$, for Example 4.6

	SBVM	El-Gamel (2012)
$\mathit{ϵ}$	Err	Err
${10}^{-2}$	$5.62\times {10}^{-11}$	$1.59\times {10}^{-7}$
${10}^{-3}$	$1.35\times {10}^{-11}$	$8.43\times {10}^{-7}$
${10}^{-6}$	$5.90\times {10}^{-13}$	$1.49\times {10}^{-6}$
${10}^{-8}$	$2.08\times {10}^{-13}$	$4.78\times {10}^{-7}$
${10}^{-10}$	$1.02\times {10}^{-12}$	$1.73\times {10}^{-6}$

This problem was chosen to demonstrate the performance of the SBVM on a singularly perturbed two-point boundary value system. It is seen from Table 6 that SBVM is more accurate than the method in El-Gamel (2012).

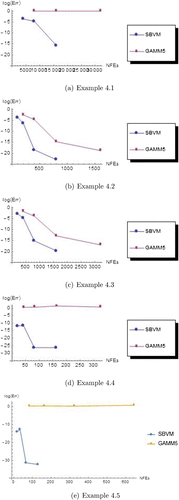
4.1. Comparison of SBVM and GAMM6

We further discuss the superiority of the SBVM over the generalized Adams–Moulton method (GAMM6) given in Brugnano and Trigiante (1998). The GAMM6 was chosen for comparison with the SBVM because it is also of order six and has been applied as a BVM. The efficiency curves for the two methods are given in Figure 2 for Examples 4.1 to 4.5.

Figure 2. Efficiency curves for Examples 4.1–4.5.

4.2. Hyperbolic PDEs

Example 4.7

We consider the following one-dimensional nonlinear sine-Gordon equation given in Dehghan and Shokri (2008).$$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}-sin(u),-3<x<3,0<t<1,\hfill \\ \hfill u(x,0)& =4arctan(e^{\frac{x}{\sqrt{1-C^2}}}),\hfill \\ \hfill u_t(x,0)& =-\frac{4C{e}^{\frac{x}{\sqrt{1-C^2}}}}{\sqrt{1-C^2}(1+e^{2\frac{x}{\sqrt{1-C^2}}})}.\hfill \end{array}$$

The exact solution is given by $u(x,t)=4arctan(\text{sech}(x)t)$, C is the velocity of the solitary wave, and the boundary conditions are given accordingly. The problem is solved for $C=0.5$, $\mathrm{\Delta }t=0.125$, and $\mathrm{\Delta }x=0.04$. The results for the first component are given in Table 7. In order to solve this PDE using the SBVM, we carry out the semi-discretization of the spatial variable x using the second-order finite difference method to obtain the following second-order system in the second variable t.(17) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{{\mathit{\partial }}^2{u}_m}{\mathit{\partial }{t}^2}-\frac{(u_{m+1}-2u_m+u_{m-1})}{{(\mathrm{\Delta }x)}^2}=g_m,\hfill & 0<t<1,=m=1,\dots ,M-1,\hfill \\ u(x_m,0)=u_m,\hfill & u_t(x_m,0)=u_m^{\prime },\hfill \end{array}\right.\end{array}$$(17)

where $\mathrm{\Delta }x=(b-a)/M$, $x_m=a+m\mathrm{\Delta }x$, $m=0,1,\dots ,M$, $\mathbf{u}={[u_1(t),\dots ,u_M(t)]}^T$, $\mathbf{g}={[g_1(t),\dots ,g_m(t)]}^T$, $u_m(t)\approx u(x_m,t)$ and $g_m(t)\approx g(x_m,t)=sin(u_m)$, which can be written in the form(18) $$\begin{array}{c}\hfill {\mathbf{u}}^{″}=\mathbf{f}(t,u),\end{array}$$(18)

subject to the boundary conditions $\mathbf{u}(t_0)={\mathbf{u}}_0,{\mathbf{u}}^{\prime }(t_0)={\mathbf{u}}_0^{\prime }$

where $\mathbf{f}(t,u)=Au+g$, and A is an $M-1\times M-1$, matrix arising from the semi-discretized system, and $\mathit{g}$ is a vector of constants (Figure 3).  

Table 7. Results, with $\mathit{\omega }=10$, for Example 4.7

x	SBVM	Exact	Err
0.125	0.121956	0.121956	$1.30\times {10}^{-7}$
0.25	0.113469	0.113469	$2,94\times {10}^{-7}$
0.375	0.105573	0.105572	$4.51\times {10}^{-7}$
0.5	0.0982256	0.0982249	$6.49\times {10}^{-7}$
0.625	0.0913892	0.0913884	$8.41\times {10}^{-7}$
0.75	0.0850284	0.0850273	$1.03\times {10}^{-6}$
0.875	0.0791101	0.0791088	$1.25\times {10}^{-6}$
1.00	0.0736035	0.0736021	$1.44\times {10}^{-6}$

Figure 3. Graphical evidence for Example 4.7.

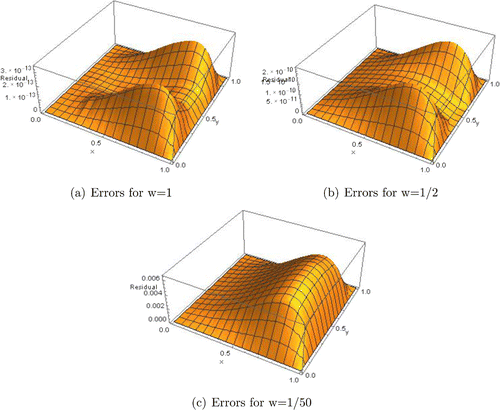
Example 4.8

We consider the wave equation given in Franco (1995).

A problem representing a vibrating string with speed $\mathit{\omega }$ is given by(19) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}-x(1-x)\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+({\mathit{\omega }}^2-2)u=0,0<x<1,0<t\le 5,\hfill \\ u(0,t)=0,u(1,t)=0,u(x,0)=x(1-x),u_t(x,0)=0.\hfill \end{array}\right.\end{array}$$(19)

where the initial and Dirichlet boundary conditions have been chosen such that the solution is given by $u(x,t)=x(1-x)cos\mathit{\omega }t$. In order to solve this PDE using the SBVM, we carry out the semi-discretization of the spatial variable x using the second-order finite difference method to obtain the following second-order system in the second variable t (Figures 4 and 5).(20) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{{\mathit{\partial }}^2{u}_m}{\mathit{\partial }{t}^2}-x_m(1-x_m)+\frac{(u_{m+1}-2u_m+u_{m-1})}{{(\mathrm{\Delta }x)}^2}+({\mathit{\omega }}^2-2)u_m=g_m,\hfill & m=1,\dots ,M-1,\hfill \\ u(x_m,0)=x_m(1-x_m),\hfill & u_t(x_m,0)=0,0<t\le 5,\hfill \end{array}\right.\end{array}$$(20)

where $\mathrm{\Delta }x=(b-a)/M$, $x_m=a+m\mathrm{\Delta }x$, $m=0,1,\dots ,M$, $\mathbf{u}={[u_1(t),\dots ,u_M(t)]}^T$, $\mathbf{g}={[g_1(t),\dots ,g_m(t)]}^T$, $u_m(t)\approx u(x_m,t)$ and $g_m(t)\approx g(x_m,t)=0$, which can be written in the form(21) $$\begin{array}{c}\hfill {\mathbf{u}}^{″}=\mathbf{f}(t,u),\end{array}$$(21)

subject to the boundary conditions $\mathit{u}(t_0)={\mathbf{u}}_0,{\mathit{u}}^{\mathbf{\prime }}(t_0)={\mathbf{u}}_0^{\prime }$ where $\mathit{f}\mathbf{(}\mathit{t}\mathbf{,}\mathit{u}\mathbf{)}\mathbf{=}\mathit{A}\mathit{u}\mathbf{+}\mathit{g}$, and A is an $M-1\times M-1$ matrix arising from the semi-discretized system, and $\mathbf{g}$ is a vector of constants.

Figure 4. Graphical evidence for Example 4.8.

4.3. Elliptic PDEs

In this section, the performance of a block extension of the LMM is tested on four problems, which include the Poisson equation, Laplace equation subject to Neumann boundary conditions, and Laplace equation subject to Dirichlet boundary conditions.

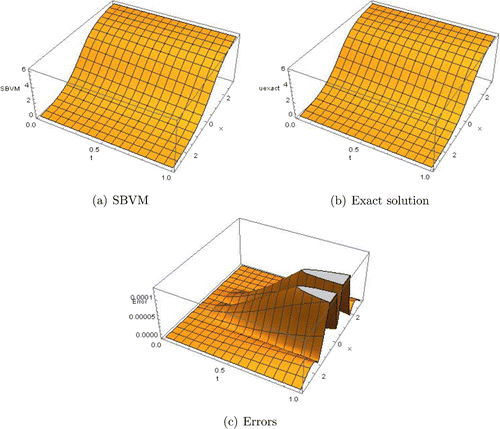
Example 4.9

We solve the given Poisson equation (see Xu & Wang, 2011)(22) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}=2(3x+x^2+y^2),\hfill & (x,y)\mathit{ϵ}\mathrm{\Omega }=[0,1]\times [0,1],\hfill \\ u(x,y)=x^2(x+y^2)+2,\hfill & (x,y)\mathit{ϵ}\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}\right.\end{array}$$(22)

The exact solution is given by $u(x,y)=x^2(x+y^2)+2$. In order to solve this PDE using the SBVM, we carry out the semi-discretization of the spatial variable x using the second-order finite difference method to obtain the following second-order system in the second variable y.(23) $$\begin{array}{c}\hfill \frac{{\text{d}}^2{u}_m}{\text{d}{y}^2}+\frac{(u_{m+1}-2u_m+u_{m-1})}{{(\mathrm{\Delta }x)}^2}=g(x_m,y),m=1,\dots ,M-1,\end{array}$$(23)

where $\mathrm{\Delta }x=(b-a)/M$, $x_m=a+m\mathrm{\Delta }x$, $m=0,1,\dots ,M$, $\mathbf{u}={[u_1(y),\dots ,u_{M-1}(y)]}^T$, $\mathbf{g}={[g_1(y),\dots ,g_m(y)]}^T$, $u_m(y)\approx u(x_m,y)$ and $g_m(y)\approx g(x_m,y)=2(3x_m+x_m^2+y^2)$, which can be written in the form(24) $$\begin{array}{c}\hfill {\mathbf{u}}^{″}=\mathbf{f}(y,u),\end{array}$$(24)

subject to the boundary conditions $\mathit{u}(y_0)={\mathit{u}}_0,\mathit{u}(y_N)={\mathit{u}}_N$, where $\mathit{f}\mathbf{(}\mathit{y}\mathbf{,}\mathit{u}\mathbf{)}\mathbf{=}\mathit{A}\mathit{u}\mathbf{+}\mathit{g}$, and $\mathit{A}$ is an $M-1\times M-1$ matrix arising from the semi-discretized system, and $\mathit{g}$ is a vector of constants.

Figure 5. Graphical evidence for Example 4.9.

5. Conclusion

We have proposed a continuous linear multistep method with trigonometric coefficients from which a symmetric main method as well as additional methods are reproduced and applied as a SBVM to solve systems of second-order initial and boundary value problems of the form ${\mathbf{y}}^{″}=f(x,y)$, without first reducing the system into an equivalent first order. Moreover, the method is successfully applied to solve hyperbolic and elliptic partial differential equations, such as the sine-Gordon and the Poisson equations. The convergence and stability properties of the SBVM are discussed. Numerical experiments are performed to show the accuracy of the method.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

S.N. Jator

S.N. Jator is currently a professor of Mathematics and the chair of the Department of Mathematics and Statistics, Austin Peay State University, Clarksville, Tennessee, U.S.A. His research interests include Numerical Analysis, Mathematical Biology, Ordinary and Partial Differential Equations, Financial Mathematics, and Predictive Analytics.