Optical solitons in a power-law media with fourth-order dispersion by three integration methods

Abstract

In this paper, the extended trial equation method, the $exp(-\mathrm{\Omega }(\eta ))$-expansion method and the $tan(\varphi (\eta )/2)$-expansion method are used in examining the analytical solution of the non-linear Schrödinger equation (NLSE) with fourth-order dispersion. The proposed methods are based on the integration method and a wave transformation. The NLSE with fourth-order dispersion is an equation that arises in soliton radiation, soliton communications with dispersion caused by the hindrance in presence of higher order dispersion terms. We successfully get some solutions with the kink structure.

Keywords:

• The non-linear Schrödinger equation with fourth-order dispersion
• The extended trial equation method
• The $exp(-\mathrm{\Omega }(\eta ))$-expansion method
• The $tan(\varphi (\eta )/2)$-expansion method

AMS Subject Classifications:

• 02.60.Lj
• 02.70.Wz
• 02.90.+p
• 04.30.Nk

Public Interest Statement

In the present paper, the extended trial equation method, the $exp(-\mathrm{\Omega }(\eta ))$-expansion method and the $tan(\varphi (\eta )/2)$-expansion method are used in examining the analytical solution of the non-linear Schrodinger equation (NLSE) with fourth-order dispersion. The proposed methods are based on the integration method and a wave transformation. The NLSE with fourth-order dispersion is an equation that arises in soliton radiation, soliton communications with dispersion caused by the hindrance in presence of higher order dispersion terms. We successfully get some solutions with the kink structure.

1. Introduction

Searching for the new analytical solutions to non-linear evolution equations (NEEs) plays a vital role in the study of non-linear physical aspects. Non-linear evolution equation are often used to express complex models that arise in the various fields of non-linear sciences, such as; plasma physics, quantum mechanics, biological sciences and so on.

There are many non-linear physical phenomena in nature that are described by non-linear equations of partial differential equations. Nowadays, with rapid development of symbolic computation systems, the search for the exact solutions of non-linear equations of PDEs has attracted a lot of attention. Recently, a variety of approaches has been proposed and applied to the non-linear equations of PDEs, including the Exp-function method (Ekici, Mirzazadeh, Sonmezoglu, Zhou, Triki, Ullah, & Biswas, 2017; Manafian, 2015; Manafian & Lakestani, 2015a), the generalized Kudryashov method (Zhou, Ekici, Sonmezoglu, Manafian, Khaleghizadeh, & Mirzazadeh, 2016), the extended Jacobi elliptic function expansion method (Ekici, Zhou, Sonmezoglu, Manafian, & Mirzazadeh, 2017; Mirzazadeh, Ekici, Sonmezoglu, Ortakaya, Eslami, & Biswas, 2016), the improve $tan(\varphi /2)$-expansion method (Manafian, 2016; Manafian, 2017; Manafian & Lakestani, 2016a, b; Manafian, Lakestani, & Bekir, 2016), the $G^{\prime }/G$-expansion method (Manafian & Lakestani, 2015b; Manafian & Lakestani, 2017; Sindi & Manafian, 2016), the generalized $G^{\prime }/G$-expansion method (Zinati & Manafian, 2017), the Bernoulli sub-equation function method (Baskonus, 2017; Bulut & Baskonus, 2016; Baskonus & Bulut, 2016a; Baskonus, Koç, & Bulut, 2016), the sine-Gordon expansion method (Baskonus, 2016; Baskonus & Bulut, 2016b; Baskonus, Bulut, & Atangana, 2016; Yel, Baskonus, & Bulut, 2017), the Ricatti equation expansion (Inc, Kilic, & Baleanu, 2016; Zhou, 2016), the formal linearization method (Mirzazadeh & Eslami, 2015), the Lie symmetry (Tchier, Yusuf, Aliyu, & Inc, 2017) and so on.

Extended trial equation method is one of the robust techniques to look for the exact solutions of non-linear partial differential equations that has received special interest owing to its fairly great performance. For example, Mohyud-Din and Irshad (2017) explored new exact solitary wave solutions of some non-linear PDEs arising in electronics using the extended trial equation method. Mirzazadeh et al. (2017) adopted he extended trial equation method to obtain analytical solutions to the generalized resonant dispersive non-linear Schrödinger’s equation with power law nonlinearity. Ekici et al. (2017) found the exact soliton solutions to magneto-optic waveguides that appear with Kerr, power and log-law nonlinearities using the extended trial equation method.

This paper will adopt three integration schemes that are known as the extended trial equation method, the $exp(-\mathrm{\Omega }(\eta ))$-expansion method, and the $tan(\varphi (\eta )/2)$-expansion method that will reveal soliton solutions as well as other solutions. The system for the model is studied here to investigate exact solution structures. We note that this system has not yet been studied using the afore-mentioned methods.

The rest of the paper is ordered as follows: Analysis of model is presented in Section 2. In Sections 3, 4, and 5, the extended trial equation method, the $exp(-\mathrm{\Omega }(\eta ))$-expansion method, and the $tan(\varphi (\eta )/2)$-expansion method are given. Application of methods are given in sections . In Sections 6, 7, and 8, applications of the NLSE with fourth-order dispersion are given and derived exact solutions. Finally, the conclusion is given in Section 9.

2. Analysis of model

In this section, we briefly outline the model used in this study. The dimensionless form of the NLSE with fourth-order dispersion (Kohl & Biswas, 2017; Kohl, Biswas, Milovic, & Zerrad, 2008; Wazwaz, 2006) is given by:(2.1) $$\begin{array}{c}\hfill i{q}_t+a{q}_{\mathit{xx}}-b{q}_{\mathit{xxxx}}+c{|q|}^{2m}q=0,\end{array}$$(2.1)

where a, b, and c represent, respectively, the coefficients of group velocity dispersion, fourth-OD term and power-law nonlinearity. The 1-soliton solution of Equation (2.1) is given by the following:(2.2) $$\begin{array}{c}\hfill q(x,t)=u(x,t)e^{i\varphi (x,t)},\end{array}$$(2.2)

in which u(x, t) and $\varphi (x,t)$ represent, respectively, amplitude and phase component of the soliton. Applying the phase component of the soliton(2.3) $$\begin{array}{c}\hfill \varphi (x,t)=-kx+wt+\theta ,\end{array}$$(2.3)

where k is the frequency of the soliton, w is the wave number, while $\theta$ is the phase constant, obtain the following terms with the help of (2.2) and (2.3)(2.4) $$\begin{array}{c}\hfill i{q}_t=(i{u}_t-u{\varphi }_t)e^{i\varphi },\end{array}$$(2.4) (2.5) $$\begin{array}{c}\hfill q_{\mathit{xx}}=(u_{\mathit{xx}}-2ik{u}_x-k^{2}u)e^{i\varphi },\end{array}$$(2.5) (2.6) $$\begin{array}{c}\hfill q_{\mathit{xxxx}}=(u_{\mathit{xxxx}}-4ik{u}_{\mathit{xxx}}-6k^2{u}_{\mathit{xx}}+4i{k}^3{u}_x+k^{4}u)e^{i\varphi }.\end{array}$$(2.6)

By substituting (2.4)–(2.6) and decomposing into real and imaginary parts gives(2.7) $$\begin{array}{c}\hfill \mathbf{R}ealpart:(w+a{k}^2+b{k}^4)u-c{u}^{2m+1}-(a+6b{k}^2)u_{\mathit{xx}}+b{u}_{\mathit{xxxx}}=0,\end{array}$$(2.7) (2.8) $$\begin{array}{c}\hfill \mathbf{I}maginarypart:u_t-2k(a+2b{k}^2)u_x+4bk{u}_{\mathit{xxx}}=0.\end{array}$$(2.8)

Via the transformation $\eta =B(x-vt)$, Equations (2.7) and (2.8) are reduced to the following non-linear ODEs:(2.9) $$\begin{array}{c}\hfill (w+a{k}^2+b{k}^4)u-c{u}^{2m+1}-B^2(a+6b{k}^2)u^{″}+b{B}^4{u}^{″″}=0,\end{array}$$(2.9) (2.10) $$\begin{array}{c}\hfill -Bv{u}^{\prime }-2kB(a+2b{k}^2)u^{\prime }+4bk{B}^3{u}^{″\prime }=0.\end{array}$$(2.10)

After integrating Equation (2.10) respect to $\eta$ and simplification, we get the following non-linear ordinary differential equation:(2.11) $$\begin{array}{c}\hfill -(v+2k(a+2b{k}^2))u+4bk{B}^2{u}^{″}=0,\end{array}$$(2.11)

or(2.12) $$\begin{array}{c}\hfill u^{″}=\frac{v+2k(a+2b{k}^2)}{4bk{B}^2}u.\end{array}$$(2.12)

By inserting (2.12) into Equation (2.9), then it yields(2.13) $$\begin{array}{c}\hfill \left[(w+a{k}^2+b{k}^4)-\frac{(a+6b{k}^2)(v+2k(a+2b{k}^2))}{4bk{B}^2}\right]u-c{u}^{2m+1}+b{B}^4{u}^{″″}=0.\end{array}$$(2.13)

Utilizing the balance principle technique, between $u^{2m+1}$ and $u^{″″}$, we obtain the following relationship as:(2.14) $$\begin{array}{c}\hfill (2m+1)M=M+4\Rightarrow M=\frac{2}{m},\end{array}$$(2.14)

using the following transformation:(2.15) $$\begin{array}{c}\hfill u(\eta )=U{(\eta )}^{\frac{2}{m}},\end{array}$$(2.15)

Equation (2.13) reduced to the following ODE:(2.16) $$\begin{array}{c}\hfill -c{m}^{4}u{U}^8+\left[w+a{k}^2+b{k}^4-\frac{(a+6b{k}^2)(v+2k(a+2b{k}^2))}{4bk{B}^2}\right]m^4{U}^4-4b{B}^4(m-1)(m-2)(3m-2){(U^{\prime })}^4+\end{array}$$(2.16) $$24B^4(2bm-3b{m}^2+b{m}^3)U{U}^{\prime 2}{U}^{″}-6B^{4}b{m}^2(m-2)U^2{(U^{″})}^2-8B^{4}b{m}^2(m-2)U^2{U}^{\prime }{U}^{″\prime }+2B^{4}b{m}^3{U}^3{U}^{″″}=0.$$

3. Extended trial equation method

The current method described here is the extended trial equation method which was utilized to find traveling wave solutions of LPD model which can be understood through the following steps:

Step 1. We assume that the given non-linear PDE(3.1) $$\begin{array}{c}\hfill \mathcal{N}(u,u_x,u_t,u_{\mathit{xx}},u_{\mathit{tt}},...)=0.\end{array}$$(3.1)

Utilizing the wave transformation(3.2) $$\begin{array}{c}\hfill u(x_1,x_2,...,x_N,t)=u(\eta ),\eta =k\left(\sum _{j=1}^N{x}_j-\lambda t\right),\end{array}$$(3.2)

where $\lambda \ne 0$ and $c\ne 0$. Substituting (3.2(3.2) $$\begin{array}{c}\hfill u(x_1,x_2,...,x_N,t)=u(\eta ),\eta =k\left(\sum _{j=1}^N{x}_j-\lambda t\right),\end{array}$$(3.2) ) into Equation (3.1) yields a non-linear ordinary differential equation,(3.3) $$\begin{array}{c}\hfill \mathcal{Q}(u,k{u}^{\prime },-k\lambda u^{\prime },k^2{u}^{″},k^2{\lambda }^2{u}^{″},...)=0.\end{array}$$(3.3) Step 2. Take the transformation and trial equation as follows:(3.4) $$\begin{array}{c}\hfill u(\eta )=\sum _{i=0}^{\delta }{\tau }_i{\mathrm{\Gamma }}^i,\end{array}$$(3.4)

where(3.5) $$\begin{array}{c}\hfill {({\mathrm{\Gamma }}^{\prime })}^2=\mathrm{\Omega }(\mathrm{\Gamma })=\frac{\mathrm{\Phi }(\mathrm{\Gamma })}{\mathrm{\Psi }(\mathrm{\Gamma })}=\frac{{\xi }_{\theta }{\mathrm{\Gamma }}^{\theta }+...+{\xi }_1\mathrm{\Gamma }+{\xi }_0}{{\zeta }_{ϵ}{\mathrm{\Gamma }}^{ϵ}+...+{\zeta }_1\mathrm{\Gamma }+{\zeta }_0}.\end{array}$$(3.5)

Using the Equations (3.4) and (3.5), we can find(3.6) $$\begin{array}{c}\hfill {(u^{\prime })}^2=\frac{\mathrm{\Phi }(\mathrm{\Gamma })}{\mathrm{\Psi }(\mathrm{\Gamma })}{\left(\sum _{i=0}^{\delta }i{\tau }_i{\mathrm{\Gamma }}^{i-1}\right)}^2,\end{array}$$(3.6) (3.7) $$\begin{array}{c}\hfill u^{″}=\frac{{\mathrm{\Phi }}^{\prime }(\mathrm{\Gamma })\mathrm{\Psi }(\mathrm{\Gamma })-\mathrm{\Phi }(\mathrm{\Gamma }){\mathrm{\Psi }}^{\prime }(\mathrm{\Gamma })}{2{\mathrm{\Psi }}^2(\mathrm{\Gamma })}\left(\sum _{i=0}^{\delta }i{\tau }_i{\mathrm{\Gamma }}^{i-1}\right)+\frac{\mathrm{\Phi }(\mathrm{\Gamma })}{\mathrm{\Psi }(\mathrm{\Gamma })}\left(\sum _{i=0}^{\delta }i(i-1){\tau }_i{\mathrm{\Gamma }}^{i-2}\right),\end{array}$$(3.7)

where $\mathrm{\Phi }(\mathrm{\Gamma })$ and $\mathrm{\Psi }(\mathrm{\Gamma })$ are polynomials. Substituting these terms into Equation (3.1) yields an equation of polynomial $\mathrm{\Lambda }(\mathrm{\Gamma })$ of $\mathrm{\Gamma }$:(3.8) $$\begin{array}{c}\hfill \mathrm{\Lambda }(\mathrm{\Gamma })={\varrho }_s{\mathrm{\Gamma }}^s+...+{\varrho }_1\mathrm{\Gamma }+{\varrho }_0=0.\end{array}$$(3.8)

By utilizing the balance principle on (3.8), we can determine a relation of $\theta ,ϵ$ and $\delta$. We can take some values of $\theta ,ϵ$ and $\delta$.

Step 3. Setting each coefficient of polynomial $\mathrm{\Lambda }(\mathrm{\Gamma })$ to zero to derive a system of algebraic equations:(3.9) $$\begin{array}{c}\hfill {\varrho }_i=0,i=1,2,...,s.\end{array}$$(3.9)

By solving the system (3.9(3.9) $$\begin{array}{c}\hfill {\varrho }_i=0,i=1,2,...,s.\end{array}$$(3.9) ), we will obtain the values of ${\xi }_0,{\xi }_1,...,{\xi }_{\theta }$, ${\zeta }_0,{\zeta }_1,...,{\zeta }_{\sigma }$ and ${\tau }_0,{\tau }_1,...,{\tau }_{\delta }$.

Step 4. In the following step, we obtain the elementary form of the integral by reduction of Equation (3.5), as follows:(3.10) $$\begin{array}{c}\hfill \pm (\eta -{\eta }_0)=\int \frac{d\mathrm{\Gamma }}{\sqrt{\mathrm{\Omega }(\mathrm{\Gamma })}}=\int \sqrt{\frac{\mathrm{\Psi }(\mathrm{\Gamma })}{\mathrm{\Phi }(\mathrm{\Gamma })}}d\mathrm{\Gamma },\end{array}$$(3.10)

where ${\eta }_0$ is an arbitrary constant.

4. The $exp(-\mathrm{\Omega }(\eta ))$-Expansion Method

In this section, we describe the $exp(-\mathrm{\Omega }(\eta ))$-expansion method which was utilized to find traveling wave solutions of non-linear partial differential equations. This approach is based on the $exp(-\mathrm{\Omega }(\eta ))$-expansion method (Khan & Akbar, 2014; Rayhanul Islam et al., 2015). We consider the following steps:

Step 1. We suppose that given non-linear partial differential equation for u(x, t) to be in the form:(4.1) $$\begin{array}{c}\hfill \mathcal{N}(u,u_x,u_t,u_{\mathit{xx}},u_{\mathit{tt}},...)=0,\end{array}$$(4.1)

which can be converted to an ODE(4.2) $$\begin{array}{c}\hfill \mathcal{Q}(U,B{U}^{\prime },-Bv{U}^{\prime },B^2{U}^{″},B^2{v}^2{U}^{″},...)=0,\end{array}$$(4.2)

by the transformation $\eta =B(x-vt)$ is the wave variable. Also, B and v are constants to be determined later.

Step 2. We suppose the solution of non-linear equation (4.2(4.2) $$\begin{array}{c}\hfill \mathcal{Q}(U,B{U}^{\prime },-Bv{U}^{\prime },B^2{U}^{″},B^2{v}^2{U}^{″},...)=0,\end{array}$$(4.2) ) can be expressed by a rational polynomial in $F(\eta )$ as the following:(4.3) $$\begin{array}{c}\hfill U(\eta )=\sum _{j=0}^M{\xi }_j{F}^j(\eta ),\end{array}$$(4.3)

where $F(\eta )=exp(-\mathrm{\Omega }(\eta ))$ and ${\xi }_j(0\le j\le M)$, are constants to be determined, such that ${\xi }_M\ne 0$, and, $\mathrm{\Omega }=\mathrm{\Omega }(\eta )$ satisfies the following ordinary differential;(4.4) $$\begin{array}{c}\hfill {\mathrm{\Omega }}^{\prime }=\mu F^{-1}(\eta )+F(\eta )+\lambda .\end{array}$$(4.4)

The following exact analytical solutions (Hafez, Alam, & Akbar, 2015; Hafez, Nur Alam, & Akbar, 2014) can be considered from Equation (4.4):

Solution-1: If $\mu \ne 0$ and ${\lambda }^2-4\mu >0,$ then we have(4.5) $$\begin{array}{c}\hfill \mathrm{\Omega }(\eta )=ln\left(-\frac{\sqrt{{\lambda }^2-4\mu }}{2\mu }tanh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\eta +E)\right)-\frac{\lambda }{2\mu }\right),\end{array}$$(4.5)

where E is integral constant.

Solution-2: If $\mu \ne 0$ and ${\lambda }^2-4\mu <0,$ then we have(4.6) $$\begin{array}{c}\hfill \mathrm{\Omega }(\eta )=ln\left(\frac{\sqrt{-{\lambda }^2+4\mu }}{2\mu }tan\left(\frac{\sqrt{-{\lambda }^2+4\mu }}{2}(\eta +E)\right)-\frac{\lambda }{2\mu }\right).\end{array}$$(4.6) Solution-3: If $\mu =0$, $\lambda \ne 0,$ and ${\lambda }^2-4\mu >0,$ then we get(4.7) $$\begin{array}{c}\hfill \mathrm{\Omega }(\eta )=-ln\left(\frac{\lambda }{exp(\lambda (\eta +E))-1}\right).\end{array}$$(4.7) Solution-4: If $\mu \ne 0$, $\lambda \ne 0,$ and ${\lambda }^2-4\mu =0,$ then we get(4.8) $$\begin{array}{c}\hfill \mathrm{\Omega }(\eta )=ln\left(-\frac{2\lambda (\eta +E)+4}{{\lambda }^2(\eta +E)}\right).\end{array}$$(4.8) Solution-5: If $\mu =0$, $\lambda =0,$ and ${\lambda }^2-4\mu =0,$ then we get(4.9) $$\begin{array}{c}\hfill \mathrm{\Omega }(\eta )=ln\left(\eta +E\right),\end{array}$$(4.9)

where ${\xi }_j(0\le j\le M)$, $\lambda$ and $\mu$ are constants to be determined. The value M can be identified by taking the balance principle which is based on the relationship between the highest order derivatives and the highest degree of the non-linear terms occurring in Equation (4.2).

Step 3. Substituting (4.3) into Equation (4.2) with the value of M obtained in Step 2. collecting the coefficients of $F(\eta )$, then setting each coefficient to zero, we can get a set of overdetermined equations for ${\xi }_0,{\xi }_1,...,{\xi }_M$$\lambda$, and $\mu$ with the aid of symbolic computation Maple. Solving the algebraic equations including coefficients of ${\xi }_0,{\xi }_1,...,{\xi }_M$$\lambda$, and $\mu$ into (4.3) we get to exact solution of considered problem.

5. Description of the $tan(\varphi (\eta )/2)$-expansion method

The $tan(\varphi /2)$-expansion method is a well-known analytical method. In this paper, we propose to develop this method, but prior to that we give a detailed description of the method throughout the following steps:

Step 1. We suppose that the given NPDE for u(x, t) to be in the form:(5.1) $$\begin{array}{c}\hfill \mathcal{N}(u,u_x,u_t,u_{\mathit{xx}},u_{\mathit{tt}},...)=0,\end{array}$$(5.1)

which can be converted to an ODE as:(5.2) $$\begin{array}{c}\hfill \mathcal{Q}(u,B{u}^{\prime },-Bv{u}^{\prime },B^2{u}^{″},B^2{v}^2{u}^{″},...)=0,\end{array}$$(5.2)

by the transformation $\eta =B(x-vt),$ as wave variable. Also, B and v9 are constants to be determined later.

Step 2. Suppose the traveling wave solution of Equation (5.2) can be expressed as follows:(5.3) $$\begin{array}{c}\hfill u(\eta )=\sum _{k=0}^M{A}_k{tan}^k\left(\frac{\varphi (\eta )}{2}\right),\end{array}$$(5.3)

where $A_k(0\le k\le M)$ are constants to be determined, such that $A_M\ne 0$ and $\varphi =\varphi (\xi )$ satisfies the following ordinary differential equation:(5.4) $$\begin{array}{c}\hfill {\varphi }^{\prime }(\eta )=\lambda sin(\varphi (\eta ))+\mu cos(\varphi (\eta ))+\delta .\end{array}$$(5.4) Step 3. To determine m. This, usually, can be accomplished by balancing the linear term(s) of highest order with the highest-order non-linear term(s) in Equation (5.2). But, the positive integer m can be determined by considering the homogeneous balance between the highest order derivatives and non-linear terms appearing in Equation (5.2). Moreover, precisely, we define the degree of $u(\eta )$ as $D(u(\eta ))=m$, which gives rise to degree of another expression as follows:(5.5) $$\begin{array}{c}\hfill D\left(\frac{d^{q}u}{d{\eta }^q}\right)=m+q,D\left(u^p{\left(\frac{d^{q}u}{d{\eta }^q}\right)}^s\right)=mp+s(m+q),\end{array}$$(5.5) Step 4. Substituting (5.3) into Equation (5.2) with the value of M obtained in Step 3. Collecting the coefficients of $tan{(\varphi /2)}^k$, $cot{(\varphi /2)}^k(k=0,1,2,...,M)$, then setting each coefficient to zero, we can get a set of overdetermined equations for $A_0,A_k(k=1,2,...,)$$\lambda ,\mu$, and $\delta$ with the aid of symbolic computation Maple. Solving the algebraic equations, then substituting $A_0,A_1,...,A_M,B,v$ in (5.3).

Consider the following special solutions of Equation (5.4):

Family 1: When $\mathrm{\Delta }={\lambda }^2+{\mu }^2-{\delta }^2<0$ and $\mu -\delta \ne 0$, then $\varphi (\eta )=2arctan\left[\frac{\lambda }{\mu -\delta }-\frac{\sqrt{-\mathrm{\Delta }}}{\mu -\delta }\right.$$\left.tan\left(\frac{\sqrt{-\mathrm{\Delta }}}{2}\tilde{\eta }\right)\right].$

Family 2: When $\mathrm{\Delta }={\lambda }^2+{\mu }^2-{\delta }^2>0$ and $\mu -\delta \ne 0$, then $\varphi (\eta )=2arctan\left[\frac{\lambda }{\mu -\delta }+\frac{\sqrt{\mathrm{\Delta }}}{\mu -\delta }tanh\left(\frac{\sqrt{\mathrm{\Delta }}}{2}\tilde{\eta }\right)\right].$

Family 3: When ${\lambda }^2+{\mu }^2-{\delta }^2>0$, $\mu \ne 0$ and $\delta =0,$ then $\varphi (\eta )=2arctan\left[\frac{\lambda }{\mu }+\frac{\sqrt{{\mu }^2+{\lambda }^2}}{\mu }tanh\left(\frac{\sqrt{{\mu }^2+{\lambda }^2}}{2}\tilde{\eta }\right)\right].$

Family 4: When ${\lambda }^2+{\mu }^2-{\delta }^2<0$, $\delta \ne 0$ and $\mu =0,$ then $\varphi (\eta )=2arctan\left[-\frac{\lambda }{\delta }+\frac{\sqrt{{\delta }^2-{\lambda }^2}}{\delta }tan\left(\frac{\sqrt{{\delta }^2-{\lambda }^2}}{2}\tilde{\eta }\right)\right].$

Family 5: When ${\lambda }^2+{\mu }^2-{\delta }^2>0$, $\mu -\delta \ne 0$ and $\lambda =0,$ then $\varphi (\eta )=2arctan\left[\sqrt{\frac{\mu +\delta }{\mu -\delta }}tanh\left(\frac{\sqrt{{\mu }^2-{\delta }^2}}{2}\tilde{\eta }\right)\right].$

Family 6: When $\lambda =0$ and $\delta =0,$ then $\varphi (\eta )=arctan\left[\frac{e^{2\mu \tilde{\eta }}-1}{e^{2\mu \tilde{\eta }}+1},\frac{2e^{\mu \tilde{\eta }}}{e^{2\mu \tilde{\eta }}+1}\right].$

Family 7: When $\mu =0$ and $\delta =0,$ then $\varphi (\eta )=arctan\left[\frac{2e^{\lambda \tilde{\eta }}}{e^{2\lambda \tilde{\eta }}+1},\frac{e^{2\lambda \tilde{\eta }}-1}{e^{2\lambda \tilde{\eta }}+1}\right].$

Family 8: When ${\lambda }^2+{\mu }^2={\delta }^2$, then $\varphi (\eta )=-2arctan\left[\frac{(\mu +\delta )(\lambda \tilde{\eta }+2)}{{\lambda }^2\tilde{\eta }}\right].$

Family 9: When $\delta =\lambda$, then $\varphi (\eta )=-2arctan\left[\frac{(\lambda +\mu )e^{\mu \tilde{\eta }}-1}{(\lambda -\mu )e^{\mu \tilde{\eta }}-1}\right].$

Family 10: When $\delta =-\lambda$, then $\varphi (\eta )=2arctan\left[\frac{e^{\mu \tilde{\eta }}+\mu -\lambda }{e^{\mu \tilde{\eta }}-\mu -\lambda }\right].$

Family 11: When $\mu =-\delta$, then $\varphi (\eta )=-2arctan\left[\frac{\lambda e^{\lambda \tilde{\eta }}}{\delta e^{\lambda \tilde{\eta }}-1}\right].$

Family 12: When $\mu =0$ and $\lambda =\delta$, then $\varphi (\eta )=-2arctan\left[\frac{\delta \tilde{\eta }+2}{\delta \tilde{\eta }}\right].$

Family 13: When $\lambda =0$ and $\mu =\delta$, then $\varphi (\eta )=2arctan\left[\delta \tilde{\eta }\right].$

Family 14: When $\lambda =0$ and $\mu =-\delta$, then $\varphi (\eta )=-2arctan\left[\frac{1}{\delta \tilde{\eta }}\right],$

Family 15: When $\lambda =0$ and $\mu =0$, then $\varphi (\eta )=\delta \tilde{\eta }+C.$

Family 16: When $\mu =\delta$ then $\varphi (\eta )=2arctan\left[\frac{e^{\lambda \tilde{\eta }}-\delta }{\lambda }\right],$ where $\tilde{\eta }=\eta +C$.

6. Application of ETEM for the NLSE with fourth-order dispersion

This illustrates the performance of the analytical algorithm proposed. To this end, we use the Equation (2.16) as:(6.1) $$\begin{array}{c}\hfill -c{m}^4{U}^8+\left[w+a{k}^2+b{k}^4-\frac{(a+6b{k}^2)(v+2k(a+2b{k}^2))}{4bk{B}^2}\right]m^4{U}^4-4b{B}^4(m-1)(m-2)(3m-2){(U^{\prime })}^4+\end{array}$$(6.1) $$24B^4(2bm-3b{m}^2+b{m}^3)U{U}^{\prime 2}{U}^{″}-6B^{4}b{m}^2(m-2)U^2{(U^{″})}^2-8B^{4}b{m}^2(m-2)U^2{U}^{\prime }{U}^{″\prime }+2B^{4}b{m}^3{U}^3{U}^{″″}=0.$$

We can determine values of $\delta ,\theta ,$ and $ϵ$, by balancing $U^8$ and $U^3{U}^{″″}$ in Equation (6.1) as follows:(6.2) $$\begin{array}{c}\hfill 2\delta =\theta -ϵ-2.\end{array}$$(6.2)

For different values of $\delta ,\theta ,$ and $ϵ$, we have the following cases:

Case I: $\delta =1,\theta =4$, $\text{and}$$ϵ=0$.

If we take $\delta =1,\theta =4$, and $ϵ=0$ for Equations (3.4) and (3.5), then we obtain(6.3) $$\begin{array}{c}\hfill U(\eta )={\tau }_0+{\tau }_1\mathrm{\Gamma },\end{array}$$(6.3) (6.4) $$\begin{array}{c}\hfill {(U^{\prime }(\eta ))}^2=\frac{{\tau }_1^2({\xi }_4{\mathrm{\Gamma }}^4+{\xi }_3{\mathrm{\Gamma }}^3+{\xi }_2{\mathrm{\Gamma }}^2+{\xi }_1\mathrm{\Gamma }+{\xi }_0)}{{\zeta }_0},\end{array}$$(6.4)

where ${\xi }_4\ne 0$ and ${\zeta }_0\ne 0$. Solving the algebraic equation system (3.9) yields

$\bullet$First set of parameters:(6.5) $$\begin{array}{c}\hfill {\tau }_0=\sqrt[4]{\frac{{\xi }_0}{{\xi }_4}}{\tau }_1,{\tau }_1={\tau }_1,v=v,k=k,{\xi }_0={\xi }_0,{\xi }_1=4\sqrt[4]{{\xi }_0^3{\xi }_4},{\xi }_2=6\sqrt{{\xi }_0{\xi }_4},{\xi }_3=4\sqrt[4]{{\xi }_0{\xi }_4^3},\end{array}$$(6.5) $${\xi }_4={\xi }_4,{\zeta }_0={\zeta }_0,B=m{\tau }_1\sqrt[4]{\frac{c{\zeta }_0^2}{4{\xi }_4^{2}b(3m+2)(m+2)(m+1)}},w=\frac{2k{a}^2+20b^2{k}^5+av+12a{k}^{3}b+6b{k}^{2}v}{4bk}.$$

Substituting these results into Equations (3.5) and (3.10), we get(6.6) $$\begin{array}{c}\hfill \pm (\eta -{\eta }_0)=\int \frac{\mathrm{\Pi }d\mathrm{\Gamma }}{\sqrt{{\mathrm{\Gamma }}^4+4\sqrt[4]{\frac{{\xi }_0}{{\xi }_4}}{\mathrm{\Gamma }}^3+6\sqrt{\frac{{\xi }_0}{{\xi }_4}}{\mathrm{\Gamma }}^2+4\sqrt[4]{\frac{{\xi }_0^3}{{\xi }_4^3}}\mathrm{\Gamma }+\frac{{\xi }_0}{{\xi }_4}}}=\int \frac{\mathrm{\Pi }d\mathrm{\Gamma }}{\sqrt{{\left(\mathrm{\Gamma }+\sqrt[4]{\frac{{\xi }_0}{{\xi }_4}}\right)}^4}},\mathrm{\Pi }=\sqrt{\frac{{\zeta }_0}{{\xi }_4}}.\end{array}$$(6.6)

Integrating (6.6), we obtain the solutions to the Equation (6.1) as follows:

First solution:(6.7) $$\begin{array}{c}\hfill \pm (\eta -{\eta }_0)=-\frac{\mathrm{\Pi }}{\mathrm{\Gamma }+\sqrt[4]{\frac{{\xi }_0}{{\xi }_4}}}\Rightarrow \mathrm{\Gamma }=-\sqrt[4]{\frac{{\xi }_0}{{\xi }_4}}-\frac{\mathrm{\Pi }}{\eta -{\eta }_0}=-\sqrt[4]{\frac{{\xi }_0}{{\xi }_4}}-\frac{\mathrm{\Pi }}{m{\tau }_1\sqrt[4]{\frac{c{\zeta }_0^2}{4{\xi }_4^{2}b(3m+2)(m+2)(m+1)}}(x-vt)-{\eta }_0}.\end{array}$$(6.7)

Therefore, the solution for the NLSE with fourth-order dispersion will be as:(6.8) $$\begin{array}{c}\hfill q(x,t)={\left\{-\frac{\sqrt{\frac{{\zeta }_0}{{\xi }_4}}}{m{\tau }_1\sqrt[4]{\frac{c{\zeta }_0^2}{4{\xi }_4^{2}b(3m+2)(m+2)(m+1)}}(x-vt)-{\eta }_0}\right\}}^{\frac{2}{m}}{e}^{i\left(-kx+\frac{2k{a}^2+20b^2{k}^5+av+12a{k}^{3}b+6b{k}^{2}v}{4bk}t+\theta \right)},\end{array}$$(6.8)

where $k,{\zeta }_0,{\xi }_4,{\tau }_1,v,$ and ${\eta }_0$ can be selected as free constants.

Case II: $\delta =1,\theta =5$, $\text{and}$$ϵ=1$.

If we take $\delta =1,\theta =5$, and $ϵ=1$ for Equations (3.4) and (3.5), then we obtain(6.9) $$\begin{array}{c}\hfill U(\eta )={\tau }_0+{\tau }_1\mathrm{\Gamma },\end{array}$$(6.9) (6.10) $$\begin{array}{c}\hfill {(U^{\prime }(\eta ))}^2=\frac{{\tau }_1^2({\xi }_5{\mathrm{\Gamma }}^5+{\xi }_4{\mathrm{\Gamma }}^4+{\xi }_3{\mathrm{\Gamma }}^3+{\xi }_2{\mathrm{\Gamma }}^2+{\xi }_1\mathrm{\Gamma }+{\xi }_0)}{{\zeta }_0+{\zeta }_1\mathrm{\Gamma }},\end{array}$$(6.10)

where ${\xi }_5\ne 0$ and ${\zeta }_0\ne 0$. Solving the algebraic equation system (3.9) yields

$\bullet$First set of parameters:(6.11) $$\begin{array}{c}\hfill {\tau }_0=\sqrt[4]{\frac{{\xi }_1}{{\xi }_5}}{\tau }_1,{\tau }_1={\tau }_1,v=v,k=k,{\xi }_0=0,{\xi }_1={\xi }_1,{\xi }_2=4\sqrt[4]{{\xi }_1^3{\xi }_5},{\xi }_3=6\sqrt{{\xi }_1{\xi }_5},\end{array}$$(6.11) $${\xi }_4=4\sqrt[4]{{\xi }_1{\xi }_5^3},{\xi }_5={\xi }_5,{\zeta }_0=0,{\zeta }_1={\zeta }_1,$$$$B=m{\tau }_1\sqrt[4]{\frac{c{\zeta }_1^2}{4{\xi }_5^{2}b(3m+2)(m+2)(m+1)}},w=\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}.$$

Substituting these results into Equations (3.5) and (3.10), we get(6.12) $$\begin{array}{c}\hfill \pm (\eta -{\eta }_0)=\int \frac{\sqrt{\frac{{\zeta }_0}{{\xi }_5}\mathrm{\Gamma }}d\mathrm{\Gamma }}{\sqrt{{\mathrm{\Gamma }}^5+4\sqrt[4]{\frac{{\xi }_1}{{\xi }_5}}{\mathrm{\Gamma }}^4+6\sqrt{\frac{{\xi }_1}{{\xi }_5}}{\mathrm{\Gamma }}^3+4\sqrt[4]{\frac{{\xi }_1^3}{{\xi }_5^3}}{\mathrm{\Gamma }}^2+\frac{{\xi }_1}{{\xi }_5}\mathrm{\Gamma }}}=\int \frac{\sqrt{\frac{{\zeta }_0}{{\xi }_5}}d\mathrm{\Gamma }}{\sqrt{{\left(\mathrm{\Gamma }+\sqrt[4]{\frac{{\xi }_0}{{\xi }_4}}\right)}^4}},\end{array}$$(6.12)

in which is investigated in (6.7) and (6.8).

$\bullet$Second set of parameters:(6.13) $$\begin{array}{c}\hfill {\tau }_0={\tau }_0,{\tau }_1={\tau }_1,v=v,k=k,{\xi }_0=\frac{{\tau }_0^4{\zeta }_0{\xi }_5}{{\tau }_1^4{\zeta }_1},{\xi }_1=\frac{{\xi }_5{\tau }_0^3({\zeta }_1{\tau }_0+4{\zeta }_0{\tau }_1)}{{\tau }_1^4{\zeta }_1},{\xi }_2=\frac{2{\xi }_5{\tau }_0^2(2{\zeta }_1{\tau }_0+3{\zeta }_0{\tau }_1)}{{\tau }_1^3{\zeta }_1},\end{array}$$(6.13) $${\xi }_3=\frac{2{\xi }_5{\tau }_0(3{\zeta }_1{\tau }_0+2{\zeta }_0{\tau }_1)}{{\tau }_1^2{\zeta }_1},{\xi }_4=\frac{{\xi }_5(4{\zeta }_1{\tau }_0+{\zeta }_0{\tau }_1)}{{\tau }_1{\zeta }_1},{\xi }_5={\xi }_5,{\zeta }_0={\zeta }_0,{\zeta }_1={\zeta }_1,$$$$B=m{\tau }_1\sqrt[4]{\frac{c{\zeta }_1^2}{4{\xi }_5^{2}b(3m+2)(m+2)(m+1)}},w=\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}.$$

Substituting these results into Equations (3.5) and (3.10), we get(6.14) $$\begin{array}{c}\hfill \pm (\eta -{\eta }_0)=\int \frac{\sqrt{\frac{{\zeta }_0}{{\xi }_5}+\frac{{\zeta }_1}{{\xi }_5}\mathrm{\Gamma }}d\mathrm{\Gamma }}{\sqrt{{\mathrm{\Gamma }}^5+\frac{4{\zeta }_1{\tau }_0+{\zeta }_0{\tau }_1}{{\tau }_1{\zeta }_1}{\mathrm{\Gamma }}^4+\frac{2{\tau }_0(3{\zeta }_1{\tau }_0+2{\zeta }_0{\tau }_1)}{{\tau }_1^2{\zeta }_1}{\mathrm{\Gamma }}^3+\frac{2{\tau }_0^2(2{\zeta }_1{\tau }_0+3{\zeta }_0{\tau }_1)}{{\tau }_1^3{\zeta }_1}{\mathrm{\Gamma }}^2+\frac{{\tau }_0^3({\zeta }_1{\tau }_0+4{\zeta }_0{\tau }_1)}{{\tau }_1^4{\zeta }_1}\mathrm{\Gamma }+\frac{{\tau }_0^4{\zeta }_0}{{\tau }_1^4{\zeta }_1}}}=\end{array}$$(6.14) $$\int \frac{\sqrt{\frac{{\zeta }_0}{{\xi }_5}+\frac{{\zeta }_1}{{\xi }_5}\mathrm{\Gamma }}d\mathrm{\Gamma }}{\sqrt{\frac{{({\tau }_1\mathrm{\Gamma }+{\tau }_0)}^4({\zeta }_1\mathrm{\Gamma }+{\zeta }_0)}{{\tau }_1^4{\zeta }_1}}}=\int \frac{\sqrt{\frac{{\zeta }_1}{{\xi }_5}}d\mathrm{\Gamma }}{{\left(\mathrm{\Gamma }+\frac{{\tau }_0}{{\tau }_1}\right)}^2}=-\frac{\sqrt{\frac{{\zeta }_1}{{\xi }_5}}}{\left(\mathrm{\Gamma }+\frac{{\tau }_0}{{\tau }_1}\right)},$$

where(6.15) $$\begin{array}{c}\hfill \mathrm{\Gamma }=-\frac{{\tau }_0}{{\tau }_1}-\frac{\sqrt{\frac{{\zeta }_1}{{\xi }_5}}}{\eta -{\eta }_0}\end{array}$$(6.15)

or(6.16) $$\begin{array}{c}\hfill \mathrm{\Gamma }=-\frac{{\tau }_0}{{\tau }_1}-\frac{\sqrt{\frac{{\zeta }_1}{{\xi }_5}}}{m{\tau }_1\sqrt[4]{\frac{c{\zeta }_1^2}{4{\xi }_5^{2}b(3m+2)(m+2)(m+1)}}(x-vt)-{\eta }_0}.\end{array}$$(6.16) Case III: $\delta =2,\theta =6$, $\text{and}$$ϵ=0$.

If we take $\delta =2,\theta =6$, and $ϵ=0$ for Equations (3.4) and (3.5), then we obtain(6.17) $$\begin{array}{c}\hfill U(\eta )={\tau }_0+{\tau }_1\mathrm{\Gamma }+{\tau }_2{\mathrm{\Gamma }}^2,\end{array}$$(6.17) (6.18) $$\begin{array}{c}\hfill {(U^{\prime }(\eta ))}^2=\frac{{({\tau }_1+{\tau }_2\mathrm{\Gamma })}^2({\xi }_6{\mathrm{\Gamma }}^6+{\xi }_5{\mathrm{\Gamma }}^5+{\xi }_4{\mathrm{\Gamma }}^4+{\xi }_3{\mathrm{\Gamma }}^3+{\xi }_2{\mathrm{\Gamma }}^2+{\xi }_1\mathrm{\Gamma }+{\xi }_0)}{{\zeta }_0},\end{array}$$(6.18)

where ${\xi }_6\ne 0$ and ${\zeta }_0\ne 0$. Solving the algebraic equation system (3.9) yields

$\bullet$First set of parameters:(6.19) $$\begin{array}{c}\hfill {\tau }_0=\frac{{\tau }_1^2}{4{\tau }_2},{\tau }_1={\tau }_1,{\tau }_2={\tau }_2,v=v,k=k,\alpha =\frac{{\tau }_1}{{\tau }_2},{\xi }_0=\frac{1}{64}{\alpha }^6{\xi }_6,{\xi }_1=\frac{3}{16}{\alpha }^5{\xi }_6,\end{array}$$(6.19) $${\xi }_2=\frac{15}{16}{\alpha }^4{\xi }_6,{\xi }_3=\frac{5}{2}{\alpha }^3{\xi }_6,{\xi }_4=\frac{15}{4}{\alpha }^2{\xi }_6,{\xi }_5=3\alpha {\xi }_6,{\xi }_6={\xi }_6,{\zeta }_0={\zeta }_0,$$$$B=m{\tau }_2\sqrt[4]{\frac{c{\zeta }_0^2}{64{\xi }_6^{2}b(3m+2)(m+2)(m+1)}},w=\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}.$$

Substituting these results into Equations (3.5) and (3.10), we get(6.20) $$\begin{array}{c}\hfill \pm (\eta -{\eta }_0)=\int \frac{\sqrt{\frac{{\zeta }_0}{{\xi }_6}\mathrm{\Gamma }}d\mathrm{\Gamma }}{\sqrt{{\mathrm{\Gamma }}^6+\frac{{\xi }_5}{{\xi }_6}{\mathrm{\Gamma }}^5+\frac{{\xi }_4}{{\xi }_6}{\mathrm{\Gamma }}^4+\frac{{\xi }_3}{{\xi }_6}{\mathrm{\Gamma }}^3+\frac{{\xi }_2}{{\xi }_6}{\mathrm{\Gamma }}^2+\frac{{\xi }_1}{{\xi }_6}\mathrm{\Gamma }}+\frac{{\xi }_0}{{\xi }_6}}=\int \frac{\sqrt{\frac{{\zeta }_0}{{\xi }_6}}d\mathrm{\Gamma }}{\sqrt{{\left(\mathrm{\Gamma }+\frac{\alpha }{2}\right)}^6}}=-\frac{1}{2}\sqrt{\frac{{\zeta }_0}{{\xi }_6}}\frac{1}{{\left(\mathrm{\Gamma }+\frac{\alpha }{2}\right)}^2},\end{array}$$(6.20)

or(6.21) $$\begin{array}{c}\hfill \mathrm{\Gamma }=-\frac{{\tau }_1}{2{\tau }_2}+\sqrt{-\frac{1}{2}\sqrt{\frac{{\zeta }_0}{{\xi }_6}}\frac{1}{(\eta -{\eta }_0)}}.\end{array}$$(6.21)

Therefore, the exact solution for the power law with fourth-order dispersion will be as:(6.22) $$\begin{array}{c}\hfill q(x,t)=e^{-i(kx+\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}t+\theta )}\left\{{\tau }_0-\frac{{\tau }_1^2}{2{\tau }_2}+{\tau }_1\sqrt{-\frac{1}{2}\sqrt{\frac{{\zeta }_0}{{\xi }_6}}\frac{1}{m{\tau }_2\sqrt[4]{\frac{c{\zeta }_0^2}{64{\xi }_6^{2}b(3m+2)(m+2)(m+1)}}(x,t)-{\eta }_0}}\right.\end{array}$$(6.22) $${\left.+{\tau }_2{\left(-\frac{{\tau }_1}{2{\tau }_2}+\sqrt{-\frac{1}{2}\sqrt{\frac{{\zeta }_0}{{\xi }_6}}\frac{1}{m{\tau }_2\sqrt[4]{\frac{c{\zeta }_0^2}{64{\xi }_6^{2}b(3m+2)(m+2)(m+1)}}(x,t)-{\eta }_0}}\right)}^2\right\}}^{\frac{2}{m}}.$$

7. Application of EEM for power-law media with fourth-order dispersion

As the second method, we use EEM for Equation (6.1) which is given as:(7.1) $$\begin{array}{c}\hfill -c{m}^4{U}^8+\left[w+a{k}^2+b{k}^4-\frac{(a+6b{k}^2)(v+2k(a+2b{k}^2))}{4bk{B}^2}\right]m^4{U}^4-4b{B}^4(m-1)(m-2)(3m-2){(U^{\prime })}^4+\end{array}$$(7.1) $$24B^4(2bm-3b{m}^2+b{m}^3)U{U}^{\prime 2}{U}^{″}-6B^{4}b{m}^2(m-2)U^2{(U^{″})}^2-8B^{4}b{m}^2(m-2)U^2{U}^{\prime }{U}^{″\prime }+2B^{4}b{m}^3{U}^3{U}^{″″}=0.$$

Considering the homogenous balance method between $U^8$ and $U^3{U}^{″″}$, we obtain the following relationship for M:(7.2) $$\begin{array}{c}\hfill 8M=3M+M+4,\end{array}$$(7.2) (7.3) $$\begin{array}{c}\hfill M=1,\end{array}$$(7.3)

If we take $M=1$, for Equation (4.3), then we obtain(7.4) $$\begin{array}{c}\hfill U(\eta )={\xi }_0+{\xi }_{1}F(\xi ),\end{array}$$(7.4)

where ${\xi }_1\ne 0$. By substituting (7.4) into Equation (7.1) and collecting all terms with the same order of $F(\xi )$ together, in which are converted into polynomial in $F(\eta )$. Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for ${\xi }_0,{\xi }_1,\lambda ,\mu ,B$ and v. Solving the algebraic equation system yields.

$\bullet$First set of parameters:(7.5) $$\begin{array}{c}\hfill \lambda =\frac{2{\xi }_0}{{\xi }_1},\mu =\frac{{\xi }_0^2}{{\xi }_1^2},k=k,{\xi }_0={\xi }_0,{\xi }_1={\xi }_1,v=v,\end{array}$$(7.5) $$B=m{\xi }_1\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}},w=\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}.$$

Substituting these results into (4.3), using (4.8) we get(7.6) $$\begin{array}{c}\hfill q(x,t)={(-1)}^{\frac{2}{m}}{e}^{i\left(-kx+\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}t+\theta \right)}{\left\{\frac{m{\xi }_0^2\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}}(x-vt)}{m{\xi }_0{\xi }_1\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}}(x-vt)+{\xi }_1}\right\}}^{\frac{2}{m}},\end{array}$$(7.6)

where $k,v,{\xi }_0,{\xi }_1$, and $\theta$ are arbitrary constants.

8. Application of TEM for power-law media with fourth-order dispersion

As the third method, we use TEM for Equation (6.1) which is given as:(8.1) $$\begin{array}{c}\hfill -c{m}^4{U}^8+\left[w+a{k}^2+b{k}^4-\frac{(a+6b{k}^2)(v+2k(a+2b{k}^2))}{4bk{B}^2}\right]m^4{U}^4-4b{B}^4(m-1)(m-2)(3m-2){(U^{\prime })}^4+\end{array}$$(8.1) $$24B^4(2bm-3b{m}^2+b{m}^3)U{U}^{\prime 2}{U}^{″}-6B^{4}b{m}^2(m-2)U^2{(U^{″})}^2-8B^{4}b{m}^2(m-2)U^2{U}^{\prime }{U}^{″\prime }+2B^{4}b{m}^3{U}^3{U}^{″″}=0.$$

Using the homogenous balance method between $U^8$ and $U^3{U}^{″″}$, we take $M=1$, for Equation (4.3), then we will acquire(8.2) $$\begin{array}{c}\hfill U(\eta )=A_0+A_{1}tan\left(\frac{\varphi (\eta )}{2}\right),\end{array}$$(8.2)

where $A_1\ne 0$. By substituting (7.4) into Equation (7.1) and collecting all terms with the same order of $tan\left(\frac{\varphi (\eta )}{2}\right)$ together, in which are converted into polynomial in $tan\left(\frac{\varphi (\eta )}{2}\right)$. Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for $A_0,A_1,\lambda ,\mu ,\delta ,B$ and v. Solving the algebraic equation system yields.

$\bullet$First set of parameters:(8.3) $$\begin{array}{cc}& \lambda =0,\mu =-\delta ,k=k,A_0=0,A_1=A_1,v=v,\hfill \\ \hfill & B=\frac{m{A}_1}{\mu }\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}},w=\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}.\hfill \end{array}$$(8.3)

Substituting these results into (4.3), using Family 14 of Section 5, we get(8.4) $$\begin{array}{c}\hfill q_1(x,t)=e^{i\left(-kx+\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}t+\theta \right)}{\left\{\frac{-1}{\frac{m}{\mu }\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}}(x-vt)+C}\right\}}^{\frac{2}{m}},\end{array}$$(8.4)

where k, v, C, and $\theta$ are arbitrary constants.

$\bullet$Second set of parameters:(8.5) $$\begin{array}{c}\hfill \lambda =\frac{2A_0{A}_1}{A_0^2-A_1^2}\mu ,\mu =\mu ,\delta =\frac{A_0^2+A_1^2}{A_0^2-A_1^2}\mu ,k=k,A_0=A_0,A_1=A_1,v=v,\end{array}$$(8.5) $$B=\frac{m(A_0^2-A_1^2)}{A_1\mu }\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}},w=\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}.$$

Substituting these results into (4.3(4.3) $$\begin{array}{c}\hfill U(\eta )=\sum _{j=0}^M{\xi }_j{F}^j(\eta ),\end{array}$$(4.3) ), using Family 14 of Section 5, we get(8.6) $$\begin{array}{c}\hfill q_2(x,t)=e^{i\left(-kx+\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}t+\theta \right)}{\left\{A_0-\frac{2A_0{A}_{1}m\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}}(x-vt+C)+2}{2A_{1}m\sqrt[4]{\frac{c}{4b(3m+2)(m+2)(m+1)}}(x-vt+C)}\right\}}^{\frac{2}{m}},\end{array}$$(8.6)

where $k,v,C,A_0,A_1$, and $\theta$ are arbitrary constants.

$\bullet$Third set of parameters:(8.7) $$\begin{array}{c}\hfill \lambda =\delta ,\mu =0,\delta =\delta ,k=k,A_0=A_0,A_1=A_0,v=v,\end{array}$$(8.7) $$B=\frac{m{A}_0}{\delta }\sqrt[4]{\frac{4c}{b(3m+2)(m+2)(m+1)}},w=\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}.$$

Substituting these results into (4.3(4.3) $$\begin{array}{c}\hfill U(\eta )=\sum _{j=0}^M{\xi }_j{F}^j(\eta ),\end{array}$$(4.3) ), using Family 12 of Section 5, we get(8.8) $$\begin{array}{c}\hfill q_3(x,t)=e^{i\left(-kx+\frac{20k^5{b}^2+va+2a^{2}k+6v{k}^{2}b+12b{k}^{3}a}{4bk}t+\theta \right)}{\left\{A_0+\frac{m{A}_0\sqrt[4]{\frac{4c}{b(3m+2)(m+2)(m+1)}}(x-vt+C)+2}{m\sqrt[4]{\frac{4c}{b(3m+2)(m+2)(m+1)}}(x-vt+C)}\right\}}^{\frac{2}{m}},\end{array}$$(8.8)

where $k,v,C,A_0$, and $\theta$ are arbitrary constants.

9. Conclusion

In this study, by utilizing three integration methods with the help of Maple 13, we investigated the solutions of the NLSE with fourth- order dispersion. We obtained some new kink wave solutions. All the obtained solutions in this study verified the NLSE with fourth-order dispersion, we checked this using the same program in Maple 13. We observed that our results might be helpful in detecting the soliton radiation, soliton communications where arising as a hindrance in presence of higher order dispersion terms. The afore-mentioned methods are powerful and efficient mathematical tool that can be used with the aid of symbolic software such as Maple or Mathematica in exploring search for the solutions of the various non-linear equations arising in the various field of non-linear sciences.

Additional information

Funding

The author received no direct funding for this research.

Notes on contributors

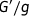
Jalil Manafian

Jalil Manafian is a postdoctoral researcher of “Department of Mathematics, Mathematical of Sciences, University of Tabriz, Tabriz, Iran”. The author has published more than 60 papers of which 50 papers include ISI. My important interest of research activities are: (1) Analytical methods in the fields of optical soliton, optik, non-linear quantum, problems in engineering, inverse scattering method, Tan-expansion method, generalized $G^{\prime }/g$-expansion method, He semi-variational principle method, Hirota bilinear method (2) Numerical Methods in the fields of wavelets, multi-wavelets, Block pulse method, and so on. (3) Semi-analytical methods including Homptopy methods (HAM, HPM, OHAM), DTM and VIM, and so on. The author is interested in the fields of non-linear integral, integral-differential equations and non-linear PDEs.