The characterization of mathematical reasoning through an analysis of high school curricula and textbooks in Morocco

Abstract

This research paper aims to characterize Mathematical Reasoning (MR) in teaching and learning of mathematics in high-school education. To achieve this goal and reveal the status of Mathematical Reasoning as a concept, we analyze the content of curricula and official textbooks of the initial and second year of high school in Morocco. Our analytical framework focuses on the commognitive perspective, exploiting the different components of MR presented in literature. The results obtained from this study using a quantitative approach show that MR occupies a central place in mathematics education at Moroccan high school, but the use of some structural and procedural aspects is still too limited.

Keywords:

• mathematical reasoning
• high school education
• Mathematics textbooks
• structural aspect of mathematical reasoning
• procedural aspect of mathematical reasoning
• quantitative approach
• Chi-square test

1. Introduction

In the high school mathematics curricula and pedagogical guidelines (Ministry of National Education [MEN], 2007), the projected goals of mathematics teaching highlight the value of mathematical culture and its contribution to the integration of citizens into an ever-developing society. These objectives aim to provide students with positive values and attitudes that will generate confidence in their ability to practice mathematics and appreciate its contribution to individual and societal development, as well as in students’ ability to solve problems and communicate mathematically and to use mathematical reasoning.

This mathematical reasoning (MR) is operationalized through a set of actions:

“To develop their ability to practice mathematical exploration through appropriate models, recognize and apply inductive and deductive reasoning, use the various means of demonstration, assimilate methods of reasoning and apply them, to develop conjectures, proofs and their evaluation, to find out the validity of ideas and acquire precision of ideas and formulation of judgments, to give examples and counter-examples and develop their ability to estimate the strength of the use of reasoning as a part of mathematics” (Kingdom of Morocco, 2007, p. 5).

In the teaching profession, where we should prepare lessons, the essential issues are to develop (or choose) tasks that lead students to the desired learning. In this paper, we focus on the development of mathematical reasoning. However, what does it mean to develop mathematical reasoning for students? and what is mathematical reasoning to begin with?

Mathematical Reasoning (MR) is a fundamental concept in mathematics teaching and learning. According to Elder and Paul (2001), it is the implication of a set of interrelated intellectual processes, which involve knowledge, experiences, and different mental gestures. As for Brousseau (2000, p. 1), Mathematical Reasoning is a mixture of deductive reasoning and inductive imagination, activated by a familiar manipulation of images that prepares students to tackle other mathematical theories.

The analysis of MR definitions in the literature on mathematics teaching has made it possible to note some convergences, differences, and even lacks associated with MR. Incorporating the processes found in the literature on MR has highlighted the conceptual ambiguity surrounding MR and its importance in learning intuitively without definition or characterization (Jeannotte, 2015). For Jeannotte, MR is a process of communication with others or with oneself that allows statements to be inferred from other statements based on the analysis of the research literature on MR in mathematics teaching and the adoption of a commognitive perspective (Sfard, 2008, 2012). A study is necessary in the attempt to characterize mathematical reasoning through an analysis of mathematics curricula and textbooks in high school.

Since textbook analysis receives a great attention from researchers, it is important to consider the different studies that address it. Especially in MR research in school math textbooks.

Stacey and Vincent (2009) presented a qualitative and quantitative elaboration of the modes of reasoning, which underlie the explanations. They examined the nature of reasoning explanation and proof that is presented in the eighth-grade mathematics textbooks in Australia. Also, they explored whether the low frequency of reasoning mathematics lessons reflects a low frequency of reasoning. The results showed that most of the textbooks made some attempt to explain each rule rather than presenting “rules without reasons” but the main purpose appeared to be rule derivation or justification in preparation for practical exercises, rather than using explanations as thinking tools. Textbooks generally did not distinguish between the deductive legitimacies and other modes of reasoning.

Thompson et al. (2012) have conducted detailed content analyses about the nature and extent of reasoning and proof embodied in the written curriculum of 20 contemporary high-school mathematics US textbooks, particularly on topics on algebra or functions. This study showed that the extent of proof-related reasoning varied by topic and textbook. Overall, about 50% of the identified properties in the 3 topic areas were justified, with about 30% of the addressed properties justified with a general argument and about 20% justified with an argument about a specific case. However, opportunities for students to use proof-related reasoning in the exercise sets were also rare. Overall, less than 6% of the exercises in the lessons we analyzed involved proof-related reasoning, with developing an argument and investigating a conjecture being the most commonly occurring type of proof-related reasoning among the categories we coded.

Bieda et al. (2014) investigated the nature of opportunities to engage in reasoning-and-proving in elementary mathematics textbooks to determine what opportunities exist in student text materials for students to engage in reasoning-and-proving, such as making claims, justifying claims, evaluating claims and what aspects of reasoning-and-proving are prompted by tasks in elementary grades curricula and how frequently and consistently do those opportunities appear in the text materials. The results mentioned that the curriculum used in elementary mathematics classrooms may not be sufficient, as written, to provide students with meaningful opportunities to learn to generate and evaluate mathematical claims; the average percentage of tasks we sampled across seven elementary mathematics textbooks related to RP was only 3.7%.

Fujita and Jones (2014) present an analysis of the geometry chapters of a selected mathematics textbook currently in common use by students aged between 13 and 14 in Grade 8. We focus on proof and proving, and on what opportunities textbooks provide for what G. J. Stylianides (2009, p. 259) calls “reasoning-and-proving” (RP). The study mentioned that the emphasis in the textbook is on “direct” proofs of geometrical statements, accompanied by activities, which encourage students to form conjectures. The manner in which the mathematical proof is built up in the textbook is through proving various geometrical statements. Given the evidence about how curricula approaches influence students’ views of geometry of students. The result also showed that most Grade 8 students in Japan can construct suitable proofs—usually based on congruent triangles and that the same students may not fully appreciate the necessity or generality of mathematical proof.

Sidenvall et al. (2015) examined how the type of reasoning affects the possibilities to solve textbook tasks in a Swedish high-school context. The relation between types of mathematical reasoning required, and the rate of correct task solutions were studied.

This study demonstrates that students get few opportunities to learn creative mathematically founded reasoning (CMR). Rote learning and superficial reasoning were common, and 80% of all attempted tasks were correctly solved using such imitative strategies. The results reveal as well that textbooks’ worked examples and theory sections are not used as an aid by the student in task-solving. Hence, it would be of importance to examine how the answers section should be constructed and used to assist students’ development of CMR.

Hong and Choi (2018) have analyzed and compared reasoning and proving opportunities in geometry lessons from American standard-based high-school textbook series, and high-school textbooks from Korea, one of the top-performing countries, in geometry, where reasoning and proving is most prevalent (Otten et al., 2014). And that to understand how these textbooks provide student opportunities to engage in reasoning and proving activities and, to determine that similarities and differences are observed in reasoning and proving opportunities in Korean and standards–based American high-school textbooks.

The analysis of textbook exposition and exercise problems of this study shows that textbooks from these two countries provide quite different reasoning and proving opportunities for students. On the one hand, Korean textbooks provide opportunities to read and become familiar with deductive proofs in their exposition. While Korean textbooks provide only a few opportunities for students to make conjectures and prove statements themselves.

Johar and Yusniarti (2018) employed descriptive qualitative method to identify the distribution and the Level of Cognitive Demands (LCD) of the proportional problems included in each chapter in the Year 7 and Year 8 of the Indonesian mathematics textbook of the 2013 curriculum (2014 revised edition) and to identify the cognitive level the proportional reasoning problems found. The results reveal that the distribution of the proportional reasoning problems in the Year 7 and Year 8 textbooks of the 2013 curriculum is not equal. The proportional reasoning problems were only found in the three of 17 chapters, which represent different LCDs including Lower-LCD (Low-M and Low-P) and Higher-LCD (High-P). Out of 69 proportional reasoning problem found in the textbooks, the percentage of higher-LCD problems (n = 29; 42.03%) is less than lower-LCD (n = 40; 57.97%).

More recently, Fu et al. (2022) explored the opportunities for students to learn about reasoning and proof (RP) by examining the narratives of algebra content of three popular series of mathematics textbooks in China. This study provides a unified analytical framework to present RP within the exercises and narratives.

The results show that the proportion of RP tasks was less than 40% and there was no significant statistical difference in the number of RP components by grade among the three series of textbooks.

In this article, we focus on the characterization of mathematical reasoning in the Moroccan secondary school curriculum through the analysis of the textbooks of the first and second year of the baccalaureate following the content analysis approach (Landry, 1997) to interpret and infer. We analyze textbooks by addressing the following question: what is the place that concerns the MR in the Moroccan curriculum and how can we characterize this MR through the activities proposed in the textbooks?

For this, we first present the conceptual model of mathematical reasoning and the analytical framework supported by a theoretical anchoring. Then, we outline the research methodology, analysis, comparison with the Chi-square test and interpretation of the results.

2. A conceptual model of mathematical reasoning

Through corpus exploration and after a deep analysis of the literature on Mathematical Reasoning, with the aim to develop and validate a conceptual model of mathematical reasoning for teaching and learning in high school. Jeannotte (2015) carried out an anasynthesis process (Legendre, 2005; see, Figure 1) which made it possible to define MR as a commognitive process (Sfard, 2008; a process of communication with others or oneself, which infer mathematical statements from other mathematical statements). To keep nine commognitive processes that are meta-discursive (derive statements about objects or mathematical relationships by exploring the relationships between them; Balacheff, 1988; Cabassut, 2005; Pedemonte, 2002; Pólya, 1968; Stylianides et al., 2002), grouped into two major categories: the processes related to the search for similarities and differences, and processes related to the search for validation.

Figure 1. Caption: Anasynthesis approach adapted from Legendre 1993-2005 (Jeannotte, 2015, p. 57)

The anasynthesis process carried out by Jeannotte (2015) to define MR as a commognitive process and to characterize MR structures.

The similarity search processes involve different commognitive acts and aim to infer a statement about the already developed objects or mathematical relationships, namely: generalizing, conjecturing, identifying a pattern, comparing, and classifying. The validation research processes, namely: justifying, proving and formal proving; rather aim to infer a statement about the epistemic value of a statement (expressed the degree of certainty or conviction attached to a proposition) “the epistemological value must be clarified by the aspects” (Duval, 1995). Exemplifying is an MR process that comprises studying a problem using several examples (Mason, 1994) and supports both the processes related to the search for similarities and differences and the processes related to the search for validation.

In literature, the process of anasynthesis has made it possible to characterize four MR structures, which highlight the different constituent elements of a reasoning process and the relationships that unite them, namely the deductive, inductive, abductive and analogy structure (Simon, 1996; Cabassut, 2005; Duval, 1995; Lithner, 2000, 2008; Meyer, 2010).

From this methodological approach, a conceptual model was developed (see, Figure 2). It is defined with two aspects: the structural aspect (which refers to how the discursive elements fit together in an ordered system, which describes both the elements and the relationships, the maintain with each other) and the process aspect (which refers to MR as a discursive activity: the description of activities within the framework of a type of interaction. (Kerbrat-Orecchioni and Traverso (2004)).

Figure 2. Caption: Conceptual model of MR (Jeannotte, 2015 p 269).

This conceptual model was developed by a methodological approach. It is defined with two aspects: the structural aspect (which refers to how the discursive elements fit together in an ordered system, which describes both the elements and the relationships, the maintain with each other) and the process aspect (which refers to MR as a discursive activity: the description of activities within the framework of a type of interaction.

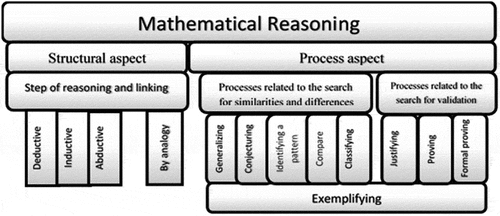
This model defines MR according to two essential aspects:

Structural aspect based on the literature that deals with mathematical logic, there are deductive, inductive, abductive, and analogy structures. The process aspect emerges from a more varied corpus that uses several action verbs in connection with MR (which resembles to the kinds of tasks in the sense of the anthropological theory of didactics developed by Chevallard (1998). It contains eight reasoning processes, including five processes related to the search for similarities and differences, and three processes related to the search for validation:

Generalizing: (…): an MR process that infers narratives about a set of mathematical objects or a relation between objects of the set from a subset of the former (G.J. Stylianides, 2008).

Conjecturing: (…) by looking for similarities and differences, it becomes possible to infer a statement about a regularity or relationship with which the associated epistemic value is reasonable and has the potential for mathematical theorization.

Identifying a pattern: (…) aims to infer a statement about a recursive relation or mathematical relations by looking at similarities and differences between different objects.

Comparing: (…) allows us to infer, by looking for similarities and differences a statement about mathematical objects and relationships (Jeannotte, 2015, p. 270).

Classifying: (…) allows deducing statements about classes that rely on properties or definitions by looking at the similarities and differences between mathematical objects.

Justifying: (…) is an MR process, which, by researching data, allows for mathematical inference and foundation, and allows an edit of the epistemic value of a statement.

Proving: (…) allows inference and mathematical foundation by researching data. This process is constrained by statements accepted by the class community (set of accepted statements) which are true (from the point of view of the expert’s mathematical discourse) and available without further justification; a final deductive restructuring; achievements that are appropriate and known or accessible to the class (Balacheff, 1988, 2008; Reid, 2010).

Formal proving (is referred to, an action derivative of formal proof (a term generally used in the mathematics education research literature)): (…) it allows inference and mathematical foundation through data research to change the epistemic value from plausible to true. It is constrained by statements accepted by the class community (set of accepted statements) which are true (from the point of view of the expert’s mathematical discourse) and systematized in a mathematical theory; a final deductive restructuring; achievements formalized and accepted by the class community and by the mathematics community (Jeannotte, 2015, pp. 271–272).

2.1. Choice of model

MR is a broad concept. In the literature, it manifests itself in different aspects. It has been approached in many ways and treated from different points of view. In education, there is a variety of subjects dealing with MR.

The study conducted by Jeannotte, 2015) and the model resulting from the in-depth analysis of the literature aimed to characterize MR and conceptualize it to fully understand the concept of MR, hence our choice of this model. In addition, to the fact that this model is designed for MR in education as much as it is a communication activity; it also has the potential to study the development of MR in students.

“This model could serve as a starting point for the study of the development of MR by students by bringing to light the vocabulary, discursive rules, visual mediators, routines, and statements used and managed during MR” (Jeannotte, 2015, p297).

“This model proposes to characterize MR from a commognitive perspective by posing MR as a commognitive process. As an inferential process, it extends mathematical discourse by generating statements from other statements “ (Jeannotte, 2005, p293).

2.2. Presentation of the analysis grid

We elaborated a detailed grid (Table 1) to present the elements of the model proposed by Jeannotte, 2015. In this grid, we find the two aspects of MR: the structural aspect defined by its four steps, led by their definitions and their epistemological value, and some clarifying examples presented by Jeannotte, 2015. The process aspect defined in two categories, led by their definition, their epistemological value and their connections with the structural aspect and other processes.

Table 1. Developed MR analysis grid from the model provided by Jeannotte, 2015)

MR: Structural aspect
Definition	Epistemic value	Examples
Deductive Step:
- infers an affirmation based on data and a rule. The form: data-rule-result.	True	- Start with a statement (true or false), then develop a discourse by using rules or adding them and then moving to the affirmation. - link to form a long deductive chain (reasoning by the absurd or by disjunction of cases)
Inductive Step:
- infers a rule from data and assertion about that data. - It would go from the particular to the general. - The form: data-result therefore rule.	Probable	- Observe data, identify patterns, and draw a conclusion or a rule. -Start with a data and a result to derive a rule (all the numbers that end with 0, 2, 4, 6, or 8 are even).
Abductive Step:
- is of two types: a first that infers data from a statement and a rule, a second that infers data and a rule from an assertion. -For Peirce (1878), abduction makes it possible to infer elements that seek to explain the assertion, and to explore data to validate a statement. -The form: Result-affirmation-rule-data.	Likely	- From an affirmation and a rule, we deduce other data necessary to make a concluding statement. - example of a rhombus (lozenge): To show that a rhombus is a square, we claim ABCD is a rhombus, and we have the rule that a rhombus with a right angle is a square, so we conclude that the data we need is the right angle.
by Analogy Step:
-infers statements about a source object and a target object depending on their similarities and differences. -It combines at least two elementary steps. These two steps can be of different elementary structures: Inductive and deductive, abductive and deductive. -It only takes form in a series of steps.	Probable	- Problem: finding the number of points making up the n^th: triangular number. First inductive step: Data: triangular number; Statement: can be arranged in a triangle; Inferred rule: the n^th triangular number suggests a similarity with the measure of the area that represents it. S Second deductive step: Data: the area of the triangle; Rule: inferior to the previous step.
MR: Process aspect
The processes of searching for similarities and differences
Definition	Epistemic value	Linking process aspects with structural aspects
Generalizing:
-Infers narratives about a set of mathematical objects or a relation between objects of the set from a subset of this set. - Extend the domain of application of a statement.	probable to sure	- Structured in the inductive step. - Abductive step plays a role in the validation processes. - Reasoning by analogy requires inferring statements depending on their similarities and differences. -relies on the process “exemplify”.
Conjecturing:
-Infers a statement about pattern or relation, which the epistemic value attached to it; is plausible and has potential for mathematical theorizing. - Infers statements that have the potential to enrich a mathematical theory.	probable	- Structured in the inductive step. - Abductive step plays a role in the validation processes. - Reasoning by analogy requires inferring statements based on their similarities and differences. - It relies on the process of “exemplify”.
Identifying a pattern:
-infers a statement about a recursive relationship between different mathematical objects or relationships by looking at similarities and differences between those mathematical objects or relationships. -Constructs a statement about a recursive relationship between mathematical objects.	Different from probable	- Structured in inductive step. - The abductive step plays a role in validation processes - Reasoning by analogy requires inferring statements based on their similarities and differences. - relies on the process of “exemplify”.
Comparing:
-infers a statement about mathematical objects and relationships by looking at similarities and differences. -Constructs a statement that identifies similarities and differences between mathematical objects or relationships.		- The abductive step plays a role in the validation processes. - Reasoning by analogy requires inferring statements based on their similarities and differences. - relies on the process of “exemplify”.
Classifying:
-infers statements about classes of mathematical objects by looking for similarities and differences between them, based on mathematical properties or definitions. - Constructs a statement about classes of mathematical objects or relationships.	probable	- The abductive step plays a role in the validation processes. - Reasoning by analogy requires inferring statements depending on their similarities and differences. -Relies on the process “exemplify”
Validation research processes
Justifying:
-is an MR process, which, by researching data, allows for mathematical inference and foundation, and allows for modification of the epistemic value of a statement.	Likely to more likely or likely to be true or false.	-The abductive step plays a role in the validation processes. - Relies on the process “exemplify”.
Proving:
-Is a MR process which, by researching data; permits inference and mathematical foundation - It allows systematizing the discourse, always to theorize the mathematical discourse.	Probable to true.	-The abductive step plays a role in validation processes - Requires restructuring into a sequence of deductive steps. - Relies on the process “exemplify”.
Formal proving:
- An MR process that searches for data, warrant and backing.	Likely to be true.	- The abductive step does not play a role in validation processes - Relies on the process “exemplify”

3. Methodology

Mathematical Reasoning is a fundamental concept in mathematics’ education. The reasoning is a line of thought, a way of thinking, that is adopted to produce assertions and reach conclusions (Lithner, 2000).MR has a critical function in improving students’ thinking through activities that can characterize students’ mathematical reasoning and develop MR, not the discourse.

In this study, the chosen data processing method is Content Analysis. Landry (1997) explicitly points out that this analysis method may be relevant to studying textbook content.

With the aim to have an overview of MR, we have analyzed the content of the Moroccan high school mathematics curricula. And to identify several pieces of information about MR: the degree of its presence, its diversity, and its effectiveness in solving mathematical problems; We relied on an analysis grid based on Jeannotte (2015) model that relates to the use of different processes and aspects of MR and the overlap between its various elements.

Our methodological choice was made according to the approach proposed by Landry (1997) which can be summarized as determination of the objectives; pre-analysis; analysis; evaluation of the reliability and validity of the data; analysis and interpretation of the results.

3.1. Objectives

In this study, we will examine the concept of MR from the perspective of teaching and learning. We will focus on determining its status in Moroccan high-school curricula and the different ways in which it is addressed in these curricula and textbooks.

That leads us to bring out elements of answers to the following questions:

• Does the MR presented in the Moroccan curriculum and textbooks follow the model presented in Part 1? In addition, to what extent is it a communication discourse?

• Are there any activities in the curriculum and textbooks that help develop MR in Common Core and first-year Baccalaureate students? How can we characterize MR through these activities?

3.2. Pre-analysis

3.2.1. A sample of the study

The mathematics textbooks selected for this research paper are the most widespread and most used in Moroccan classrooms (Table 2). The Ministry of National Education, Vocational Training, Higher Education, and Scientific Research in Morocco approves them as part of implementing the educational reform created in the early year of 2005.

Table 2. Selected textbooks

Grade	Textbook	Language	Collection	Edition	Year of the 1st edition
CCS	Fi rihab riyadiyat	Arabic	FI RIHAB	2013	2005
	Najah fi riyadiyat	Arabic	ANAJAH	2010	2005
	Wahat riyadiyat	Arabic	AL WAHA	2005	2005
1BAC. Exp science	Fi rihab riyadiyat	Arabic	FI RIHAB	2006	2006
	Jayid fi riyadiyat	Arabic	AL JAYID	2006	2006

The most popular mathematics collections of the first year of high school (Common Core Science: CCS) are as follows: Fi rihab riyadiyat (Men, 2005aa), Najah fi riyadiyat (Men, 2006a), Wahat riyadiyat (Men, 2005) and the two most popular collections of the second year of high school (first-year baccalaureate experimental science stream: first BAC. Exp science) are as follows: Fi rihab riyadiyat (Men, 2006a), Jayid Fi riyadiyat (Men, 2006a).

We also look at the educational guidelines and specific programs designed for the teaching of mathematics in the high-school grades (2007) and the educational guidelines and programs for the international stream of the Moroccan baccalaureate: French option (2014).

3.2.2. Data collection

First, we analyzed the official pedagogical guidelines of the school grades selected to determine what they say about Mathematical Reasoning in the different fields of mathematics: algebra, arithmetic, geometry, analysis, and statistics.

Second, we analyzed the textbooks of the two selected grades: activities, exercises of various types, and problems … to extract the type of reasoning treated in these books. Precisely, what process aspect is approached, and which structural aspect is used in these textbooks. In addition, with the help of tables and statistical graphs, we could clearly see the frequency of each one of these aspects in each mathematical field.

3.2.3. The pre-analysis processes

We used an iterative approach in the development of data collection tools (analysis of mathematics programs, pedagogical guidelines, textbooks, etc.) we had not carried out a complete analysis of the data, instead we readjusted the relevance of the data collected to better prepare the next ones. In fact, we found ourselves in a situation of analysis like what Huberman and Miles (1991) has called “analysis during data collection”, which often ensures the relevance of the data collected:

“ … The researcher can alternate a period of reflection on the data already collected and the development of new strategies to collect others, often of better quality; this can be an effective means of correcting systematic flaws that have remained unnoticed … ”

Deslauriers (1991) has also mentioned that the analysis stage is not only carried out after collecting all the data, but that the stage of writing notes and the appropriation of research tools often make up phases of pre-analysis.

For the analysis of the program and the selected textbooks, we are based on the grid presented in part 1.2. First, we began by identifying the structural aspects in each exercise and mathematical activity according to the definition and characterization of each structural step. Then, we identified the process aspects: the processes related to the search for similarities and differences and the processes related to the search for validation based on their definitions and detailed explanations. Finally, we used connections between structural and process aspects to validate what we found because of the overlap between the two aspects.

3.2.3.1. Pre-analysis of the official instructions

The Moroccan Official Mathematics Instructions are pedagogical guidelines that present a uniform frame of reference at the national level and provide pedagogical and didactical organizations for this discipline. After the last implementation of the pedagogical reform in November 2007, new guidelines have been operationalized. These begin with an introduction where there is a global overview on the Moroccan program, then parts dedicated to each school level in which we find lessons grouped in mathematical fields, namely: Arithmetic, Geometry (spatial, analytical), Analysis, Statistics for the CCS grade, and Geometry, Algebra, Analysis for 1st BAC. Exp science.

In 2014, the international baccalaureate: French option; was included but there was no change in the official instructions except for translating texts into French.

3.2.3.2. Pre-analysis of textbooks

We have carried out an exhaustive analysis of all the activities and exercises that appear in the textbooks sample, which have been selected (section 2.2.1). We have identified the structural and process aspect of MR for each part analyzed on all the sectors of each mathematical field (Tables 3). The identification was first written directly on the copies of the manual, and then typed in tables (column: parts analyzed, line: fields) showing the frequency of their appearance. To come out with some preliminary results, we have grouped the results found, this time, in a table that reflects the number of aspects studied in each mathematical field, and then we made statistical graphs using Excel software. This method of quantitative analysis has made it possible to see the existence, variety, and frequency of these aspects in the Moroccan mathematics’ program.

Table 3. The parts analyzed in the CCS and the first-year BAC. Exp sciences collections

Grade	CCS			1BAC. Exp science
Textbooks	Fi rihab riyadiyat, 2013, edition: Men, 2005a, Arabic.	Najah fi riyadiyat, 2010, edition: 2005, Arabic.	Wahat riyadiyat, 2005, edition: 2005, Arabic.	Fi rihab riyadiyat, 2006, edition: 2006-1562, Arabic	Jayid fi riyadiyat, 2006, edition: 2006-1656, Arabic.
Part analyzed In each textbook,	- Introductory activities - Application exercises - Supporting exercises - Reinforcement exercises	- Introductory activities - Application exercises - Supporting exercises Reinforcement Exercises - In-depth exercises - Problems	- Introductory activities - Exercises with solutions (methods) - Exercises to invest in learning - Exercises for evaluation and reinforcement of acquired knowledge - Problems - Challenges	- Introductory activities - Knowledge investment exercise - Learning integration exercise - Application exercises - Reinforcement exercises - In-depth exercises and synthesis	- Introductory activities - Application exercises - Exercises with solutions - Reinforcement exercises - Synthesis exercises - Problem

To have a better identification, we have analyzed all the parts that appeared in each textbook as illustrated above in Table 3 for the CCS and the 1^st year BAC. Exp science. Using also the grouping mentioned in the pedagogical guidelines as shown in Table 4.

Table 4. Organization of the CCS &1BAC. Exp science mathematical content

Grade	Mathematics fields	Lessons included (areas)
CCS	Arithmetic	Arithmetic in $\mathbb{N}$ Numbers sets Order in $\mathbb{N}$ Polynomial Equations, inequalities, System
	Geometry	Vector Calculus Projection on the plane The line in the plane Trigonometry Transformation in the plan Scalar product Geometry in space
	Analysis	Functions
	Statistics	Descriptive statistics
1BAC. Exp science	Geometry	Barycenter in the plane Rotation in the plane Analytical study of the scalar product and applications Vectors space Analytical study of space
	Algebra & Analysis	Notions of logic Numerical sequences Trigonometric calculation Numerical functions (generalities, limits, derivation, graphic representation

3.3. Method of analysis

Besides descriptive analysis (Frequency, percentages, averages) that allow us to provide a general overview of the place of mathematical reasoning in the mathematics curriculum and textbooks, we resorted, as did the researcher Jeannotte (2015), to a study that is based on the grid for analyzing students’ reasoning in problem solving.

For the analysis of the textbooks, we have assembled the data found for each lesson according to its mathematical field, and to better visualize the results obtained, we have grouped this within tables that show the frequency of the existing aspects for each type of processes according to the model of Jeannotte (2015).

Content analysis is a set of implicit and explicit methodological techniques for analyzing texts based on interpretation, deduction, and inference. Using objective and rigorous procedures on the one hand and subjective on the other (Bardin, 1977), we managed to reduce bias and increase reliability and validity of the data (Van der Maren, 1996).

Content analysis has three main chronological phases: pre-analysis, exploitation of data and materials, and processing of results for inference and interpretation:

• Pre-analysis, this is the preliminary stage of intuition and organization to operationalize and systematize the initial ideas to reach an outline or an analysis plan. According to Bardin (2001) and L’Écuyer (2011), this phase consists of three tasks: choice of documents through the so-called “floating reading” as indicated by Bardin (2001), Elaboration of indicators and organizing them systematically as precise and reliable indicators (Bardin, 1977) based on which the final interpretation is made.

• The exploitation of data and materials consists of categorizing, proceeding to coding, and counting or enumerating operations according to previously formulated instructions or pre-established reading grids. It is composed of two key steps: the categorization operation that includes the elaboration or application of a grid of categories and the coding/counting of the units where the categories are applied to the corpus and therefore, the analysis grids are filled in according to the chosen unit of recording on the one hand and to the unit of numeration, i.e.,:

3.4. Evaluation of the reliability and validity of data

Regarding the validity, we referred in this work to the conceptual model of MR (Jeannotte, 2015) and because of it; we have developed the grid that we used as a basis for data collection. The validity of the different components of the grid is carried out according to the work of Jeannotte (2015), Jeannotte & Kieran (2017) and according to the most recognized authors and researchers in the field. For the reliability of the results got: stability, reproducibility, and accuracy (Landry, 1997). Given the sample size and the procedure of the analysis, which consists in reading the mathematical activities and having the grid in front of the eyes to determine which MR is present and often this detection procedure was repeated at least twice to be sure of the result, we consider that our results respect the expected level of reliability, while considering the margin of error that can be committed during the collection of data or the results and the risk of deriving incorrect conclusions (Landry, 1997 page 346).

3.5. Analysis and interpretation of results

In this stage, we propose interpretations of the results found and we make inferences using quantitative analysis of the collected data:

• Determine the existence of structural and process aspects of MR.

• Observe the frequency of occurrence of each of these aspects first in the analyzed parts and then in the mathematical areas in question.

• Compare the different textbooks analyzed and synthesize the results.

3.5.1. Analysis of the official pedagogical guidelines

The analysis of the introductory part of the official pedagogical orientations, shows the great interest (see, Figure 3) that the Moroccan program gives to develop the ability of the student to use mathematical reasoning and these, through the development of its ability in the pedagogical orientations of mathematics, qualifying secondary (2007 p 5):

Figure 3. Translation of extracts from mathematics pedagogical guidelines, high school grades (2007 p 6).

The extracts from mathematics pedagogical guidelines, high-school grades in Morocco about mathematical reasoning.

• Practice mathematical discovery through appropriate models.

• Recognize inductive and deductive reasoning and its applications.

• Acquire the ability to use different demonstrations.

• Suspect, prove, and evaluate findings.

• Think accurately and make judgments.

• Be certain of the validity of one’s ideas.

• Estimate the ability to use reasoning as a part of mathematics.

Based on these pedagogical guidelines (Figure 3), we have noted that besides the use of reasoning there had been a mention of some structural and process aspects. The analysis made on the content of each lesson in each category of the mathematical fields for both grades led to the same inductions. Here are some extracts of this case (Figure 4 for the CCS level and Figure 5 for first BAC. Exp sciences):

Figure 4. Excerpts from mathematics pedagogical orientations, high school CCS (2014 p 2, 3, 4, 7).

The extracts from mathematics pedagogical orientations high school which shows pedagogical recommendations of Common Core Science (CCS) level.

Figure 5. Excerpts from mathematics pedagogical orientations, high school grades 1st BAC. Exp sciences (2014 p 17, 18)

The extracts from mathematics pedagogical orientations high school which shows pedagogical recommendations of first-year baccalaureate experimental science stream (first BAC. Exp science) level.

A persistence in writing clear and correct reasoning has been noticed frequently. Thus, the presence of MR in these pedagogical orientations and especially as structural aspects: inductive, deductive and the process aspect: formal proving.

The presentation of certain types of reasoning in the 2^nd year of Baccalaureate orientations: Contrapositive, absurdity, recurrence … reinforces the use of MR aspects.

3.5.2. Analysis of CCS textbooks

In this section, we present the results found for each textbook of the CCS grade, followed by a comparison between the textbooks and a synthesis concerning the three textbooks at this level.

For the textbook Fi rihab (Men, 2005aa), first, concerning the structural aspects (see, Figure 6), we found a dominance of the deductive step, and this is noticeable especially in geometry with an outlier, an average value in arithmetic and a low rate in analysis. Regarding the field of statistics, we found a total absence of this process. This is because the exercises and problems treated for this field are purely practical, direct statistical rules.

Figure 6. The presence of structural aspects of MR by mathematical fields in the CCS textbook “Fi rihab” (2005a).

The analysis of structural aspects in the textbook Fi rihab (Men,2005a) shows a dominance of the deductive step especially in geometry.

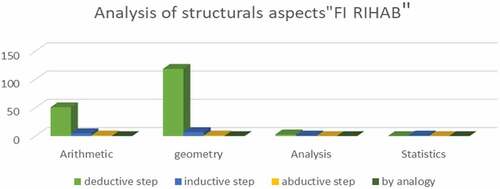
Then, for the inductive phase, it is used in the four fields, with a higher presence in geometry. Finally, for abductive and by analogy aspects, we have seen a very weak appearance of the abductive step and a lack for the step by analogy in all mathematical fields.

Since geometry preoccupies the most significant part of the textbook, we can deduce that the structural aspect the most used is the deductive step, which is manifested in statements to develop the mathematical discourse by deducing statements and results.

As in the example (Figure 8) “show that $\sqrt{2}$ is not a rational number” we have a sequence of deductive steps starting with a data (false, reasoning by the absurd) to arrive at an assertion while using rules.

Second, concerning the process aspect (Figure 7), we have noted a limited use of the first-type to search for similarities and differences in all mathematical fields. In arithmetic, we have noticed that the process of “comparing” is used a little more than the process of “generalizing” and “conjecturing”. As for “classifying”, it is never used. Then, for geometry, all the processes were used with a low frequency (18%). Only “conjecturing” was used for analysis and statistics but with a moderate frequency (10%). For the second type: search for validation, we noticed that the most widespread process is “formal proving” which is significantly used in arithmetic, analysis and in geometry, followed by the process “proving” and “justifying,” which are frequent successively in geometry and arithmetic.

Figure 7. The presence of the process aspects of MR according to the mathematical fields taught in the CCS textbook:” Fi rihab” (2005a)

The analysis of the process aspect in the Fi rihab manual (Men,2005a), noted a limited use of the first type of similarity and difference search in all mathematical domains. As for the validity process, the most common process is the “formal proving “ which is used significantly in arithmetic, analysis, and geometry.

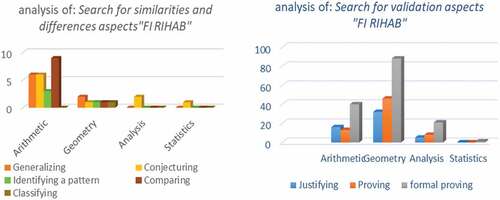
Figure 8. Translate of some exercises and problems from the CCS textbook “ Fi rihab” (2005a) pages 25, 33.

The figures illustrate an activity, and a solved exercise in which we see the existence of the MR that is defined by the structural aspects deductive (exercise) inductive (activity) with an overlap with the process aspects.

The following figures illustrate some examples of the analyzed parts. In this case, it is an activity, and a solved exercise in which we see the existence of the MR that is defined by the structural aspects deductive (exercise) inductive (activity) with an overlap with the process aspects: formal proving, justifying, comparing, identifying a pattern, and generalizing.

For the second textbooks analyzed Najah fi riyadiyat (Men, 2006a).

According to the analysis of the structural aspects (Figure 9), we noticed a significant presence of the deductive step in geometry with a frequency of 72%, and in arithmetic compared with the other fields: a 28% frequency in analysis and statistics, and a very weak appearance in the analysis domain. It has also been observed that the abductive step is used moderately and the inductive step weakly in the fields of geometry and arithmetic. Finally, we have noted that there is a complete absence of structural aspects in the statistical field.

Figure 9. The presence of structural aspects of MR by mathematical fields in the CCS textbook “Najah (2006a)”.

The analysis of structural aspects in the textbook Najah (Men,2006a) noticed a significant presence of the deductive step in geometry, and in arithmetic compared with the other fields.

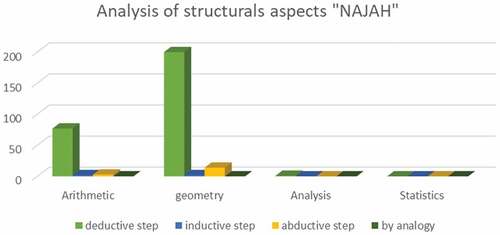
Figure 10. The presence of the process aspects of MR according to the mathematical domains in the TCS Najah manual (2006a).

The analysis of the process aspects of MR in the TCS Najah manual (2006a) noticed a weak use of the similarity and deference searches in the arithmetic and geometry fields. As for the processes of search for validation, showed a very high use of the process “formal proving” in geometry.

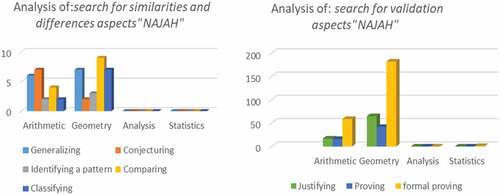
We carried out an analysis of the process aspects, and we observed that there is a weak use of the similarity and deference searches in the arithmetic and geometry fields. As for the processes of search for validation, we observed a very high use of the process “formal proving” in geometry and subsequently, it is the most dominant one, since geometry occupies almost 43% of the curriculum, and it is present with a significant percentage in the arithmetic field. For the processes “proving” and “justifying” their use is quite significant in geometry with a small shift in favor of “justifying” but they are of average use in arithmetic. In the fields of analysis and statistics, there was a total absence using the process aspects.

Eventually, we deduce that the structural aspect most used on the totality of the Najah textbook is the deductive step with a sequence of process aspects with the processes: “formal proving,” “proving,” “generalizing,” “comparing,” and “conjecturing.”

Below are some parts analyzed in the fields of geometry and arithmetic, in which the structures of the MR appear, namely the structural aspect: deductive such as the activity of two irrational numbers (Figure 11) and the inductive such as the activity of the trigonometric formula of the scalar product (Figure 11) as well as different types of process aspects.

Figure 11. Translation of some exercises and problems from “Najah textbook in mathematics” for CCS students (2016) pages 25, 226.

Some parts analyzed in the fields of geometry and arithmetic, in which the structures of the MR appear, namely the structural aspect: deductive such as the activity of two irrational numbers and the inductive such as the activity of the trigonometric formula of the scalar product as well as different types of process aspects.

We have carried out the same procedure when studying the last textbook; “Wahat Riyadiyat” (Men, 2005). First, we analyzed the structural aspects according to the graph (Figure 12). We can see a dominance of the deductive step, a medium presence of the abductive step, and a low frequency of the inductive step in the geometry field. In addition, we have noticed an average rate of the deductive step and low use of the abductive and inductive steps for the arithmetic field. Finally, we found no exercise or problem using structural aspects for the analysis and statistics branches except for a very inefficient use of the deductive step in the analysis domain. As far as the step by analogy is concerned, we have noticed a total absence of it in all the mathematical fields.

Figure 12. The presence of structural aspects of MR according to the mathematical fields in the Wahat riyadiyat textbook of the CCS (2005)

The analysis of structural aspects in the textbook Wahat riyadiyat (Men,2005) indicated a dominance of the deductive step that appears in the geometry field.

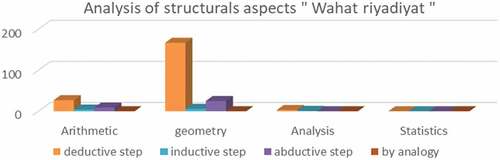
Figure 13. The presence of the process aspects of MR according to the mathematical fields in the CCS textbook “Wahat riyadiyat”.

The analysis of the aspects “search for similarities and differences”, noticed a significant rate of the process “identifying a pattern “ and an average use of the processes “generalizing”, “comparing” and “classifying” in the geometry field, as for the aspects: search for validation the analysis showed an aberration of the process “formal proving” in geometry, followed by a significant value for the process “justifying”; an average use of the “formal proving” process.

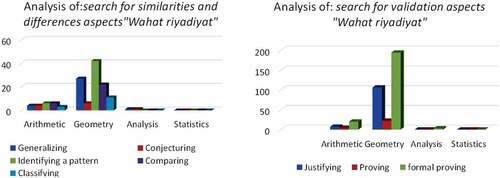
Next are the process aspects. Regarding the aspects “search for similarities and differences”, we have noticed:

• A significant rate of the process “identifying a pattern “ and an average use of the processes “generalizing”, “comparing” and “classifying” in the geometry field; a low use of all the processes “search for similarities and differences” in the arithmetic field;

• A very low use of the processes “generalizing” and “conjecturing”; the analysis domain.

• Moreover, an absence of use for all these processes in the last field.

As for the aspects: search for validation, there is:

• an aberration of the process “formal proving” in geometry, followed by a significant value for the process “justifying”;

• an average use of the “formal proving” process and a low use of the other processes in the arithmetic field;

• Finally, a very low use of the “formal proving” process and a radical absence of the other processes in the areas of analysis and arithmetic.

It is concluded that the most used structural aspect in this textbook is the deductive step with a sequence of the process aspects through the processes: “formal proving,” “justifying,” “identifying a pattern,” “generalizing,” and “comparing “.

In Figure 14, are some examples of the exercises and activities in which we can note the overlap between the different aspects of MR.

Figure 14. translation of some exercises and problems given in the CCS textbook “AL WAHA” pages: 24,201.

The excerpts from exercises and activities in the textbook Wahat riyadiyat (Men,2005) of which we could identify an MR is characterized according to structural and process aspects.

Subsequently, excerpts from example exercises and activities in the manual Wahat Riyadiyat (Men, 2005) of which we could identify an MR is characterized according to these two aspects.

According to the study of the program and the textbooks of the common core science grade, we noticed that the Moroccan program grants importance to mathematical reasoning and especially in the fields of arithmetic and geometry.

We have also noticed a richness in the use of both types of processes, whether structural or process aspects and the connection between the two, in the different exercises that besides there are several kinds and variety.

Also, we can see from the comparison of all the textbooks that the deductive reasoning is the most common reasoning especially in the field of geometry. Which allows us, to say that in this level, the Moroccan program targets as an objective the acquisition of competences related to the deductive reasoning in their priority. This is evident in the introduction of reasoning, such as reasoning by the absurd, reasoning by disjunction of cases through employing special cases of deductive reasoning repeatedly and over the course of several exercises. These are helping students to work more on the development of their mathematical reasoning at the level of CCS.

3.5.3. Analysis of the textbook of 1st year BAC. Exp science

While studying the textbook Jayid (Men, 2006a), we have found that for the structural aspect, there was a dominance (see, Figure 15) of the deductive phase in the two mathematical areas that characterize the program of the first year of high school: geometry and algebra-analysis. Then, we’ve noticed a very low occurrence of the inductive step in both those fields, and an almost total absence of the processes: “abductive” and “by analogy”.

Figure 15. The presence of the structural aspects of MR according to the mathematical fields taught in the 1^st year BAC. Exp sciences textbook: “Men, 2006b)”.

The analysis of the structural aspect in the first year of high school, showed a dominance of the deductive phase in the two mathematical areas that characterize the program: geometry and algebra-analysis. Then, it was noticed a very low occurrence of the inductive phase in these two areas, and an almost total absence of the processes: “abductive” and “by analogy”.

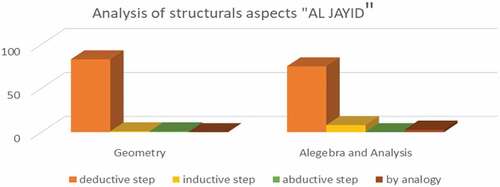
Concerning the process aspect (Figure 16), we have noted an average use of the first type “search for similarities and differences” in two mathematical fields. In geometry, all the processes were used with a low frequency, whereas in algebra-analysis, we saw that all the processes were almost present with a similar frequency, except for the processes “identifying a pattern“ and “comparing” which were used more frequently. For the second type “search for validation”, we have seen that the most widespread is the process “justifying” in geometry, “justifying” “ formal proving “ in algebra-analysis.

Figure 16. The presence of the process aspects of MR according to the mathematical fields in the textbook “Men, 2006b)” of 1^st year BAC. Exp sciences.

The analysis of the aspect of the processes has revealed that in geometry all the processes were used with low frequency, while in algebra-analysis all the processes were almost present with similar frequency, except for the processes “identify a pattern” and “compare” which were used more frequently. For the second type “search for validation”, the most common was the process “justify” in geometry, “justify” “formal proving” in algebra-analysis.

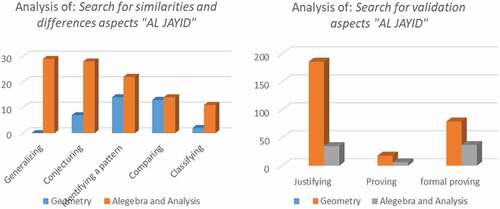
Figure 17. Translation of some exercises and problems from the textbook Jayid of 1^st year BAC. Exp sciences (pages: 17, 58)

These illustrations, taken from the Jayid textbook 1st year BAC. Exp sciences, present some examples in which the MR is present.

To conclude, we have noticed that the deductive step is the most dominant in both fields. By making an analogy, we could deduce that it is based on the process aspects (formal proving, proving, comparing, conjecturing, and generalizing).

The illustrations below, taken from the textbook Jayid, present some examples in which MR is present through these process and structural aspects.

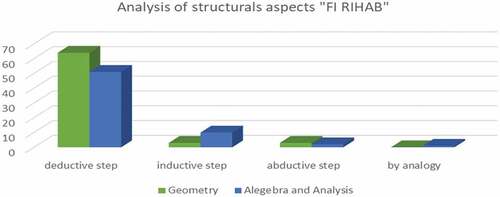
For the structural aspects in the textbook Fi rihab (Men, 2006a), we have observed a dominance of the deductive step (Figure 18) in both fields and an absence of all other steps.

Figure 18. The presence of structural aspects of MR according to mathematical fields in “Men, 2006a)”: a textbook for 1^st year BAC. Exp science.

The analysis of structural aspects in the Fi rihab manual (Men,2006a), indicated a dominance of the deductive stage in both areas and an absence of all other stages.

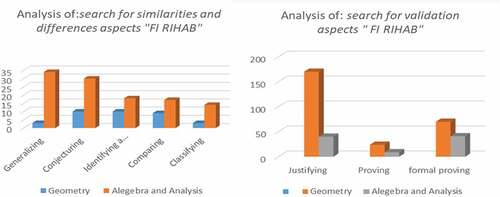
Concerning the process aspect (Figure 19), we noticed a high and similar frequency of all aspects of the first type “search for similarities and differences” in all the mathematical fields. As for the second type “search for validation”, we have noted that the most widespread is the process “justifying” in geometry followed by the process “formal proving”, while there is an average use of two processes “justifying” and “formal proving” in algebra and analysis, and a weak presence of the process “proving”.

Figure 19. The presence of the process aspects of the MR according to the mathematical fields in “Men, 2006a)”: a textbook for 1^st year BAC. Exp science.

The presence of the processual aspects of MR, showed a high and similar frequency of all aspects of the first type “search for similarities and differences” in all mathematical domains. As for the second type “search for validation”, the most widespread process is the “justify” process in geometry followed by the “formal proving” process, while there is an average use of two processes “justify” and “formal proving” in algebra and analysis, and a low presence of the “prove” process.

The illustrations below are samples of some elements analyzed in the textbook “Fi Rihab”, in which we have been able to recognize some structural and process aspects.

Figure 20. Some exercises and problems of the Fi rihab riyadiyat textbook for 1st year BAC. Exp science pages: 25, 30, 87.

Samples of some elements analyzed in the textbook “Fi Rihab”, in which we have been able to recognize some structural and process aspects.

Comparing the structural aspect, it has been noticed that deductive is present in the two textbooks with high frequencies in both mathematical fields. As for the other aspects, they are also present similarly in both textbooks but with minor frequencies.

3.5.4 Comparison of the analyzed textbooks

After the analysis of each textbook, we could develop results regarding the existence and frequency of structural and process aspects of MR. To have an overview of MR at each level; we made an analysis that compares the identification of MR between the analyzed textbooks.

For the CCS level, we found the following results for the three textbooks. The tables below (Table 5) give an overall view of the frequency of structural and process aspects, which allowed us to compare them.

Table 5. Comparison of the percentages concerned with structural aspects in the three CCS textbooks

Structural aspects Mathematical fields		Textbooks analyzed at the CCS Grade
		« Fi rihab riyadiyat »	« Najah fi riyadiyat »	« Wahat riyadiyat»
Arithmetic	deductive step	94%	93%	84%
	inductive step	5%	1%	13%
	abductive step	1%	6%	3%
	by analogy	0%	0%	0%
Geometry	deductive step	89%	94%	67%
	inductive step	9%	2%	10%
	abductive step	2%	4%	23%
	by analogy	0%	0%	0%
Analysis	deductive step	75%	100%	75%
	inductive step	25%	0%	25%
	abductive step	0%	0%	0%
	by analogy	0%	0%	0%
Statistics	deductive step	0%	0%	0%
	inductive step	100%	0%	0%
	abductive step	0%	0%	0%
	by analogy	0%	0%	0%

First, concerning MR’s (Table 5) structural aspects, it was found that the deductive step is present with approximate frequencies in the three textbooks, as well as in the mathematical fields with very high percentages in geometry and arithmetic activities, and that justifies its dominance. As for the inductive step, also in the three manuals, it is present almost with the same frequencies (low frequencies) and what is also the case for the abductive and by analogy steps except that of a shallow frequency to null.

Regarding the process aspects (Table 6), we have seen that for the aspect “search for similarities and difference”, there are variations for these processes in all the textbooks. For example, for the aspect “generalizing” is present with the highest frequency (84%) in the textbook “ Men (2005)” mainly in the field of geometry compared with its low frequency in the textbook “Meyer (2010)” with a percentage of 25% and the same is noticed in the other mathematical fields.

Table 6. Comparison between the percentages of process aspects in the three CCS grade textbooks

Process aspects Mathematical fields		Textbooks analyzed at CCS grade
		« Fi rihab riyadiyat »	« Najah fi riyadiyat »	« Wahat riyadiyat»
Arithmetic	Generalizing	25%	54%	84%
	Conjecturing	10%	22%	55%
	Identifying a pattern	25%	60%	88%
	Comparing	0%	31%	79%
	Classifying	100%	78%	79%
	Justifying	60%	79%	94%
	Proving	69%	72%	85%
	Formal proving	58%	75%	90%
Geometry	Generalizing	75%	46%	13%
	Conjecturing	60%	78%	36%
	Identifying a pattern	75%	40%	12%
	Comparing	90%	69%	21%
	Classifying	0%	22%	21%
	Justifying	30%	21%	6%
	Proving	19%	28%	15%
	Formal proving	27%	24%	9%
Analysis	Generalizing	0%	0%	3%
	Conjecturing	20%	0%	9%
	Identifying a pattern	0%	0%	0%
	Comparing	10%	0%	0%
	Classifying	0%	0%	0%
	Justifying	10%	0%	0%
	Proving	12%	0%	0%
	Formal proving	14%	0%	1%
Statistics	Generalizing	0%	0%	0%
	Conjecturing	0%	0%	0%
	Identifying a pattern	0%	0%	0%
	Comparing	0%	0%	0%
	Classifying	0%	0%	0%
	Justifying	0%	0%	0%
	Proving	0%	0%	0%
	Formal proving	1%	1%	0%

For grade of first-year BAC exp. Science, we made a comparison using the table 7 below:

Table 7. Comparison of the percentages that concern the structural aspects in the three textbooks of the 1^st year BAC exp. Science grade

Structural aspects Mathematical fields		Textbooks analyzed for 1^st year Bac grade
		Al jayid fi riyadiyat	Fi rihab riyadiyat
Geometry	deductive step	98%	92%
	inductive step	1%	4%
	abductive step	1%	4%
	by analogy	1%	0%
Analysis-algebra	deductive step	87%	80%
	inductive step	9%	16%
	abductive step	0%	3%
	by analogy	4%	1%

For the process aspects, it has been noticed that the deductive step is present in the two textbooks with high frequencies in both mathematical fields (table 8). As for the other aspects, they are also present similarly in both textbooks but with minor frequencies.

Table 8. Comparison of the percentages that concern the process aspects in the three textbooks of the 1^st year BAC exp. Science grade

Process aspects Mathematical fields		Textbooks 1st year BAC exp. Science
		Al jayid fi riyadiyat	Fi rihab riyadiyat
Geometry	Generalizing	0%	8%
	Conjecturing	20%	25%
	Identifying a pattern	39%	36%
	Comparing	48%	35%
	Classifying	15%	18%
	Justifying	84%	81%
	Proving	75%	73%
	formal proving	68%	63%
Analysis-algebra	Generalizing	100%	92%
	Conjecturing	80%	75%
	Identifying a pattern	61%	64%
	Comparing	52%	65%
	Classifying	85%	82%
	Justifying	16%	19%
	Proving	25%	27%
	Formal proving	32%	37%

3.5.5 Chi-square Test

For a significant comparison of the percentages that concern the structural aspects of the CCS and the first-year BAC exp. Science grade, we used the chi-square test statistics. First, we Defined the null hypothesis and the alternative hypothesis:

H0 = Structural aspects and textbooks are independent

Ha = Structural aspects and textbooks are dependent

Second, we putted the data into table, and we calculated the row-wise sum of items for each row and the column-wise sum of items for each column, then we calculated the expected frequencies and the Chi-statistic value.

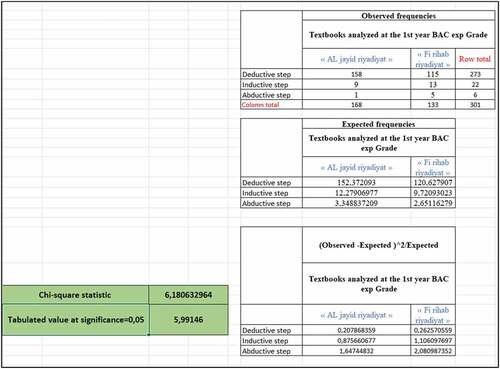
We assumed a significance level (or margin of error) equal a 0.05 (generally) .and a degree of freedom in our case: 4 for CCS grade and 2 for first-year BAC exp. Science grade (DOF = (Number of rows—1) x (Number of columns—1))

Based on the tabulated and calculated value, we concluded that:

For CCS grade looking at the box corresponding to column 0.05 and row 4 in chi-square table (figure), we find the value 9,48,773. In other words, there would be, for our table, a 5% chance that the chi-square exceeds this value (and a 95% chance that it is lower). Since the calculated value 39,67,443,193 is greater than this value, we rejected the null hypothesis. This means that the structural aspects and textbook are dependent, showing that the choice of textbooks has an impact on the practice of the structural aspect of MR, i.e., some textbooks perform better than others.

For first-year BAC exp. Science grade Looking at the box corresponding to column 0.05 and row 2 in chi-square table we find the value 5,99,146. As the calculated value 6,180,632,964 is greater than this value Hence rejected the null hypothesis. That means structural aspects and textbooks are dependent, same conclusion as above for the CCS grade comparison.

4. Discussion and conclusion

This study aimed to characterize Mathematical Reasoning in Moroccan high-school education through an analysis of the curriculum and the textbooks.

Based on the conceptual model developed by Jeannotte (2015) which defines MR in two fundamental aspects. An analysis grid was developed and used as a reference in the curriculum’s analysis that we carried out after selecting the sample on which the study was based: the mathematics textbooks of the 1^st year (CCS) and the 2^nd year (1st BAC. Exp science) of high school that have been approved by the Ministry of National Education.

As for the used methodological approach, it is content analysis (Landry, 1997). This approach enabled us to provide elements that helped answer the questions and make these objectives more precise. For the analysis phase, a qualitative data analysis was carried out to specify, identify and characterize MR in all the mathematical activities in the textbooks by examining the existence and frequency of MR processes and the overlap between structural processes and process aspects.

After having analyzed the selected textbooks, we found that for the CCS level, there is a dominance of the deductive process step in the main mathematical areas of this level: geometry and arithmetic, followed by the inductive step but with a very low rate and almost an absence of the other steps. The most used process aspects are formal proving, proving, comparing, conjecturing, and generalizing. For the first BAC grade. Exp science, we also found, after having analyzed the two widespread textbooks, that the most dominant step in the two textbooks is the deductive step in both fields: geometry and algebra/analysis, while the other steps are rarely present, or even missing in some cases. Concerning the process aspects in the first BAC. Exp science textbook “Jayid”, the first type “search for similarities and differences” was found to be used moderately in both fields of mathematics. However, the second type “search for validation”, we have noted that the most widespread process is “justifying” in geometry and “justifying”, “formal proving” in algebra and analysis.

In the light of this study, we conclude that the textbooks studied do not sufficiently prepare students to break with the dominance of calculation techniques for an effective entry into a commognitive thinking where the exploitation of the different components of the MR presented in the model of Jeannotte (2015) will be put in place. Indeed, institutional intentions through pedagogical orientations and curricula are not concretized in a relevant way according to the intention of the designers of the textbooks that are analyzed. Mathematical reasoning is present in secondary school programs, with a certain frequency in all mathematical fields constituting the program of each school year analyzed with a dominance of the deductive process step (Presence of 90% in the CCS and 95% in the first BAC. Exp science) which makes it possible to say that the Moroccan program gives more importance to deductive reasoning in the first two years of high school. This result is consistent with the study conducted in Australia by Stacey and Vincent (2009), who presented a qualitative and quantitative elaboration of the modes of reasoning that underlie the explanations. They deduced that textbooks generally did not distinguish between the legitimates of deductive reasoning and other modes of reasoning.

And for the processual aspects of the MR there was a variety in the use of the different aspects, with a dominance of the process “demonstrate” by the reason for the overlap between the two aspects of the MR. This is close to the research results of Denisse et al. (2012) who conducted detailed content analyses on the nature and extent of reasoning and evidence incorporated into the planned curriculum of American textbooks of contemporary high-school mathematics, particularly on algebra or function topics. This study showed that the scope of reasoning related to the evidence varied by topic and textbook. This was verified by the comparison made between the textbooks, which generally showed that the mathematical reasoning varied according to the textbooks, which was further approved with the Chi-square test, which showed that the MR presented by their structural aspect are dependent on the textbooks. This means that the choice of textbooks influences the practice of mathematical reasoning here in its structural aspect, i.e. there are textbooks that treat this aspect well than others and therefore it gives students more opportunities to work on their reasoning than the others.

This research introduced an analysis of all the mathematical blocks to see the presence of each type in the Moroccan program to provide a global vision. It is as a first step to know how to focus on an appropriate methodological framework of one of these blocks in subsequent articles, in order to be more profound and with prospects to conceive a conceptual model of mathematical reasoning.

Figure 21. The Chi square test statistics of the CCS grade.

The comparison of CCS textbooks with Chi-square shows that structural aspects and textbooks are dependent and the null hypothesis (structural aspects and textbooks are independent) was rejected because the calculated value: 39.67443193 is greater than the tabulated value at a significance equal to 0.05.

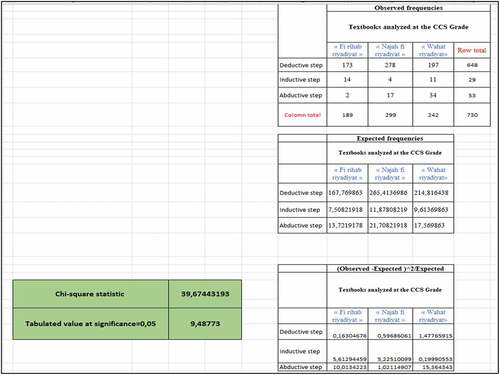
Figure 22. The comparison of 1st year BAC exp. Science textbooks with Chi-square shows that structural aspects and textbooks are dependent and the null hypothesis (structural aspects and textbooks are independent) was rejected because the calculated value (6,180632964) is greater than the tabulated value at a significance equal to 0.05 (5,99146).

Disclosure statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Meryem Nhiry

Meryem Nhiry Department of Math & info, Hassan First University of Settat, Settat, Morocco e-mail: [email protected], ORCID ID: https://orcid.org/0000-0003-1392-6710