The difference of mean waiting times between two classes of customers in a single-server FIFO queue: An experimental study

Abstract

Previous studies have shown that the distribution of mean waiting times of different classes of customers is different for each class in a GI/G/1 queue with FIFO discipline. This experimental simulation study is motivated by those results as it investigates which are the conditions causing a difference of mean waiting times between two classes of customers using a FIFO discipline. Results from the study show that having a difference in the squared coefficient of variation of inter-arrival times between classes is the most important factor to determine whether a difference of mean waiting times between two classes exists. Furthermore, if a difference of mean service times between the two classes exists, the class with the highest mean service time will tend to have the smallest mean waiting time between the two classes, resulting in an unfair policy.

Keywords:

• queueing theory
• GI/G/1
• discrete event simulation
• design of experiments
• multi-class queue

Public Interest Statement

The common assumption in any service or production facility is that the FIFO discipline is one of the fairest service disciplines since serving customers in the order of arrival will result in an equal expected queueing time for all types of customers, contrary to a priority-based service. However, this study presents some results that challenge that assumption when some particular probabilistic conditions exist. Firstly, we found that the type of customers with the highest variance between consecutive arrivals were the customers with the highest average queueing times. Secondly, results showed that the type of customers that needed more service time were the customers with the lowest queueing time, a result that would seem particularly unfair for the customers with lower service time needs.

1. Introduction

Multi-class queueing systems are used to represent systems where inter-arrival and service processes cannot be modelled by a single probability function because different types of customers with different behaviours arrive to the server facilities in order to be processed.

Due to the importance of the topic of multi-class queueing systems to the practice of Operations Management (OM), this topic has been extensively studied; see, for example, the books by Jaiswal (1968), Bolch, Greiner, de Meer, and Trivedi (1998) and Gross, Shortie, Thompson, and Harris (2008) for a summary of results of multi-class queueing systems and priority queueing.

One of the most practical and well-known results concerned with multi-class queueing systems is that the customers with the highest priority in a M/G/1 queue have the lowest mean waiting time, compared with the other customers (Sztrik, 2016). Conversely, the lowest priority customers have the highest mean waiting time of all the customers. Furthermore, for any multi-class M/G/1 queueing system without priorities and a FIFO service discipline, all classes of customers have the same waiting time distribution (Boxma & Takine, 2003), even if the arrival and service rates are different among customer classes.

However, some contrasting results can be found in the studies by Van Houdt and Blondia (2002) and He (2012), where it was shown that, for multi-class single server queues with non-Poissonian arrivals and FIFO discipline, the steady-state probability distributions of the waiting times of different classes were different.

In particular, He (2012) showed an example of a two-class GI/G/1 system, with batch arrivals and with different arrival and service rates for each class, where the class with the highest arrival rate and the highest service rate (or the quickest service time) was the class with the highest mean waiting time.

These results are somewhat counter-intuitive as it would be expected that any priority discipline for ordering queues would be fair with the customers with the lowest mean service times by a resulting low mean waiting time (Wierman, 2011) or at least that the FIFO discipline would provide an equal and fair service for all the customers (Avi-Itzhak & Levy, 2004), regardless of class characteristics.

Thus, we think that the topic of the difference of mean waiting times among different customer classes is worth further investigation as various subjects regarding the difference of mean waiting times are yet to be studied. The objective of this paper can be summarised in the following research statements that will be investigated:

(1)	A difference of steady-state mean waiting times between two distinct classes of customers commonly exists on a GI/G/1/FIFO queueing system.
(2)	The difference of mean waiting times between two classes is only present in systems where the SCV of inter-arrival times is different from 1 as there is no difference of mean waiting times between two classes with different arrival and service rates in an M/G/1 system, where the Squared Coefficient of Variation (SCV) of inter-arrival times is 1.
(3)	The difference of mean waiting times between two classes is caused by a difference on the utilisation that each class creates on the system, independently of the differences between mean arrival and service rates.

Therefore, this paper is concerned with investigating the three previously stated statements. In order to fulfil this objective, an experimental simulation study of a GI/G/1 queue with two-classes of customers was developed.

The remaining of this paper is organised as follows. Section 2 presents a literature review. Section 3 describes the methodology used to develop this study. Results of the study are shown in Section 4 while a discussion of the results is presented in Section 5. Finally, Section 6 gives the conclusions of the study.

2. Literature review

Most of the research concerned with single-server multi-class systems has studied queueing systems with priority rules (see, for example, Abate & Whitt, 1997; Al Hanbali, Alvarez, & van der Heijden, 2015; Caldentey, 2001; Horvath, 2005; Sleptchenko, Selen, Adan, & van Houtum, 2015; Stanford, Taylor, & Ziedins, 2014; Whitt, 1994), where a class of customers, arbitrarily or depending on some characteristic, receives service before other classes, effectively prioritising their service.

There have been a number of studies specifically concerned with studying single-server multi-class queueing systems with a FIFO discipline and different service time distributions for each class. For example, the papers of Takine (2001), Boxma and Takine (2003) and Masuyama and Takine (2003) present a methodology to build the distribution of the total number of customers in the queue and the distribution of the number of customers of each class.

Moreover, Van Houdt and Blondia (2002) proposed an algorithm to calculate the waiting time probability distribution of different classes with batch arrivals. Van Houdt and Blondia present an example where, under the FIFO discipline, the waiting time distribution of each class is different from the other classes. Le Ny (2006) developed exact formulas for the stationary probabilities of the total number of customers in queue and the number of customers of each class considering a two-class M/M/1 queueing system.

In addition, He (2012) proposed a methodology to calculate the probability distributions of queue lengths, cycle times, and waiting times for semi-Markov arrival processes and phase-type distributions. He presents an example where the mean waiting time of different customer classes varies between classes under the FIFO discipline, contrary to the characteristics of a M/G/1/FIFO queue where the distribution of the waiting times of all classes is the same (Boxma & Takine, 2003) due to the PASTA property (Wolff, 1982). Finally, De Clercq, Laevens, Steyaert, and Bruneel (2013) studied the steady-state distribution of the number of customers in queue and the waiting times of different classes for a discrete-time queueing system.

Therefore, to the best of our knowledge, no study has specifically addressed the issue of the difference of mean waiting times between two classes of customers in a GI/G/1/FIFO queue or has particularly studied the queueing conditions in which different classes in a FIFO queue have different mean waiting times.

3. Methodology

The analytical approach has been the most commonly used methodology for studying queueing systems. However, it has seldom been used to study the topic of multi-class GI/G/1 queues due to the extreme difficulty of obtaining exact expressions for non phase-type distributions, including the GI/G/1 system (Wolff, 1970).

Moreover, the lognormal distribution was selected to model the distribution of inter-arrival and service times because it can describe the typical shape of the probability distribution of service times with varying values of SCV using two simple parameters (Baker & Altheimer, 2012). Thus, an exact analysis of the waiting time distributions for each class will be a very difficult task because the lognormal density function cannot be represented as a semi-Markovian process, hindering the ability to model the complete queueing process with exact methods, e.g. Matrix Analytic Method (Neuts, 1981; Latouche & Ramaswami, 1999).

Therefore, Discrete Event Simulation (Law, 2014) was selected as the modelling approach since it can model the behaviour of different queueing systems and is well suited for experimental studies where the system’s parameters are required to vary among experiments.

The primary response of this study is the difference between the mean waiting times of the two classes, calculated as the ratio between the mean waiting time of class one and the mean waiting time of class two.(1) $$\mathit{\theta }=\frac{\overline{W_1}}{\overline{W_2}}$$(1)

being that, $\overline{W_1}$ is the mean waiting time of class 1, $\overline{W_2}$ is the mean waiting time of class 2 and, θ is the ratio between mean waiting times of the two classes of customers.

Additionally, to investigate which factors cause a difference between mean waiting times, a number of system’s parameters were selected for the experimental study. The SCV of the inter-arrival times of class 1 (SCV_A1) and class 2 (SCV_A2) and the SCV of service times of class 1 (SCV_S1) and class 2 (SCV_S2) were selected as main factors since one of the objectives was to investigate whether a difference between mean waiting times existed only in systems with a SCV of inter-arrival times different than 1.

The total utilisation of the system (ρ), was also selected as one of the main factors of the study, as it has been shown that it is one of the most important factors in the resulting waiting times of GI/G/1 queues (Bolch, et.al 1998; Shanthikumar, Ding, & Zhang, 2007). Furthermore, different values of server’s utilisation per class (ρ₁ for class 1, ρ₂ for class 2) were also selected to investigate whether the source of the difference in mean waiting times of different classes is caused by a difference in the specific utilisation that each class imposes on the system or exclusively due to a difference in mean arrival rates or mean service rates.

Following suggestions from the Design of Experiments methodology (Gutiérrez & de la Vara, 2012) different low and high values for all the factors were selected. The actual values for each level are shown in Table 1. Thus, the total number of experiments resulted in 288.

Table 1. Values for each factor level

Factor	Factor level
	Low	Medium	High
SCVA1	0.5		1
SCVA2	0.5		1
SCVS1	0.5		1
SCVS2	0.5		1
ρ	0.85		0.95
ρ1 (ρ = 0.85)	0.350	0.425	0.500
ρ2 (ρ = 0.85)	0.500	0.425	0.350
ρ1 (ρ = 0.95)	0.400	0.475	0.550
ρ2 (ρ = 0.95)	0.550	0.475	0.400
Source of differences in load between ρ1 and ρ2	Arrival rates	Service rates	Both

Moreover, the study was designed to have three sets of experiments with exactly the same values for all factors since the source of the variation on the specific utilisation levels per class changed on those three experiments. Thus, the values of inter-arrival and service SCV,ρ₁ and ρ₂, were constant while the source of the specific loads for each class changed. That is, for the first of those three experiments, the mean service times were equal for both classes while the mean inter-arrival time changed between classes to attain the desired values for ρ₁ and ρ₂.

The second experiment considered the same mean inter-arrival time for both classes while the mean service time changed between classes. Finally, both the mean inter-arrival time and mean service time changed between classes in a proportional way in the third experiment to attain the specific desired utilisation level per class. For example, for a desired ρ₁ = 0.350 in the third experiment, class 1 will impose a lower load on the system than class 2 (ρ₂ = 0.500) and, consequently, class 1 will have a proportionally higher mean inter-arrival time and higher mean service time than class 2.

Experimental values were calculated using the following formulas concerning a single-server queueing system:

(2) $$\mathit{\rho }={\mathit{\rho }}_1+{\mathit{\rho }}_2$$(2) (3) $$\mathit{\rho }=\frac{E(S)}{E(A)},{\mathit{\rho }}_1=\frac{E(S_1)}{E(A_1)}\text{and}{\mathit{\rho }}_2=\frac{E(S_2)}{E(A_2)}$$(3)

(4) $$\frac{1}{E(A)}=\frac{1}{E(A_1)}+\frac{1}{E(A_2)}$$(4)

(5) $$E(S)=\frac{E(A)}{E(A_1)}E(S_1)+\frac{E(A)}{E(A_2)}E(S_2)$$(5)

being that, E(S) is the expected value of the conjunct service time considering both classes, and E(S₁) and E(S₂) are the mean service times of class 1 and 2, respectively, E(A) is the expected value of the conjunct inter-arrival time considering both classes, E(A₁) and E(A₂) are the mean inter-arrival times of class 1 and 2, respectively.

The experimental design setting was defined with the intention of investigating which could be the cause of the differences of mean waiting times between the two classes, namely, a difference between mean inter-arrival times, a difference between mean service times or a simple difference between the utilisation levels of each class.

After defining all the factorial values the actual parameters of the four lognormal distributions per experiment were calculated considering the following characteristics of the lognormal distribution:(6) $$E(X)=e^{\mathit{\mu }+{\mathit{\sigma }}^2/2}$$(6) (7) $$\text{Var}(X)=(e^{{\mathit{\sigma }}^2}-1)e^{2\mathit{\mu }+{\mathit{\sigma }}^2}$$(7)

(8) $$\text{SCV}(X)=e^{{\mathit{\sigma }}^2}-1$$(8)

being that, X is a random variable modelled by the lognormal distribution, μ is the mean parameter of the associated normal distribution and, σ² is the variance parameter of the associated normal distribution.

Furthermore, since the objective of this study is concerned with finding steady-state mean waiting times of two different classes of customers, initial transient states were estimated using Welch’s method (1983). The initial transient period was estimated to be 10,000 customers. The simulation length was set to 1,000,000 customers following suggestions from Chen and Kelton (2006) to reach good steady-state estimations of cycle times. A total of 10 replications per experiment were run considering the time constraints of running the complete lot of experiments. Simio simulation software Version 8.139 (Kelton, Smith, & Sturrock, 2014) was used to run the experiments.

After running the experiments, a t-test of paired data was conducted to analyse whether the differences of mean waiting times between two classes were significant for the same experiments. Statistical analyses were done using Minitab Version 17.2.1.

4. Results

The experimental design of this study generated a total of 288 experiments. In 79 of those experiments it was found that no statistically significant differences were present between the mean waiting times of class 1 and class 2. All experiments with no statistically significant differences were found when the SCV of inter-arrival times of both classes were equal, as Table 2 shows.

Table 2. Number of experiments with no statistically significant differences of mean waiting times between two classes at different levels of inter-arrival and service times’ SCV

SCV1A	SCV2A	SCV1S				Total
		0.5		1.0
		SCV2S
		0.5	1.0	0.5	1.0
0.5	0.5	9	6	9	10	34
	1.0	0	0	0	0	0
1.0	0.5	0	0	0	0	0
	1.0	10	11	11	13	45
Total		19	17	20	23	79

Furthermore, a big proportion of the experiments with no statistically significant differences were experiments where the utilisation levels of both classes were equal (Table 3). It can be seen in Table 3 that a high level of system’s utilisation (0.95) resulted in higher number of experiments with no differences between classes. In addition, various experiments did not have statistically significant differences between mean waiting times when the arrival rate was different between classes and the service rate remained constant (“Arrival” as the source of differences in load between classes).

Table 3. Number of experiments with no statistically significant differences of mean waiting times between classes at different levels of utilisation compared with various sources of differences in load between classes

Utilisation	ρ1 vs. ρ2	Source of differences in load between classes
		Arrival	Both	Service	Total
0.85	ρ1 < ρ2	5	0	0	5
	ρ1 = ρ2	7	7	7	21
	ρ1 > ρ2	2	0	0	2
0.95	ρ1 < ρ2	8	3	2	13
	ρ1 = ρ2	8	8	8	24
	ρ1 > ρ2	8	2	4	14
Total		38	20	21	79

It is worth noting that half the experiments with a system’s utilisation of 0.95 and ρ₁ equal to ρ₂ resulted in no statistically significant differences between mean waiting times. Similarly, half the experiments with a system’s utilisation of 0.95 and the mean inter-arrival times as the source of differences in load between classes (same mean service times for the two customer classes) resulted in no statistically significant differences between classes. These mentioned experiments had equal values for SCV_1A and SCV_2A. On the other hand, all of the experiments with different SCV_1A and SCV_2A (144 experiments) resulted in statistically significant differences between the mean waiting times of each class. The complete results of experiments with no statistically significant differences can be found in the Table A1 in Appendix A.

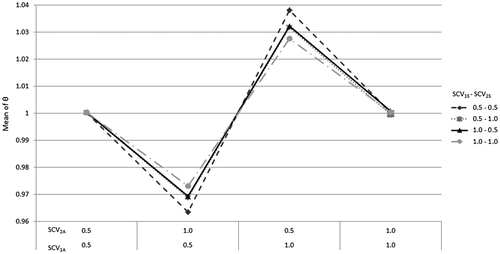
On the other hand, Figure 1 shows the global impact that the SCV of inter-arrival times has on the mean proportion of mean waiting times between the two classes (θ) since the biggest differences are reached when the SCV of the inter-arrival times of class 1 is different from class 2. Thus, considering these experiments, the higher the SCV_A for one class was, the higher the waiting time for that class resulted. It can also be seen that, despite the fact that the impact that the SCV_S has on θ is minimal, it does seem to have an impact when the SCV_A is different between classes. Interestingly, the biggest difference between mean waiting times of classes is attained when the SCV_S is 0.5 for both classes. Contrariwise, the impact of having different values for SCV_1A and SCV_2A is diminished by having a SCV_S equal to 1 for both classes.

Figure 1. Mean value of θ for different values of SCV of inter-arrival and service times.

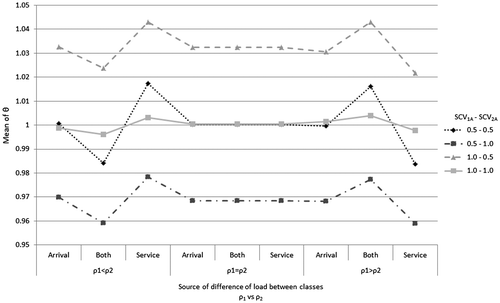
The impact that the source of differences in load between classes has on the mean θ can be clearly seen in Figure 2, as well as the impact of the utilization level. As it was tentatively expected, equalling the load that each customer class imposed on the system resulted in generally no differences between the waiting times of different classes. Experiments with the same mean service rate but different mean arrival rate (“Arrival” lines in Figure 2) accounted for little variation between classes whereas experiments with the same mean arrival rate but different mean service rates between classes (“Service” lines in Figure 2) and experiments with different arrival rates and different service rates between classes (“Both” lines in Figure 2) created significant differences of mean waiting times between classes, particularly for experiments with a system’s utilisation value of 0.85.

Figure 2. Mean value of θ for different system’s utilisation values depending on different sources of differences in load between classes.

The “Service” and “Both” lines in Figure 2 present contrasting results because, to produce a ρ₁ value less than ρ₂, the mean service time of class 1 had to be lower than the mean service time of class 2 while maintaining the same inter-arrival time for both classes for “Service” experiments. In contrast, for “Both” experiments, the mean service time and the mean inter-arrival time of class 1 were both higher than for class 2, imposing a lower load on the system. This result shows that, for this set of experiments, the class with the highest mean service time is the class with the lowest mean waiting time, independently of the differences between mean arrival rates. This characteristic can also be seen in Table 3, where all of the experiments with “Service” or “Both” sources of differences in load for an utilisation level of 0.85 had statistically significant differences of mean waiting times between different classes.

These results show that having different arrival rates between the two classes does not create a significant effect on the difference between mean waiting times but having different service rates results in a difference of mean waiting times between different classes.

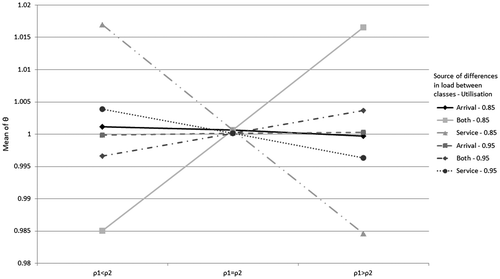
The relation between SCV_A and the source of differences in load between classes is shown in Figure 3 where it is shown that different values of mean service times between classes caused a higher impact on experiments with a SCV_A equal to 0.5 for both classes (the dotted line in the middle of Figure 3) than for experiments with different SCV_A values between classes (the upper and lower lines in Figure 3). Figure 3 also shows how experiments with SCV_A equal to 1 for both classes are the ones that are affected the least by a difference of mean service times between different classes. The complete results regarding θ for all the experiments can be found in the Table A2 in Appendix A.

Figure 3. Mean values of θ for different SCV values of inter-arrival times and various sources of differences in load between classes.

5. Discussion

A number of patterns regarding the LN/LN/1/FIFO queue with two classes of customers can be appreciated from the experimental results of this study. Firstly, if a class of customer has a SCV_A equal to 1 and the other has a SCV_A equal to 0.5, the class with the highest SCV_A will have the highest mean waiting time.

Secondly, when both classes have the same SCV_A, the class with the highest mean service time will have the lowest mean waiting time. If both classes have different SCV_A, the class with the highest mean service time will have a smaller mean waiting time compared with an experiment with equal service times for both classes. These results support the findings presented by He (2012). On the other hand, a difference of mean arrival rates between the two classes does not seem to produce a significant difference on the mean waiting times of both classes.

Finally, the system’s utilisation imposes a restriction on the magnitude of the difference of mean waiting times between classes as the number of experiments with no statistically significant differences between the mean waiting times was higher for a 0.95 utilisation level than for a 0.85 utilisation level. This pattern is related with the notion that utilisation reduces output variability (Al Hanbali, Mandjes, Nazarathy, & Whitt, 2011; Buzacott & Shanthikumar, 1993; Wu, 2005). Thus, a higher utilisation reduces the general effect that inter-arrival variability has on system’s performance (Hopp & Spearman, 2000).

After evaluating these patterns, we can address the three statements suggested at the introduction of the study. Results showed that the difference of mean waiting times between two classes of customers is commonly present in a GI/G/1/FIFO queue as only 79 out of the 288 experiments did not have a statistically significant difference of mean waiting times between the two classes. Thus, results suggest that statement one is true: A difference of steady-state mean waiting times between two distinct classes of customers commonly exists on a GI/G/1/FIFO queueing system

Moreover, statistically significant differences were found between the mean waiting times of the two classes even in experiments where the SCV of inter-arrival times was 1 for both classes. This suggests that the difference of mean waiting times between two classes is present in single-server queueing systems with non-Poissonian arrivals, independently of the value of the SCV of inter-arrival times. This conclusion shows that statement 2 of the study is false, as not only systems with a SCV different from 1 present a difference of mean waiting times between classes. This result suggests that non-Poissonian arrivals can cause a difference of means between classes, irrespective of the SCV of inter-arrival times.

Finally, results show that the load that each class imposes on the system is not a necessary condition for creating a difference of mean waiting times between classes, that is, a difference between the utilisation factors of each class is not the main cause of a difference of mean waiting times between classes because experiments with different arrival rates but equal service rates and equal inter-arrival SCV did not have statistically significant differences.

However, having different service times for each class of customers does create a difference of mean waiting times between classes. Therefore, the conclusions of this study suggest that the third statement of this study is false, as the difference on the utilisation that each class creates on the system is not a cause, on itself, of a difference of mean waiting times between classes. Differences of mean waiting times between classes are created by either a difference in the SCV of inter-arrival times or by a difference on mean service times.

5.1. Implications of the results of the study

The two main results from this study create some relevant and contrasting implications to the OM practice. The first main result of this study, i.e. the class with the highest SCV of inter-arrival times will have the highest expected mean waiting time of the two classes, is a result that is consistent with common queueing theory results: to improve performance, reduce variability. Thus, it should be expected that the customers with the lowest variable arrivals will have the lowest expected waiting time, without any consideration for their mean arrival rate.

It could be argued that this result is fair for this class of customers as they are creating a lower penalty on system’s performance by a reduced variability, being that the topic of fairness has proven to be a topic worth investigating by various authors (Avi-Itzhak & Levy, 2004; Hahne, Choudhury, & Maxemchuk, 1990; Kim, Yoon, & Yeom, 2011; Wu, Wu, & Lin, 2007).

The second main result of this study, suggesting that the class of customers with the highest mean service times tend to have reduced mean waiting times when compared with customers with lower service times, presents a fairness problem for this type of queueing systems since the class of customers that needs more server time is the class that could expect to wait less time in the queue. Despite the fact that this is a characteristic of this system, this issue would be hard to justify to the customers that have the lowest mean service times; therefore, this type of systems would need to impose a different queueing discipline than the FIFO discipline, for example, the Shortest Expected Processing Time (SEPT) discipline, to improve the perceived fairness of their system.

5.2. Future research and limitations of the study

Since the main considerations regarding the experimental design of this study were practical, a number of limitations can be found in the results of this study to further investigate these findings.

Firstly, this study considered a GI/G/1 system with lognormal distributions with SCV values of 0.5 and 1.0. Results from this study could be limited by only having considered two values of SCV. Further studies that consider SCV values higher than 1 and lower than 0.5 are needed to analyse whether the conclusions of this study continue to hold.

A second limitation can be found in the fact that only two different utilisation factors were considered. More research is needed to study the behaviour of a two-class GI/G/1 system with FIFO discipline with different levels of traffic intensity.

6. Conclusions

This study was concerned with studying in which conditions does a difference of mean waiting times between two classes of customers are present in a GI/G/1/FIFO queue. Thus, an experimental study was prepared using Discrete Event Simulation to study the exploratory research questions of this paper.

Results from this study show that a difference of the squared coefficients of variation of inter-arrival times between the two classes is the most important factor causing a difference of mean waiting times since the class with the lowest squared coefficient of variation was the class with the lowest mean waiting time.

Moreover, a difference of mean service times between classes has also been found to be a factor causing a difference of mean waiting times between two classes of customers as the class with the highest mean service time is the class with the lowest mean waiting time.

Funding

The authors received no direct funding for this research.

Additional information

Notes on contributors

Rodrigo Romero-Silva

Rodrigo Romero-Silva received his PhD in Industrial Engineering in 2012 by TECNUN, University of Navarra, Spain. He is currently an Assistant Professor at Universidad Panamericana in Mexico City and an actual member of the National Researchers System (SNI) with funding from CONACYT. His research focus is concerned with the effects of variability on the performance of production and service systems.

Margarita Hurtado

Margarita Hurtado Hernandez holds a PhD in Industrial Engineering (Universidad de Navarra, Spain). She is the current Director of the Industrial Engineering Bachelor and Professor of the Operations Management Department at Universidad Panamericana (Mexico). She’s also the co-author of the books “El Puente” and “Top 60 mistakes made by Small and Medium Businesses and how to avoid them”.

Appendix A

Table A1. Experiments with no statistically significant differences between the mean waiting time of class 1 and class 2

Table

Utilisation	SCV1A	SCV2A	SCV1S	SCV2S	ρ1 vs. ρ2
					ρ1 < ρ2			ρ1 < ρ2			ρ1 < ρ2
					Source of differences in load between classes
					Arrival	Both	Service	Arrival	Both	Service	Arrival	Both	Service
0.85	0.5	0.5	0.5	0.5	1	0	0	1	1	1	0	0	0
				1.0	0	0	0	0	0	0	1	0	0
			1.0	0.5	1	0	0	1	1	1	0	0	0
				1.0	1	0	0	1	1	1	1	0	0
		1.0	0.5	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
			1.0	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
	1.0	0.5	0.5	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
			1.0	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
		1.0	0.5	0.5	0	0	0	1	1	1	0	0	0
				1.0	0	0	0	1	1	1	0	0	0
			1.0	0.5	1	0	0	1	1	1	0	0	0
				1.0	1	0	0	1	1	1	0	0	0
0.95	0.5	0.5	0.5	0.5	1	0	0	1	1	1	1	0	0
				1.0	1	0	0	1	1	1	1	0	0
			1.0	0.5	1	0	0	1	1	1	1	0	0
				1.0	1	0	0	1	1	1	1	0	0
		1.0	0.5	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
			1.0	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
	1.0	0.5	0.5	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
			1.0	0.5	0	0	0	0	0	0	0	0	0
				1.0	0	0	0	0	0	0	0	0	0
		1.0	0.5	0.5	1	1	0	1	1	1	1	0	1
				1.0	1	0	1	1	1	1	1	1	1
			1.0	0.5	1	1	0	1	1	1	1	0	1
				1.0	1	1	1	1	1	1	1	1	1

Table A2. Value of θ for all of the study’s experiments

Table

Utilisation	SCV1A	SCV2A	SCV1S	SCV2S	ρ1 vs. ρ2
					ρ1 < ρ2			ρ1 = ρ2			ρ1 > ρ2
					Source of differences in load between classes
					Arrival	Both	Service	Arrival	Both	Service	Arrival	Both	Service
0.85	0.5	0.5	0.5	0.5	1.00139	0.96918	1.03412	1.00027	1.00027	1.00027	0.99843	1.03159	0.96759
				1.0	1.00143	0.97595	1.02561	1.00092	1.00092	1.00092	0.99930	1.02494	0.97309
			1.0	0.5	1.00045	0.97538	1.02875	1.00020	1.00020	1.00020	0.99874	1.02458	0.97628
				1.0	1.00078	0.97984	1.02251	1.00077	1.00077	1.00077	0.99928	1.02039	0.97952
		1.0	0.5	0.5	0.94871	0.92823	0.96541	0.94588	0.94588	0.94588	0.94467	0.96384	0.92675
				1.0	0.95788	0.93936	0.97101	0.95389	0.95389	0.95389	0.95176	0.96859	0.93501
			1.0	0.5	0.95553	0.93964	0.96859	0.95439	0.95439	0.95439	0.95473	0.96928	0.94274
				1.0	0.96248	0.94738	0.97311	0.96006	0.96006	0.96006	0.95937	0.97261	0.94775
	1.0	0.5	0.5	0.5	1.05780	1.03807	1.07847	1.05683	1.05683	1.05683	1.05344	1.07743	1.03537
				1.0	1.04677	1.03217	1.06045	1.04770	1.04770	1.04770	1.04577	1.06434	1.03212
			1.0	0.5	1.04978	1.03317	1.06855	1.04759	1.04759	1.04759	1.04339	1.06460	1.02922
				1.0	1.04161	1.02883	1.05454	1.04120	1.04120	1.04120	1.03831	1.05559	1.02713
		1.0	0.5	0.5	0.99817	0.99165	1.00633	1.00019	1.00019	1.00019	1.00234	1.00860	0.99413
				1.0	0.99757	0.99275	1.00373	0.99928	0.99928	0.99928	1.00138	1.00589	0.99431
			1.0	0.5	0.99927	0.99437	1.00608	1.00090	1.00090	1.00090	1.00296	1.00746	0.99643
				1.0	0.99860	0.99490	1.00384	1.00015	1.00015	1.00015	1.00205	1.00526	0.99648
0.95	0.5	0.5	0.5	0.5	1.00040	0.99167	1.00856	0.99998	0.99998	0.99998	1.00028	1.00837	0.99156
				1.0	1.00007	0.99342	1.00653	1.00004	1.00004	1.00004	1.00020	1.00664	0.99291
			1.0	0.5	1.00046	0.99331	1.00725	1.00006	1.00006	1.00006	1.00054	1.00651	0.99384
				1.0	1.00017	0.99450	1.00585	1.00014	1.00014	1.00014	1.00046	1.00539	0.99458
		1.0	0.5	0.5	0.98101	0.97616	0.98505	0.98045	0.98045	0.98045	0.98108	0.98387	0.97585
				1.0	0.98430	0.98011	0.98766	0.98360	0.98360	0.98360	0.98373	0.98654	0.97880
			1.0	0.5	0.98337	0.98017	0.98657	0.98359	0.98359	0.98359	0.98482	0.98639	0.98111
				1.0	0.98595	0.98292	0.98873	0.98581	0.98581	0.98581	0.98657	0.98822	0.98292
	1.0	0.5	0.5	0.5	1.01942	1.01698	1.02430	1.01950	1.01950	1.01950	1.01883	1.02421	1.01436
				1.0	1.01557	1.01434	1.01896	1.01623	1.01623	1.01623	1.01632	1.02010	1.01274
			1.0	0.5	1.01664	1.01424	1.02125	1.01645	1.01645	1.01645	1.01528	1.02029	1.01176
				1.0	1.01374	1.01249	1.01703	1.01406	1.01406	1.01406	1.01355	1.01739	1.01063
		1.0	0.5	0.5	0.99903	0.99887	1.00142	1.00077	1.00077	1.00077	1.00076	1.00129	1.00012
				1.0	0.99923	0.99861	1.00085	1.00038	1.00038	1.00038	1.00062	1.00071	0.99991
			1.0	0.5	0.99928	0.99935	1.00154	1.00099	1.00099	1.00099	1.00062	1.00138	1.00047
				1.0	0.99935	0.99912	1.00094	1.00064	1.00064	1.00064	1.00057	1.00090	1.00032