A benchmark study on the efficiency of unconstrained optimization algorithms in 2D-aerodynamic shape design

Abstract

Optimization algorithms are used in various engineering applications to identify optimal shapes. In this work, we benchmark several unconstrained optimization algorithms (Nelder–Mead, Quasi-Newton, steepest descent) under variation of gradient estimation schemes (adjoint equations, finite differences). Flow fields are computed by solving the Reynolds-Averaged Navier–Stokes equations using the open source computational fluid dynamics code OpenFOAM. Design variables vary from $N=2$ to $N=364$. The efficiency of the optimization algorithms are benchmarked in terms of: (a) computation time, and (b) applicability and ease of use. Results for lift optimizations are presented for airfoils at a Reynolds number of $\text{Re}=50,000$. As a result, we find for a small number of design variables $N\approx 5$ or less, the computational efficiency of all optimization algorithms to be similar, while the ease of use of the Nelder–Mead algorithm makes it a perfect choice for a low number of design variables. For intermediate and large number of design variables, gradient-based algorithms with gradient estimation through the solution of adjoint equations are unbeaten.

Keywords:

• airfoil optimization
• airfoil parametrization
• computational fluid dynamics
• OpenFOAM
• gradient-based
• gradient-free
• adjoint approach
• optimization
• automatic design

Public Interest Statement

The design of aerodynamic shapes is a challenging task in many engineering applications such as wind turbine rotors. Since aerodynamic profiles are highly complex geometries, improving these is not straight forward. Thus, optimization algorithms are needed for the design of such airfoils. Additionally, the flow around airfoils is complex, showing flow phenomena like stagnation, separation, reattachment. These cannot be captured by reduced order models, which makes the usage of computational fluid dynamics necessary.

Here, computational fluid dynamics are combined with optimization algorithms. The different set-ups are compared regarding stability, convergence and ease of use. This investigation is a necessary basis for further work within the design process of aerodynamic shapes in order to select a suitable optimization strategy.

1. Introduction

Optimization of 3D aerodynamic shapes in fully-turbulent, instationary flow fields is still an open question due to: (a) the high number of design variables, (b) the high number of design goals, (c) the lack of efficient and proven optimization algorithms for this type of applications, which safely and robustly deliver optimal shapes and (d) the extensive computational costs for high-order methods. As such, a large amount of work has been done on simplified problems with significantly reduced complexity. Specifically, the optimization of 2D airfoils with stationary flow fields has attracted some attention (Mohammadi & Pironneau, 2001), since it is in the reach of today’s computational technology. Results from such optimizations can be used as a base for many engineering applications, e.g. in the design of wind turbine blades using standard methods based on the blade element momentum theory (BEM) (Schepers, 2012). Besides, stationary analysis is often used, since the designer is interested in an averaged and not time-dependent airfoil shape. Therefore, we strongly believe that the sound understanding of the 2D aerodynamic shape optimization problem with stationary flow fields is of fundamental importance for the optimization of 3D aerodynamic shapes for fully-turbulent flow fields, with a large number of design goals, to be achieved in the future.

Practical design problems in product development are highly complex, since huge amounts of design goals have to be treated on the same time (Bünner, 2014). The same is true for aerodynamic shape optimization, since in practice the design goals or technical specifications are not restricted to a single operating point, but are to be fulfilled on several operating points or even along a characteristic curve (variation of wind velocity, variation of angle of attack and others). Besides, for the optimal design, not only aerodynamic properties have to be considered. Additionally, mechanical properties including mechanical load, fatigue, manufacturability and material and manufacturing costs are to be taken into account. As a consequence, there is a strong need for optimization techniques, which are able to handle thousands to hundred-thousands of design goals on the basis of a sound mathematical framework.

It turns out that unconstrained optimization is not the appropriate mathematical container to handle a large number of design goals as required by optimization problems in product development. Even if used in many cases, the method of weighted sums can only be a proper method to condense a low number of design goals, not more than 2 or 3, into a single goal function. The method of weighted sums is not the proper tool to treat many (e.g. more than 5) design goals, since it introduces a large number of undefined parameters (the weighting parameters) into the optimization problem (Bünner, 2014). Nevertheless when using computational fluid dynamics (CFD), the majority of work in 2D aerodynamic shape optimization has been in the realm of unconstrained optimization. The reason behind is its simplicity and robustness. The severe drawback of using unconstrained optimization is that in many cases the optimization results are unrealistic or impractical and require major after-optimization adaption work, since important design goals and operating points have been simply omitted in the optimization problem.

On the other side, constrained optimization delivers a powerful mathematical framework to model a large number of design goals. Here, the design goals are modelled as non-linear inequality constraints, and the optimization problem turns, in fact, into a feasibility problem. Along these development lines, modern algorithms, which are capable to safely and robustly solve large constrained non-linear optimization problems (NLP), have demonstrated the ability to solve practical product development optimization problems. For instance algorithms from the SQP family (Nocedal, 2006; Schittkowski, 1986) have identified optimal designs for product development problems with many, up to hundred-thousands, of design goals in the field of optimal high fidelity design (van de Braak, Bünner, & Schittkowski, 2004), optimal wind turbine airfoil design (Grasso, 2011), optimal turbine design (Nagel, 2004) and optimal 2D airfoil design (Bünner, 2014). On this basis, it is possible to create a robust workflow, which is able to deliver safely and numerically highly efficient optimal designs. In some applications, gradients, as requested by modern optimization routines, can be computed safely, with low numerical costs. In other applications, the computation of gradients remains a challenge. In many applications, e.g. wind turbines or aeroplanes, aerodynamic shapes have been improved in several design phases during many years of research and development. It is expected that in further optimization only small improvements are possible. Thus a computational method with high fidelity, such as CFD, is necessary, since other low fidelity methods based on models and approximations do not offer the necessary level of detail. This leads to high requirements regarding the searching efficiency of the optimization algorithm, as the computational cost of the flow solver is already comparably large.

During the optimization, the aerodynamic characteristics of the airfoils have to be evaluated several times. Many authors use fast but low order methods based on potential flow theory coupled with boundary layer corrections in their optimizations (Bak, Gaudern, Zahle, & Vronsky, 2014; Dahl & Fuglsang, 1998; Grasso, 2010; Méndez, Munduate,& San Miguel, 2014). There, the Navier–Stokes equations are simplified, e.g. vorticity is zero, and in principle, these methods also could be used in the following benchmark study due to the simple optimization problems, but future applications of the optimization shall deal with 3D shapes, which create vortices, and turbulent flow fields at high Reynolds numbers. Since the computation of 3D flows need a numerical tool with high fidelity, CFD based on the Reynolds-Averaged Navier–Stokes equations (RANS), will be used in this benchmark study. CFD is able to predict the aerodynamic forces with a higher accuracy and can be used in more general applications. For the computation of the flow field, the open-source library OpenFOAM-2.3.0 (OpenCFD, n.d.) is used.

For the optimization of 2D airfoils, a fundamental step is the choice of shape parametrization. Parametrizations with a low number of parameters are available, such as the well-known NACA parametrizations (Abbott & von Doenhoff, 1949). A medium number of parameters is provided by Bézier or spline parametrizations (Salomon, 2006; Shahrokhi & Jahangirian, 2008). A high number of design parameters is used, when the points of the numerical grid on the surface of the geometry are used for pointwise discretization of the shape itself. In this work, the grid nodes on the surface of the airfoil geometry are referred to as surface points.

On the basis of CFD simulations, several optimization strategies have been applied for 2D shape optimization. Several parametrizations have been used and consequently, the number of design variables varies tremendously from case to case. By far the most work has been done in the framework of unconstrained optimization, where the Nelder–Mead algorithm (Nelder & Mead, 1965), algorithms from the widespread family of Newton or Quasi-Newton type with gradient information provided by finite differences (Broyden, 1970; Fletcher, 1970; Gill, Murray, & Wright, 1974; Shanno, 1970), steepest descent with gradient estimation on the basis of the solution of adjoint equations (Soto, Löhner, & Yang, 2002) and finally genetic or so-called evolutionary algorithms (Mehnel, 2007; Schramm, Stoevesandt, & Peinke, 2015) are used. Also some work has been done in the framework of constrained optimization, where algorithms from the SQP-family (Bünner, 2014; Grasso, 2012) or, respectively, genetic or evolutionary algorithms (Asouti, Kyriacou, & Giannakoglou, 2014; Roy, 2016; Vasant, 2013) were used. In principle, algorithms can be combined in various ways, e.g. a combination of heuristic or stochastic algorithms with gradient-based algorithms is possible (Garg, 2015; Montillet, Yu, Bonenberg, & Roberts, 2016; Senvar, Turanoglu, & Kahraman, 2013; Vasant, 2012,2014). Since this work is supposed to be a base for optimizations of aerodynamic shapes, which are close to an optimum, only algorithms are considered, which can find local optima. Thus a combination of algorithms is not in the aim of this work.

Still, it remains a challenge to compare the quality of optimization approaches for optimal 2D aerodynamic shape design, and to identify the most promising approaches, since design spaces are not identical, termination conditions for different optimization algorithms are different and it is not obvious how to quantify computational efficiency in a universal way. As a consequence, even if every single optimization strategy is successful in its own, several open questions remain in the light of these different optimization strategies:

(1)	Which optimization algorithms are most efficient in terms of numerical costs?
(2)	Which optimization algorithms are robust and comparably easy to use?
(3)	Which algorithms require a high level of knowledge and maintenance to be used successfully in engineering practice?

 

The aim of this benchmark study is to address the fundamental questions of numerical efficiency, robustness, stability and ease of use for four different unconstrained optimization techniques as they are applied on the identical 2D aerodynamic shape optimization problem: (1) Nelder–Mead algorithm (Nelder & Mead, 1965; Press, Teukolsky, & Vetterling, 1986), (2) Method of steepest descent with step size control (Nocedal, 2006; Press et al., 1986) with gradient estimation on the basis of the solution of adjoint equations, (3) Quasi-Newton algorithm with Broyden–Fletcher–Goldfarb–Shanno (BFGS) Hessian reconstruction (Broyden, 1970; Fletcher, 1970; Nocedal, 2006; Press et al., 1986; Shanno, 1970) with (3a) finite differences gradient calculation or with (3b) gradient calculations on the basis of the solutions of adjoint equations. The number of design variables is varied form $N=2$ up to $N=346$ and therefore offers a wide range of design spaces.

The paper is organized as follows: firstly, the definition of the benchmark problem is described in Section 2. In Section 3, the shape parametrizations, as used in this benchmark study, are introduced. In Section 4, the optimization algorithms under investigation are explained. In Section 5, the simulation and optimization cases are presented up to the necessary depth. The results of the benchmark study are presented in Section 6. Finally, conclusions are drawn and research lines are identified for future research on 3D aerodynamic constrained shape optimization for fully turbulent flow fields, on the basis of this benchmark study.

2. Benchmark problem for 2D-aerodynamic unconstrained shape optimization with variable number of design variables

In order to benchmark airfoil optimization for optimization algorithms with a varying numbers of design variables from $N=2$ to $N=346$, it is of crucial importance to define a proper benchmark optimization problem. The optimization problem needs to allow:

• a unique definition of the termination condition for different optimization, algorithms

• a unique definition of the design goal for a varying number of design, variables N

• a unique definition of the computational efficiency.

 

On the basis of an N-dimensional shape parametrization, $s\in R^N$, the benchmark optimization problem is stated as follows:

(1)	What are the numerical costs for a chosen optimization algorithm to identify a shape with lift coefficient $c_l^{\ast }$ starting from any initial shape $s_0$ with vanishing lift coefficient $c_l(s_0)=0$?
(2)	How easy is it for a user to fulfil this task for a chosen optimization algorithm, and how much inside knowledge and maintenance work is required?

  Formally, the benchmark problems writes as: start with a set of I initial shapes $s_{0,i},i=1,\dots ,I$ in the N-dimensional design space with zero lift $c_l(s_{0,i})=0,i=1,\dots ,I$. For each initial shape, the unconstrained optimization problem(1) $$\begin{array}{cc}& minf\left(s\right)s\in R^N\hfill \end{array}$$(1) (2) $$\begin{array}{cc}& f(s)=\frac{1}{2}{\left(c_l\left(s\right)-c_l^{\ast }\right)}^2+\tilde{p}\hfill \end{array}$$(2)

is solved. The goal function f(s) depends on the selected parametrization s, which determines the coordinates of the two-dimensional shape. Quadratic penalty functions $\tilde{p}$ are used to realise box constraints for the design parameters. These box constraints define minimal and maximal values for the design parameters, such that all feasible values can be imagined within a box spanned within the defined range.

The optimization algorithms are iterative and perform several optimization iterations j, $s_{0,i}\to s_{1,i}\to \cdots \to s_{J,i}$ until the optimization algorithm terminates for $j=J$. Here, an universal termination condition has to be chosen, which applies equally well for all tested optimization algorithms. Since a first-order convergence information is not available for all optimization algorithms, a simple termination condition is needed. Consequently, as termination condition a simple condition on the goal function f is applied: $\frac{1}{2}{\left(c_l\left(s_j\right)-c_l^{\ast }\right)}^2\le {10}^{-6}$ for all $j\ge J$.

For each initial state $s_{0,i}$, the total sum of the CFD iterations needed to identify the optimal shape $s_{J,i}$ is recorded as a measure for the computational efficiency. Note, the number of optimization steps is not a proper measure for computational efficiency, since the computational costs for optimization steps differ widely for different optimization algorithms, but the total number of CFD iterations includes CFD iterations needed for gradient calculations. Finally, as a measure for the efficiency of the different optimization algorithms, the total number of CFD iterations averaged over all initial airfoil geometries and overall I optimization runs is used. If the solution of adjoint equations is needed, the CFD iterations for solving these equations are summed up as well as the CFD iterations for finite-differencing. The optimization problem shown in Equation (1) is an unconstrained non-linear optimization problem with N design variables. Loosely speaking, the benchmark problem is posed in such a way that the optimization algorithm performs I optimizations with I different initial shapes $\{s_0^i\in H_0,i=1,\dots ,I\}$. The optimization algorithm starts to change the shape until the cost function drops below ${10}^{-6}$, which refers to a difference below 0.141% between the current and goal lift coefficients. This is referred to as the final state close to $H^{\ast }$.

3. Parametrization of the shapes

In this section, the parametrizations of the airfoil shape, as applied in this paper, are presented. First, the parametrization based on the 4-digit NACA equation with two design parameters is shown. Then, a parametrization based on Bézier curves with 14 design variables is used. Finally, a free shape parametrization based on the surface points, which are the grid nodes on the surface of the airfoil geometry, is described. In the following, mesh movement describes the update of the numerical grid according to the update of the airfoil geometry within each optimization step.

3.1. NACA equation with 4-digits

The 4-digit NACA airfoils parametrization (Abbott & von Doenhoff, 1949; Jacobs, Ward, & Pinkerton, 1935) is highly useful to describe simple airfoils, as it allows to describe an airfoil shape based on the few variables $c,t,m,p$ which are chord, maximum thickness, camber and location of maximal camber, respectively.

In order to assure high numerical grid quality during the optimization, the chord is kept constant at $c=1$ as well as the location of maximal camber at $p=0.4$. This leads to $s=(t,m)$ as design parameters, i. e. a two-dimensional design space. Thickness and camber are updated according to the optimization step and the new airfoil geometry is solved by additional equations for cambered 4-digit NACA airfoils (Jacobs et al., 1935) based on the updated design parameters. The new position of the surface points is then directly calculated based on the updated NACA parameters. The movement of the surface points is damped down in the computational grid by a Laplace equation using an inverse distance method, which is available in OpenFOAM by default.

3.2. Bézier Curves

Bézier curves are often used to generate smooth shapes and thus are suitable for parametrizing airfoils. As in the work from Grasso (2010), four Bézier curves are used to represent the airfoil shape, two on the suction and pressure side each. The connections of the single curves are at leading and trailing edge as well as the two points at maximum thickness. The cubic Bézier curves $\mathit{B}$ consist of four points ${\mathit{P}}_{0...3}$ and the curve parameter t. The design parameters s are then the control points of the used Bézier curves:(3) $$\begin{array}{c}\hfill \mathit{B}={(1-t)}^3{\mathit{P}}_0+3{(1-t)}^{2}t{\mathit{P}}_1+3(1-t)t^2{\mathit{P}}_2+t^3{\mathit{P}}_3,0\le t\le 1.\end{array}$$(3)

Allowing deformation in x- and y-direction, this would result into 32 design parameters, but due to the 4 connecting points this number is reduced to 24. Using the same limitations as Grasso (2010), i.e. removing design variables in x- or y-direction for smooth transitions between the connected curves, the total number of design parameters reduces further to a design space $N=14$, which still offers a high flexibility in the design of airfoil shapes. For the update of the numerical grid using a geometry defined by Bézier curves, two different approaches are used. Using the adjoint approach to compute gradients leads to high quality requirements regarding the numerical grid. Therefore, a mesh movement was implemented based on the mesh motion approach by Jameson and Reuther (1994). The applicability of this mesh movement in combination with adjoint gradient estimation is described by the authors in Schramm, Stoevesandt, and Peinke (2016). For the other application of Bèzier curve defined geometries, namely finite differences, an automatized remeshing for 2D profiles was implemented in Matlab, such that there is no mesh movement needed for this set-up.

3.3. Free shape deformation

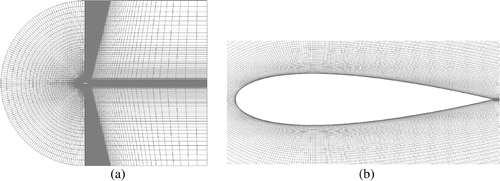
The adjoint approach, which is further explained in Section 4.5, leads to gradient information at every surface point of the numerical grid. In general, this allows to use every surface point as an independent design parameter. In this study, the points are moved along the surface normals, leading to $N=364$ design parameters. The numerical grid showing all possible design parameters, e.g. the surface points, is shown in Figure 1. The high degree of freedom for such a large amount of design parameters can lead to problems regarding the mesh motion, e.g. counter-oriented motion of two neighbouring points close to the leading edge could lead to negative cell volumes within the numerical grid. Therefore a movement of the points is only allowed in the direction normal to airfoil surface, as it was shown that sufficiently small movements can be reduced to a motion in normal direction (Castro, Lorenzo, Palacios, & Zuazua, 2007). Thus the surface points moving in normal direction are the design parameters s for this parametrization. The adjoint approach, as it is implemented here, cannot handle discontinuities, which occur at the trailing edge (Anderson & Venkatakrishnan, 1997). To avoid this problem, the trailing edge and a few adjacent faces are fixed, here the last 4% of the chord, are fixed.

The cells in the boundary layer usually have a high aspect ratio in order to have a low amount of total cells, but still a good resolution of the boundary layer. In some cases, the general mesh movement in OpenFOAM can lead to errors in the numerical grid, as the used step sizes could be larger than the size of the boundary layer cells. A movement of the numerical grid with such a condition must be handled carefully to assure a high cell quality after the mesh update. Therefore, the previously described mesh motion implemented by the authors Schramm et al. (2016) is used for free shape deformation with $N=364$ design parameters.

Figure 1. Numerical grid used for the evaluation of the goal function. (a) C-grid of the full domain and (b) Close-up view of the airfoil (here NACA 0020).

4. Optimization methods

An overview of the unconstrained optimization methods and algorithms, which are benchmarked in this paper, is given in this section. At first, the Nelder–Mead algorithm, which does not require any gradients, is described. Then, the method of steepest descent and the Quasi-Newton algorithm are presented. These require gradients, which are computed by finite differences or the adjoint approach.

4.1. Nelder–Mead (Downhill Simplex) algorithm

The Nelder–Mead (NM) method, which is also known as downhill simplex, is a simple, robust, easy-to-use, heuristic unconstrained optimization algorithm, which requires a continuous goal function - indeed, non-differentiable goal functions are okay (Nocedal, 2006). The Nelder–Mead algorithm relies on the “movement” of an $N+1$-dimensional simplex in N-dimensional design space, according to simple, heuristic rules. Its robustness and simplicity, especially since gradient information is not required, makes the Nelder–Mead algorithm to the work horse in engineering. Typical termination conditions for a Nelder–Mead search are step sizes in the design space, or in the goal function.

Special care has to be taken to the choice of the initial simplex, since this strongly determines the efficiency of the algorithm. As the Nelder–Mead proceeds from iteration to iteration the improvement in goal function has to be monitored until a properly set termination condition is reached. All in all, the Nelder–Mead algorithm is easy to use and requires little insight into the intricacies of optimization theory.

4.2. Method of steepest descent

The method of steepest descent (SD) is a first-order method, which requires a continuous and differentiable goal function (Nocedal, 2006). The iterative algorithm applies at each iteration a search directed to the steepest descent. For this, obviously, gradient information is needed. Due to the lack of a step size, a line search is applied at each iteration step. Often the norm of the gradient is used a first-order termination condition for a steepest descent search.

As in most cases, the optimal search direction (pointing to the minimum) differs largely from the gradient direction, the steepest descent search results in a highly inefficient, but typical zigzag pattern. Consequently, the method of steepest descent has found little applicability in practice, since its performance is in most cases largely inferior to second-order methods, like the Quasi-Newton method. For high-dimensional design spaces, though, the method of steepest descent can be advantageous, since it does not require the estimation of the inverse Hessian, which scales with the number of design variables.

The set-up and maintenance of a steepest descent method is not simple, but also not too difficult. Special care has to be taken for the accuracy of the gradient estimation. Besides, parameters of the line search and termination condition have to be set properly, and have to be monitored as the optimization proceeds.

Using the method of steepest descent based on gradients calculated using the adjoint approach in combination with the free shape parametrization has shown to be impractical, as can be seen in Section 4.5.1. Thus, a smoothing is applied to the gradients, where the gradient of each design parameter is smoothed using weighted gradients of the neighbouring design parameters. Especially in areas of large flow parameter gradients, e.g. close to the stagnation point or the suction peak, this increases the quality of the optimization result. Still, a weighted smoothing influences the gradient direction and therefore is not a pure steepest descent method any more.

4.3. The family of Quasi-Newton methods

All members of the family of Quasi-Newton methods are second-order methods, which require a continuous and two-times differentiable goal function. In Quasi-Newton methods, the second-order information (Hessian) is not computed directly. Instead, the Hessian is estimated with the help of an iterative procedure, where the BFGS and Davidon–Fletcher–Powell(DFP) schemes are most successful, on the basis of gradient information only (Nocedal, 2006). To build up proper information inside the approximated Hessian, typically N iterations are needed in an N-dimensional design space. This is one of the weaknesses of Quasi-Newton methods, which makes it unstable and inefficient for a large number of design variables. The typical termination conditions for Quasi-Newton algorithms is the norm of the gradient. On the basis of the Hessian, Quasi-Newton methods can derive proper search directions pointing to the minimum (and to the steepest descent), with a proper step length. As such, the methods are highly efficient and inefficient zigzag search paths are avoided.

4.4. Gradient estimation by finite differences

A common approach to approximate gradients is the use of finite differences (FD), which are based on Taylor’s theorem (Nocedal, 2006). Some codes use first-order forward differences, but here second-order central differences are used. Beside the approximation and neglect of higher order terms, a principal problem of finite differences is the evaluation of the step size h, which determines the magnitude of the change of the design parameters. A too small step size can lead to round-off errors whereas a too big step size can result in truncation errors. An improper choice of the step size can thus lead to erroneous gradients and poor optimization results. In practice, before using finite differences, a sound gradient and noise study is required to identify proper step sizes for each design variable. If step sizes are chosen properly and noise in the goal function is not too large, FD is a reliable and stable gradient estimator. The computational cost for FD is comparably high, since the number of goal function evaluations scales linearly with the number of design variables. With this, in the realm of shape optimization in fluid dynamics, FD requires tremendous computational resources, since (a) the number of design variables is high, and (b) the computational cost for a single evaluation of the goal function is high. In this paper, the symmetrical FD scheme is used, where proper step sizes had been chosen in each case, with the help of a gradient study.

4.5. Gradient estimation by the adjoint approach

Various authors propose the adjoint method for the computation of the gradients (Papadimitriou & Giannakoglou, 2006; Othmer, 2008; Soto & Löhner, 2004). By this the high computational cost of FD for a large number of design variables can be avoided, since the computational effort is independent of the number of design variables. But another set of partial differential equations—the adjoint equations—have to implemented and solved numerically. In practice, the adjoint approach for gradient estimation imposes several additional tasks on the CFD practitioner, such as implementation of the adjoint equations and maintenance of the convergence behaviour of a second set of field equations. Besides, the continuous adjoint equations often impose simplifications, i.e. the adjoint turbulent viscosity is often assumed to be identical as the one from the primal flow field.

As such, both is benchmarked here, gradient estimation via FD and via the solution of adjoint equations. In this paper, the continuous adjoint approach is used, since OpenFOAM is highly suitable for the implementation of continuous equations. The implementation of the adjoint field follows the available adjoint solver for ducted flows by Othmer, de Villier and Weller (2007). Therein the adjoint turbulent viscosity is supposed to be equal to the turbulent viscosity of the flow field. This approximation is widely used in the literature and referred to as “frozen turbulence”. As the adjoint field is “driven” by the flow parameters, a high convergence of the flow field is required for correct adjoints to the flow field. This leads to high quality requirements regarding the numerical grid and a careful case set-up. In this work, the flow field is pre-converged, before the adjoint field is solved, which leads to a stable and converging adjoint field. The iterations needed for pre-convergence are added to the total amount of iterations needed for the optimization case.

The gradient information can be used directly for pure free shape parametrization, or treated further, e.g. by smoothing the gradient field or by projecting the gradients to design parameter of a lower design space. The adjoint method computes gradients on the whole geometry surface, which can also be interpreted as production sensitivities. The designer can use the size of the sensitivities to define the importance and range of production tolerances. In the process, large sensitivities indicate where tolerances should be fulfilled and low tolerances where can be higher. By this, the production costs can be controlled precisely.

4.5.1. Preliminary study on free shape optimization using the adjoint approach and steepest descent for 364 design variables

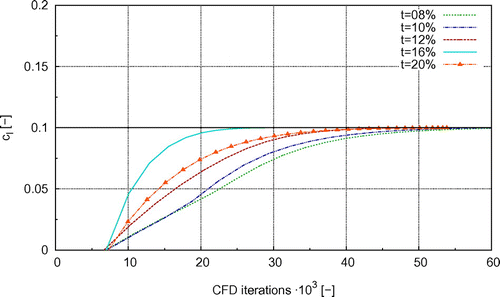
In order to show the potential and drawback of free shape deformation, a preliminary study on optimizing an airfoil using the adjoint approach and steepest descent for all surface points as design parameters is conducted. Figure 2 shows the development of the lift coefficient during this optimization. The initial lift is $c_l=0.0496$ and the goal is to increase the lift to $c_l^{\ast }=0.0530$, which corresponds to an increase of nearly 7%. The goal function is a quadratic least square function as shown in Equation (1), without any penalty functions. In this example, all surface points are free to move and the gradients are neither smoothed nor transformed in any way. Only the last 4% of the chord are fixed in position. As mentioned before, this is necessary, since the adjoint approach as it is implemented here does not support discontinuities.

Figure 2. Evolution of lift coefficient $c_l$ against CFD iterations with $N=364$ design variables using method of steepest descent (goal lift coefficient $c_l^{\ast }=0.0530$).

Figure 3. Close-up views of leading (left) and trailing (right) edge of the initial airfoil and optimized shape, where the optimization uses method of steepest descent with $N=364$ design variables (goal lift coefficient $c_l^{\ast }=0.0530$).

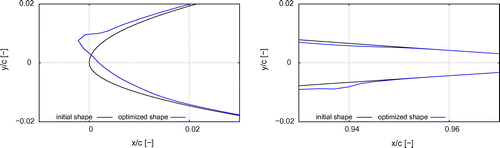
The resulting shapes of this optimization are shown in Figure 3, where a close-up view of leading and trailing edge are shown. Since the adjoint field and therefore also the gradients are driven by the flow field, relatively large geometry changes are expected at areas with large changes in the flow field. The overall changes in the geometry are small and thus only close-up views of the leading and trailing edge are presented. It can be seen that the trailing edge geometry (last 4% of the chord) is not changed due to the fixed surface points and that a bump occurs at the leading edge. This bump may not be useful for a practical application of this airfoil, but it is mathematically correct, since the goal lift coefficient is reached.

The tendency of developing bumps can lead to issues with convergence of the primal and adjoint field. Hence, a free shape parametrization can only be used, if changes in the goal function and thus the shape deformations are small. This was the case for the presented example, but will not hold for the following optimizations. In order to overcome such a problem additional smoothing approaches can be used, e.g. use of regularization methods (Hojjat, 2015; Jameson & Vassber, 2000; Soto et al., 2002). Also a projection of gradients to a lower design space can be applied to overcome infeasible geometries, which is presented in the following Section 4.6.

For free shape deformation in this work, a simple smoothing of the gradients is applied by weighted averaging over neighbouring surface points. This results in a reduction of the effective design variables, but still each airfoil point is moved individually. For convenience, the number of $N={364}^{\ast }$ parameters is used in the following sections, but is marked with a star as the reader should remember that the number of parameters is affected by the applied smoothing.

Beside the use of the adjoint approach for optimization, a practical application is the use of the gradient information for sensitivity maps. The designer can manually include the sensitivities of a given objective function in the design process of a geometry. This is rather a cumbersome improvement process instead of an optimization, but can be done in cases, when too many constraints have to be considered, e.g. aerodynamic optimizations of car outlines (Othmer, 2014).

4.6. Projection of gradients

The strength of the adjoint approach is that the gradient computation does not scale with the number of design parameters and thus each airfoil point can be used as an individual design variable. In practice this is rarely done, since high gradients in the primal flow lead to strong adjoint gradients in the affected regions, resulting in uneven deformations such as bumps. These can be mathematically correct results of an optimization, but they are seldom suitable for standard engineering applications, which can be seen in Figure 3, where the large flow acceleration along the leading edge leads to large gradients in some regions and therefore to large deformations. At the same time, the flow is rather steady between 20–90% of the chord, such that the gradients are not pronounced in this area and the movements are small.

The grid on the surface of the airfoil contains 364 surface points and the adjoint method leads to gradient information on each of these points. Thus a projection from these 364 gradients on less design parameters N is implemented, which is necessary when using a parametrization with less design variables, such as the NACA equation or Bézier curves in combination with the adjoint method. A projection allows an exact transfer of the information gained by the gradient of the goal function $f(s(x,y))$ defined within the numerical grid coordinate system based on $(x,y)$ to the chosen design parameter defined in the parametrization equation, e.g. Bèzier control points.

A reduction to very few design variables might not be useful in combination with the adjoint approach, as the solution of the adjoint equations needs some additional computational effort, which may not pay off, e.g. when only two parameters are used. However, it is done in this work in order to compare the different optimization algorithms and to evaluate when the adjoint approach increases the speed of the optimization and when standard finite-differencing is sufficient for the gradient computation. Besides, a projection of the gradients to lower dimensions also applies an indirect smoothing.

The chain rule is used for the gradients of the goal function $f(x(s),y(s))$ within the two-dimensional coordinate system where the surface points are defined in. The x- and y-coordinates depend on the selected parametrization parameter $s_m$ of the chosen parametrization, e.g. the NACA parameters or the control points of the Bézier curves. The gradient of the cost function with respect to the design parameters then is:(4) $$\begin{array}{c}\hfill \frac{\mathit{\partial }f}{\mathit{\partial }{s}_m}=\sum _{k=1}^K\left(\frac{\mathit{\partial }f}{\mathit{\partial }{x}_k}\frac{\mathit{\partial }{x}_k}{\mathit{\partial }{s}_m}+\frac{\mathit{\partial }f}{\mathit{\partial }{y}_k}\frac{\mathit{\partial }{y}_k}{\mathit{\partial }{s}_m}\right),\end{array}$$(4)

where K are the airfoil points in total. The gradients $\frac{\mathit{\partial }f}{\mathit{\partial }{x}_k}$, $\frac{\mathit{\partial }f}{\mathit{\partial }{y}_k}$ are calculated by the adjoint method on each surface point k with its different x- and y-components, respectively. This projection of gradients is exact, since for each design parameter the gradients along the whole surface are taken into account. It can easily be extended for 3D applications by adding the z-direction.

5. Simulation and optimization set-ups

The following benchmark is done for five initially symmetric airfoils at a Reynolds number of $\text{Re}=50,000$ and an angle of attack of $AoA=0^{\circ }$, with zero lift coefficient $c_l(s_0)=0$. In order to ensure a good comparability, five initially symmetric airfoils with different initial thickness’ of 8, 10, 12, 16 and 20% are optimized. Different parametrizations are used within different optimization methods, but the general CFD set-up of the simulations is the same in order to ensure a valuable comparison. The numerical grid as it is used here is a compromise between the different optimization methods in this work. The Nelder–Mead algorithm is generally able to handle a higher amount of noise in the objective function than a Quasi-Newton method. The adjoints are driven by the primal flow field and any numerical error is directly transferred to the adjoint field, leading to noise in the gradient evaluation. Thus a fine grid is needed in the adjoint approach, but a coarse grid could be used with the Nelder–Mead algorithm and a standard RANS simulation of an airfoil could probably also deliver adequate results with a coarse grid. For practical applications, the computational accuracy has to be high in order to find improvements over airfoils, which are commonly in use. In principle, the simple airfoils in this work could also be optimized with a smaller accuracy, when using Nelder–Mead algorithm. But for the gradient computation (via adjoints or finite differences), a reasonably high accuracy is necessary. This necessity is the minimum limitation for the computational costs and any higher accuracy is not computed in order to limit the costs. After some preliminary testing, the grids are created as described in the following. They allow a comparability of the different optimization methods without leading to a predominance of a single method due to its own strengths in the mesh requirements. The numerical grids are block-structured, hexahedral C-grids with a domain size of approx. Fifteen chord lengths and nearly 50,000 cells, where the airfoil surface consists of 364 faces. The RANS equations are closed by the Spalart–Allmaras turbulence model without transition (Spalart & Allmaras, 1992) and in order to fully resolve the flow in the boundary layer the dimensionless wall distance is at $y^{+}\approx 0.7$. The grid of the symmetric NACA airfoil with 20% relative thickness is shown in Figure 1. Standard boundary conditions, such as Dirichlet and zero Neumann, are used for the flow simulations.

Table 1 summarizes all nine different optimization cases, which are benchmarked in this paper: two cases Nelder–Mead, four cases Quasi-Newton and three cases steepest descent. The first two cases do not require gradient estimation. In two cases, gradient estimation via finite differences is used. In five cases, gradient estimation via the solution of the adjoint equations is used, including gradient projection, if needed. There is no Quasi-Newton used with $N=364$ design parameters, since the approximation of the Hessian is computationally too expensive and with these design parameters the algorithm may easily lead to grid errors as discussed in Section 4.5.

The needed CFD iterations for five airfoil optimizations are averaged, in which the optimizations aim at lift coefficients of $c_l^{\ast }=0.1$ and $c_l^{\ast }=0.2$. Thus a total of $9·5·2=90$ optimizations are conducted.

Table 1. Optimization set-ups with different optimization methods and number of design parameters (“FD” refers to gradients by finite differences)

Nelder–Mead		Quasi-Newton		Steepest descent
Design parameters	Gradient estimation	Design parameters	Gradient estimation	Design parameters	Gradient estimation
2	–	2	FD/Adjoints	2	Adjoints
14	–	14	FD/Adjoints	14	Adjoints
–	–	–	–	${364}^{\ast 1}$	Adjoints

${}^{\ast 1}$Smoothing with neighbouring values is applied on the gradients, such that the effective amount of design parameters is reduced. Still, each grid point is moved individually.

By tuning the initial configuration, e.g. step sizes, Hessians or initial simplex, the user could improve each optimization process individually. This influences the stability and convergence behaviour of the optimization and would bias the comparison. Thus the first step of the optimization should lead to a lift coefficient within the range of 40–60% of the goal lift coefficient. In order to reach convergence, the goal function f(s) has to drop below ${10}^{-6}$ for all following optimization steps. Thus $\frac{1}{2}{\left(c_l(x)-c_l^{\ast }\right)}^2\le {10}^{-6}$ is applied.

6. Results

In the following, the convergence behaviour of the different optimization set-ups is compared and the needed amount of total CFD iterations is evaluated. This also includes the necessary iterations for computing the gradients via the adjoint approach or via finite-differencing. Finally, the ease of use is compared as well, summing up the experiences of the authors within this work.

6.1. Evolution of the lift coefficient

In order to check the convergence behaviour of the various optimization set-ups, the evolution of the lift coefficient over the total CFD iterations is analyzed. The results of two cases using the NACA parametrization with $N=2$ is shown in Figure 4, where the upper graph shows the optimization of an airfoil with the initial thickness of 8% and the lower one for the initial thickness of 20%.

In both cases, an obvious difference between the gradient-free and the gradient-based optimization can be seen. The Nelder–Mead algorithm uses big steps in the beginning, which leads to high changes of the lift coefficient and produces a zigzag pattern. This algorithm needs less CFD iterations between two optimization steps than the gradient-based methods, which use smaller optimization steps, and the Nelder–Mead converges only a little slower than the other methods. The method of steepest descent uses more optimization steps to reach the goal lift coefficient, where an automatic reduction of the step size is used every time the cost function becomes bigger than in the previous step. The Quasi-Newton algorithm (QN) needs a similar amount of CFD iterations as the steepest descent, but less optimization steps due to the additional information provided by the approximated Hessian. Here, providing the Hessian for the QN consumes more CFD iterations, which depletes the advantage of less needed optimization steps.

The course of the adjoint Quasi-Newton in Figure 4(a) is similar to the Quasi-Newton using finite differences, where as in Figure 4(b) for an airfoil with an initial thickness of 8% the courses are very different. The amount of total CFD iterations are of similar size, but the lift coefficient overshoots the goal lift coefficient significantly when using the adjoint approach.

Figure 4. Evolution of lift coefficient $c_l$ over CFD iterations using $N=2$ design variables (NACA parametrization) and different optimization methods for a goal lift coefficient of $c_l^{\ast }=0.1$. (a) Initial airfoil thickness of 8% and (b) Initial airfoil thickness of 20%. Notes: “NM” refers to Nelder-Mead; “QN FD” refers to Quasi-Newton and gradients by finite differences; “QN adj” refers to Quasi-Newton and gradients by the adjoint approach; “SD adj” refers to steepest descent and gradients by the adjoint approach.

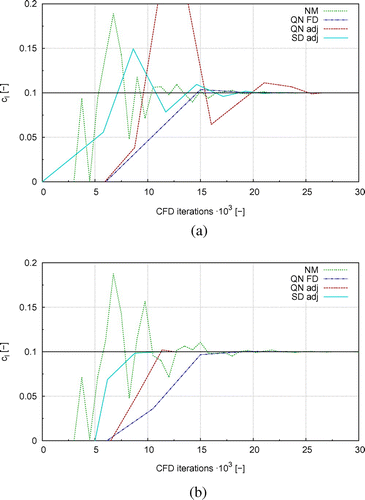
Figure 5. Evolution of lift coefficient $c_l$ over CFD iterations using $N=14$ design variables (Bézier parametrization) and different optimization methods for a goal lift coefficient of $c_l^{\ast }=0.1$. (a) Initial airfoil thickness of 8% and (b) Initial airfoil thickness of 20%.Notes: “NM” refers to Nelder-Mead; “QN FD” refers to Quasi-Newton and gradients by finite differences; “QN adj” refers to Quasi-Newton and gradients by the adjoint approach; “SD adj” refers to steepest descent and gradients by the adjoint approach.

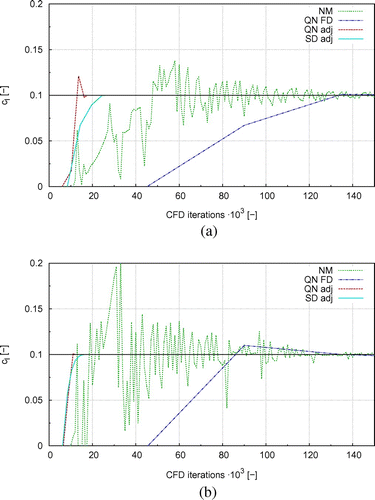
This could result from a noisy gradient computation and thus a bad approximation of the Hessian. Another possible influence on the convergence could be the airfoil thickness itself, since a thicker airfoil is less sensitive to geometry changes than the thin airfoil. Thus, similar initial step sizes for airfoils of different thickness’ may have different influence on the lift coefficient.

A further tuning of the initial Hessian could be a possible solution, but is not done here in order to ensure a fair comparison of the different methods. Also it is a known effect of the QN algorithm that the first optimization steps are prone to errors, as the approximation of the Hessian using the BFGS method needs up to $2·N$ iterations until it reaches a reliable state (Nocedal, 2006).

The behaviour when using the Bézier parametrization with $N=14$ design variables is different than in the previous cases. The results of the evolution for two initial airfoils are shown in Figure 5, where the upper graph shows the optimization of an airfoil with an initial thickness of 8% and the lower one shows the results of an initial thickness of 20%.

For both cases, the Nelder–Mead algorithm (NM) shows a zigzag pattern as before and needs more than 150,000 CFD iterations in total. The use of finite differences with the Quasi-Newton method (QN) also needs more than 150,000 CFD iterations to reach the given convergence criteria of $\frac{1}{2}{\left(c_l(x)-c_l^{\ast }\right)}^2\le {10}^{-6}$. In contrast, using the adjoint approach leads to a much faster convergence and the amount of total CFD iterations is in the order of the previous cases when $N=2$ design variables were used, underlining the independence of the adjoint approach regarding the amount of design variables. The method of steepest descent needs a little more CFD iterations than Quasi-Newton, where the information of an approximated Hessian is used. Figure 6 shows the results of steepest descent with $N={364}^{\ast }$ design variables, where the initial airfoils have a different thickness. The optimization starting with an initial airfoil thickness of 16% converges faster than starting with other airfoils, which need approx. the same amount of CFD iterations. This difference could result from a smoother flow behaviour around this airfoil in combination with a good response to design parameter changes at this airfoil thickness and was also noticed at other parametrizations.

Figure 6. Evolution of lift coefficient $c_l$ over CFD iterations using $N={364}^{\ast }$ design variables and steepest descent using gradients by the adjoint approach for a goal lift coefficient $c_l^{\ast }=0.1$. Initial airfoils have different thickness t.

6.2. Comparison of total CFD iterations needed

Table 2 shows the CFD iterations for the different optimization set-ups averaged over all five airfoils and sorted by the two goal lift coefficients $c_l^{\ast }=0.1$ and $c_l^{\ast }=0.2$, respectively. In all cases with fully converged optimizations, the higher goal lift coefficient leads to an increase in needed CFD iterations. This can be expected since the higher goal is further away from the initial shape with zero lift. As mentioned in Section 5, no Quasi-Newton with $N=364$ design parameters is used due to the high computational costs for the Hessian approximation and expectable errors in the numerical grid.

Using the adjoint approach with $N=2$ design variables, the method of steepest descent needs a similar amount of CFD iterations as the Quasi-Newton method. Using $N=14$ design variables instead, the use of the Hessian leads to a faster convergence than a simple steepest descent, because of the advantageous information from the Hessian. Additional CFD iterations are needed for an accurate approximation of the Hessian and for the adjoint approach with $N=14$ design variables the beneficial use of the Hessian outbalances this extra computational effort.

The adjoint approach scales with a factor close to 1, in case of Quasi-Newton even below 1, which results from the overshoot due to possibly noisy gradients as it was shown in Figure 4(a) for $N=2$. The Nelder–Mead algorithm (NM) scales superlinearly and needs approximately nine times more iterations for $N=14$ than for $N=2$ design parameters. The optimization using finite differences scales superlinearly with a factor of approximately 14, since the gradients have to be computed for each design variable separately.

Table 2. Comparison of the needed CFD iterations for the different optimization set-ups averaged over all five airfoils (more $+$ means higher ease of use)

Optimization method	Design variables	Gradient calculation method	Averaged number of CFD iterations ($\times {10}^3$)		Ease of use
			$c_l^{\ast }=0.1$	$c_l^{\ast }=0.2$
Nelder–Mead	2	–	21.5	24.2	+++
	14	–	191.8	217.6	+++
Steepest descent	2	Adjoints	14.9	16.0	+
	14	Adjoints	18.3	23.2	+
	364${}^{\ast }$	Adjoints	42.2	74.9	+
Quasi-Newton	2	Adjoints	15.3	19.7	+
	2	Finite differences	18.6	23.1	++
	14	Adjoints	14.9	16.1	+
	14	Finite differences	261.0	297.0	++

Comparing the optimizations using different amounts of design parameters, the advantage of the adjoint method becomes clear. While the effort for Nelder-Mead or finite differences increases with the number of design parameters—sometimes even dramatically, the adjoint approach barely scales with the amount of design variables. Using gradients via the adjoint approach shows that the number of CFD iterations is nearly independent from the number of design parameters, which proofs the theoretical idea of this method (at least for the simple cases presented here).

Table 2 also shows the ease of use of the different methods, which is evaluated by the authors experience of robustness, stability and user knowledge needed for each method. For the presented cases, the Nelder–Mead algorithm is the easiest and most robust method. Also the dependence on the quality of the CFD computations is not as high as for other methods. Quasi-Newton using finite differences needs more user knowledge, but is more robust than the continuous adjoint approach, which requires more experience of the user.

In summary, Nelder–Mead or gradient-based methods using finite difference might be more stable and less sensitive to the initial optimization set-up, but they scale with the number of design parameters. The adjoint approach is more sensitive to the initial set-up, i.e. mesh quality and user experience, but barely depends on the number of design variables. Both, the optimization using finite differences and the adjoint method, require a certain level of quality for the CFD computation and lead to requirements in the pre-processing, e.g. the preparation of the numerical grid and the numerical schemes.

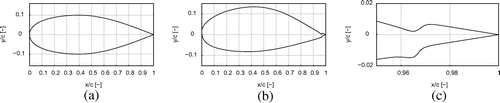
6.3. Comparison of final airfoil shapes

Beside the convergence of each method, the final airfoil shape is of importance and Figure 7 shows the shapes resulting from the different optimization strategies for a goal lift coefficient of $c_l^{\ast }=0.2$ with $N=2$ design variables (NACA parametrization) with an initial thickness of 20%. During the optimization, the camber increases from the initially symmetric airfoil in order to generate lift. Beside the result from the steepest descent, the optimized shapes are similar to each other. This is also an effect of the chosen parametrization due to few design variables. Here, the geometries have to follow the NACA equation and therefore always stay within the range of this airfoil type. Note that the optimization is unconstrained and thus the thickness may vary.

Figure 8 shows the shapes resulting from the different optimizations for a goal lift coefficient of $c_l^{\ast }=0.2$ with $N=14$ design variables (Bézier parametrization) with an initial thickness of 20%. The shapes resulting from Nelder–Mead and Quasi-Newton using finite differences are similar. In contrast, the results from the same optimizer, i.e. Quasi-Newton, depend on the gradient estimation and differ from each other. This can be explained by a different computation of the gradients, where each method includes a varying noise leading to unequal gradients and Hessians. The resulting shape using steepest descent is completely different than the others. It seems to be similar to the case when using $N=2$ design variables, but is also different to that one. Note, the optimization problem is posed in a way that the solution space is large and many solutions are possible, which means that identical shapes would only result due to coincidence. Similarities, as they appear here, are not a sign for a better solution or a higher level of convergence.

Figure 7. Initial airfoil (20% thickness) and optimized shapes resulting from different optimization strategies for a goal lift coefficient of $c_l^{\ast }=0.2$ and $N=2$ design variables (NACA parametrization). (a) Initial airfoil, (b) Nelder-Mead, (c) Steepest Descent with gradients via the adjoint approach (d) Quasi-Newton with gradients by finite differences and (e) Quasi-Newton with gradients via the adjoint approach.

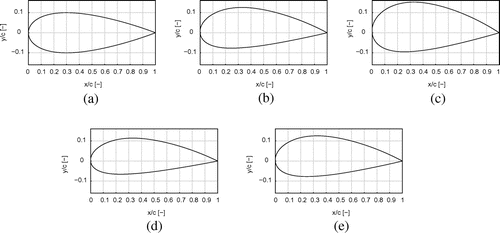
Figure 8. Initial airfoil (20% thickness) and optimized shapes resulting from different optimization strategies for a goal lift coefficient of $c_l^{\ast }=0.2$ and $N=14$ design variables (Bézier parametrization). (a) Initial airfoil, (b) Nelder-Mead, (c) Steepest Descent with gradients via the adjoint approach, (d) Quasi-Newton with gradients by finite differences and (e) Quasi-Newton with gradients via the adjoint approach.

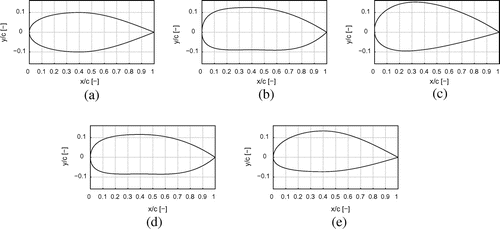
Figure 9 shows the shape resulting from the use of steepest descent with $N={364}^{\ast }$ design variables for a goal lift coefficient of $c_l^{\ast }=0.2$ with an initial thickness of 20%. The shape is different from the previous shapes, since it has more degrees of freedom, although it should be noted that such a shape is only possible when the gradients are smoothed as discussed in Section 4.5.1. Note the shape close to the trailing edge, where the optimization produces a bump resulting from fixed points at the trailing edge. As mentioned, this fixing is necessary in order to use the adjoint approach with surface points as design parameters, since the high quality of the numerical grid has to be maintained. Still, the gradients are computed correctly (aside from noise terms), which can be concluded from the resulting cambered airfoil, where the shape near the trailing edge bends downwards in order to generate lift. Further work would be needed in order to formulate a different smoothing or more stable mesh movement for avoiding inflection points even in this region.

Summed up, the final shapes show that constraints are necessary for meaningful optimization, as the airfoils may not be suitable for some engineering applications.

Figure 9. Initial airfoil (20% thickness) and optimized shape resulting from steepest descent with gradients via the adjoint approach for a goal lift coefficient of $c_l^{\ast }=0.2$ and 364 design variables. (a) Initial airfoil, (b) Steepest Descent with gradients via the adjoint approach and (c) Close-up view of trailing edge when using Steepest Descent with gradients via the adjoint approach.

7. Conclusions

The presented work deals with the unconstrained shape optimization of 2D airfoils using different optimization configurations. The gradient-free Nelder–Mead algorithm is compared with two gradient-based methods, the method of steepest descent and Quasi-Newton. In both methods, the gradients are computed by the adjoint approach, but also finite differences are used within the Quasi-Newton method. The airfoil shape is parametrized by the 4-digit NACA equation ($N=2$ design parameters), a set of Bézier curves ($N=14$ design parameters) and by a free shape parametrization ($N=364$ design parameters), where each airfoil surface point is an individual design parameter.

The results show that the Nelder–Mead algorithm works well with a small number of design parameters and is then comparably fast as the gradient-based methods. Using more design variables, the computational effort for Nelder–Mead as well as finite differences increases superlinearly. Only the adjoint approach is able to converge within a similar amount of total CFD iterations, nearly independent from the number of design parameters, which is in accordance with the theory of the approach.

However, the requirements of user knowledge and experience needed for a successful optimization with Nelder–Mead are the lowest, since this algorithm does not need any gradient information and hence is more robust than the gradient-based methods. The use of finite differences need a careful set-up of the step sizes and eventually a tuning of the initial Hessian, whereas the adjoint approach is less stable and requires the most user knowledge of these presented methods.

The questions raised in the introduction addressed the efficiency regarding computational costs, the robustness of the algorithms as well as the ease of use and the needed user knowledge beforehand. To recommend an optimization method best suitable to the readers problem and to answer those questions, the following can be concluded:

(1)	The Quasi-Newton method using the adjoint approach is most efficient when using $N=14$ or more design variables.
(2)	The Nelder–Mead method is most robust and comparably easy to use.
(3)	The adjoint approach clearly requires the highest level of knowledge and maintenance.

 

Future analysis should be done in the course of constrained optimizations. Also more complex cases at higher angles of attack or multi-point optimizations should be investigated. Large-scale problems can be optimized with all presented methods, but the computational effort will increase dramatically, if not the gradient computation via the adjoint approach is used. For the shown optimization algorithms, a suitable parametrization for large scales has to be defined. In case of the adjoint approach with many design variables, improvements in gradient smoothing should be developed. Another possible development step would be the inclusion of structural constraints, leading to multi-disciplinary optimization. This adds extra design restrictions, but may lead to more practical designs in future.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

L. Vorspel

ForWind is the joint Center for Wind Energy Research with basic research ranging broadly in engineering and physics. Computational fluid dynamics (CFD) are used to investigate the interaction between turbulence and wind turbines, e. g. by fluid-structure-coupled simulations of turbines.

Fraunhofer IWES ensures investments in technological developments in the field of wind energy through its validation services. One focus is the enhancement of numerical methods within OpenFOAM and its use for aerodynamic applications, e.g. simulating full rotor blades within aero-servo-elastic conditions.

The Institute for Computational Engineering (ICE) at the University for Applied Sciences NTB, Switzerland is devoted to bringing state-of-the art results from mathematics to industry and engineering departments. Special emphasis is on the fruitful application of optimization algorithms for automatic design of technical systems.