On comparison of tuning method of FOPID controller for controlling field controlled DC servo motor

Abstract

In this paper, the Simulated Annealing (SA) optimization method is introduced to estimate the parameters of Fractional Order Proportional-Integral-Differential (FOPID) controller for controlling a field-controlled DC servo motor. The parameters are evaluated for considering a transfer function of controlling a field-controlled DC servo motor and its performance is observed for unit step response. Also, the parameters of FOPID controller are calculated using the traditional techniques such as Genetic Algorithm (GA) and frequency domain design method based on constrained optimization for the sake of comparison of performance with respect to simulated annealing method. A detail study on all the specified techniques is discussed in this paper.

Keywords:

• FOPID
• fractional calculus
• frequency domain design
• genetic algorithm
• simulated annealing

Public Interest Statement

Fractional Order Proportional Integral Differential Controller (FOPID) has gained more attention over the conventional PID controller as it has two extra control parameters. Moreover the FOPID controller offers more robustness, good tracking ability, less sensitive to external disturbances and iso-damping property of step response. In literature, various tuning methods for tuning of FOPID controller has been proposed to achieve faster response while minimizing the steady state error. In this paper, the Simulated Annealing (SA) optimization method is introduced to estimate the parameters of FOPID controller for controlling a field controlled DC servo motor. Here in this paper the performance comparison of PID and FOPID has been done on the basis of unit step response.

1. Introduction

In the recent years, modern control theories have made great advances. Control techniques including unified feedback control, optimal control, predictive control, neural network control, fuzzy logic control and so on, have been developed significantly. Nevertheless, the PID control technique has still been widely used in many industrial applications such as process control, motor drives, flight control, etc. More than 90% of the control loops in industry are PID based control loop (Åström, & Hägglund, 1988). This is mainly because of PID controller possesses robust performance to fulfill the global change of industry process, simple structure to be easily understood by engineers, and easiness to design and implement.

Lately, there are increasing interests to enhance the performance of PID controller by using the idea of fractional calculus, which deals with fractional or non-integer order of derivative and integral. Fractional order PID controller proposed by Podlubny is a generalization of the classical PID controller using the fractional calculus (Podlubny, 1999). Its transfer function is described by Equation (1). A Fractional Order Proportional-Integral-Differential (FOPID) controller is characterized by five parameters, i.e. the Proportional gain ($K_p$) the integral gain ($K_i$), the derivative gain ($K_d$), integral order ($\mathit{\lambda }$) and derivative order ($\mathit{\mu }$).(1) $$\begin{array}{c}\hfill G_c(s)=K_p+K_i{s}^{-\mathit{\lambda }}+K_d{s}^{\mathit{\mu }}\end{array}$$(1)

Many research results show that FOPID controller has better performance and robustness than classical PID controller. So that, the FOPID controller parameter tuning is a critical and major issue (Cominos & Munro, 2002). In the literature, many formulations have been documented to design FOPID controller. These approaches can be classified into two types: analytic methods (Bouafoura & Braiek, 2010; Edet & Katebi, 2016) and heuristic methods (Maione, Punzi, & Li, 2013). In the analytic type, the parameters of FOPID controller are tuned by reducing a nonlinear objective function depending on the specifications given by the designers (Edet & Katebi, 2016).

2. Classical PID vs. fractional order PID controller

Although the classical PID controller works well regarding the fulfillment of the design specification. But with the change of parameters value and aging the output tends to deteriorate and deviate. The classical PID Controller do not have the capability to cope with the changing parameter (Monje, Vinagre, Feliu, & Chen, 2008). With this the output tends to deviate from its nominal value, which force the system towards instability or a region of low efficiency. Moreover the classical PID controllers have only three parameter to tune which limit the tuning strategy. The integral constant and the derivative constant in classical PID controller are related to each other (generally regarded as “$\mathit{\alpha }$” in literature) (Chen, Hu, & Moore, 2003). Therefore the classical PID controller have very little scope for tuning. As a consequent the robustness of a control system cannot be increased with the help of this existing parameter and this limits, the use of classical PID controller in the future prospects.

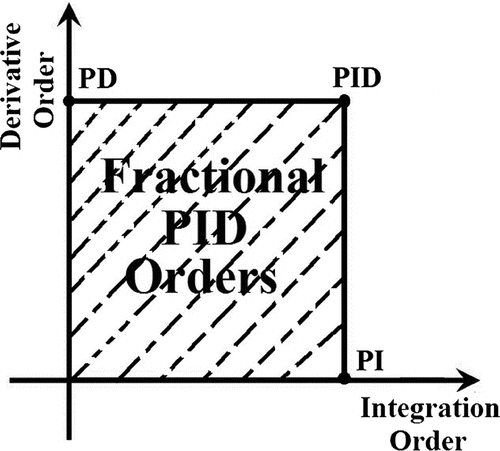
The limitation of a classical PID controller can be overcome by the introduction of additional tuning parameter that is the order of integrator and differentiator (Vinagre, Podlubny, Dorcak, & Feliu, 2000). Naturally, besides setting proportional gain $K_p$, integral gain $K_i$ and derivative gain $K_d$, we have two more parameter $\mathit{\lambda }$ and $\mathit{\mu }$, which widens the scope of control system design (Li, Yang, Peng, & Wang, 2006). The fractional order controller generalizes the integer order PID controller design and expands it from point to plane (Vu & Lee, 2013). This expansion adds more flexibility to control system design and we can control our real world process more accurately (Maiti, Biswas, & Konar, 2008). This is shown in Figure 1.

Figure 1. Expanding from point to plane.

With the help of fractional order PID controller it is possible to design a controller to ensure that the closed loop system is robust to gain variation and step response exhibits an iso-damping property (phase-bode plot of the system is flat at the gain crossover frequency) as a result system gets more robustness to gain variation (Chen et al., 2003). The width of flat phase region can be adjusted with the help of fractional order phase shaper (Chen, Moore, Vinagre, & Podlubny, 2004) resulting into a more robust system. $P{I}^{\mathit{\lambda }}{D}^{\mathit{\mu }}$ controllers are less sensitive to parameter variation.

As most of the real world process can be efficiently modeled with the help of fractional order differential equation rather than integer ones (Podlubny, 1999). Therefore fractional order controller is naturally suitable for these fractional order models to imply a better control.

3. Fractional calculus and approximation of fractional order transfer function

The concept of FO controller means, controllers can be explained by fractional-order differential equations. Of the various definitions of fractional derivatives, the Grunwald–Letnikov (Miller, 1993) and Riemann–Liouville (Eckert, Kupper, & Hohmann, 2014) definitions are the most widely used. These definitions are required for the realization of discrete control algorithms.(2) $$\begin{array}{c}\hfill D_t^{v}f(t)=\left\{\begin{array}{cc}\frac{1}{\mathrm{\Gamma }(-v)}\underset{a}{\overset{t}{\int }}{(t-x)}^{-v-1}f(\mathit{\tau })d\mathit{\tau }\hfill & v<0\hfill \\ \frac{d^{n}f}{d{t}^n}\hfill & a=n\in N\hfill \\ \frac{d^n}{d{t}^n}\left[{D_t}^{-(n-\mathit{\alpha })}f(t)\right]\hfill & 0\le n-1<\mathit{\alpha }<n\hfill \\ \frac{1}{\mathrm{\Gamma }(n-\mathit{\alpha })}\frac{d^n}{d{t}^n}\left[\underset{a}{\overset{t}{\int }}\frac{f(\mathit{\tau })}{{(t-\mathit{\tau })}^{\mathit{\alpha }-n+1}}d\mathit{\tau }\right]\hfill \end{array}\right\}\end{array}$$(2)

Here, $\mathit{\tau }(·)$ is the Eulers gamma function (Davis, 1959) given by Equation (3).(3) $$\begin{array}{c}\hfill \mathrm{\Gamma }(x)=\underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{x-1}dt,x>0\end{array}$$(3)

With special case when $x=n$$$\begin{array}{c}\hfill \mathrm{\Gamma }(n)=(n-1)!\end{array}$$

The Laplace transformation of Reimann-Lioville definition (Munkhammar, 2004) is discussed in Equations (5) and (6).(4) $$\begin{array}{cc}& L\{D^{-\mathit{\alpha }}f(t)\}=s^{-\mathit{\alpha }}F(s)\hfill \end{array}$$(4) (5) $$\begin{array}{cc}& L\{D^{\mathit{\alpha }}f(t)\}=s^{\mathit{\alpha }}F(s)-\sum _{k=0}^{k=n}{s^k\left[D^{\mathit{\alpha }-k-1}f(t)\right]}_{t=0}\hfill \end{array}$$(5)

where$$\begin{array}{c}\hfill (n-1\le \mathit{\alpha }\le n)\end{array}$$

These two equation represent the Laplace transformation of fractional order system. In practice, fractional order differentiators or integrators cannot exactly be achieved or implemented in real time application because they represent an infinite dimensional linear filter (Padhee, Gautam, Singh, & Kaur, 2011). A band-limit FOC (Fractional order control) implementation is important in practice i.e. finite-dimensional approximation of FOC in a proper range of frequencies. There are several approximation methods that can directly give the approximate s-transfer function of fractional order differentiator and integrator. The well-known approximation is given by Oustaloup (2000). Oustaloup approximation makes use of a recursive distribution of zeros and poles. The approximating transfer function is given in Equation (7).(6) $$\begin{array}{c}\hfill s^{\mathit{\alpha }}\approx k\prod _{n=1}^N\frac{1+(s/{\mathit{\omega }}_{z,n})}{1+(s/{\mathit{\omega }}_{p,n})}\end{array}$$(6)

The approximation is valid in the frequency range [${\mathit{\omega }}_l,{\mathit{\omega }}_n$ ]. Gain k is adjusted so that both sides of Equation (7) shall have unit gain at 1 rad/sec. The number of zeros and poles N is chosen beforehand. The better performance of approximation strongly depends on N, low values of N lead to simple approximations and can cause the appearance of ripple in both gain and phase behaviors while highest values of N will be computationally heavier though such a ripple can be removed. Frequencies of zeros and poles in Equation (7) are given as(7) $$\begin{array}{cc}& {\mathit{\omega }}_{z,1}={\mathit{\omega }}_l\sqrt{\mathit{\eta }}\hfill \end{array}$$(7) (8) $$\begin{array}{cc}& {\mathit{\omega }}_{p,n}={\mathit{\omega }}_{z,n}\mathit{\epsilon },n=1,2,3,\dots ,N\hfill \end{array}$$(8) (9) $$\begin{array}{cc}& {\mathit{\omega }}_{z,n+1}={\mathit{\omega }}_{p,n}\mathit{\eta }n=1,2,3,\dots ,N-1\hfill \end{array}$$(9) (10) $$\begin{array}{cc}& \mathit{\epsilon }=({\mathit{\omega }}_h/{\mathit{\omega }}_l)\hfill \end{array}$$(10) (11) $$\begin{array}{cc}& \mathit{\eta }={({\mathit{\omega }}_h/{\mathit{\omega }}_l)}^{(1-\mathit{\alpha })/N}\hfill \end{array}$$(11)

The case $\mathit{\alpha }<0$ can be handled by inverting Equation (7). So, the approximation becomes unsatisfactory; for that reason, it is usual to split fractional powers of s like this $|\mathit{\alpha }|>1$(12) $$\begin{array}{c}\hfill s^{\mathit{\alpha }}=s^n{s}^{\mathit{\delta }}\end{array}$$(12)

where $\mathit{\alpha }=n+\mathit{\delta }$, $n\in Z$, $\mathit{\delta }\in \left[0,1\right]$.

As a result, only the latter term has to be approximated.

4. Transfer function of field controller DC servo motor

Field controlled DC servo motor arrangement is mainly used in small servo application (Alshehhi, 2014). We have used it as the main system to be controlled. Mathematical model is built in Laplace domain and the transfer function between angular position and field voltage neglecting disturbance torque comes out to be(13) $$\begin{array}{c}\hfill G(s)=\frac{\mathit{\theta }(s)}{V_f(s)}=\frac{K_m/B{R}_f}{s({\mathit{\tau }}_{f}s+1)({\mathit{\tau }}_{L}s+1)}\end{array}$$(13)

where ${\mathit{\tau }}_f=L_f/R_f$ and ${\mathit{\tau }}_L=J/b$

where $L_f$ is field inductance, $R_f$ is field resistance, J is motor inertia constant, B is speed damping coefficient and $K_m$ is motor torque constant. Applying the parameters given in Appendix A in Equation (13) we get the following equation.(14) $$\begin{array}{c}\hfill G(s)=\frac{\mathit{\theta }(s)}{V_f(s)}=\frac{1.91}{s^3+21s^2+20s}\end{array}$$(14)

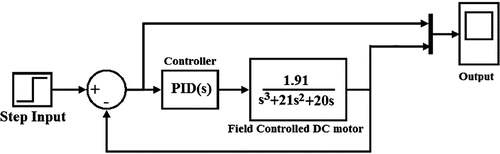
Here output is taken as the instantaneous position of motor and input is taken as field voltage. The equation shows that the system has a dynamics of third order. The system is analyzed by closed loop step response after that the characteristic of uncompensated is determined by time and frequency domain specification (Singhal, Padhee, & Kaur, 2012) then, the system is compensated by designing appropriate controller. The controller is tuned by different tuning algorithm and the performance is compared for relative dominance of different tuning strategy.

5. Analysis of uncompensated system

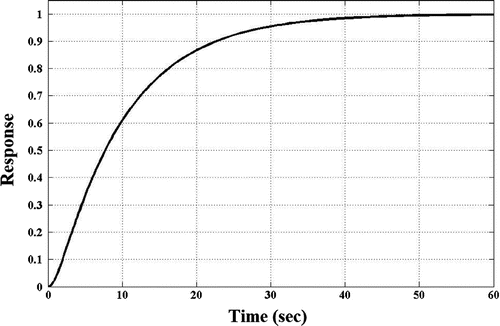
The system is modeled in MATLAB, SISO design tool (Granda, 2002) is used to determine the characteristic of uncompensated system (Hanselman & Littlefield, 1995). The graph of closed loop step response is given in Figure 2.

Figure 2. Step response of uncompensated system.

The step response shows that the response is an over damped response having rise time of 20.7 sec, settling time of 37.6 sec, zero steady state error and no overshoot. This much rise time and settling time made the system very sluggish and slow. Therefore the system needs compensation so that the characteristics should be in tolerable limit.

6. Controller topology and tuning strategies

It is desired to design a controller to meet the following design specification: Rise time less than 1 sec, settling time less than 1.5 sec, zero steady state error and percent overshoot less than 10%. For achieving the desired specification PID and FOPID are tuned by different tuning algorithm. The controller is put in series with the plant with unity feedback. The overall structure of controlled system is given in Figure 3:

Figure 3. Block diagram with PID controller tuned by ZN tuning rule.

The PID controller is first tuned with classical integer order PID controller with the help of genetic algorithm based optimization approach to find the maximum performance that can be obtained by classical PID controller (Kushwah & Patra, 2014). Then we switched to the fractional order PID controller firstly tuned by genetic algorithm based minimization then simulated annealing based minimization (Bandyopadhyay, Saha, Maulik, & Deb, 2008) and finally with the frequency domain design based on constrained minimization in order to obtain the better result and finally compare all the result by generating closed loop step response.

For tuning the controller with the help of genetic algorithm and simulated annealing method, firstly an optimization problem is formulated whhich requires generating an objective function. The objective function is formulated in Section 6.1. Tuning of FOPID by frequency domain design based on constrained minimization is dealt in Section 6.2.

6.1. Time domain design

Here firstly optimization a problem is formulated and then minimize the objective function using different search technique.

6.1.1. Formulation of objective function by dominant pole placement method of controller design

Our approach is based on the root locus method (dominant pole method) of designing PID controllers. As in the traditional root locus method, the peak overshoot $M_p$ and rise time $t_{rise}$ are specified, then from these specifications damping ratio $\mathit{\zeta }$ and the undamped natural frequency ${\mathit{\omega }}_n$ are calculated according to Equations (15) and (16).(15) $$\begin{array}{cc}& \mathit{\zeta }=-\frac{ln(M_p)}{\sqrt{{\{ln(M_p)\}}^2+{\mathit{\pi }}^2}}\hfill \end{array}$$(15) (16) $$\begin{array}{cc}& {\mathit{\omega }}_n=\frac{\mathit{\pi }-{tan}^{-1}\left(\frac{\sqrt{1-{\mathit{\zeta }}^2}}{\mathit{\zeta }}\right)}{t_{rise}\sqrt{1-{\mathit{\zeta }}^2}}\hfill \end{array}$$(16) (17) $$\begin{array}{cc}& p_{1,2}=-\mathit{\zeta }{\mathit{\omega }}_n\pm j{\mathit{\omega }}_n\sqrt{1-{\mathit{\zeta }}^2}=-a\pm jb\hfill \end{array}$$(17)

where $a=\mathit{\zeta }{\mathit{\omega }}_n,b={\mathit{\omega }}_n\sqrt{1-{\mathit{\zeta }}^2}$.

Using these computed values of $\mathit{\zeta }$ and ${\mathit{\omega }}_n$, desired positions of the dominant poles p1, 2 of the closed loop system are determined as:

Let $G_p(s)$ be the transfer function of the process to be controlled, $G_c(s)$ the transfer function of the controller to be designed and H(s) the transfer function of the feedback path. Then, the closed loop transfer function of the controlled system is given as-(18) $$\begin{array}{c}\hfill T(s)=\frac{G(s)}{1+G(s)H(s)}\end{array}$$(18) $G(s)=G_c(s)·G_p(s)$ being the forward path transfer function. Assuming unity feedback, then $H(s)=1$. In this case, the characteristic equation becomes $1+G(s)=0$,(19) $$\begin{array}{cc}& 1+G_c(s)G_p(s)=0\hfill \end{array}$$(19) (20) $$\begin{array}{cc}& 1+G(s)·\frac{P(s)}{Q(s)}=0\hfill \end{array}$$(20) (21) $$\begin{array}{cc}& Q(s)+G_c(s)·P(s)=0\hfill \end{array}$$(21)

where P(s) and Q(s) are respectively the numerator and denominator polynomials of G(s), P(s) and Q(s) have no common factor. As p1, 2 is poles of the closed loop system, each of them must be a root of the characteristic equation and hence must satisfy Equation (21). Thus, putting $s=p_1=-a+jb$ in Equation (21), we get(22) $$\begin{array}{cc}& Q\left(p_1\right)+G_c\left(p_1\right)P\left(p_1\right)=0\hfill \end{array}$$(22) (23) $$\begin{array}{cc}& Q(-a+jb)+(K_p+K_i{(-a+jb)}^{-\mathit{\lambda }}+K_d{(-a+jb)}^{\mathit{\delta }})·P(-a+jb)=0\hfill \end{array}$$(23)

Equation (23) is a complex equation in five unknowns, namely $K_p,K_i,K_d,\mathit{\lambda },\mathit{\mu }$ and our problem of designing a controller that makes the closed loop system dominant poles to be coincide with p1,2 now reduces to determining the set of values of [$K_p,K_i,K_d,\mathit{\lambda },\mathit{\mu }$] for which Equation (23) holds good. But as the number of unknowns exceed the number of equations, there exists an infinite number of solution sets and the equations can not be unambiguously solved by traditional methods. This necessitates the application of random global search techniques, which, in turn, requires the formulation of a suitable objective function.

Let R = Real part and I = Imaginary part of the L.H.S. of Equation (23) and(24) $$\begin{array}{c}\hfill P={tan}^{-1}\frac{I}{R}\end{array}$$(24)

we define(25) $$\begin{array}{c}\hfill F(K_p,T_i,T_d,\mathit{\lambda },\mathit{\mu })=\left|R\right|+\left|I\right|+\left|P\right|\end{array}$$(25)

as our objective function. Clearly, f0, in general, and $f=0$ if and only if $R=0$ and $I=0$ and $P=0$, i.e. if and only if Equation (23) is satisfied. So, we now employ different search technique to scour the five-dimensional search space and find the optimal solution set [$K_p,K_i,K_d,\mathit{\lambda },\mathit{\mu }$] for which $f=f_{min}=0$. This method of finding the parameter of PID and FOPID is widely used in control engineering.

6.1.2. Genetic algorithm based tuning of PID controller

Genetic algorithm (Goldberg & Holland, 1988) belongs to the group of optimization methods called as non- traditional optimization methods. GA tries to imitate natural genetics and natural selection. The main philosophy behind GA is survival of the fittest. As a result GA is used primarily for maximization problems in optimization. GA don’t suffer from the basic setback of traditional optimization methods such as getting stuck in local minima. This is because GA works on the principle of natural genetics, which incorporates large number of randomness. There are basically three operators of genetic algorithm, namely reproduction, crossover and mutation. These operators are used till, the genetic algorithm finds the optimal values.

For searching good set of value of $K_p,K_i$ & $K_d$ by genetic algorithm firstly an optimization problem is formulated using Equation (25) and then minimize the fitness function by genetic algorithm.

The process we want to control has the transfer function given by Equation (13). Controller is designed such that closed loop system exhibits maximum over shoot of 10% and rise time less than 1 second. From Equations (15) and (16) the value of damping ratio and undamped natural frequency comes out to be 0.35 and 2 rad/sec. The dominant pole for the closed loop system should lie at $P1,2=-0.7+j1.87$ and $-0.7-j1.87$. From Equation (19), for $P1=-0.7+j1.87$, the characteristics equation can be written as:(26) $$\begin{array}{cc}& {\left(1+\left(\frac{1.91}{s^3+21s^2+20s}\right)\left(K_p+\frac{K_i}{s}+K_{d}s\right)\right)}_{p_1}=0\hfill \end{array}$$(26) (27) $$\begin{array}{cc}& 1+\frac{1.91}{{(-0.7+j1.87)}^3+21{(-0.7+j1.87)}^2+20(-0.7+j1.87)}.K_p+\frac{K_i}{(-0.7+j1.87)}+K_d(-0.7+j1.87))=0\hfill \end{array}$$(27)

which is a complex equation, after separating real and imaginary part(28) $$\begin{array}{cc}& R=1.91K_p-0.3354K_i-1.337K_d-70.1444\hfill \end{array}$$(28) (29) $$\begin{array}{cc}& I=3.5717K_d-0.9K_i-21.3683\hfill \end{array}$$(29) (30) $$\begin{array}{cc}& P={tan}^{-1}\left(\frac{3.5717K_d-0.9K_i-21.3683}{1.91K_p-0.3354K_i-1.337K_d-70.1444}\right)\hfill \end{array}$$(30)

We formulate the fitness function as $F=|R|+|I|+|P|$ and use genetic algorithm to search for good set of value of $K_p,K_i,K_d$. For optimization Matlab optimization toolbox is used, the parameter of genetic algorithm is set to as given in Table 1.

Table 1. Parameter of GA PID controller

Parameter	Value
Lower bound [$K_p$   $K_i$   $K_d$]	[1 1 1]
Upper bound [$K_p$   $K_i$   $K_d$]	[1000 500 500]
Population size	50
Crossover	Scattered
Crossover fraction	0.8
Mutation fraction	0.011
Stopping criteria (iterations)	70
Selection	Stochastic uniform

After performing the minimization of objective function in MATLAB the value of function converge to 0.2891 after 70 generation. The value of $K_p$, $K_i$ and $K_d$ comes out to be 199.506, 450.55 and 119.513 respectively. The transfer function of PID controller is given as(31) $$\begin{array}{c}\hfill G_c(s)=199.506+\frac{450.55}{s}+119.513s\end{array}$$(31)

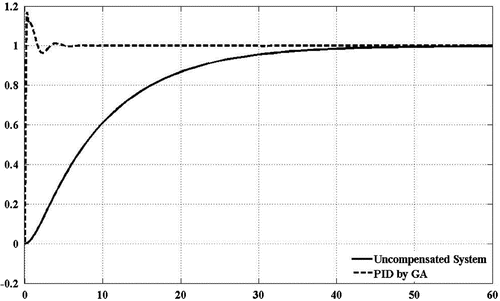
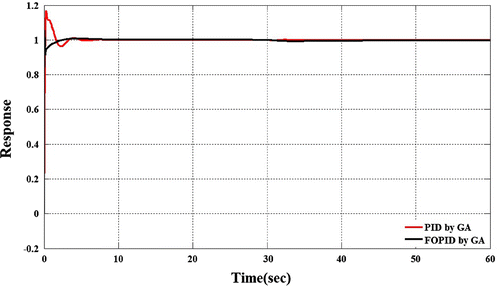
Now we plot the time responses for unit step input in Figure 4 for: uncontrolled system, system controlled by PID controller tuned by genetic algorithm based minimization. A step disturbance is also introduced in the system to check the system robustness with respect to disturbance signal.

Figure 4. Step response of uncompensated, and PID tuned by genetic algorithm.

The graph show significant improvement in closed step response comparing to uncompensated system. From Table 2 it is clear that there is significant improvement in step response in term of rise time, settling time, peak over shoot. But the specification of overshoot less than 10% is still not achieved. As genetic algorithm has a very high tendency towards global optimum, genetic algorithm gives the limit of performance that can be obtained from PID controller. For obtaining better result we need extra parameter so that the desired specification can be met.

Table 2. Response characteristic for step input

Response specification	Response without compensation	PID tuned by GA
Rise time	20.7 sec	0.815 sec
Peak overshoot	0.00%	16.85%
Settling time	37.6 sec	7.24 sec
Steady state error	0.00	0.00

From Table 2 it is clear that there is significant improvement in step response in term of rise time, settling time, peak over shoot. But the specification of overshoot less than 10% is still not achieved. As genetic algorithm has a very high tendency towards global optimum, genetic algorithm gives the limit of performance that can be obtained from PID controller. For obtaining better result we need extra parameter so that the desired specification can be met.

For this we switch to the fractional order PID controller which is the generalization of PID controller using the concept of fractional calculus. Podlubny shows the dominance of FOPID over classical PID controller in term of fulfillment of various performance indices as it has two more parameter to tune.

6.1.3. Genetic algorithm based tuning of FOPID controller

In fractional order PID controller, apart from the three tuning parameters ($K_p,K_i$ and $K_d$) there are two additional tuning parameters that is $\mathit{\lambda }$ & $\mathit{\mu }$. The range of $\mathit{\lambda }$ and $\mathit{\mu }$ can be anything, but in our problem we restrict it in between 0 and 2. Again the controller is designed such that such that closed loop system exhibits maximum over shoot of 10% and rise time less than 1 second. From Equations (15) and (16) the dominant pole for the closed loop system should lie at $P1,2=-0.7+j1.87$ and $-0.7-j1.87$.

From Equation (19) the characteristic equation is given as-(32) $$\begin{array}{c}\hfill 1+\left(\frac{1.91}{s^3+21s^2+20s}\right)\left(K_p+\frac{K_i}{s^{\mathit{\lambda }}}+K_d{s}^{\mathit{\mu }}\right)=0\end{array}$$(32)

Solving the equation at dominant pole(33) $$\begin{array}{cc}& 1+\frac{1.91}{{(-0.7+j1.87)}^3+21{(-0.7+j1.87)}^2+20(-0.7+j1.87)}·(K_p+\frac{K_i}{{(-0.7+j1.87)}^{\mathit{\lambda }}}\hfill \\ \hfill +K_d{(-0.7+j1.87)}^{\mathit{\mu }})=0\end{array}$$(33)

This is a complex equation. Separating real and imaginary parts(34) $$\begin{array}{cc}& R=1.91K_p+1.91K_i{2}^{-\mathit{\lambda }}cos(1.93\mathit{\lambda })+1.91K_d{2}^{\mathit{\mu }}cos(1.93\mathit{\mu })-70.1444\hfill \end{array}$$(34) (35) $$\begin{array}{cc}& I=1.91K_d{2}^{\mathit{\mu }}sin(1.93\mathit{\mu })-1.91K_i{2}^{-\mathit{\lambda }}sin(1.93\mathit{\lambda })-21.3683\hfill \end{array}$$(35) (36) $$\begin{array}{cc}& P={tan}^{-1}\left(\frac{1.91K_d{2}^{\mathit{\mu }}sin(1.93\mathit{\mu })-1.91K_i{2}^{-\mathit{\lambda }}sin(1.93\mathit{\lambda })-21.3683}{1.91K_p+1.91K_i{2}^{-\mathit{\lambda }}cos(1.93\mathit{\lambda })+1.91K_d{2}^{\mathit{\mu }}cos(1.93\mathit{\mu })-70.1444}\right)\hfill \end{array}$$(36)

Again the fitness function is given as $F=|R|+|I|+|P|$ and we use genetic algorithm to search for good set of value of $K_p,K_i,K_d,\mathit{\mu }$ and $\mathit{\lambda }$. The parameter of genetic algorithm is set as given in Table 3.

Table 3. Parameter of GA FOPID

Parameter	Value
Lower bound [$K_p,K_i,K_d,\mathit{\mu }$$\mathit{\lambda }$]	[1, 1, 1, 0, 0]
Upper bound [$K_p,K_i,K_d,\mathit{\mu }$$\mathit{\lambda }$]	[1000, 500, 500, 2, 2]
Population size	60
Crossover	Scattered
Crossover fraction	0.8
Mutation	0.01
Stopping criteria	400
Selection	Stochastic uniform

After optimization, the function converge to 0.06028 after 100 generation and the value of $K_p,K_i,K_d,\mathit{\mu }$ and $\mathit{\lambda }$ comes out to be 132, 8, 200, 0.835 and 1.3 respectively. The transfer function of FOPID controller is given as(37) $$\begin{array}{c}\hfill G(s)=132+\frac{8}{S^{0.835}}+200s^{1.3}\end{array}$$(37)

Now we plot the time responses for unit step input in Figure 5 for FOPID controller tuned on the basis of genetic algorithm and compare the result with the classical integer order PID controller. A step disturbance is also introduced in the system to check the system robustness with respect to noise signal.

Figure 5. Comparison of PID and FOPID tuned by GA.

The graph show significant improvement in closed step response comparing to integer order PID controller. Various step response characteristics are compared in Tables 4 and 5.

Table 4. Response characteristic for step input

Response specification	PID tuned by genetic algorithm	FOPID tuned by genetic algorithm
Rise time	0.815 sec	0.06 sec
Peak overshoot	16.85%	5.4%
Settling time	7.24 sec	1.1 sec
Steady state error	0.00	0.00

Table 5. Response characteristic for step input

Response specification	PID tuned by GA	FOPID tuned by GA
Peak undershoot	3%	0.6%
Settling time	3 sec	0.0 sec

From Tables 4 and 5 it is clear that there is significant improvement in step response in term of rise time, settling time, peak over shoot and also in characteristic related to step disturbance. The response shows a very high robustness for step disturbance, it only show a under shoot of 0.6% which is very low as compared to integer order PID controller. The settling time for disturbance is 0 sec as the system response always remain in tolerable limit, this is due to the extra robustness obtained due to the two more degree of freedom of FOPID controller.

In the next section we use simulated annealing to search the parameter of controller.

6.1.4. Simulated annealing based tuning for FOPID controller

Annealing is the process of slow cooling of metal. Simulated Annealing is point to point stochastic guided random search global optimization technique which mimics the process of annealing. This optimization method was first proposed by Kirpatrick, Gellet and Vecchi in 1983. Simulated annealing (SA) (Yachen & Yueming, 2008) is used to solve unconstrained and bound-constrained optimization problems. When a metal is at high temperature the atoms present within the metals having high energy state move randomly in a high speed.

But as the metal start cooling the atoms looses its energy and ultimately orients itself in a crystalline state having lowest energy. But if the cooling process is very fast then the atoms might reach to semicrystalline state having energy higher than the crystalline state. This is equivalent to getting trapped in a local minima or premature convergence. But if the cooling rate is slow and controlled then this phenomena can be avoided. So cooling rate here is a very important parameter. This cooling rate is controlled according to the Boltzmann Probability distribution which can be given by Equation (38).(38) $$\begin{array}{c}\hfill P(E)=e^{{}^{(\frac{-\mathrm{\Delta }E}{kT})}}\end{array}$$(38)

where P (E) is the probability of energy distribution, k is the Boltzmann constant, T is the temperature and $\mathrm{\Delta }E$ is the change is energy. From Equation (38) we can easily conclude that if T increases there is a uniform probability of the atoms to be at any energy state, but if T decreases the probability of the atoms to be at a higher energy state reduces. At each of the iterations of the simulated annealing algorithm, a new point is randomly generated. The distance of the new point from the current point, or the extent of the search, is based on a probability distribution with a scale proportional to the temperature.

The algorithm not only accepts all new points that lower the objective function F (in case of minimizing problem), but also, accepts certain points that raise the objective function with a probability according to the Boltzmann probability distribution. As this algorithm searches the sample space very rigorously it becomes very robust and is used in solving very complex, noisy and discrete problems. For optimization we take $k=1$, $\mathrm{\Delta }E$ is equivalent to the change in objective function and T is the control parameter.

6.1.5. Algorithm of simulated annealing (SA)

 

Step 1:	Select an Initial Point x (0) and a stopping criterion. Start with a very high value of temperature (T) and set the counter t on Zero i.e t = 0.
Step 2:	Calculate the neighboring point $x(t+1)$.
Step 3:	Find $\mathrm{\Delta }E(\mathrm{\Delta }E=E(t+1)-E(t))$. If $\mathrm{\Delta }E$ is less then Zero then accept it and increment the counter. But if the $\mathrm{\Delta }E$ is greater the zero then unlike the conventional algorithm ,instead of straight forward rejecting it create a random number Y in between zero and one and if Y is less than or equal to $e^{{}^{(\frac{-\mathrm{\Delta }E}{kT})}}$ increment the t to (t+1). Otherwise go to step 2.
	Step 4 :- If the magnitude of the difference between two points is less then the stopping criteria and the temperature (T) is small, stop the process. Otherwise reduce the temperature and repeat the step 2.

In this case also we use the same equation as Equation (19) as the fitness function and optimize the result using simulated annealing and find the parameter of FOPID that is the value of $K_p,K_i,K_d,\mathit{\lambda }$ and $\mathit{\mu }$. The parameter of simulated annealing is set as given in Table 6. The lower and upper bounds of FOPID controller parameter integral order ($\mathit{\lambda }$) and derivative order ($\mathit{\mu }$) are $0\le \mathit{\lambda }\le 2.0$ and $0\le \mathit{\mu }\le 2.0$.

Table 6. Parameter of SA for FOPID

Parameter	Value
Initial value	[148, 39.42, 47.4, 0.229, 0.813]
Lower bound [$K_p,K_i,K_d,\mathit{\lambda },\mathit{\mu }$]	[1, 1, 1, 0, 0]
Upper bound [$K_p,K_i,K_d,\mathit{\lambda },\mathit{\mu }$]	[1000, 500, 500, 2, 2]
Max iteration	15,550
Function tolerance	0.000001
Annealing function	0.8
Re-annealing interval	100

After optimization, the function converge to 0.0204 after 8569 iteration and the value of $K_p,K_i,K_d,\mathit{\lambda }$ and $\mathit{\mu }$ comes out to be 103.1981, 103.5293, 48.0151, 0.6262 and 1.2737 respectively.

Transfer function of FOPID controller is given as:(39) $$\begin{array}{c}\hfill G_c(s)=103.1981+\frac{103.5293}{s^{0.6262}}+48.0151s^{1.2737}\end{array}$$(39)

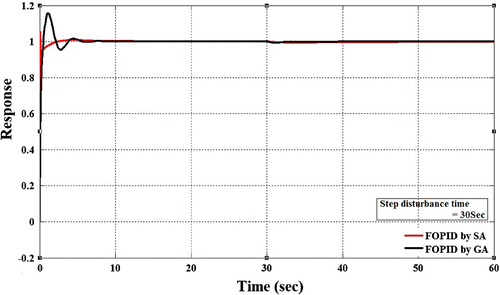
Again we plot the time responses for unit step input in Figure 6 for FOPID controller tuned on the basis of simulated annealing and compare the result with FOPID controller tuned by genetic algorithm.

Figure 6. Comparison of FOPID controller by SA and GA.

Time response characteristics of FOPID controller tuned by genetic algorithm and simulated annealing are shown in Tables 7 and 8 from which comparison can be made between them.

Table 7. Response characteristic for step input

Response specification	FOPID tuned by genetic algorithm	FOPID tuned by simulated annealing
Rise time	0.06 sec	0.33 sec
Peak overshoot	5.4%	15.68%
Settling time	1.1 sec	3.4 sec
Steady state error	0.00	0.00

Table 8. Response characteristic for step disturbance input to the system

Response specification	FOPID tuned by genetic algorithm	FOPID tuned by genetic algorithm
Peak undershoot	0.6	0.7
Settling time	0.0 sec	0.0 sec

From the curve it is observed the response obtained from simulated annealing based tuning approaches is inferior as compared to the FOPID based on genetic algorithm. Instead the response is far better as compared to integer order PID controller tuned based on genetic algorithm. Now we switch to the next tuning method which is frequency domain design based on constrained minimization.

6.2. Frequency domain design based on constrained minimization for FOPID controller

It is an optimization based frequency domain tuning method proposed by Monje et al. (2008). This takes two extra specifications on maximum value of magnitude of sensitivity and complementary sensitivity function along with the specification presented in minimization (Monje et al., 2008) frequency domain design of FOPID controller.

6.2.1. Design specifications and compensation problem

 

(1)	No steady-state error: Properly implemented a fractional integrator of order $k+\mathit{\lambda }$, k, N, $0<\mathit{\lambda }<1$, is, for steady error cancellation as efficient as integer order integrator of order $k+1$.
(2)	Phase margin $({\mathit{\varphi }}_m)$and gain crossover frequency $({\mathit{\omega }}_{cg})$specifications: The conditions must be fulfilled (40) $$\begin{array}{cc}& |G_c(j{\mathit{\omega }}_{cg})G_p(j{\mathit{\omega }}_{cg}){|}_{dB}=0dB\hfill \\ \hfill & Arg(G_c(j{\mathit{\omega }}_{cg})G_p(j{\mathit{\omega }}_{cg}))=-\mathit{\pi }+{\mathit{\varphi }}_m\hfill \end{array}$$(40) where $G_c(s)$ is controller and $G_p(s)$ is the plant transfer function and ${\mathit{\omega }}_{cg}$ is the gain cross over frequency. With this condition the phase is forced to be flat at ${\mathit{\omega }}_{cg}$ and so, to be almost constant within an interval around ${\mathit{\omega }}_{cg}$. It means that the system is more robust to gain changes and the overshoot of the response is almost constant within the interval.
(3)	Robustness to variations in the gain of the plant: To this respect, the next constraint must be fulfilled (41) $$\begin{array}{c}\hfill {\left(\frac{d(Arg(G_c(j\mathit{\omega })G_p(j\mathit{\omega })))}{d\mathit{\omega }}\right)}_{\mathit{\omega }={\mathit{\omega }}_{cg}}=0\end{array}$$(41) With this condition the phase is forced to be flat at ${\mathit{\omega }}_{c}g$ and so, to be almost constant within an interval around ${\mathit{\omega }}_{c}g$. It means that the system is more robust to gain changes and the overshoot of the response is almost constant within the interval
(4)	Robustness to high frequency noise: Complementary sensitivity function T(j) indicates the robustness to measurement noise and other un-modulated system dynamics. To have good time response T(j) should have small value at higher frequencies. For this it must be fulfilled the condition as in Equation (43): (42) $$\begin{array}{c}\hfill {\left|T(j\mathit{\omega })=\frac{G_c(j\mathit{\omega })G_p(j\mathit{\omega })}{1+G_c(j\mathit{\omega })G_p(j\mathit{\omega })}\right|}_{dB}\le AdB\end{array}$$(42) and $\forall \mathit{\omega }\ge {\mathit{\omega }}_t\text{rad/sec}$. Where A is the desired noise attenuation for frequencies $\mathit{\omega }>{\mathit{\omega }}_t$ rad/sec.
(5)	To ensure a good output disturbance rejection: Sensitivity function S(j) indicates the ability of the system to suppress load disturbances and achieve good set-point tracking. To have good time response under disturbed condition the S(j) should have small value at low frequency. For this it must fulfill the condition: (43) $$\begin{array}{c}\hfill {\left|S(j\mathit{\omega })=\frac{1}{1+G_c(j\mathit{\omega })G_p(j\mathit{\omega })}\right|}_{dB}\le BdB\end{array}$$(43) and $\forall \mathit{\omega }\le {\mathit{\omega }}_s\text{rad/sec}$ with B the desired value of the sensitivity function for frequencies $\mathit{\omega }<{\mathit{\omega }}_s$ rad/sec. A set of five of these six specifications can be met by the closed-loop system, since the fractional controller C(s) has five parameters to tune. In this case, the specifications considered are those in Equations (39)–(44), ensuring a robust performance of the controlled system to gain changes and noise and a relative stability and bandwidth specifications. The condition of no steady-state error is fulfilled just with the introduction of the fractional integrator properly implemented, as commented before.

 

6.2.2. The problem of nonlinear minimization

From the specifications above, a set of five nonlinear equations with five unknown parameters [$K_p,K_d,K_i,\mathit{\lambda },\mathit{\mu }$] is obtained. The complexity of this set of nonlinear equations is very significant. The function used for this purpose is called fmincon (.), which finds the constrained minimum of a function of several variables (Coleman & Zhang, 2011). In our case, the specification in Equation (38) is taken as the main function to minimize, and the rest of specifications are taken as constraints for the minimization, all of them subjected to the optimization parameters defined within the function fmincon($·$) (Tepljakov, Petlenkov, & Belikov, 2011).

The transfer function of field controlled DC servo motor we want to control is given by Equation (13). The controller is designed to fulfill the following design specification in frequency domain.

(1)	Gain crossover frequency, ${\mathit{\omega }}_{cg}$ = 1 rad/sec
(2)	Phase margin, ${\mathit{\varphi }}_m$ = 0.73267 rad = 42 degree
(3)	Robustness to the gain variation must be fulfilled
(4)	${\left|T(j\mathit{\omega })\right|}_{dB}\le -20dB,\forall \mathit{\omega }\ge {\mathit{\omega }}_t$ = 10 rad/sec
(5)	${\left|S(j\mathit{\omega })\right|}_{dB}\le -20dB,\forall \mathit{\omega }\le {\mathit{\omega }}_s$ = 0.1 rad/sec

Now using the design specification and the condition given in Equations (39)–(44), we formulate the nonlinear equations as in Equation (45): Putting ${\mathit{\omega }}_{cg}$ = 1 rad/sec in Equation (38)(44) $$\begin{array}{cc}& 20log\left\{0.06744{\left({\left(K_p+K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)}^2+{\left(K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}-K_{i}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)}^2\right)}^{\frac{1}{2}}\right\}=0\hfill \end{array}$$(44)

Putting the value of phase margin ${\mathit{\varphi }}_m$ = 0.73267 rad and ${\mathit{\omega }}_{cg}$ = 1 rad/sec in Equation (41)(45) $$\begin{array}{c}\hfill \begin{array}{c}0.002\left(K_p+K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)-K_{i}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}+K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}=0\hfill \end{array}\end{array}$$(45)

For ${\mathit{\omega }}_{cg}$ = 1 rad/sec in Equation (42)(46) $$\begin{array}{cc}& \left(K_p+K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)\left(K_d\mathit{\mu }sin\mathit{\mu }\frac{\mathit{\pi }}{2}+K_i\mathit{\lambda }sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)\hfill \\ \hfill & -\left(K_{d}sin\mathit{\mu }\frac{\mathit{\pi }}{2}-K_{i}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)\left(K_d\mathit{\mu }cos\mathit{\mu }\frac{\mathit{\pi }}{2}-K_i\mathit{\lambda }cos\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)\hfill \\ \hfill & -0.55\left({\left(K_p+K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)}^2+{\left(K_{d}sin\mathit{\mu }\frac{\mathit{\pi }}{2}-K_{i}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)}^2\right)=0\hfill \end{array}$$(46)

For $\mathit{\omega }$ = 20 $>{\mathit{\omega }}_t$ in Equation (42)(47) $$\begin{array}{cc}& {\left(K_p+{20}^{-\mathit{\lambda }}\times K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+{20}^{\mathit{\mu }}\times K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)}^2+{\left({20}^{\mathit{\mu }}\times K_{d}sin\mathit{\mu }\frac{\mathit{\pi }}{2}-{20}^{-\mathit{\lambda }}\times K_{i}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)}^2-2.74\times {10}^{-3}\hfill \\ \hfill & \times \left(\begin{array}{c}{\left(1.91\left(K_p+{20}^{-\mathit{\lambda }}\times K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+K_d\times {20}^{\mathit{\mu }}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)-8400\right)}^2\hfill \\ +{\left(1.91\left(K_d\times {20}^{\mathit{\mu }}sin\mathit{\mu }\frac{\mathit{\pi }}{2}-{20}^{-\mathit{\lambda }}\times K_{i}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)-76000\right)}^2\hfill \end{array}\right)\le 0\hfill \end{array}$$(47)

For $\mathit{\omega }$ = 0.001 le 0.01 rad/sec in Equation (45)(48) $$\begin{array}{cc}& 0.04-3.6481{\left(K_p+0.001\times K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+0.{001}^{\mathit{\mu }}\times K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)}^2\hfill \\ \hfill & -{\left(1.91\left(K_d\times 0.{001}^{\mathit{\mu }}sin\mathit{\mu }\frac{\mathit{\pi }}{2}-0.{001}^{-\mathit{\lambda }}\times K_{d}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)+0.02\right)}^2\le 0\hfill \end{array}$$(48)

Equation (45) is taken as the main function to minimize and rest of the equation is taken as the constraint. Equations (38) and (39) serves as the nonlinear equality constraint and Equations (40) and (41) as nonlinear inequality constraint. Therefore the function to minimize is given as(49) $$\begin{array}{c}\hfill F=20log\left(0.06744\sqrt{{\left(K_p+K_{i}cos\mathit{\lambda }\frac{\mathit{\pi }}{2}+K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}\right)}^2+{\left(K_{d}cos\mathit{\mu }\frac{\mathit{\pi }}{2}-K_{i}sin\mathit{\lambda }\frac{\mathit{\pi }}{2}\right)}^2}\right)\end{array}$$(49)

The parameters of FOPID are searched in such a way that the function F takes minimum value fmincon(.) result depend on the initial value, therefore it is always better to take some known good initial value. In our work we take the parameter of FOPID obtained in genetic algorithm as initial point. Parameter of fmincon(.) solver in active set algorithm is set as given in Table 9.

Table 9. Parameter of fmincon solver

Parameter	Value
Start point	[132 8 200 0.835 1.3]
Lower bound [$K_p,K_i,K_d$, $\mathit{\lambda }$, $\mathit{\mu }$]	[1, 1, 1, 0, 0]
Upper bound [$K_p,K_i,K_d$, $\mathit{\lambda }$, $\mathit{\mu }$]	[1000, 500, 500, 2, 2]
Max iteration	400
Max function evaluation	400 $\times$ (No. of variable) = 2,000
Parameter tolerance	0.000001

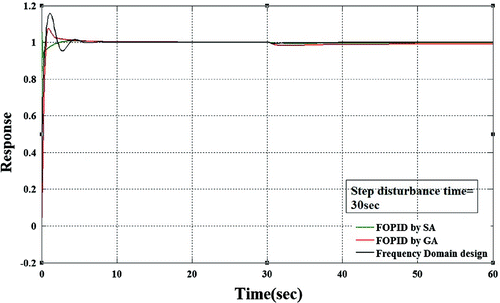
After running the algorithm in MATLAB the function converges to 25.02083 after 13 iteration. The value of FOPID parameter $K_p,K_i,K_d,\mathit{\lambda }$ and $\mathit{\mu }$ comes out to be 1.148, 39.419, 47.403, 0.229 and 0.813. Now we generate step response and compare the result with the response obtained with genetic algorithm and simulated annealing method.

Figure 7. Comparison between GA, SA and frequency domain design.

The curve shows a single overshoot which slowly settles down to steady states value. A steady state error is introduced of about 0.002 which is insignificant as far as our system is concerned. The response shows arise time of 0.4751 sec, peak over shoot 7.5% and settling time of 2 sec.

In the next section a comparison is made on the performance characteristics of three FOPID controller tuned by genetic algorithm simulated annealing and frequency domain design (Figure 7).

Table 10. Response characteristic for step input

Response specification	FOPID tuned by GA	FOPID tuned by SA	FOPID tuned by frequency domain design
Rise time	0.06 sec	0.33 sec	0.4751
Peak overshoot	5.4%	15.68 %	75%
Settling time	1.1 sec	3.4 sec	2sec
Steady state error	0.00	0.00	0.002

Table 11. Response characteristic for step disturbance input to the system

Response specification	FOPID tuned by GA	FOPID tuned by SA	FOPID tuned by frequency domain design
Peak undershoot	0.6%	0.7%	1.75%
Settling time	0.0 sec	0.0 sec	0.00 sec

From Tables 10 and 11 it is clear that this method gives a slightly higher rise time, peak over shoot and settling time, but the response is far better than the response of integer order PID controller and simulated annealing based FOPID controller.

7. Comparison of all tuning method

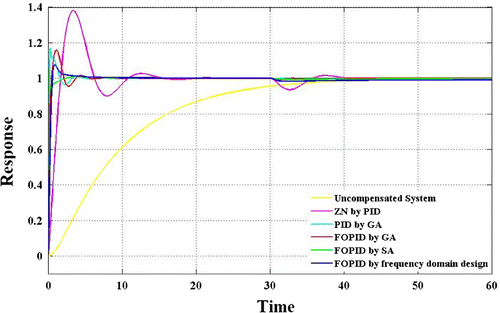
In this section we have compared the result of closed loop step response obtained from different tuning strategy used so far and find which tuning method is best one. The system is simulated for 60s, a step disturbance is introduced after 30 sec of step input to the system. The graph shown in Figure 8 the relative merits of PID and FOPID under different tuning strategy.

Figure 8. Step response comparison of all tuning method.

Table 12. Comparison of step response of all system

Response specification	PID tuned by GA	FOPID tuned by GA	FOPID tuned by SA	FOPID frequency domain design
Rise time	0.815 sec	0.06 sec	0.33 sec	0.4751 sec
Peak overshoot	16.85%	5.4%	15.68 %	7.5%
Settling time	7.24 sec	1.1 sec	3.4 sec	2 sec
Steady state error	0.00	0.00	0.00	0.002

Table 13. Comparison of step response of all system

Response specification	PID tuned by GA	FOPID tuned by GA	FOPID tuned by SA	FOPID frequency domain design
Peak undershoot	3%	0.6%	0.7%	1.75%
Settling time	3 sec	0.00 sec	0.00 sec	0.00 sec

Tables 12 and 13 clearly shows that the performance characteristics obtained from FOPID is better in all respect. Among the FOPID tuned by different tuning method, genetic algorithm based approaches shows the best result in term of rise time, peak over shoot and settling time. Among FOPID SA based approaches gives highest over shoot of 15.68% and highest settling time of 3.4 sec. The results of frequency domain design and genetic algorithm is very close to each other.

8. Conclusion

In this paper we have used different tuning method to set the parameter of PID and FOPID to control a field controlled DC servo motor. Then performance comparison of PID and FOPID has been done on the basis of unit step response. After comparison of all the results it is found that FOPID is better in all respect whether it is rise time settling time or peak overshoot. Among the FOPID the best result is obtained by genetic algorithm based optimization approaches. Although the response obtained by frequency domain design based on constrained minimization by fmincon(.) is well in comparison with genetic algorithm approach but the complexity of obtaining the nonlinear constraint is very significant in frequency domain design. Also the output of fmincon(.) depend on the initial guess or starting point which is not the case in genetic algorithm.

The performance obtained from FOPID tuned by simulated annealing is inferior as compared to FOPID tuned by genetic algorithm and frequency domain design method but far better than integer order PID controller. Moreover simulated annealing takes large number of iteration and more time to converge and also its output depend on the initial guess or start point. Simulated annealing based optimization instead of being a global search technique, in our system seems to give local optimum point but the point is acceptable as far as the characteristic of the step response is concerned.

Additional information

Funding

This work is funded by National Institute of Technology, Arunachal Pradesh under project entitled “New Simulated annealing based optimal tuning of Fractional Order Proportional-Integral-Derivative (PID) Controller” and National Research Foundation [grant number 97823]. Authors would like to thank NIT Arunachal Pradesh for funding this project.

Notes on contributors

Shantanu Chatterjee

Shantanu Chatterjee is currently working as an assistant professor in the Department of Electrical Engineering at NIT, Arunachal Pradesh, India. Before joining NIT Arunachal Pradesh he has worked at CSIR-CMERI, India as Sr. Research Fellow for 1 year. He has more than 4 years of experience in research and teaching field. His research interest includes PID Controller tunings, Active Power Filters, Smart Grid & Anti Islanding, and Power Electronics Applications in Renewable Energy System. He has papers published in Elsevier and different IEEE conferences.

Appendix 1

Specification of field controlled dc servo motor

 

Table

Rated power P	10 HP
Rated armature voltage ($V_a$)	240 V
Field winding resistance ($R_f$)	1.39 ohm
Field winding inductance ($L_f$)	0.1 Henry
Field winding current ($I_f$)	10 Ampere
Applied field voltage ($V_f$)	300 V
Motor torque constant (K)	0.05 N-m/A
Moment of inertia of motor (J)	0.02 Kgm${}^2$
Viscous friction coefficient (B)	0.02 N-m/rad/sec