An evolutionary approach for the offsetting inventory cycle problem

Abstract

In inventory management, a fundamental issue is the rational use of required space. Among the numerous techniques adopted, an important role is played by the determination of the replenishment cycle offsetting which minimizes the warehouse space within a considered time horizon. The NP-completeness of the Offsetting Inventory Cycle Problem (OICP) has led the researchers towards the development and the comparison of specific heuristics. We propose and implement a genetic algorithm for the OICP, whose effectiveness is validated by comparing its solutions with those found by a mixed integer programming model. The algorithm, tested on realistic instances, shows a high reduction of the maximum space and a more regular warehouse saturation with negligible increase of the total cost. This paper, unlike other papers currently available in literature, provides instances data and results necessary for reproducibility, aiming to become a benchmark for future comparisons with other OICP algorithms.

Keywords:

• replenishment cycle offsetting
• genetic algorithm
• inventory management
• OICP
• offsetting inventory cycle problem
• warehouse space
• joint replenishment problem
• mixed integer programming

Public Interest Statement

One of the main issues in industrial companies concerns a proper inventory management and a suitable use of the warehouse space. Consequently, several techniques have been proposed to manage, in an efficient and effective way, the inventory and the limited warehouse space. The evolutionary approach proposed in this paper can be useful to manage the orders of a large amount of items/products with the aim of using in a better way the whole warehouse space, allowing larger order quantities while satisfying the market demand. In particular, the developed algorithm allows us to select the order quantities, which minimize ordering, holding and purchasing costs, and sets the optimal time of the first replenishment of each item in order to minimize the volume peak of the warehouse. Unlike other previous studies, this paper also provides data of instances and results of the algorithm applications to make possible future comparisons with other approaches.

1. Introduction

Inventory management is among the activities that show more criticality in an increasingly complex company environment. In the literature, many techniques have been investigated to optimize the use and management of the inventory in a warehouse. Among the most used models, the classic Wilson model allows minimization of the total cost through the use of an optimal lot for each item. The joint replenishment problem (JRP) of a family of items is based on the same assumptions as the Wilson model. It considers a uniform and deterministic demand for each item available in the storage, no shortages allowed, and no quantity discount. Consequently, cost savings could be achieved by coordinating the replenishment of N items. In the general JRP, since the quantities of each item are ordered for the first time at the initial instant of the considered period, the maximum occupied space occurs at the beginning of the period, and in the following days, the space will be used inefficiently with a resulting non-regular saturation of the warehouse. From this consideration, some heuristics have been developed with the aim of shifting the instant of first replenishment of the items and looking for the optimal offset that allows minimizing the maximum volume peak and guaranteeing a more regular saturation (e.g. Boctor, 2010; Murthy, Benton, & Rubin, 2003; Moon, Cha, & Kim, 2008; Yao & Chu, 2008). In this way, inefficiency can be avoided to a considerable extent, resulting in optimization of the inventory management process. This is a particularly complex problem, known in literature as Offsetting Inventory Cycle Problem (OICP) that cannot be solved optimally in polynomial time (Gallego, Shaw, & Simchi-Levi, 1992). Some heuristic approaches were implemented to obtain a good solution in a reasonable time. Anyway, to date, none of them have been validated and tested on instances of large dimensions showing the consequences of heuristic application in terms of warehouse space trend, value of maximum volume peak, and economic impact. In fact, although in some papers heuristics have been proposed and applied to small instances, none of them has detailed of data and results, therefore comparisons turn out to be impossible. This manuscript, according to the guidelines of Barr, Golden, Kelly, Resende, and Stewart (1995) for an appropriate representation of experimental results, provides all information necessary for reproducibility of the instances, aiming to become a benchmark for any future comparison. Furthermore, most of the papers regarding the OICP are based on mathematical assumptions (explained in detail at the end of the Literature Review Section) which, on one hand, reduce the problem complexity and, on the other hand, make the instances less realistic. Differently from what proposed up to now, this paper focuses on realistic instances data without any simplified assumption.

A heuristic procedure focused on the shifting of the first replenishment cycle of items in a warehouse and able to overcome the limits just highlighted, is designed, implemented, validated, and finally tested on new reproducible instances, proving its effectiveness through the achievement of a high minimization of the maximum peak during the considered time horizon and an optimal use of the space in the warehouse with a negligible increase of the total cost.

The paper, after a review of the state of the art related to the JRP and to the problem of offsetting inventory replenishment cycles, provides its detailed description and presents a genetic algorithm for its solution. Such algorithm is first validated with instances of small-medium dimension and then applied to two instances of more realistic dimensions showing its potentiality in terms of a more effective use of storage space.

2. Literature review

The JRP has been studied over 30 years. In 1989 Arkin proved that the JRP is an NP-hard problem; therefore, heuristics may be used for solving it, and many researches have addressed it (Cha, Moon, & Park, 2008; Kaspi & Rosenblatt, 1991; Khouja, Michalewicz, & Satoskar, 2000; Lee & Yao, 2003; Tsai, Tsai, & Huang, 2009; Van Eijs, 1993; Viswanathan, 1996; Wang, He, Wu, & Zeng, 2012; Wildeman, Frenk, & Dekker, 1997). A review of the JRP literature up to the late 1980s was conducted by Aksoy and Selcuk Erenguc (1988) and Goyal and Satir (1989), while Khouja and Goyal (2008) present an interesting review of all the articles about this issue from 1989 to 2005.

Actually, there are many resource restrictions in inventory systems (e.g., space or budget), but the classic JRP does not consider this issue. For this reason, if a constraint is violated (e.g., the required space is greater than the available space), many textbooks suggest using Lagrange multipliers to find reduced order quantities that allow respecting the resource constraint (Hadley & Whitin, 1963; Johnson & Montgomery, 1974; Tersine, 1976). Many scientific papers have been written on this issue, in particular, the most recent are Amaya, Carvajal, and Castaño (2013), Haksever and Moussourakis (2005), Hoque (2006), Moon and Cha (2006), Yao (2007).

Another possible approach to the multi-item inventory system with resource constraints, particularly considered in the literature, assumes that all the items have a common and fixed cycle time (which represents the time between order (TBO) for each item). The most interesting papers in this frame are Chiu, Lin, Sheu, and Ho (2014), Haji and Mansuri (1995), Hall (1998), Rosenblatt and Rothblum (1990), Thomas and Hartley (1983), and Zoller (1977).

Other researchers focused their attention instead on the joint replenishment policy in which the cycle of each item is an integer multiple of an established basic cycle time (Goyal (1973); Kaspi and Rosenblatt (1983); Silver (1976)). More recently, Yao, Chu, and Lin (2008) studied this type of problem, suggested that the warehouse is supplied at the beginning of a basic period and proposed a new heuristics to generate a program for minimizing the maximum warehouse space, whereas Miranda, Fera, Iannone, and Riemma (2015) proposed a technique based on lot size modification in order to respect space limits with a reduced impact on the total warehousing cost.

However, the main problem of the JRP is that all the items are ordered at the beginning of the considered time horizon and, as a consequence, a maximum occupied space will occur at time t = 0 and will used inefficiently for the rest of the time. To solve this problem, as anticipated in the Introduction section, the offsetting can be carried out of N different items’ replenishment cycles that share a common space, and it is necessary to distribute the arrivals in an “intelligent” way in order to minimize the maximum peak in the warehouse, namely, the joint storage requirements for the items. This type of problem, which we are going to debate in this paper, is often called the “staggering problem” or “offsetting inventory cycle problem (OICP)”. In 1992, Gallego et al. showed that the staggering problem is NP-complete even if only one item has a different reorder interval and, thus, it is not possible to find the optimal solution in polynomial time, but a heuristic technique must be used.

Researches on the offsetting issue are rather few. Teo, Ou, and Tan (1998) deal with the OICP; however, the first real turning point came only in 2003 with the work of Murthy, Benton, and Rubin. Such authors considered the presence of space constraints and presented an interesting heuristics for offsetting independent and unrestricted ordering cycles for items in order to minimize their joint storage requirements over an infinite time horizon when warehouse space is limited. Given that the procedure developed by Murthy et al. represents the benchmark of many subsequent works in this field, from now on, we will call it the Murthy, Benton, and Rubin procedure (MBRP). Later, Moon et al. (2008) proposed an MIP model both for a finite and an infinite time horizon and a genetic algorithm and compared their procedures with the one previously presented by Murthy et al. (2003). Yao and Chu (2008) also conducted theoretical analysis based on Fourier series and Fourier transforms and proposed a procedure to calculate the maximum warehouse space requirement and showed the improvements compared with the MBRP. Then, Boctor (2010) proposed a new formulation of the MBRP and a heuristic algorithm based on simulated annealing through which they achieved the same results as Moon et al. (2008). Subsequently, Boctor and Bolduc (2012) presented two heuristic approaches for solving the staggering problem and obtained good performances, while Croot and Huang (2013) studied this problem from the viewpoint of probability theory and proposed a series of algorithms for the OICP. Boctor and Bolduc (2015) presented two heuristic solution approaches to solve a bi-objective problem with the aim of minimizing the ordering and holding costs and the maximum required storage. In contrast, Franciosi, Miranda, Iannone, and Lambiase (2015) developed a first algorithm targeted to determine the optimal offsetting of item inventory cycles stored in the same warehouse. Finally, Russell and Urban (2016) proposed two heuristics for the OICP and they analysed new variants of the problem concerning a continuous-time framework as well as the effect of stochastic demand.

Most of the analysed papers consider the time horizon equal to the least common multiplier (LCM) of the times between orders (TBOs) associated to the items, since the maximum peak occurs during this time interval. In Yao et al. (2008) the authors proved that if this assumption holds then it is possible to fix the first replenishment instant of an item j at time zero without loss of generality. Thanks to this idea, it is possible to reduce the size of the problem, since all the variables associated to the item j are fixed a priori, and to reduce the symmetry issues that heavily affect the OICP.

Russell and Urban (2016) carried out some tests to verify the performance improvements obtained by fixing the first replenishment instant of one or more items. Moreover, they applied the different symmetry breaking parameters provided by CPLEX to state what is the best configuration to use for the OICP. For instance, on an instance with only 20 items CPLEX requires about 16 h to optimally solve it whereas, the same instance is solved in only 12 min by fixing the first replenishment instant of an item.

Due to the LCM assumption, the time horizon considered for the OICP is usually a finite value, for instance the 360 days of a year. In several papers concerning the OICP the authors select the TBOs as divisors of the time horizon assuring, in this way, that the first replenishment instant of, at least, one item can be fixed a priori. However, the choice of selecting the TBOs as divisors of the time horizon can be too much restrictive for companies that need to define the TBO of each item with the aim of reducing the stock management cost. For this reason, in this paper the time horizon is fixed to 220 days, corresponding to average number of annual working days, and the TBOs are chosen within the range 1–220 without restrictions. Consequently, TBOs may not be divisors of 220 and then the LCM assumption does not hold in our instances and no first replenishment instants can be fixed a priori. This choice makes the problem more realistic but even more complex and it represents a significant novelty of this paper compared to the existing literature. Moreover, since the daily demand is equal to the ratio between the replenishment quantity and the TBO, its value can be fractional as well as the peak value.

Such considerations together with the necessity to provide data and results of the instances, have led the authors to propose a heuristic able to solve realistic and reproducible cases.

3. Problem description and formulation

The goal of the OICP is to find the optimal offsetting of each item with the aim of decreasing the maximum volume peak in the warehouse and, consequently, stabilizing the saturation of the storage for better management of space.

The Wilson model is widely used for supply problems, and it determines the optimal ordering lot for each item, known as EOQ, which minimizes the sum of the purchasing, ordering, and holding costs. Furthermore, for simplification, this model fixes the first replenishment time for each item to the initial instant of the time horizon, and thus, the items will be available simultaneously in the warehouse with a consequent remarkable peak in volume at the initial time and a considerably unsaturated warehouse in the following days.

The example below better explains the problem just described.

Consider the data reported in Table 1: storage space, daily demand, TBOs, and EOQ for each item.

Table 1. Data of the example

Item	Storage space per unit time (m^3)	Daily demand	Time between orders - TBO (days)	Economic order quantity - EOQ
#1	1	3	3	9
#2	1	2	10	20
#3	1	5	6	30

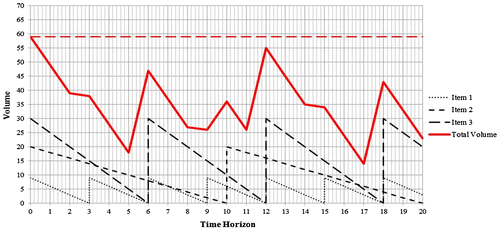
If it considers a time horizon fixed to 20 days, the space required separately from the three items is shown in the Figure 1, indicated by black dotted lines, while the total space requirement without offsetting, namely, with the application of the Wilson model, is shown by a red line. It can be seen that the maximum peak occurs at the initial instant of the time horizon and is equal to 59 m³.

Figure 1. Space requirement without offsetting.

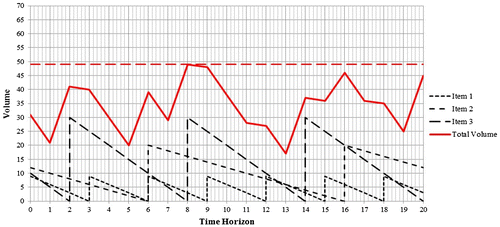
When the offsetting is carried out, the items are ordered for the first time on days zero, six, and two, as shown in the Figure 2, and not simultaneously at the beginning of the time horizon. Consequently, the initial quantities are set equal to 9, 12, and 10, respectively. As can be seen, the maximum peak does not occur at the initial instant of the time horizon; it is lower than the previous one and is equal to 49 m³. In this manner, it is possible to have better management of space.

Figure 2. Space requirement with offsetting.

In this simple example, there are only three items in the storage, but in the real cases, the number of items involved significantly increases; therefore, the aforementioned problem is much more remarkable. Consequently, there are two main criticalities to face in the OICP:

(1)	Violation of potential space constraints.
(2)	Bad management of the warehouse due to nonhomogeneous saturation of space.

In the present work, the same assumptions of Franciosi et al. (2015), Moon et al. (2008), and Murthy et al. (2003) about the OICP are used: the daily demand is deterministic and constant, the replenishment is instantaneous, the TBO is known and constant for each item over a finite time horizon, and shortages and backlogs are not allowed. The objective is to minimize the maximum peak during the considered time horizon. Since the total space requirement pattern is periodic, the maximum peak will occur in the time interval from t = 0 to t = LCM (TBO₁, …, TBO_N), where LCM is the least common multiple and corresponds to the whole time horizon. However, in real cases that involve a large number of items, the LCM of the TBOs may become very high, leading to an overblown time horizon. For this reason, we use a finite time horizon T that makes the problem more realistic, as also explained by Franciosi et al. (2015). In our case, T is fixed to 220 days, which approximately correspond to a working year.

To each item j, three parameters are associated: demand d_j, time between orders TBO_j, and replenishment quantity Q_j = d_j·TBO_j. The formulation of the OICP is based on two sets of variables: x_jt and I_jt. The binary variable x_jt is equal to 1 if and only if an order for item j occurs at time t, with t = 0, 1, ..., TBO_j−1. The variable I_jt represents the inventory level for item j at time t, with t = 0, 1, ..., T. Finally, we introduce a variable S_max equal to the maximum storage space required for all items in the time interval t ∈ [0, T]. Since the d_j values can be not integers, I_jt and S_max are continuous variables.(1) $$\left(\text{MIP}\right)min{S}_{max}$$(1)

subject to:(2) $$\sum _{t=0}^{{\text{TBO}}_j-1}{x}_{jt}=1j=1,\dots ,N$$(2) (3) $$I_{j0}=Q_j{x}_{j0}+d_j\sum _{t=1}^{{\text{TBO}}_j-1}t{x}_{jt}j=1,\dots ,N$$(3) (4) $$I_{jt}=I_{j(t-1)}+Q_j{x}_{jt}-d_{j}j=1,\dots ,N;t=1,\dots ,{\text{TBO}}_j-1$$(4) (5) $$S_{max}\ge \sum _{j=1}^N{s}_j{I}_{jk\left(j\right)}k\left(j\right)=\left\{\begin{array}{cc}t\hfill & \text{if}t<{\text{TBO}}_j\hfill \\ mod\left(t/{\text{TBO}}_j\right)\hfill & \text{if}t\ge {\text{TBO}}_j\hfill \end{array}\right.t=0,\dots ,T$$(5) (6) $$x_{jt}\in \left\{0,1\right\}j=1,\dots ,N;t=0,\dots ,{\text{TBO}}_j-1$$(6) (7) $$I_{jt}\ge 0j=1,\dots ,N;t=0,\dots ,{\text{TBO}}_j-1$$(7) (8) $$S_{max}\ge 0$$(8)

The objective function (1) minimizes the maximum space required in the warehouse over the considered time horizon T. Constraints (2) force the first replenishment instant of any item j to occur within the range [0, TBO_j−1]. Constraints (3) and (4) ensure that the value of variables I_jt coincides with the inventory level of item j at time t. More in details, due to the constraints (2) we know that there is exactly one x_jt equal to 1 into the constraints (3). Now, if x_j0 = 1 then the inventory level of the item j is equal to Q_j because the replenishment instant for the item j is zero. Otherwise, if x_jt = 1 then I_j0 is equal to t times the daily demand d_j. About the constraint (4), if x_jt = 0 then I_jt is equal to the inventory level of item j at time t−1 minus the daily demand d_j. Otherwise, if x_jt = 1 then I_jt is given by replenishment quantity Q_j minus the daily demand d_j. Finally, for any instant of time t, constraints (5) force the variable S_max to be greater than or equal to the sum of the inventory level of all items.

The MIP model will be used to verify the effectiveness of the genetic algorithm, described in the next section. This comparison will show that the genetic algorithm is able to find good solutions even for large instances that involve many items in a warehouse.

4. Genetic algorithm

Genetic algorithms are bioinspired metaheuristic techniques introduced by Holland (1975) in his book Adaptation in Natural and Artificial Systems. These techniques, based on natural selection and evolution, reproduce the evolutionary process of the species. The genetic algorithms consider a population of chromosomes (or individuals) that represent feasible or unfeasible solutions to the problem. The quality of an individual, namely, how the solution is good for the problem, is measured by a fitness function created ad hoc for the specific problem. Therefore, a genetic algorithm is an iterative search procedure whose purpose is optimizing the fitness function. Starting from an initial population, normally generated randomly, a genetic algorithm produces new generations usually containing better individuals than the previous ones: the algorithm progresses to the global optimum of the fitness function.

The great ability of a GA to explore in depth the solutions space and the possibility to effectively manage the constraints through the setting of few parameters, make the genetic algorithm, among evolutionary algorithms, potentially suitable for the OICP.

It is necessary to appropriately set the parameters of the genetic algorithm to obtain good solutions. The possible parameters are known thanks to the many articles and books presented in the literature: Aytug, Khouja, and Vergara (2003), Dowsland (1996), Hua and Huang (2006), Li and Gen (1996), Maiti, Bhunia, and Maiti (2006), Mitchell (1998), and Yokota, Gen, Li, and Kim (1996) are examples of guidelines for GA configuration and setting.

In the OICP, the variables (individuals of the genetic algorithm) are restricted to integer values.

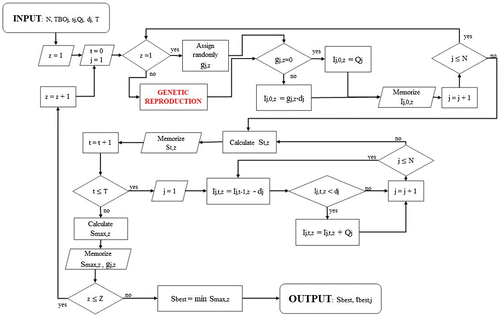
The logic of our genetic algorithm is explained by the flowchart in Figure 3 and through the pseudo-code in Figure 4. The algorithm randomly assumes (for the first generation, z = 1) the values of the first replenishment instant for each item, and in subsequent generations, it researches, through genetic reproduction, the values of g_j,z that lead to the minimization of the maximum peak S_max.

Figure 3. Flowchart of the genetic algorithm.

Figure 4. Pseudo-code of the genetic algorithm.

Starting from the first item (j = 1), initial instant of time (t = 0), and first generation (z = 1), the genetic algorithm randomly assigns the first replenishment instant for the first item (g_1,1), and if g_1,1 = 0, the initial quantities I_1,0,1 = Q₁; otherwise $I_{1,0,1}=g_{1,1}·d_1$. The values of I_1,0,1 are memorized. The procedure is repeated for each item j, and then the total storage space required for all items is calculated according to the equation(9) $$S_{0,z}=\sum _{j=1}^N{s}_j·I_{j,0,z}$$(9)

From the following day until the last day of the time horizon T is reached, the algorithm calculates the present quantities in the warehouse according to the equation(10) $$I_{j,t,z}=I_{j,t-1,z}+Q_j-d_j,$$(10)

in which Q_j = 0 if I_j,t−1,z ≥ d_j, while $Q_j=d_j·{\text{TBO}}_j$ if $I_{j,t-1,z}<d_j$. Moreover, the total space S_t,z occupied by the items every day is calculated. At the end of this iterative procedure, the algorithm computes the maximum space occupied by the items during the time horizon T and memorizes this value, according to the equation(11) $$S_{max}=\underset{t}{max}\left\{S_{t,z}\right\}.$$(11)

The aforementioned procedure is repeated for all generations considering the genetic reproduction that leads to the best values of the first replenishment instants (t_best,j) and the optimal value of the maximum space required by the items in the warehouse (S_best). When the maximum number of generation Z is reached, the algorithm memorizes and shows the best value of the maximum space required by items in the warehouse (S_best) and the corresponding best first replenishment instant for every item (t_best,j) that led to the value S_best. Generally, as the algorithm is structured, S_best coincides with S_max of the last generation.

In the following paragraphs, we present the choices made for each parameter of the genetic algorithm.

4.1. Chromosome representation and initial population

In our genetic algorithm, the length of each chromosome (individual) is equal to the number of items within the warehouse; accordingly, each chromosome has as many genes as the items considered and each gene j represents the first replenishment instant g_j,z of the corresponding item j. Therefore, it is necessary that the gene is an integer between 0 (if g_j,z = 0, it means that the lot will be ordered for the first time at the initial instant as in the Wilson model) and TBO_j −1 for each item. If we consider the example of three items presented in Section 3, the individual representation of the solution shown in Figure 2 is the following:

Table

0

6

2

The initial population, namely the first set of solutions, is created randomly, and the population size is fixed equal to 50 individuals after a tuning phase carried out with a range of individuals between 20 and 200 in several instances and with different number of items. By increasing the population size over 50 individuals, we observed a negligible improvement of the solutions found with a significant increase in the computational time.

4.2. Fitness function

The fitness function evaluates the goodness in the individuals of the population. In our problem, the fitness of each chromosome is equal to the maximum peak obtained according to the value of each gene. In every generation, the algorithm will choose individuals with the best fitness value for the following generation that minimizes the space according to Equation (1).

4.3. Methods for selecting individuals

The chosen technique used for the selection of parents is the tournament selection, which involves running several tournaments among individuals chosen at random from the population; then, the individual with the best fitness value, namely the winner of the tournament, is selected for the following crossover. The tournament size is set equal to three. The tournament selection is explained and studied in several previous articles such as Blickle and Thiele (1995), Goldberg and Deb (1991), Miller and Goldberg (1995), which affirmed that tournament selection is a useful, simple, and robust selection mechanism commonly used in GAs. Moreover, Goldberg and Deb (1991) showed that tournament selection has better or equivalent convergence and computational time complexity properties when compared to any other reproduction operator that exists in the literature. Finally, as clearly explained by Deb (2000), to manage constraints the tournament selection is combined with a penalty function, which allows easily selecting only feasible individuals for next generations.

4.4. Operators to vary genetic composition of individuals during the reproduction: Crossover and mutation

The individuals that survive to the selection step undergo a change through the application of the crossover and mutation operators with the aim of generating new individuals in the next generation.

In our case, “Laplace crossover” and “power mutation” have been chosen as reproduction operators. Laplace crossover is a parent centric real coded operator based on Laplace distribution and it was introduced by Deep and Thakur (2007a), while power mutation is an operator based on power distribution described by Deep and Thakur (2007b). Deep and Thakur (2007a, 2007b) tested Laplace crossover and power mutation operators on several algorithms and on 20 benchmark problems available in global optimization literature showing that the GA using jointly such operators emerged as the best. Moreover, these operators integrate a truncation procedure for integer restrictions (Deep, Singh, Kansal, & Mohan, 2009), necessary in our GA for getting integer variables. According to Deep et al. (2009), the crossover rate and the mutation rate are respectively fixed to 0.8 and 0.005.

4.5. Stopping criteria

The established stopping condition is a maximum number of generations. In fact, as indicated in the detailed review conducted by Aytug et al. (2003) concerning the use of genetic algorithms to solve production and operations-management problems, the most common criterion used for stopping a genetic algorithm is a fixed number of generations. After a series of simulations with a large variety of instances, the number of generations, which more often permits the convergence to the optimal solution or very close to the optimal solution/upper bound of MIP model, is fixed to 300. In fact, a number of generations equal to 300 is the right compromise between obtained results and acceptable run times: when the number of generations increases, the run time consequently increases, while the result remains almost constant.

5. Validation

With the aim of testing the validity and the effectiveness of the two aforementioned procedures, both have been applied to the example presented in the literature by Murthy et al. (2003). The data of the Murthy et al. example (occupied space and TBO for each item), which consider nine items, are shown below in Table 2.

Table 2. Data of Murthy et al.’s example

Item j	1	2	3	4	5	6	7	8	9
sjQj	100	200	81	144	150	160	90	60	50
TBOj	4	5	9	12	15	8	6	12	2

As previously mentioned, the fixed time horizon is equal to a working year (T = 220 days).

The Wilson model was applied to this example and, as can be seen in the following table, the highest volume peak without offsetting is equal to 1035 m³. It occurs at the beginning of the considered time period because all the lots Q_j are ordered simultaneously at the initial instant of the time horizon (g_j = 0, ∀ j). Murthy et al., through their procedure, obtained a maximum volume peak equal to 875 m³ with a reduction of 15.46%. Instead, with the application of the offsetting through the MIP model and the genetic algorithm, we are able to obtain a maximum peak equal to the optimum value of 760 m³, with a percentage reduction of the occupied volume equal to 26.57%.

As shown in Table 3, the maximum peak values found by genetic algorithm and MIP model coincide and this means that the genetic algorithm solves optimality this example. Therefore, in Table 3, the first replenishment instant for each item (g_j) and the corresponding space occupied at the initial instant for each item (I_j,0·s_j), which leads to the maximum volume peak equal to 760 m³, are reported.

Table 3. Application of the two procedures to Murthy et al.’s example

	Without offsetting		Murthy et al. model		MIP model		Genetic algorithm
Item	gj	Ij,0·sj	gj	Ij,0·sj	gj	Ij,0 · sj	gj	Ij,0 · sj
#1	0	100	0	100	3	100	0	100
#2	0	200	4	160	1	80	1	40
#3	0	81	0	81	5	54	1	9
#4	0	144	0	144	1	24	6	72
#5	0	150	0	150	3	40	8	80
#6	0	160	6	120	5	120	2	40
#7	0	90	5	75	4	75	3	45
#8	0	60	4	20	7	40	0	60
#9	0	50	1	25	0	25	1	25
Max peak (m^3)	1,035		875		760		760
Peak day	0		0		38		42
% Reduction	–		15.46%		26.57%		26.57%

Notes: The values in bold are representative of the results obtained through the application of MIP model and genetic algorithm on the Murthy et al.’s example.

Figure 5 shows the space requirement without offsetting and with the application of the genetic algorithm during the considered time horizon T: the black line represents the occupied space with the application of the classic Wilson model without offsetting; the red line, instead, represents the space requirement after the application of the genetic algorithm.

Figure 5. Murthy et al. Case. Comparison between the space requirement with and without offsetting.

A reduction of the storage space is possible and a more regular saturation of the warehouse permits a more correct management of the items and the space.

The next section shows the results obtained with the application of the MIP model and the genetic algorithm to eight new instances of different dimension, whose data are reported in the Appendix A.

6. Experimental tests

The purpose of the computational tests presented in this section is to study the effectiveness and the performance of our genetic algorithm. Both the genetic algorithm and the MIP model have been applied to several instances with 10, 20, 30, 40, 50, 80, and 200 items, respectively.

Table 4 reports the range of values in which are included the main characteristics of the considered items in all cases: the daily demand, the TBOs, and, consequently, the economic order quantity. For simplification, the specific volume is fixed to 1 m³/unit.

Table 4. Characteristics of the items

Characteristic	Measure Unit	Range
Daily demand (dj)	Units/day	1–106
Time between order (TBOj)	Days	1–220
Economic order quantity (Qj)	Units	74–3,748

Table 5 reports the results obtained by the application of the MIP model to the different instances.

Table 5. MIP model results

	MIP model
Case study	Upper bound (m^3)	Lower bound (m^3)	Run time (sec)	Stop motivation	GAP (%)
9 items	760.00	760.00	3.55	Optimal	0.00
10 items	2,854.00	2,854.00	229.95	Optimal	0.00
20 items	7,121.00	6,902.06	10,810.01	AbortTimeLim	3.07
30 items	12,352.00	12,210.00	10,810.03	AbortTimeLim	1.14
40 items	13,795.00	13,585.30	10,810.03	AbortTimeLim	1.52
50 items	17,602.00	17,131.80	10,810.04	AbortTimeLim	2.67
80 items	27,689.00	27,024.60	10,810.08	AbortTimeLim	2.40
200 items	73,309.00	72,477.70	10,810.18	AbortTimeLim	1.13

It has to be noted that, since the peak value can be a not integer value, the upper bounds reported in the following table are rounded up to the closest integer value.

The MIP model was coded in C++ on an OSX platform running on an Intel i5 2.9 GHz processor with 16 GB of RAM and solved by using the Concert library of IBM ILOG CPLEX 12.5. We fixed a limit of 3 h and 8 GB of memory for the resolution of each instance. In each row of the table, the upper and lower bounds computed by the MIP model for that instance, the computational time, the stop status, and the gap between the upper and lower bound are reported. Obviously, when an optimal solution is found, the upper and lower bounds coincide and the gap is equal to 0%.

The instances with 9 and 10 items are optimally solved by the MIP model, while it reaches the time limit on the instances with 20 items, 30 items, 40 items, 50 items, 80 items and 200 items. The gap values are low and the upper bounds found by the MIP model are close enough to the optimal solution.

Table 6 shows the solution values found by MIP model and genetic algorithm in each case study. Moreover, the run times of the genetic algorithm and the percent gap between the maximum peaks of the two procedures are reported.

Table 6. Comparison between the results of the two procedures

	MIP model	Genetic Algorithm
Case study	Max Volume Peak (m^3)	Max Volume Peak (m^3)	Run Time (s)	Gap (%)
9 items	760	760	87	0.000
10 items	2,854.00	2,881.00	88	0.946
20 items	7,121.00	7,229.00	110	1.517
30 items	12,352.00	12,660.00	137	2.494
40 items	13,795.00	14,147.00	177	2.552
50 items	17,602.00	18,019.00	206	2.369
80 items	27,689.00	28,489.00	294	2.889
200 items	73,309.00	75,682.00	733	3.237

The genetic algorithm is able to obtain the optimum value only for the instance with 9 items, while, in the other cases, it finds solutions very close to the upper bounds of the MIP model with a percent error always lower than 3.3%. Regarding performance, the genetic algorithm produces results very fast, requiring less than 5 min to solve all the instances up to 80 items and 12 min for the instance with 200 items. Since the running time is so low, we tested the algorithm even on larger instances, which involve, respectively, 1,000 and 2,000 items within the boundaries of a company warehouse. The results of these tests are described in the next section.

6.1. Larger instances (1,000 and 2,000 items)

The genetic algorithm was applied to two more realistic cases of companies managing, respectively, 1,000 and 2,000 items in the warehouse. Table 7 reports the ranges in which the main data of the instances are included, namely, daily demand, TBOs, specific volume, unit purchasing cost, unit ordering cost, and unit holding cost for each case.

Table 7. Ranges of values for instances

Characteristic	Measure unit	Range 1,000 items	Range 2,000 items
Daily demand (dj)	Units/day	1–108	1–110
Time between order (TBOj)	Days	1–202	1–373
Specific volume (sj)	m^3/unit	0.002–1	0.002–1
Unit purchasing cost (pj)	€/unit	0.1–7	0.1–7
Unit ordering cost (Clj)	€/order	50–100	50–100
Unit holding cost (kj)	€/(unit·day)	0.001–0.05	0.001–0.05

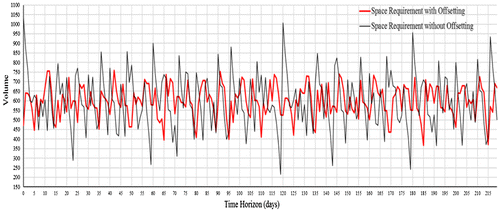
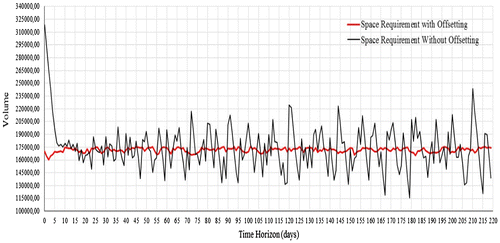
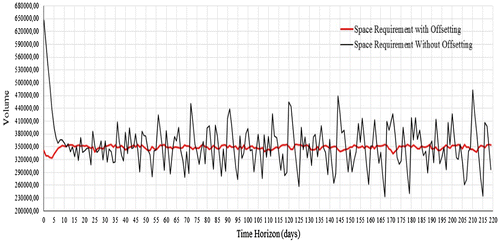
Once the data was collected, the economic order quantity Q_j has been calculated and, considering the classic Wilson model that established the presence of all quantities for the first time at t = 0, it obtains a maximum volume peak equal to 318,488 m³ for the case of 1,000 and 645,813.24 m³ for the case of 2,000 items. Both peaks occur on the initial instant of the first day.

With the application of the proposed genetic algorithm, the maximum volume peak is equal to 175,813 m³ for the case of 1,000 items, which occurs on day 217 with a reduction of occupied space of approximately 44.8%. In the case of 2,000 items, the genetic algorithm obtains a maximum peak equal to 355,386.67 m³, which occurs on the day 46, with a reduction of the occupied space of approximately 45%.

Figures 6 and 7 show the respective space requirements for the two cases during the considered time horizon T: the black line represents the occupied space with the application of the classic Wilson model without offsetting; the red line represents the space requirement after the application of the genetic algorithm.

Figure 6. 1,000 item case. Comparison between the space requirement with and without offsetting.

Figure 7. 2,000 item case. Comparison between the space requirement with and without offsetting.

In both cases, a huge difference between the two procedures regarding the occupied volume, the saturation of the warehouse, can be observed. Moreover, with the application of offsetting through the genetic algorithm, better management of the warehouse is possible, and a major space, usable for other items or for potential safety stocks, is made available.

Furthermore, in real cases it is fundamental to consider the costs. Table 8 presents the total purchasing, ordering, and holding costs associated with 1,000 items and 2,000 items and incurred by the company with both the Wilson model and the genetic algorithm.

Table 8. Comparing the costs

	1,000 item instance		2,000 item instance
Characteristic	Wilson model	Genetic algorithm	Wilson model	Genetic Algorithm
Purchasing cost (€)	38,375,050	38,375,050	75,632,639	75,632,639
Ordering cost (€)	1,373,354	1,336,834	2,766,932	2,693,515
Holding cost (€)	1,371,553	1,335,040	2,769,247	2,695,727
Extra ordering cost (€)	–	71,325	–	145,386
Extra holding cost (€)	–	22,865	–	46,464
Total cost (€)	41,119,957	41,141,114	81,168,818	81,213,731
Max volume (m^3)	318,488	175,813	645,813.24	355,386.67

As evidenced in Table 8, the purchasing cost remains constant in the two cases because such cost does not depend on the specific lot, but only on the daily demand, the time horizon, and the unit purchasing price.

Instead, the ordering and holding costs depend on the specific lot. For this reason, with the application of the genetic algorithm, it is necessary to consider an extra ordering cost and an extra holding cost for the hypothesized initial quantities that must satisfy the demand of the first days until the first replenishment fixed by the genetic algorithm occurs. However, the considered time horizon is always the same and, for this reason, the ordering and holding costs (associated to the lot Q_j) with the genetic algorithm are inferior to the Wilson model because in the initial days only the initial quantities with the associated extra ordering and holding costs have to be considered. After the first replenishment and until the end of the time horizon, the ordering and holding costs are the same associated to the lot Q_j, and so they are calculated in the same way for the two models.

In both cases, the total cost with the application of the genetic algorithm is greater, but the difference, about 0.8% for both cases, is negligible if compared with the value of the total ordering and holding cost calculated for each case and with the obtained reduction of the occupied space.

7. Conclusions

The present paper deals with the OICP. A genetic algorithm, whose features have been accurately chosen for this problem, has been introduced and then validated through comparison with the solutions computed by an MIP model. The data and results of all instances used for the validation are reported in order to make possible their reproducibility and future comparisons in the OICP field.

The algorithm has shown good performance also on realistic cases, which involved a large number of items and without any simplified mathematical assumption. The obtained solutions reveal that a huge reduction in the space requirement is possible and that a more regular saturation of the warehouse allows for a better use of space. Therefore, the algorithm is suitable for any type of instance and it is able to handle real cases in effective way.

Further research could be focused on testing different heuristic techniques, applying them to real cases, and comparing the results. Another possible next step would concern a model modification by including in it the space constraint imposed by the finite dimension of the warehouse, as usually happens in many logistic problems. In this last case, the objective function won’t be the occupied space minimization but the minimization of the total cost of stock management with the respect of the new space constraint.

Notations
	=	The following notations were used in this paper:
j	=	index for each item
N	=	number of items
T	=	finite time horizon
z	=	index for each genetic algorithm generation
Z	=	maximum number of genetic algorithm generations
xjt	=	binary variable that indicates, for each item, when an order occurs
gj	=	integer variable that indicates the first replenishment instant for each item j
gj,z	=	integer variable that indicates the first replenishment instant for each item j at each generation z
dj	=	daily demand for the jth item
TBOj	=	time between orders for the jth item
Qj	=	replenishment quantity for the jth item
Ij,t	=	quantity of the jth item present in the warehouse at time t
Ij,t,z	=	quantity of the jth item present in the warehouse at time t and at generation z
sj	=	space required per unit time for the jth item
St,z	=	total storage space required for all items at time t and at generation z
Smax	=	maximum storage space required for all items in the finite time horizon T
Smax,z	=	maximum storage space required for all items in the finite time horizon T at each generation z
Sbest	=	best value of the maximum occupied space
tbest,j	=	best first replenishment instant for the jth item

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Chiara Franciosi

This work originates from the collaboration of the Department of Industrial Engineering and the Department of Mathematics of University of Salerno, Italy. Chiara Franciosi is a PhD student in Industrial Engineering at University of Salerno; her current research interests include Inventory Management, Industrial Maintenance Management, and Sustainable Manufacturing.

Francesco Carrabs

Francesco Carrabs is assistant professor at the Department of Mathematics of University of Salerno; his research interests include combinatorial optimization, heuristics, metaheuristics, hybrid heuristics for mixed integer linear programming problems, vehicle routing problems.

Raffaele Cerulli

Raffaele Cerulli is Associate Professor at the Department of Mathematics of University of Salerno; his research interests include combinatorial optimization problems, mainly on mathematical models and algorithm design for covering problems on graphs and wireless sensor networks problems.

Salvatore Miranda

Salvatore Miranda is Associate Professor at the Department of Industrial Engineering of University of Salerno; his research interests include Operations Management, Maintenance, Human Reliability Analysis, Simulation, Logistics and Inventory Management.

Appendix A

Table

#Item	Q10
1–10	617	677	81	193	238	341	692	219	524	603

Table

#Item	TBO10
1–10	6	20	81	32	30	23	115	17	8	10

Table

#Item	Q20
1–10	113	823	741	423	562	442	274	1,043	443	803
11–20	612	1,343	594	565	406	426	412	508	550	596

Table

#Item	TBO20
1–10	23	39	9	11	6	8	14	33	44	38
11–20	10	14	14	14	9	7	9	9	7	7

Table

#Item	Q30
1–10	544	326	370	726	547	249	160	1,470	1,316	607
11–20	618	544	583	972	1,145	485	986	200	335	520
21–30	2,961	420	178	756	686	410	1,086	441	505	189

Table

#Item	TBO30
1–10	7	8	10	10	13	83	40	22	14	9
11–20	7	8	10	13	19	6	10	25	19	10
21–30	51	16	15	10	8	7	33	5	12	38

Table

#Item	Q40
1–10	261	521	643	408	1,169	192	592	696	396	143
11–20	535	514	706	303	692	501	1,510	614	330	459
21–30	331	74	108	354	263	422	654	327	548	1,378
31–40	862	792	962	197	304	1,424	442	636	2,023	345

Table

#Item	TBO40
1–10	11	5	10	19	32	19	13	10	11	20
11–20	7	9	9	14	10	8	21	11	13	9
21–30	19	74	36	13	10	11	9	8	91	15
31–40	10	24	13	25	10	24	25	6	38	10

Table

#Item	Q50
1–10	502	108	652	844	558	428	399	332	520	585
11–20	1,647	465	857	865	325	339	741	478	356	891
21–30	1,021	150	2,424	989	332	501	641	1,076	486	273
31–40	127	735	1,298	385	762	189	1,183	570	382	293
41–50	130	297	850	679	354	162	944	563	438	560

Table

#Item	TBO50
1–10	63	27	7	11	8	9	10	7	8	39
11–20	36	13	15	12	11	12	9	9	18	14
21–30	13	21	25	19	14	12	15	11	6	39
31–40	42	7	16	9	9	27	15	6	10	8
41–50	33	15	12	10	44	23	21	24	219	22

Table

#Item	Q80
1–10	576	1,269	644	560	334	363	376	381	501	298
11–20	525	503	1,115	475	612	674	1,781	474	775	737
21–30	192	482	524	581	363	97	307	624	407	753
31–40	435	539	329	331	179	469	1,200	789	708	263
41–50	466	485	1,010	453	484	433	544	956	551	679
51–60	583	914	755	339	648	964	422	461	233	883
61–70	354	778	683	174	429	413	2,551	227	1,188	1,237
71–80	1,533	484	566	1,604	458	244	465	374	200	786

Table

#Item	TBO80
1–10	9	14	8	11	8	16	7	22	20	27
11–20	12	42	31	8	8	7	21	5	30	8
21–30	19	14	7	13	14	49	16	7	10	58
31–40	12	6	10	9	45	6	15	9	13	88
41–50	33	5	11	7	8	6	21	10	6	9
51–60	8	10	31	10	7	37	8	8	16	16
61–70	14	9	11	58	15	14	43	17	33	39
71–80	26	6	13	25	7	22	9	8	20	24

Table

#Item	Q200
1–10	518	769	808	450	322	730	725	739	415	603
11–20	508	353	894	266	3,140	1,348	552	138	415	324
21–30	105	543	388	1,068	710	289	579	288	1,030	758
31–40	473	238	622	646	732	820	529	449	2,923	1,106
41–50	461	491	1,017	517	599	569	192	371	692	422
51–60	299	1,013	1,033	1,532	1,538	501	1,519	1,704	507	810
61–70	1,015	660	326	1,143	427	610	559	690	364	295
71–80	191	1,095	424	782	315	606	537	520	1,511	628
81–90	150	622	644	546	573	775	101	484	414	184
91–100	320	494	361	342	363	558	157	631	634	1,120
101–110	2,258	466	174	1,387	416	496	444	519	395	525
111–120	1,375	392	3,748	1,061	456	549	160	289	519	91
121–130	251	597	236	1,895	558	983	544	416	2,265	709
131–140	369	746	554	770	315	474	681	729	247	646
141–150	551	598	387	806	701	1,472	1,287	506	581	827
151–160	831	190	743	151	932	400	515	369	345	351
161–170	405	468	449	417	124	595	707	251	472	1,044
171–180	566	661	582	1,063	360	840	777	519	718	386
181–190	681	306	646	391	618	679	589	1,471	85	562
191–200	534	588	561	1,982	647	475	1,524	594	355	915

Table

#Item	TBO200
1–10	10	17	135	10	7	8	9	18	9	10
11–20	6	10	10	10	34	17	15	23	13	20
21–30	35	9	15	33	15	13	6	17	13	10
31–40	9	22	11	9	8	12	9	9	29	17
41–50	6	5	20	7	12	11	21	13	9	10
51–60	13	18	13	26	17	10	17	34	9	8
61–70	11	9	82	52	5	7	7	33	11	10
71–80	27	17	6	17	8	17	23	20	16	37
81–90	25	16	19	12	15	12	51	9	10	20
91–100	11	7	9	14	11	8	26	10	14	14
101–110	24	11	22	14	35	7	9	7	10	6
111–120	15	12	44	14	16	55	18	11	7	46
121–130	63	10	12	20	7	13	11	13	33	10
131–140	7	9	9	9	45	53	15	9	12	9
141–150	8	6	10	10	9	49	16	8	7	13
151–160	17	38	8	38	18	11	17	17	11	13
161–170	6	7	220	7	41	10	10	13	9	20
171–180	8	8	8	15	8	11	18	10	8	10
181–190	8	7	7	14	13	7	6	16	43	8
191–200	31	7	6	20	9	6	54	13	6	2