Three hybrid GAs for discounted fixed charge transportation problems

Abstract

The problem of allocating heterogeneous fleet of vehicles to the existing distribution network for dispensing products from a manufacturing firm to a set of depots is considered. It is assumed a heterogeneous fleet of vehicles with the given capacities and total costs consisting of a discounted fixed cost and a variable cost proportional to the amount shipped is employed for handling products. To minimize the total transportation costs, the problem is modeled in a form of the nonlinear mixed integer program. Due to the NP hard complexity of the mathematical model, three prioritized K-mean clustering hybrid GAs, by incorporating two new heuristic algorithms, are proposed. The efficiency of the algorithms is compared and the best one is designated. The designated algorithm is compared with CPLEX as well as two recently cited algorithms, and the results supported its high effectiveness and efficiency in terms of solution quality and CPU time.

Keywords:

• manufacturing logistics
• prioritized K-mean clustering hybrid genetic algorithm
• fixed charge transportation model
• discounted transportation cost. MILP model

Public Interest Statement

Distribution is a step in the economic process which brings goods and services from those who make them to those who use them. Some of the most important steps of distribution are transportation, packaging, storage, and advertising. Goods transportation is important because it enables trade between people, which is essential for the development of civilizations. Since transportation contributes the highest cost among the related elements in logistics systems, the improvement of transport efficiency could change the overall performance of a logistics system. In this paper the problem of designing a cost efficient transportation system for goods distribution is considered. In this system it is assumed that the transportation costs are the sum of its fixed cost and a variable cost and a discount mechanism is applied to the fix cost. However, the solution approaches for solving such problem suffers from computational complexity. Therefore, we assembled three hybrid heuristic algorithms to obtain a suitable solution for the proposed problem.

1. Introduction

Transport is an integral part of the supply chain and the most significant contributor to logistics costs. While logistics is a process of planning, implementing, and controlling the efficient flow of products, information, and funds, transport is a core component of logistics, moving goods between different points in the supply chain. In fact, the backbone of the entire supply chain is the transportation management that makes it possible to achieve the well-known seven Rs; the right product in the right quantity and the right condition, at the right place, at the right time, for the right customer at the right cost. Transportation is a critical part of any global logistics effort because of the long distances that can separate a firm from its customers. Among five primary modes of transportation, rail, road, pipeline, water and air, trucks carry the highest percentage of the weight and value of goods in (Transportation Statistics Annual Report, 2013). Since logistics is often insensitive to transport costs; the total costs of transport should be analyzed more thoroughly.

In this paper, the problem of assigning vehicle type to an existing transportation network, to minimize total transportation costs, is considered. The proposed problem is motivated by a vehicle depot assignment in the transportation model of a food industrial group (called SIG). Although the problem is modeled based on the transportation structure of the SIG, but it is not an attempt for proposing a direct solution for the SIG problem. Moreover, it is to propose a more generalized version of the transportation model which can later be adapted to the SIG and similar problems. In this context, the problem of allocating heterogeneous fleet of vehicles to an existing distribution network for dispensing products from a manufacturing firm to a set of depots with the objective of minimizing total transportation costs is considered. It is assumed that a limited number of vehicles, with various capacities, are available for transporting various products from a manufacturing firm to set depots. The transportation costs are the sum of its fixed cost and a variable cost incurred proportionately to the travel distance, and discount mechanism is applied to the fix cost depending on the number of vehicles to be rented. To handle the problem, a mathematical model, in the form of nonlinear zero-one integer programming is developed. The developed mathematical programming model is an NP-hard problem, Due to the computational complexity of the model, any exact solution approach for handling a real-world case is expected to suffer from the computer time and memory requirements. Therefore, only heuristic approaches can handle such problems. Among these approaches, the use of the genetic algorithms (GAs) seems to be very promising (Molla-Alizadeh-Zavardehi, Sadi Nezhad, Tavakkoli-Moghaddam, & Yazdani, 2013). We therefore developed three prioritized cluster encoding hybrid GAs as the solution approaches for the proposed mathematical model.

For evaluating the efficiency of the proposed algorithms, an extensive computational experiment is conducted. Through this experiment the solutions of the proposed algorithms are compared and the best algorithm is designated. Then this algorithm is compared with a conventional solution approach using CPLEX software, and the results are reported in Section 6.3. The results reveal that the designated algorithm is capable of providing good quality solutions with minimal computational effort. Also, the designated algorithm is compared with two recently cited algorithms and showed that it outperforms the challenging algorithms.

2. Literature review

Transportation is an important function of logistics system. Statistic indicates the largest contribution to logistic costs is transportation. United states business logistics costs are $1.45 trillion US dollar in 2014, and the transportation costs for the same year run nearly one trillion US dollar that constitute over 65% of the total logistics costs (Wilson, 2015). Design of a cost-efficient distribution network and a better utilization of vehicles for transporting goods have been studied and implemented in several real-world instances. One of these studies is an experiment begun in 1994 0at Eindhoven University in The Netherlands, which aimed for the integration of research, education and knowledge transfer to industry (Donselaar & Sharman, 1998). This experiment focused on the transportation and distribution sector in a province in the Netherlands. Bhadury, Khurana, Peng, and Zong (2006) developed a comprehensive methodology to optimize the planning of acquiring motor carriers in transportation companies. As a case study, a Canadian transportation company was selected and the current acquisition planning for heavy trucking equipment was examined. Other research works on the real-life implementation of distribution systems can be found in Olhager, Pashaei, and Sternberg (2015), Wanke (2014), and Yam and Tang (1996).

Although transportation is as an important element of logistics and supply chain success, yet it is often ignored as a source of competitive advantage. Caplice and Sheffi (2003) presented the concept of optimization-based procurement for transportation services. Tracey (2004) proposed a structural equation modeling for examining the impact of inbound and outbound transportation performance on the manufacturing cost reduction. Goossens and Spieksma (2009) considered a generalization of the ordinary transportation problem with some exclusionary side constraints. It is confirmed that the proposed model is NP-hard. Then Waldherr, Poppenborg, and Knust (2015) presented a new extension of the bottleneck transportation problem with additionally auxiliary resources for supporting the transports. A transportation system in which a single commodity has to be sent from supply to demand nodes for satisfying the total demand was considered.

Fixed charge transportation problems are the extension of the classical transportation problems, where fixed costs are incurred at every rout irrelative to its shipping amount. The fixed charge transportation problem was first considered by Hirsch and Dantzig (1968) in which it is shown to be NP hard. Other early works considering different types of the fixed charge transportation problems are due to Sandrock (1988), Kowalski and Lev (2008), Adlakha, Kowalski, and Lev (2010). But till date, there exist several open problems applicable in real life in this area. An efficient method to solve nonlinear fixed charge transportation problem is proposed by Xie and Jia (2012). Acharya, Basu, and Das (2013) developed a modified method for fixed charge transportation problem. Varma and Kumar (2015) have demonstrated how non-linear transportation problem can be solved efficiently by minimizing time and cost. In this work they proposed several methods to find solutions to transportation problems. Klose (2008) focused on fixed charge transportation problem and presented two methods based on a dynamic programming and implicit enumeration. Jo, Li, and Gen (2007) contemplated the nonlinear fixed charge transportation problem and presented a spanning tree-based GA. Aguado (2009) considered fixed charge transportation problem and proposed a Lagrangean relaxation and a decomposition method. Loch and Silva (2014) presented a heuristic algorithm, comparing the quality solution and computational time with the CPLEX software. Hajiaghaei-Keshteli, Molla-Alizadeh-Zavardehi, and Tavakkoli-Moghaddam (2010) addressed the nonlinear fixed-charge transportation problem using a spanning tree-based genetic algorithm. A priority-based GA for fixed charge transportation problems is appied in Lotfi and Tavakkoli-Moghaddam (2013). A hybrid PSO for solving the fixed charge transportation problem is proposed in El-Sherbiny and Alhamali (2013).

Das, Basu, and Acharya (2013) considered fixed charge capacitated transportation problem with non-linear objective functions and linear constraints and presented a local optimum condition of this problem with an algorithm for solving this transportation problem. Anholcer (2015) investigated the nonlinear generalized transportation problems where the transportation costs and the costs that depend on the amount of good delivered to the destination points are strictly convex functions and provided a method of solving the proposed problems. Krile (2013) considered a transport planning problem for cost minimization on the voyage route with multiple loading/unloading ports. A heuristic algorithm was developed to find the transshipment costs. Through a computational experiment it was demonstrated that the proposed algorithm can handle complex shipping problems with limited computing power. Vaisi and Tavakkoli-Moghaddam (2015) presented a non-linear integer programming model for a cross-dock problem with the objective of minimizing the total transportation cost, and a genetic algorithm is proposed. Othman, Rostamian-Delavar, Behnam, and Lessanibahri (2011) claimed that the Fixed Charge Transportation Problem is a more comprehensive type of transportation problem and is categorized as the NP-hard problems. Due to computational complexity two genetic algorithm were proposed the problem. Two fuzzy logic controllers (FLC) were also developed to automatically tune two critical parameters of cross over and mutation operators and applied to one of these two GAs. Finally the results from the simple conventional GA and automatically tuned GA are compared together. This comparison demonstrated that the GA that is tuned with FLC reach the local optimum remarkably faster. Molla-Alizadeh-Zavardehi, Mahmoodirad, and Rahimian (2014) tackled the NP hard problem of the step fixed-charge transportation by presenting a set of genetic algorithms. Several crossover and mutation operators were proposed for improving the efficiency and convergence of the proposed algorithms. The efficiency of the proposed GAs were then compared with the simulated annealing (SA) and showed that the GAs were more robust and consistently outperformed the SA for all instances. Other works considering fixed charge transportation problems are appeared in Jawahar, Gunasekaran, and Balaji (2012), Molla-Alizadeh-Zavardehi et al. (2013), Sheng et al. (2006), Sanei, Mahmoodirad, Niroomand, Jamalian, and Gelareh (2015), and Sun, Aronson, McKeown, and Drinka (1998).

Discounted fixed cost transportation can be considered as a version of fixed cost transportation problem. This is considered to be an NP-hard problem since the cost structure causes the value of the objective function to behave like a step function (Altassan, El-Sherbiny, & Sasidhar, 2013). Numerous models have been developed to overcome this issue. For models considering discounted price according to the variation of quantities refer to Blazewicz, Bouvry, Kovalyov, and Musial (2014), and Osuji, Ogbonna – Chukwudi, and Jude (2014). Yousefi, Afshari, and Hajiaghaei-Keshteli (2017) developed a GA for fixed charge transportation problem with discounted mechanism. Ghseemi Tari (2016) proposed A mathematical programming model in the form of the discrete nonlinear optimization problem. Then a hybrid dynamic programming algorithm is developed for finding the optimal solution. To increase the computational efficiency of the solution algorithm, several concepts and routines, such as the imbedded state routine, surrogate constraint concept, and bounding schemes, are incorporated in the dynamic programming algorithm. A real-world case problem is selected and solved by the proposed solution algorithm, and the optimal solution is obtained.

Genetic algorithms are good at taking large, potentially huge search spaces and navigating them, looking for optimal combinations of variables (Alaei & Ghassemi-Tari, 2011; Ghassemi-Tari & Alaei, 2013). They are capable to finding solution to NP hard Problems such as travelling salesman, and nonlinear cost transportation problems (Panchal & Panchal, 2015). Improving the computational efficiency of GA by presenting a non random initial population have been considered in several papers (Ghassemi-Tari & Meshkinfam, 2017; Meshkinfam & Ghassemi Tari, 2016; Pandey, Chaudhary, & Mehrotra, 2014; Wu, Liu, Tang, Li, & Yu, 2017). Use of GA for optimization of transportation networks usually involves the analysis of a large data-set. In order to mine a high dimensional data-set, a efficient dimension reduction method is very crucial. Several methods have been proposed to find an efficient reduction of the dimension of a high dimensional data-set without affecting the original data. In this regards, K-means is one the most effective approaches. Krishna and Murty (1999) proposed a novel hybrid GA for obtaining a globally optimal partition of a given data-set into a specified number of clusters. The recent research attempts using K-means concept are due to Ayyagari, Sivakumar, and Kannan (2014), Chittu and Sumathi (2011), Dash and Dash (2012), and Patil and Argiddi (2014). A vehicle allocation problem involving a heterogeneous fleet of vehicles for delivering products from a manufacturing firm to a set of depots has been considered in Ghassemi Tari and Hashemi (2016). The aim was to assign the proper type and number of vehicle to each depot route to minimize the total transportation costs, consist of fixed cost and variable cost. In this work, first a mathematical programming model was proposed and then a priority-based GA was proposed. The computational results revealed that the proposed algorithm was capable of providing the astonishing solutions with minimal computational effort, comparing with the CPLEX solutions. A similar problem has been contemplated in Hashemi and Ghassemi (2018) and a Prufer-based GA was presented. The efficiency of this algorithm was also compared with the solution obtained by CPLEX and the results revealed that the proposed algorithm was capable of providing good quality solutions with the minimum CPU time.

In this manuscript we integrated several search routines in the powerful approach of the GA and employed the K-mean clustering for efficiently searching over the high dimensional data-set in order to develop three hybrid GAs capable of solving a general version of the fixed charge discounted transportation cost problems. In the following sections, the scope of the proposed problem followed by the developing process of the hybrid algorithm will be presented.

3. Scope of the problem

Consider a directed graph G = (N, A) with the set A of directed arcs, and the set N of nodes representing a manufacturer and depots. The manufacturer is indexed 0 and depots are indexed from 1 to n. Customer in depot j has a known demand with the total goods weight of W _j , j ∈ N. There are m types of vehicles, and the capacity of the vehicle type i in term of the weight it can deliver is designated by q _i . The routing transportation cost of a vehicle type i is the sum of its fixed cost F _i and a variable cost of c _ij incurred proportionately to the travel distance to depot j. The total number of available vehicles is limited especially for some types of heavy loading vehicles, for which the total number of available type i vehicle is designated as T _i . It is also assumed that there exists a discount policy for the vehicles to be rented. This discount varies according to the number of rented vehicles and is applied on their fixed cost. By this discount policy, if the number of rented type i vehicles is less than $n_i^1$ the renting companies ask for the fixed cost of $F_i^1.$ If the number of type i vehicles is greater than or equal to $n_i^1,$ but less than $n_i^2$, when $n_i^1<n_i^2,$ the renting companies charge a discounted value of $F_i^2$ as the fixed charge. Let us consider x _ij as the number of typei vehicles for transporting the products to depot j. Assuming there are as many as v number of discount intervals, the general formula for determining the fix cost can be written as follow:$$F_i=\left\{\begin{array}{cc}0\hfill & \text{if}\sum _{j=1}^n{x}_{\mathit{ij}}=0,\forall i=1,2,\dots ,m\hfill \\ F_i^1\hfill & \text{if}\sum _{j=1}^n{x}_{\mathit{ij}}<n_i^1,\forall i=1,2,\dots ,m\hfill \\ F_i^2\hfill & \text{if}{n}_i^1\le \sum _{j=1}^n{x}_{\mathit{ij}}<n_i^2,\forall i=1,2,\dots ,m\hfill \\ \text{M}\hfill & \text{M}\hfill \\ F_i^v\hfill & \text{if}{n}_i^v\le \sum _{j=1}^n{x}_{\mathit{ij}}\le T_i,\forall i=1,2,\dots ,m\hfill \end{array}\right.$$

where $F_i^1>F_i^2>\cdots >F_i^v$

It is also assumed that the distribution network has already been designed and therefore the distances from the manufacturing firm to depots are fixed and are given. The objective is assigning a set of vehicles to each depot, to minimize the total transporting costs of delivering products from the manufacturing firm to the set of designated depots. The mathematical model is developed and will be presented in the following section.

4. Mathematical model

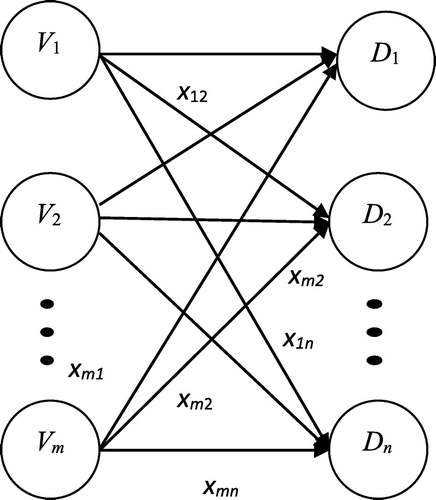
We can now develop a mathematical programming model for the proposed problem. Considering M as a known large number, we can define the decision variables and parameters of the mathematical model as follow:

m	=	Number of vehicle types
n	=	Number of depots
q i	=	Capacity of vehicle type i (i = 1,2,…, m)
c ij	=	Variable cost of using vehicle type i for depot j, (i = 1,2,…, m, j = 1,2,…, n)
F i	=	Fixed cost of using vehicle type i, (i = 1,2,…, m)
T i	=	Total number of available vehicle type i, (i = 1,2,…, m)
W j	=	Demand quantity of depot j, (j = 1,2,…, n)
D j	=	Distance of depot j from manufacturing firm, (j = 1,2,…, n)
x ij	=	Number of vehicle type i used for transporting products to depot j, (i = 1,2,…, m, j = 1,2,…, n)

(1) $$Min{X}_0=\sum _{i=1}^m\sum _{j=1}^n{F}_i{x}_{\mathit{ij}}+\sum _{i=1}^m\sum _{j=1}^n{c}_{\mathit{ij}}{x}_{\mathit{ij}}$$(1)

Subject to:(2) $$\sum _{i=1}^m{q}_i{x}_{\mathit{ij}}\ge W_j\forall j=\text{1,2,}\cdots \text{,}n$$(2) (3) $$\sum _{j=1}^n{x}_{\mathit{ij}}\le T_i\forall i=1,2,\cdots ,m$$(3) (4) $$F_i=(y_i^0-1)+y_i^1{F}_i^1+y_{{}_i}^2{F}_i^2+\cdots +y_i^t{F}_i^v\text{For}i=1,2,\cdots m$$(4) (5) $$-M(1-y_{{}_i}^s)+\sum _{j=1}^n{x}_{\mathit{ij}}\le v_i^s\text{- 1}\forall i=1,2,\cdots ,m,s=1,2,\cdots ,t-1$$(5) (6) $$M(1-y_i^{s+1})+\sum _{j=1}^n{x}_{\mathit{ij}}\ge v_i^s\forall i=1,2,\cdots ,m,s=1,2,\cdots ,t-1$$(6) (7) $$M(1-y_i^t)+\sum _{j=1}^n{x}_{\mathit{ij}}\ge v_i^t=T_i\forall i=1,2,\cdots ,m$$(7) (8) $$\sum _{k=0}^t{y}_i^k=1\forall i=1,2,\cdots ,m$$(8) (9) $$y_i^s=0,1\forall i=1,2,\cdots ,m\text{and}s=\text{1,2,}\cdots \text{,}t$$(9) (10) $$x_{\mathit{ij}}\in N-\{0\}\forall j=1,2,\cdots ,n\text{and}i=1,2,\cdots ,m$$(10)

5. Proposed solution algorithms

The problem of distributing products from a manufacturing firm to a set of distinct depots to minimize the transportation fixed and variable costs when a discounting mechanism is applied is considered as NP-hard problem. Thus there is no optimal approach to obtain the solution of the real-world sized problem in a polynomial computational time. Due to this fact a suitable approach could be the generic search optimization algorithm. This is to be explored in this research.

In transportation systems with the heterogeneous vehicles, several factors such as the delivery distances and the amount of the depot demand affect the decision-making concerning the selection of the vehicle types. Considering the real world conditions, the variable transportation cost of handling a unit of products is smaller for a higher capacity vehicle, comparing to a lower capacity one, while the fixed transportation costs are incurred exactly oppositely.As it will be seen an individual vehicle type and an individual depot each representing a genome of a chromosome in the proposed algorithm. Now referring to the processes of developing a genetic algorithm, the use of crossover and mutation operators require the interchange of at least two of the vehicles types which are selected in the previous iterations for transporting the products to a pair of depots. By this interchange, there would be an unreasonable act if we let a heavy capacity vehicle is assigned to a depot with a lower remaining demand/ shorter distance. Realizing this fact, we should design a solution algorithm through which the vehicles with more loading capacity are allocated to the distribution depots having more remaining demand/longer distance from the manufacturing plant. Due to the above mentioned considerations; a multidimensional clustering mechanism consists of the distance and the demand of depots is proposed. We then incorporated this mechanism in conjunction with apriority-based encoding, and a heuristic procedure for constructing the initial population, to develop a hybrid genetic algorithm.

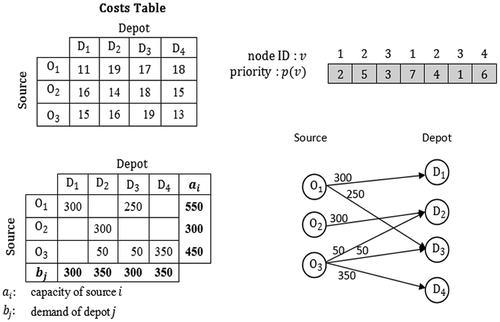
Let us first describe how we implement the priority encoding GA on a conventional transportation network. Figure 1 illustrates a transportation problem having three source nodes and four sink nodes which is used as a sample of transportation with its corresponding priority-based encoding. The size of chromosome in this network is determined as the total number of the source nodes and the sink nodes which is seven in this case. Denoting the chromosome size by N, a genome of this chromosome is selected randomly using the uniform distribution with the range of 1 to N. therefore, highest priority of N is assigned to this genome Now by letting N = N−1, the priority is assigned to each of the remaining genome.

Figure 1. A sample of transportation with its corresponding priority-based encoding.

Now to develop a prioritized based GA, consider the transportation model as depicted in Table 1 and in Figure 2. To adapt the proposed problem to a transportation network, we let every source node is represented as a vehicle type, and every sink node is represented as a depot. By this, the capacity of a source node is determined by its associated number of available vehicle type, and the demand of a sink node is determined by its associated dept’s demand. Considering T _i as the limited number of the vehicle type i and W _j as the demand of depot j, the loading capacity of the vehicle type i can be defined by q _i .

Table 1. Transportation table for the proposed problem

Figure 2. A transportation graph.

Moreover, to propose prioritized clustering based GA, the distribution depots are clustered based on their distance from the manufacturing plant and the amount of their demands. By this clustering process, we can incorporate a heuristic rule into the genetic algorithm through which a higher priority is assigned to the cluster member with longer average distance/higher average amount of demand for selecting the vehicle type.

5.1. Clustering distribution depots

There are two major factors for selecting the vehicle type to obtain the lowest transportation costs. One of these factors is the demand of each depot and the other is the distance between the manufacturing plant and the location of a depot. Considering this fact, a heuristic rule is incorporated to the proposed hybrid algorithms in which these two factors are used as the means of clustering. For applying this clustering procedure in a multidimensional space, the distance and the demand are shown respectively on the axes (X, Y) of the Cartesian coordinates. Therefore, denoting the distance and the demand of depot j by d _i and w _j respectively, in the Cartesian coordinates, any point in (X, Y) is shown as:$$(x_j,y_j)=(d_j,W_j)\forall j=1,2,\cdots ,n$$

Among the existing data clustering, the K-means has been most widely used. To enhance the performance of ​​the proposed algorithm, we employed the k-mean data clustering as well.

5.2. Prioritizing the clusters

To assign priority index to each cluster the average distances and demands of the members in each cluster are calculated and following steps will be performed.

1. Step 1. Designate the cluster with the largest average distance (LAD), to the manufacturing site. Select the cluster with the largest average in case of two or more clusters with the differential LADs of less than 100. Then assign the priority index k to the selected cluster.

2. Step 2. Eliminate the selected cluster from the list.

3. Step 3. If k = 0, stop, otherwise let k = k − 1, and go to step 1.

5.3. Initial solution

Two heuristic algorithms are proposed for obtaining the initial solution. Then each of these two solutions is incorporated into the GA for developing two hybrid GAs.

5.3.1. Heuristic algorithm I

The length of each chromosome in each cluster is defined by the its containing number of depots. That is; if there are K clusters, we will have K chromosomes in each of the initial solution. However, the lengths of the K chromosomes are varied according to the number of depots containing in each cluster. therefore, if the number of clusters is K and there are T depots in cluster t and if we consider $\left|L_T\right|$as the length of chromosome t, the value of its each gene, which illustrates the priority of its related depot, is an integer value in the range [$1,\left|L_T\right|$]. To generate the initial population, a priority encoding hybrid genetic algorithm is used to generate the chromosomes of each cluster. Note that the vehicles with the larger capacity generally have smaller unit cost. Due to this, a procedure is incorporated in the algorithm by which heavy vehicles are fully loaded first. Then, the remaining load then will be allocated according to the priority procedure. Let V denotes the set of source nodes (vehicles), D denotes the sink node (a depot in each cluster), pk(j) denotes the value of each gene in the kth chromosome corresponding to the kth cluster, and x _ij denotes the quantity of goods shipped from the source node i (with the vehicle i) to the sink node j (depot j). Then, heuristic algorithm I can be illustrated by the following flowchart:

Algorithm I

$$\begin{array}{cc}\text{Rel}\text{(1)}& \begin{array}{c}\text{Let}{x}_{i^{\ast }{j}^{\ast }}=x_{i^{\ast }{j}^{\ast }}+Min\{[W_{j^{\ast }}/q_{i^{\ast }}],T_{i^{\ast }}\},T_{i^{\ast }}-x_{i^{\ast }{j}^{\ast }},\text{and}\\ W_j=\left\{\begin{array}{cc}{W}_j-q_i{x}_{\mathit{ij}}& \text{for}{x}_{\mathit{ij}}=T_i\\ 0& \text{for}{x}_{\mathit{ij}}=[W_j/q_i]\end{array}\right.\end{array}\end{array}$$

Subroutine I

5.3.2. Heuristic algorithm II

This heuristic algorithm is developed based on the well-known concept of inner sum product rule. By this rule, the value of $AB=\sum \overline{a}\ast \overline{b}$ is minimized by ordering the elements of vector a in non-increasing order and the elements of vector bin non-decreasing order. Based on this rule, consider a transportation table in which the depots are considered as the sing nodes and the different vehicle types as the source nodes as follow:

In this Table 2 deports are ordered in non-increasing order of their distance from the manufacturing firm and appeared by this order in columns from left to right (D _j ’s). That is, the first column represents the depot with the largest distance to the manufacturing firm. Similarly, vehicles are ordered in non-decreasing order of their variable transportation costs (Cij) and appeared by this order in rows from top to down (Vi’s).The associated capacity of vehicles is appeared in the last column (q _i ’s) and the associated demand of depots is appeared in the last row (W _j ’s). Finally the volumeof load which is transporting from vehicle i to depot j is shown by variable x _ij . Using this Table 2 a near optimal solution can be obtained using the Subroutine II. Then for generating n solutions, Heuristic Algorithm II can be performed.

Table 2. Transportation table of the proposed heuristic Algorithm I

Subroutine II

Algorithm II

5.4. Hybrid genetic algorithms

The above preliminary procedures enable us to develop a hybrid genetic algorithm for solving the proposed problem. Using these procedures, the main steps of the proposed algorithm are conducted as below:

At the beginning of a run of the genetic algorithm a large population of random chromosomes is created. Each one, when decoded will represent a different solution to the problem at hand. Let’s say there are N chromosomes in the initial population. Then, the following steps are repeated until a solution is found.

5.4.1. Steps of hybrid GA-I

Flowchart of Hybrid GA-I can be presented as follow:

The above flowchart presents the major steps of Hybrid GA-I. the operators of this algorithm are described in the following subsections of this paper.

Based on Hybrid GA-I, two additional hybrid algorithms are proposed. The steps of these two additional algorithms are the same as Hybrid GA-I, except the first step for generating one of the initial populations. That is; in Hybrid GA-II, one of the initial population is generated using Heuristic Algorithm II, and in Hybrid GA-III, one of the initial population is selected among the best solutions obtained by Heuristic Algorithm I and Heuristic Algorithm II.

Before finalizing the development of the proposed algorithm, we performed a preliminary computational experiment for finding the most appropriate values of p _c and p _m . Through this experiment the values of p _c and p _m were determined as 90 and 50% respectively. In the following subsections the operators of the proposed algorithms are described.

5.4.2. The hybrid genetic algorithm operators

As it was mentioned earlier, the new generations are produced through the execution of the hybrid genetic algorithm operators. For the proposed algorithm the selection, crossover and mutation operators are developed and described as follow:

5.4.2.1. Selection operator

Since the objective function tries to minimize the total cost, the best solutions are the ones that have the least objective function values. Elitist and roulette wheel selection operators are the most used methods in designing a genetic algorithm.

In elitist selection method, the most appropriate member (s) of each population, and in roulette wheel selection method, the more appropriate member (s) with higher probability, will be selected. For a problem with minimizing objective function, a method for calculating fitness value with respect to the objective function has to be determined, in a way that better chromosomes, with smaller objective function values to be given lesser fitness values. For this purpose, suppose the objective function value and the fitness value for the kth chromosome respectively, denoted by z _k and f _k . So, the fitness value is considered as; $f_k=\frac{1}{z_k}$. For use of the roulette wheel selection method, the selection probability for each chromosome must be determined. Suppose that the selection probability for the kth chromosome is shown with p _k . If n is equal to the population size, the selection probability and the cumulative probability for each chromosome is calculated by Equations (11) and (12) respectively.(11) $$p_k=\frac{f_k}{\sum _{i=1}^n{f}_i}k=1,2,\cdots ,n$$(11) (12) $$q_k=\sum _{i=1}^n{p}_{i}k=1,2,\cdots ,n$$(12)

In the roulette wheel selection, the n intervals [0,q ₁], [$q_1,q_2]$ … [$q_k,q_{k+1}$] … [$q_n,1$,] are considered. In every selection, a random number between zero and one will be generated. Then the chromosome corresponding to the interval of the generated number will be selected.

To select the parents from the parent population for mutation and crossover operator, the roulette wheel selection method is used. All generated chromosomes by crossover and mutation operator are added to the current population, and finally for selecting the population of the next generation, the elitist selection method is used. Since it is more likely that the superior parents can produce superior offsprings, transmitting better solutions from each generation to the next generation is essential. That is why the elitist selection method has been chosen for selecting the chromosomes and transmitting them to the next generation.

It should be noted that the fitness values of the chromosomes related to different clusters which have the same number in the population are equal to each other. This is because of the fact that each problem solution is obtained by decoding the chromosomes with the same cluster number.

5.4.2.2. Crossover Operator

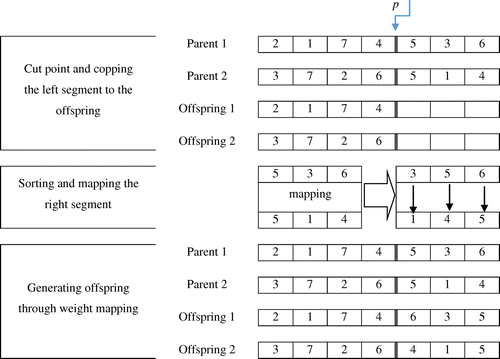
In this algorithm, the number of the chromosomes which are generated using the crossover operator is considered equal to P _c % of the total population size. The crossover operator which is used is known as the Weight Mapping Crossover and is separately applied to the chromosomes of each cluster. In other words, first the chromosomes of the first cluster are considered. Two chromosomes are selected using roulette wheel selection method, and the crossover operator is applied to them; the process is continued until producing new chromosomes equal to the P _c % of the total population size. Then, the same process is implemented on the next cluster and repeated to the last cluster. The crossover operator of the weighted mapping crossover is employed. This type of crossover operator is the one-point crossover operator, so like other one-point crossover operators; the first cut-point is randomly selected.

As showed in Figure 3, first we choose a random cut point p. using this cut, the values of the genes in the left segments of the first and second parent respectively, are copied to the genes in the left segments of the first and second offsprings. Then we get a mapping relation-ship by sorting the weight of the right segments s ₁[⋅] and s ₂[⋅]. As one-cut point crossover, it generates the offspring v ₁’[⋅] and v ₂’[⋅] by exchange substrings between parents v ₁[⋅] and v ₂[⋅]; legalize offspring with mapping relationship and thus, two new chromosomes are produced.

Figure 3. Example of weight mapping crossover operator.

5.4.2.3. Mutation Operator

Mutation Operator is used to make a change in the structure of the chromosome and in its current sequence. In other words, it is used to produce a new sequence, but similar to the current sequence of the mutated chromosome. The number of chromosomes generated by this operator, is considered equal to P _m % of the total population size. In this algorithm, similar to the crossover operator, the mutation operator is separately applied to the chromosomes of each cluster. In other words, first the chromosomes of the first cluster are considered. One chromosome is selected using the roulette wheel selection method, and the mutation operator is applied to it; the process is continued until producing new chromosomes equal in number to the P _m % of the total population size. Then, the same process is implemented on the next cluster and repeated to the last cluster.

There are four types of mutation operators, namely; swap, inversion, displacement, and inserting mutation. In this research we performed a preliminary computational experiment to select the mutation operator which provides the smallest gap from the optimum. Through this experiment we found swap mutation as the most appropriate operator.

6. Computational experiments

The motivation of this research comes from a real-world problem in a developing country in which a dairy manufacturer attempts to find the best allocation of the vehicles for transporting its dairy products to its depot. The area of this country is over 1,600,000 square kilometers which is categorized as a middle sized country. Considering the transportation coverage as well as the other attributes of this real-world problem, the experimental data for constructing the test problems are randomly generated.

6.1. Generation of the test problems

The test problems are categorized, according to the number of depots, in three different sizes. Considering n as the number of depots, the small size test problems are those having n ≤ 45, while the medium and large size problems we have 45 < n < 150, and 150 ≤ n ≤ 650 respectively. For each category 24 test problems with different values of n were contemplated. Five types of vehicles with loading capacities of 3, 6, 12, 18, and 24 tons are considered. The data for transportation cost consisting of the fixed and variable costs are determined as follows:

Letting $F_i^d$ denotes the fixed cost of vehicle i, discounted according to the allocated load d, with three load allocations as follow:$$F_i^d=\left\{\begin{array}{c}{F}_i^1\text{if}0\le \sum _{j=1}^n{x}_{\mathit{ij}}<1/2T_i\hfill \\ F_i^2\text{if}1/2T_i\le \sum _{j=1}^n{x}_{\mathit{ij}}<1/2T_i+1/3T_i\hfill \\ F_i^3\text{if}1/2T_i+1/3T_i\le \sum _{j=1}^n{x}_{\mathit{ij}}\le T_i\hfill \end{array}\right.$$

The values of $F_{q_i}^d$ for the vehicles with different capacities of q _i (q _i  = 1, 2, 3, 4, 5), are as follows:$$F_1^1=120,F_1^2=90,F_1^3=60,F_2^1=130,F_2^2=100,F_2^3=70,F_3^1=150,F_3^2=120,F_3^3=90,F_4^1=180,F_4^2=150,F_4^3=120,F_5^1=210,F_5^2=180,F_5^3=150.$$

To generate the variable costs a uniform density function with the range of [20–200] is generated and assigned to the routes. To consider the real world considerations, We let the variable costs are increased as the distances are increased. We also let the unit variable cost (cost/weight) is decreased as the vehicles with higher capacity are allocated. The depots demands were generated using a uniform density function with the range of [40–400]. The depots distances from the manufacturing site were generated using a uniform density function with the range of [100–2000]. As another real world consideration, no limitation is imposed on the number of vehicles with the capacities of 3 and 6 tons. To impose limitation on the number of other vehicle types, while preventing the trivial solutions, the following cases were contemplated:

If limitations have to be imposed on only two types of vehicles, the data are generated using the uniform density function of U[a−b], as:

The number of 24 tons vehicles = İ( ∑ W _j /24) * U[0.25 − 0.75]İ

The number of 18 tons vehicles = İ∑ W _j /18) * U[0.50 − 1.10]İ

To impose a limitation on three types of vehicles the data are generated as;

The number of 24 tons vehicles = İ∑ W _j /24) * U[0.15 − 0.50]İ

The number of 18 tons vehicles = İ∑ W _j /18) * U[0.20 − 0.55]İ

The number of 12 tons vehicles = İ∑ W _j /12) * U[0.25 − 0.65]İ

To impose a limitation on more than three types of vehicles the data are generated as;

The number of 24 tons vehicles = İ∑ W _j /24) * U[0.10 − 0.45]İ

The number of 18 tons vehicles = İ∑ W _j /18) * U[0.15 − 0.50]İ

The number of 12 tons vehicles = İ∑ W _j /12) * U[0.20 − 0.60]İ

The number of 6 tons vehicles = İ∑ W _j /6İ

The number of 3 tons vehicles = İ∑ W _j /3İ

Where the symbol İaİ indicates the largest integer value less than or equal to a.

6.2. Algorithm parameter tuning

For tuning the parameters, we chose Hybrid GA-I. The interaction effects of two parameters at a time on the gaps of the objective function values and the computational time is evaluated using the solution of Hybrid GA-I and the CPLEX solution (S-CPLEX). A factorial experimental design is performed considering each parameter as a factor. Table 3 illustrates the parameters (factors) and their associated levels of the proposed genetic algorithm. The solution gap and the gap on computational time are determined by Equations (13) and (14) respectively.(13) $${\text{Gap}}_S=\frac{S_{\text{HybridGA}-I}-S_{\text{CPLEX}}}{S_{\text{CPLEX}}}\times 100$$(13) (14) $${\text{Gap}}_T=\frac{T_{\text{HybridGA}-I}-T_{\text{CPLEX}}}{T_{\text{CPLEX}}}\times 100$$(14)

Table 3. Hybrid GA-I parameters and their associated levels

No.	Parameters(Factors)	Level of factors
		1	2	3	4	5
1	Population size	m×n	2×m×n	(m×n)/2
2	Number of iterations	m×n	2×m×n	(m×n)/2
3	Crossover types	One point	Two points	Position based
4	Mutation types	Insert	Swap	Inversion	Displacement	Prufer
5	Crossover rates	% 70	% 80	% 90
6	Mutation rates	% 30	% 40	% 50

Notes: n: the number depots, and m: the number of vehicle types.

To determine the main effects of the “population size” and the “number of iterations”, as well as their interaction effects, the Gap _S and Gap _T are calculated, while other three factors are ignored in these calculations. Then a similar experiment is performed for the pair of the “crossover types” and the “mutation types” as well as the pair of “crossover rates” and the “mutation rates”. Through these experiments a set parameter with the smallest Gap _S is selected. It is to be noted that the Gap _S and Gap _T were fairly correlated throughout these experiments.

6.3. Computational results

In this section the efficiency of the proposed algorithms will be evaluated. The different scenarios are considered for assessing the performance of the proposed algorithms. In first scenario, the hybrid algorithms are compared with each other and the best one will be designated. Then, the designated algorithm is compared it with CPLEX. Finally, two recently cited algorithms will be used to evaluate the efficiency of the designated algorithm.

6.3.1. Comparison of the proposed hybrid algorithms

For evaluating the efficiency of the proposed hybrid algorithms, 24 test problems are classified per different number of depots and different number of vehicle types. Then for each class, five test problems are randomly generated and solved by the proposed hybrid algorithm. Table 4 presents the results of this computational experiment. In this table the objective function of the solutions, denoted by “OF V”, and the CPU time of the algorithms are reported. Based on these values, the hybrid algorithm having the lowest objective function value and CPU time are designated and presented by bold numbers. As it is revealed, hybrid GA-III provides the best objective function values for 23 out of 24 instances and provided the lowest CPU times in most of instances. Therefore, we designated this algorithm for the further computational experiments.

Table 4. Comparison of the three-proposed hybrid GAs

# of Depot	#of VT	Hybrid GA-I		Hybrid GA-II		Hybrid GA-III
		OF V	Time	OF V	Time	OF V	Time
30	2	112,858.7	0.07	111,912.5	0.08	110,768.0 *	0.06 **
	3	140,373.0	0.14	138,993.1	0.14	138,195.0 *	0.12 **
	4	130,434.0	0.01 **	131,036.0	0.02	118,698.7 *	0.01 **
	5	174,377.7	0.16 **	171,482.0	0.18	157,129.8 *	0.16 **
60	2	244,281.3	0.61	245,035.0	0.68	241,253.0 *	0.55 **
	3	304,442.0	1.49	292,351.0	1.37	284,876.0 *	1.42 **
	4	395,623.3	0.61	381,415.9	0.55	361,424.5 *	0.16 **
	5	328,800.7	1.79	329,011.0	1.57	294,296.2 *	1.70 **
90	2	370,489.0	2.52	368,888.0	2.44	347,801.7 *	2.04 **
	3	508,420.7	0.07 **	501,729.0	0.07 **	465,363.3 *	0.07 **
	4	485,942.0	0.44 **	480,681.9	0.54	446,588.9 *	0.51
	5	405,751.3 *	1.13	454,167.0	0.87	407,588.1	0.93 **
150	2	611,199.0	13.54	608,331.4	12.11	583,778.0 *	11.16 **
	3	725,513.7	0.23	727,184.7	0.22	666,565.3 *	0.20 **
	4	832,339.3	0.24	744,687.5 *	0.23 **	744,687.5 *	0.27
	5	658,344.0	39.47	631,591.0	37.82 **	586,504.4 *	41.57
350	2	1,587,707.0	235.73	1,569,993.0	233.14 **	1,472,111.0 *	245.61
	3	1,792,511.3	3.17	1,633,529.6	3.77	1,525,112.1 *	2.27 **
	4	2,116,080.0	16.86	2,200,482.0	17.02	2,071,240.5 *	15.52 **
	5	2,197,789.3	59.03	2,214,821.0	51.8	1,990,434.6 *	49.49 **
550	2	2,470,977.0	5.33 **	2,411,663.0	7.23	2,404,568.0 *	5.33 **
	3	2,846,752.3	7.13	2,699,352.7	6.14 **	2,463,048.9 *	8.41
	4	3,358,537.3	134.07	3,274,611.0	132.17 **	2,999,522.4 *	168.01
	5	3,534,212.0	1889.34	3,393,211.0	1882.09 **	2,677,537.6 *	2035.57

* Best OF V (Bold number).

** Best CPU time (Bold number).

6.3.2. Comparing hybrid GA-III with CPLEX

A mathematical programming model was presented in Section 4 of this paper. As it can be realized, the objective function of this model, consists of two parts. The first part which defines the fixed costs has a nonlinear relation.In order to assess the performance of Hybrid GA-III, CPLEX software is employed. However, we first need to convert the mathematical problem to a linear form. For converting the first part of the objective function to a linear relation, we can rewrite the relations as below:(15) $$\text{Fixed cost}=\sum _{i=1}^m\sum _{j=1}^n{F}_i{x}_{\mathit{ij}}=\sum _{i=1}^m\sum _{j=1}^n(y_i^1{F}_i^1+y_{{}_i}^2{F}_i^2+\cdots +y_i^t{F}_i^t)x_{\mathit{ij}}$$(15)

If T _i is the upper limit of $\sum _{j=1}^n{x}_{\mathit{ij}}$, we can convert the integer variable x _ij to the series of zero-one variable z _ij ’s by the following relation:(16) $$x_{\mathit{ij}}=2^0{z}_{\mathit{ij}}^0+2^1{z}_{\mathit{ij}}^1+2^2{z}_{\mathit{ij}}^2+\cdots +2^{f_i}{z}_{\mathit{ij}}^{f_i},\text{where}{f}_i\le ⌈\frac{log\left(\frac{T_i+1}{2}\right)}{log2}⌉$$(16) (17) $$t_{\mathit{ijs}}=y_i^s{x}_{\mathit{ij}}\Rightarrow t_{\mathit{ijs}}=2^0{y}_i^s{z}_{\mathit{ij}}^0+2^1{y}_i^s{z}_{\mathit{ij}}^1+2^2{y}_i^s{z}_{\mathit{ij}}^2+\cdots +2^{f_i}{y}_i^s{z}_{\mathit{ij}}^{f_i}$$(17) (18) $$\text{Fixed cost}=\sum _{i=1}^m\sum _{j=1}^n(F_i^1{t}_{ij1}+F_i^2{t}_{ij2}+\cdots +F_i^v{t}_{\mathit{ijv}})=\sum _{i=1}^m\sum _{j=1}^n\sum _{s=1}^v{F}_i^s{t}_{\mathit{ijs}}$$(18) (19) $$y_i^s+z_{\mathit{ij}}^r-2t_{\mathit{ijs}}^r\ge 0\forall i=1,2,\cdots ,m,j=1,2,\cdots ,n,s=1,2,\cdots ,v,\text{and}r=0,1,2,\cdots ,f_i$$(19) (20) $$y_i^s+z_{\mathit{ij}}^r-t_{\mathit{ijs}}^r\le 1\forall i=1,2,\cdots ,m,j=1,2,\cdots ,n,s=1,2,\cdots ,v,\text{and}r=0,1,2,\cdots ,f_i$$(20) (21) $$\text{Then we have}\sum _{i=1}^m\sum _{j=1}^n\sum _{s=1}^t{F}_i^s{t}_{\mathit{ijs}}=\sum _{i=1}^m\sum _{j=1}^n\sum _{s=1}^t\sum _{r=0}^{f_i}{F}_i^s(2^r{t}_{\mathit{ijs}}^r)$$(21)

Using this fixed cost the mathematical model can be written as:(22) $$Min{X}_0=\sum _{i=1}^m\sum _{j=1}^n\sum _{s=1}^t\sum _{r=0}^{f_i}{F}_i^s(2^r{t}_{\mathit{ijs}}^r)+\sum _{i=1}^m\sum _{j=1}^n\sum _{r=0}^{f_i}{c}_{\mathit{ij}}(2^r{z}_{\mathit{ij}}^r)$$(22)

Subject to:(23) $$\sum _{j=1}^n\sum _{r=0}^{f_i}{2}^r{z}_{\mathit{ij}}^r\le T_i\forall i=1,2,\cdots ,m$$(23) (24) $$\sum _{i=1}^m\sum _{r=0}^{f_i}{q}_i(2^r{z}_{\mathit{ij}}^r)\ge W_j\forall j=1,2,\cdots ,n$$(24) (25) $$-M(1-y_i^s)+\sum _{j=1}^n\sum _{r=0}^{f_i}{2}^r{z}_{\mathit{ij}}^r\le v_i^s\text{- 1}\forall i=1,2,\cdots ,m\text{and}s=1,2,\cdots ,t-1$$(25) (26) $$-M(1-y_i^s)+\sum _{j=1}^n\sum _{r=0}^{f_i}{2}^r{z}_{\mathit{ij}}^r{x}_{\mathit{ij}}\le v_i^t\forall i=1,2,\cdots ,m$$(26) (27) $$M(1-y_i^s)+\sum _{j=1}^n\sum _{r=0}^{f_i}{2}^r{z}_{\mathit{ij}}^r\ge v_i^{s-1}\forall i=1,2,\cdots ,m\text{and}s=2,3,\cdots ,t$$(27) (28) $$x_{\mathit{ij}}=\sum _{r=0}^{f_i}{2}^r{z}_{\mathit{ij}}^r\forall i=1,2,\cdots ,m,\text{and}j=1,2,\cdots ,n$$(28) (29) $$y_i^s+z_{\mathit{ijs}}^r-t_{\mathit{ijs}}^r\le 1\forall i=1,2,\cdots ,m,j=1,2,\cdots ,n,s=1,2,\cdots ,t,\text{and}r=0,1,2,\cdots ,f_i$$(29)

For every 72 test problems (24 test problems in each category; small, medium and large instances), with different values of m and n five problems were randomly generated and solved via the Hybrid GA-III and CPLEX software. Tables 5 through 7 illustrate the results of this computational experiment. Table 5 is dedicated to the results of small sized test problems. In this Table 24 test problems are classified according to different values of m and n. In column two, the number of depots are presented. In class of the small sized problems, six different scenarios of, 20, 25, 30, 35, 40 and 45 are considered for the number of depots. For each scenario, the number of the vehicle types of 2, 3, 4, and 5 are contemplated (column 3). As the result 24 different scenarios are defined. Then the test problems are solved by the proposed algorithm and the CPLEX software. The results obtained by the designated algorithm and the CPLEX software are illustrated in columns 4 to 6 and columns 7 to 9 respectively. Columns 5 and 6 present the average values of the objective function (denoted by Ave OF value) and average computational time of the proposed algorithm respectively. Similarly, columns 7 and 8 present the same values obtained by the CPLEX software respectively. Due to the computational complexity of the problems, the optimal solution of some of the small sized problem couldn’t be obtained by the CEPLEX software. Therefore, in this column, the problems are either marked as “optimal”, or marked as “LB” for those which the optimal are not reached. in this column. Finally, the last two columns of this table illustrate the gap in objective function values, marked as “OF Gap” and the gap in execution time, marked as “Time Gap”, respectively, using the following mathematical relations:(30) $$OFGap=(Ave.OF\text{value of Hybrid GA-III-}OF\text{value of CPLEX})/OF\text{value of CPLEX}.$$(30) (31) $$TimeGap=(Ave.Time\text{of Hybrid GA-III-}Time\text{of CPLEX})/Time\text{of CPLEX}.$$(31)

Table 5. Computational results of the small sized problems

				Hybrid GA-III		CPLEX			Appraisal
Test problem	# of Depot	# of Vehicle types	Pop size	Ave OF value	Ave Time (S)	OF value	Time (S)	Type of solution	OF gap	Time gap
1	20	2	40	85,456.00	0.03	85,456.00	10.48	Optimal	0.00	99.71
2	25	2	50	113,103.54	0.04	112,063.00	13.73	Optimal	0.92	99.71
3	30	2	60	110,768.00	0.06	110,768.00	10.75	Optimal	0.00	99.44
4	35	2	70	132,469.26	0.11	131,469.00	9.91	Optimal	0.76	98.89
5	40	2	80	139,677.00	0.17	139,677.00	21.86	Optimal	0.00	99.22
6	45	2	90	180,971.51	0.23	180,894.00	91.15	Optimal	0.04	99.75
7	20	3	60	85,348.00	0.05	85,348.00	26.83	Optimal	0.00	99.81
8	25	3	75	129,138.24	0.08	128,325.00	21.81	Optimal	0.63	99.63
9	30	3	90	138,195.00	0.12	138,195.00	22.84	Optimal	0.00	99.47
10	35	3	105	170,818.56	0.24	169,502.00	56.45	Optimal	0.77	99.57
11	40	3	120	174,156.84	0.38	172,469.00	65.22	Optimal	0.97	99.42
12	45	3	135	208,882.74	0.57	207,909.00	433.30	Optimal	0.47	99.87
13	20	4	80	125,603.66	0.08	125,402.00	2043.10	Optimal	0.16	100.00
14	25	4	100	158,028.52	0.01	158,194.00	1429.05	LB	BTL	100.00
15	30	4	120	118,698.69	0.01	123,916.00	1491.30	LB	BTL	100.00
16	35	4	140	213,445.59	0.04	213,199.00	1409.65	LB	0.12	100.00
17	40	4	160	173,337.00	0.08	177,444.00	1119.54	LB	BTL	99.99
18	45	4	180	249,525.44	0.09	252,912.00	997.74	LB	BTL	99.99
19	20	5	100	105,899.20	0.05	109,186.00	854.22	LB	BTL	99.99
20	25	5	125	106,319.76	0.05	105,948.00	1211.93	LB	0.35	100.00
21	30	5	150	157,129.78	0.16	169,940.00	1314.44	LB	BTL	99.99
22	35	5	175	161,082.79	0.16	162,805.00	1217.19	LB	BTL	99.99
23	40	5	200	279,527.36	0.3	278,974.00	1263.73	LB	0.20	99.98
24	45	5	225	224,234.81	0.74	225,350.00	1564.31	LB	BTL	99.95

In Tables 6 and 7 similar results for the medium and large sized test problems are illustratedrespectively. From the results of this experiment we can conclude that the designated algorithm can obtain the robust solutions in a very short computational time. As it can be seen, the CPLEX cannot find the optimal solutions for the problems with more than 4 vehicles. It is stopped either due to the excessive computational time or computational memory with the results of a non-integer solution or non-optimal solution. However, since we can consider these solutions as the lower bound of the optimal solutions, it can be concluded that the gap between the solution obtained by the proposed algorithm and the optimal solution are so small. Note that in several instances the solution of Hybrid GA-III is better than the lower bound of CPLEX (denoted by BTL in Column OF Gap). With regard of the computational time, we certainly can conclude that the computational time of Hybrid GA-III is so tiny comparing to the computational time of the CPLEX. In case of applying the approach to a real-world instance, this can be considered as the most important future of the proposed algorithm.

Table 6. Computational results of the medium sized problems

				Hybrid GA-III		CPLEX			Appraisal
Test problem	# of Depot	# of Vehicle types	Pop size	Ave OF value	Ave time (S)	OF value	Time (S)	Type of solution	OF gap	Time gap
1	50	2	100	221,749.00	0.34	221,749.00	57.82	Optimal	0.00	99.41
2	60	2	120	241,253.00	0.55	241,253.00	19.06	Optimal	0.00	97.11
3	70	2	140	327,849.20	1.02	320,983.00	86.67	Optimal	2.09	98.82
4	80	2	160	330,094.23	1.69	321,196.00	48.08	Optimal	2.70	96.49
5	90	2	180	347,801.70	2.04	355,842.00	228.81	Optimal	0.00	99.11
6	100	2	200	376,741.00	3.32	376,741.00	359.01	Optimal	0.00	99.08
7	50	3	150	255,474.00	0.76	255,474.00	120.09	Optimal	0.00	99.37
8	60	3	180	284,116.17	1.42	285,650.00	1267.89	Optimal	BTL	99.89
9	70	3	210	350,065.53	0.07	351,746.00	1371.81	LB	BTL	99.99
10	80	3	240	408,103.00	0.06	408,190.00	1301.66	LB	BTL	100.00
11	90	3	270	465,363.30	0.07	499,423.00	1526.85	LB	BTL	100.00
12	100	3	300	460,434.00	8.26	460,434.00	5399.21	Optimal	0.00	99.85
13	50	4	200	272,866.30	0.12	272,537.00	728.68	LB	0.12	99.98
14	60	4	240	361,424.16	0.16	387,990.00	417.41	LB	BTL	99.96
15	70	4	280	459,951.04	0.13	460,820.00	1566.17	LB	BTL	99.99
16	80	4	320	500,008.42	0.27	498,213.00	2002.26	LB	0.36	99.99
17	90	4	360	446,588.91	0.51	471,929.00	1586.69	LB	BTL	99.97
18	100	4	400	541,335.01	0.51	540,364.00	2677.50	LB	0.18	99.98
19	50	5	250	282,448.33	0.72	280,186.00	624.41	LB	0.80	99.88
20	60	5	300	294,296.17	1.70	321,552.00	2771.70	LB	BTL	99.94
21	70	5	350	349,683.45	2.06	352,410.00	1693.47	LB	BTL	99.88
22	80	5	400	398,478.08	10	392,946.00	1962.72	LB	1.39	99.49
23	90	5	450	407,588.08	0.93	434,258.00	2043.08	LB	BTL	99.95
24	100	5	500	458,222.36	1.86	454,687.00	1838.19	LB	0.77	99.90

Table 7. Computational results of the large sized problems

				Hybrid GA-III		CPLEX			Appraisal
Test problem	# of Depot	# of Vehicle types	Pop Size	Ave of value	Ave time (S)	OF value	Time (S)	Type of solution	OF gap	Time gap
1	150	2	300	583,778.00	13.54	583,778.00	461.07	Optimal	0.00	97.06
2	250	2	500	1,189,084.00	89.37	1,089,084.00	5268.81	Optimal	8.41	98.30
3	350	2	700	1,472,111.00	245.61	1,472,111.00	1007.50	Optimal	4.94	75.62
4	450	2	900	1,893,915.95	787.85	1,877,224.00	2422.07	Optimal	0.88	67.47
5	550	2	1100	2,404,568.00	5.33	2,404,568.00	327.04	LB	0.00	98.37
6	650	2	1300	2,875,046.08	3248.92	2,743,017.00	7016.97	LB	4.59	53.70
7	150	3	450	666,565.27	0.2	708,231.00	1322.96	LB	BTL	99.98
8	250	3	750	1,255,934.55	0.68	1,258,262.00	4197.25	LB	BTL	99.98
9	350	3	1050	1,525,112.05	2.27	1,680,355.00	4044.16	LB	BTL	99.94
10	450	3	1350	2,319,943.58	3.88	2,313,796.00	1935.76	LB	0.26	99.80
11	550	3	1650	2,463,048.79	8.41	2,791,528.00	7237.02	LB	BTL	99.88
12	650	3	1950	3,562,674.20	80.07	3,512,785.00	7839.38	LB	1.40	98.98
13	150	4	600	744,687.52	0.27	966,241.00	521.79	LB	BTL	99.95
14	250	4	1000	1,380,900.80	3.59	1,401,988.00	5639.52	LB	BTL	99.94
15	350	4	1400	2,071,240.46	15.52	2,803,780.00	1061.18	LB	BTL	98.54
16	450	4	1800	2,672,793.20	61.13	2,658,101.00	8010.54	LB	0.55	99.24
17	550	4	2200	2,999,522.43	168.01	3,241,147.09	3055.96	LB	0.26	94.50
18	650	4	2600	3,962,693.84	190.09	4,511,222.69	3313.92	LB	BTL	94.26
19	150	5	750	586,504.44	41.57	627,399.00	2308.92	LB	BTL	98.20
20	250	5	1250	1,410,137.28	81.56	1,392,492.00	5733.54	LB	1.25	98.58
21	350	5	1750	1,990,434.04	49.49	2,040,618.77	622.21	LB	BTL	92.05
22	450	5	2250	2,936,188.78	342.51	2,129,218.89	3462.38	LB	27.48	90.11
23	550	5	2750	2,677,537.57	2035.44	3,728,023.97	3816.35	LB	BTL	46.67
24	650	5	3250	3,975,060.90	333.76	4,319,182.95	1295.63	LB	BTL	74.24

Note: An illustrative example of the mathematical model and its solution by CPLEX software is presented in the Appendix 1 of this manuscript.

6.3.3. Comparing Hybrid GA-III with existing algorithms

To evaluate the efficiency of the Hybrid GA-IIIwith the existing algorithm, a priority-based GA (Ghassemi Tari, 2016) and a Prufer based GA (Hajiaghaei-Keshteli et al., 2010) are selected from literature. Then 24 of the test problems are also solved by the Hybrid GA-III and the cited Gas. The results of this computational experiment are presented in Tables 8 and 9. In Table 8 the first two columns illustrate the size of the problem, namely; the number of depots indicated by (# of Depot); and the number of vehicle types indicated by “# of VT”. Columns 3 and 4 of this table present the objective function value indicated by “OF V” and the computational time indicted by “Time” of the Hybrid GA-III respectively. The same measures for the priority-based GA are presented in columns 5, and 6.Finally the percentage of improvement on the objective function value and computational time are calculated by the following relations and are respectively demonstrated in the last two columns.(32) $$OFV\%=(OFV\text{of the priority}-OFV\text{of Hybrid GA-III})/OFV\text{of the priority}$$(32) (33) $$Time\%=(Time\text{of the priority}-Time\text{of Hybrid GAIII})/Time\text{of the priority}$$(33)

Table 8. Comparison of the proposed hybrid algorithm with a priority-based GA

# of Depot	#of VT	Hybrid Algorithm III		Priority Algorithm		Improvement (%)
		OF V	Time	OF V	Time	OF V	Time
30	2	110,768.0	0.06	112,793.7	0.06	1.80	0.00
	3	138,195.0	0.12	140,453.7	0.15	1.61	20.00
	4	118,698.7	0.01	127,238.7	0.07	6.71	85.71
	5	157,129.8	0.16	175,208	0.49	10.32	67.35
60	2	241,253.0	0.55	244,174	0.59	1.20	6.78
	3	284,116.2	1.42	303,704	1.42	6.45	0.00
	4	361,424.5	0.16	395,291	0.48	8.57	66.67
	5	294,296.2	1.70	329,193	5.34	10.60	68.16
90	2	347,801.7	2.04	370,001.7	2.41	6.00	15.35
	3	465,363.3	0.07	509,899.3	0.73	8.73	90.41
	4	446,588.9	0.51	486,895.7	1.75	8.28	70.86
	5	407,588.1	0.93	451,895.3	21.28	9.80	95.63
150	2	583,778.0	13.54	608,170.7	15.55	4.01	12.93
	3	666,565.3	0.20	723,840.7	4.47	7.91	95.53
	4	744,687.5	0.27	814,662.7	9.89	8.59	97.27
	5	586,504.4	41.57	653,496.7	158.66	10.25	73.80
350	2	1,472,111.0	245.61	1,572,456	371.66	6.38	33.92
	3	1,525,112.1	2.27	1,799,277	82.73	15.24	97.26
	4	2,071,240.5	15.52	2,093,592	264.15	1.07	94.12
	5	1,990,434.6	49.49	2,239,327	518.54	11.11	90.46
550	2	2,404,568.0	5.33	2,484,227	48.84	3.21	89.09
	3	2,463,048.9	8.41	2,850,156	82.73	13.58	89.83
	4	2,999,522.4	168.01	3,351,702	1192.16	10.51	85.91
	5	2,677,537.6	2035.57	3,653,620	2777.46	26.72	26.71
Average						8.28	61.41

Table 9. Comparison of the proposed hybrid algorithm with a Prufer-based GA

# of Depot	#of VT	Hybrid Algorithm III		Prufer Algorithm		Improvement (%)
		OF V	Time	OF V	Time	OF V	Time
30	2	110,768.0	0.06	113,096.67	0.14	2.06	57.14
	3	138,195.0	0.12	140,973.33	0.39	1.97	69.23
	4	118,698.7	0.01	127,633.00	0.27	7.00	77.78
	5	157,129.8	0.16	179,231.67	0.83	12.33	78.31
60	2	241,253.0	0.55	244,653.67	1.50	1.39	57.14
	3	284,116.2	1.42	292,552.33	5.60	2.88	69.23
	4	361,424.5	0.16	397,393.67	1.71	9.05	96.30
	5	294,296.2	1.70	335,656.67	13.99	12.32	80.72
90	2	347,801.7	2.04	370,431.33	6.50	6.11	63.33
	3	465,363.3	0.07	512,486.67	1.64	9.20	74.64
	4	446,588.9	0.51	489,450.00	8.81	8.76	90.64
	5	407,588.1	0.93	460,136.33	55.13	11.42	87.85
150	2	583,778.0	13.54	608,270.33	46.28	4.03	68.62
	3	666,565.3	0.20	724,689.00	11.61	8.02	95.73
	4	744,687.5	0.27	819,122.00	48.53	9.09	94.21
	5	586,504.4	41.57	667,427.00	346.28	12.12	98.31
350	2	1,472,111.0	245.61	158,027.00	1171.11	6.84	70.74
	3	1,525,112.1	2.27	1,802,210.70	184.34	15.38	98.28
	4	2,071,240.5	15.52	2,113,510.70	587.68	2.00	99.44
	5	1,990,434.6	49.49	2,369,564.30	491.89	16.00	88.00
550	2	2,404,568.0	5.33	2,497,393.00	50.69	3.72	79.03
	3	2,463,048.9	8.41	2,859,327.00	856.27	13.86	98.77
	4	2,999,522.4	168.01	3,420,727.00	1818.04	12.31	97.36
	5	2,677,537.6	2035.57	3,825,053.70	2657.56	30.00	89.94
Average						9.08	83.37

The same results are reported for Prufer-based GA in Table 9. Referring to these tables, it can be realized that the average computational time of Hybrid GA-III on average is more than 60% faster than priority-based GA and more than 80% faster than Prufer-based GA. Also, it is shown that the average objective value of Hybrid GA-III is 8.28% better than the priority-based GA and is 9.08% better than the Prufer-based GA.

7. Conclusions

In this paper, the problem of assigning the most appropriate type of vehicles to the transportation routes in an existing distribution system to minimize the total transportation costs was considered. The problem involves a heterogeneous fleet of vehicles having various capacities, for delivering a set of goods from a manufacturing firm to its depots. It is assumed that transportation costs consist of a fixed cost and a variable cost which is incurred proportionately to the travel distance. Also, there is a discount mechanism which is applied to the fixed part of the transportation costs, varying according to the number of vehicles to be rented. The proposed problem is challenged by a fleet vehicles depots assignment problem in a food industrial group of a developing country. However, instead of solving this real-world problem a more generalized form of this problem was considered. A mathematical model in the form of nonlinear mixed zero-one integer programming was proposed. Due to the computational complexity of the proposed mathematical programming model for the real-world scenarios, three hybrid meta-heuristic approaches for obtaining a good solution of the problem were developed. Two heuristic algorithms for selecting a lower cost vehicle to depots were first developed. The solutions of each of these heuristics were considered as the initial population of a new proposed prioritized K-mean cluster encoding GA. By incorporating different combinations of the solutions of these two heuristic algorithms, as the initial population of GA, three hybrid GAs were constructed. By a factorial experimental design, the operators of the genetic algorithm are defined and tuned for obtaining the best results. Furthermore, an extensive computational experiment was conducted for evaluating the performance of the proposed algorithm. In this experiment 72 test problems were categorized in three different classes according to their sizes. Then, for every class of 72 test problems, five test problems, using the concept of the pseudo-random number, were generated. Three different scenarios were considered for assessing the performance of the proposed algorithms. In first scenario, the hybrid algorithms were compared with each other and due to high performance of Hybrid GA-III, it was designated as the best one. Then, Hybrid GA-III was compared with CPLEX. Finally, two recently cited algorithms, a priority-based GA, and a Prufer-based GA were used to evaluate the efficiency of the designated algorithm. The results of these scenarios indicated the superiority of the proposed solution approaches.

In this research, we considered a general version of vehicles allocation to distribution routes of a discounted fixed charge transportation network with total transportation costs as performance measure and proposed three prioritized K-mean clustering hybrid Gas. The Proposed algorithms showed to be efficient both in terms of speed and quality. Some other major contributions of this work can be summarized as follow:

•	A nonlinear mathematical program is proposed and is converted to a linear MILP.
•	The efficiency of proposed algorithms are compared with each other and the best one is designated.
•	The efficacy of the designated algorithm is compared with the solution of CPLEX software and its efficiency is confirmed.
•	The computational efficiency of the designated algorithm is compared with two recently cited algorithms and shown that it outperforms the existing algorithms.

Funding

The authors received no direct funding for this research.

Supplementary material

Supplementary material for this article can be accessed at https://doi.org/10.1080/23311916.2018.1463833.

Additional information

Notes on contributors

Farhad Ghassemi Tari

Farhad Ghassemi Tari is working as an associate professor in the Department of Industrial Engineering at Sharif University of Technology. He received his PhD and MSc in Industrial Engineering from Texas A & M University, and his Bachelor degree in Industrial Engineering from Sharif University of Technology. His major fields of research are; applied operations research, facility layout design, sequencing & scheduling, and transportation planning.

Appendix 1

Consider a small example consists of 5 depots and two vehicle types with the following parameters:

m = 2; n = 5, q ₁ = 24, q ₂ = 18, T ₁ = 8, T ₂ = 48$$W_1=124,W_2=203,W_3=125,W_4=230,W_5=150$$ $$c_{11}=301,c_{12}=369,c_{13}=348,c_{14}=253,c_{15}=304$$ $$c_{21}=239,c_{22}=360,c_{23}=283,c_{24}=301,c_{25}=301$$ $$F_1=\left\{\begin{array}{c}\begin{array}{cc}210& 0<V_1<4\end{array}\\ \begin{array}{cc}180& 4\le V_1<7\end{array}\\ \begin{array}{cc}150& 7\le V_1\le 8\end{array}\end{array}\right.$$

Where $V_1=\sum _{j=1}^5{x}_{1j}$ $$F_2=\left\{\begin{array}{c}\begin{array}{cc}180& 0<V_2<4\end{array}\\ \begin{array}{cc}150& 4\le V_2<7\end{array}\\ \begin{array}{cc}120& 7\le V_2\le 8\end{array}\end{array}\right.$$

Where $V_2=\sum _{j=1}^5{x}_{2j}$

Variables:

x _ij :Number of vehicle type i used for transporting products to depot j(i = 1, 2; j = 1, 2, …, 5)

$y_i^s$: Binary variable(i = 1, 2; s = 1, 2, 3)

The mathematical model of this problem is written as follows:$$Min{X}_0=\sum _{i=1}^2\sum _{j=1}^5{F}_i{x}_{\mathit{ij}}+\sum _{i=1}^2\sum _{j=1}^5{c}_{\mathit{ij}}{x}_{\mathit{ij}}$$

Subjected to:$$\begin{array}{c}\sum _{i=1}^2{q}_i{x}_{\mathit{ij}}\ge W_j\forall j=1,2,\dots ,5\hfill \\ \sum _{j=1}^5{x}_{\mathit{ij}}\le T_i\forall i=1,2\hfill \\ F_1=210y_1^1+180y_1^2+150y_1^3\hfill \\ F_2=180y_2^1+150y_2^2+120y_2^3\hfill \end{array}$$ $$\begin{array}{c}{y}_1^1+y_1^2+y_1^3=1\hfill \\ y_2^1+y_2^2+y_2^3=1\hfill \end{array}$$ $$\begin{array}{c}-M(1-y_1^1)+\sum _{j=1}^5{x}_{\mathit{ij}}\le 3\hfill \\ -M(1-y_2^1)+\sum _{j=1}^5{x}_{\mathit{ij}}\le 23\hfill \end{array}$$ $$\begin{array}{c}M(1-y_1^2)+\sum _{j=1}^5{x}_{\mathit{ij}}\ge 4\hfill \\ M(1-y_2^2)+\sum _{j=1}^5{x}_{\mathit{ij}}\ge 24\hfill \end{array}$$ $$\begin{array}{c}-M(1-y_1^2)+\sum _{j=1}^5{x}_{\mathit{ij}}\le 6\hfill \\ -M(1-y_2^2)+\sum _{j=1}^5{x}_{\mathit{ij}}\le 39\hfill \end{array}$$ $$\begin{array}{c}M(1-y_1^3)+\sum _{j=1}^5{x}_{\mathit{ij}}\ge 7\hfill \\ M(1-y_2^3)+\sum _{j=1}^5{x}_{\mathit{ij}}\ge 40\hfill \end{array}$$ $$\begin{array}{c}-M(1-y_1^3)+\sum _{j=1}^5{x}_{\mathit{ij}}\le 8\hfill \\ -M(1-y_2^3)+\sum _{j=1}^5{x}_{\mathit{ij}}\le 48\hfill \end{array}$$ $$\begin{array}{c}{y}_i^s=0,1\forall i=1,2\text{and}s=\text{1,2,3}\hfill \\ x_{\mathit{ij}}\in N-\{0\}\forall j=1,2,\dots ,5\text{and}i=1,2\hfill \end{array}$$

$\Rightarrow \text{Fixed - Cost}=\sum _{i=1}^2\sum _{j=1}^5{F}_i{x}_{\mathit{ij}}=\sum _{j=1}^5(210y_1^1+180y_1^2+150y_1^3)x_{1j}+\sum _{j=1}^5(180y_2^1+150y_2^2+120y_2^3)x_{2j}$. If T _i is the upper limit of $\sum _{j=1}^n{x}_{\mathit{ij}},$ we can convert the integer variable x _ij to the series of zero-one variable z _ij ’s by the following relation:

$x_{\mathit{ij}}=2^0{z}_{\mathit{ij}}^0+2^1{z}_{\mathit{ij}}^1+2^2{z}_{\mathit{ij}}^2+\cdots +2^{f_i}{z}_{\mathit{ij}}^{f_i},\text{where}{f}_i\le ⌈\frac{log\left(\frac{T_i+1}{2}\right)}{log2}⌉.$ $$\to T_1=8\Rightarrow f_1\le 3,T_2=48\Rightarrow f_2\le 5$$ $$\Rightarrow x_{1j}=2^0{z}_{1j}^0+2^1{z}_{1j}^1+2^2{z}_{1j}^2+2^3{z}_{1j}^3;\forall j=1,2,\dots ,5$$ $$x_{2j}=2^0{z}_{2j}^0+2^1{z}_{2j}^1+2^2{z}_{2j}^2+2^3{z}_{2j}^3+2^4{z}_{2j}^4+2^5{z}_{2j}^5;\forall j=1,2,\dots ,5$$

Let:$$t_{\mathit{ijs}}=y_i^s{x}_{\mathit{ij}}\Rightarrow t_{\mathit{ijs}}=2^0{y}_i^s{z}_{\mathit{ij}}^0+2^1{y}_i^s{z}_{\mathit{ij}}^1+2^2{y}_i^s{z}_{\mathit{ij}}^2+\cdots +2^{f_i}{y}_i^s{z}_{\mathit{ij}}^{f_i};\forall i=1,2;j=1,2,\dots ,5;s=1,2,3$$ $$\Rightarrow \text{Fixed - Cost}=\sum _{i=1}^2\sum _{j=1}^5{F}_i{x}_{\mathit{ij}}=\sum _{j=1}^5(210y_1^1+180y_1^2+150y_1^3)(2^0{z}_{1j}^0+2^1{z}_{1j}^1+2^2{z}_{1j}^2+2^3{z}_{1j}^3)$$ $$+\sum _{j=1}^5(180y_2^1+150y_2^2+120y_2^3\text{)(}{2}^0{z}_{2j}^0+2^1{z}_{2j}^1+2^2{z}_{2j}^2+2^3{z}_{2j}^3+2^4{z}_{2j}^4+2^5{z}_{2j}^5)=$$

$\sum _{j=1}^5(210y_1^1{z}_{1j}^0+2(210)y_1^1{z}_{1j}^1+...+2^3(150)y_1^3{z}_{1j}^3)+\sum _{j=1}^5(180y_2^1{z}_{2j}^0+2(150)y_2^1{z}_{2j}^1+...+2^3(120)y_2^3{z}_{2j}^3)=$ $\sum _{i=1}^2\sum _{j=1}^5\sum _{s=1}^3\sum _{k=0}^{f_i}{F}_i^s(2^k{y}_i^s{z}_{\mathit{ij}}^k$) = $\sum _{i=1}^2\sum _{j=1}^5\sum _{s=1}^3{F}_i^s{t}_{\mathit{ijs}}$

Let:

$t_{\mathit{ijs}}^r=y_i^s{z}_{\mathit{ij}}^r\Rightarrow t_{\mathit{ijs}}=2^0{t}_{\mathit{ijs}}^0+2^1{t}_{\mathit{ijs}}^1+2^2{t}_{\mathit{ijs}}^2+\cdots +2^{f_i}{t}_{\mathit{ijs}}^{f_i};\forall i=1,2;j=1,2,...,5;s=1,2,3$ $y_i^s+z_{\mathit{ij}}^r-t_{\mathit{ijs}}^r\le 1\forall i=1,2;j=1,2,\cdots ,5;s=1,2,3;r=0,1,2,\cdots ,f_i$ $y_i^s+z_{\mathit{ij}}^r-2t_{\mathit{ijs}}^r\ge 0\forall i=1,2;j=1,2,\cdots ,5;s=1,2,3;r=0,1,2,\cdots ,f_i$

Then we have:$$\sum _{i=1}^2\sum _{j=1}^5\sum _{s=1}^3{F}_i^s{t}_{\mathit{ijs}}=\sum _{i=1}^2\sum _{j=1}^5\sum _{s=1}^3\sum _{r=0}^{f_i}{F}_i^s(2^r{t}_{\mathit{ijs}}^r)$$

Using this fixed cost the mathematical model can be written as:$$Min{X}_0=\sum _{i=1}^2\sum _{j=1}^5\sum _{s=1}^3\sum _{r=0}^{f_i}{F}_i^s(2^r{t}_{\mathit{ijs}}^r)+\sum _{i=1}^2\sum _{j=1}^5\sum _{r=0}^{f_i}{c}_{\mathit{ij}}(2^r{z}_{\mathit{ij}}^r)$$

Subjected to:$$\sum _{i=1}^2\sum _{r=0}^{f_i}{q}_i(2^r{z}_{\mathit{ij}}^r)\ge W_j\forall j=1,2,\cdots ,5$$ $$\sum _{j=1}^5\sum _{r=0}^{f_i}{2}^r{z}_{\mathit{ij}}^r\le T_i\forall i=1,2$$ $$\begin{array}{c}-M(1-y_1^1)+\sum _{j=1}^5\sum _{r=0}^3{2}^r{z}_{1j}^r\le 3\hfill \\ -M(1-y_2^1)+\sum _{j=1}^5\sum _{r=0}^5{2}^r{z}_{2j}^r\le 23\hfill \end{array}$$ $$\begin{array}{c}M(1-y_1^2)+\sum _{j=1}^5\sum _{r=0}^3{2}^r{z}_{1j}^r\ge 4\hfill \\ M(1-y_2^2)+\sum _{j=1}^5\sum _{r=0}^5{2}^r{z}_{2j}^r\ge 24\hfill \end{array}$$ $$\begin{array}{c}-M(1-y_1^2)+\sum _{j=1}^5\sum _{r=0}^3{2}^r{z}_{1j}^r\le 6\hfill \\ -M(1-y_2^2)+\sum _{j=1}^5\sum _{r=0}^5{2}^r{z}_{2j}^r\le 39\hfill \end{array}$$ $$\begin{array}{c}M(1-y_1^3)+\sum _{j=1}^5\sum _{r=0}^3{2}^r{z}_{1j}^r\ge 7\hfill \\ M(1-y_2^3)+\sum _{j=1}^5\sum _{r=0}^5{2}^r{z}_{2j}^r\ge 40\hfill \end{array}$$ $$\begin{array}{c}-M(1-y_1^3)+\sum _{j=1}^5\sum _{r=0}^3{2}^r{z}_{1j}^r\le 8\hfill \\ -M(1-y_2^3)+\sum _{j=1}^5\sum _{r=0}^5{2}^r{z}_{2j}^r\le 48\hfill \end{array}$$ $$x_{1j}=\sum _{r=0}^3{2}^r{z}_{1j}^{r}j=1,2,\cdots ,5$$ $$x_{2j}=\sum _{r=0}^5{2}^r{z}_{2j}^{r}j=1,2,\cdots ,5$$ $$t_{1js}=\sum _{r=0}^3{2}^r{t}_{1js}^{r}j=1,2,\cdots ,5\text{;and}s=1,2,3$$ $$y_1^s+z_{1js}^r-t_{1js}^r\le 1j=1,2,\cdots ,5;s=1,2,3;r=0,1,2,3$$ $$y_1^s+z_{1js}^r-2t_{1js}^r\ge 0j=1,2,\cdots ,5;s=1,2,\text{3;}r=0,1,2,3$$ $$y_2^s+z_{2js}^r-t_{2js}^r\le 1j=1,2,\cdots ,5;s=1,2,3;r=0,1,\dots ,5$$

Using the CPLEX software the optimal solution is obtained as follow:$$x_{\mathit{ij}}=\left[\begin{array}{c}\begin{array}{ccc}0& 4& \begin{array}{ccc}0& 0& 1\end{array}\end{array}\\ \begin{array}{ccc}7& 6& \begin{array}{ccc}7& 13& 7\end{array}\end{array}\end{array}\right],y_i^s=\left[\begin{array}{c}\begin{array}{ccc}0& 1& 0\end{array}\\ \begin{array}{ccc}0& 0& 1\end{array}\end{array}\right]$$

Objective function= X ₀ = 18,063

Execution time = 00:00:07:71

The CPLEX code is presented as follow:

/*********************************************

* OPL 12.3.0.1 Model

* Author: Zahra

* Creation Date: 2013/4/18 at 22:13:13

*********************************************/

usingCPLEX;

intNum_Depot = 5;

intNum_VehicleKind = 2;

intNum_Discount = 3;

intMax_p = 5;

rangen = 1..Num_Depot;

rangem = 1..Num_VehicleKind;

rangek = 1..Num_Discount;

rangep = 0..(Max_P + 1);

intVar_Cost[m,n] = ...;

intDemand_Val[n] = ...;

intCapacity[m] = ...;

intAvailable_Vehicle[m] = ...;

intFix_Cost[k,m] = ...;

intNumber_Discount[k,m] = ...;

intP[m] = ...;

intM = 1,000,000;

dvarintX[m,n];

dvarbooleanY[m,k];

dvarbooleanz[m,n,p];

dvarbooleant[m,n,k,p];

/*Objective function

– – – – – – – – – – – – – – – – – – –*/

minimize((sum(iinm,jinn,sink,rin0..P[i])

  Fix_Cost[s,i]*(2^r)*t[i,j,s,r])+

  (sum(iinm,jinn,rin0..P[i])

  Var_Cost[i,j]*(2^r)*z[i,j,r]));

/*Constrains

– – – – – – – – – – – – – – – – – – –*/

subjectto{

/*Supplying Demand of each depot

– – – – – – – – – – – – – – – – – – –*/

forall(jinn)

sum(iinm,rin0..P[i])

Capacity[i]*(2^r)*z[i,j,r] >=Demand_Val[j];

/*Limitation on available Vehicle of each kind

– – – – – – – – – – – – – – – – – – –*/

forall(iinm)

sum(jinn,rin0..P[i](2^r)*z[i,j,r] <=Available_Vehicle[i];

forall(iinm,sin1..(Num_Discount-1))

-M*(1-Y[i,s])+(sum(jinn,rin0..P[i])(2^r)*z[i,j,r])

<= Number_Discount[s,i]-1;

forall(iinm)

-M*(1-Y[i,Num_Discount]) + (sum(jinn,rin0..P[i])(2^r)*z[i,j,r])

<=Number_Discount[Num_Discount,i];

forall(iinm,sin2..Num_Discount)

M*(1-Y[i,s]) + (sum(jinn,rin0..P[i])(2^r)*z[i,j,r])

>=Number_Discount[s-1,i];

forall(iinm)

sum(sink)Y[i,s] ==1;

/*Convert Variables X[m,n,k] to zero-one variables

– – – – – – – – – – – – – – – – – –*/

forall(iinm,jinn)

X[i,j] ==sum(rin0..P[i])(2^r)*z[i,j,r];

forall(iinm,jinn,sink,rin0..P[i]){

Y[i,s]+z[i,j,r] -t[i,j,s,r] <=1;

Y[i,s]+z[i,j,r] -2*t[i,j,s,r] >=0;

}

/*Variables X[m,n,k] is positive*/

– – – – – – – – – – – – – – – – – – –*/

forall(iinm,jinn,sink)

X[i,j]>=0;

}

.dat file: Reading and Writing Data in Excel file

/*********************************************

* OPL 12.3.0.1 Data

* Author: Zahra

* Creation Date: 2013/4/18 at 22:13:13

*********************************************/

SheetConnectionsheet(“XXSmall Size Test Problems.xlsx”);

Var_CostfromSheetRead(sheet, “Sheet1!B3:F4”);

Demand_ValfromSheetRead(sheet, “Sheet1!B19:F19”);

CapacityfromSheetRead(sheet, “Sheet1!B27:C27”);

Available_VehiclefromSheetRead(sheet, “Sheet1!B28:C28”);

Fix_CostfromSheetRead(sheet, “Sheet1!B30:C32”);

Number_DiscountfromSheetRead(sheet, “Sheet1!B33:C35”);

PfromSheetRead(sheet, “Sheet1!B36:C36”);

XtoSheetWrite(sheet, “Sheet1!B42:F43”);

YtoSheetWrite(sheet, “Sheet1!B52:D53”);