Peristaltic transport of two-layered blood flow using Herschel–Bulkley Model

Abstract

The present article investigates the peristaltic transport of a Herschel–Bulkley fluid in an axisymmetric tube. The governing equations are solved using the long wavelength and small Reynolds number approximation. The closed-form solutions are obtained and analyzed for the effects of the fluid behavior index, amplitude ratio, and yield stress on pressure, pressure rise, frictional force, and streamlines. The present model reveals that the increase in flux against pressure rise for a Newtonian fluid is less when compared with Herschel–Bulkley fluid. Further, these changes are opposite to the behavior of frictional force against pressure rise. Also, it is noticed that pressure rise for a fixed value of amplitude ratio in Herschel–Bulkley model is more significant than that of a Newtonian, Power-law, and Bingham model. Furthermore, it is observed that, for small values of yield stress, there is not much difference between Herschel–Bulkley and Power-law fluids.

GRAPHICAL ABSTRACT

Keywords:

• Bingham plastic
• frictional force
• Herschel-Bulkley fluid
• peristalsis
• power law
• pressure rise
• yield stress

PUBLIC INTEREST STATEMENT

The present investigation on peristaltic transport of blood has been of utmost interest to researchers in recent times due to its wide application in the field of Medicine. The peristaltic transport occurs in the movement of bolus through esophagus, chime in the gastrointestinal tract, spermatozoa in the cervical canal, ovum in the fallopian tube, transportation of urine through the ureter, and flow of blood in the blood vessel. The mechanism of peristaltic motion has also found applications in biomedical engineering to design and construct many useful devices such as blood pump machine, toxic liquid in nuclear industry, finger and roller pumps, and dialysis machine.

1. Introduction

Peristalsis is a mechanism of the progressive propagation of wave contraction and expansion along the walls of a distensible tube. Physiologically, any tubular smooth muscle structure has an inherent neuromuscular property, which exhibits peristaltic action. The body uses these characteristics to mix and push forward the contents of the tube, like movement of food through the esophagus, chime in the gastrointestinal tract, spermatozoa in the cervical canal, ovum in the fallopian tube, transportation of urine through the ureter, and flow of blood in the blood vessel. The mechanism of peristaltic motion has also found applications in biomedical engineering to design and construct many useful devices such as blood pump machine and dialysis machine (Jaggy, Lachat, Leskosek, Znd, & Turina, 2000; Nisar, Afzulpurkar, Mahaisavariya, & Tuantranont, 2008).

The mechanism of peristalsis has been of scientific interest for many researchers since the preliminary investigation by Latham (1966), several experimental and theoretical studies have been carried out to explore peristaltic action in different situations. Initial works were carried out by assuming the small wave number, amplitude ratio, and Reynolds number (Burns & Parkes, 1967; Fung & Yih, 1968; Jaffrin, 1973; Jaffrin & Shapiro, 1971; Raju & Devanathan, 1972; Shapiro, Jaffrin, & Weinberg, 1969; Weinberg, Eckstein, & Shapiro, 1971). The viscosity close to the wall of the tube has been observed to be not quite the same as that in the central region for some biological systems and thinking about this reality, Shukla, Parihar, Rao, and Guptha (1980) studied two-layered peristaltic flows through tubes and channels using Stoke’s approximations. It was observed that the effect of frictional force decreases and the flow flux increases with a reduction in fluid viscosity. Srivastava and Srivastava (1982) investigated the two-layered peristaltic transport consisting of Newtonian fluid in an axisymmetric tube. Their study emphasizes the effects of viscosity variation on two-layered peristaltic transport in a non-uniform tube. Srivastava and Srivastava (1984) investigated the peristaltic movement using Casson model and found that, under a given set of conditions, the magnitude of the pressure rise is smaller in the model without a peripheral layer, when compared to those with an outer layer. By considering the two-layered power-law fluid model, Usha and Ramachandra (1997) noticed that the positive or negative mean flow was due to the rheology of the peripheral layer. Further, comparative study was carried out by Misra and Pandey (2002) for the axisymmetric and channel flow. Akram, Hanif, Nadeem, and Zhongmin (2014) investigated peristaltic transport with the help of Maxwell model by taking porous channel. Recently, several authors used non-Newtonian models to study the physiological behaviors of different fluids under various assumption and geometries (Manjunatha & Rajashekhar, 2018; Prasad, Vajravelu, Vaidya, Shivakumara, & Basha, 2016; Vajravelu, Prasad, Vaidya, Basha, & Ng, 2017).

The above-mentioned non-Newtonian models do not explain the complex physiological behavior of blood. In the case of suspensions of cells, the plasma of blood influences it to behave like non-Newtonian fluid at moderate shear rates. This nonlinearity can be modeled using either Casson or Herschel–Bulkley model. The study on using both Casson and Herschel–Bulkley models were carried out by Blair and Spanner (1974). They concluded that the blood obeys Casson model at moderate shear rates. Further, they also noticed that there is no much change among Casson and Herschel–Bulkley plots of experimental data at moderate shear rates. However, the utilization of Herschel–Bulkley model over Casson model is more suitable since it contains one more additional parameter (fluid behavior index) and can be utilized for low shear rates where the Casson model fails to clarify the different physiological behaviors of blood. Furthermore, the Herschel–Bulkley model can be reduced to different models, for example, Newtonian, Power-law, and Bingham plastic for a pertinent value of yield stress and fluid behavior index. Due to their generality, many researchers have made use of Herschel–Bulkley model to study the peristaltic transport in different physiological conditions. Vajravelu, Sreenadh, and Babu (2005) investigated the two-layered peristaltic transport using Herschel–Bulkley fluid. Later, Vajravelu et al. (2005a, 2006) extended their work on peristaltic transport to the inclined tube and two-layered geometry, respectively.

Maiti and Misra (2013) explored the peristaltic transport of a couple stress fluid in a porous channel. Their investigation was inspired toward the physiological fluid of blood in the micro-circulatory framework by assessing the particle size effect. It was additionally uncovered that it is conceivable to increment both pumping and pressure by expanding amplitude proportion and couple stress parameter and by lessening the permeability. Manjunatha, Basavarajappa, Thippeswamy, and Hanumesh (2013), (2014) contemplated the peristaltic transport of two and three-layered fluid with varying amplitude proportion. For the examination, they used Herschel–Bulkley model to ascertain the physiological parameters. Vajravelu, Sreenadh, Devaki, and Prasad (2015, 2016) carried out investigations on peristaltic transport by considering the elastic tube. For modeling the peristaltic flow, Herschel–Bulkley and Casson’s models were used. Recently, a detailed survey regarding peristaltic transport of physiological fluids was carried out by (Suresh & Hemadri, 2016; Thanesh & Kavitha, 2016).

The present study investigates the two-layered peristaltic transport using a non-Newtonian Herschel–Bulkley model. The closed-form solutions are obtained for velocity, flow rate, pressure gradient, pressure rise, and frictional force. Further, the results of various other models (Power-law, Bingham plastic, and Newtonian) are discussed as a special case of Herschel–Bulkley model for a fixed value of yield stress and fluid behavior index. Furthermore, the present investigation helps in understanding the movement of food bolus through gastrointestinal tract, the flow of blood in narrow arteries (where the shear rates are low) and the thrombus formation of blood.

2. Formulation of the problem

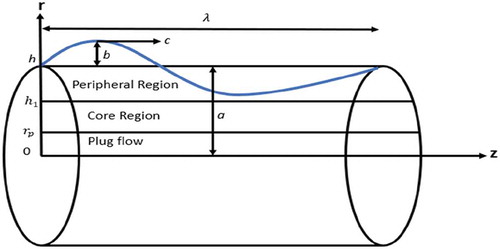
Consider the peristaltic flow of a steady, laminar, incompressible Herschel–Bulkley fluid in an axisymmetric tube (Figure 1) with radius $a$. The flow is axisymmetric and encourages the choice of the cylindrical coordinate system to study the problem. The wall deformation due to the propagation of an infinite sinusoidal wave train of peristaltic waves is represented by

(1) $h(z,t)=a+bsin\left[\frac{2\pi }{\lambda }(z-ct)\right]$(1)

Figure 1. Geometric representation of peristaltic waves in a tube.

where b is the amplitude, $\lambda$ is the wavelength, c is the wave propagation speed, and t is the time.

The flow becomes steady in the wave frame $(r,\theta ,z)$ moving with velocity $c$ away from the fixed frame $\left(R,\mathrm{\Theta },Z\right)$ given by

(2) $r=R,z=Z-ct,\psi =\mathrm{\Psi }-\frac{R^2}{2},p\left(z,t\right)=P(Z),$(2)

where $p$ and $P$ are pressures, $\psi$ and $\mathrm{\Psi }$ are stream functions, in the wave and fixed frames of references, respectively.

3. Mathematical model

The equations of motion in the wave frame of references, moving with speed c under the long wavelength approximation and by neglecting the wall slope and inertial terms (Shapiro et al., 1969), is written as

(3) $\frac{1}{r\prime }\frac{\mathrm{\partial }}{\mathrm{\partial }r\prime }\left(r\prime {\tau }_{r\prime z\prime }\right)=-\frac{\mathrm{\partial }P\prime }{\mathrm{\partial }z\prime }$(3)

(4) $\frac{\mathrm{\partial }P\prime }{\mathrm{\partial }r\prime }=0$(4)

where ${\tau }_{r\prime z\prime }$ for Herschel–Bulkley fluid is given by Chaturani & Narasimhan (1988)

(5) $-\frac{\mathrm{\partial }{u}_i^{\prime }}{\mathrm{\partial }r\prime }=f\left(\tau \right)={\left[\frac{1}{k}\left({\tau }_{r\prime z\prime }-{\tau }_0\right)\right]}^{\frac{1}{n_i}},{\tau }_{r\prime z\prime }\ge {\tau }_0,$(5)

(6) $-\frac{\mathrm{\partial }{u}_i^{\prime }}{\mathrm{\partial }r\prime }=f\left(\tau \right)=0,{\tau }_{r\prime z\prime }\le {\tau }_0.$(6)

It is worth mentioning that above Herschel–Bulkley model reduces to Bingham fluid when $n_i=1\mathrm{a}\mathrm{n}\mathrm{d}K=\mu$ (Newtonian viscosity); to the power-law fluid when ${\tau }_0=0\mathrm{a}\mathrm{n}\mathrm{d}K=\mu$ and to the Newtonian fluid when $n_i=1,K=\mu$, and ${\tau }_0=0$. It is important to note that the plug core radius increases with the yield stress ${\tau }_0$ and with the fluid behavior index $n_i$.

The variables are rendered dimensionless by the following transformations

(7) $p=\frac{a^{n+1}p\prime }{\lambda \mu c^n},r=\frac{r\prime }{a},z=\frac{z\prime }{\lambda },u_i=\frac{{u\prime }_i}{c},{\tau }_0=\frac{a^n{\tau }_0^{\prime }}{c^n\mu },{\tau }_{rz}=\frac{\tau {\prime }_{r\prime z\prime }{a}^n}{\mu c^n},{\tau }_a=\frac{\tau {\prime }_a{a}^n}{\mu c^n}$(7)

Making use of the non-dimensional quantities in Equation (7), the governing equations (5) and (6) (after dropping the primes) take the form as,

(8) $\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}r\left[{\left(-\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }r}\right)}^{n_i}+{\tau }_0\right]=-\frac{\mathrm{\partial }p}{\mathrm{\partial }z},{\tau }_{rz}\ge {\tau }_0,i=1,2,$(8)

(9) $\frac{\mathrm{\partial }{u}_i^{\prime }}{\mathrm{\partial }r\prime }=0,{\tau }_{rz}\le {\tau }_0.$(9)

The corresponding non-dimensional boundary conditions are

(10) $\begin{array}{c}{u}_1=u_p\mathrm{a}\mathrm{t}r=r_p\\ u_1=u_2\mathrm{a}\mathrm{t}r=h_1\\ u_1^{\prime }=0\mathrm{a}\mathrm{t}r=0\\ u_2=-1\mathrm{a}\mathrm{t}r=h\end{array}$(10)

The expression for velocities $u_1$, $u_2$, and $u_p$ are obtained on solving Equations (8) and (9) satisfying the boundary conditions (10), we get

(11) $u_1=\frac{2}{P(K_1+1)}\left[{\left(\frac{Ph}{2}-{\tau }_0\right)}^{K_1+1}-{\left(\frac{Pr}{2}-{\tau }_0\right)}^{K_1+1}\right]-1$(11)

(12) $u_2=\frac{2}{P(K_2+1)}\left[{\left(\frac{Ph}{2}-{\tau }_0\right)}^{K_2+1}-{\left(\frac{Pr}{2}-{\tau }_0\right)}^{K_2+1}\right]-1$(12)

The upper limit of plug flow region for ${\tau }_0=\frac{\mathrm{P}}{2}{r}_p\mathrm{a}\mathrm{t}r=r_p$ is obtained as $r_p=\frac{2{\tau }_0}{P}$ and for ${\tau }_{rz}={\tau }_h$ at $r=h$ (Bird et al., 1976), we get $P=\frac{2{\tau }_h}{h}$.

Hence, from the above results, we have

(13) $\frac{r_p}{h}=\frac{{\tau }_0}{{\tau }_h}=\tau$(13)

The plug flow velocity at $r=r_p$, using Equations (11) and (13) is given by

(14) $u_p=\frac{2}{P(K_1+1)}\left[{\left(\frac{Ph}{2}-{\tau }_0\right)}^{K_1+1}-{\left(\frac{P{r}_p}{2}-{\tau }_0\right)}^{K_1+1}\right]-1$(14)

where $r_p=\frac{2{\tau }_0}{P}$, $P=-\frac{\mathrm{\partial }p}{\mathrm{\partial }z}$, $K_1=\frac{1}{n_1}$, $K_2=\frac{1}{n_2}$

The instantaneous flow rate $q$ across any cross-section of the artery is defined as given below:

(15) $q=q_p+q_1+q_2$(15)

(16) $q=2\underset{0}{\overset{r_p}{\int }}r{u}_{p}dr+2\underset{r_p}{\overset{h_1}{\int }}r{u}_{1}dr+2\underset{h_1}{\overset{h}{\int }}r{u}_{2}dr$(16)

(17) $q_p=\frac{2r_p^2}{P(1+K_1)}{\left[\frac{Ph}{2}-{\tau }_0\right]}^{1+K_1}-r_p^2$(17)

(18) $q_1=-{\frac{16\left[{\tau }_0+\frac{P{h}_1}{2}(K_1+2)\right]\left[\frac{P{h}_1}{2}-2\right]}{P^3(K_1+1)(K_1+2)(K_1+3)}}^{K_1+2}+(h_1^2-r_p^2)\left[\frac{2}{P(K_1+1)}{\left(\frac{Ph}{2}-{\tau }_0\right)}^{K_1+1}\right]$(18)

$q_2=\frac{-16}{P^3(K_2+1)(K_2+2)(K_2+3)}\left[{\left(\frac{Ph}{2}-{\tau }_0\right)}^{K_2+2}\left({\tau }_0+\frac{Ph}{2}(K_2+2)\right)\right.$

(19) $-\left.{\left(\frac{P{h}_1}{2}-{\tau }_0\right)}^{K_2+2}\left({\tau }_0+\frac{P{h}_1}{2}(K_2+2)\right)\right]+(h^2-h_1^2)\left[\frac{2}{P(K_2+2)}\right.\left.{\left(\frac{Ph}{2}-{\tau }_0\right)}^{K_2+1}-1\right]$(19)

where $q_p,q_1\mathrm{a}\mathrm{n}\mathrm{d}{q}_2$ are respectively the plug, core, and peripheral region flow rates. The dimensionless time-averaged flux $\bar{Q}$ is obtained as

(20) $\bar{Q}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{h}{\int }}r(u_i-1)drdz=q+\underset{0}{\overset{1}{\int }}{h}^{2}dz=q+1+\frac{{\epsilon }^2}{2}$(20)

4. Pumping characteristics

The pressure rise ($\mathrm{\Delta }P$) over one cycle of the wave is given by

(21) $\mathrm{\Delta }P=-\underset{0}{\overset{1}{\int }}{\left[\frac{Q(K+1)(K+2)(K+3)2^K}{h^{K+3}{\left(1-\tau \right)}^{K+1}\left\{(K+1)(K+2)+2\tau \left(\tau +K+1\right)\right\}}\right]}^{\frac{1}{K}}dz$(21)

The dimensionless frictional force $F$ at the wall across one wavelength is

$F=\underset{0}{\overset{1}{\int }}{h}^2\left(-\frac{\mathrm{\partial }P}{\mathrm{\partial }z}\right)dz$

(22) $F=\underset{0}{\overset{1}{\int }}{\left[\frac{Q(K+1)(K+2)(K+3)2^K}{h^{3-K}{\left(1-\tau \right)}^{K+1}\left\{(K+1)(K+2)+2\tau \left(\tau +K+1\right)\right\}}\right]}^{\frac{1}{K}}dz$(22)

Equations (21) and (22) are solved numerically by Weddle’s rule using MATLAB.

5. Results and discussion

The solutions for pressure rise and frictional force with corresponding boundary condition are obtained using MATLAB. The effects of yield stress to wall shearing stress $(\tau )$, amplitude ratio $(\epsilon )$ and fluid behavior index $(n)$ on pressure rise $(\mathrm{\Delta }P)$, frictional force $(F)$, pressure gradient $(P)$, and streamlines $(\psi )$ for Newtonian, Power-law, Bingham plastic, and Herschel–Bulkley models are analyzed and presented graphically through Figures 2–16.

Figure 2. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{\tau }$ with $\mathit{\epsilon }=\mathbf{0.6}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}\mathbf{=}\mathbf{3}$.

Figure 3. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{\epsilon }$ with $\mathit{\tau }\mathbf{=}\mathbf{0.2}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}\mathbf{=}\mathbf{3}$.

Figure 4. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{n}$ with $\mathit{\epsilon }\mathbf{=}\mathbf{0.6}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{\tau }=\mathbf{0.2}$.

Figure 5. $\mathit{F}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{\tau }$ with $\mathit{\epsilon }=\mathbf{0.6}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}=\mathbf{3}$.

Figure 6. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{\epsilon }$ with $\mathit{\tau }=\mathbf{0}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}=\mathbf{1}$.

Figure 7. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{\epsilon }$ with $\mathit{\tau }=\mathbf{0}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}=\mathbf{3}$.

Figure 8. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{n}$ with $\mathit{\epsilon }=\mathbf{0.6}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{\tau }=\mathbf{0}$.

Figure 9. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{\epsilon }$ for $\mathit{\tau }=\mathbf{0.2}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}=\mathbf{1}$.

Figure 10. $\mathrm{\Delta }\mathit{P}$ v/s $\bar{\mathit{Q}}$ for varying $\mathit{\tau }$ with $\mathit{\epsilon }=\mathbf{0.6}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}=\mathbf{1}$.

Figure 11. $\mathit{P}$ v/s $\mathit{z}$ for varying (a) $\mathit{\tau }$ (b) $\mathit{\epsilon }$ and (c) $\mathit{n}$ with $\mathit{\epsilon }=\mathbf{0.5},\mathit{\tau }=\mathbf{0.5}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}=\mathbf{0.3}$.

Figure 12. $\mathit{P}$ v/s $\mathit{z}$ with varying (a) $\mathit{\tau }$ (b) $\mathit{\epsilon }$ and (c) $\mathit{n}$ with $\mathit{\epsilon }=\mathbf{0.5},\mathit{\tau }=\mathbf{0.5}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{n}=\mathbf{0.3}$.

Figure 13. $\mathit{P}$ v/s $\mathit{z}$ for varying $\mathit{\epsilon }$ with $\mathit{n}=\mathbf{1}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{\tau }=\mathbf{0}$.

Figure 14. Pressure v/s $z$ for power-law model with varying (a) $\mathit{\epsilon }$ (shear thickening), (b) $\mathit{\epsilon }$ (shear thinning), (c) $\mathit{n}$ (shear thickening) and (d) $\mathit{n}$ (shear thinning) with $\mathit{\epsilon }=\mathbf{0.5}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{\tau }=\mathbf{0}$.

Figure 15. $\mathit{P}$ v/s $\mathit{z}$ for Bingham plastic model with varying (a) $\mathit{\tau }$ and (b) $\mathit{\epsilon }$.

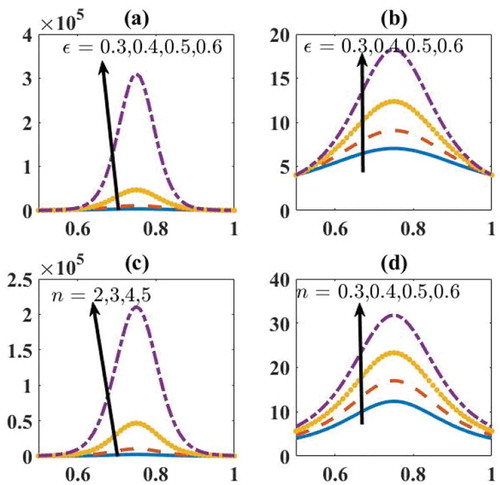
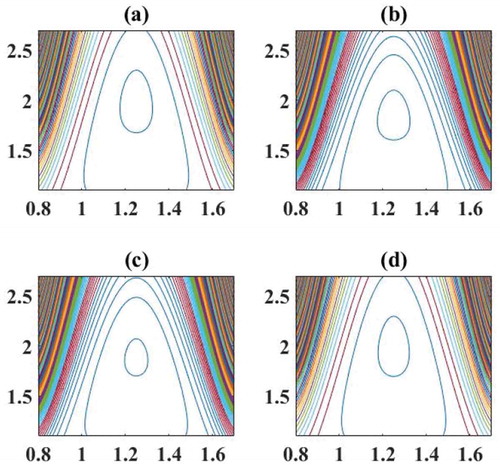
Figure 16. Streamlines for (a) Herschel–Bulkley, (b) Bingham plastic, (c) Newtonian, and (d) Power-law fluid.

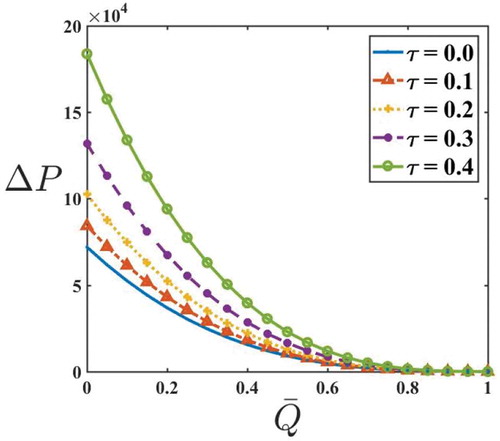
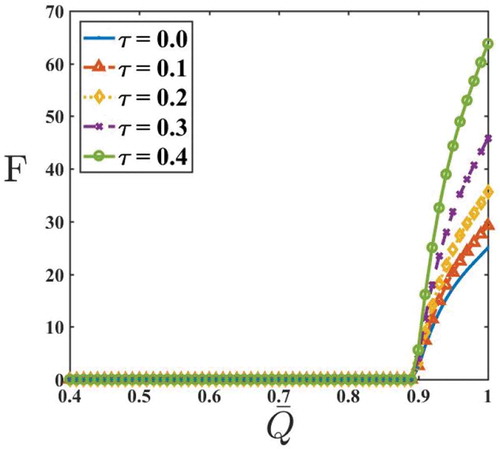
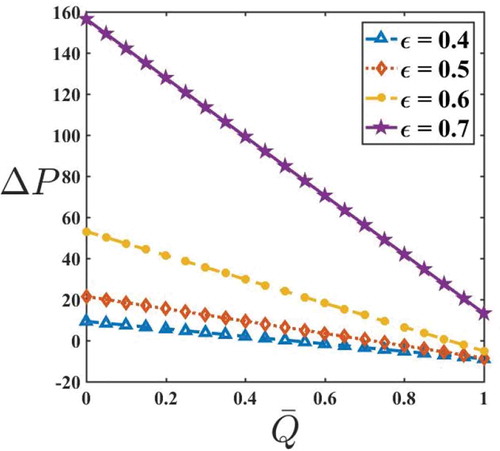
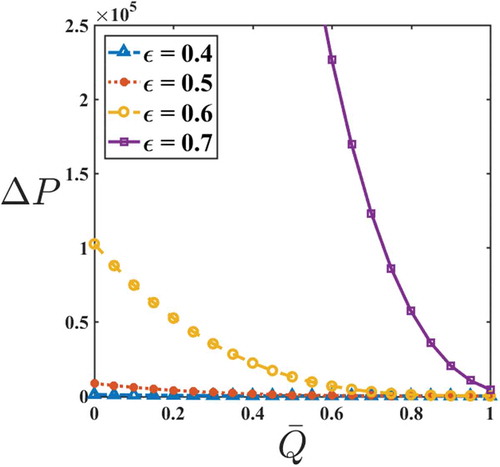
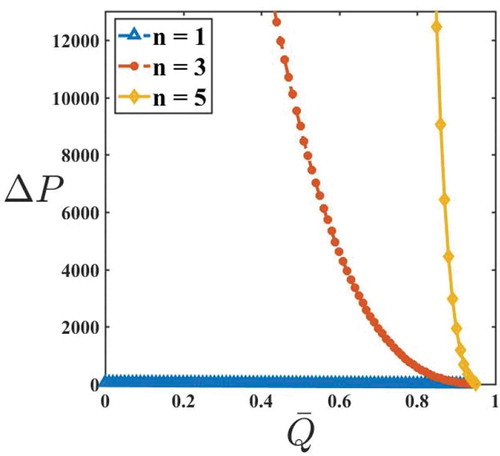
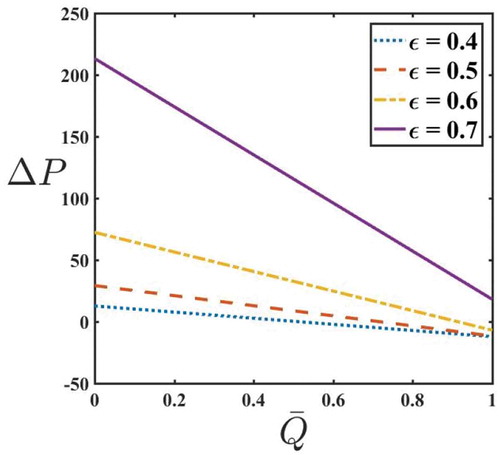
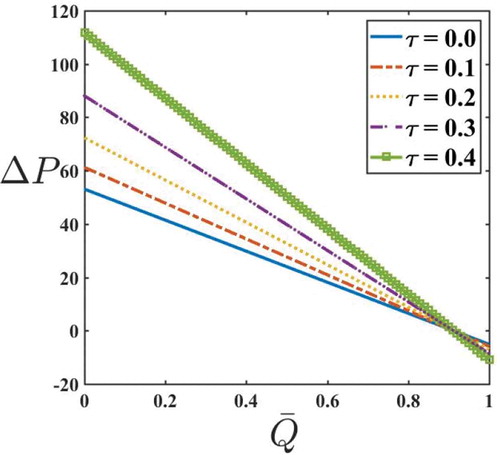
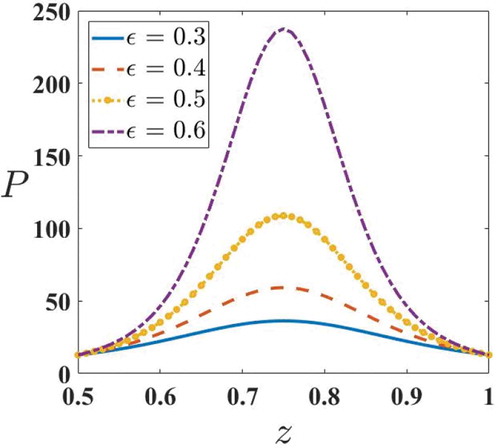
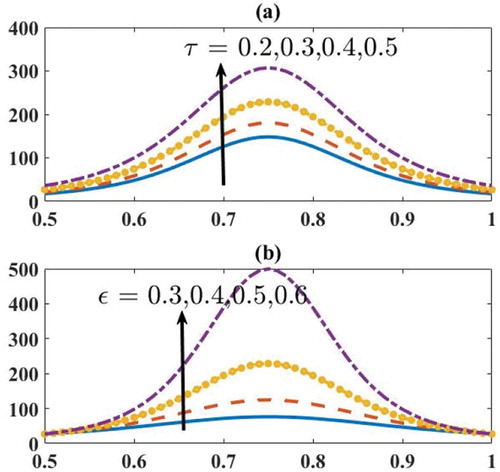
Figures 2–4 are plotted to see the effects of yield stress, amplitude ratio, and fluid behavior index on pressure rise and frictional force for a Herschel–Bulkley fluid. Figure 2 depicts the variation of $\tau$ on $\mathrm{\Delta }P$ and $\bar{Q}$. It is observed that an increase in the value of $\tau$ increases $\mathrm{\Delta }P$ in an axisymmetric tube. This is because of the existence of $\tau$ in the model. Moreover, $\mathrm{\Delta }P$ decreases with an increase in $\bar{Q}$. The variation of $\epsilon$ on $\mathrm{\Delta }P$ and $\bar{Q}$ is shown in Figure 3. It is noticed that an increase in the value of $\epsilon$ increases the pressure rise. This is mainly due to the increase in the height of the sinusoidal wave which requires more $\mathrm{\Delta }P$ for the movement of blood through the tube. 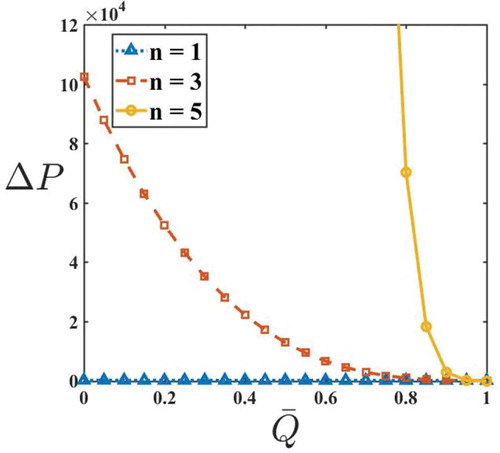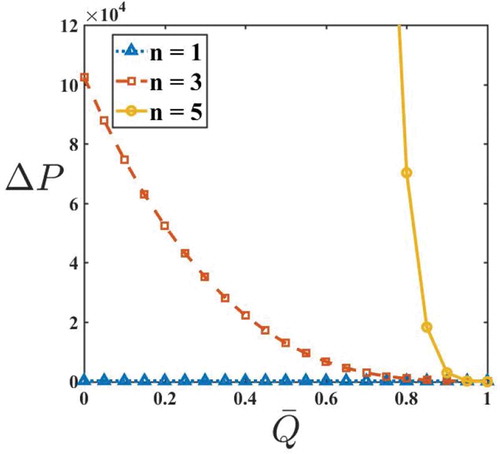The variation of $n$ on $\mathrm{\Delta }P$ and $\bar{Q}$ shows the significant increase in $\mathrm{\Delta }P$ for small variation in $n$ (Figure 4). This appreciable amount of increase in $\mathrm{\Delta }P$ is due to the shear-thickening property of blood.

The variations of $\tau$ on $F$ and $\bar{Q}$ are plotted in Figure 5. It is noticed that the behavior of $F$ is opposite to that of $\mathrm{\Delta }P$. The above observations of $\tau$, $\epsilon$, and $n$ on $\mathrm{\Delta }P$ and $F$ are in concurrence with the results of Shapiro et al. (1969) and Vajravelu et al. (2005).

Figure 6 shows the results for a Newtonian fluid $(\tau =0,n=1)$. It is observed that the behavior of $\epsilon$ remains to be the same as that of Herschel–Bulkley fluid, but $\mathrm{\Delta }P$ required for a particular value of $\epsilon$ is less when compared with Herschel–Bulkley fluid. This is mainly due to the absence of $\tau$. Figures 7 and 8 are plotted for the effects of $\epsilon$ and $n$ on $\mathrm{\Delta }P$ and $\bar{Q}$ for Power-law fluids. It is noticed from Figure 7 that an increase in the values of $\epsilon$ increases $\mathrm{\Delta }P$ in an axisymmetric tube. Similar behavior is observed for an increase in $n$ (Figure 8). Figures 9 and 10 illustrate the variation of $\epsilon$ and $\tau$ on $\mathrm{\Delta }P$ and $\bar{Q}$ for Bingham-plastic fluids. The variations of $\epsilon$ and $\tau$ show the same trend as that of Herschel–Bulkley fluid, but $\mathrm{\Delta }P$ required is less when compared with Herschel–Bulkley and Power-law fluids.

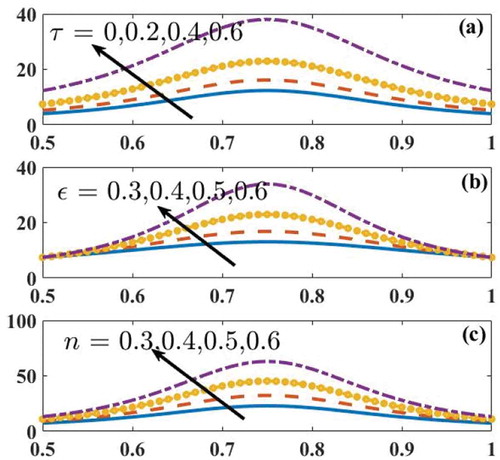
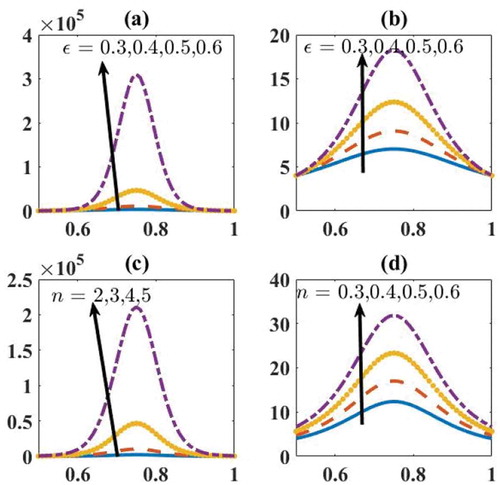
Figures 11 and 12 illustrate the pressure graphs for Herschel–Bulkley fluid. Figure 11 shows the variations of $\tau$, $\epsilon$ and $n$ $(n>1)$ on pressure. As expected, the pressure gradient $P$ is maximum at the narrowest part of the tube, that is, $z=0.75$. The main reason is to maintain the same flow rate through narrow part in comparison with the wider part of the tube to satisfy the conservation of mass. Further, for positive $P$, an adverse pressure gradient is registered (which opposes the flow) in the range$z\in [0,1]$. It is observed that the magnitude of pressure increases with an increase in $\tau$, $\epsilon$, and $n$. Similar behavior is observed on pressure for the variation of $\tau$, $\epsilon$, and $n$ when $(n<1)$ (Figure 12). Figure 13 depicts the variation of $\epsilon$ on pressure for a Newtonian fluid. It is noticed that the magnitude of pressure increases for an increase in $\epsilon$. Also, it is observed that the magnitude of pressure increases with an increase in the value of $\epsilon$ and $n$ for Power-law fluids (Figure 14). Similar variations in pressure are observed for an increase in the values of $\tau$ and $\epsilon$ for Bingham-plastic fluids (Figure 15). Thus, from Figures 11–15, it is noticed that the maximum pressure is required for pumping the Herschel–Bulkley fluid and minimum pressure for Newtonian fluid.

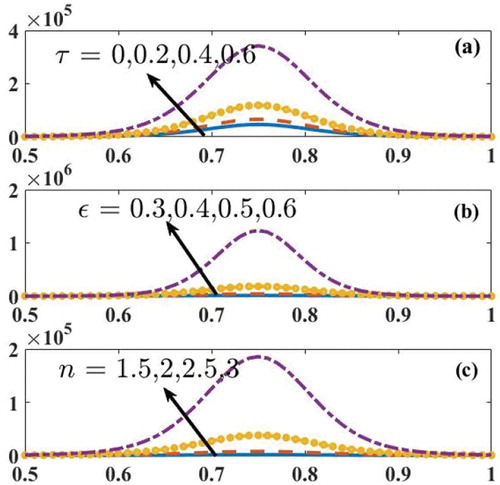
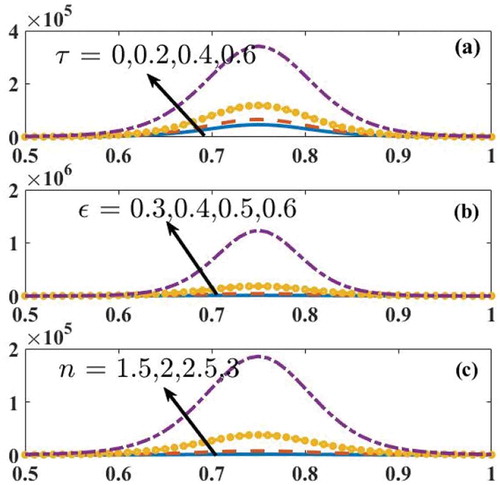
The most essential part of peristalsis is trapping. It is by and large the arrangement of inside flowing bolus. The generation of inside flowing bolus in a fluid is implanted by different stream, which is named as trapping phenomenon. These trapped boluses move alongside sinusoidal movement of peristaltic wave. This phenomenon is particularly useful in understanding the flow of bolus through gastrointestinal tract and the formulation of thrombus in blood. Figure 16 is plotted to see the formation of trapped bolus for Herschel–Bulkley, Bingham, Newtonian, and Power-law fluids. From the figure, it is noticed that an increase in the value of $\tau$ increases the volumeof trapped bolus for Herschel–Bulkley, Bingham, and Newtonian fluid. Further, from Newtonian and Power-law fluids, it is observed that the fluid behavior index enhances the volumeof trapped bolus. Also, for small values of $\tau$, there is not much difference between Herschel–Bulkley and Power-law fluids.

6. Conclusions

The present article deals with the study of the peristaltic motion of blood in the human circulatory system. The results are presented for Herschel–Bulkley, Power-law, Bingham-plastic, and Newtonian fluids. The effects of amplitude ratio, yield stress, and fluid behavior index are studied on pressure, pressure rise, and frictional force. The study has the potential of significant application in the field of medicine, biomedical engineering, and technology. Some of the interesting findings are as follows:

• The pressure rise increases with increase in the value of yield stress, amplitude ratio, and fluid behavior index for Newtonian, Power law, Bingham, and Herschel–Bulkley fluid, respectively.

• The pressure rise for a particular value of amplitude ratio in Herschel–Bulkley model is greater than that of Newtonian, Power law, and Bingham model.

• The pressure rise in all the cases, namely, Newtonian, Power law, Bingham, and Herschel-Bulkley, decreases with an increase in the time-averaged flux.

• The magnitude of pressure gradient increases with an increase in the value of yield stress, amplitude ratio, and fluid behavior index.

• The presence of yield stress, amplitude ratio, and fluid behavior index enhances the flux in an axisymmetric tube.

• The volumeof trapped bolus increases with an increase in the value of yield stress parameter.

Nomenclature

$a$: radius of the tube

$r_p$ _: radius of plug region

$P$: pressure gradient

$b$: amplitudes

$t$: time

$c$: wave speed

$(r,z)$: radial and axial coordinates

$u_p$: velocity in plug region

$u_1$: velocity in core region

$u_2$: velocity in peripheral region

$h$: length of the tube

$n_i$: fluid behavior index

$q$: volumetric flow rate

$q_p$: flux in plug region

$q_1$: flux in core region

$q_2$: flux in peripheral region

$\bar{Q}$: time averaged flux

$\mathrm{\Delta }P$: pressure rise per wavelength

$F$: frictional force at the wall

Greek symbols

$\lambda$: wavelength

$\mu$: viscosity

${\tau }_0$: yield stress

$\tau$: ratio of yield stress to wall shearing stress

$\epsilon$: amplitude ratio

Cover Image

Source:

Acknowledgements

The authors appreciate the constructive comments of the reviewers, which led to definite improvement in the article.

Additional information

Notes on contributors

G. Manjunatha

Dr G. Manjunatha received his BSc Degree in Mathematics from the Gulbarga University, Gulbarga, India, in 1994. He then received his MSc and PhD degrees from Gulbarga and Kuvempu University, India, in 1996 and 2009, respectively. Dr G. Manjunatha is currently working as an Associate Professor Senior Scale at the Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal. He serves as a referee for several reputed international journals. Dr G. Manjunatha research interests include Mathematical Modeling, Biomechanics, fluid mechanics, and Numerical Analysis