Tube model predictive control for a class of nonlinear discrete-time systems

Abstract

This paper signifies a tube model predictive control for discrete time uncertain nonlinear systems in the presence of bounded disturbances. The problem of obtaining robustness against parametric uncertainty is renewed to the problem of grasping robustness against additional bounded disturbance. The nominal control law is achieved through the same computational burden as that of standard MPC with guaranteed stability. Also, ancillary control law is accomplished by H∞ control approach to stabilize the states despite parametric uncertainty and disturbances. A simulation example is exploited to show the effectiveness and applicability of the method.

Keywords:

• discrete time system
• H∞ control
• robust tube model predictive control
• compressor surge control
• uncertain nonlinear system

PUBLIC INTEREST STATEMENT

Uncertain nonlinear systems control is one of the real challenges in the industry. In addition to the problem of optimizing the control signal, issues of disturbance and uncertainty entering the model should also be taken into account. This paper presents a new predictive control method for covering the above effects, in which, in addition to being robust to the disturbance and uncertainty, optimization is considered in each sampling.

1. Introduction

Model predictive control (MPC) is one of the typical control methods for large-scale, constrained nonlinear systems in process industry (Qin & Badgwell, 2003). At each sampling instant, a finite horizon open-loop optimal control problem is solved which uses an explicit process model and state measurement. A control chain is achieved, and the first control action in this chain is applied to the plant. At the next sampling instant, the optimization problem is again solved using new measurements, and the control input is updated. An outstanding advantage of MPC is its capability to handle the issues of non-linearity, constraints, and performances flexibility within an optimal control setting (Mayne, Rawlings, Scokaert, & Rao, 2000; Raimondo, Limon, Lazar, Magni, & Camacho, 2009).

Nevertheless, due to the presence of uncertainty in parameter or structure of processes and exogenous disturbances, a system with nominally asymptotically stable MPC controller can be propelled to an infeasible region or unstable regime (Chisci, Rossiter, & Zappa, 2001; Grimm, Messina, Tuna, & Teel, 2004). A popular method for handling system uncertainties and disturbances is to develop Robust Model Predictive Control (RMPC) schemes which optimize over feasible state feedback control policies. There are several ways for designing robust MPC controllers in perturbed nonlinear systems. One way is to rely on the inherent robustness properties of nominally stabilizing MPC algorithms, as it was done in the work by Grimm, Messina, Tuna, & Teel (2003); Limon, Alamo, & Camacho (2002a); Magni, De Nicolao, & Scattolini (1998); Scokaert, Rawlings, & Meadows (1997). Another approach is to incorporate knowledge about the disturbances in the MPC problem formulation via open-loop worst case scenarios. This includes MPC algorithms based on open-loop min–max optimization problems (Canale & Milanese, 2003; Chen, Gao, Wang, & Findeisen, 2007; Goulart, Kerrigan, & Alamo, 2009), and MPC algorithms, based on tightened constraints (Chisci et al., 2001, 2001; Limon, Alamo, & Camacho, 2002b).

While the min–max formulation provides a natural way for studying the robustness of MPC, its computational expensive demand is distinguished and the complexity of resulting optimization problem grows exponentially with increase of prediction horizon (Lee & Yu, 1997). Moreover, its consequences in such controllers that mainly consider “worst-case” disturbances make an unrealistic scenario which have a poor performance even if the disturbance is close to zero. Constraint tightening approaches avoid computational complexity by using a nominal prediction model and tightened constraint sets. Tube MPC, as one of them, reduces the online computational burden involving fixed tightened sets. The algorithms utilize both a state feedback control law and a control action. The control action, calculated online, steers the nominal system states to the equilibrium. The state feedback control law keeps the actual trajectory of the constrained system in disturbance invariant sets centered along the nominal trajectory.

Recently, some references considered the linear system formulation to develop their robust model predictive control (Chisci et al., 2001; Mayne & Langson, 2001; Raković, 2012). In this paper, we extend these results to additive discrete time uncertain nonlinear systems. A new tube MPC method is described here for the optimization of closed loop process dynamics with fast and reliable real-time solution. The main contribution is converting robustness of parametric uncertainty into easier problem of an added bounded disturbance. Also, the proposed tube MPC uses $H_{\mathrm{\infty }}$ control approach for solving an ancillary MPC problem, which serves to contain the trajectories of the actual system in a tube around the nominal trajectory. This tube-based robust MPC algorithm can deal with bounded disturbances and uncertainties which provides a strong guarantee of robust stability. The method maintains feasible controlled trajectories while obtains good nominal control performance.

The rest of this article is organized as follows. In Section 2, problem setup is described. Section 3 presents a robust tube model predictive control law for additive uncertain nonlinear systems. In order to demonstrate the validity of the approach, surge control of a centrifugal compressor is presented in Section 4. Section 5 provides the concluding remarks.

2. Problem setup

Consider a nonlinear discrete time dynamical system described by

(1) $x\left(k+1\right)=Ax\left(k\right)+f\left(x\left(k\right)\right)+g\left(x\left(k\right)\right)\theta +B_{d}d\left(k\right)+Bu\left(k\right)$(1)

where $x\in R^{n_x}$ is the state of the system, $u\in R^{n_u}$ is the control input, $\theta$ is system uncertainty, and $d\in R^{n_d}$ is the bounded exogenous disturbance that lies in a compact set

(2) $D:=\left\{d\in R^{n_d}|||d||\le d_{max}\right\}$(2)

which contains the origin, i.e. $d\left(k\right)\in D$ for $k\ge 0$. Also, system is subject to constraints

(3) $x\left(k\right)\in X,u\left(k\right)\in U\mathrm{\forall }k>0$(3)

$A,B,B_d$ are constant matrices and $f\left(x\right):R^{n_x}\to R^{n_x}$, $g\left(x\right):R^{n_x}\to R^{n_x}$ are continuous nonlinear functions that satisfy the Lipchitz condition

(4) $\begin{array}{rl}& ||f\left(x_1\right)-f\left(x_2\right)||\le ||L_1{x}_1-x_2||\mathrm{\forall }{x}_1,x_2\in X\\ & ||g\left(x_1\right)-g\left(x_2\right)||\le ||L_2{x}_1-x_2||\mathrm{\forall }{x}_1,x_2\in X\end{array}$(4)

$L_1$, $L_2$ are diagonal matrices with positive constant known numbers.

The nominal system is described by

(5) $\bar{x}\left(k+1\right)=A\bar{x}\left(k\right)+f\left(\bar{x}\left(k\right)\right)+g\left(\bar{x}\left(k\right)\right)\bar{\theta }+B\bar{u}\left(k\right)$(5)

where $\bar{\theta }$ is certain known ${\theta }_{min}<\bar{\theta }<{\theta }_{max}$. Assume that $x\left(k\right)$ can be measured in real time and error between the actual and nominal system is described by

(6) $e\left(k\right)=x\left(k\right)-\bar{x}\left(k\right)$(6)

The aim of the paper is to design a control signal with both nominal controller and state feedback control (ancillary control), i.e.

(7) $u\left(k\right)=\bar{u}\left(k\right)+v\left(k\right)$(7)

which guarantees the robustness of actual system in presence of parametric uncertainty and disturbance. Also, it possesses a slight computational demand. Hence, the dynamic of error system is given as

(8) $e\left(k+1\right)=Ae\left(k\right)+f\left(x\left(k\right)\right)-f\left(\bar{x}\left(k\right)\right)+g\left(x\left(k\right)\right)\theta -g\left(\bar{x}\left(k\right)\right)\bar{\theta }+B_{d}d\left(k\right)+Bv\left(k\right)$(8)

By describing

(9) $\tilde{\theta }=\theta -\bar{\theta }$(9)

We have

(10) $e\left(k+1\right)=Ae\left(k\right)+f\left(x\left(k\right)\right)-f\left(\bar{x}\left(k\right)\right)+\left(g\left(x\left(k\right)\right)-g\left(\bar{x}\left(k\right)\right)\right)\bar{\theta }+g\left(x\left(k\right)\right)\tilde{\theta }+B_{d}d\left(k\right)+Bv\left(k\right)$(10)

(11) $h\left(x,\bar{x},e\right)=Ae\left(k\right)+f\left(x\left(k\right)\right)-f\left(\bar{x}\left(k\right)\right)+\left(g\left(x\left(k\right)\right)-g\left(\bar{x}\left(k\right)\right)\right)\bar{\theta }$(11)

(12) $\text{wleft(k right) = left[{matrix{ {gleft({xleft(k right)} right)mathop tildetheta} cr {dleft(k right)} cr } } right]matrix{ {wleft(k right) in W: = left{ {w in {R^{{n\_w}}}| ||w|| le {w\_{max}}} right}} cr {forall k ge 0} cr }}$(12)

Finally, it obtains

(13) $e\left(k+1\right)=h\left(x,\bar{x},e\right)+B_{w}w\left(k\right)+Bv\left(k\right)$(13)

Definition 1. A set ${\mathrm{\Omega }}_c\subset X\subset R^{n_x}$ is a robust control invariant set for error system (13) if and only if there is an ancillary feedback control law $v\left(.\right)$ with $v\left(.\right)+\bar{u}\left(.\right)\subseteq U\in R^{n_u}$ such that $\mathrm{\forall }v\left(.\right)\in {\mathrm{\Omega }}_c$ and $\mathrm{\forall }w\in W$, the trajectories $v\left(k\right)$ remain in ${\mathrm{\Omega }}_c$ for all $k\ge 0$.

Definition 2. A dynamic system is asymptotically ultimately bounded if a set of initial conditions of the system converges asymptotically to a bounded set.

3. Robust tube model predictive control

In this section, a robust tube MPC based on $H_{\mathrm{\infty }}$ approach is proposed for ensuring robust stability in the face of parametric uncertainty and disturbance. Control signal has two components: a nominal controller obtained from online optimization problem subject to nominal dynamics and ancillary controller which aims at steering the trajectories of the error system (13) to the origin, i.e. the trajectory of system (1) to the nominal trajectories.

A. Nominal controller design

The nominal optimal control problem is subject to the nominal dynamics (5), i.e. there are no uncertainties and disturbances. The nominal control problem for the current state $x\left(k\right)$, which is an online solution, is formulated as follows:

(14) $\begin{array}{c}\begin{array}{c}minimizeJ\left(k\right)\\ \bar{u}\left(k+i|k\right)i=0,1,2,\dots ,N\end{array}\\ s.t\\ \begin{array}{c}\bar{x}\left(k+1\right)=A\bar{x}\left(k\right)+f\left(\bar{x}\left(k\right)\right)+g\left(\bar{x}\left(k\right)\right)\bar{\theta }+B\bar{u}\left(k\right)\\ \bar{x}\left(k\right)\in X\\ \bar{u}\left(k\right)\in U\end{array}\end{array}$(14)

The nominal cost function is defined as follows:

(15) $J\left(k\right)=\sum _{i=0}^N\left({\bar{x}}^{\prime }\left(k+i|k\right)\bar{Q}\bar{x}\left(k+i|k\right)+{\bar{u}}^{\prime }\left(k+i|k\right)\bar{R}\bar{u}\left(k+i|k\right)\right)$(15)

Here, $N$ is the prediction horizon, $\bar{Q}$ and $\bar{R}$ are positive definite weighting matrices. The online nominal calculated controller is used to generate nominal state trajectory and ancillary control law $v\left(k\right)$ is used to keep the error system (6) in an invariant set centered on the nominal trajectory.

The following algorithm can be employed to stabilize the system:

Algorithm 1

Step 0: At time $k=0$, set $\bar{x}\left(0\right)=x\left(0\right)$, in which $x\left(0\right)$ is the current state.

Step 1: At time $k$ and current states $\left(\bar{x}\left(k\right),x\left(k\right)\right)$, solve problem (14) to obtain the nominal control action $\bar{u}\left(k\right)$ and actual control action $u\left(k\right)=\bar{u}\left(k\right)+v\left(k\right)$.

Step 2: Apply the control $u\left(k\right)$ to the system (1), during the sampling interval $\left[k,k+1\right]$.

Step 3: Measure the states $x\left(k+1\right)$ at the next time instant $k+1$ of the system (1) and compute the successor states $\bar{x}\left(k+1\right)$ of the nominal system (5) under the nominal control $\bar{u}\left(k\right)$.

Step 4: Set $\left(\bar{x}\left(k\right),x\left(k\right)\right)=\left(\bar{x}\left(k+1\right),x\left(k+1\right)\right)$, $k=k+1$ and go to Step 1.

We should notice that only the nominal model is used for prediction and the online computational burden of scheme is as same as standard MPC. General results of the proposed algorithm are stated by the following theorem.

Theorem 1.

Assuming $X$, $v$, ${\mathrm{\Omega }}_c$ are given and optimization problem is feasible at $k=0$; Then

Proof:

Since the online optimization problem only uses the “measured” state of nominal system and the nominal system dynamics, it does not depend on the uncertainties and disturbances at all.

1. Optimization problem is feasible for all $\ge 0$.

2. According to algorithm 1, the trajectory of the system (1) under control law is asymptotically ultimately bounded.

3. The closed-loop system is input-to-state stable.

Thus, if the optimization problem has a feasible solution at $k=0$, recursive feasibility is guaranteed (Chen & Allgöwer, 1998). According to Magni, De Nicolao, Scattolini, & Allgower (2003), there is a finite quantity $\beta \left(x_0\right)$, $\beta \left(0\right)=0$, such that

$||\bar{x}\left(k\right)||\le \beta \left(||x_0||,k\right)\mathrm{\forall }k\ge 0$

Because $e\left(k\right)\in {\mathrm{\Omega }}_c$, there is a class $\mathrm{K}$ function such that

$\begin{array}{rl}& ||e\left(k\right)||\le \gamma \left(sup||w\left(i\right)||\right)\mathrm{\forall }k>0\\ & 0\le i\le k\end{array}$

Finally, according to $\bar{x}\left(0\right)=x\left(0\right)$ and $x\left(\mathrm{k}\right)=\bar{x}\left(\mathrm{k}\right)+e\left(k\right)$

$\begin{array}{rl}& x\left(k\right)\le \beta \left(x_0,k\right)+\gamma \left(supw\left(i\right)\right)\mathrm{\forall }k\ge 0\\ & 0\le i\le k\end{array}$

Therefore, by using of algorithm 1, system (1) is asymptotically ultimately bounded and closed-loop system is input-to-state stable (Khalil, 2002).

B. Ancillary controller design

In this section, $H_{\mathrm{\infty }}$ approach is used to obtain the ancillary control law. The main idea is originated from Magni et al. (2003), where $H_{\mathrm{\infty }}$ approach is used to compute an auxiliary central law with its associated robust invariant set. By some modifications, the idea is used for computing ancillary control law.

Theorem 2

The control law $v\left(k\right)$ can be found by solving $H_{\mathrm{\infty }}$ control problem for the system (13). To do this, a $n\times n$ square matrix, $P$ and a symmetric matrix $M$ must be defined.

(16) $M=\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right]$(16)

$M_{11}=B^{\prime }PB+R$

$M_{12}=M_{21}=B^{\prime }P{B}_w$

$M_{22}=B_w^{\prime }P{B}_w-{\gamma }^{2}I$

where $\gamma$ is the designing parameter. The quadratic function is also defined as

(17) $V\left(e\right)=e^{\prime }Pe$(17)

According to Magni et al. (2003), suppose there exists a positive definite matrix $P$ such that

$\left(i\right)M_{22}<0$

$\left(ii\right)-P+{\left(A+L_1+L_2\right)}^{\prime }P\left(A+L_1+L_2\right)+Q-{\left(A+L_1+L_2\right)}^{\prime }P\left[\begin{array}{cc}B& B_w\end{array}\right]M^{-1}{\left[\begin{array}{cc}B& B_w\end{array}\right]}^{\prime }P\left(A+L_1+L_2\right)<0$

Then, the control law $v\left(k\right)=\kappa \left(x,\bar{x},e\right)$ becomes

(18) $\left[\begin{array}{c}\kappa \left(x,\bar{x},e\right)\\ \xi \left(x,\bar{x},e\right)\end{array}\right]=-M^{-1}{\left[\begin{array}{cc}B& B_w\end{array}\right]}^{\prime }Ph\left(x,\bar{x},e\right)$(18)

With

(19) ${\mathrm{\Omega }}_c=\left\{e:e^{\prime }Pe\le \alpha \right\}$(19)

where $\alpha$ is a finite positive constant. The matrix $P$ can also be derived by solving a discrete time $H_{\mathrm{\infty }}$ algebraic Riccati equation as follows:

Proof.

(20) $P=A{\left(A+L_1+L_2\right)}^{\prime }P\left(A+L_1+L_2\right)+Q-{\left(A+L_1+L_2\right)}^{\prime }P\left[\begin{array}{cc}B& B_w\end{array}\right]M^{-1}{\left[\begin{array}{cc}B& B_w\end{array}\right]}^{\prime }P{\left(A+L_1+L_2\right)}^{\prime }PA+Q-A^{\prime }P\left[\begin{array}{cc}B& B_w\end{array}\right]M^{-1}{\left[\begin{array}{cc}B& B_w\end{array}\right]}^{\prime }PA$(20)

Define

(21) $\text{Hleft({x,bar x,e,v,w} right) = Vleft({h + Bv + {B\_w}w} right) - Vleft(e right) \& lt - left({e'Qe + v'Rv - {gamma ^2}||w{^2}}|| right)}$(21)

(22) ${\left(h+Bv+B_{w}w\right)}^{\prime }P\left(h+Bv+B_{w}w\right)-e^{\prime }Pe+e^{\prime }Qe+v^{\prime }Rv-{\gamma }^2{w}^{\prime }w<0$(22)

(23) $h^{\prime }Ph+e^{\prime }\left(Q-P\right)e+v^{\prime }\left(B^{\prime }PB+R\right)v+w^{\prime }\left(B_w^{\prime }P{B}_w-{\gamma }^{2}I\right)w+2\left[\begin{array}{cc}{v}^{\prime }& w^{\prime }\end{array}\right]\left[\begin{array}{c}{B}^{\prime }Ph\\ B_w^{\prime }Ph\end{array}\right]+2v^{\prime }{B}^{\prime }P{B}_{w}w<0$(23)

(24) $h^{\prime }Ph+e^{\prime }\left(Q-P\right)e+\left[\begin{array}{cc}{v}^{\prime }& w^{\prime }\end{array}\right]M\left[\begin{array}{c}v\\ w\end{array}\right]+\left[\begin{array}{cc}{v}^{\prime }& w^{\prime }\end{array}\right]\left[\begin{array}{c}{B}^{\prime }Ph\\ B_w^{\prime }Ph\end{array}\right]<0$(24)

And by computing (24) for $v=\kappa \left(x,\bar{x},e\right)$ and $w=\kappa \left(x,\bar{x},e\right)$

(25) $H\left(x,\bar{x},e,\kappa \left(x,\bar{x},e\right),\xi \left(x,\bar{x},e\right)\right)=h^{\prime }Ph+e^{\prime }\left(Q-P\right)e+\left[\begin{array}{cc}{\kappa }^{\prime }\left(x,\bar{x},e\right)& {\xi }^{\prime }\end{array}\left(x,\bar{x},e\right)\right]M\left[\begin{array}{c}\kappa \left(x,\bar{x},e\right)\\ \xi \left(x,\bar{x},e\right)\end{array}\right]-2\left[\begin{array}{cc}{\kappa }^{\prime }\left(x,\bar{x},e\right)& {\xi }^{\prime }\end{array}\left(x,\bar{x},e\right)\right]M\left[\begin{array}{c}\kappa \left(x,\bar{x},e\right)\\ \xi \left(x,\bar{x},e\right)\end{array}\right]<0$(25)

(26) $h^{\prime }Ph+e^{\prime }\left(Q-P\right)e-h^{\prime }P\left[\begin{array}{cc}B& B_w\end{array}\right]M^{-1}\left[\begin{array}{c}{B}^{\prime }\\ B_w^{\prime }\end{array}\right]Ph<0$(26)

According to (11)

(27) ${\left(Ae+f\left(x\right)-f\left(\bar{x}\right)+\left(g\left(x\right)-g\left(\bar{x}\right)\right)\bar{\theta }\right)}^{\prime }P\left(Ae+f\left(x\right)-f\left(\bar{x}\right)+\left(g\left(x\right)-g\left(\bar{x}\right)\right)\bar{\theta }\right)+e^{\prime }\left(Q-P\right)e-{\left(Ae+f\left(x\right)-f\left(\bar{x}\right)+\left(g\left(x\right)-g\left(\bar{x}\right)\right)\bar{\theta }\right)}^{\prime }P\left[\begin{array}{cc}B& B_w\end{array}\right]M^{-1}\left[\begin{array}{c}{B}^{\prime }\\ B_w^{\prime }\end{array}\right]P\left(Ae+f\left(x\right)-f\left(\bar{x}\right)+\left(g\left(x\right)-g\left(\bar{x}\right)\right)\bar{\theta }\right)<0$(27)

According to Lipschitz conditions (4), we have

(28) $e^{\prime }\left({\left(A+L_1+L_2\right)}^{\prime }P\left(A+L_1+L_2\right)+Q-P-{\left(A+L_1+L_2\right)}^{\prime }P\left[\begin{array}{cc}B& B_w\end{array}\right]M^{-1}\left[\begin{array}{c}{B}^{\prime }\\ B_w^{\prime }\end{array}\right]P\left(A+L_1+L_2\right)\right)e<0$(28)

There exist positive constants followed$\left(ii\right)$ such that

(29) $H\left(x,\bar{x},e,\kappa \left(x,\bar{x},e\right),\xi \left(x,\bar{x},e\right)\right)\le -\epsilon ||e{ }^2||\mathrm{\forall }e\in {\mathrm{\Omega }}_1=\left\{e:||e||\le r_1\right\}$(29)

By Taylor expansion theorem

(30) $H\left(x,\bar{x},e,v,w\right)=H\left(x,\bar{x},e,\kappa \left(x,\bar{x},e\right),\xi \left(x,\bar{x},e\right)\right)+\frac{1}{2}{\left[\begin{array}{cc}v-\kappa \left(x,\bar{x},e\right)& w-\xi \left(x,\bar{x},e\right)\end{array}\right]}^{\prime }R\left[\begin{array}{c}v-\kappa \left(x,\bar{x},e\right)\\ w-\xi \left(x,\bar{x},e\right)\end{array}\right]$(30)

where the first-order term is evaluated and terms of order are null. If the system is controlled by $v\left(k\right)=\kappa \left(x,\bar{x},e\right)$ then

(31) $H\left(x,\bar{x},e,\kappa \left(x,\bar{x},e\right),w\right)=H\left(x,\bar{x},e,\kappa \left(x,\bar{x},e\right),\xi \left(x,\bar{x},e\right)\right)+\frac{1}{2}{\left(w-\xi \left(x,\bar{x},e\right)\right)}^{\prime }{R}_{22}\left(w-\xi \left(x,\bar{x},e\right)\right)$(31)

Because $M_{22}<0$ and by using of (29)

(32) $H\left(x,\bar{x},e,\kappa \left(x,\bar{x},e\right),w\right)\le H\left(x,\bar{x},e,\kappa \left(x,\bar{x},e\right),\xi \left(x,\bar{x},e\right)\right)\le -\epsilon ||e{ }^2||\begin{array}{c}\mathrm{\forall }e\in {\mathrm{\Omega }}_1=\left\{e:||e||\le r_1\right\}\\ allw\in W\end{array}$(32)

From (21) and (32), it follows that

(33) $V\left(h+Bv+B_{w}w\right)\le V\left(e\right)-\left(e^{\prime }Qe+v^{\prime }v-{\gamma }^2||w{ }^2||\right)-\epsilon ||e{ }^2||\le V\left(e\right)-\epsilon e{ }^2\begin{array}{c}\mathrm{\forall }\in {\mathrm{\Omega }}_c=\left\{e:V\left(e\right)\le \alpha \right\}\subset {\mathrm{\Omega }}_1\\ allw\in W\end{array}$(33)

And that ${\mathrm{\Omega }}_c$ is an invariant set with the origin as an interior point for the system. In the next section, the introduced tube MPC law will be applied to compressor system for exemplifying the derived results.

4. Surge control of a centrifugal compressor

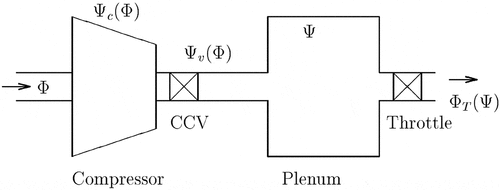
In this section, to illustrate the effectiveness of the proposed method, the Tube_MPC law is applied to a centrifugal compressor in order to surge control. Figure 1 shows the diagram of compression system with close coupled valve (CCV) actuator.

Figure 1. The compressor system with CCV actuator

The system is described by

$\dot{\psi }=\frac{1}{4B^2{l}_c}\left(\varphi -{\varphi }_T\left(\psi \right)+d_{\varphi }\left(\xi \right)\right)$

(34) $\dot{\varphi }=\frac{1}{l_c}\left({\psi }_c\left(\varphi \right)-\psi -{\psi }_V\left(\varphi \right)+d_{\psi }\left(\xi \right)\right)$(34)

where $\psi$ is the coefficient of increase in compressor pressure, $\varphi$ is the coefficient of compressor’s mass flow, ${\psi }_c\left(\phi \right)$ is the characteristic of the compressor, $d_{\varphi }\left(\xi \right),d_{\psi }\left(\xi \right)$ are the disturbances of flow and pressure, $B$ is the Greitzer’s parameter, $l_c$ is the length of ducts and compressor, and ${\varphi }_T\left(\psi \right)$ is the characteristic of throttle valve

(35) ${\varphi }_T\left(\psi \right)={\gamma }_T\sqrt{\psi }$(35)

${\gamma }_T$ is also the valve’s yield.

Considering ${\psi }_V\left(\varphi \right)$ as the input for system control and $x_1=\psi ,x_2=\varphi$, discrete time nonlinear equations of (34) according to Euler approximation with T sampling time are

$x_1\left(k+1\right)=x_1\left(k\right)+\frac{T}{4B^2{l}_c}\left(x_2\left(k\right)-{\gamma }_T\sqrt{x_1\left(k\right)}+d_{\varphi }\left(k\right)\right)$

(36) $x_2\left(k+1\right)=x_2\left(k\right)+\frac{T}{l_c}\left({\psi }_c\left(x_2\left(k\right)\right)-x_1\left(k\right)-u\left(k\right)+d_{\psi }\left(k\right)\right)$(36)

Rewriting above equation according to (1), we have

(37) $\left[\begin{array}{c}{x}_1\left(k+1\right)\\ x_2\left(k+1\right)\end{array}\right]=A\left[\begin{array}{c}{x}_1\left(k\right)\\ x_2\left(k\right)\end{array}\right]+f\left(x\left(k\right)\right)+g\left(x\left(k\right)\right)\theta +B_d\left[\begin{array}{c}{d}_{\varphi }\left(k\right)\\ d_{\psi }\left(k\right)\end{array}\right]+Bu\left(k\right)$(37)

where

$A=\left[\begin{array}{cc}1& \frac{T}{4B^2{l}_c}\\ -\frac{T}{l_c}& 1\end{array}\right]$, $B=\left[\begin{array}{c}0\\ -\frac{T}{l_c}\end{array}\right]$, $B_d=\left[\begin{array}{cc}\frac{T}{4B^2{l}_c}& 0\\ 0& \frac{T}{l_c}\end{array}\right]$, $f\left(x\left(k\right)\right)=\left[\begin{array}{c}0\\ \frac{T}{l_c}{\psi }_c\left(x_2\left(k\right)\right)\end{array}\right]$,

(38) $g\left(x\left(k\right)\right)=\left[\begin{array}{c}-\sqrt{x_1\left(k\right)}\\ 0\end{array}\right]$(38)

and $\theta ={\gamma }_T$ has parametric uncertainty in the system. The nominal model for the system (37) is defined as

(39) $\left[\begin{array}{c}{\bar{x}}_1\left(k+1\right)\\ {\bar{x}}_2\left(k+1\right)\end{array}\right]=A\left[\begin{array}{c}{\bar{x}}_1\left(k\right)\\ {\bar{x}}_2\left(k\right)\end{array}\right]+\left[\begin{array}{c}0\\ \frac{T}{l_c}{\psi }_c\left({\bar{x}}_2\left(k\right)\right)\end{array}\right]+\left[\begin{array}{c}-\sqrt{{\bar{x}}_1\left(k\right)}\\ 0\end{array}\right]{\bar{\gamma }}_T+B\bar{u}\left(k\right)$(39)

The above equations satisfy the mentioned conditions for designing the proposed controller. By using the error system (13), we have $B_w=\left[\begin{array}{cc}1& \frac{T}{4B^2{l}_c}\\ 1& \frac{T}{l_c}\end{array}\right]$ and $w\left(k\right)=\left[\begin{array}{cc}-\sqrt{x_1\left(k\right)}\left({\gamma }_T-{\bar{\gamma }}_T\right)& d_{\varphi }\left(k\right)\\ 0& d_{\psi }\left(k\right)\end{array}\right]$.

Since the control signal is a CCV output, the first constraint is considered as follows:

(40) $\bar{u}\left(k\right)>0$(40)

The maximum and minimum values for compressor flow are the second constraint:

(41) $-{\varphi }_m\le \varphi \left(k\right)\le {\varphi }_{Choke}$(41)

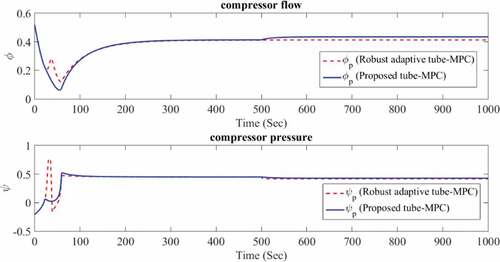
Solving the optimization problem (14) and the law (18) gives nominal and ancillary control signals, respectively. To demonstrate the various features of the proposed method, a set of simulation is performed. Compressor parameters in simulation are same (Gravdahl & Egeland, 1999). The states and control signal for compression system using the proposed method are shown in Figures 2–10. Also, it is compared with robust adaptive tube-MPC (Ziabari, Jahed-Motlagh, Salahshoor, Ramezani, & Moarefianpuor, 2017) to demonstrate the effectiveness of the proposed controller. Disturbance and uncertainty are same (Ghanavati, Salahshoor, Motlagh, Ramazani, & Moarefianpour, 2018; Ziabari et al., 2017)

Figure 2. Flow and pressure of compressor

In all of the simulations, compressor initially operates in steady state where the value of throttle valve is ${\gamma }_T=0.65$. At t = 500s, the value of throttle valve is reduced to ${\gamma }_T=0.6$, which causes the compressor insert into surge. The initial points of process are $\left(x_1\left(0\right),x_2\left(0\right)\right)=\left(0.5189,-0.2\right)$ in the left side of the surge line and the initial points of model are $\left(x_1\left(0\right),x_2\left(0\right)\right)=\left(1,1\right)$. The $\bar{\theta }$ of the model is ${\bar{\gamma }}_T=0.65$. 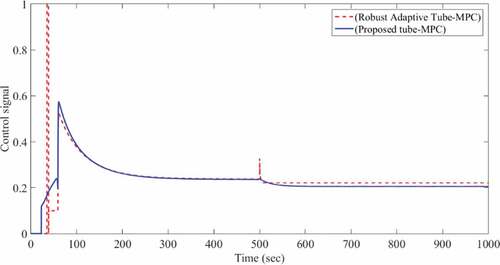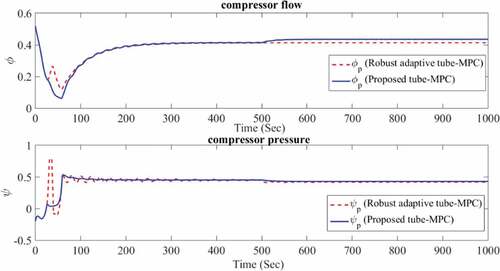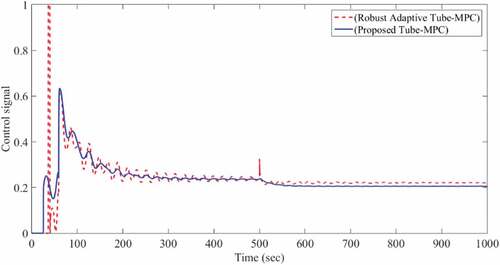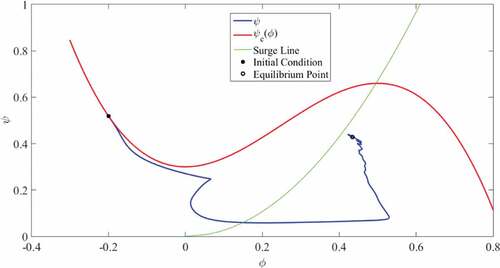Also, there is no external disturbance on the compressor system in first mode. It can be observed that the controller had been able to stabilize the system well. Figure 2 presents the flow and pressure and Figure 3 shows the history of the optimal solution of the control problem.

Figure 3. Control signal

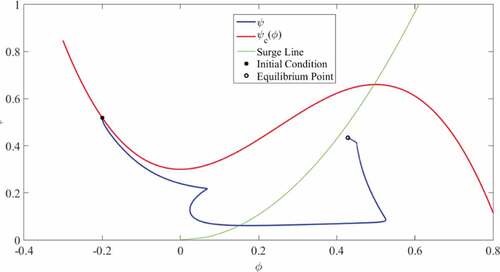
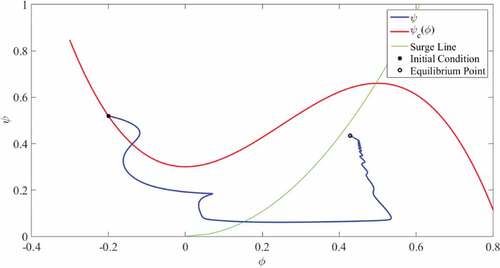
Figure 4 shows the trajectory of compressor in a performance curve. It shows how the controller prevents the compressor from entering the surge area.

Figure 4. Compression system trajectories

In the second mode, it is assumed that some transitory disturbances are applied to the system. These disturbances are modeled as

(42) $\begin{array}{c}{d}_{\varphi }\left(k\right)=0.15e^{-0.015k}cos\left(0.2k\right)\\ d_{\psi }\left(k\right)=0.1e^{-0.005k}sin\left(0.3k\right)\end{array}$(42)

Figure 5 shows the values of flow and pressure. As can be seen, despite the existing disturbances, the controller has been able to repulse it and control the surge. The control signal is shown in Figure 6.

Figure 5. Flow and pressure of compressor

Figure 6. Control signal

The trajectory of the compressor is also shown in Figure 7, and it conveys the ability of the controller for disturbance rejection.

Figure 7. Compression system trajectories

In the third mode, it is assumed that some stable disturbances are applied to the system. These disturbances are modeled as follows:

(43) $\begin{array}{c}{d}_{\varphi }\left(k\right)=0.02sin\left(0.1k\right)+0.02cos\left(0.4k\right)\\ d_{\psi }\left(k\right)=0.02sin\left(0.1k\right)+0.02cos\left(0.4k\right)\end{array}$(43)

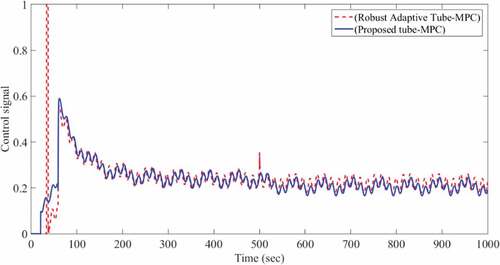
After simulation, the values of flow and pressure are shown in Figure 8, which show that the controller has been able to stabilize the system, in spite of the existence of disturbances and uncertainty.

Figure 8. Flow and pressure of compressor

The control signal for surge prevention is also presented in Figure 9.

Figure 9. Control signal

The performance curve for the compressor is also shown in Figure 10. It can be seen that in spite of the existence of disturbance and uncertainty, the controller has been able to prevent surge.

Figure 10. Compression system trajectories

As can be seen, simulation results illustrate the robustness of the proposed controller to steer the centrifugal compressor against disturbance and change in throttle valve gain.

It should be noticed that in all simulations, the control signal obtained from the proposed method is far from the specified limit and accompanied with lower slew rate than the robust adaptive tube-MPC method (Ziabari et al., 2017).

5. Conclusion

A tube MPC scheme with guaranteed recursive feasibility is derived for discrete-time uncertain nonlinear systems subject to bounded disturbances based on the robust control invariant sets. Control design methodology solves two problems: the optimal control problem with computational burden as the standard MPC, that is solved online includes the nominal system without uncertainties and disturbances to define a central guidance path and the ancillary problem to steer the states toward the central path despite uncertainties and disturbances. Numerical simulation illustrates that the proposed controller can successfully stabilize the states within expected neighborhood of the origin.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Hashem Imani Marrani

Hashem Imani Marrani is Ph.D. in Control and System Engineering in Science and Research branch, Islamic Azad University, Tehran, Iran. His research interests include Nonlinear Control, MPC, and Nonlinear Fiber Optics.

Samane Fazeli

Samane Fazeli was born in Torbat-e Heydarieh, Iran. She is a Ph.D. student and received M.Sc. degrees with honors in electrical engineering from Islamic Azad University, Science and Research Branch, Tehran, Iran. Her research interests include model predictive control, time delay systems, and robust control.

Hamid Malekizade

Hamid Malekizade is an assistant professor at the Department of Electrical Engineering, Imam Khomeini Maritime University, Nowshahr, Iran. His main fields of interest are stabilizing marine systems and robust model predictive control.

Hasan Hosseinzadeh

Hasan Hosseinzadeh was born in 1979 in Ardabil, Iran. He received his BSc in 2003 from Payam Noor University Ardabil, MSc from Sistine and Baluchistan University in 2006 and Ph.D. from Karaj Azad University in 2013. His research interests are Mathematical analysis and its applications, differential equations, image processing, and other related mathematical fields.