On self-sustained detonation

Abstract

Steady and self-sustained detonation is a fundamental element for combustion theory. There is already a theory on it, however, author of this work found that the theory is not perfect and it is necessary to develop new theory, which is the objective of this work. To that end, author firstly discusses the deficiencies of the existing theory. Then, based on the work [1], author introduced a new theoretic model for the self-sustained detonation, an eigenvalue problem. The new model removes the deficiencies in the existing theory and can produce all the information of the detonation, including its speed and structure. This paper focuses on the theoretic analysis on the new concept and is the first part of the work. A direct numerical simulation (DNS) for the self-sustained detonation was carried out as well. Comparison of the results of the DNS, the new theoretic model and the existing theory shows that the introduced new model produced the results identical with the DNS results but significantly different from the results done by the existing theory. This is the second part of the work.

Keywords:

• self-sustained detonation
• Chapman-Jouguet detonation
• speed of combustion wave propagation
• eigenvalue problem
• combustion velocity

PUBLIC INTEREST STATEMENT

Detonation is an important mode of chemical combustions. When it is driven by the chemical reactions and without action of other external forces, the detonation is called self-sustained detonation. The self-sustained detonation is a fundamental element of any other detonations. Traditional theory deems that the self-sustained detonation is determined by the chemical reaction heat only and independent of the reaction speeds. Thus, the self-sustained detonation is always weakest and slowest of all the possible detonation modes. Nonetheless, numerical investigation into the detonation by author and other researchers find that the real detonation is not like what the traditional theory describes. It is controlled by not only the reaction heat but also the reaction speeds. In order to explain this discovery, the works in this paper setup a new theoretic model. This new model well interprets the discovery and provides a new concept or understanding on self-sustained detonation.

1. Statement of the Problem

When a premixed combustible gaseous mixture ignites, an explosion frequently occurs if the mixture has sufficiently high energy density and the chemical reaction rates are rapid enough. The explosion takes place of two forms. One is fast deflagration and the other is detonation (Bjerketvedt, Bakke, & Wingerden, 1997). The main discrimination of these two forms of explosions lies in that the former has an expansion of the mixture, i.e., decrease of the mixture density, in the chemical reaction zone, compared with the unreacted mixture, while the latter generates a more denser mixture within the chemical reaction zone. The two explosions all propagate with fast speed and produce high over-pressure. The fast deflagration, however, is often unstable, which would result in deflagration-to-detonation transition (DDT).

Different from fast deflagration, detonation is a supersonic combustion wave and always associated with a very strong shock wave. As a result, the produced overpressure is usually more than 10 times that generated by the fast deflagration. Hence, from a safety point of view, the detonation is hopefully avoided. In some other applications, e.g., pulsejet engine, however, the detonation is necessary but hopefully controllable. Therefore, whatever the applications are, it is all required for us to fully and correctly understand detonation propagation.

A detonation is comprised of two layers: a leading shock wave and an associated chemical reaction zone or flame. The chemical reactions are major source or force to drive the combustion wave movement. In practical application, however, many external factors such as rough wall, obstacle, heat transfer with the surrounding and inlet stream flow (“piston-driven in shock tube”), etc. have significant influences or actions on the detonation propagation. Therefore, it is necessary to distinguish the detonation purely driven by the reactions from the others. In combustion theory (Glassman & Yetter, 2008; Landau & Lifshitz, 2011; Law, 2006; Williams, 1985), if a detonation is significantly affected or acted by some external factors, the detonation is referred as to being the overdriven. To contrary, when detonation propagation is maintained by its chemical reactions only and is not affected from the external factors, this detonation is called self-sustained detonation. The self-sustained detonation has its own autonomous dynamics, represents the inherent nature of detonation (Kasimov & Stewart, 2004), and therefore plays a fundamental role in combustion theory and applications.

Theoretically one curve, Rankine–Hugoniot curve, and one straight line, Rayleigh line, are frequently used to represent combustion wave propagations in a premixed medium (Glassman & Yetter, 2008; Law, 2006; Williams, 1985). Rankine–Hugoniot curve expresses the relationship of the pressures and specific volumes, i.e., density reciprocals, before and after the chemical reactions of combustion waves, while Rayleigh line reflects the speed of combustion wave propagations. When the total heat released by the reactions, which can be estimated by chemical energy of an unreacted fuel, is known, Rankine–Hugoniot curve will be fixed. The Rankine–Hugoniot curve however tells us that the detonation with the corresponding release heat can have infinitely many possible modes of propagations (Glassman & Yetter, 2008; Law, 2006; Williams, 1985). Each mode corresponds to a point at the upper branch of the Rankine–Hugoniot curve. Amid the infinitely many possible modes there is a particular mode, called Chapman–Jouguet (C–J) detonation that has the minimal propagation speed. The C–J detonation is of an attribute that the flow velocity at the end of reaction zone is equal to the local sonic speed. This attribute is called C–J condition in literature (Shapiro, 1953).

A fundamental problem on self-sustained detonation is to find detonation speed. When the detonation speed is known, the Rayleigh line will be defined. The cross point between this Rayleigh line and the Rankine–Hugoniot is the corresponding detonation. How to decide the detonation speed, author of this work finds, is still problematic.

In order to explain the problem clearly, our discussion is restricted to one-dimensional and frictionless flows on which we have already had well-developed fluid dynamics theories (Courant & Friedrichs, 1976; Landau & Lifshitz, 2011; Shapiro, 1953) to be used. At present, the theory on detonation deems that a 1D self-sustained detonation is C–J detonation corresponding to its chemical reaction release heat. The major reason to support this theory can be explained in what follows, e.g., see Fickett (1979). The flow of detonation is divided into two parts in the wave-fixed reference frame. One is steady reacting flow from the shock wave to the end of the reaction zone. The second one is the unsteady flow behind the flow of first part. Their interface is the boundary for both flows. In order to block the interference coming from the unsteady flow of second part to the first part flow, the boundary, i.e., at the end of reaction zone must be sonic flow, since all the unsteady flow disturbances toward the reaction zone propagate with the local sonic speed subtracting the flow velocity (Courant & Friedrichs, 1976; Landau & Lifshitz, 2011). When the flow is sonic flow at the boundary, the upstream propagating speed is zero so that the reacting flow can keep steady. If the sonic point is at the end of the reaction zone, the detonation must be C–J detonation.

This theory does not always work well. Fickett and Davis (1979) introduced an interesting example: a detonation with two reactions, one is exothermic and the other is endothermic. The exothermic reaction is faster than the endothermic. As a result, the heat addition process must be ended in somewhere inside the reaction zone. Because of the second endothermic reaction, applying the principle of Rayleigh heat-addition flows (Shapiro, 1953), we can see that the flow at the end of the whole reactions must be subsonic. Therefore, no C–J detonation exists. For this two-reaction case, however, we can still apply the approach for the C–J self-sustained detonation theory and assume that the flow at the end of the exothermic reaction but within the reaction zone is sonic such that the possible disturbances will be blocked before the end of the exothermic reaction. The detonation produced by this assumption is called pathological detonation in literature, e.g., see Higgins (2012). The pathological detonation lies in above the C–J detonation on Rankine–Hugoniot curve, and therefore propagates much faster and generates much more overpressure than the C–J detonation.

Nonetheless, following the method of Fickett and Davis, we may make a three-reaction detonation. The first reaction is fast exothermic, the second is middle-fast endothermic and the third is slow exothermic. Since reaction heats and rates are free variables, we can set them such that when the flow at the end of first reaction is set to be sonic, i.e., the detonation is pathological detonation, the flow at the end of third reaction, because of being exothermic, can be sonic flow as well, i.e., the detonation should be C–J detonation. Alternatively, when the flow at the end of third reaction is set to be sonic, i.e., the detonation is C–J detonation, the first reaction, since the flow at its end is sonic flow as well, will cause the flow in the whole reaction zone to be unsteady. As a result, both theories above are not applicable for this three-reaction case.

In addition, these theories for self-sustained detonation suffer from another fatal deficiency, i.e., self-sustained detonation maintained by its reactions only propagates without any relationship of its reaction rates. Common-sense experience tells us that the reaction rates may be the most key factor for combustion wave propagation modes, e.g., no DDT takes place if the reaction rates are slow (Liu, 2012, 2015). The existing theories, however, say that the self-sustained detonation is independent of its reaction rates that is very difficult to be understood.

From the above discussion, we see that the key problem for determining detonation speed is how to specify the boundary condition at the end of reaction zone. Recently, Liu (2016) developed a general theory for self-sustained combustion wave propagation. In Liu’s theory, the boundary condition is Neumann boundary condition which is theoretically at the infinitely far from the detonation front and the above interference of unsteady flow therefore disappears. The similar theoretic model can be seen in Kee, Grcar, Smooke, Miller, and Meeks (2000). The combustion waves produced by them are closely related to their reaction rates. Therefore, applying these theoretic models to build up theoretic frame for self-sustained detonation may be better.

Not only does the new theoretic frame include the transport effect on combustion wave propagations but also the effect of the material compressibility is contained in it. The objective of this work is an attempt to build up new conceptual frame on self-sustained detonation based on this theory. This is part one of the work—theoretic analysis. Author of this work also did a lot of direct numerical simulations (DNS) on one-dimensional self-sustained detonations recently. The numerical results show that the expansion zone behind the shock wave in the wave-fixed reference frame is almost constant when detonation is getting steady. Therefore, there is no the so-called interference of unsteady flow considered in the traditional theory and C–J condition is not necessary for determining the self-sustained detonation. The numerical simulation results fully support the conclusions in this paper which will be submitted to the Journal as the second part of the work soon.

2. Mathematic Model for Self-sustained Detonations

The chemical reactions are the only force for driving self-sustained detonation movement. Hence, a rigorous mathematic model for the self-sustained detonations must be eigenvalue problem, something like self-sustained laminar flame (von Karman & Penner, 1954). The basic equations for the eigenvalue problem describe the detonation propagation with respect to the wave-fixed frame of reference, which are the same as Liu (2016) and are written as

(1) $\frac{\mathrm{\partial }\left(\rho u\right)}{\mathrm{\partial }x}=0$(1)

(2) $\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[\rho u^2+p-\frac{4}{3Re}\frac{\mathrm{\partial }u}{\mathrm{\partial }x}\right]=0$(2)

(3) $\frac{\mathrm{\partial }\left(\rho uE+up\right)}{\mathrm{\partial }x}=-h_0^T\cdot \rho \dot{\omega }+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\gamma \frac{4M^2}{3Re}\cdot u\frac{\mathrm{\partial }u}{\mathrm{\partial }x}+\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)$(3)

(4) $\frac{\mathrm{\partial }\left(\rho uY\right)}{\mathrm{\partial }x}-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{1}{ScRe}\rho \frac{\mathrm{\partial }Y}{\mathrm{\partial }x}\right)=\rho \dot{\omega }$(4)

(5) $p=\rho T$(5)

It can be seen that the mathematic models (1)–(5) contain the effects of both transport terms and material compressibility, even though the effects of the transport terms play an insignificant role in fast combustion wave propagations (Clarke, 1983).

For the sake of generalization, the above equations are normalized as the dimensionless form in which a length, l, the sound speed, density, pressure and temperature at the unreacted states of the reactant mixture, $a_0$, ${\rho }_0$, $p_0$ and $T_0$, are used for the reference length, velocity, density, pressure and temperature, respectively. The Equation (1)(1) $\frac{\mathrm{\partial }\left(\rho u\right)}{\mathrm{\partial }x}=0$(1) is for the mass conservation, (2) for the momentum conservation, (3) for the energy conservation, (4) for the fraction of chemical species and (5) is the equation for the thermodynamic state of mixture. In the equations, $u$, $\rho$, $p$, $T$, $E$, $Y$, $h_0$ and $\dot{\omega }$denote the flow velocity, density, pressure, temperature, total energy, vector of mass fraction of reactants, vector of heats of combustion (enthalpy of formation) and vector of reactant production rates, respectively, in which $\sum Y_i=1$ and $\sum {\omega }_i=0$.

The reactant production rates are related to the rates of the chemical reactions. In combustion theory, the chemical reactions can be represented as

$\text{matrix{ {sum nu\_i^{{'^k}{R\_i} to sum {nu\_i^{{''^k}{R\_i},} } } \& {k = 1,2, cdots ,M} cr }}$

where $R_i$ is the reactant or product, measured by its concentration by volume and ν is a coefficient that will be explained below. The rate of a chemical reaction satisfies the law of mass action, that is,

$\begin{array}{cc}{r}_k=C_k(T)\rho \prod Y_i^{{\nu }_i^{{\prime }^k}},& k=1,2,\cdots ,M\end{array}$

where $C_k$ and ${{\nu }_i^{\prime }}^k$ are the proportionality factor and the order of the reaction with respect to the species i. The proportionality factor can be written as modified Arrhenius form:

$C_k(T)=A_k{T}^{{\beta }_k}{e}^{-\frac{E_a^k}{RT}}$

where $A_k$, $E_a^k$,$T$ and $R$ are the preexponential factor, activation energy, temperature and universal gas constant, respectively and ${\beta }_k$ is a constant. The reactant production rate with respect to the species i can be therefore represented as

${\dot{\omega }}_i=\sum \left\{({\nu }_i^{{{ }^{\prime \prime }}^k}-{\nu }_i^{{\prime }^k})\cdot r_k\right\}$

If the reaction in combustion follows first-order Arrhenius kinetics, the above reactant production rate can be further simplified.

Mathematical model for a self-sustained combustion wave in the laboratory reference frame is a Cauchy problem. When it is transformed to the wave-fixed reference frame such as the case of this paper, the problem becomes steady and boundary conditions are necessary. The boundary conditions at the cold boundary (unreacted mixture side) are of Dirichlet type and can be expressed as (6) in which, $u_0$, is the speed of detonation propagation, an unknown to be found.

(6) $\left(\begin{array}{cccccc}u,& \rho ,& p,& T,& E,& Y\end{array}\right)\left|{ }_{x=-\mathrm{\infty }}\right.=\left(\begin{array}{cccccc}{u}_0,& {\rho }_0,& p_0,& T_0,& E_0,& Y_0\end{array}\right)$(6)

In order to make the problem well-posed, other two homogeneous boundary conditions (7) and (8) at the fully reacted mixture side are necessary.

(7) $\left(\begin{array}{cccccc}\frac{\mathrm{\partial }u}{\mathrm{\partial }x},& \frac{\mathrm{\partial }\rho }{\mathrm{\partial }x},& \frac{\mathrm{\partial }p}{\mathrm{\partial }x},& \frac{\mathrm{\partial }T}{\mathrm{\partial }x},& \frac{\mathrm{\partial }E}{\mathrm{\partial }x},& \begin{array}{cc}Y,& \frac{\mathrm{\partial }Y}{\mathrm{\partial }x}\end{array}\end{array}\right)\left|{ }_{x=+\mathrm{\infty }}\right.=\left(\begin{array}{cccccc}0,& 0,& 0,& 0,& 0,& \begin{array}{cc}{Y}_{\mathrm{\infty }},& 0\end{array}\end{array}\right)$(7)

(8) $\left(\begin{array}{cccccc}\frac{\mathrm{\partial }u}{\mathrm{\partial }x},& \frac{\mathrm{\partial }\rho }{\mathrm{\partial }x},& \frac{\mathrm{\partial }p}{\mathrm{\partial }x},& \frac{\mathrm{\partial }T}{\mathrm{\partial }x},& \frac{\mathrm{\partial }E}{\mathrm{\partial }x},& \frac{\mathrm{\partial }Y}{\mathrm{\partial }x}\end{array}\right)\left|{ }_{x=-\mathrm{\infty }}\right.=\left(\begin{array}{cccccc}0,& 0& 0& 0& 0& 0\end{array}\right)$(8)

where $Y_0$ and $Y_{\mathrm{\infty }}$denote respectively the mass fractions before and after the reactions. As the speed of detonation is unknown, the problems (1)–(8) form an eigenvalue problem. There is always a zero solution or a trivial solution for the above eigenvalue problem. Nonetheless, what we seek for is the non-zero solutions of the problem, i.e., non-trivial solutions.

In the problems (1)–(8), there is no external force such as “piston strength” before the flame or external disturbance in the post-reaction zone. Therefore, the non-trivial solutions, if they exist, should be those that are driven and maintained by their chemical reactions only, that is, self-sustained detonations.

Now let us have a look at the difference between the theoretic model introduced in this work and traditional theory. In the traditional theory, the C–J condition can be applied to determine the speed of detonation in (6). As a result, the boundary condition (8) becomes unnecessary. As the speed of detonation is known, the problems (1)–(7) can be uniquely solved for the structure of detonation. This is the approach of the traditional theory to obtain self-sustained detonations.

Nonetheless, the discussion in Section 1 shows that C–J condition cannot be as the necessary condition for self-sustained detonation, and thence the eigenvalue problem introduced above has an additional boundary condition (8). The introduction of this boundary condition causes the speed and structure of detonation produced by the eigenvalue problem to be different from those of the C–J detonation. In Section 2.1, a new necessary condition for self-sustained detonation will be obtained through analytically solving the eigenvalue problems (1)–(8) that enable us to determine the speed and structure of self-sustained detonations very easily.

2.1. A new necessary condition for self-sustained detonations

There is an analytic solution for the speed of detonation in the problems (1)–(8), which can be represented by the form of integration. For example, when the chemical reaction is involved in only one species, we may directly integrate the Equations (1)(1) $\frac{\mathrm{\partial }\left(\rho u\right)}{\mathrm{\partial }x}=0$(1) and (4(4) $\frac{\mathrm{\partial }\left(\rho uY\right)}{\mathrm{\partial }x}-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{1}{ScRe}\rho \frac{\mathrm{\partial }Y}{\mathrm{\partial }x}\right)=\rho \dot{\omega }$(4) ), and obtain the formula for the eigenvalues of the above eigenvalue problem.

(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9)

where $m\equiv {\rho }_{+\mathrm{\infty }}{u}_{+\mathrm{\infty }}={\rho }_{0^{+}}{u}_{0^{+}}$ is actually the eigenvalue or detonation speed to be found, and $0^{+}$is the coordinate just behind the shock wave. Nonetheless when the reactions include the chemical species more than one, the above simple method for the solution becomes incapable and the problem is more complex. The paper of Liu (2016) gives a general solution. Applying it to (1)–(8), we will have a formula for the speed of detonation, i.e., eigenvalue of the eigenvalue problem:

(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10)

where $\bar{p}=p_{+\mathrm{\infty }}/p_{0^{+}}$, $\bar{\rho }={\rho }_{+\mathrm{\infty }}/{\rho }_{0^{+}}$ and $\gamma$ is the radio of specific heats. From the formulae (9) and (10), we see that the detonation propagation is indeed relevant to the chemical reaction rates or kinetics. In the coming section, one will see that the formula (9) or (10) plays a key role to determine the speed and structure of detonations.

2.2. Calculational method

In order to obtain the detailed contents of the detonations, we need to numerically solve the problems (1)–(8). It is worth noting that the boundary conditions (6)–(8) are specified at $x=\pm \mathrm{\infty }$. Directly and accurately numerically solving the problem is therefore not easy. Having the integration formula (9) or (10), however, the difficulty can be overcome. With the help of (9) or (10), an algorithm is devised as follows. In the below algorithm, steps (3) and (4) are crucial, since they ensure that the numerical solutions to be found exactly satisfy the boundary conditions (6)–(8).

(0) Assume that thermodynamic state ahead of detonation, ${\rho }_0$, $p_0$ and $T_0$, are known.

(1) Guess a detonation speed, $u_0^0$

(2) Integrate the Equations (1)(1) $\frac{\mathrm{\partial }\left(\rho u\right)}{\mathrm{\partial }x}=0$(1) –(8)(8) $\left(\begin{array}{cccccc}\frac{\mathrm{\partial }u}{\mathrm{\partial }x},& \frac{\mathrm{\partial }\rho }{\mathrm{\partial }x},& \frac{\mathrm{\partial }p}{\mathrm{\partial }x},& \frac{\mathrm{\partial }T}{\mathrm{\partial }x},& \frac{\mathrm{\partial }E}{\mathrm{\partial }x},& \frac{\mathrm{\partial }Y}{\mathrm{\partial }x}\end{array}\right)\left|{ }_{x=-\mathrm{\infty }}\right.=\left(\begin{array}{cccccc}0,& 0& 0& 0& 0& 0\end{array}\right)$(8) .

(3) Calculate a new detonation speed, $u_0$, using Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) (9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10)(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) .

(4) If $\left|u_0-u_0^0\right|<\epsilon$, the calculation stops, otherwise update $u_0^0$ and go to (1) for a new iteration until the convergent criterion is met.

Some readers may think that the Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) ) is trivial and the steps (3) and (4) in the above algorithm are always satisfied for any given $u_0^0$, that is, chemical reaction kinetics has no influence for the selection of detonation speed. Such readers have a misunderstanding on self-sustained detonation. A simple example can assist these readers to understand the role of the Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) ) and correct their misunderstanding. Assuming the given detonation speed in the above algorithm, $u_0^0$, is the speed of C–J detonation, then the chemical reactions have to be so that the flow velocity at the end of the reaction zone is guaranteed to be equal to the local sonic speed. The chemical reactions, however, are controlled by their individual kinetics. Not all the chemical reaction kinetics can ensure that the flow velocity equals the sonic local speed. For example, pathological detonation (see Section 1), in which the flow velocity at the end of heat addition must not be sonic speed, and therefore the speed of C–J detonation must be changed and updated. When applying (9) or (10) to update $u_0^0$, since (9) or (10) is the exact solution for the speed of detonation with any chemical reaction kinetics, we will obtain the corrected speed for the detonation. This example clearly shows the role of reaction kinetics or (9) and (10) in determining detonation propagation mode.

In practical computations, the computational domain is always finite. In order to calculate the eigenvalue problem in this finite domain accurately, a dynamically mesh-adaptive refinement is necessary. In the dynamically mesh-adaptive refinement procedure, the domain is dynamically moved so that it covers all the flame and mesh-adaptive refinement is applied so that the flame zone is meshed by many nodes, say, 5,000 nodes in this work. In addition, the convergence criterion in this work is set as $\left|u_0-u_0^0\right|<\epsilon =1\times {10}^{-5}$.

3. Results and Discussions

The numerical solutions for the eigenvalue problem described in Section 2 are presented in this section, which will show the detailed contents of detonation.

For the sake of theoretic analysis, the first-order Arrhenius kinetics is employed in all the numerical computations:

(11) $\dot{\omega }=AY{e}^{-\frac{E_a}{T}}$(11)

where $\dot{\omega }$, $A$, $Y$ and $E_a$ denote the reaction rate, preexponential factor, mass fraction of reactants and activation energy, respectively. The reader is reminded to note that $A$ and $E_a$ in the Equation (11)(11) $\dot{\omega }=AY{e}^{-\frac{E_a}{T}}$(11) are dimensionless.

The reaction kinetics (11) has two control parameters, $A$ and $E_a$. Their values are taken in the range $\left(\begin{array}{c}0,+\mathrm{\infty }\end{array}\right)$. All the values in the range form the whole possible kinetics, which is called kinetics space. Now we numerically study into the solution for the problems (1)–(8) on the kinetics space.

Here emphasized is that all the equations to be solved in this work are dimensionless, in which the sound speed, density, pressure and temperature at the unreacted states of the reactant mixture, $a_0$, ${\rho }_0$, $p_0$ and $T_0$, are used for the reference velocity, density, pressure and temperature, respectively. Thus, all the results presented in this section are without units.

3.1. Existence of self-sustained detonation propagation modes

The input parameters for the case study are given in Table 1. One can see that the three cases have same combustion heat but different reaction kinetics. The speeds and structures of the detonations corresponding to the input parameters are calculated by the algorithm in Section 2.2. That is, given a speed of detonation, if it is equal to the speed of detonation calculated by (9) or (10), then this detonation is self-sustainable, otherwise simply abandon it and try another new speed of detonation.

Table 1. The input parameters

	Case 1	Case 2	Case 3
Heat of combustion ($q_0$)	4.0	4.0	4.0
Ratio of specific heats ($\gamma$)	1.25	1.25	1.25
Preexponential factor ($A$)	$2\times {10}^5$	$2\times {10}^5$	$2\times {10}^5$
Activation energy ($E_a$)	15	20	25
Re, Pr, M, Sc	$1.0\times {10}^6$, 0.78, 0.8704, 1.0

The calculated results show that not any given speeds can be the eigenvalue for the problems (1)–(8), because of the restriction of the Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) ) (see steps (3) and (4) of the numerical algorithm in Section 2.2). In the other words, when the Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) ) is applied as criterion, those modes that are not self-sustainable will be eliminated and only self-sustained detonation propagation modes remain. As a result, the Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) ) can be used to select the modes of detonation propagations from the upper branch of the Rankine–Huhoniot curve. The selected modes will be self-sustainable.

Instead of the Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) ), if C–J condition is used as the criterion, we will get only C–J detonation. Hence the difference between the concept of self-sustained detonation introduced in this work and the traditional one is only in the criterion to exclude non self-sustainable modes from all the modes at the upper branch of the Rankine-Huhoniot curve. As the Equation (9)(9) $m\equiv {\int }_{0^{+}}^{+\mathrm{\infty }}\rho \left(\dot{\omega }+\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\right)dx$(9) or (10(10) $m\equiv \left(\gamma -1\right){\left[ln\left(\frac{{\bar{\rho }}^{\gamma }}{\bar{p}}\right)\right]}^{-1}{\int }_{0^{+}}^{+\mathrm{\infty }}\frac{\left[h_0^T\cdot \rho \dot{\omega }-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\frac{\gamma }{\left(\gamma -1\right)RePr}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\right]}{T}dx$(10) ) is resulted from the chemical reaction kinetics, the criterion proposed in this work is therefore more reasonable over the C–J condition.

Tables 2–4 list the found modes of self-sustained detonation propagations for each case with the input parameters given in Table 1, using the algorithm in Section 2.2. In the list, the speeds of detonations, i.e., the eigenvalues of the problem, are $M_0$. It is noted that the speeds of detonations are normalized by the reference sonic speed already. In the list, $M_{vonNeumann}$and $M_b$denote the Mach number at von Neumann or post-shock state and Mach number at the end of reaction zone, respectively.

Table 2. Modes of self-sustained detonation for $q_0=4.0$, $E_a=15.0$ and $A=2\times {10}^5$

Mode	$M_0$	$M_{vonNeumann}$	$M_b$
1	3.376743	0.414326	0.526127
2	3.315874	0.417547	0.534179
3	3.086795	0.431175	0.569955
4	2.980451	0.438432	0.590382
5	2.929255	0.442168	0.601356
6	2.830782	0.449843	0.625065
7	2.783512	0.453774	0.637918
8	2.737575	0.457759	0.651532
9	2.347324	0.499725	0.904438

Table 3. Modes of self-sustained detonation for $q_0=4.0$, $E_a=20.0$ and $A=2\times {10}^5$

Mode	$M_0$	$M_{vonNeumann}$	$M_b$
1	3.394151	0.413433	0.523917
2	3.081351	0.431530	0.570932
3	2.999363	0.437093	0.586529
4	2.920474	0.442826	0.603324
5	2.736526	0.457852	0.651858
6	2.668285	0.464100	0.674635
7	2.635349	0.467262	0.686947
8	2.603229	0.470442	0.699970
9	2.571958	0.473634	0.713795
10	2.456424	0.486314	0.779776
11	2.430386	0.489379	0.799976
12	2.405806	0.492349	0.822336
13	2.362338	0.497788	0.876312

Table 4. Modes of self-sustained detonation for $q_0=4.0$, $E_a=25.0$ and $A=2\times {10}^5$

Mode	$M_0$	$M_{vonNeumann}$	$M_b$
1	3.459172	0.410199	0.516000
2	3.343662	0.416058	0.530439
3	3.306379	0.418064	0.535483
4	3.269685	0.420097	0.540652
5	3.198022	0.424242	0.551383
6	3.163033	0.426355	0.556956
7	3.128592	0.428495	0.562676
8	3.094691	0.430661	0.568550
9	3.061322	0.432854	0.574587
10	2.996145	0.437319	0.587177
11	2.964323	0.439591	0.593751
12	2.902183	0.444212	0.607508
13	2.871852	0.446561	0.614717
14	2.812648	0.451331	0.629868
15	2.783767	0.453752	0.637845
16	2.755364	0.456196	0.646117
17	2.727436	0.458662	0.654706
18	2.699984	0.461148	0.663639
19	2.673008	0.463655	0.672947
20	2.646512	0.466179	0.682664
21	2.620500	0.468720	0.692832
22	2.594979	0.471275	0.703499
23	2.569959	0.473841	0.714722
24	2.545456	0.476416	0.726568
25	2.521487	0.478995	0.739122
26	2.498081	0.481573	0.752485
27	2.453114	0.486699	0.782186
28	2.431671	0.489226	0.798905
29	2.411043	0.491710	0.817235

As a comparison, if C–J condition is used for the criterion, the C–J detonation corresponding to the parameters of Table 1 is obtained. The speed of the C–J detonation is 2.327088. Since C–J detonation is independent of the reaction kinetics, there is only one mode of C–J detonation propagation for all the three cases given in Table 1. Comparing it with the results in Tables 2–4, we found that all the speeds of detonations in Tables 2–4 are faster than that of the C–J detonation.

Distribution of the modes of the eigenvalue problems (1)–(8) is mathematically called spectrum distribution. Tables 2–4 show that the spectra exist and distribute with discrete manner. With the increase of the activation energy, the spectrum distribution becomes dense. A further study of the properties of the eigenvalue problem and its spectrum structure is under way.

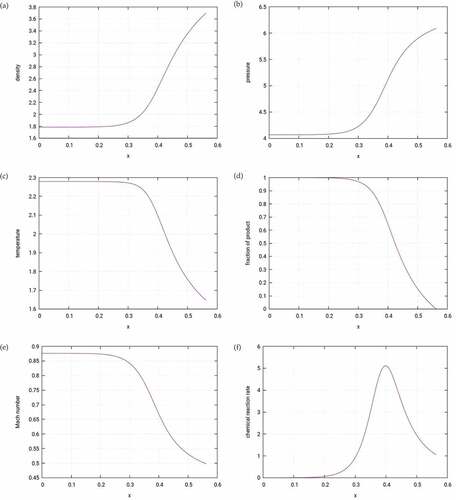
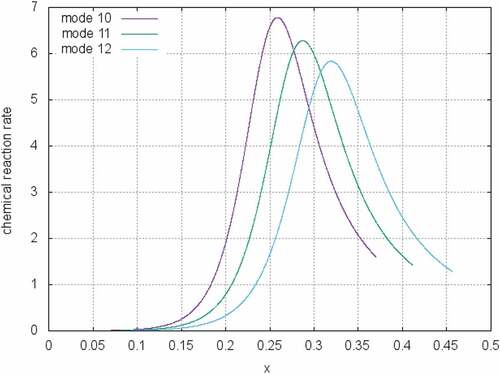
Now we continue to study the structure of the detonation produced by the eigenvalue problem. To this end, the profiles of the density, pressure, temperature and Mach number of the mixture of the mode 13 in the Table 3 are illustrated in Figure 1. In Figure 1, the fraction of product and reaction rate are displayed as well. Seeing the figure, x = 0.562385 is the location of Neumann post-shock point. Passing that point, the chemical reaction starts. Figure 1(a–c,e) shows the mixture flow in the reaction zone. It is seen that the flow completely follows the principle of Rayleigh heat addition flows. Figure 1(d,f) presents the fraction of product and reaction rate. One can see that the reaction velocity increases in the beginning phase. The fastest reaction is reached at about x = 0.4 and then the reaction begins with decaying. The reaction rates of the three modes in Table 3 are plotted in Figure 2. It is observed that with the increase of detonation speeds the reaction zone becomes narrow and the fastest rates (the peak value of reaction rates) are getting faster.

Figure 1. Structures of detonation calculated from the eigenvalue problem, (a) density of mixture, (b) pressures of mixture, (c) temperatures of mixture, (d) Mach numbers in flame, (e) fraction of product, (f) reaction rate

Figure 2. Reaction rates of three detonation propagation modes corresponding to the mode 10, mode 11 and mode 12 in Table 3

3.2. The minimal detonation speeds

Given a kinetics from the kinetics space (11), it is asked what is the minimal eigenvalue of the problems (1)–(8) or the minimal possible detonation speed.

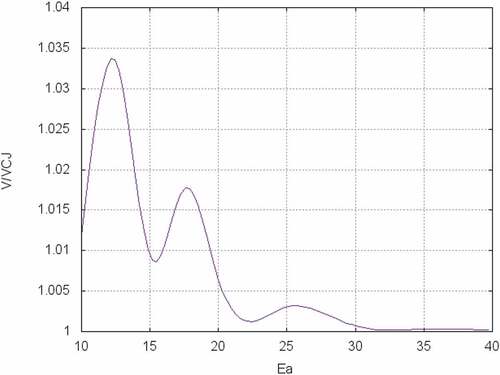
To answer this question, the minimal eigenvalues for $q_0=5.0$, $A={10}^5$ and $E_a=\begin{array}{c}10,12.5,15,17.5,20,22.5,25,27.5,30,32.5,35,40\end{array}$are searched for. The found the solutions, which are normalized by the C–J detonation speed, are plotted in Figure 3. It is seen that all the values are larger than the C–J detonation speed. With the increase of the activation energy, $E_a$, however, the ratio of the eigenvalue to the C–J detonation speed trends to unity. This appears to suggest that the C–J detonation is the solution of the eigenvalue problem in the case at $E_a=+\mathrm{\infty }$

Figure 3. Ratios of the minimal detonation speeds produced by the eigenvalue problem and their C–J detonation speeds, here E_a is the activation energy (${\mathit{q}}_{\mathbf{0}}=5.0$, $\mathit{A}={10}^5$ and $\gamma \mathbf{=}\mathbf{1.25}$)

3.3. Comparison with direct numerical simulations

An alternative approach to find self-sustained detonations is to solve Cauchy problem corresponding to (1)–(5). The Cauchy problem has no boundary condition and describes a developing process of detonation from its ignition to become steady state. The purpose of solving the Cauchy problem is to verify the new theoretic model proposed in this work. The detailed results will be submitted as the second part of this work. Here is an example only.

The speed of the combustion wave propagation simulated by NDS is observed and recorded. The numerical results show when a reaction kinetics is fixed, the simulated combustion wave propagation will trend to a same mode with the same speed whatever ignition energy is applied to initiate the wave propagation. The different ignition energy only influences the ignition processes in the initial phase. After the ignitions, all the simulated cases are approaching to identical.

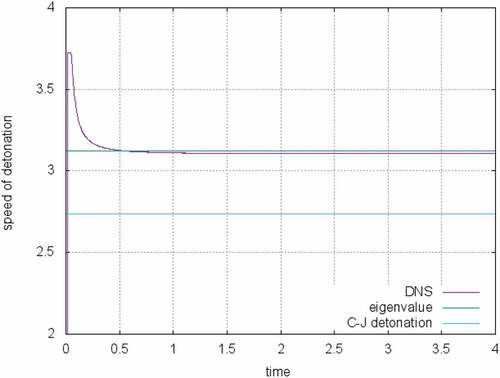
Development of a simulated detonation speed is illustrated in Figure 4. The input parameters for this case is $q_0=5.0$, $A=2\times {10}^5$, $E_a=15$ and $\gamma =\mathrm{1..32}$. As comparison, the detonation speed calculated by the new model proposed in this work and C–J detonation speed are plotted in Figure 4 as well. One can see that the steady detonation propagation mode simulated by DNS is definitely not the C–J detonation. The calculated eigenvalue problem gives multiple modes, one of which is very close to the one of DNS. Therefore, it is a DNS evidence to support the new model introduced in this work.

Figure 4. Comparison of the speed of detonations produced by DNS with the detonation speed predicted by the eigenvalue problem and C–J detonation speed (${\mathit{q}}_{\mathbf{0}}=5.0$, $\mathit{A}=2\times {10}^5$, ${\mathit{E}}_{\mathit{a}}=15$ and $\mathit{\gamma }=\mathrm{1..32}$)

Conclusions

After analysis of the existing theory on self-sustained detonation, author of this work found its deficiencies and therefore it is necessary to develop new theory. To that end, a new theoretic model is introduced, which removes the deficiency. In particular, the self-sustained detonation generated by the new theory is closely related to the chemical kinetics or reaction rates. This is an important difference between the new theory and traditional theory.

Additional information

Funding

The author received no direct funding for this research.

Notes on contributors

Weiming Liu

Weiming Liu is a researcher in computational fluid dynamics (CFD). His research areas mainly lie in three aspects, turbulence modelling, flows in complex geometries such as turbomachinery and flows with complex processes such as chemically reacting flows and phase-changing flows. His research activities are mainly to develop numerical schemes and computational algorithms to obtain high accuracy numerical solutions for the flow problems in these three areas.