Full article: CTLBO: Converged teaching–learning

Formulae display: $MathJax Logo$ ?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.

Abstract

Teaching–learning–based optimization (TLBO) is an algorithm based on the influence of a teacher on the output of learners in a class. This method has shown to be more effective and efficient than other optimizations in finding the maximum solutions. In this paper, a new improved version of TLBO algorithm, called the converged teaching-learning-based optimization (CTLBO), is presented. In fact, it combines a proposed convergence operator with the teacher phase to find better solutions with a higher convergence rate. The method is tested on some benchmark problems and the results are compared with the original TLBO and other popular evolutionary algorithms. Furthermore, the introduced algorithm is used for optimization of fuzzy tracking control of a walking humanoid robot. In elaboration, fuzzy tracking control, which has appropriate membership functions and error indices, is employed in this paper as a promising intelligent approach to control the nonlinear dynamics of a humanoid robot. Summation of integrals of absolute angle errors and absolute control efforts is regarded as the objective function addressed by both TLBO and CTLBO algorithms in the present investigation.

Keywords:

PUBLIC INTEREST STATEMENT

Teaching–learning–based optimization (TLBO) is an algorithm based on the influence of a teacher on the learners in a class. The process of TLBO is divided into two parts. The first part is called “teacher phase”, and the second part is named the “learner phase”. The teacher phase means learning from the teacher, while the learner phase indicates learning through the interaction between learners. In this paper, in order to improve the performance of the TLBO algorithm, the teacher phase is combined with a novel convergence formula to modify the converging process. The method is tested on some benchmark problems and the results are compared with the original TLBO and other popular evolutionary algorithms. The comparative study confirms that CTLBO is a promising global optimization approach and superior other algorithms in terms of accuracy, speed, robustness, and efficiency.

1. Introduction

Optimization is referred to as the process of finding the best answer among other available answers and is used for design of most engineering and economical systems in order to minimize a defined objective. Traditional techniques often fail to solve optimization problems that have many local optima and thus there remains a need for efficient and effective optimization techniques. Continuous research is being conducted into this field, indicating that the nature-inspired meta-heuristic optimization methods are better than the traditional ones. Moreover, evolutionary algorithms are widely used as the most modern heuristic minimization methods. In fact, the optimization algorithms of this special type such as genetic algorithm (Back, Citation1996; Holland, Citation1975) ant colony optimization (Chen, Xiao, Li, Wang, & Huo, Citation2018), bee colony optimization (Karaboga & Akay, Citation2009), particle swarm optimization (Kennedy, Citation2011), championship sports leagues (Kashan, Citation2014), imperialist competitive algorithm (Atashpaz-Gargari & Lucas, Citation2007), team game algorithm (Mahmoodabadi, Rasekh, & Zohari, Citation2018) and the artificial root foraging optimizer (Ma, Zhu, Liu, Tian, & Chen, Citation2015) are known as meta-heuristic population-based algorithms.

The teaching-learning-based optimization algorithm, which is also an evolutionary one, was originally introduced by R.V. Rao in 2011 for mechanical design optimization problems (Rao, Savsani, & Vakharia, Citation2011). It was later extended for continuous non-linear large-scale problems (Rao, Savsani, & Vakharia, Citation2012). In recent years, this algorithm was highlighted mainly due to its strong ability to find the global optimum point. For instance, in 2013, Satapathy et al. proposed a teaching-learning-based optimization, according to the orthogonal design, for solving global optimization problems and called it OTLBO (Satapathy, Naik, & Parvathi, Citation2013a). Afterwards, they introduced a weighted teaching-learning-based algorithm and proved its superiority in comparison with other approaches (Satapathy, Naik, & Parvathi, Citation2013b). In addition, the multi-objective optimization of heat exchangers was proposed by Rao et al. in 2013, using a modified TLBO algorithm (Rao & Patel, Citation2013). More details about multi-objective improved teaching-learning-based optimization algorithm were presented by Rai in 2017 (Rai, Citation2017).

The two main highlighted issues of TLBO are its speed and accuracy to find the global optimum point. Hence, the main contribution and motivation of this paper is the improvement of TLBO via increasing the convergence speed to reach better results with higher accuracy in shorter time. The considered convergence operator, which has a performance probability, is added to the teacher phase of the algorithm. In order to prove the effectiveness and success of the proposed scenario, it was challenged by both mathematical test functions and real world design problems. The numerical results show that not only the new algorithm has a better performance in comparison with the original TLBO, but also it is more accurate than other well-known evolutionary algorithms.

2. Teaching–learning–based optimization

The process of TLBO is divided into two parts. The first part is called “teacher phase”, and the second part is named the “learner phase”. The teacher phase means learning from the teacher, while the learner phase indicates learning through the interaction between learners (Venkata Rao, Citation2016).

2.1. Teacher phase

In this algorithm, a teacher is the learner that has the best level of knowledge. The teacher can only improve the mean performance of class depending on the class capability. Let ${\overset{ˉ}{M}}^{K}$ be the mean situation of the population at iteration $K$ ; and ${\overset{ˉ}{X}}_{t e a c h e r}^{K}$ be the teacher situation, which tries to move ${\overset{ˉ}{M}}^{K}$ towards its own level. Then, a solution is updated according to the difference between mean and teacher situations as follows:

(1)

{\overset{ˉ}{X}}_{d i f f}^{K} = {\overset{ˉ}{r}}_{K} \times ({\overset{ˉ}{X}}_{t e a c h e r}^{K} - T F \times {\overset{ˉ}{M}}^{K})

(1)

(2)

{\overset{ˉ}{X}}_{n e w}^{K + 1} = {\overset{ˉ}{X}}_{o l d}^{K} + {\overset{ˉ}{X}}_{d i f f}^{K}

(2)

where, $T F$ is the teaching factor, and ${\overset{ˉ}{r}}_{K}$ denotes a vector of random numbers in range [0,1]. The value of $T F$ can be either 1 or 2 as below:

(3)

T F = r o u n d [1 + r a n d (0, 1)]

(3)

2.2. Learner phase

In this phase, the learners increase their knowledge through interaction between themselves. A learner learns something new if another learner has more knowledge than it. In mathematical terms, for any ${\overset{ˉ}{X}}_{i}$ , the learner ${\overset{ˉ}{X}}_{j}$ is randomly selected ( $i \neq j$ ), and if $f ({\overset{ˉ}{X}}_{i}) \leq f ({\overset{ˉ}{X}}_{j})$ then:

(4)

{\overset{ˉ}{X}}_{n e w}^{K + 1} = {\overset{ˉ}{X}}_{o l d}^{K} + {\overset{ˉ}{r}}_{K} \times ({\overset{ˉ}{X}}_{j} - {\overset{ˉ}{X}}_{i})

(4)

and in reverse, if $f ({\overset{ˉ}{X}}_{i}) > f ({\overset{ˉ}{X}}_{j})$ then:

(5)

{\overset{ˉ}{X}}_{n e w}^{K + 1} = {\overset{ˉ}{X}}_{o l d}^{K} + {\overset{ˉ}{r}}^{K} \times ({\overset{ˉ}{X}}_{i} - {\overset{ˉ}{X}}_{j})

(5)

3. CTLBO

In order to improve the performance of the TLBO algorithm, the teacher phase is combined with a novel convergence formula to modify the converging process. Let $p \in [0, 1]$ be the convergence probability and $q \in [0, 1]$ be a random number; if $p < q,$ then the following operator should be implemented to generate the new situation from the old one:

(6)

{\overset{ˉ}{X}}_{n e w}^{K + 1} = {\overset{ˉ}{X}}_{o l d}^{K} + {\overset{ˉ}{r}}_{K} \times (C \times {\overset{ˉ}{X}}_{t e a c h e r}^{K} - 2 {\overset{ˉ}{X}}_{o l d}^{K})

(6)

where, $C$ is the social learning factor, inspired by the PSO algorithm (Mahmoodabadi & Ziaei, Citation2019), and represents the attraction of a learner towards the success of the class (teacher). With a small value of this parameter, learners are allowed to move around their personal position, while its large value helps particles to converge to the best solution of the class. Previous researches on PSO algorithm suggest that the best solutions are determined when $C$ is linearly increased, over the iterations, from 0.25 to 1.25 (Mahmoodabadi & Bisheban, Citation2014). In addition, for simplicity, the value of the convergence probability is set at $p = 0.5$ . If the convergence probability condition is not satisfied, then the original teacher phase formulation, i.e. 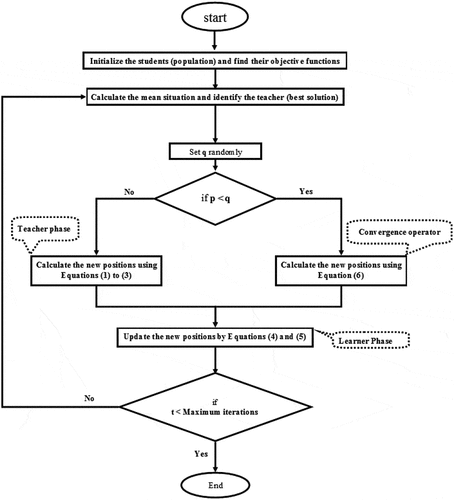EquationEquations (1(1) ${\overset{ˉ}{X}}_{d i f f}^{K} = {\overset{ˉ}{r}}_{K} \times ({\overset{ˉ}{X}}_{t e a c h e r}^{K} - T F \times {\overset{ˉ}{M}}^{K})$ (1) –Equation3(3) $T F = r o u n d [1 + r a n d (0, 1)]$ (3) ), would be used for each student. A flowchart of the proposed algorithm is illustrated in Figure . Besides, Figure delivers a comparison of the population distribution of TLBO and CTLBO for the sphere test function (Table ) with 50 students in three running phases. This simple investigation exhibits the higher convergence speed of CTBLO and its ability to adapt to a time-varying environment.

Figure 1. Flowchart of the CTLBO algorithm

Figure 2. Comparison of the position of students in three stages for the sphere test function, obtained by TLBO and CTLBO algorithms

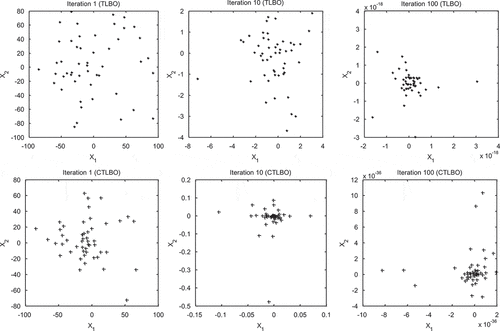
Table 1. Optimization test functions

Display Table

4. Comparison regarding mathematical test functions

In order to evaluate the accuracy and convergence speed of the proposed algorithm, several test functions with different characteristics are employed (Table ). At first, the performance of the proposed algorithm is assessed in respect of solution accuracy through comparison with harmony search algorithm (HSA) (Geem, Kim, & Loganathan, Citation2001), ant colony optimization (ACO) (Dorigo, Citation1992), artificial bee colony optimization (ABC) (Karaboga, Citation2010) and the teaching-learning-based optimization (TLBO) (Rao et al., Citation2012). These assessments are accomplished at same conditions such as the number of function evaluations, population size and dimensions. In this experiment, dimensions (D) of the test functions are taken as 5, 10, 30, 50 and 100 with a maximum number of function evaluations 100,000. The results are presented in Table in terms of the mean and the standard deviation (SD) (EquationEquations (7)(7) $m e a n (F) = \overset{ˉ}{F} = \frac{1}{n} (\sum_{i = 1}^{n} |F_{i} (x)|)$ (7) and (Equation8(8) $S D = \sqrt{\frac{1}{n - 1} (\sum_{i = 1}^{n} {(F_{i} (x) - \overset{ˉ}{F})}^{2})}$ (8) ), respectively) of the solution errors obtained in 30 ( $n = 30$ ) independent runs by each algorithm.

(7)

m e a n (F) = \overset{ˉ}{F} = \frac{1}{n} (\sum_{i = 1}^{n} |F_{i} (x)|)

(7)

(8)

S D = \sqrt{\frac{1}{n - 1} (\sum_{i = 1}^{n} {(F_{i} (x) - \overset{ˉ}{F})}^{2})}

(8)

Table 2. Comparison of results in terms of the mean and the standard deviation for HS, ACO, ABC, TLBO and CTLBO

Download CSV Display Table

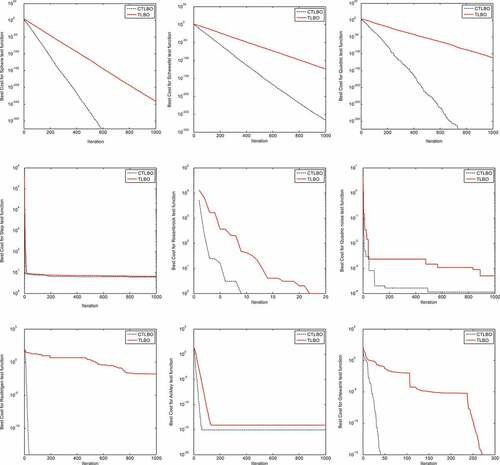
These simulations demonstrate that the CTLBO achieves the global optimum in the optimization of complex multimodal functions: sphere, quadric, step, Rastrrigen and Griewank. Although TLBO outperforms CTLBO and others on Rosenbrok for dimensions 5, 10 and 30; its solutions for other dimensions (50 and 100) are worse than those of the CTLBO. Further, CTLBO can successfully jump out of the local optima on most of the multimodal functions and surpasses all the other algorithms on functions Rastrrigen, Ackley and Griewank. It is noticeable that the global optimum of Schwefel’s function is far away from any of the local optima, and the global best solutions of Rastrigin are surrounded by a large number of local optima (Liang, Qin, Suganthan, & Baskar, Citation2006; Parrott & Li, Citation2006). The ability to avoid being trapped into local optima and achieve global optimal solutions suggests that the CTLBO can indeed benefit from the convergence operator.

Additionally, Figure represents the comparison of the evolutionary processes for four different test functions with respect to convergence characteristics. Generally speaking, these graphs reveal that CTLBO offers a much higher speed than TLBO over the test functions.

Figure 3. Convergence performance of TLBO and CTLBO on the test functions

5. Optimum design of the fuzzy controller

5.1. Dynamics and modeling of the humanoid robot

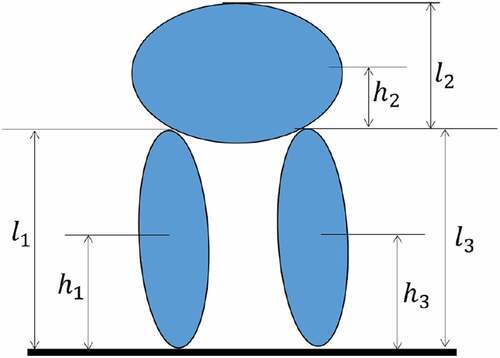
The humanoid robot, walking in the vertical plane, is simulated by means of a three-link model as shown schematically in Figure (Mahmoodabadi, Taherkhorsandi, & Bagheri, Citation2014). The first link is considered the stance leg on the ground; the second link represents the head, arms, and trunk; while the third link refers to the swing leg. These links move freely in the vertical plane, and their parameters are given in Table which is the anthropometric table for a humanoid robot with 171 cm height and 74 kg weight (Mahmoodabadi et al., Citation2014).

Table 3. Anthropometric parameters of the humanoid robot model

Display Table

The Newton-Euler approach is used to obtain the dynamical equations of the model (Mahmoodabadi et al., Citation2014). Moreover, $θ$ ₁ $, θ$ ₂ and $θ$ ₃ are the angles between the first, second and third links and their assumed vertical lines, respectively.

Figure 4. Parameters of the humanoid robot based upon the anthropometric table

5.2. Fuzzy tracking control of the humanoid robot

The proposed fuzzy tracking control is based upon a closed-loop fuzzy system. The state variable vector is chosen as ${[x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}]}^{T} = {[θ_{1}, {\dot{θ}}_{1}, θ_{2}, {\dot{θ}}_{2}, θ_{3}, {\dot{θ}}_{3}]}^{T} .$ The errors, in turn, could be defined as follows:

(9)

e_{i} = x_{i}^{d} - x_{i}, (i = 1, 2, \dots, 6)

(9)

where, $x_{i}^{d} (i = 1, 2, \dots, 6)$ are the desired state values. The new error index parameters introduced for the inputs of fuzzy system would be defined as below:

(10)

E_{i} = \frac{e_{i}}{|x_{i}^{d}| + |x_{i}|} (i = 1, 2, \dots, 6)

(10)

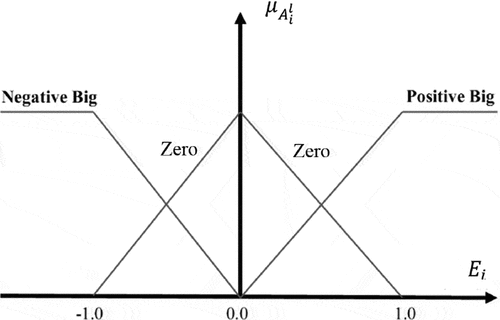
Furthermore, the constructed rules are mentioned in Table ( ${\overset{ˉ}{y}}_{i}$ ); and the considered membership functions are shown in Figure ( $μ_{A_{i}^{l}}$ ). Besides, the inference result $f_{i}$ should be calculated through the product-sum gravity method using the following equation (Mahmoodabadi et al., Citation2014):

(11)

f_{i} = \frac{\sum_{l = 1}^{M} {\overset{ˉ}{y}}_{i}^{l} μ_{A_{i}^{l}} (E_{i})}{\sum_{l = 1}^{M} μ_{A_{i}^{l}} (x_{i})}, i = 1, 2, \dots, 6

(11)

in which, $M$ stands for the number of rules. Finally, the control efforts, $u_{1}, u_{2}$ and $u_{3}$ are obtained by the following equations:

(12)

u_{1} = w_{1} f_{1} + w_{2} f_{2} u_{2} = w_{3} f_{3} + w_{4} f_{4}

(12)

$u_{3} = w_{5} f_{5} + w_{6} f_{6}$

where, $w_{1}, w_{2}, w_{3}, w_{4}, w_{5}$ and $w_{6}$ denote the weighting constants and are usually identified by a trial-and-error process. An appropriate approach to choose these factors is to employ optimization algorithms such as TLBO.

Table 4. Rule modules for the input items

Display Table

Figure 5. Membership function for the fuzzy control of the humanoid robot

5.3. Comparison of the optimal control problem solutions

In order to challenge the performance of the introduced controller, the desired trajectories of joint angles are obtained through using third-degree polynomials as follows:

(13)

x_{1}^{d} = - 0.0165 t^{3} + 0.1246 t^{2} - 0.2711 t - 0.0083

(13)

(14)

x_{2}^{d} = - 0.0147 t^{3} + 0.1132 t^{2} - 0.2519 t + 0.2103

(14)

(15)

x_{3}^{d} = - 0.0492 t^{3} + 0.4122 t^{2} - 1.1035 t + 3.14

(15)

where, $t$ signifies the time. These desired trajectories cause the zero-moment point to move into the stability polygon, and thus provide stability for the robot. In this paper, the sum of integrals of absolute angle errors and absolute control efforts is regarded as the objective function which should be minimized.

(16)

o b j e c t i v e f u n c t i o n = \sum_{i = 1}^{6} \int |e_{i}| d t + \sum_{i = 1}^{3} \int |u_{i}| d t

(16)

In addition, vector [ $w_{1}, w_{2}, w_{3}, w_{4}, w_{5}, w_{6}$ ] contains the selective parameters obtained by the trial-and-error process, which are all positive constants and lie in a general region as $0 < w_{i} < 1000$ ( $i = 1, 2, \dots, 6$ ). Sum of integrals of absolute angle errors and absolute control efforts is a function of this vector’s components. For the present optimization problem, the population size is set at 20, and the maximum iteration is also fixed at 50.

The optimum objective functions and the corresponding design variables acquired by TLBO and CTLBO are illustrated in Table . The corresponding joint angles and velocities are illustrated in Figure , while Figure shows the related errors of the obtained optimum design variables by the CTLBO.

Figure 6. Desired and the tracking trajectories of the joint angles and velocities for the optimal design variables obtained by CTLBO

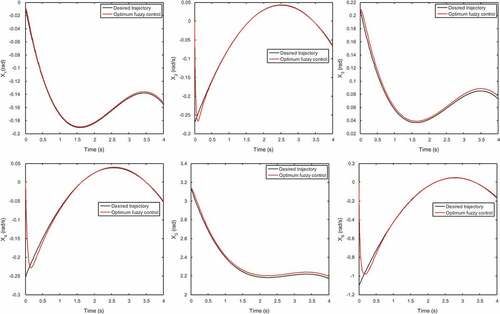
Figure 7. Tracking errors of the joint angles and velocities for the optimal design variables obtained by CTLBO

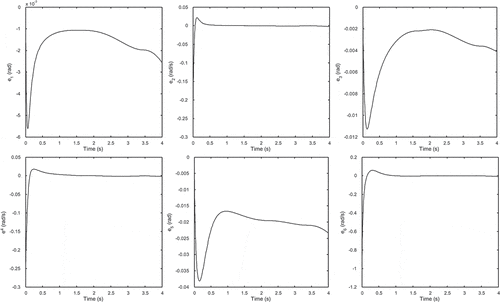
Table 5. Objective functions and design variables acquired by TLBO and CTLBO

Display Table

6. Conclusion

In this study, TLBO has been extended to CTLBO by utilizing two processes. The first has been implemented for increasing the convergence speed, and the second has been applied to avoid being trapped into local optima. The CTLBO has comprehensively been evaluated on several well-known benchmark functions, and the results have been compared with those of other recently introduced optimization algorithms. This analysis has demonstrated the feasibility and efficiency of the proposed strategies in terms of convergence speed, global optimality, solution accuracy and the algorithm reliability. Furthermore, as a real application, the considered algorithms have been utilized for optimum design of a fuzzy controller for a humanoid robot. The numerical results have been depicted to illustrate the feasibility and efficiency of the CTLBO in comparison with TLBO for a nonlinear complicated problem.

Cover Image

Source: The humanoid robot, walking in the vertical plane, is simulated by means of a multi-link model. The first links are considered the stance leg on the ground; the second links represent the head, arms, and trunk; while the third links refer to the swing leg. These links move freely in the vertical plane.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

M. J. Mahmoodabadi

M. J. Mahmoodabadi received his BS and MS degrees in Mechanical Engineering from Shahid Bahonar University of Kerman, Iranin 2005 and 2007, respectively. He received his Ph.D. degree in Mechanical Engineering from the University of Guilan, Rasht, Iran in 2012. He worked for 2 years in the Iranian textile industries. During his research, he was a scholar visitor with Robotics and Mechatronics Group, University of Twente, Enchede, the Netherlands for 6 months. Now, he is an Associate Professor of Mechanical Engineering at the Sirjan University of Technology, Sirjan, Iran. His research interests include optimization algorithms, nonlinear and robust control and computational methods.

Roya Ostadzadeh was born in Lar, Fars, Iran in 1994. She received his BS degree in Engineering Sciences from Sirjan University of Technology, Sirjan, Iran in 2016 .Her research interests include optimization, artificial intelligence and robotics.

References

Atashpaz-Gargari, E., & Lucas, C. (2007). Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. In Proceedings of IEEE Congress on Evolutionary Computation, Singapore.
Google Scholar
Back, T. (1996). Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms. New York, NY: Oxford University Press.
Google Scholar
Chen, L., Xiao, C., Li, X., Wang, Z., & Huo, S. (2018). A seismic fault recognition method based on ant colony optimization. Journal of Applied Geophysics, 152, 1–14. doi:10.1016/j.jappgeo.2018.02.009
Web of Science ®Google Scholar
Dorigo, M. (1992). Optimization, learning and natural algorithms ( PhD thesis). Politecnico di Milano, Italy.
Google Scholar
Geem, Z. W., Kim, J. H., & Loganathan, G. V. (2001). A new heuristic optimization algorithm: harmony search. Simulation, 76, 60–68. doi:10.1177/003754970107600201
Google Scholar
Holland, J. (1975). Adaptation in natural and artificial systems: An introductory analysis with application to biology. Control and Artificial Intelligence. England: University of Michigan Press.
Google Scholar
Karaboga, D. (2010). Artificial bee colony algorithm. Scholarpedia, 5(3), 6915. doi:10.4249/scholarpedia.6915
Google Scholar
Karaboga, D., & Akay, B. 2009. Artificial bee colony (ABC), harmony search and bees algorithms on numerical optimization. In Innovative Production Machines and Systems Virtual Conference, Cardiff, UK.
Google Scholar
Kashan, A. H. (2014). League Championship Algorithm (LCA): An algorithm for global optimization inspired by sport championships (Vol. 16, pp. 171–200). Applied Soft Computing. doi: 10.1016/j.asoc.2013.12.005
Google Scholar
Kennedy, J. (2011). Particle swarm optimization. In C. Sammut, & G. I. Webb (Eds.), Encyclopedia of machine learning (pp. 760–766). Boston, MA: Springer.
Google Scholar
Liang, J. J., Qin, A. K., Suganthan, P. N., & Baskar, S. (2006). Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Transactions on Evolutionary Computation, 10(3), 281–295. doi:10.1109/TEVC.2005.857610
Web of Science ®Google Scholar
Ma, L., Zhu, Y., Liu, Y., Tian, L., & Chen, H. (2015). A novel bionic algorithm inspired by plant root foraging behaviors. Applied Soft Computing, 37, 95–113. doi:10.1016/j.asoc.2015.08.014
Web of Science ®Google Scholar
Mahmoodabadi, M. J., & Bisheban, M. (2014). An online optimal linear state feedback controller based on MLS approximations and a novel straightforward PSO algorithm. Transactions of the Institute of Measurement and Control, 36(8), 1132–1142. doi:10.1177/0142331214537014
Web of Science ®Google Scholar
Mahmoodabadi, M. J., Rasekh, M., & Zohari, T. (2018). TGA: Team game algorithm. Future Computing and Informatics Journal, 3(2), 191–199. doi:10.1016/j.fcij.2018.03.002
Google Scholar
Mahmoodabadi, M. J., Taherkhorsandi, M., & Bagheri, A. (2014). Optimal robust sliding mode tracking control of a biped robot based on ingenious multi-objective PSO. Neurocomputing, 124, 194–209. doi:10.1016/j.neucom.2013.07.009
Web of Science ®Google Scholar
Mahmoodabadi, M. J., & Ziaei, A. (2019). Inverse dynamics based optimal fuzzy controller for a robot manipulator via particle swarm optimization. Journal of Robotics, 2019, 1–10. doi:10.1155/2019/5052185
Web of Science ®Google Scholar
Parrott, D., & Li, X. D. (2006). Locating and tracking multiple dynamic optima by a particle swarm model using speciation. IEEE Transactions on Evolutionary Computation, 10(4), 440–458. doi:10.1109/TEVC.2005.859468
Web of Science ®Google Scholar
Rai, D. P. (2017). Comments on “A note on multi-objective improved teaching-learning based optimization algorithm (MO-ITLBO)”. International Journal of Industrial Engineering Computations, 8(2), 179–190. doi:10.5267/j.ijiec.2016.11.002
Google Scholar
Rao, R. V., & Patel, V. (2013). An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems. Scientia Iranica, 20(3), 710–720.
Web of Science ®Google Scholar
Rao, R. V., Savsani, V. J., & Vakharia, D. (2011). Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Design, 43(3), 303–315. doi:10.1016/j.cad.2010.12.015
Web of Science ®Google Scholar
Rao, R. V., Savsani, V. J., & Vakharia, D. (2012). Teaching–learning-based optimization: an optimization method for continuous non-linear large scale problems. Information Sciences, 183(1), 1–15. doi:10.1016/j.ins.2011.08.006
Web of Science ®Google Scholar
Satapathy, S. C., Naik, A., & Parvathi, K. (2013a). A teaching learning based optimization based on orthogonal design for solving global optimization problems. Springer Plus, 2(1), 130. doi:10.1186/2193-1801-2-130
PubMedGoogle Scholar
Satapathy, S. C., Naik, A., & Parvathi, K. (2013b). Weighted teaching-learning-based optimization for global function optimization. Applied Mathematics, 4(3), 429. doi:10.4236/am.2013.43064
Google Scholar
Venkata Rao, R. (2016). Teaching learning based optimization algorithm and its engineering applications. Switzerland: Springer. ISBN: 9783319227313.
Google Scholar

CTLBO: Converged teaching–learning–based optimization