Investigation of the interfacial instability in a non-Boussinesq density stratified flow using linear stability theory

Abstract

The main goal of this study is investigating the interfacial instability in the shear density stratified flow in non-Boussinesq regime using linear stability theory. In the current study, the pseudospectral collocation method employed Chebyshev polynomials is applied to solve two coupled eigenvalue equations. Using the linear stability analysis in the temporal framework, the effects of various parameters on the flow instability have been studied. Obtained results in the present paper are showing that increasing the bed slope, the flow becomes more unstable; also at R = 1, Kelvin–Helmholtz and Holmboe waves appear. Furthermore, Holmboe waves were not observed only at θ = 0. This study shows that at R ≠ 1, in addition to observing Kelvin–Helmholtz and Holmboe waves with higher growth rates, by increasing the bed slope, the growth rate and the number of Kelvin–Helmholtz modes increase. With an improved understanding of the instability mechanisms and features with including the non-Boussinesq effects, one can confirm some of the previous experimental results and offer new indications to observations that have not been fully explained. In designing laboratory experiments to observe Holmboe waves and estimating their wavelengths and phase speeds the results of present paper are also could be useful.

Keywords:

• Interfacial instability
• linear stability analysis
• stratified shear flows
• non-Boussinesq

PUBLIC INTEREST STATEMENT

The mixing between two or more fluids can influence both of them. In oceans, lakes and seas this phenomenon occurs mainly due to waves at the interface of the flows. Some of these waves have unique features and can be predicted by means of some theoretical methods (called linear stability). In this paper, some of the interfacial waves in non-Boussinesq regime (one of the main assumptions in theories has been ignored in the current paper to make the theory closer to the reality) is investigated and the parameters affect these waves are indicated.

1. Introduction

Stratified flows are important in the study of the atmosphere and oceans. Gravity or density currents are the most frequent among the atmosphere and ocean streams which are a subset of stratified flows. These flows are caused by the force of gravity and its effect on the density difference of the flow relative to the surrounding fluid or the environment. The density difference could be due to temperature differences (such as lakes or atmosphere), salt concentration (such as the estuary of the rivers, the sea or ocean), particles (like turbidity currents) or other materials. Gravity currents can move below, above or through the surrounding fluid. The density difference between the two fluids are the main cause of this kind of flows (Middleton, 1993).

Interfacial instabilities affect the behavior of stratified flows. An improved understanding of the interfacial instabilities in stratified shear flows can aid to forecast exchange flow rates and vertical mixing rates. The importance of this forecasting is because of its control on the vertical transfer of salt, heat, nutrients, pollutants and momentum in stratified flows. A noteworthy quantity of mixing in the interior ocean and atmosphere is produced by the formation of shear instabilities in density stratified flows (Nourmohammadi, Afshin, & Firoozabadi, 2011). It is probable to predict instabilities using linear stability analysis. The results of such tool provide a theoretical estimation of initial instability frequency or wavelength, the instability growth rate, knowledge that is serious for understanding and controlling shear flows (Khavasi & Firoozabadi, 2018, 2019).

The shearing between the layers causes interfacial instability in stratified shear flows. However, the density difference in the flow plays also a significant role on determination of the type of instability. It has been found that two types of instability can usually occur in these flows; the most frequently observed and investigated is Kelvin–Helmholtz instability which has major role on mixing of the fluids. This instability is characterized by its overturning billowing patterns, cats-eye structure and its capability to mix effectually. The chance of occurring Kelvin–Helmholtz instability is when the stratification is not strong and the thickness of density transition layer between two layers of different densities is comparable to the shear layer thickness. This mode of instability travels at approximately average velocity between the two layers. Another mode of instability known as Holmboe. This mode seems when the stratification is strong and the density transition layer is much thinner than that of the shear layer. It has been shown in theoretical and numerical works that this mode of instability consists of two traveling waves in opposite directions and the same growth rate (the imaginary part of wave speed). Both theoretical and experimental investigations have been found that the speed of Holmboe waves’ grows with Richardson number (Khavasi & Firoozabadi, 2019).

In contrast with Kelvin–Helmholtz mode, Holmboe modes are not stabilized again as stratification increases. One of the main features of Holmboe instability is cusping waves fairly similar to surface water waves in which mixed fluid builds up at the cusp of Holmboe wave. Finally, mixed fluid is expelled as a wisp into the upper (lower) layer. Unlike Kelvin–Helmholtz instability, Holmboe instability does not cause complete overturning of the density interface. It was found that Holmboe instabilities grow more slowly than Kelvin–Helmholtz instabilities, the total amount of mixing may be comparable, though. (Holmboe, 1962; Khavasi & Firoozabadi, 2019).

Instability at the interface of shear flows has been studied by many researchers, including Hazel (Hazel, 1972), Smyth and Winter (Smyth & Winters, 2003), Alexakis (Alexakis, 2009), Rahmani (Rahmani, Lawrence & Seymour 2011), Khavasi et al. (Khavasi & Firoozabadi, 2018, 2019) numerically and experimentally, and also, Haigh and Lawrence (Haigh & Lawrence, 1999), Ortiz et al. (Ortiz, Chomaz, & Loiseleux, 2002), Alexakis (Alexakis, 2005) and Barros and Choi (Barros & Choi, 2014) analytically studied the effect of various parameters on characteristics of Kelvin–Helmholtz or Holmboe instabilities. These researchers studied the effect of changing Richardson number or changing the ratio of shear layer thickness to density layer thickness, the effect of presence of boundaries, slope effect, mechanism of instability, and different appeared modes of instabilities and instabilities in different geometries.

Khavasi et al. (Khavasi, Firoozabadi, & Afshin, 2013) proved that viscosity stabilizes the flow where its effect is not the same in different wavelengths. Lin et al. (Lin, Xia, & Bao, 2014) studied hydrodynamic instability of nanofluids in a channel by means of linear stability analysis. They found that the existence of particles makes the flow more stable, however, they cannot completely make the current stable. Senatore et al. (Senatore, Davis, & Jacobs, 2015) investigated the effect of non-uniformity in bulk particle mass loading on the linear development of a particle-laden shear layer by means of a stochastic Eulerian-Eulerian model. They showed that non-uniform loading of small-inertia particles (Stokes number < 0.2) may destabilize the inviscid mixing layer development. Amini et al. (Amini, Khavasi, & Asadizanjani, 2016) used linear stability method to study the effect of particle on density current. Their two-way coupled approach showed that the increasing number of particles makes the current more stable. Barmak et al. (Barmak, Gelfgat, Ullmann, & Brauner, 2017) examined the applicability of the Squire’s transformation for stability analysis of stratified two-phase flow in horizontal and inclined channels. They proved that 2D perturbations are the critical ones also for the case of inclined channel. Oladosu et al. (Oladosu, Hasnain, Brown, Frigaard, & Alba, 2019) studied experimentally density-stable displacement flow of immiscible fluids in inclined pipes. They found that compared to the previously studied miscible limit observe behavior at the interface between the two fluids where the displaced fluid stays “pinned” to the lower wall of the pipe upon pumping the displacing one.

In the mentioned researches, Boussinesq approximation is applied. Barros and Choi (Barros & Choi, 2011) investigated the stability of shear density stratified flow by means of linear stability in non-Boussinesq regime. They used linear profiles for density and velocity to analytically solve the eigenvalue equations.

In some cases of real flows the density difference is such that Boussinesq assumption is not valid furthermore, so, it could be useful to investigate the flow behavior and its instability in non-Boussinesq regime. In this study, the interfacial instability in the non-Boussinesq stratified density current was evaluated using linear stability theory. Non-Boussinesq stability of density currents have not been studied yet by use of linear stability theory applying Chebyshev polynomials.

2. Materials and methods

The aim of the present study was to obtain the instability characteristics, such as unstable waves appeared in various Richardson numbers, on the inclined substrate in the non-Boussinesq stratified density flow. To study the behavior of the flow, growth rate and phase speed in terms of the effective parameters in the flow such as Richardson number, R ($={\delta }_{\mathrm{v}}/{\delta }_{\rho }$ where ${\delta }_{\mathrm{v}}$ is the velocity and ${\delta }_{\rho }$ is the density layer thickness) and bed slope have been studied. Also, the flow behavior at high Richardson numbers (Richardson of 0 to 5, in the previous papers of the authors; for example (Khavasi & Firoozabadi, 2018, 2019; Khavasi et al., 2013); it has been seen that some new modes of instability can be found in higher values of Richardson number) will be examined and the effect of slope will be studied as well.

Figure 1 shows a schematic of the studying flow. This two-dimensional flow is assumed to include continuous layers and without diffusion.

Figure 1. Schematic of the problem under study with velocity profiles U (y) and the base concentration of ρ (y) of a two-layer flow. δ_ρ is the density layer thickness and δ_V is the shear layer thickness. g is gravitational acceleration and θ is the bed slope

According to the linear stability theory in the process of obtaining the equations, the multiplication of two perturbations and terms with derivatives higher than the second order of perturbations are neglected. In addition, it is assumed that the base flow is parallel, i.e. the velocity perpendicular to the surface, V, equals zero, and velocity components as well as the concentration of the base flow are only functions of the direction perpendicular to the flow and do not change in the transverse direction.

In this study, the Boussinesq assumption has been ignored and the following normal modes have been used for the stream function of velocity and density fluctuations terms:

(1) $\begin{array}{rl}& \psi \left(x,y,t\right)=\mathrm{\Re }\left[\phi \left(y\right)e^{ik\left(x-ct\right)}\right]\\ & \rho \left(x,y,t\right)=\mathrm{\Re }\left[\phi \left(y\right)e^{ik\left(x-ct\right)}\right]\end{array}$(1)

Where $\mathrm{\Re }$ represents the real part. $\psi$ is the stream function, ϕ is the complex amplitude of the stream function for a normal mode with real wavenumber k. c is the complex phase speed and also $i=\sqrt{-1}$. x and y directions are defined in Figure 1.

As a result, in order to investigate the instability of the stratified flow, the final non-dimensional equations become as Equations 2(2) $\begin{array}{rl}& \left[\left(u-c\right)\left({\phi }_{yy}-{\alpha }^2\phi \right)\right]-u_{yy}\phi +\frac{{\varphi }_y}{{\rho }_0}\left[\left(u-c\right){\phi }_y-\phi u_y\right]=\frac{J}{{\rho }_0}\left[\varphi cos\theta +\frac{{\varphi }_y}{i\alpha }sin\theta \right]+\\ & \frac{1}{i\alpha \mathrm{R}\mathrm{e}}\left[{\phi }_{yyyy}-2{\alpha }^2{\phi }_{yy}+{\alpha }^4\phi \right]\end{array}$(2) and 3(3) $\left(u-c\right)\phi ={\rho }_y\varphi$(3) :

(2) $\begin{array}{rl}& \left[\left(u-c\right)\left({\phi }_{yy}-{\alpha }^2\phi \right)\right]-u_{yy}\phi +\frac{{\varphi }_y}{{\rho }_0}\left[\left(u-c\right){\phi }_y-\phi u_y\right]=\frac{J}{{\rho }_0}\left[\varphi cos\theta +\frac{{\varphi }_y}{i\alpha }sin\theta \right]+\\ & \frac{1}{i\alpha \mathrm{R}\mathrm{e}}\left[{\phi }_{yyyy}-2{\alpha }^2{\phi }_{yy}+{\alpha }^4\phi \right]\end{array}$(2)

(3) $\left(u-c\right)\phi ={\rho }_y\varphi$(3)

where all parameters are dimensionless and $J$ is the Richardson number which will play an important role in analyzing the results. u(y) and ρ(y), are the non-dimensional background flow velocity and density profiles and will be defined in the following section. α= α_r+iα_i where α_r and α_i are the (non-dimensional) wavenumber and the spatial amplification rate, respectively. Also, ω= ω_r+iω_i where ω_r and ω_i are the (non-dimensional) frequency and the temporal amplification rate of the perturbation, respectively. y subscript is the differentiation with respect to normal direction. In the above equations c= ω/α=c_r+ic_i is the complex wave speed and $J=\sigma g{\delta }_v/V^2$ is the bulk (local) Richardson number (where $\sigma$ is a typical density measure). φ and ϕ represent the complex amplitude of the density and stream function disturbances. The following boundary conditions are imposed

$\varphi (\pm \mathrm{\infty })=\phi (\pm \mathrm{\infty })=\varphi \prime (\pm \mathrm{\infty })=\phi \prime (\pm \mathrm{\infty })=0$

These equations can be solved by both numerical and analytical methods. In this study, these equations are discretized with pseudo-spectral collocation using Chebyshev polynomials ignoring the Boussinesq assumption (Khavasi et al., 2013).

For unlimited environments, Rational Chebyshev functions are used, which can be written as follows:

(4) $T{B}_n\left({\hat{y}}_i\right)=T_n\left(y_i\right)$(4)

where $TB$and $T$are rational and (normal) Chebyshev polynomials. And the change of variables:

(5) $\stackrel{\wedge }{{\mathrm{y}}_{\mathrm{i}}}=\beta {\mathrm{y}}_{\mathrm{i}}/\sqrt{1-}{\mathrm{y}}_{\mathrm{i}}^2{\mathrm{y}}_{\mathrm{i}}\in ,\left(-\mathrm{\infty },\mathrm{\infty }\right),\stackrel{\wedge }{{\mathrm{y}}_{\mathrm{i}}}\in \left[-1,1\right]$(5)

is used, where $\beta$ is the weight function. For$\beta <1$, the maximum density occurs in the origin. Also, the velocity and gradient concentration is maximum at the origin, where there is the smallest gridding, so $\beta <1$ is a good choice for the problem of study. At $0.2<\beta <0.3$, the most accurate responses with the lowest cost of computing are obtained (Khavasi et al., 2013), which in the present study, the same solution has been coded and used applying non-Boussinesq conditions, to solve the equations.

3. Results, discussion, and analysis

The main novelty of this study is using linear stability theory employing the pseudospectral collocation method with Chebyshev polynomials in temporal framework to inspect the hydrodynamic instability characteristics of the shear density stratified flow in non-Boussinesq regime. In this study, the effect of various parameters such as slope, wave number and the ratio of thickness of the shear layer to density layer concentration (R) on the interfacial instability in the stratified flow, will be discussed by solving ‏Equations (2(2) $\begin{array}{rl}& \left[\left(u-c\right)\left({\phi }_{yy}-{\alpha }^2\phi \right)\right]-u_{yy}\phi +\frac{{\varphi }_y}{{\rho }_0}\left[\left(u-c\right){\phi }_y-\phi u_y\right]=\frac{J}{{\rho }_0}\left[\varphi cos\theta +\frac{{\varphi }_y}{i\alpha }sin\theta \right]+\\ & \frac{1}{i\alpha \mathrm{R}\mathrm{e}}\left[{\phi }_{yyyy}-2{\alpha }^2{\phi }_{yy}+{\alpha }^4\phi \right]\end{array}$(2) and 3(3) $\left(u-c\right)\phi ={\rho }_y\varphi$(3) ). To solve instability equations in linear instability method, the velocity profiles and concentration of the base flow should be determined. The hyperbolic tangent profiles are of conventional profiles to choose for velocity and concentration of the base flow. All the profiles have been achieved based on experimental data and curves crossing these results, and with regard to ease of application of hyperbolic tangent profiles (as well as the possibility of comparison with previous researches), these profiles will be used for velocity (u (y)) and concentration (ρ (y)) of the base flow.

$u\left(y\right)=tanh\left(y\right)\rho \left(y\right)=tanh\left(Ry\right)$

In which tanh is hyperbolic tangent. It should be noted that linear stability theory in temporal framework has some limitations that make its results somehow different from reality: the main is the assumption of linearization (eliminating higher-order terms in obtaining the instability equations) and the other limiting assumption is using normal modes which is not exactly the same as the real perturbations. Using temporal framework is also not exactly realistic, because, it assumes the growth of perturbations just in time.

3.1. The effect of slope on the stratified flow instability

To investigate the effect of slope, the equation governing the flow instability is obtained from the Equations (2(2) $\begin{array}{rl}& \left[\left(u-c\right)\left({\phi }_{yy}-{\alpha }^2\phi \right)\right]-u_{yy}\phi +\frac{{\varphi }_y}{{\rho }_0}\left[\left(u-c\right){\phi }_y-\phi u_y\right]=\frac{J}{{\rho }_0}\left[\varphi cos\theta +\frac{{\varphi }_y}{i\alpha }sin\theta \right]+\\ & \frac{1}{i\alpha \mathrm{R}\mathrm{e}}\left[{\phi }_{yyyy}-2{\alpha }^2{\phi }_{yy}+{\alpha }^4\phi \right]\end{array}$(2) and 3(3) $\left(u-c\right)\phi ={\rho }_y\varphi$(3) ) assuming $\frac{1}{Re}\to 0$ (to eliminate the effect of viscosity and just investigate the slope influence).

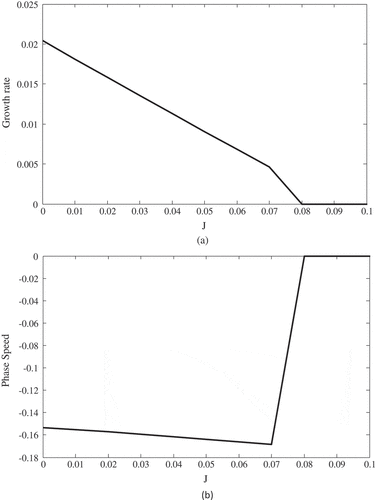
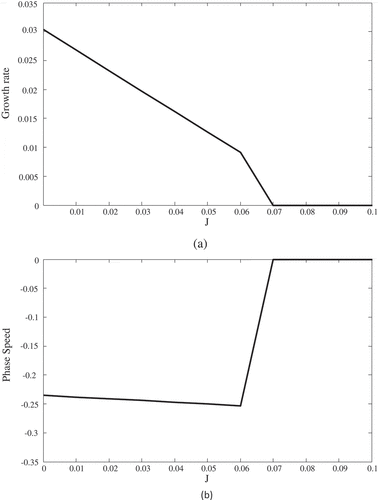
Changes in the growth rate and the phase speed at ${\alpha }_{\mathrm{r}}=$ 0.3 and ${\alpha }_{\mathrm{r}}=$ 0.5 in terms of the J, at slopes 0 and 0.2, are shown, respectively, in Figures (2–5). In the figures, the horizontal axis indicates the Richardson number and vertical axis has been represented in two sections of phase speed (c*_r= α_rc_r) and growth rate (ω_i). Also, the solid lines of the graph is indicating the first mode and the dashed lines show the second mode.

Figure 2. Changes of (a) growth rate and (b) phase speed for ${\alpha }_r=0.3$ and $\theta =0$

In Figure 2, it can be seen that the flow becomes stable at J = 0.08.

Figure 3. Changes of (a) growth rate and (b) phase speed (the legend is same as part a) for ${\alpha }_r=0.3$ and $\theta =0.2$. Solid line is the first mode (Kelvin–Helmholtz) and dotted line is the second mode (Holmboe) of instability

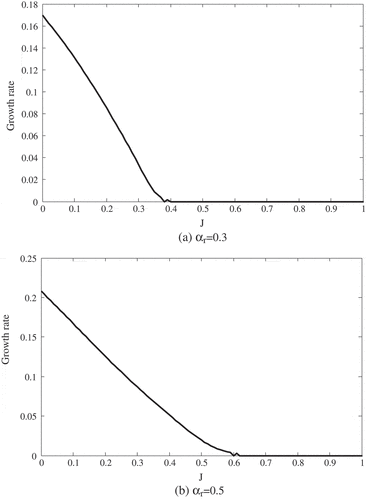
In Figure 3, first, the appeared Kelvin–Helmholtz waves become stable at J = 0.1 and then, Holmboe waves appear at J = 0.4. By increasing J, at about J = 0.4, the second mode of Kelvin–Helmholtz waves appears.

Figure 4. Changes of (a) growth rate and (b) phase speed for ${\alpha }_r=0.5$ and $\theta =0$

Figure 4 shows that the flow becomes stable at J = 0.07. In this case, only Kelvin–Helmholtz waves appears, and Holmboe waves cannot be seen.

Figure 5. Changes of (a) growth rate and (b) phase speed for ${\alpha }_r=0.5$ and $\theta =0.2$

In Figure 5, first, the appeared Kelvin – Helmholtz waves gets stable and then, at J = 0.6 the Holmboe waves appear and grow at higher Richardson numbers.

It can be concluded that in the non-Boussinesq conditions, at R = 1 and θ = 0, the Holmboe waves does not appear. The figures also show that in a determined Richardson number, by increasing the slope, the growth rate will be higher. Also, at each slope, the growth rate decreases with increasing J, i.e. the flow is going to be stable, but the Kelvin–Helmholtz waves may appear again after becoming stable.

Figure 5 shows that the second mode of Kelvin–Helmholtz also can appear. From this figure, it is clear that by increasing the slope, the growth rate of unstable range increases. Using the physics governing the shear flows, the effect of slope on the flow’s instability can be explained as follows: since the slope, reduces the buoyancy force component (g’cosθ) which stabilizes the flow, and increases the component accelerating the flow (g’sinθ), eventually results in increasing the flow’s instability.

3.2. Changes of R at different slopes

In the previous section, the effect of slope was studied at R = 1. Since the ratio of velocity thickness to density layer thickness are not equal in general and in reality (i.e., usually R ≠ 1), so it is better to check the case R ≠ 1 at different slopes. In Figures 6 and 7, the graphs of the growth rate are shown for ${\alpha }_r=0.5$ and $\theta =0.2$.

Figure 6. Temporal growth rate in terms of Richardson number for R = 3 and Ө = 0

Figure 6 shows that at R = 3, the flow becomes stable in ${\alpha }_r=0.3$ at J ≅ 0.38 and ${\alpha }_r=0.5$ at J ≅ 0.6. In this case, similar to the R = 1 case only Kelvin–Helmholtz waves appear.

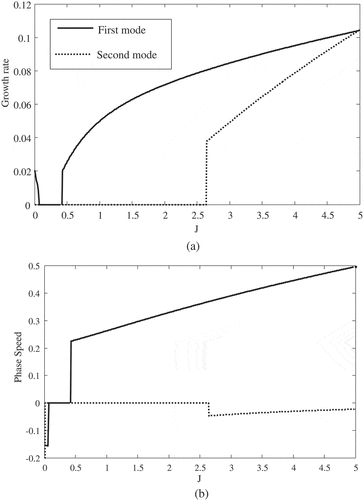
Figure 7. Time growth rate in terms of Richardson number for R = 5 and Ө = 0.2.. Solid line is the first mode (Kelvin–Helmholtz) and dotted line is the second mode (Holmboe) of instability. The legend is same as Figure 3

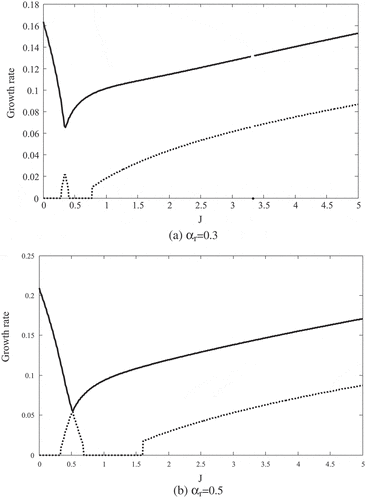
Figure (7(a)) shows that the appeared Kelvin–Helmholtz wave tends to become stable, but changes its behavior at J ≅ 0.3 and suddenly its growth rate increases dramatically. In the second mode, the Kelvin–Helmholtz waves are merged and changed at J ≅ 1.6, and Holmboe wave appears. In Figure (7(b)) primarily, the first and second modes of kelvin–Helmholtz reach to each other at J ≅ 0.5 and the second mode stabilizes, and re-appears at J ≅ 1.6. Also in the first mode, first the Kelvin–Helmholtz wave appears and then, the Holmboe wave appears at J ≅ 3.2.

These figures show that by increasing the slope, as mentioned in the previous section, the growth rate increases and the stability areas for non-zero slope are different from the areas with a slope of zero.

It should be noted that with increasing wave number, on the same conditions, the stability increases. Reducing the chances of the Holmboe mode presence and increasing the chances of the presence of the Kelvin–Helmholtz mode in the same α_r, J and R, by increasing the slope can be explained as follows: the Holmboe mode occurs in conditions where the Richardson number is high, and the Kelvin–Helmholtz mode is created when the Richardson number is small, this means that if the ratio of buoyancy force to inertia force is remarkable, the Holmboe mode appears, and if the ratio of inertial force to buoyancy force be considerable, the Kelvin–Helmholtz mode emerges.

4. Conclusion

Using linear stability method and normal modes, first, the instability equations were obtained for a double-layered flow with density layer and on an inclined bed. Using these equations, the flow stability was evaluated in the temporal framework. To solve the equations, the pseudo-spectral method with Chebyshev polynomials is used. The base velocity and concentration profiles were selected as hyperbolic tangent. The results of the present paper shows that instability characteristics of the stratified flow considering the non-Boussinesq regime is different from the cases with Boussinesq approximation (Khavasi et al., 2013). The results of the present paper can be useful in the prediction of the unstable modes in reality and designing experiments in which the Boussinesq approximation is meaningless. It is also shown that different parameters can affect the stability features of the stratified shear layers. The precise prediction of unstable waves can help the better understanding of influential parameters on mixing and entrainment.

Parametric study in the temporal framework is showed that:

• At R = 1 by increasing the slope, the range of the flow instability and the growth rate of the unstable mode increases. In terms of Boussinesq assumption, only Kelvin–Helmholtz waves appeared (Holmboe Waves are not seen), but in this study, the Holmboe is not appeared only at θ = 0.

• In R ≠ 1 by increasing the slope, the growth rate of Kelvin–Helmholtz mode increases. Meanwhile, the number of Kelvin–Helmholtz modes also increases.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Ehsan Khavasi

This paper is a part of the project of studying stratified shear layers or more specifically gravity currents. As interfacial instability can have significant effect on the behavior of the current, so, it is studied in the present paper. The corresponding author (Ehsan Khavasi) is now working on numerical and experimental modeling of gravity currents in which interfacial instability always occurs and influential.