GMRES based numerical simulation and parallel implementation of multicomponent multiphase flow in porous media

Abstract

This article considered the numerical simulation of multicomponent multiphase flow in porous media. The resulting system of nonlinear equations linearized by the Newton-Raphson method and solved with the iterative Generalized minimal residual method (GMRES) algorithm. To achieve better convergence, we used the ILU(0) preconditioner to the GMRES algorithm. As a result, we used a completely implicit scheme called the Newton-ILU0-GMRES algorithm to solve the problem of interest. Based on the obtained sequential algorithm, we implemented a parallel algorithm using Message Passing Interface (MPI) technology. Additionally, we made comparisons between the parallel program of the presented algorithm and the parallel program using the ready-made Portable Extensible Toolkit for Scientific Computation (PETSc) library. We developed an MPI parallel algorithm and tested it on the MVS-10P supercomputer of the Interdepartmental Supercomputer Center of the Russian Academy of Sciences.

Keywords:

• multicomponent multiphase flow
• Newton-Raphson method
• GMRES
• MPI technology

PUBLIC INTEREST STATEMENT

Reducing the cost of oil production is an urgent task for every oil company. For this purpose, companies use models of the production process to identify optimal conditions. During modelling, multiphase liquid flows into porous media, and taking into account the multicomponent nature of hydrocarbon phases allows one to obtain more accurate calculation results. Increasing the accuracy of these calculations leads to an increase in the runtime. This problem is solved by the development of parallel algorithms that will run on supercomputers. In this article, the authors consider the development of a parallel algorithm to solve such oil problems.

1. Introduction

The development of high-performance computing (HPCwire: Global News on High Performance Computing, 2020) enables the solving of major scientific and applied problems in various fields. For example, supercomputers can be loaded with weather and climate forecasting tasks, acoustic tasks, hydrodynamics, medical preparations manufacturing tasks, and biological research (Akhmed-Zaki et al., 2017; Farrukh, 2018; Yeshmukhametov et al., 2017).

Using supercomputers can significantly accelerate the solution of problems when using numerical methods. One of these tasks is forecasting oil and gas production in specific oil and gas fields. Modelling multicomponent multiphase fluid (oil and gas) flow in porous media (in oil reservoirs) is relevant and, at the same time, a complex problem of hydrodynamic simulation. To solve such problems, various methods and schemes are used (Aceto et al., 2006; Ahmed, 2006; Borisov et al., 2013; Chen, 2006; Chen et al., 2006; Edwards et al., 2018; Javidi & Ahmad, 2013; Imankulov et al. 2018; Zheng & Yin, 2014), some of which are iterative methods for solving linear systems (Lacroix et al., 2003; Mittal & Al-Kurdi, 2002; Vabishchevich & Vasilyeva, 2011; Wang et al., 2013).

To speed up scientific calculations, various technologies are used, such as Open Multi-Processing (OpenMP) (Iryanto & Gunawan, 2017; Werneck et al., 2016), Message Passing Interface (MPI) (Akhmed-Zaki et al., 2019; Pannala et al., 2003), Open Computing Language (OpenCL) (Khramchenkov & Khramchenkov, 2018), Compute Unified Device Architecture (CUDA) (McClure et al., 2014; Zaza et al., 2016) and fragmented programming (Akhmed-Zaki et al., 2019; Malyshkin & Perepelkin, 2011).

In this paper, the equation system of multicomponent multiphase flow in porous media, which is linearized by the Newton-Raphson method is solved, and at each iteration for solving the linear equation system, the generalized minimal residual method (GMRES) (Saad & Schults, 1986) is used with the ILU(0) preconditioner. The method, called Newton-ILU(0)-GMRES, is the combination of the Newton-Raphson method and GMRES algorithm with ILU0 preprocessing to develop a reliable and efficient method. A parallel implementation of the considered problem is realized by the MPI programming interface, which is the main tool in the development of parallel programs for supercomputers. In the future, a project to develop an active knowledge management system to solve the multicomponent fluid flow problem is planned (Akhmed-Zaki et al., 2019). The result of this project will be a system that will automatically choose the a solution method, one of which is the method described in this article, for practical problems.

2. Mathematical model and numerical method

The one-dimensional problem of compositional fluid flow in a porous medium is considered. Compositional flow involves multiple components, and the one-dimensional problem of compositional fluid flow in a porous medium is considered. Compositional flow involves multiple components and three phases, and there is a mass transfer between the vapour and liquid phases. The model has the following assumptions:

• the flow process is isothermal,

• the components form at most three phases (e.g., vapour, liquid, and water),

• there is no mass interchange between the water and the hydrocarbon (vapour, liquid) phases.

• the diffusion/dispersion effect is negligible.

We describe the compositional model that has been widely used in the petroleum industry because the general compositional model is very difficult to solve.

At point A, water is pumped in, which, due to the difference in pressure through porous media, moves to point B. Liquid/vapor is pumped from point B as shown in Figure 1. The distribution of water, vapour, and liquid in the porous medium should be calculated.

Figure 1. Layout diagram.

Let us consider a mathematical model of the multicomponent flow of three-phase fluid in a porous medium. We write the law of conservation of mass for each component (Chen, 2006; Chen et al., 2006):

(1) $\frac{\mathrm{\partial }\left(\varphi {\xi }_{\omega }{S}_{\omega }\right)}{\mathrm{\partial }t}+\mathrm{\nabla }\cdot \left({\xi }_{\omega }{u}_{\omega }\right)=q_{\omega },\frac{\mathrm{\partial }\left(\varphi \left[x_{mo}{\xi }_o{S}_o+x_{mg}{\xi }_g{S}_g\right]\right)}{\mathrm{\partial }t}+\mathrm{\nabla }\cdot \left(x_{mo}{\xi }_o{u}_o+x_{mg}{\xi }_g{u}_g\right)=q_m$(1)

(2) $u_{\alpha }=\frac{-k_{r\alpha }}{{\mu }_{\alpha }}k\left(\mathrm{\nabla }{p}_{\alpha }-{\rho }_{\alpha }\mathrm{\wp }\mathrm{\nabla }z\right),\alpha =\omega ,o,g.$(2)

(3) ${\sum }_{m=1}^{N_c}{x}_{mo}=1,{\sum }_{m=1}^{N_c}{x}_{mg}=1.$(3)

(4) $S_{\omega }+S_o+S_g=1.$(4)

(5) $p_{co\omega }=p_o-p_{\omega },p_{cgo}=p_g-p_o.$(5)

(6) $\begin{array}{rl}& f_{mo}\left(p_o,x_{1o},x_{2o,}\dots ,x_{N_{c}o}\right)=f_{mg}\left(p_g,x_{1g},x_{2g},\dots ,x_{N_{c}g}\right)\\ & f_{m\alpha }=p_{\alpha }{x}_{m\alpha }{\phi }_{m\alpha },m=1,2,\dots ,N_c,\alpha =o,g.\end{array}$(6)

where $S_w$, $S_o$, and $S_g$ are the saturations of the water, oil and gas phase, respectively; $x_{m\alpha }$ is the mole fraction of component m in phase α; ${\xi }_{\alpha }$ is the molar density of phase $\alpha$; $\varphi$ and $k$ are the porosity and permeability, respectively, of the rock; ${\mu }_{\alpha }$ is the viscosity; $p_{\alpha }$ is the phase pressure, $p_{co\omega }$ and $p_{cgo}$ are the capillary pressures; $k_{r\alpha }$ is the relative phase permeability; $u_{\alpha }$ is the velocity of phase α; $q_w$ and $q_m$ are the molar velocities of the water flow and m-th component, respectively; $f_{mo}$ and $f_{mg}$ are the fugacity functions; and ${\phi }_{m\alpha }$ is the fugacity coefficient of component m in phase $\alpha$.

Distribution of chemical components in the hydrocarbon phase described by the K-value method (Pederson & Christensen, 2008). The thermodynamic behaviour of fluids under reservoir conditions are described by the Peng-Robinson equations of state (Peng & Robinson, 1976).

The system of nonlinear Equations (1)(1) $\frac{\mathrm{\partial }\left(\varphi {\xi }_{\omega }{S}_{\omega }\right)}{\mathrm{\partial }t}+\mathrm{\nabla }\cdot \left({\xi }_{\omega }{u}_{\omega }\right)=q_{\omega },\frac{\mathrm{\partial }\left(\varphi \left[x_{mo}{\xi }_o{S}_o+x_{mg}{\xi }_g{S}_g\right]\right)}{\mathrm{\partial }t}+\mathrm{\nabla }\cdot \left(x_{mo}{\xi }_o{u}_o+x_{mg}{\xi }_g{u}_g\right)=q_m$(1) —(6(6) $\begin{array}{rl}& f_{mo}\left(p_o,x_{1o},x_{2o,}\dots ,x_{N_{c}o}\right)=f_{mg}\left(p_g,x_{1g},x_{2g},\dots ,x_{N_{c}g}\right)\\ & f_{m\alpha }=p_{\alpha }{x}_{m\alpha }{\phi }_{m\alpha },m=1,2,\dots ,N_c,\alpha =o,g.\end{array}$(6) ) is linearized by the Newton-Raphson method.

In the (l+ 1)-th layer of the Newton iterative process, the value of the unknowns is updated by the following law (Chen et al., 2006):

(7) $\begin{array}{rl}& x_{mo}^{n+1,l+1}=x_{mo}^{n+1,l}+\mathrm{\Delta }{x}_{mo}^{n+1,l+1},m=1,2,\dots ,N_c-1,\\ & {\mathrm{Z}}_{mo}^{n+1,l+1}={\mathrm{Z}}_{mo}^{n+1,l}+\mathrm{\Delta }{\mathrm{Z}}_{mo}^{n+1,l+1},m=1,2,\dots ,N_c-1,\\ & L^{n+1,l+1}=L^{n+1,l}+\mathrm{\Delta }{L}^{n+1,l+1},\\ & F^{(n+1,l+1)}=F^{(n+1,l)}+\mathrm{\Delta }{F}^{(n+1,l+1)},\\ & S^{n+1,l+1}=S^{n+1,l}+\mathrm{\Delta }{S}^{n+1,l+1},\\ & p^{n+1,l+1}=p^{n+1,l}+\mathrm{\Delta }{p}^{n+1,l+1}.\end{array}$(7)

The resulting system of linear Equations (7)(7) $\begin{array}{rl}& x_{mo}^{n+1,l+1}=x_{mo}^{n+1,l}+\mathrm{\Delta }{x}_{mo}^{n+1,l+1},m=1,2,\dots ,N_c-1,\\ & {\mathrm{Z}}_{mo}^{n+1,l+1}={\mathrm{Z}}_{mo}^{n+1,l}+\mathrm{\Delta }{\mathrm{Z}}_{mo}^{n+1,l+1},m=1,2,\dots ,N_c-1,\\ & L^{n+1,l+1}=L^{n+1,l}+\mathrm{\Delta }{L}^{n+1,l+1},\\ & F^{(n+1,l+1)}=F^{(n+1,l)}+\mathrm{\Delta }{F}^{(n+1,l+1)},\\ & S^{n+1,l+1}=S^{n+1,l}+\mathrm{\Delta }{S}^{n+1,l+1},\\ & p^{n+1,l+1}=p^{n+1,l}+\mathrm{\Delta }{p}^{n+1,l+1}.\end{array}$(7) is reduced to the following form, as shown by Chen et al. (2006):

(8) $Ax=b$(8)

There are several well-known methods for solving systems of algebraic equations of this type; direct methods, such as the Gauss method or LU decomposition, are not suitable for systems with sparse matrices since there is the possibility of overflow (Higham, 2011). The Conjugate gradient method (CG) is designed for systems with symmetric matrices, and the Biconjugate Gradient Method (BiCG) has slow convergence (Van der Vorst, 2003). In this work, system (8) was solved by the iterative method GMRES, which is a widely used Krylov subspace method (Saad, 2003).

To reduce the number of iterations in the computation, preconditioning was used as an explicit or implicit modification of the system of linear equations, making it possible to simplify the solution. One of the widely used methods for finding the preconditioner is incomplete LU (ILU) decomposition of the original matrix A (Mittal & Al-Kurdi, 2003). We choose ILU(0) (Chow & Saad, 1997) as a preconditioner for the GMRES algorithm, which was found by decomposing matrix A by a fine-grained ILU factorization algorithm. As a result, for the numerical solution of the given problem for solving a system of linear equations, (8) uses the Newton-ILU0-GMRES algorithm as a fully implicit scheme.

3. Parallel algorithm

To implement the parallel algorithm of the GMRES, we need to determine the parts of the calculations that can be the basis of parallelization.

For instance, the GMRES algorithm consists of the following steps:

1. Initialization. Choose $x_0$, compute $r=b-A{x}_0$, solve $Pw=r$ and compute $v_1=\frac{W}{{∥w∥}_2}$

2. Arnoldi iteration. Iterate m times: j = 1,2, …,m. The specific Arnoldi algorithm is as follows:

for i = 1, …, m

$Pw=A{x}_i$

for k=1, …, i

$h_{k,i}=\left(w,v_k\right)$

$w=w-h_{k,i}{v}_k$

$endk$

$h_{i+1,i}={∥w∥}_2$

$v_{j+1}=\frac{W}{h_{i+1,i}}$

end i

1. Compute the approximate solution $x^m=x^0+Q_{n,m}{y}_m$. Here, minimizes ${∥\beta \xi -H_{m,m}y∥}_2$; $Q_{n,k}$ is an $n\times k$ matrix, the column vector of the matrix is composed of $v_{1,}{v}_2,\dots ,v_k$ orthogonal vectors, and $H_{mm}$ is the Hessenberg matrix.

2. Determination. Compute $r^m=b-x^m$, stop if the condition is met: otherwise let $x^0=x^m$ and go back to a) and recalculate. The convergence condition by which the method stops is given by an arbitrary number ε.

In this GMRES algorithm, there are common operations such as matrix-matrix multiplication, matrix-vector multiplication, vector-vector multiplication and vector norm calculation in steps of a), b) and c). These operations could be implemented in parallel with data decomposition. In a) and b) steps of the GMRES algorithm, P is used as the ILU(0) preconditioner.

4. Existing libraries

The GMRES algorithm can be implemented on some well-known libraries, such as Intel MKL (Intel® Math Kernel Library Developer Reference, 2020), MATLAB (MathWorks, 2020), Portable, Extensible Toolkit for Scientific Computation (PETSc) (Abhyankar et al., 2018). In this work, the PETSc library was chosen for comparisons with our Newton-ILU0-GMRES MPI parallel implementation since this tool implements parallel versions of different methods for solving linear and nonlinear equations.

During the review, it was revealed that it was impossible to use the ILU(0) preconditioner in a parallel program with PETSc; by default, the Jacobi block preconditioner is used instead.

5. Testing results of the numerical experiment

5.1. Verification of the convergence of the algorithm with preconditioning

The testing of the program was carried out on matrices corresponding to the cases when the number of grid point schemes varied from 500 to 8000. The parameters of the matrix are shown in Table 1.

Table 1. Parameters of the matrix

Matrix designation	#1	#2	#3	#4	#5
Number of grid points	500	1000	2000	4000	8000
Size of matrix A	$3000\times 3000$	$6000\times 6000$	$12000\times 12000$	$24000\times 24000$	$48000\times 48000$

From this table, the size of the matrix being solved is 6 times larger than the number of grid points. For example, the size of matrix #5, which corresponds to the case when the number of points of the difference grid is 8000, is $48000\times 48000$ because 6 Equations (7)(7) $\begin{array}{rl}& x_{mo}^{n+1,l+1}=x_{mo}^{n+1,l}+\mathrm{\Delta }{x}_{mo}^{n+1,l+1},m=1,2,\dots ,N_c-1,\\ & {\mathrm{Z}}_{mo}^{n+1,l+1}={\mathrm{Z}}_{mo}^{n+1,l}+\mathrm{\Delta }{\mathrm{Z}}_{mo}^{n+1,l+1},m=1,2,\dots ,N_c-1,\\ & L^{n+1,l+1}=L^{n+1,l}+\mathrm{\Delta }{L}^{n+1,l+1},\\ & F^{(n+1,l+1)}=F^{(n+1,l)}+\mathrm{\Delta }{F}^{(n+1,l+1)},\\ & S^{n+1,l+1}=S^{n+1,l}+\mathrm{\Delta }{S}^{n+1,l+1},\\ & p^{n+1,l+1}=p^{n+1,l}+\mathrm{\Delta }{p}^{n+1,l+1}.\end{array}$(7) are written for each point.

Problem (8) was solved by the Newton-GMRES algorithm without a preconditioner and with the ILU(0) preconditioner. The graph of the change in the solution residuals with the execution of a certain number of iterations for various cases is shown in Figure 2.

Figure 2. The residual plot for matrices #1—#3 when solving with the Newton-GMRES algorithm without a preconditioner and when solving with the Newton-ILU(0)-GMRES algorithm.

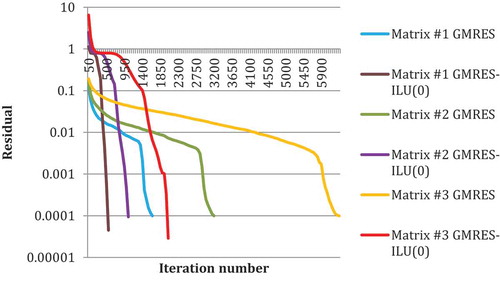
As seen in Figure 2, for all the matrices tested, the Newton-ILU(0)-GMRES algorithm converges in less than three times the number of iterations than the Newton-GMRES algorithm. Based on this result, further tests were conducted only on the Newton-ILU (0)-GMRES algorithm.

5.2. Comparison of the Newton-ILU(0)-GMRES algorithm with the PETSc library

To compare our parallel program of Newton-ILU(0)-GMRES algorithm and the program using the PETSc library, tests were carried out on a personal 8-core computer, since it was not possible to install third-party libraries on a supercomputer. The results are shown in the following Table 2.

Table 2. Comparison of the Newton-ILU(0)-GMRES algorithm with the PETSc library

Number of processors	Newton-ILU(0)-GMRES, s	PETSc, s
1	6.11	3.21
2	35.64	52.45
4	23.24	128.13
8	36.18	277.25

The tests were carried out on a 3000×3000 matrix, which corresponds to the case when the number of nodes of the difference scheme of (1)—(6) was 500. As we can see from Table 2, in parallel calculations, the implementation of the Newton-ILU(0)-GMRES algorithm runs faster than the program using PETSc. The comparisons shown above are not under the same conditions, as different preconditioners were used in different parallel implementations. However, the implementation of the presented Newton-ILU(0)-GMRES algorithm is faster than the PETSc version on the same personal computer.

5.3. Test results of the Newton-ILU(0)-GMRES parallel algorithm

Test runs for the considered problem (8) were made on the MVS-10P supercomputer of the Interdepartmental Supercomputer Center of the Russian Academy of Sciences, which includes nodes with two Xeon X5450 processors and 8 GB of RAM for each node. The test results are shown in Table 3.

Table 3. The runtimes of the parallel program in MPI

Matrix Number designation of processors	#1	#2	#3	#4	#5
1	3.74	48.38	334.24	1 688.74	20 219.34
8	1.19	7.57	53.82	394.74	2 942.02
64	2.59	12.03	64.16	389.68	2 565.59
128	2.95	12.66	65.25	395.58	2 569.01
256	4.39	17.29	82.75	450.28	2 798.32
512	11.53	42.56	202.01	866.98	4 185.07

As we can see from the test results, the parallel program running on 8 processors achieved the shortest runtime. As the size of the task increases, the parallel application achieves the shortest calculation time running on 64 processors, but it is not much different from the runtime of a parallel program running on 8, 128 and 256 processors. The reason is because with an increase in the number of processors, the computation time on each processor decreases, and the time spent on communications increases.

It can be seen that the runtimes on 64 and 128 processors are about the same. This finding is explained by the fact that on 64 processors, the communication time is less than the computation time, and on 128 processors, the computation time is less than the communication time, but in total, the time consumed is almost the same.

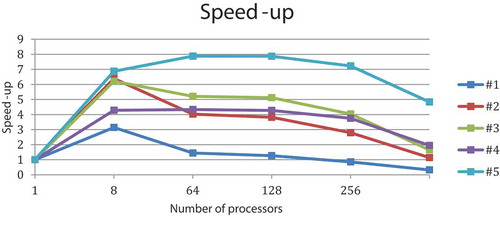
For matrix #1 on 256 and 512 processors, the parallel program is slower than the sequential program. With an increase in the size of the matrix, for instance, for matrices #2—#5, the runtime of the parallel program decreases compared to the sequential program. This regularity makes it possible to predict that with an increase in the size of the matrix, in large numbers of processors, acceleration also increases. Figure 3 shows the parallel program acceleration. It can be concluded that it makes sense to run the parallel algorithm of the method on a large number of processors but only with large of matrix that cannot fit in the memory of a single node.

Figure 3. Acceleration of the parallel algorithm.

On matrix #1 with 256 and 512 processes, the parallel program considers it slower than the sequential one. With an increase in the size of the matrix for instance, on matrix #2—matrix #5, the runtime of the parallel program decreases compared to the sequential one. This regularity makes it possible to predict that with an increase in the size of the matrix, in large numbers of processes, acceleration also increases. Figure 3 shows the parallel program acceleration. It can be concluded that the parallel algorithm of the method makes sense to run on a large number of processors, only on large sizes that cannot fit in the memory of one node.

6. Conclusion

This research examines the parallel implementation of the Newton-ILU0-GMRES algorithm for a multicomponent three-phase flow problem. The considered problem is compared to the parallel implementation of the presented method and parallel program with the PETSc library on an 8-core personal computer. The results have shown that the presented Newton-ILU(0)-GMRES algorithm achieves faster convergence than the Newton-GMRES algorithm and has a shorter runtime than the parallel program with PETSc. Tests were also carried out with different node sizes and numbers of processes on supercomputers. The study showed that on a large number of processes, the MPI program runs better in large-scale tasks. In future research, we plan to consider other variants of the method to improve the efficiency of the parallel algorithm. In particular, we plan to consider other options instead of the Arnoldi iteration and develop a fragmented algorithm (Akhmed-Zaki et al., 2019) that will allow users to not to spend time on the implementation of communications.

Additional information

Funding

This work was supported by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan [Grant No. AP05130366].

Notes on contributors

Danil V. Lebedev

Danil Lebedev has a PhD in computer science and is an acting associate professor in the Department of Computer Science of Al-Farabi Kazakh National University. The authors of the article are employees of the Scientific Research Institute of Mathematics and Mechanics, operating in Al-Farabi Kazakh National University and are engaged in problems of modelling the flow of liquids and distributed data processing.