Optimal design of an adaptive robust proportional-integral-derivative controller based upon sliding surfaces for under-actuated dynamical systems

Abstract

This paper presents a novel adaptive robust proportional-integral-derivative (PID) controller for under-actuated dynamical systems via employing the advantages of the PID control and sliding surfaces. The related control gains as adjustable parameters are computed during the control process using gradient descent techniques and the chain derivative rule. Based on the design of control rules, the genetic algorithm optimization is utilized in order to find the optimal values of the learning rates and initial conditions of the control gains. The suggested strategy is implemented successfully to stabilize the cart-pole and ball-beam systems. Lastly, the simulation results demonstrate the efficacy of the proposed controller to control such under-actuated dynamical systems as well as its superiority in comparison with other recently introduced methods.

Keywords:

• Adaptive robust controller
• proportional-integral-derivative controller
• sliding mode
• under-actuated dynamical systems
• genetic algorithm optimization

PUBLIC INTEREST STATEMENT

The proportional-integral-derivative (PID) control approach is one of the simplest and most common control methods widely used in industries throughout the world. Due to its straightforward structure, the application of this control approach for a wide range of engineering problems is feasible. In fact, this technique is an appropriate scheme for the control of linear fully actuated systems, and there are different approaches to adjust the gains of the controllers designed for such systems. However, it is complicated and sometimes infeasible to reach an exact performance for the control of the under-actuated systems. To address this problem, this paper presents a novel adaptive robust PID controller for under-actuated dynamical systems via employing the advantages of gradient descent techniques, sliding surfaces and genetic algorithm optimization.

1. Introduction

The proportional-integral-derivative control approach is one of the simplest and most common control methods widely used in industries throughout the world. Due to its straightforward structure, the application of this control approach for a wide range of engineering problems is feasible (Astrom et al., 2001; Astrom & Hagglund, 2001). In fact, this technique is an appropriate scheme for the control of linear fully actuated systems, and there are different approaches to adjust the gains of the controllers designed for such systems (Dwyer, 2009). However, it is complicated and sometimes infeasible to reach an exact performance for the control of the under-actuated systems. Therefore, to address this problem, a number of different effectual approaches have been proposed to combine with the PID control scheme, such as fractional robust method (Beschi et al., 2016) adaptive based neural network method (Milovanović et al., 2016), reference model-based adaptive approach (Sarhadi et al., 2016), fuzzy systems (Moradi et al., 2016; Kumar & Kumar), nonlinear robust semi-fuzzy approach (Londhe et al., 2016), sliding mode concepts (Lochan et al., 2016), fuzzy sliding mode ideas (Tavakoli & Seifi, 2016), and so on.

While the gains of the PID control approach are commonly obtained via trial and error methods, finding these parameters via scientific approaches will help to enhance its efficacy. Recent studies illustrate that evolutionary algorithms are considered as one of the most efficient ways to gain the optimal values of these parameters. For instance, the genetic algorithm has been utilized in order to adjust the parameters of the PID control (Jiménez et al., 2015). Furthermore, a gravitational search algorithm has been used to optimize the design of the Posicast PID control systems (De Moura Oliveira et al., 2015). A teaching-learning-based optimization algorithm has been employed to design the fuzzy-PID control approach (Sahu et al., 2015). Particle swarm optimization has been employed to gain the optimal parameters of the PID controller for an air heater temperature control system (Sungthong & Assawinchaichote, 2016). Once more, an improved gravitational search algorithm has been used in order to optimally design an adaptively fast fuzzy fractional order PID controller for a pumped storage hydro unit (Xu et al., 2016). An improved chaotic krill herd algorithm has been employed to tune the parameters of a PID control approach (Yaghoobi & Mojallali, 2016). A bacterial swarm optimization algorithm has been utilized to gain the optimal parameters of classical and fractional PID control approaches (Özdemir et al., 2015). The particle swarm optimization approach has been implemented to find the gains of the robust PID adaptive controller for exoskeletons (Belkadi, Oulhadj, Touati, Safdar, Khan, & Daachi, Belkadi et al., 2017). A real-coded genetic algorithm has been applied for optimal design of the PID control for a reactor (Mousakazemi et al., 2018). A whale optimization algorithm has been suggested to tune proportional-integral-derivative controllers and utilized for AVR systems (Mosaad et al., 2019). A fuzzy self-tuning PID controller has been optimized using a tribe-DE optimization algorithm and a rule weight adjustment method for load frequency control of interconnected multi-area power systems (Jalali et al., 2020). Finally, an optimal fuzzy adaptive robust PID control system has been implemented via a particle swarm optimization scheme for an active suspension system (Mahmoodabadi & Nejadkourki, 2020).

On the other hand, the under-actuated systems have fewer control efforts than their degrees of freedom and display some advantages such as energy saving, cost decreasing and easy installation. Due to their importance and applications as well as control complications, handling and stabilization of these systems have been widely studied by researchers. To name but a few, a robust adaptive antiswing control approach has been investigated for an underactuated crane system with two parallel payloads and rail length constraint (Zhang et al., 2016). A feedback control method has been introduced for a class of under-actuated mechanical systems obviating matching conditions (Mehra et al., 2017). A new scheme related to the LMI-based sliding mode control has been studied for an underactuated moment gyroscope system (Keshtkar et al., 2018). A continuous sliding-mode control methodology has been proposed for underactuated systems having the relative degree of one and two (Ovalle et al., 2019). An optimal adaptive hybrid controller has been employed for a fourth-order under-actuated nonlinear inverted pendulum system (Mahmoodabadi & Khoobroo Haghbayan, 2020). A sliding mode control scheme has been suggested for a class of underactuated systems with non-integrable momentum (Chen & Van, 2020). An optimum fuzzy combination of robust decoupled sliding mode and adaptive feedback linearization controllers has been implemented for uncertain under-actuated nonlinear systems (Mahmoodabadi & Soleymani, 2020). The tackling mismatched uncertainty has been analyzed for the robust constraint-following control of underactuated systems (Yin et al., 2020). A new optimal robust adaptive fuzzy controller has been examined for a class of non-linear under-actuated systems (M. J. Mahmoodabadi & Rafee, 2020). A supervised learning algorithm has been realized for stabilization of the underactuated dynamical systems (Monga & Moehlis, 2020). An optimal hybrid adaptive controller based on the multi-objective evolutionary algorithms has been executed for an under-actuated nonlinear ball and wheel system (Pezhman et al., 2020). Besides, there are some other control methods, such as the resilient control which can also provide such flexibility (Shang, 2018a; Shang,, 2020).

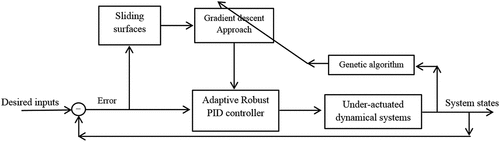
The present research work is endeavored to modify the authors' previous study (Mahmoodabadi et al., 2011) by employing the PID controller in conjunction with sliding mode surfaces used for adaptation laws based upon the gradient descent approach. More precisely, an adaptive robust PID control approach is proposed in order to overcome the dynamical challenges of under-actuated systems. Indeed, the gains of the PID control method are adjustable parameters which are determined during the control process via an appropriate adaptive mechanism so that the sliding surface is automatically minimized and the stability of the closed-loop system is guaranteed. Furthermore, in order to minimize the overshoot and settling time of the system states, the optimum parameters of the controller are obtained by the genetic algorithm optimization.

The rest of this paper is organized as follows. Section 2 describes basic definitions for the under-actuated systems. Section 3 represents the proposed adaptive robust PID control approach. The genetic algorithm optimization is briefly explained in Section 4. The suggested scenario is implemented on the ball-beam and cart-pole systems, and the results are illustrated in Section 5. The paper is concluded in Section 6.

2. Under-actuated systems

In the under-actuated systems, the number of control inputs is less than the number of degrees of freedom. On the other hand, fully actuated systems have a control input for every degree of freedom (Reyhanoglu et al., 1996).

It can be noted that the under-actuated systems have advantages such as energy saving, lower costs of production and easy installation compared to the fully actuated ones. However, the control of the under-actuated systems is challenging owing to the limited number of control inputs. There exists an increasing interest in the control approaches of the under-actuated dynamics systems due to (1) their extensive applications for stability of ships, airplanes, helicopters, submarines, robots, vehicles, etc., and (2) as well as owing to the high probability of physical problems or defects in fully actuated systems and turning these systems into under-actuated systems.

Eq. (1)(1) $\stackrel{=}{q}{f}_1\left(\dot{q},q,t\right)+f_2\left(\dot{q},q,t\right)u$(1) illustrates the dynamics of a system having n degree-of-freedom; where,$q$ (n × 1) is the position vector, $u$ (n × 1) is the control input vector, and $t$ corresponds to time.

(1) $\stackrel{=}{q}{f}_1\left(\dot{q},q,t\right)+f_2\left(\dot{q},q,t\right)u$(1)

Based on Eq. (1(1) $\stackrel{=}{q}{f}_1\left(\dot{q},q,t\right)+f_2\left(\dot{q},q,t\right)u$(1) ), the fully actuated and under-actuated systems can be mathematically defined as Eq. (2) and Eq. (3) respectively.

(2) $rank\left[f_2\left(\dot{q},q,t\right)\right]=dimansion\left[q\right]$(2)

(3) $rank\left[f_2\left(\dot{q},q,t\right)\right]<dimansion\left[q\right]$(3)

3. Adaptive robust PID control

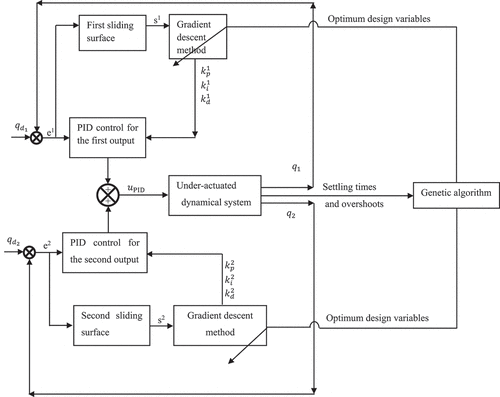
The control approach proposed in this study combines the advantages of the PID control and sliding mode, whereas its details are elaborated as follows. The general scheme of the PID controller for a system having two outputs can be considered as follows.

(4) $u_{pid}=K_p^1{e}^1+K_i^1\int e^{1}dt+K_d^1\frac{d{e}^1}{dt}+K_p^2{e}^2+K_i^2\int e^{2}dt+K_d^2\frac{d{e}^2}{dt}+C$(4)

where $e^1$ and $e^2$represent the error signals of the first and second outputs, respectively. $K_p^1$,$K_i^1$ and $K_d^1$ respectively denote the proportional and integral derivative gains of the first output. $K_p^2$, $K_i^2$ and $K_d^2$ are the proportional; and integral derivative gains of the second output. $\mathrm{C}$ is a constant parameter to eliminate the effects of fixed external forces.

The difference between an adaptive controller and a non-adaptive controller involves the fact that the gains of the first one are timely tuned. In order to adjust these gains, a mechanism based upon the system signals and states is employed. In this paper, for the robust regulation of the PID control gains, the surfaces defined in the sliding mode controllers (Mohamed et al., 2012; Qiu et al., 2020; G. Wang et al., 2020; Y. Wang et al., 2020) for the first and the second outputs are, respectively, calculated as follows.

(5) $S^1=q_1-q_{1d}$(5)

(6) $S^2=q_2-q_{2d}$(6)

In which, $q_1$ represents the first output of the system, while $q_{1d}$ is its desired value. Moreover,$q_2$ denotes the second output of the system, and $q_{2d}$ is its desired value. Now, by using the gradient descent technique and the chain derivative rule, the following formulae are obtained to adaptively evaluate the gains of the PID controller based on the robust sliding surfaces (Cahng & Yan, 2005).

(7) ${\dot{K}}_p^1={\gamma }_p^1\frac{\mathrm{\partial }{S}^1{\dot{S}}^1}{\mathrm{\partial }{K}_p^1}={\gamma }_p^1\frac{\mathrm{\partial }{S}^1{\dot{S}}^1}{\mathrm{\partial }{u}_{pid}}\frac{\mathrm{\partial }{u}_{pid}}{\mathrm{\partial }{K}_p^1}\cong {\gamma }_p^1{S}^1{e}^1$(7)

(8) ${\dot{K}}_i^1={\gamma }_i^1\frac{\mathrm{\partial }{S}^1{\dot{S}}^1}{\mathrm{\partial }{K}_i^1}={\gamma }_i^1\frac{\mathrm{\partial }{S}^1{\dot{S}}^1}{\mathrm{\partial }{u}_{pid}}\frac{\mathrm{\partial }{u}_{pid}}{\mathrm{\partial }{K}_i^1}\cong {\gamma }_i^1{S}^1{\int }^{e^1}dt$(8)

(9) ${\dot{K}}_d^1={\gamma }_d^1\frac{\mathrm{\partial }{S}_p^1{\dot{S}}_p^1}{\mathrm{\partial }{K}_d^1}={\gamma }_d^1\frac{\mathrm{\partial }{S}_p^1{\dot{S}}_p^1}{\mathrm{\partial }{u}_{pid}}\frac{\mathrm{\partial }{u}_{pid}}{\mathrm{\partial }{K}_d^1}\cong {\gamma }_d^1{S}^1{\dot{e}}_d^1$(9)

(10) ${\dot{K}}_p^2={\gamma }_p^2\frac{\mathrm{\partial }{S}^2{\dot{S}}^2}{\mathrm{\partial }{K}_p^2}={\gamma }_p^2\frac{\mathrm{\partial }{S}^2{\dot{S}}^2}{\mathrm{\partial }{u}_{pid}}\frac{\mathrm{\partial }{u}_{pid}}{\mathrm{\partial }{K}_p^2}\cong {\gamma }_p^2{S}^2{e}^2$(10)

(11) ${\dot{K}}_i^2={\gamma }_i^2\frac{\mathrm{\partial }{S}^2{\dot{S}}^2}{\mathrm{\partial }{K}_i^2}={\gamma }_i^2\frac{\mathrm{\partial }{S}^2{\dot{S}}^2}{\mathrm{\partial }{u}_{pid}}\frac{\mathrm{\partial }{u}_{pid}}{\mathrm{\partial }{K}_i^2}\cong {\gamma }_i^2{S}^2{\int }^{e^2}dt$(11)

(12) ${\dot{K}}_d^2={\gamma }_d^2\frac{\mathrm{\partial }{S}^2{\dot{S}}^2}{\mathrm{\partial }{K}_d^2}={\gamma }_d^2\frac{\mathrm{\partial }{S}^2{\dot{S}}^2}{\mathrm{\partial }{u}_{pid}}\frac{\mathrm{\partial }{u}_{pid}}{\mathrm{\partial }{K}_d^2}\cong {\gamma }_d^2{S}^2{\dot{e}}^2$(12)

where ${\gamma }_p^1$, ${\gamma }_i^1$, ${\gamma }_d^1$, ${\gamma }_p^2$,${\gamma }_i^2$ and ${\gamma }_d^2$ are the learning rates with regard to the gains of the controller. In this study, these learning rates as well as the initial conditions of the control gains are considered as the design variables for the optimization process and would be found utilizing the genetic algorithm.

Figure 1 displays the block diagram of the introduced optimal adaptive robust PID controller for the under-actuated systems. In this approach, the error signals are applied to calculate the sliding mode surfaces. The computed surfaces are employed in the gradient descent block to find the adaptive gains of the PID controller. The optimum values of the constant parameters are discovered by using the block optimization-based genetic algorithm.

Figure 1. Block diagram of the proposed adaptive robust proportional integral derivative controller

4. Genetic algorithm

The genetic algorithm is a comprehensive searching approach which imitates the natural evolutionary biology. In fact, this optimization algorithm uses the concept of the survival of the fittest to find superior solutions for a defined problem. In each generation, the solutions selected via the operators of the natural genetic present estimations for the final solutions. Looking into the history of this algorithm, it was initially introduced by John Holland (Holland, 1975) in 1975 at the University of Michigan, and afterward, it has been widely used by many researchers to address advanced optimization problems. In order to apply the genetic algorithm, an objective function must be defined for the evaluation of the fitness of the chromosomes. Indeed, the value of the fitness gained from the objective function has a direct effect on the survival of each evolutionary member of the population. The crossover and mutation operators would be used in order to generate a new population. In the first operator, two new members (offsprings) are generated by two selected chromosomes (parents) to have a new crossover population with the similar information about the parents. On the other hand, in the mutation, one part of a chromosome is selected according to the probability rules and is arbitrarily changed. If $N$ represents the size of the population, $P_c$ denotes the probability of the crossover process, and $P_m$ is the probability of the mutation process, then the crossover operator works on $P_c\times N$of the total chromosomes, and the mutation operator is implemented on $P_m\times N$member of the population. In this paper, the size of the initial population, the maximum number of iterations, the probabilities of the mutation and crossover operators are considered as 50, 200, 0.3 and 0.8, respectively. The flowchart of the proposed method is illustrated in Figure 2 to show the operation of the overall control system.

Figure 2. Flowchart of the introduced control method

5. Illustrative examples

5.1. Ball-beam system

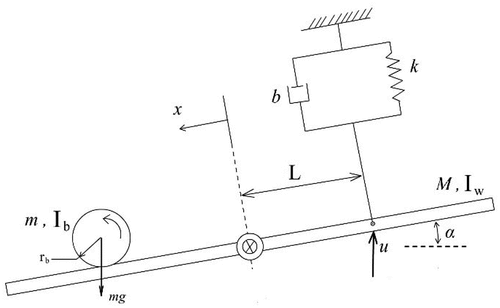
The ball-beam system is a nonlinear under-actuated mechanism which involves a rolling ball on a rotating beam as illustrated in Figure 3. In the open-loop condition, it is an open loop unstable system because if the angular position of the beam is considered constant with respect to the horizontal axis, the position of the ball would be infinitely increased due to the gravitational force of the earth.

Figure 3. Mechanical structure of the ball-beam system

Therefore, the controller must regulate the rotational angle of the beam in order to place the ball in the desired position. The nonlinear dynamical equations of this system obtained by the Lagrange method can be written as follows.

(13) $(m+\frac{I_b}{{r_b}^2})+\left(m{r_b}^2+I_b\right)\frac{1}{r_b}\ddot{\alpha }-mx{\dot{\alpha }}^2=mgsin\alpha$(13)

(14) $\left(m{x}^2+I_b+I_w+m{r_b}^2\right)\ddot{\alpha }\left(2m\dot{x}x+b{L}^2\right)\dot{\alpha }+k{L}^2\alpha +\left(m{r_b}^2+I_b\right)\frac{1}{r_b}\ddot{x}-mgxcos\alpha =uLcos\alpha$(14)

where, $x$ is the position of the ball while$\dot{x}$and$\ddot{x}$represent its velocity and acceleration, respectively. Moreover, $\alpha$ is the angle of the beam with respect to the horizontal axis, while $\dot{\alpha }$ and $\ddot{\alpha }$, respectively, demonstrate its angular velocity and acceleration. Further, $m$ is the mass of the ball, $r_b$ represents the effective radius of the ball, $b$ denotes the equivalent viscous damping coefficient of the system, $L$is the distance between the force direction and the center of the beam, $k$represents the equivalent spring coefficient of the system, $I_w$is the inertia moment of the beam with respect to its center of gravity, $I_b$ represents the inertia moment of the ball with respect to its center of gravity, and $u$denotes the control effort.

The dynamical equations of the ball-beam system after linearization around the equilibrium point could be stated as follows.

(15) $\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\\ {\dot{x}}_3\end{array}\\ {\dot{x}}_4\end{array}\\ {\dot{x}}_5\end{array}\\ {\dot{x}}_6\end{array}\right]=\left[\begin{array}{cccc}0& I_o& 0& \begin{array}{cc}0& \begin{array}{cc}0& 0\end{array}\end{array}\\ 0& 0& I_0& \begin{array}{cc}0& \begin{array}{cc}0& 0\end{array}\end{array}\\ 0& A& 0& \begin{array}{cc}0& \begin{array}{cc}B& a_2\times b_3\end{array}\end{array}\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ C\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}{I}_o\\ \begin{array}{c}0\\ D\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}{I}_0\\ E\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ -a_{2}L\\ 0\\ 0\\ F\end{array}\right]u$(15)

where${\left[x_1,{\mathrm{x}}_2,x_3,x_4,x_5,x_6\right]}^T={\left[{\int }^{\alpha },\alpha ,\dot{\alpha },{\int }^x,x,\dot{x}\right]}^T$ . Furthermore, the other parameters are defined as follows.

(16) $A=-a_2{a}_3+\left(\frac{2m\times a_1\times a_2\times a_3\times x_o^2}{I_o}\right)$(16)

(17) $B=a_3\left(m{x}_o^2+b_1\right)+a_2{b}_4$(17)

(18) $C=\frac{-I_{o}m{x}_o^2{a}_3{b}_1}{\left(m^2{x}_o^4+b_1^{2}2m{b}_1{x}_o^2\right)}-3a_1{a}_2{b}_5{m}^2{x}_o^4\left(3a_{1}m{x}_o^2+2a_1{b}_1-a_2{b}_5\right)+\frac{b_1\left(-a_1{b}_1+a_2{b}_2\right)}{I_o}$(18)

(19) $D=\frac{b_4{I}_o}{m{x}_o^2+m{b}_1}-a_3{b}_5-\frac{a_2{b}_4{b}_5}{m{x}_o^2+b_1}$(19)

(20) $E=\frac{-b_3\left(I_o+a_2{b}_5\right)}{m{x}_o^2+b_1}$(20)

(21) $F=\frac{\mathrm{l}}{\left(m{x}_o^2+b_1\right)\left(I_o+a_2\times b_5\right)}$(21)

(22) $a_1=m+I_b/r^2$(22)

(23) $a_2=(m{r}^2+I_b)/r$(23)

(24) $a_3=mg$(24)

(25) $b_1=I_b+I_w$(25)

(26) $b_2=2m$(26)

(27) $b_3=b{L}^2$(27)

(28) $b_4=k{L}^2$(28)

(29) $b_5=(m{r}^2+I_b)/r$(29)

(30) $I_o=a_1(m{x}_o^2+b_1)-a_2{b}_5$(30)

Moreover, in the design of a proper control effort for this system, the following physical constraints must be satisfied.

• The constraint on the control force: $\left|u\right|\le 6N$

• The constraint on the position of the ball: $\left|x_2\right|\le 0.7m$

• The constraint on the angle of rotation: $\left|x_5\right|\le 0.2rad$

Moreover, to make a fair comparison, the numerical values of the physical specifications of the ball-beam system provided in Table 1 are selected from (Mahmoodabadi et al., 2011). In fact, the performance of the introduced adaptive robust PID control approach based upon the genetic algorithm optimization is contrasted with the performance of a linear feedback controller based upon the particle swarm optimization presented in (Mahmoodabadi et al., 2011).

Table 1. The physical specifications of the ball-beam system

Parameter	$m$	$r_b$	$L$	$I_w$	$b$	$k$	$I_b$
Value	2.7 × 10^−1 kg	1.8 × 10^−2 m	4.9 × 10^−1 m	1.4025  × 10^−1 kg.m^2	1 N.s/M	1 × 10^−3 N/M	4.32 × 10^−5 kg.m^2

In order to optimize the gains of the control approach designed for the ball-beam system, the objective function is defined as the summation of the normalized values of the settling times and overshoots of the ball and the beam. The optimal values of the design variables related to the proposed control method are illustrated in Table 2.

Table 2. The optimal values of the control gains for the proposed approach

Control gain	$K_p^1(0)$	$K_i^1(0)$	$K_d^1(0)$	$K_p^2(0)$	$K_i^2(0)$	$K_d^2(0)$
Optimum value	−8.7916	−2.0321  × 10^−3	−5.0116	−1.9696  × 10^1	−3.7000  × 10^−1	−5.0671
Control gain	${\gamma }_p^1$	${\gamma }_i^1$	${\gamma }_d^1$	${\gamma }_p^2$	${\gamma }_i^2$	${\gamma }_d^2$
Optimum value	−9.9680	1.6700  × 10^−2	6.0285	−1.6796  × 10^1	1.4113	−2.4732

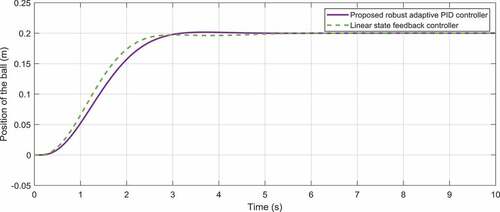
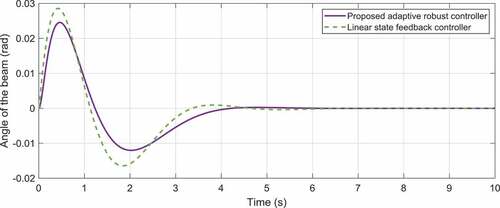
Moreover, Table 3 provides the optimal values of the settling time and overshoot of the ball-beam system obtained from the adaptive robust PID control approach and the linear feedback control method introduced in (Mahmoodabadi et al., 2011). These values are calculated for initial conditions $x_1(0)=0$, $x_2(0)=0$, $x_3(0)=0$, $x_4(0)=0$, $x_5(0)=0$, $x_6(0)=0$, and for desired values $x_{1d}=0.2t$ and $x_{2d}=0.2$, $x_{3d}=0$, $x_{4d}=0$, $x_{5d}=0$, $x_{6d}=0$ simulated in 10 s.

Table 3. The comparison of the settling times and overshoots for the ball and the beam

Controller	Normalized settling time (s)		Normalized overshoot (m)
	Ball	Beam	Ball	Beam
Adaptive robust PID (this work)	2.94	5.41	9.08 × 10^−4	2.45 × 10^−2
Linear state feedback (Mahmoodabadi et al., 2011)	5.31	6.22	1.25 × 10^−2	2.84 × 10^−2

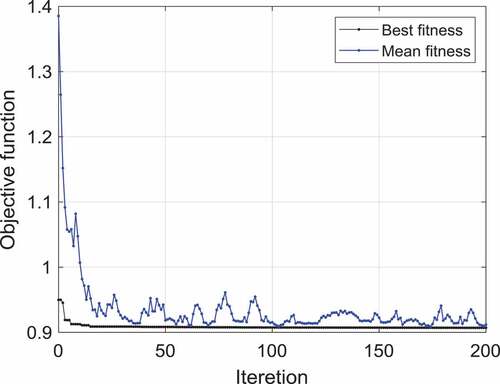
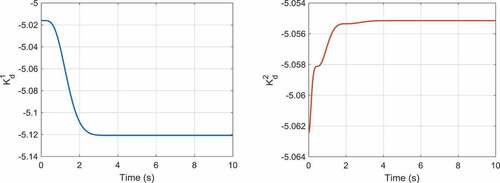
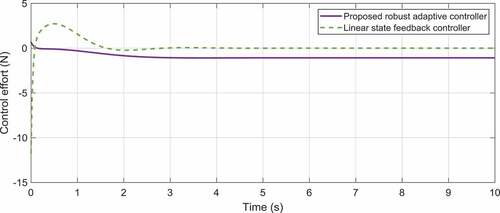
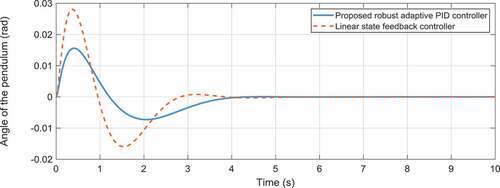
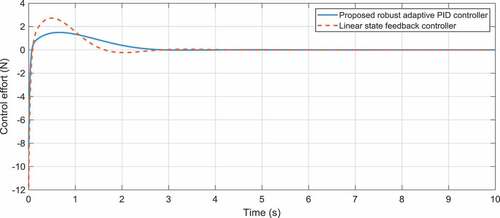
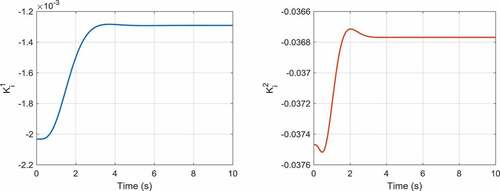
The optimization graph of this example is illustrated in Figure 4 for the population size of 50 and maximum iteration 200. The time responses of the proportional, integral and derivative gains related to the first and second outputs are correspondingly demonstrated in Figures 5–7. Moreover, Figures 8 and 9 illustrate the ball’s position and the beam’s angle obtained by the two control approaches. As these figures elucidate, the overshoots and settling times obtained by the adaptive robust control approach are significantly less than those for the control method proposed in (Mahmoodabadi et al., 2011). Moreover, the most interesting result is that the maximum absolute value of the control effort proposed by the adaptive robust PID controller is, indeed, significantly less than that for the linear feedback control scheme (Figure 10). It is noticeable that the remaining control effort in the static regime is utilized to overcome the viscous damping.

Figure 4. Optimization trajectory for the adaptive robust PID control of the ball-beam system

Figure 5. The time behaviors of the proportional gains for the first and second outputs of the ball-beam system

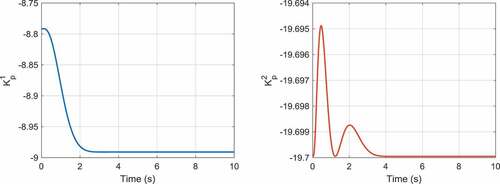
Figure 6. The time behaviors of the integral gains for the first and second outputs of the ball-beam system

Figure 7. The time behaviors of the derivative gains for the first and second outputs of the ball-beam system

Figure 8. The comparison of the time responses of the ball’s position

Figure 9. The comparison of the time response of the beam’s angle

Figure 10. The comparison of the time response of the control effort for the ball-beam system

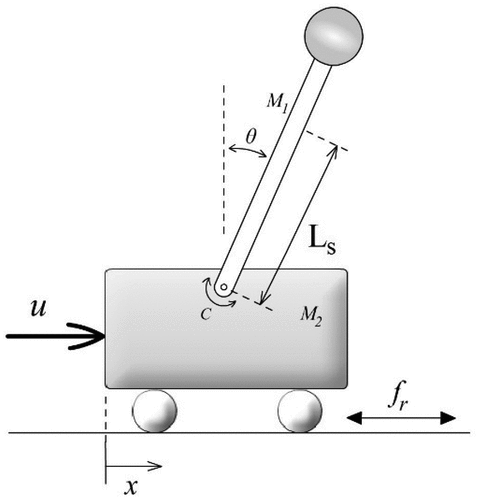
5.2. Cart-pole system

The physical structure of the cart-pole system is shown in Figure 11, which involves a cart as well as a pole attached to it. The general form of governing equations of this system obtained using Lagrange approach could be stated as follows.

(31) $I\ddot{\theta }+C\dot{\theta }-M_1{L}_{s}gsin\theta +M_1{L}_s\ddot{x}cos\theta =0$(31)

(32) $M\ddot{x}+f_r\dot{x}+M_1{L}_s\left(\ddot{\theta }cos\theta -{\dot{\theta }}^{2}sin\theta \right)=u$(32)

Figure 11. The physical structure of the cart-pole system

where $x$is the position of the cart, $\dot{x}$ represents the velocity of the cart, $\ddot{x}$ illustrates the acceleration of the cart, $\theta$ denotes the angle of the pole with respect to the vertical axis, $\dot{\theta }$ corresponds to the angular velocity of the pole, $\ddot{\theta }$ demonstrates the angular acceleration of the pole, $M_1$ represents the mass of the pole, $M=M_1+M_2$, and $M_2$ is the mass of the cart, $L_s$ denotes the length of the pole with respect to its center of mass, $f_r$ is the friction coefficient related to the contact surface of the cart with the ground. $I$ represents the inertia moment of the pole around its center of mass, $C$ is the rotational friction coefficient of the pole, $g$denotes the gravitational acceleration of the earth, and $u$is the control effort. The state vector of the system is considered as follows.

(33) ${\left[x_1,x_2,x_3,x_4,x_5,x_6\right]}^T={\left[{\int }^x,x,\dot{x},{\int }^{\theta },\theta ,\dot{\theta }\right]}^T$(33)

The system’s dynamical model linearized around the equilibrium point is illustrated in Eq. (34).

(34) $\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ \begin{array}{c}{\dot{x}}_4\\ {\dot{x}}_5\\ {\dot{x}}_6\end{array}\end{array}\right]=\frac{1}{1_o}\left[\begin{array}{cccc}0& I_o& 0& \begin{array}{cc}0& \begin{array}{cc}0& 0\end{array}\end{array}\\ 0& 0& IM-{(M_1{l}_s)}^2& \begin{array}{cc}0& \begin{array}{cc}0& 0\end{array}\end{array}\\ 0& 0& -I{f}_r& \begin{array}{cc}0& \begin{array}{cc}-{(M_1{l}_s)}^{2}g& M_1{l}_{s}C\end{array}\end{array}\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ M_1{l}_s{f}_r\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}{I}_o\\ \begin{array}{c}0\\ M{M}_1{l}_{s}g\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}IM-{(M_1{l}_s)}^2\\ -CM\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ \begin{array}{c}{x}_4\\ x_5\\ x_6\end{array}\end{array}\right]+\frac{1}{1_o}\left[\begin{array}{c}0\\ 0\\ I\\ 0\\ 0\\ -M_1{l}_s\end{array}\right]$(34)

Furthermore, the following constraints with regard to the physical conditions of the system must be satisfied.

• The constraint on the control effort: $\left|u\right|\le 20N$

• The constraint on the cart’s rail: $\left|x_2\right|\le 0.5m$

• The constraint on the rotational angle: $\left|x_5\right|\le 0.1745rad$

The numerical values of the physical characteristics of the inverted pendulum system are displayed in Table 4 according to (Mahmoodabadi et al., 2011). The vectors of the initial conditions and the final desired position are, respectively, considered according to Eqs. (35)(35) $x_0={\left[0,0,0,0,0,0\right]}^T$(35) and (36(36) $x_d={\left[0.2,0,0,0,0,0\right]}^T$(36) ).

(35) $x_0={\left[0,0,0,0,0,0\right]}^T$(35)

(36) $x_d={\left[0.2,0,0,0,0,0\right]}^T$(36)

Table 4. The physical characteristics of the cart-pole system

Parameter	$M_1$	$M_2$	$I_s$	$I$	$f_r$	$C$
value	0.36 kg	4 kg	0.451 m	0.08433 kg m^2	10 kg/s	0.00145 kgm^2/s

In order to find the optimum values of the control gains for the inverted pendulum system, the objective function is considered as the summation of the normalized values of the settling time and overshoot of the cart and the pendulum. Further, the constraints on the range of the control input and the movement of the cart and the pole must be met. In this study, the performance of the adaptive robust PID control approach optimized via the genetic algorithm is compared with that of the linear feedback control method optimized via the particle swarm optimization reported in (Mahmoodabadi et al., 2011). The optimum coefficients found by the proposed approach are presented in Table 5. In this table, $K_p^1(0)$, $K_i^1(0)$, $K_d^1(0)$, $K_p^2(0)$, $K_i^2(0)$ and $K_d^2(0)$ are the initial conditions for the gains of the control method. The obtained values for the settling time and overshoot of the cart and the pole resulting from the adaptive robust PID control approach and the linear feedback control method introduced in Mahmoodabadi et al. (2011) are illustrated in Table 6.

Table 5. The optimum gains of the proposed control approach for the cart-pole system

Control gain	$K_p^1(0)$	$K_i^1(0)$	$K_d^1(0)$	$K_p^2(0)$	$K_i^2(0)$	$K_d^2(0)$
Optimum value	4.2407 × 10^1	7.1593  × 10^−2	9.1467 × 10^1	4.1983 × 10^2	−1.0138  × 10^2	1.3700 × 10^2
Control gain	${\gamma }_p^1$	${\gamma }_i^1$	${\gamma }_d^1$	${\gamma }_p^2$	${\gamma }_i^2$	${\gamma }_d^2$
Optimum value	5.0149 × 10^2	−5.281  × 10^−1	9.1551 × 10^1	3.2287 × 10^2	2.0089 × 10^2	8.3789 × 10^1

Table 6. The comparison of the settling times and overshoots for the cart-pole system

Controller	Normalized settling time (s)		Normalized overshoot (m)
	Cart	Pendulum	Cart	Pendulum
Adaptive PID	3.0784	3.6079	2.7372$\times {10}^{-4}$	1.56$\times {10}^{-2}$
Linear state feed back	5.11	6.22	3$.14\times {10}^{-3}$	2.21$\times {10}^{-2}$

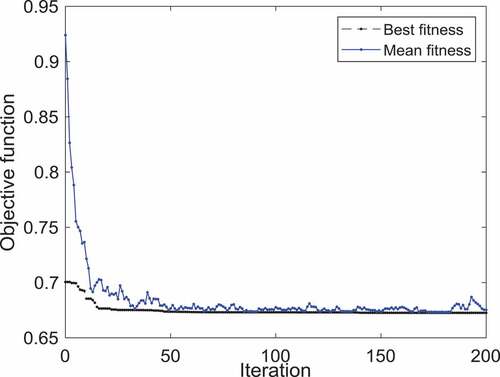
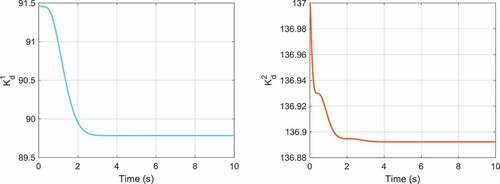
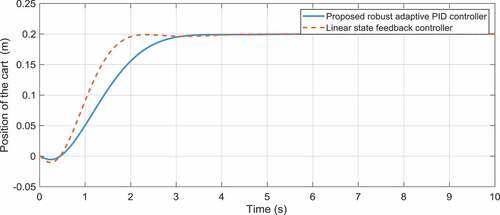
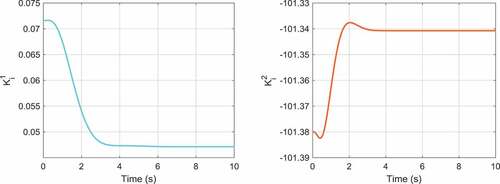
In Figure 12, the optimization graph obtained by the genetic algorithm for the adaptive robust PID control of the inverted pendulum system is illustrated. The time histories of the control gains of the first and second outputs are depicted in Figures 13–15. On the other hand, the position of the cart and the angle of the pole are displayed in Figures 16 and 17. As these figures illustrate, the proposed adaptive robust control method has lower overshoots and shorter settling times compared to the results of the controller introduced in Mahmoodabadi et al. (2011) for the cart-pole system. However, the significant outcome is that the maximum absolute value of the control effort for the proposed controller is highly less than that for the method suggested in (Mahmoodabadi et al., 2011) (Figure 18).

Figure 12. Optimization trajectory for the adaptive robust PID control of the cart-pole system

Figure 13. The time behaviors of the proportional gains for the first and second outputs of the cart-pole system

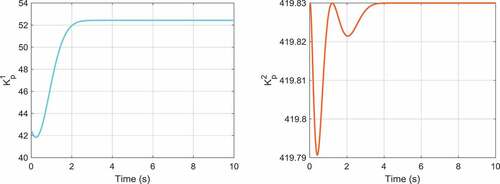
Figure 14. The time behaviors of the integral gains for the first and second outputs of the cart-pole system

Figure 15. The time behaviors of the derivative gains for the first and second outputs of the cart-pole system

Figure 16. The comparison of the time responses of the cart’s position

Figure 17. The comparison of the time response of the pole’s angle

Figure 18. The comparison of the time response of the control effort for the cart-pole system

6. Conclusions

In this paper, the challenging problem of the control of the under-actuated systems is effectively addressed via a novel optimum adaptive robust PID control approach. To this end, the proportional-integral-derivative control scheme is designed for the under-actuated systems, and the related parameters are adaptively computed using the gradient descent method and robust sliding mode surfaces. Indeed, an appropriate objective function based on the summation of the normalized settling times and overshoots is considered, and the optimal values of the design variables are obtained. Furthermore, the stabilization capabilities of the proposed controller are examined on the ball-beam and cart-pole systems, and the obtained results are compared with the results of the other methods introduced in the literature. Finally, the results demonstrate the capabilities of the proposed adaptive robust PID control approach for the control of the under-actuated systems via providing lower overshoots, shorter settling times and less energy consumption.

The future works related to this research could be mentioned as follows:

1. Applying the introduced strategy on the real dynamical system to evaluate the experimental results.

2. Implementation of the multi-criteria optimization approach to display the related Pareto front.

3. Utilizing the fuzzy systems to achieve more accurate results.

4. Employing the suggested method on the nonlinear dynamical systems.

5. Using the adaptive robust PID controller to handle the structural and un-structural uncertainties of the real systems.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

M.J. Mahmoodabadi

Mohammad Javad Mahmoodabadi received his BS and MS degrees in Mechanical Engineering from Shahid Bahonar University of Kerman, Iran in 2005 and 2007, respectively. He received his Ph.D. degree in Mechanical Engineering from the University of Guilan, Rasht, Iran in 2012. Now, he is an Associate Professor of Mechanical Engineering at the Sirjan University of Technology, Sirjan, Iran. His research interests include optimization algorithms, nonlinear and robust control and computational methods.

Samaneh Safi Jahanshahi was born in Sirjan, Kerman, Iran in 1993. She received her BS degree in Mechanical Engineering from Sirjan University of Technology, Sirjan, Iran in 2015. She received her MS degree in Mechanical Engineering from the University of Shahrood, Semnan, Iran in 2018. Her research interests include optimization algorithms, nonlinear and robust control, Numerical Methods, convective heat transfer, nanofluids and wavy channel.