A novel aggregation method for generating Pythagorean fuzzy numbers in multiple criteria group decision making: An application to materials selection

Abstract

Pythagorean Fuzzy Numbers are more capable of modeling uncertainties in real-life decision-making situations than Intuitionistic Fuzzy Numbers. Majority of research in Pythagorean Fuzzy Numbers, used in Multiple Criteria Decision-Making problems, has focused on developing operators and decision-making frameworks rather than the methodologies of generating the Pythagorean Fuzzy Numbers. Hence, this study aims at developing a novel aggregation method to generate Pythagorean Fuzzy Numbers from decision makers’ crisp data for Multiple Criteria Decision-Making problems. The aggregation method differs from other methods, used in generating Intuitionistic Fuzzy Numbers, by its ability to measure the uncertainty degrees in decision makers’ information and using them to generate Pythagorean Fuzzy Numbers. Initially, decision makers evaluate alternatives based on preset criteria using crisp decisions (i.e., crisp numbers) which are assigned by decision makers. A normalization method is used to normalize the given numbers from zero to one. Linear transformation is then used to identify the satisfactory and dissatisfactory elements of all normalized values. In the aggregation stage, the Sugeno fuzzy measure and Shapley value are used to fairly distribute the decision makers’ weights into the Pythagorean fuzzy numbers. Additionally, new functions to calculate uncertainty from decision-makers evaluations are developed using Takagai-Sugeno approach. An illustrative example in engineering materials selection application is presented to demonstrate the efficiency and applicability of the proposed methodology in real-life scenarios. Comparative analysis is performed to compare the results and performance of the introduced approach to other aggregation techniques.

Keywords:

• Pythagorean fuzzy numbers
• multiple criteria group decision making
• aggregation approach
• materials selection application
• Sugeno fuzzy measure
• Shapley value

PUBLIC INTEREST STATEMENT

“Group decision making is one of the most popular approaches for making critical decisions in various industries. Multiple Criteria Group Decision Making methods are commonly used to aggregate the Decision Makers’ information in order to achieve an optimal decision. Since group decision making is uncertain, the level of uncertainty and vagueness in decision-makers’ opinions need to be measured and considered for higher accuracy. This study aims at developing a novel aggregation method to generate Pythagorean Fuzzy Numbers from decision-makers’ crisp data to measure the uncertainty degrees in the information used by the decision-makers. A realistic example in engineering materials selection is presented to illustrate the efficiency of the proposed method in real life applications.”

1. Introduction

Multiple Criteria Decision Making (MCDM) is an effective technique that is used to assist decision makers (DMs) in selecting the best alternative for certain applications in various fields. The application of MCDM consists of defining a finite group of feasible alternatives and related criteria; determining the weight of each criterion and the impact of alternatives on the criteria; and defining the performance measures for ranking the alternatives (Chakraborty & Chatterjee, 2013; Jahan, Ismail, Mustapha et al., 2010). Effective formulation of MCDM problems plays a significant role in having a successful decision-making model with precise results. Typical MCDM problems are structured to allow DMs to rate each alternative with respect to each criterion. A proper mathematical representation of a MCDM problem starts with forming a decision-making matrix which includes the assigned alternatives and the listed weighted criteria as the following (Jahan, Ismail, Sapuan et al., 2010):

(1) $\begin{array}{rl}& C_1{C}_2-C_j\\ & D{\left(a_{ij}\right)}_{m\times n}=\begin{array}{c}{A}_1\\ A_2\\ -\\ A_i\end{array}\left[\begin{array}{cccc}{a}_{11}& a_{12}& -& a_{1j}\\ a_{21}& a_{22}& -& a_{2j}\\ -& -& -& -\\ a_{i1}& a_{i2}& -& a_{ij}\end{array}\right]\end{array}$(1)

where $D\left(a_{ij}\right)$ is the decision matrix and $a_{ij}$ is the rate value of the i^th alternative $(A_i:i=1,2,..,m)$ for the j^th criterion $(C_j:j=1,2,..,n)$. Weights $(w_j:j=1,2,\dots ,n)$ are assigned to each criterion and should satisfy $\sum _{j=1}^n{w}_j=1.$ Moreover, decision criteria are divided into two main categories: beneficial criteria (i.e., profit) and non-beneficial criteria (i.e., cost). Specifically, if a criterion satisfies the condition that higher scores are desirable, then it is a beneficial criterion; whereas for a criterion that satisfies the condition that lower scores are desirable, it is considered as a non-beneficial criterion.

A Multiple Criteria Group Decision Making (MCGDM) problem is often used to aggregate the DMs group information to achieve the most suitable decision (Yue, 2014b). The aim of using MCGDM techniques is to assist DMs in incorporating quantitative data with rate assessments which are constructed by collective decision-making group ideas and opinions (Liou & Chuang, 2010). The key to forming a MCGDM problem is to aggregate the rate assessments in a criterion vector into an overall criterion value of the alternative and finding the shared group decision matrix as shown in Eq. (1)(1) $\begin{array}{rl}& C_1{C}_2-C_j\\ & D{\left(a_{ij}\right)}_{m\times n}=\begin{array}{c}{A}_1\\ A_2\\ -\\ A_i\end{array}\left[\begin{array}{cccc}{a}_{11}& a_{12}& -& a_{1j}\\ a_{21}& a_{22}& -& a_{2j}\\ -& -& -& -\\ a_{i1}& a_{i2}& -& a_{ij}\end{array}\right]\end{array}$(1) .

Many MCDM tools, such as the traditional TOPSIS (Technique of Order Preference Similarity to the Ideal Solution), express decision-making problems in the form of a matrix filled with crisp data, under the assumption that the provided information is precisely defined. However, this may not be applicable in various real-life MCDM applications due to the difficulties that DMs encounter in expressing precise opinions related to some alternatives, particularly when it comes to dealing with incomplete data (Zhang, 2016). For this reason, fuzzy sets theory, which was introduced by Bellman and Zadeh (1970), has been used to assign fuzzy numbers in solving MCDM problems, considering the fuzziness in DMs’ preferences and the uncertainty of the objectives (DMs use $u_{C_j}\left(x_i\right)$ to show their satisfaction of a specific alternative $x_i$ in meeting criterion $C_j$). In addition, DMs give their opinions regarding the grade to which alternative $x_i$ doesn’t satisfy criterion $C_j$.

Atanassov (1986) introduced the Intuitionistic Fuzzy Set (IFS) theory, where DMs can show their preferences of alternative $x_i$ regarding criterion $C_j$ with reference to a membership grade, and a non-membership grade, where the sum of its membership and non-membership grades are equal to or less than 1. IFS has been widely employed in many real-world MCDM applications and problems (An et al., 2018; Hashemi et al., 2016; Kuei-Hu, 2019; Kumar & Garg, 2018; Y. Li et al., 2014; Pérez-Domínguez et al., 2018; Ren et al., 2017; Wu et al., 2013; Xue et al., 2016; Zhang et al., 2014; Zhao et al., 2017; Zhou et al., 2014). Recently, several studies aimed at developing various extensions of IFS for decision-making under uncertainty (Feng et al., 2019, 2020; Garg & Chen, 2020; Liu et al., 2018; Yager, 2017). Furthermore, Yager (2013) presented a Pythagorean Fuzzy Set (PFS) concept based on the condition that the square sum of both the membership and non-membership grades of an alternative is equal to or less than 1. The rationale is that in real-world decision-making applications, DMs present their views about the satisfactory (membership) grade and dissatisfactory (non-membership) grade for a specific alternative having a sum of grades that may be greater than 1, whereas the sum of their squares is equal to or less than 1. Yager (2014) offered a simple numerical example to illustrate this concept in which the membership grade of an alternative $x_i$ that satisfies criterion $C_j$ is equal to $\frac{\sqrt{3}}{2}$ and a non-membership grade of an alternative $x_i$ that dissatisfies criterion $C_j$ is equal to $\frac{1}{2}$. It can be noticed that $\frac{\sqrt{3}}{2}+\frac{1}{2}\ge 1;$ hence, IFS cannot define this situation. On the other hand, ${\left(\frac{\sqrt{3}}{2}\right)}^2+{\left(\frac{1}{2}\right)}^2\le 1$ can be defined by PFS. Therefore, PFS is better suited for modeling uncertainties in real-world decision-making scenarios than IFS. Several studies have been published recently showing various applications of PFS in decision-making processes (Garg, 2016; Zhang, 2016, 2017; Ali Khan et al., 2019; Bryniarska, 2020).

Previous work on fuzzy set and its extensions in group decision-making applications has mainly focused on developing operators and decision-making tools to rank the final outcomes without considering the initial step of converting crisp data into fuzzy numbers (Liang et al., 2015; Zhang, 2016; Biswas & Sarkar, 2018; Xindong, 2019; Akram, Dudek & Ilyas, 2019; Ali Khan et al., 2019; Abdullah & Goh, 2019; Khan et al., 2020; Akram, Ilyas et al., 2020; Liu & Du, 2020; Jih-Chang & Ting-Yu, 2020; Akram, Garg et al., 2020; Zhou & Chen, 2020; Guo, 2013; Das et al., 2014; Montajabiha, 2016; Liangli et al., 2017; L. Zhang, 2018; Garg & Kumar, 2020; Garg & Kaur, 2020; Darko & Liang, 2020, 2020; H. Li et al., 2021; Akram et al., 2021; Ashraf et al., 2020; Remadi & Frikha, 2020). However, limited research has addressed developing the initial aggregation phase of generating intuitionistic fuzzy numbers and its extension from decision makers’ decision information for MCGDM problems (Yue, 2008; Yue et al., 2008, 2009; Yue, 2011; Yue & Jia, 2013; Yue, 2014a; Lin & Zhang, 2016; Wan, Xu & Dong, 2016).

Since PFS properties provide extra flexibility for decision makers to express their judgments than IFS, this study aims at developing a novel aggregation method to generate PFNs from decision makers’ crisp data for MCDM problems. This aggregation method differs from other methods used in generating IFNs by its ability to measure the uncertainty degree in decision makers’ information and using it to generate PFNs.

In this paper, a new aggregation approach to convert crisp numbers into Pythagorean Fuzzy Numbers (PFNs) is introduced. It starts with an assessment process in which DMs rate each criterion with respect to a set of alternatives using crisp numbers. These numbers are then normalized to values between zero and one. Meanwhile, the satisfactory and dissatisfactory elements are identified through linear transformation of all normalized values. Furthermore, Sugeno Fuzzy measures and Shapley values are used to fairly distribute the DMs’ weights in the Pythagorean Fuzzy numbers. New functions are introduced to calculate uncertainty from DMs evaluations using Takagai-Sugeno approach. A realistic engineering materials selection application is used to compare the performance of the proposed aggregation method against other conventional methods.

2. Preliminaries

2.1. Intuitionistic Fuzzy Sets (IFSs)

An Intuitionistic fuzzy set I in a fixed set X can be represented as (Atanassov, 1986):

(2) $I=\{⟨x,I\left({\mu }_I\left(x\right),v_I\left(x\right)\right)⟩|x\in X\}$(2)

where the membership function ${\mu }_I$: X → [0, 1] describes the degree of satisfaction and the non-membership function $v_I$: X → [0, 1] describes the degree of dissatisfaction of the element x ∈ X to P, respectively. The following condition is satisfied for all x ∈ X,

(3) $0\le {\mu }_I\left(x\right)+v_I\left(x\right)\le 1$(3)

For every set of I and x $\text{isin}$ X, ${\pi }_I\left(x\right)=1-{\mu }_I\left(x\right)-v_I\left(x\right)$ is known as the degree of uncertainty of x to I.

Definition 1: Let ${\alpha }_1=I\left({\mu }_{{\alpha }_1},v_{{\alpha }_1}\right)and{\alpha }_2=I\left({\mu }_{{\alpha }_2},v_{{\alpha }_2}\right)$ be two IFNs then,

1. If $s\left({\alpha }_1\right)<s\left({\alpha }_2\right),$ then ${\alpha }_1<{\alpha }_2$;

2. If $s\left({\alpha }_1\right)>s\left({\alpha }_2\right),$ then ${\alpha }_1>{\alpha }_2$;

3. If $s\left({\alpha }_1\right)=s\left({\alpha }_2\right),$ then

   1. If $h\left({\alpha }_1\right)<h\left({\alpha }_2\right),$ then ${\alpha }_1<{\alpha }_2;$

   2. If $h\left({\alpha }_1\right)>h\left({\alpha }_2\right),$ then ${\alpha }_1>{\alpha }_2$;

   3. If $h\left({\alpha }_1\right)=h\left({\alpha }_2\right),$ then ${\alpha }_1={\alpha }_2$.

where $s\left({\alpha }_1\right)={\mu }_{{\alpha }_1}-v_{{\alpha }_1}$ and $h\left({\alpha }_1\right)={\mu }_{{\alpha }_1}+v_{{\alpha }_1}$ are the score and accuracy functions of IFN ${\alpha }_1=I\left({\mu }_{{\alpha }_1},v_{{\alpha }_1}\right)$, respectively (Xu, 2007; Xu & Yager, 2006).

2.2. Pythagorean Fuzzy Sets (PFSs)

Yager (2013, 2014) presented three key demonstrations for Pythagorean membership degrees as the following: (1) $\left(a,b\right)$ should fulfill the conditions that $a\in \left[0,1\right],\mathrm{b}\in \left[0,1\right],$ and $a^2+b^2\le 1$; (2) the polar coordinates $\left(r,\theta \right)$ should fulfill that $r\in \left[0,1\right],\theta \in \left[0,\pi /2\right]$; (3) $\left(r,d\right)$ should fulfill that $r\in \left[0,1\right],\theta \in \left[0,\pi /2\right]$, and $d=1-2\theta /\pi$. Their relationship is that $a^2+b^2=r^2$, a = $r$ cos(θ), b = $r$ sin(θ).

Definition 2: A Pythagorean fuzzy set P in a fixed set X can be represented as:

(4) $P=\{⟨x,\hspace{0.17em}P\hspace{0.17em}\left({\mu }_P\hspace{0.17em}\left(x\right),\hspace{0.17em}{v}_P\left(x\right)\right)⟩|x\hspace{0.17em}\text{isin}\hspace{0.17em}X\}$(4)

where the membership function ${\mu }_P$: X → [0, 1] describes the degree of satisfactory and the non-membership function $v_P$: X → [0, 1] describes the degree of dissatisfactory of the element x ∈ X to P, respectively, and for all x ∈ X, it satisfies

(5) $0\le {\left({\mu }_P\left(x\right)\right)}^2+{\left(v_p\left(x\right)\right)}^2\le 1$(5)

For every set of P and x $\text{isin}$ X, ${\pi }_P\left(x\right)=\sqrt{1-{\mu }_P^2\left(x\right)-v_P^2\left(x\right)}$ is known as the degree of uncertainty of x to P. Moreover, for simplification, a Pythagorean fuzzy number (PFN) will be denoted as $\beta =P\left({\mu }_{\beta },v_{\beta }\right)$, such that;0

${\mu }_{\beta }$, $v_{\beta }$ ∈ [0, 1],$({\pi }_{\beta }{)}^2=1-({\mu }_{\beta }{)}^2-(v_{\beta }{)}^2$,

(6) $({\mu }_{\beta }{)}^2-(v_{\beta }{)}^2\le 1$(6)

Zhang and Xu (2014) developed the next PFNs basic properties.

Definition 3—Proposition 1: Let ${\beta }_1=P\left(u_{{\beta }_1},v_{{\beta }_1}\right),{\beta }_2=P\left(u_{{\beta }_2},v_{{\beta }_2}\right),$ and $\beta =P\left({\mu }_{\beta },v_{\beta }\right)$, be three PFNs then,

1.${\beta }_1\oplus {\beta }_2={\beta }_2\oplus {\beta }_1$

2.${\beta }_1\otimes {\beta }_2={\beta }_2\otimes {\beta }_1$

3.$\lambda \left({\beta }_1+{\beta }_2\right)=\lambda {\beta }_1\oplus \lambda {\beta }_2,\lambda >0$

4.${\lambda }_1\beta \oplus {\lambda }_2\beta$ = $\left({\lambda }_1+{\lambda }_2\right)\beta ,{\lambda }_1,{\lambda }_2>0$

5.${\left({\beta }_1\otimes {\beta }_2\right)}^{\lambda }={{\beta }_1}^{\lambda }\otimes {{\beta }_2}^{\lambda },\lambda >0$

6.${\beta }^{{\lambda }_1}\otimes {\beta }^{{\lambda }_2}={\beta }^{({\lambda }_1+{\lambda }_2)}{\lambda }_1,{\lambda }_2>0$

Definition 4: Let ${\beta }_j=P\left(u_{{\beta }_j},v_{{\beta }_j}\right)\left(j=1,2\right)$ be two PFNs; then a natural quasi-ordering on PFNs can be expressed as ${\beta }_1\ge {\beta }_2$ if and only if $u_{{\beta }_1}\ge u_{{\beta }_2}$and $v_{{\beta }_1}\le v_{{\beta }_2}$.

To compare the magnitudes of two PFNs, the following score function is introduced (Yager, 2014; Zhang & Xu, 2014).

Definition 5: Let $\beta =P\left(u_{\beta },v_{\beta }\right)$ be a PFN; then the score function of $\beta$ score function is presented as:

(7) $s\left(\beta \right)={\left(u_{\beta }\right)}^2-{\left(v_{\beta }\right)}^2$(7)

where the score function, $s\left(\beta \right)$ ∈ [−1, 1]. For PFNs, ${\beta }_j=P\left(u_{{\beta }_j},v_{{\beta }_j}\right)\left(j=1,2\right)$, if ${\beta }_1\le {\beta }_2,$ then $s\left({\beta }_1\right)\le s\left({\beta }_2\right)$. The subsequent laws are introduced with reference to PFNs score function in order to make a comparison between two PFNs (Yager, 2014; Zhang & Xu, 2014).

Definition 6: Let ${\beta }_j=P\left(u_{{\beta }_j},v_{{\beta }_j}\right)\left(j=1,2\right)$ be two PFNs, $s\left({\beta }_1\right)$ and $s\left({\beta }_2\right)$ be the amounts of ${\beta }_1$ and ${\beta }_2$ score functions, respectively; then:

1. If $s\left({\beta }_1\right)<s\left({\beta }_2\right),$ then ${\beta }_1<{\beta }_2$;

2. If $s\left({\beta }_1\right)>s\left({\beta }_2\right),$ then ${\beta }_1>{\beta }_2$;

3. If $s\left({\beta }_1\right)=s\left({\beta }_2\right),$ then ${\beta }_1\sim {\beta }_2$;

Furthermore, Yager (2014) presented the next operator in order to aggregate PFNs.

Definition 7: Let ${\beta }_j=P\left(u_{{\beta }_j},v_{{\beta }_j}\right)\left(j=1,2,\dots ,n\right)$ be a group of PFNs and $w={\left(w_1,w_2,\dots ,w_n\right)}^T$ represent the weight vector of ${\beta }_j\left(j=1,2,\dots ,n\right)$, where $w_j$ denotes the importance level of ${\beta }_j$, fulfilling $w_j\ge 0\left(j=1,2,\dots ,n\right)$ ${\sum }_{j=1}^n{w}_j=1$, then PFNs can be aggregated using the following operator:

(8) $PFO\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right)=P({\sum }_{j=1}^n{w}_j{u}_{{\beta }_j},{\sum }_{j=1}^n{w}_j{v}_{{\beta }_j})$(8)

where PFO is called the Pythagorean Fuzzy Operator.

Illustrative Example: consider three PFNs ${\beta }_1\left(x\right)=P\left(0.7,0.4\right)$, ${\beta }_2\left(x\right)=P\left(0.8,.5\right)$, and ${\beta }_3\left(x\right)=P\left(0.5,0.4\right)$. Each PFN represents the value to which alternative $x$ satisfies and dissatisfies the criterion $\beta =\left\{{\beta }_j:j=1,2,\dots ,n\right\}$. The importance weights for the criteria are $w_1$ = 0.5, $w_2$ = 0.2, and $w_3$ = 0.3, respectively. PFNs can, therefore, be aggregated as the following: $PFO\left(\beta \left(x\right)\right)=P({\sum }_{j=1}^3{w}_j{u}_{{\beta }_j},{\sum }_{j=1}^3{w}_j{v}_{{\beta }_j})$ = (0.66, 0.42).

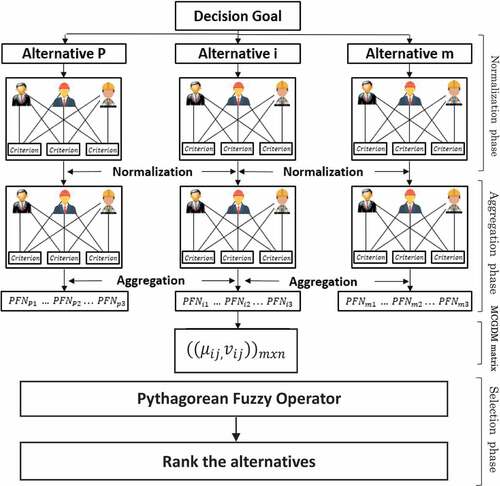
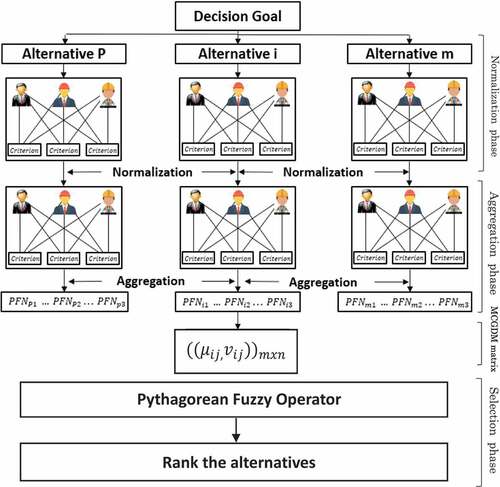
3. Proposed MCDM for Group Decision Making (MCGDM)

MCDM problems are formulated to serve the purpose of aggregating the DMs group information and thoughts to get the most suitable outcome (Yue, 2014b). In this case, a Multiple Criteria Group Decision Matrix (MCGDM) is designed as shown below:

(9) $\begin{array}{rl}& C_1\hspace{0.17em}{C}_2\hspace{0.17em}-\hspace{0.17em}{C}_n\hspace{0.17em}\\ & \hspace{0.17em}\\ & X_i={\left(r_{kj}^i\right)}_{t\times n}=\begin{array}{c}{d}_1\\ d_2\\ -\\ d_t\end{array}\left[\begin{array}{cccc}{r}_{11}^i& r_{12}^i& -& r_{1n}^i\\ r_{21}^i& { }_{22}^i& -& r_{2n}^i\hspace{0.17em}\\ -& -& -& -\\ r_{t1}^i& r_{t2}^i& -& r_{tn}^i\end{array}\right],i=1,2,\dots ,m\end{array}$(9)

$X_i={\left(r_{kj}^i\right)}_{t\times n}$ refers to the group decision matrix for i^th alternative in which each decision-maker $D=\left\{d_k:k=1,2,\dots ,t\right\}$ evaluates the importance of each given criterion $C=\left\{C_j:j=1,2,\dots ,n\right\}$ regarding alternative $x=\left\{x_i:i=1,2,\dots ,m\right\}$.

3.1. Normalization phase

Normalizing DMs data regarding performance evaluation is a significant step to begin the aggregation process. Appropriate normalization of the given numbers would facilitate converting them into Pythagorean fuzzy numbers efficiently, leading to an effective application of the MCGDM model. To start the normalization process, each group decision matrix $X_i={\left(r_{kj}^i\right)}_{t\times n}$ for each i^th alternative needs to be normalized into $R_i={\left(s_{kj}^i\right)}_{t\times n}$ using the following equations:

(10) $s_{kj}^i=\frac{r_{kj}^i-minj}{maxj-minj},forbenefecialcriteria{C}_j$(10)

(11) $s_{kj}^i=\frac{maxj-r_{kj}^i}{maxj-minj},fornon-benefecialcriteria{C}_j$(11)

where the $maxj$ and $minj$ are the highest rate and the lowest rate applied by a decision-maker $d_k$ in the evaluation system, respectively. However, in order to fit the MCGDM problem purpose, the hundred-mark system that consists of 100 being as the highest rate $(maxj)$ and 0 being as the lowest rate $(minj)$ is suggested to be used by the DMs in the assessment phase for MCGDM problems (Liu & Qiu, 1998). For this reason, equations (10)(10) $s_{kj}^i=\frac{r_{kj}^i-minj}{maxj-minj},forbenefecialcriteria{C}_j$(10) and (11(11) $s_{kj}^i=\frac{maxj-r_{kj}^i}{maxj-minj},fornon-benefecialcriteria{C}_j$(11) ) can be rewritten as:

(12) $s_{kj}^i=\frac{r_{kj}^i-0}{100},forbenefecialcriteria{C}_j$(12)

(13) $s_{kj}^i=\frac{100-r_{kj}^i}{100},fornon-benefecialcriteria{C}_j$(13)

After normalization, $R_i={\left(s_{kj}^i\right)}_{t\times n}$ matrix is represented as:

$\begin{array}{cccc}{C}_1& C_2& -& C_n\end{array}$

(14) $R_i={\left(s_{kj}^i\right)}_{t\times n}=\begin{array}{c}{d}_1\\ d_2\\ -\\ d_t\end{array}\left[\begin{array}{cccc}{s}_{11}^i& s_{12}^i& -& s_{1n}^i\\ s_{21}^i& s_{22}^i& -& s_{2n}^i\\ -& -& -& -\\ s_{t1}^i& s_{t2}^i& -& s_{tn}^i\end{array}\right],i=1,2,\dots ,m$(14)

However, the values in the normalizing column vectors in Eq. (14)(14) $R_i={\left(s_{kj}^i\right)}_{t\times n}=\begin{array}{c}{d}_1\\ d_2\\ -\\ d_t\end{array}\left[\begin{array}{cccc}{s}_{11}^i& s_{12}^i& -& s_{1n}^i\\ s_{21}^i& s_{22}^i& -& s_{2n}^i\\ -& -& -& -\\ s_{t1}^i& s_{t2}^i& -& s_{tn}^i\end{array}\right],i=1,2,\dots ,m$(14) should be within $\left[0,1\right]$ and should satisfy that the highest rate is 1 and the lowest rate is 0. The satisfactory and dissatisfactory values in the criterion/column vector $R_i=\left(s_{1j}^i,s_{2j}^i,\dots ,s_{tj}^i\right)$ need to be defined to pursue the aggregation approach.

3.2. Aggregation phase

Yue (2014b) introduced a method to generate intuitionistic fuzzy numbers, which has been criticized by Lin and Zhang (2016) for having weaknesses that result in illogical outcomes, specifically in measuring DMs weights, which hinders them impractical for real-world applications. Instead, they presented a new revised aggregation approach for IFNs by implementing the Shapley value method within the aggregation technique which forms the basis for our proposed aggregation approach in this section.

In order to determine PFNs efficiently, all crisp decisions in$R_i$ need to be aggregated within the process. The aggregation process of PFNs should consider determining three main elements: membership degree ${\mu }_{\alpha }$ (degree of satisfaction), non-membership degree ${\nu }_{\alpha }$ (degree of dissatisfaction) and hesitation degree ${\pi }_{\alpha }$ (degree of uncertainty) in which the induced numbers satisfy Eq. (5)(5) $0\le {\left({\mu }_P\left(x\right)\right)}^2+{\left(v_p\left(x\right)\right)}^2\le 1$(5) and Eq. (6(6) $({\mu }_{\beta }{)}^2-(v_{\beta }{)}^2\le 1$(6) ); respectively. Initially, some rules should be followed to define the satisfactory, dissatisfactory or uncertain values. As seen in Eq. (15(15) $s_{kj}^u=\left\{s_{kj}^i>0.5,\hspace{0.17em}{s}_{kj}^{i}aretheelementsof\hspace{0.17em}{R}_i\right\}i\in M,j\in N,k\in T$(15) ), all values are within [0,1]; thus, “0.5” will be the bound for identifying the satisfactory and dissatisfactory value.

For the criterion vector in Eq. (14(14) $R_i={\left(s_{kj}^i\right)}_{t\times n}=\begin{array}{c}{d}_1\\ d_2\\ -\\ d_t\end{array}\left[\begin{array}{cccc}{s}_{11}^i& s_{12}^i& -& s_{1n}^i\\ s_{21}^i& s_{22}^i& -& s_{2n}^i\\ -& -& -& -\\ s_{t1}^i& s_{t2}^i& -& s_{tn}^i\end{array}\right],i=1,2,\dots ,m$(14) ), let

(15) $s_{kj}^u=\left\{s_{kj}^i>0.5,\hspace{0.17em}{s}_{kj}^{i}aretheelementsof\hspace{0.17em}{R}_i\right\}i\in M,j\in N,k\in T$(15)

(16) $s_{kj}^c=\left\{s_{kj}^i<0.5,\hspace{0.17em}{s}_{kj}^{i}aretheelementsof\hspace{0.17em}{R}_i\right\}i\in M,j\in N,k\in T$(16)

A linear transformation should be made to each element to determine the satisfaction, dissatisfaction, and uncertainty degrees. The calculation of this process should take into consideration the following rules: (1) if the element value $\left(s_{kj}^u\right)$ is close to 1, then the satisfactory level is high; (2) if element value $\left(s_{kj}^c\right)$ is close to 0, then the dissatisfactory level is high; and (3) if the element values of $\left(s_{kj}^u\right)$ or $\left(s_{kj}^c\right)$ are close to 0.5, then the uncertainty level is high. The linear transformation formula can be represented as follows:

(17) $o_{ij}=\frac{s_{kj}^u-0.5}{1-0.5}i\in M,j\in N,k\in T$(17)

(18) ${\xi }_{ij}=\frac{0.5-s_{kj}^c}{0.5-0}i\in M,j\in N,k\in T$(18)

where $o_{ij}$ represents each satisfactory element of i^th alternative for the j^th criterion; and ${\xi }_{ij}$ represents each dissatisfactory element of i^th alternative for the j^th criterion.

Next, the satisfaction and dissatisfaction elements of each j^th criterion in i^th alternative are aggregated considering all DMs importance (weights), which may not all be equal. The weights are assigned based on several factors, such as educational background, experience level and authority (Lin & Zhang, 2016). In order to assign the priority of each decision-maker effectively, an evaluation process can be done by conducting surveys and interviews with the assigned committee members. Lin and Zhang (2016) used Shapely values to determine the correlative and interaction relationships among DMs; specifically, how much a DM adds to the coalition of DMs. For example, a DM whose opinion adds little to a coalition has a small Shapley value, while a DM whose opinion has significant effect on the coalition has a high Shapley value. As a result, it is a useful way for a fair division of DMs weights based on their contributions to the system. The following formula can clearly express the Shapely value mathematically:

(19) ${\mathrm{\Phi }}_k=\frac{1}{t!}\sum _{F\subseteq D\setminus \left\{d_k\right\}}\left|F\right|!\left(t-\left|F\right|-1\right)!\left[\mu \left(F{\cup }^{}\left\{d_k\right\}\right)-\mu \left(F\right)\right]\mathrm{\forall }k\in \left\{1,2,\dots ,t\right\}$(19)

${\mathrm{\Phi }}_k$ is the Shapley value, which denotes the value of the marginal contribution weighted average regarding a decision-maker $d_k$; $\mu$ is a fuzzy measure on a finite set that represents decision makers $D=\left\{d_1,d_2,\dots ,d_t\right\}$; $\mu \left(F\right)$ is the weight of the subset in group decision-making $F$, $F\subseteq D$ and it can be determined using the $\lambda$-fuzzy measures of Sugeno as follows (Sugeno, 1974a; Fatima et al., 2008):

(20) $\lambda +1=\prod _{k=1}^t\left(1+\lambda \mu \left(\{d_k\}\right)\right)$(20)

where $\lambda >-1$ and,

(21) $\mu \left(F)=\mu (\left\{d_A\right\}{\cup }^{}\left\{d_B\right\}\right)=\mu \left(d_A\right)+\mu \left(\{d_B\}\right)+\lambda \mu \left(d_A\right)\mu \left(\left\{\{d_B\right\}\right)$(21)

where $AB\in \left(1,2,\dots ,k\right)andA\ne B$.

The Sugeno $\lambda$-fuzzy measures are a function (nondecreasing) that takes into account the amounts of the estimate of the elemental fuzzy density values $\mu \left(\{d_k\}\right)$ (Leszczyński et al., 1985).

After calculating the Shapley value of each DM, the weighted averages of the satisfactory and dissatisfactory values are calculated, respectively, as:

(22) ${\kappa }_{ij}={\sum }_{k=1}^t{\mathrm{\Phi }}_k{o}_{k}i\in M,j\in N,k\in T$(22)

(23) ${\varsigma }_{ij}={\sum }_{k=1}^t{\mathrm{\Phi }}_k{\xi }_{k}i\in M,j\in N,k\in T$(23)

where ${\kappa }_{ij}$ and ${\varsigma }_{ij}$ are the weighted average satisfactory degree and the weighted average dissatisfactory degree, respectively; $\mathrm{\Phi }$ is the weight of importance of each DM with ${\mathrm{\Phi }}_k\in \left[0,1\right]$.

After finding the weighted average satisfactory and dissatisfactory values, the uncertainty of the induced numbers is calculated based on Pythagorean fuzzy sets concept in MCDM as defined by Yager (2014). In order to complete this step, the sum of the square root of satisfactory and dissatisfactory degrees is calculated as:

(24) $r=\sqrt{{\kappa }_{ij}^2+{\varsigma }_{ij}^2}$(24)

Then, the determination of theta ($\theta )$ would highly contribute to identifying the performance of the uncertainty function. Using $r$, ($\theta )$ can be calculated as follows:

(25) $cos\left(\theta \right)=\frac{\kappa }{r}$(25)

For function modeling purposes, ($\theta )$ will be transformed as follows:

(26) $d=1-\frac{\theta }{\pi }$(26)

To define the uncertainty degree in an appropriate logical and mathematical approach, a fuzzy modeling method using Takagi–Sugeno (T-K) approach is applied to build the required functions (Mohamed & Xiao, 2003). The fuzzy modeling application relies on forming fuzzy base rules that aim to explain local input–output relations between the previous experimental data in the function (Takagi & Sugeno, 1985). In order to form reasonable fuzzy base rules, the required function $F\left(x\right)$ behavior should be demonstrated precisely. As mentioned earlier, 0.5 is the bound that has been used to distinguish between the satisfactory and dissatisfactory degrees of each element; therefore, it will be used again for identifying the amount of uncertainty. In other words, if d = 0.5 then the uncertainty will be at its highest degree $f=1$ and the farthest the value from the 0.5 bound, the lower the uncertainty degree will be. Consequently, the fuzzy base rules that are going to be implemented in the modeling technique are defined as the following:

First function modeling rules (when $d>0.5,\theta <\frac{\pi }{4})$:

$R^1:\mathrm{I}\mathrm{F}riscloseto1anddiscloseto1\mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{g}_1\left(r,d\right)=0,$

$R^2:\mathrm{I}\mathrm{F}riscloseto1anddiscloseto0.5\mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{g}_2\left(x\right)=1,$

$R^3:\mathrm{I}\mathrm{F}riscloseto0\mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{g}_3\left(x\right)=1,$

Second function modeling rules (when $d<0.5,\theta <\frac{\pi }{4})$:

$R^1:\mathrm{I}\mathrm{F}riscloseto1anddiscloseto0\mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{g}_1\left(r,d\right)=0,$

$R^2:\mathrm{I}\mathrm{F}riscloseto1anddiscloseto0.5\mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{g}_2\left(r,d\right)=1,$

$R^3:\mathrm{I}\mathrm{F}riscloseto0\mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{g}_3\left(r,d\right)=1,$

For clarification, when $riscloseto1$ it will be represented as a fuzzy subset $A_1$ on the unit interval with a membership function $\left(E_{A1}\left(r\right)=r\right)$. When $riscloseto0,$ it will be represented as a fuzzy subset $A_2$ on the unit interval with a membership function ($E_{A2}\left(r\right)=1-r).$ In the first function rules, $d\in \left[0.5,1\right];$ thus, when $discloseto1$ it will be represented as a fuzzy subset $C_1$ on the unit interval with a membership function ($E_{C1}\left(d\right)=2d)$ and when $discloseto0.5$ it will be represented as a fuzzy subset $C_2$ on the unit interval with a membership function ($E_{C2}\left(d\right)=2-2d).$

In the second function rules, $d\in \left[0,0.5\right]$, when $discloseto0$ it will be represented as a fuzzy subset $N_1$ on the unit interval with a membership function ($E_{N1}\left(d\right)=2-2d)$ and when $discloseto0.5$ it will be represented as a fuzzy subset $N_2$ on the unit interval with a membership function ($E_{N2}\left(d\right)=2d).$ In general, $g_i\left(r,d\right)$ is the output of applying the i^th rule. Therefore, the uncertainty functions (A) and (B) using T-K approach to aggregate fuzzy rule bases can be represented as:

(27) $f_A\left(r,d\right)=\frac{E_{A1}\left(r\right)E_{C1}\left(d\right)\left(0\right)+E_{A1}\left(r\right)E_{C2}\left(d\right)\left(1\right)+E_{A2}\left(r\right)\left(1\right)}{E_{A1}\left(r\right)E_{C1}\left(d\right)+E_{A1}\left(r\right)E_{C2}\left(d\right)+E_{A2}\left(r\right)}d>0.5,\theta <\frac{\pi }{4}$(27)

(28) $f_B\left(r,d\right)=\frac{E_{A1}\left(r\right)E_{N1}\left(d\right)\left(0\right)+E_{A1}\left(r\right)E_{N2}\left(d\right)\left(1\right)+E_{A2}\left(r\right)\left(1\right)}{E_{A1}\left(r\right)E_{N1}\left(d\right)+E_{A1}\left(r\right)E_{N2}\left(d\right)+E_{A2}\left(r\right)}d⟨0.5,\theta ⟩\frac{\pi }{4}$(28)

It can be observed from the first function behavior that if $r$ has been placed as a fixed arc of radius, then the uncertainty function will decrease from $f_A\left(r,d\right)=1$ to $f_A\left(r,d\right)=0$ as it goes from $d=0.5$ to $d=1,$ which is similar to $\theta =\pi /4$ to $\theta =0$. Also, if $d$ is any fixed value from ($0.5<d\le 1)$ then the function will decrease from $f_A\left(r,d\right)=1$ to $f_A\left(r,d\right)=0$ as the radius increases from $r=0$ to $r=1$. Lastly, if $d=0.5$ then $f_A\left(r,d\right)=1$ and it stays the same at any $r$ value.

The uncertainty degree ${\tau }_{ij}$ can be represented as a piecewise function:

(29) ${\tau }_{ij}=\left\{\begin{array}{c}{f}_A\left(r,d\right);\{d|0.5<d\le 1\}\\ f_B\left(r,d\right);\{d|0\le d<0.5\}\\ 1;\{d|d=0.5\}\end{array}\right.$(29)

Hence, the Pythagorean Fuzzy set (PFS) in terms of the satisfactory degree and dissatisfactory degree of i^th alternative to the j^th criterion, ${\mu }_{ij}$ and ${\upsilon }_{ij}$, can be represented as PFS: $P\left({\mu }_{ij},v_{ij}\right)$, where:

(30) ${\mu }_{ij}=\sqrt{\frac{{{\kappa }_{ij}}^2}{{{\kappa }_{ij}}^2+{{\varsigma }_{ij}}^2+{{\tau }_{ij}}^2}},i\in M,j\in N$(30)

(31) ${\upsilon }_{ij}=\sqrt{\frac{{{\varsigma }_{ij}}^2}{{{\kappa }_{ij}}^2+{{\varsigma }_{ij}}^2+{{\tau }_{ij}}^2}},i\in M,j\in N$(31)

After converting all crisp data into PFNs, the collective evaluation of the Pythagorean fuzzy decision matrix $R=(C_j\left(x_i\right){)}_{m\times n}$ is constructed as:

$\begin{array}{cccc}{C}_1& C_2& -& C_n\end{array}$

(32) $R=(C_j\left(x_i\right){)}_{m\times n}=\begin{array}{c}{x}_1\\ x_2\\ -\\ x_m\end{array}\left[\begin{array}{cccc}P\left({\mu }_{11},v_{11}\right)& P\left({\mu }_{12},v_{12}\right)& -& P\left({\mu }_{1n},v_{1n}\right)\\ P\left({\mu }_{21},v_{21}\right)& P\left({\mu }_{22},v_{22}\right)& -& P\left({\mu }_{2n},v_{2n}\right)\\ -& -& -& -\\ P\left({\mu }_{m1},v_{m1}\right)& P\left({\mu }_{m2},v_{m2}\right)& -& P\left({\mu }_{mn},v_{mn}\right)\end{array}\right]$(32)

where each of the elements $C_j\left(x_i\right)=P\left({\mu }_{ij},v_{ij}\right)$ is a PFS, which indicates that the degree to which the alternative $x=\left\{x_i:i=1,2,\dots ,m\right\}$ meets the criterion $C=\left\{C_j:j=1,2,\dots ,n\right\}$ is the value ${\mu }_{ij}$ and the degree to which the alternative $x=\left\{x_i:i=1,2,\dots ,m\right\}$ doesn’t meet the criterion $C=\left\{C_j:j=1,2,\dots ,n\right\}$ is the value $v_{ij}$.

3.3. Selection phase

For a given weight vector $(w_j:j=1,2,\dots ,n)$ of criteria, we use Pythagorean fuzzy weighted averaging aggregation operator to aggregate all elements for each row of Eq. (32)(32) $R=(C_j\left(x_i\right){)}_{m\times n}=\begin{array}{c}{x}_1\\ x_2\\ -\\ x_m\end{array}\left[\begin{array}{cccc}P\left({\mu }_{11},v_{11}\right)& P\left({\mu }_{12},v_{12}\right)& -& P\left({\mu }_{1n},v_{1n}\right)\\ P\left({\mu }_{21},v_{21}\right)& P\left({\mu }_{22},v_{22}\right)& -& P\left({\mu }_{2n},v_{2n}\right)\\ -& -& -& -\\ P\left({\mu }_{m1},v_{m1}\right)& P\left({\mu }_{m2},v_{m2}\right)& -& P\left({\mu }_{mn},v_{mn}\right)\end{array}\right]$(32) as the following:

(33) $PFO\left(x_i\right)=P(\sum _{j=1}^n{w}_j{\mu }_{ij},\sum _{j=1}^n{w}_j{v}_{ij})i\in M,j\in N$(33)

where $PFO\left(x_i\right)$ is the total assessment of the alternative $x_i\left(i\in M\right)$.

Finally, the $i$^th alternatives are ranked according to the score function in a descending order.

4. The proposed algorithm

In order to simplify the implementation of the demonstrated MCGDM method, an algorithm is proposed based on generating PFNs from decision-makers’ crisp data in the following procedures:

Step 1. Forming a group decision matrix $X_i={\left(r_{kj}^i\right)}_{t\times n}$ for each i^th alternative in which each decision-maker $D=\left\{d_k:k=1,2,\dots ,t\right\}$ evaluates the importance of each criterion $C=\left\{C_j:j=1,2,\dots ,n\right\}$ regarding each alternative $x=\left\{x_i:i=1,2,\dots ,m\right\}$, as shown in Eq. (9)(9) $\begin{array}{rl}& C_1\hspace{0.17em}{C}_2\hspace{0.17em}-\hspace{0.17em}{C}_n\hspace{0.17em}\\ & \hspace{0.17em}\\ & X_i={\left(r_{kj}^i\right)}_{t\times n}=\begin{array}{c}{d}_1\\ d_2\\ -\\ d_t\end{array}\left[\begin{array}{cccc}{r}_{11}^i& r_{12}^i& -& r_{1n}^i\\ r_{21}^i& { }_{22}^i& -& r_{2n}^i\hspace{0.17em}\\ -& -& -& -\\ r_{t1}^i& r_{t2}^i& -& r_{tn}^i\end{array}\right],i=1,2,\dots ,m\end{array}$(9) .

Step 2. Normalizing each group decision matrix $X_i={\left(r_{kj}^i\right)}_{t\times n}$ into $R_i={\left(s_{kj}^i\right)}_{t\times n}$ for each alternative by using Eq. (12)(12) $s_{kj}^i=\frac{r_{kj}^i-0}{100},forbenefecialcriteria{C}_j$(12) and Eq. (13)(13) $s_{kj}^i=\frac{100-r_{kj}^i}{100},fornon-benefecialcriteria{C}_j$(13) .

Step 3. Performing linear transformation by applying Eq. (17)(17) $o_{ij}=\frac{s_{kj}^u-0.5}{1-0.5}i\in M,j\in N,k\in T$(17) and Eq. (18(18) ${\xi }_{ij}=\frac{0.5-s_{kj}^c}{0.5-0}i\in M,j\in N,k\in T$(18) ), respectively, for each criterion vector in $R_i$.

Step 4. Determining the Shapley value (weight) for each DM by applying Eq. (20(20) $\lambda +1=\prod _{k=1}^t\left(1+\lambda \mu \left(\{d_k\}\right)\right)$(20) ), Eq. (21)(21) $\mu \left(F)=\mu (\left\{d_A\right\}{\cup }^{}\left\{d_B\right\}\right)=\mu \left(d_A\right)+\mu \left(\{d_B\}\right)+\lambda \mu \left(d_A\right)\mu \left(\left\{\{d_B\right\}\right)$(21) and Eq. (19)(19) ${\mathrm{\Phi }}_k=\frac{1}{t!}\sum _{F\subseteq D\setminus \left\{d_k\right\}}\left|F\right|!\left(t-\left|F\right|-1\right)!\left[\mu \left(F{\cup }^{}\left\{d_k\right\}\right)-\mu \left(F\right)\right]\mathrm{\forall }k\in \left\{1,2,\dots ,t\right\}$(19) .

Step 5. Measuring the weighted averaged satisfactory and dissatisfactory degrees for each j^th attribute in i^th alternative with respect to all DMs weights in $R_i$ using Eq. (22)(22) ${\kappa }_{ij}={\sum }_{k=1}^t{\mathrm{\Phi }}_k{o}_{k}i\in M,j\in N,k\in T$(22) and Eq. (23(23) ${\varsigma }_{ij}={\sum }_{k=1}^t{\mathrm{\Phi }}_k{\xi }_{k}i\in M,j\in N,k\in T$(23) ), respectively.

Step 6. Calculating the uncertainty degree using Eq. (24(24) $r=\sqrt{{\kappa }_{ij}^2+{\varsigma }_{ij}^2}$(24) ), Eq. (25(25) $cos\left(\theta \right)=\frac{\kappa }{r}$(25) ), Eq. (26)(26) $d=1-\frac{\theta }{\pi }$(26) and Eq. (29(29) ${\tau }_{ij}=\left\{\begin{array}{c}{f}_A\left(r,d\right);\{d|0.5<d\le 1\}\\ f_B\left(r,d\right);\{d|0\le d<0.5\}\\ 1;\{d|d=0.5\}\end{array}\right.$(29) ), respectively, for each criterion vector in $R_i$.

Step 7. Performing the calculations in Eq. (30)(30) ${\mu }_{ij}=\sqrt{\frac{{{\kappa }_{ij}}^2}{{{\kappa }_{ij}}^2+{{\varsigma }_{ij}}^2+{{\tau }_{ij}}^2}},i\in M,j\in N$(30) and Eq. (31)(31) ${\upsilon }_{ij}=\sqrt{\frac{{{\varsigma }_{ij}}^2}{{{\kappa }_{ij}}^2+{{\varsigma }_{ij}}^2+{{\tau }_{ij}}^2}},i\in M,j\in N$(31) to obtain the final PFNs and to construct the collective evaluation Pythagorean fuzzy decision matrix in Eq. (32)(32) $R=(C_j\left(x_i\right){)}_{m\times n}=\begin{array}{c}{x}_1\\ x_2\\ -\\ x_m\end{array}\left[\begin{array}{cccc}P\left({\mu }_{11},v_{11}\right)& P\left({\mu }_{12},v_{12}\right)& -& P\left({\mu }_{1n},v_{1n}\right)\\ P\left({\mu }_{21},v_{21}\right)& P\left({\mu }_{22},v_{22}\right)& -& P\left({\mu }_{2n},v_{2n}\right)\\ -& -& -& -\\ P\left({\mu }_{m1},v_{m1}\right)& P\left({\mu }_{m2},v_{m2}\right)& -& P\left({\mu }_{mn},v_{mn}\right)\end{array}\right]$(32) .

Step 8. Determining the total assessment by Eq. (8)(8) $PFO\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right)=P({\sum }_{j=1}^n{w}_j{u}_{{\beta }_j},{\sum }_{j=1}^n{w}_j{v}_{{\beta }_j})$(8) for every $i$^th alternative.

Step 9. Using the score function in Eq. (7)(7) $s\left(\beta \right)={\left(u_{\beta }\right)}^2-{\left(v_{\beta }\right)}^2$(7) to calculate each alternative score.

Step 10. Defining the optimal ranking order of the alternatives and finding the optimal alternative per Definition 6.

Based on the score function $s\left(x_i\right)$ achieved from Step 10, the alternatives are ranked with respect to the declining values of $s\left(x_i\right)\left(i=1,2,\dots ,m\right)$ and the alternative with the highest score function is selected as the optimal one. Figure 1 shows a graphical illustration of the proposed algorithm.

Figure 1. Graphical illustration of the proposed MCGDM methodology

5. Comparisons with other methods

The proposed MCGDM approach is compared with a method which was initially introduced by Yue (2014b), and then improved and revised by Lin and Zhang (2016), based on aggregating crisp numbers into IFNs. Although, our proposed method is inspired by Yue’s idea in generating IFNs from DM crisp numbers for MCGDM problems, it aims at aggregating DM crisp thoughts into PFNs, instead. As mentioned earlier, PFN based methods are more suitable for real-life decision-making problems than IFN-based methods due to their ability to model uncertainty much better than IFNs. Additionally, using IFNs may prevent DMs from expressing their crisp decisions freely, in some situations. Consequently, they need to change their preferences to fit within IFN’s constraints. However, this problem is solved by using PFNs in decision-making models because it allows DMs to express their opinions without limitations.

Since Yue’s method (Yue, 2014b) did not consider DMs’ weights in the aggregation phase which resulted in some illogical outcomes. Lin and Zhang (2016) improved Yue’s method and introduced a revised aggregation approach that takes DMs’ weights into account. The revised method suggests implementing the Shapley value to take account of the correlation and interaction among DMs, and therefore, weights can be assigned effectively.

There are similarities and differences between the revised Yue’s method and our proposed method. In terms of similarities, both methods follow similar concepts in generating fuzzy numbers from crisp data and follow the same rules to define the satisfactory, dissatisfactory or uncertainty values in $(R_i)$ in which “0.5” is the bound for identifying the satisfactory and dissatisfactory values and all values are within the interval [0,1]. Aggregated Shapley value is used in our proposed method to calculate the parameters $({\kappa }_{ij})$ and (${\varsigma }_{ij})$, which are the weighted average satisfactory degree and the weighted average dissatisfactory degrees, respectively. In the revised Yue’s method, the Shapley value is aggregated to measure the intuitionistic fuzzy satisfactory $({\mu }_I)$, dissatisfactory ($v_I),$ and uncertainty numbers $({\pi }_I)$. Whereas, our proposed method introduces a function to calculate the uncertainty degree parameter ${\tau }_{ij}$ using fuzzy rules then aggregates it within the calculations to get the Pythagorean fuzzy satisfactory $\left({\mu }_P\right)$, dissatisfactory $(v_P)$ and uncertainty degrees $({\pi }_P)$.

The aggregation outcomes in the revised method (i.e., intuitionistic fuzzy satisfactory $({\mu }_I)$, dissatisfactory ($v_I),$ and uncertainty numbers $({\pi }_I)$) should satisfy the conditions: ${\mu }_I+v_I+{\pi }_I=1,\hspace{0.17em}0\le {\mu }_I,v_I,{\pi }_I\le 1$; whereas the outcomes of the proposed method aggregation approach should satisfy the conditions: ${{\mu }_P}^2+{v_P}^2+{{\pi }_P}^2$ = 1,$0\le {\mu }_P\left(x\right),v_P\left(x\right),{\pi }_P\left(x\right)\le 1$. Therefore, Yager’s Pythagorean membership grades properties provide extra flexibility and space to DMs more than the intuitionistic membership grades. The similarities and differences between our proposed method and the revised Yue’s method are summarized in Table 1.

Table 1. Similarities and differences between our proposed method and the revised Yue’s method

Characteristics	proposed Method	Revised Yue’s method (Lin & Zhang, 2016)
Distribution center	0.5	0.5
Generated outcomes	Pythagorean Fuzzy Numbers	Intuitionistic Fuzzy Numbers
Parameters about satisfaction	The weighted average of linearly transformed elements satisfying > 0.5	The weighted average of linearly transformed elements satisfying > 0.5
Parameters about dissatisfaction	The weighted average of linearly transformed elements satisfying < 0.5	The weighted average of linearly transformed elements satisfying > 0.5
Parameters about uncertainty	Theta resulted from the sum of the square root of satisfactory and dissatisfactory degrees	${\mathit{\pi }}_{\mathit{I}}\left(\mathit{x}\right)=1-{\mathit{\mu }}_{\mathit{I}}\left(\mathit{x}\right)-{\mathit{v}}_{\mathit{I}}\left(\mathit{x}\right)$
Conditions that need to be satisfied by the aggregated fuzzy numbers	${{\mathit{\mu }}_{\mathit{P}}}^2+{{\mathit{v}}_{\mathit{P}}}^2+{{\pi }_{\mathit{P}}}^2$ = 1,$\hspace{0.17em}0\le {\mathit{\mu }}_{\mathit{P}},\hspace{0.17em}{\mathit{v}}_{\mathit{P}},{\mathit{\pi }}_{\mathit{P}}\le 1$	${\mathit{\mu }}_{\mathit{I}}+{\mathit{v}}_{\mathit{I}}+{\mathit{\pi }}_{\mathit{I}}=1,$$\hspace{0.17em}0\le {\mathit{\mu }}_{\mathit{I}},{\mathit{v}}_{\mathit{I}},{\mathit{\pi }}_{\mathit{I}}\le 1$

6. Illustrative example

6.1. Engineering materials selection

An aerospace company intends to choose a material for the manufacturing of one of the major parts of its engine. A pre-evaluation process of the candidate materials was performed using a well-established database and software, known as Ashby charts and software. Four material candidates (alternatives) were identified to be of similar suitability for the application, as the following: Pyromet 680 (A₁), AISI 302 Wrought (A₂), Rene 80 (A₃) and Inconel 625(A₄) for further assessment. Five experts were assigned as DMs for the final assessment of the material alternatives as follows:

$d_1$: Production manager;

$d_2$: Senior materials engineer;

$d_3$: Materials department manager;

$d_4$: Quality and development department manager;

$d_5$: Senior manufacturing engineer.

The initial weight subsets of the DMs were assigned as $\mu \left(\left\{d_1\right\}\right)=$ 0.8, $\mu \left(\left\{d_2\right\}\right)=$ 0.4, $\mu \left(\left\{d_3\right\}\right)=$ 0.4, $\mu \left(\left\{d_4\right\}\right)=$ 0.2, and $\mu \left(\left\{d_5\right\}\right)=$ 0.2.

The following criteria, and weights, were suggested by the company’s research and development team to be considered in the assessment process:

C1: Max service temperature (w₁ = 0.3);

C2: Density (w₂ = 0.3);

C3: Yield strength (w₃ = 0.175);

C4: Young’s modulus (w₄ = 0.175);

C5: Cost (w₅ = 0.05).

Initially, each DM $=\left\{d_k:k=1,2,3,4,5\right\}$ rates each criterion j with respect to the material alternative i. The rating system was performed based on a scale of 0 to 100, with 0 being poorest and 100 being excellent. The collected data from the DMs, at this stage, are shown in Table 2. The three beneficial criteria were identified as max service temperature, yield strength, and Young’s modulus of elasticity.

Table 2. Materials alternatives’ evaluation rates by the DMs (Step 1)

Material	DMs	u1	u2	u3	u4	u5
A1	d1	15	18	20	62	75
	d2	10	12	25	60	70
	d3	5	14	10	70	72
	d4	12	10	20	70	70
	d5	8	5	18	68	68
	Max	100	100	100	100	100
	Min	0	0	0	0	0
A2	d1	50	35	40	62	30
	d2	45	25	30	60	15
	d3	60	25	55	71	15
	d4	45	18	30	70	18
	d5	48	15	55	65	16
	Max	100	100	100	100	100
	Min	0	0	0	0	0
A3	d1	98	40	90	95	10
	d2	98	28	95	95	5
	d3	90	25	90	88	15
	d4	90	22	95	92	15
	d5	95	15	85	90	12
	Max	100	100	100	100	100
	Min	0	0	0	0	0
A4	d1	80	10	40	60	95
	d2	80	12	35	60	90
	d3	79	15	46	66	92
	d4	82	5	32	70	80
	d5	80	10	25	68	85
	Max	100	100	100	100	100
	Min	0	0	0	0	0

The beneficial and non-beneficial criteria were normalized by Eq. (12)(12) $s_{kj}^i=\frac{r_{kj}^i-0}{100},forbenefecialcriteria{C}_j$(12) and Eq. (13(13) $s_{kj}^i=\frac{100-r_{kj}^i}{100},fornon-benefecialcriteria{C}_j$(13) ), respectively, as shown in Table 3. Linear transformation of the normalized values was performed using Eq. (17)(17) $o_{ij}=\frac{s_{kj}^u-0.5}{1-0.5}i\in M,j\in N,k\in T$(17) and Eq. (18(18) ${\xi }_{ij}=\frac{0.5-s_{kj}^c}{0.5-0}i\in M,j\in N,k\in T$(18) ), respectively. Sugeno fuzzy measure was used to find the value of the parameter $\lambda$ and the marginal contribution of each DM to every coalition using Eq. (20)(20) $\lambda +1=\prod _{k=1}^t\left(1+\lambda \mu \left(\{d_k\}\right)\right)$(20) and Eq. (21)(21) $\mu \left(F)=\mu (\left\{d_A\right\}{\cup }^{}\left\{d_B\right\}\right)=\mu \left(d_A\right)+\mu \left(\{d_B\}\right)+\lambda \mu \left(d_A\right)\mu \left(\left\{\{d_B\right\}\right)$(21) . Furthermore, Shapley values were calculated using Eq. (19)(19) ${\mathrm{\Phi }}_k=\frac{1}{t!}\sum _{F\subseteq D\setminus \left\{d_k\right\}}\left|F\right|!\left(t-\left|F\right|-1\right)!\left[\mu \left(F{\cup }^{}\left\{d_k\right\}\right)-\mu \left(F\right)\right]\mathrm{\forall }k\in \left\{1,2,\dots ,t\right\}$(19) to measure the weights (importance) of DMs as follows:

Table 3. The normalized materials alternatives’ evaluation rates by the DMs (Step 2)

Material	DMs	u1	u2	u4	u3	u5
A1	d1	0.1500	0.1800	0.2000	0.6200	0.7500
	d2	0.1000	0.1200	0.2500	0.6000	0.7000
	d3	0.0500	0.1400	0.1000	0.7000	0.7200
	d4	0.1200	0.1000	0.2000	0.7000	0.7000
	d5	0.0800	0.0500	0.1800	0.6800	0.6800
A2	d1	0.5000	0.3500	0.4000	0.6200	0.3000
	d2	0.4500	0.2500	0.3000	0.6000	0.1500
	d3	0.6000	0.2500	0.5500	0.7100	0.1500
	d4	0.4500	0.1800	0.3000	0.7000	0.1800
	d5	0.4800	0.1500	0.5500	0.6500	0.1600
A3	d1	0.9800	0.4000	0.9000	0.9500	0.9800
	d2	0.9800	0.2800	0.9500	0.9500	0.9800
	d3	0.9000	0.2500	0.9000	0.8800	0.9000
	d4	0.9000	0.2200	0.9500	0.9200	0.9000
	d5	0.9500	0.1500	0.8500	0.9000	0.9500
A4	d1	0.8000	0.1000	0.4000	0.6000	0.9500
	d2	0.8000	0.1200	0.3500	0.6000	0.9000
	d3	0.7900	0.1500	0.4600	0.6600	0.9200
	d4	0.8200	0.0500	0.3200	0.7000	0.8000
	d5	0.8000	0.1000	0.2500	0.6800	0.8500

${\mathrm{\Phi }}_1=$ 0.45762, ${\mathrm{\Phi }}_2=$ 0.18517, ${\mathrm{\Phi }}_3=$ 0.18517, ${\mathrm{\Phi }}_4=$ 0.08601, ${\mathrm{\Phi }}_5=$ 0.08601

The weighted averaging satisfactory ${\kappa }_{ij}$ and dissatisfactory ${\varsigma }_{ij}$ degrees of the material alternative A_i, regarding the criteria u_j were determined using Eq. (22)(22) ${\kappa }_{ij}={\sum }_{k=1}^t{\mathrm{\Phi }}_k{o}_{k}i\in M,j\in N,k\in T$(22) and Eq. (23(23) ${\varsigma }_{ij}={\sum }_{k=1}^t{\mathrm{\Phi }}_k{\xi }_{k}i\in M,j\in N,k\in T$(23) ), per Step 5. The uncertainty degree $({\tau }_{\mathit{i}\mathit{j}})$ was calculated using Eq. (24(24) $r=\sqrt{{\kappa }_{ij}^2+{\varsigma }_{ij}^2}$(24) ), Eq. (25(25) $cos\left(\theta \right)=\frac{\kappa }{r}$(25) ), Eq. (26)(26) $d=1-\frac{\theta }{\pi }$(26) and Eq. (29(29) ${\tau }_{ij}=\left\{\begin{array}{c}{f}_A\left(r,d\right);\{d|0.5<d\le 1\}\\ f_B\left(r,d\right);\{d|0\le d<0.5\}\\ 1;\{d|d=0.5\}\end{array}\right.$(29) ), per Step 6, as shown in Table 4. Final aggregated PFNs were obtained and a collective evaluation Pythagorean fuzzy decision matrix was formed by Eq. (30(30) ${\mu }_{ij}=\sqrt{\frac{{{\kappa }_{ij}}^2}{{{\kappa }_{ij}}^2+{{\varsigma }_{ij}}^2+{{\tau }_{ij}}^2}},i\in M,j\in N$(30) ), Eq. (31)(31) ${\upsilon }_{ij}=\sqrt{\frac{{{\varsigma }_{ij}}^2}{{{\kappa }_{ij}}^2+{{\varsigma }_{ij}}^2+{{\tau }_{ij}}^2}},i\in M,j\in N$(31) and Eq. (32(32) $R=(C_j\left(x_i\right){)}_{m\times n}=\begin{array}{c}{x}_1\\ x_2\\ -\\ x_m\end{array}\left[\begin{array}{cccc}P\left({\mu }_{11},v_{11}\right)& P\left({\mu }_{12},v_{12}\right)& -& P\left({\mu }_{1n},v_{1n}\right)\\ P\left({\mu }_{21},v_{21}\right)& P\left({\mu }_{22},v_{22}\right)& -& P\left({\mu }_{2n},v_{2n}\right)\\ -& -& -& -\\ P\left({\mu }_{m1},v_{m1}\right)& P\left({\mu }_{m2},v_{m2}\right)& -& P\left({\mu }_{mn},v_{mn}\right)\end{array}\right]$(32) ), per Step 7, as shown in Table 5. Total assessment for every alternative was determined using Eq. (8(8) $PFO\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right)=P({\sum }_{j=1}^n{w}_j{u}_{{\beta }_j},{\sum }_{j=1}^n{w}_j{v}_{{\beta }_j})$(8) ), per Step 8. Lastly, the score function was calculated using Eq. (7(7) $s\left(\beta \right)={\left(u_{\beta }\right)}^2-{\left(v_{\beta }\right)}^2$(7) ), per Step 9, and the alternatives were ranked, per Step 10, as shown in Table 6. In conclusion, material alternative A₃ (Rene 80) was deemed the best material option among the considered material alternatives for the intended manufacturing process.

Table 4. Calculated parameters from step 3—step 6

Material	Criteria	${\kappa }_{ij}$	${\varsigma }_{ij}$	$r$	$cos\hspace{0.17em}\left(\theta \right)$	$\theta$	${\tau }_{ij}$
A1	u1	0.0000	0.7727	0.7727	0.0000	${90.000}^0$	0.2272
	u2	0.0000	0.7132	0.7131	0.0000	${90.000}^0$	0.2868
	u3	0.0000	0.6219	0.6219	0.0000	${90.000}^0$	0.3780
	u4 u5	0.2863 0.4497	0.0000 0.0000	0.2863 0.4497	1.0000 1.0000	${0.0000}^0$${0.0000}^0$	0.8455 0.5503
A2	u1	0.0370	0.0306	0.0480	0.7713	${39.528}^0$	0.9941
	u2	0.0000	0.4377	0.4377	0.0000	${90.000}^0$	0.5622
	u3	0.0271	0.2000	0.2018	0.1343	${82.278}^0$	0.8328
	u4 u5	0.2848 0.0000	0.0000 0.5558	0.2848 0.5558	1.0000 0.0000	${0.0000}^0$${90.000}^0$	0.7151 0.4441
A3	u1	0.9114	0.0000	0.9114	1.0000	${0.0000}^0$	0.0885
	u2	0.0000	0.3739	0.3739	0.0000	${90.000}^0$	0.6260
	u3	0.8185	0.0000	0.8185	1.0000	${0.0000}^0$	0.1814
	u4 u5	0.8603 0.0000	0.0000 0.7879	0.8603 0.7879	1.0000 0.0000	${0.0000}^0$${90.000}^0$	0.1397 0.2120
A4	u1	0.5997	0.0000	0.5997	1.0000	${0.0000}^0$	0.4002
	u2	0.0000	0.7823	0.7827	0.0000	${90.000}^0$	0.2173
	u3	0.0000	0.2359	0.2359	0.0000	${90.000}^0$	0.7641
	u4 u5	0.2531 0.8274	0.0000 0.0000	0.2532 0.8274	1.0000 1.0000	${0.0000}^0$${0.0000}^0$	0.7468 0.1726

Table 5. Calculated parameters from step 7

Materials	u1	u2	u3	u4	u5
A1	(0.0000, 0.9594)	(0.0000, 0.9277)	(0.0000, 0.8545)	(0.3207, 0.0000)	(0.6328, 0.0000)
A2	(0.0372, 0.0307)	(0.0000, 0.6142)	(0.0316, 0.2334)	(0.3700, 0.0000)	(0.0000, 0.7812)
A3	(0.9953, 0.0000)	(0.0000, 0.5128)	(0.9763, 0.0000)	(0.9871, 0.0000)	(0.0000, 0.9656)
A4	(0.8318, 0.0000)	(0.0000, 0.9635)	(0.0000, 0.2949)	(0.3210, 0.0000)	(0.9789, 0.0000)

Table 6. Scores and ranking of the material alternatives (step 8, step 9 and step 10)

Material	Overall assessment values	Scores	Ranking
A1	(0.0878, 0.7065)	−0.4915	4
A2	(0.0815, 0.1867)	−0.0282	3
A3	(0.6408, 0.2587)	0.3437	1
A4	(0.3546, 0.3407)	0.0097	2

6.2. Comparison with Yue’s revised method

The evaluation process for the same materials alternatives was performed using Yue’s revised method for comparison purposes. The intuitionistic fuzzy satisfactory ${\mu }_{ij}$ and dissatisfactory degrees $v_{ij}$ were calculated and formed in a collective matrix as shown in Table 7. The overall evaluation values, score functions and ranking of material alternatives were determined as shown in Table 8.

Table 7. The collective evaluation of the materials using the revised method

Material	u1	u1	u2	u3	u4
A1	(0.0000,0.7727)	(0.0000, 0.7131)	(0.0000, 0.6219)	(0.2863, 0.0000)	(0.4497, 0.0000)
A2	(0.0370, 0.0305)	(0.0000, 0.4377)	(0.0271, 0.2000)	(0.2848, 0.0000)	(0.0000, 0.5558)
A3	(0.9114, 0.0000)	(0.0000, 0.3739)	(0.8185, 0.0000)	(0.8603, 0.0000)	(0.0000, 0.7879)
A4	(0.5997, 0.0000)	(0.0000, 0.7826)	(0.0000, 0.2358)	(0.2531, 0.0000)	(0.8273, 0.0000)

Table 8. Assessment values, scores and ranking of the materials using Yue’s revised method

Material	Overall assessment values	Scores	Ranking
A1	(0.0726, 0.5546)	−0.4820	4
A2	(0.0657, 0.2033)	−0.1376	3
A3	(0.5672, 0.1516)	0.2988	1
A4	(0.2656, 0.2761)	−0.0057	2

According to Table 6, our proposed method shows Rene 80 (A3) to be the optimal material for the manufacturing of the engine part with a score function of 0.3437, Inconel 625(A4) is the second best with a score function of 0.0097, Wrought (A2) is the third best with a score function of −0.0282, and Pyromet 680 (A1) is ranked last with a score function of −0.4915.

According to Table 8, Yue’s revised method shows Rene 80 (A3) as the most suitable material for the manufacturing process with a score function of 0.2988, Inconel 625(A4) is the second best with a score function of −0.0057, Wrought (A2) is the third best with a score function of −0.1376, and Pyromet 680 (A1) is ranked last with a score function of −0.4820. The final outcomes resulting from Yue’s revised method (A₃ > A₄ > A₂ > A₁) matches the recommendation resulting from our proposed approach.

6.3. Discussion of the results

It can be seen that for both methodologies final ranking results are similar. However, our approach’s results can be dissimilar with Yue’s revised method if we expand the experiment and more alternatives and criteria are added, since our aggregation approach forms the resultant fuzzy set based on aggregating the calculated uncertainty from DM’s crisp decisions. On the other hand, Yue’s revised method does not consider measuring the uncertainty level in DMs crisp data in its aggregation technique.

The uncertainty value (${\tau }_{ij}$) that results from the uncertainty function is based on (1) the amount of information stored after aggregating DM’s data represented by ($r)$ &; (2) the level of satisfactory or dissatisfactory degree represented by $\left(d\right)$ or theta $\left(\theta \right)$. Hence, aggregating the measured uncertainty value into the PFS will affect the selection phase of the decision-making process. Particularly, if the measured uncertainty value is low, the distance between the satisfactory and dissatisfactory degrees will extend (leading to a better place for the alternative in the ranking outcomes) while if the measured uncertainty value is high, the distance between the satisfactory and dissatisfactory degrees will decrease (leading to a worse place for the alternative in the ranking outcomes). Thus, it can be inferred that the generated PFNs using our proposed approach express the decision makers’ thoughts more accurately than Yue’s revised methodology.

7. Conclusion

Multiple Criteria Group Decision Making techniques have been proven for their effectiveness in facilitating the decision-making process for many engineering applications. In this work, a new method has been proposed for aggregating DMs’ thoughts into PFNs that are gathered into a collective decision-making matrix to be processed in the selection phase. The novelty of the proposed method lies in the aggregation of DMs’ crisp decisions to generate PFNs in the form of a collective decision-making matrix. In addition, uncertainty functions were developed based on Pythagorean membership grades properties and rules to measure the amount of uncertainty in DM’s crisp numbers. Finally, based on the proposed aggregation approach, a new MCGDM framework was developed by forming the generated PFNs into a collective group decision-making matrix and using the PFO to rank the final alternatives.

The proposed method was used in a realistic materials selection example for a manufacturing application and was compared to the outcomes of Yue’s revised model. Comparative analysis showed that by measuring the uncertainty level in decision makers’ evaluations, the proposed method was more effective in expressing decision makers’ information as PFS in the MCGDM matrix. The application of the proposed MCGDM method can be extended to many different applications such as logistics, materials selection, finance, healthcare and facility locations. Finally, this approach will be developed to include both quantitative and qualitative data and will be compared with other methods such as the Intuitionistic Fuzzy Dimensional Analysis for MCGDM to validate the results.

List of Abbreviations and Acronyms

DM - Decision-Maker

IFN - Intuitionistic Fuzzy Number

IFS - Intuitionistic Fuzzy Set

MCDM - Multiple Criteria Decision-Making

MCGDM - Multiple Criteria Group Decision-Making

PFN - Pythagorean Fuzzy Number

PFO - Pythagorean Fuzzy Operator

PFS - Pythagorean Fuzzy Set

TOPSIS - Technique of Order Preference Similarity to the Ideal Solution

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Alaa F. Momena

Alaa Momena is an assistant professor in the Industrial Engineering Department at University of Business and Technology (UBT), Jeddah, KSA. Dr. Momena Holds an M.S. in Engineering Management from Milwaukee School of Engineering, Milwaukee, WI, USA, and a Ph.D. in Industrial Engineering from University of Wisconsin – Milwaukee, WI, USA. Areas of research for Dr. Momena include Multiple Criteria Decision-Making models, Materials selection applications and production management.

Nidal Abu-Zahra

Dr. Abu-Zahra is an accomplished faculty member in the Materials Science and Engineering Department at the University of Wisconsin-Milwaukee. Over the past 25 years, he has been working on expanding knowledge on contemporary issues such as cost effectively harnessing solar energy, sustainability of commodity materials, and materials processing optimization. Currently, he is working on synthesizing new polymer-composite foams capable of removing heavy metal toxics from drinking water with antibacterial properties.