Influence of oriented magnetic field on natural convection in an equilateral triangular enclosure filled with water- and kerosene-based ferrofluids using a two-component nonhomogeneous thermal equilibrium model

Abstract

In this paper, hydromagnetic natural convection heat transfer in an equilateral triangular enclosure filled with water- and kerosene-based ferrofluids has been analyzed using a two-component non-homogeneous thermal equilibrium model. The enclosure is permeated by an inclined magnetic field of having uniform strength. The effects of Brownian motion and thermophoresis of the nanoparticles are incorporated into the ferrofluid model. The Galerkin weighted residual finite-element method has been employed to solve the governing nondimensional partial differential equations. Fe₃O₄-water and Co-kerosene ferrofluids have been used for the present investigation. The effects of various model parameters such as Rayleigh number, Hartmann number, and inclination angle of the magnetic field on the streamlines, isotherms, and isoconcentrations have been displayed graphically. In addition, the heat transfer augmentation for various combinations of model parameters have been done in light of the average Nusselt number from the bottom heated wall. The results indicate that increment in the magnetic field reduces the heat transfer rate, whereas increment in the magnetic field inclination angle augments the heat transfer rate significantly. The results further indicate that there exists a strong interaction between cobalt and kerosene in the presence of magnetic field which can be utilized efficiently for desired heat transfer augmentation in engineering problems.

Keywords:

• ferrofluid
• natural convection
• inclined magnetic field
• triangular enclosure
• finite-element method

Public Interest Statement

Nanofluids are relatively new class of fluids engineered by suspending nanoparticles with average sizes below 100 nm in traditional heat transfer fluids such as water, engine oil, ethylene glycol, and kerosene. Nanofluids are considered to offer important advantages over conventional heat transfer fluids. A very small amount of nanoparticles, when dispersed uniformly and suspended stably in base fluids, can provide dramatic improvements in the thermal properties of host fluids. The influence of a magnetic field on natural convection has great importance in many industrial and technological applications. Natural convection heat transfer in an equilateral triangular enclosure filled with Fe₃O₄-water and Co-kerosene ferrofluids in the presence of an inclined magnetic field is investigated using a two-component non-homogeneous thermal equilibrium model. It is found that there exists a strong interaction between cobalt and kerosene in the presence of an inclined magnetic field which can be utilized properly for desired heat transfer augmentation.

1. Introduction

The influence of a magnetic field on natural convection has great importance in many industrial and technological applications. In some cases, where the heat is transferred by natural convection mechanism, the electrically conducting fluid may be used in the presence of a magnetic field with an arbitrary inclination. Some examples of these could include the fusion reactors, metal casting, geothermal energy extractions, and crystal growth in fluids. Thus, some researchers investigated the effect of magnetic field orientation within the enclosures for two- or three-dimensional heat transfer problems and all of them revealed that the orientation of the magnetic field changed the flow field and consequently the thermal performance of the enclosure (see Alchaar, Vasseur, & Bilgen, 1995; Garandet, Alboussiere, & Moreau, 1992; Krakov & Nikiforov, 2002; Ozoe & Okada, 1989; Pirmohammadi & Ghassemi, 2009; Venkatachalappa & Subbaraya, 1993). Ece and Büyük (2006) studied natural convection flow under the action of a magnetic field in an inclined rectangular enclosure heated and cooled at the adjacent walls. Their numerical results indicate that the magnetic field suppresses the convective flow as well as the heat transfer rate. They also showed that the orientation and the aspect ratio of the enclosure, and the strength and direction of the magnetic field had significant effects on the flow and temperature fields. Sathiyamoorthy and Chamkha (2010) used different thermal boundary conditions to examine the steady laminar two-dimensional natural convection in the presence of an inclined magnetic field in a square enclosure filled with liquid gallium. They found that heat transfer decreases with an increase in the magnetic field strength. They also noted that vertically and horizontally applied magnetic fields affect the heat transfer rate differently. Grosan, Revnic, Pop, and Ingham (2009) considered the inclination angle of a magnetic field on the natural convection within a rectangular enclosure and was found that the convection mode depends upon both the strength and the orientation of the magnetic field. Their results also indicate that the applied magnetic field in the horizontal direction is most effective in suppressing the convection flow in comparison with the field along the vertical direction.

The above-literature review reveals that the existence of magnetic field has a noticeable effect on heat transfer reduction under natural convection, while in many engineering applications increasing heat transfer from solid surfaces is a goal. At this circumstance, the use of nanofluids with higher thermal conductivity can be considered as a promising solution. ${\text{Al}}_2{\text{O}}_3$–water, ${\text{TiO}}_2$–water, Cu–water are common nanofluids that are available commercially for various engineering applications for heat transfer enhancements. Although there are advanced nanofluids such as diamond-water and CNT-water but they are very costly for practical uses. Thus, we required such nanofluids which are economically cheaper and provide better heat transfer enhancements. Ferrofluid is a stable liquid that contains dispersed colloidal magnetic nanoparticles such as ${\text{Fe}}_3{\text{O}}_4$, cobalt, and nickel. Compared to the conventional non-magnetic nanofluids, there are several advantages to use ferrofluids as heat transfer media such as (i) the external magnetic field can be used to alter the properties of the solute nanoparticles (e.g. thermal conductivity and viscosity) to achieve a specific design requirements, (ii) the external magnetic field can be used to control and enhance the thermomagnetic convection in a ferrofluid, and (iii) the application of ferrofluid in heat transfer device could help to reduce the size and cost of components. In this regard, some researchers (Sheikholeslami & Ganji, 2014; Sheikholeslami & Gorji-Bandpy, 2014) show that ferrofluid provides excellent heat transfer enhancement. Sheikholeslami and Ganji (2014) investigated magnetohydrodynamic effect on ferrofluid in a semicircular annulus. They have revealed that increased solid volume fraction as well as the Rayleigh number enhances the heat transfer rate. On the other hand a decreased Hartmann number provides better heat transfer augmentation. Jafari, Tynjala, Mousavi, and Sarkomaa (2008) reported the advantage of a ferrofluid on magnetohydrodynamic convection considering cobalt-kerosene ferrofluid. Later on many researchers (Aminfar, 2013; Ashouri, Ebrahimi, Shafii, Saidi, & Saidi, 2010; Jue, 2006; Kefayati, 2014; Rahman et al., 2015; Sheikholeslami & Gorji-Bandpy, 2014; Snyder, 2003) also reported same. One-component and two-component models are popular among the numerical models of nanofluids. However, for simplification and finding the general trend as prediction to experimental work, the well-known two-component model proposed by Buongiorno (2006) is followed. This model is very popular and is used by many researchers (Bondareva, Sheremet, & Pop, 2015; Elshehabey & Ahmed, 2015; Rahman, Alam, Al-Salti, & Eltayeb, 2016; Sheremet, Pop, & Roşca, 2016). As per authors’ knowledge, the literature review revealed that using non-uniform thermal boundary conditions into the two-component non-homogeneous thermal equilibrium model in an equilateral triangular enclosure filled with ferrofluids in the presence of oriented magnetic field has not been studied yet. Therefore, in this paper, a finite-element simulation has been performed for an equilateral triangular enclosure filled with Fe₃O₄-H₂O and Co-kerosene ferrofluids considering non-uniformly heated bottom wall in the presence of an oriented magnetic field using two-component non-homogeneous thermal equilibrium model. The reason of choosing an equilateral triangular enclosure is that, it has practical applications in the field of solar thermal collectors and attics of buildings. The simulated results are shown in graphically in the form of streamlines, isotherms, and isoconcentrations for Fe₃O₄-H₂O ferrofluid. Finally, the combined effects of Hartmann number and magnetic field inclination angle on the average Nusselt number for Fe₃O₄-H₂O and Co-kerosene ferrofluids are tabulated.

2. Mathematical modeling

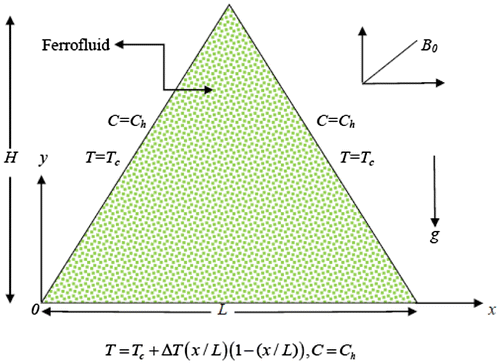
Let us consider a two-dimensional steady laminar natural convection flow inside an equilateral triangular enclosure filled with ferrofluids. The domain and boundary conditions for the buoyancy-driven heat transfer in the equilateral triangular enclosure are shown in Figure 1, where x and y are the Cartesian coordinates, L is the bottom wall length, and H is the height of the equilateral triangular enclosure. A well-defined coordinate system has been fixed, and the gravity is working along the negative y axis. It is assumed that the bottom wall of the cavity is maintained at non-uniformly varying temperatures as $T=T_c+\left(T_h-T_c\right)\left(x/L\right)\left(1-\left(x/L\right)\right)$, while the temperature of the inclined walls are kept at T_c so that T_h > T_c. The advantage of taking this boundary condition at the bottom wall of the enclosure is that it removes the singularity at the bottom edges of the corners. Due to the uniform distribution of the nanoparticles within the base fluid, the nanoparticle volume fraction on the entire domain has been taken uniform as C_h. Thermophoresis and Brownian motion effects are included in our study in the absence of any chemical reaction. The base fluid and the solid nanoparticles are in thermal equilibrium. The enclosure is permeated by a uniform magnetic field $\mathbf{B}=B_x\mathbf{i}+B_y\mathbf{j}$ of constant magnitude $B_0=\sqrt{B_x^2+B_y^2}$, where $\mathbf{i}$ and $\mathbf{j}$ are the unit vectors along the coordinate axes. The direction of the magnetic field makes an angle γ with the positive x-axis. The Boussinesq approximation has been applied to consider the density variation.

Figure 1. Physical model of the problem with boundary conditions.

Within the framework of the above-noted assumptions, the governing equations for this model can be written as (see also Elshehabey & Ahmed, 2015; Rahman et al., 2016):

Continuity equation:(1) $$\frac{\mathit{\partial }u}{\mathit{\partial }x}+\frac{\mathit{\partial }v}{\mathit{\partial }y}=0$$(1)

Momentum equation in x-direction:(2) $$\frac{\mathit{\partial }\left(u^2\right)}{\mathit{\partial }x}+\frac{\mathit{\partial }\left(uv\right)}{\mathit{\partial }y}=\frac{1}{{\mathit{\rho }}_f}\left[-\frac{\mathit{\partial }p}{\mathit{\partial }x}+{\mathit{\mu }}_f{\mathrm{\nabla }}^{2}u+{\mathit{\sigma }}_f{B}_0^2\left(vsin\mathit{\gamma }cos\mathit{\gamma }-u{sin}^2\mathit{\gamma }\right)\right]$$(2)

Momentum equation in y-direction:(3) $$\frac{\mathit{\partial }\left(uv\right)}{\mathit{\partial }x}+\frac{\mathit{\partial }\left(v^2\right)}{\mathit{\partial }y}=\frac{1}{{\mathit{\rho }}_f}\left[-\frac{\mathit{\partial }p}{\mathit{\partial }y}+{\mathit{\mu }}_f{\mathrm{\nabla }}^{2}v+{\mathit{\sigma }}_f{B}_0^2\left(usin\mathit{\gamma }cos\mathit{\gamma }-v{cos}^2\mathit{\gamma }\right)+\left(1-C_0\right)\left(T-T_c\right){\mathit{\rho }}_f{\mathit{\beta }}_{f}g-\left(C-C_0\right)\left({\mathit{\rho }}_p-{\mathit{\rho }}_f\right)g\right]$$(3)

Energy equation:(4) $$\frac{\mathit{\partial }\left(uT\right)}{\mathit{\partial }x}+\frac{\mathit{\partial }\left(vT\right)}{\mathit{\partial }y}={\mathit{\alpha }}_f{\mathrm{\nabla }}^{2}T+\frac{{\left(\mathit{\rho }{c}_p\right)}_p}{{\left(\mathit{\rho }{c}_p\right)}_f}\left\{D_B\left(\frac{\mathit{\partial }C}{\mathit{\partial }x}\frac{\mathit{\partial }T}{\mathit{\partial }x}+\frac{\mathit{\partial }C}{\mathit{\partial }y}\frac{\mathit{\partial }T}{\mathit{\partial }y}\right)\right.+\frac{D_T}{T_c}\left[{\left(\frac{\mathit{\partial }T}{\mathit{\partial }x}\right)}^2+{\left(\frac{\mathit{\partial }T}{\mathit{\partial }y}\right)}^2\right]\left.\begin{array}{c}\\ \\ \end{array}\right\}$$(4)

Conservation equation for the nanoparticles:(5) $$\frac{\mathit{\partial }\left(uC\right)}{\mathit{\partial }x}+\frac{\mathit{\partial }\left(vC\right)}{\mathit{\partial }y}=D_B{\mathrm{\nabla }}^{2}C+\frac{D_T}{T_c}{\mathrm{\nabla }}^{2}T$$(5)

where ${\mathrm{\nabla }}^2=\frac{{\mathit{\partial }}^2}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^2}{\mathit{\partial }{y}^2}$ is the Laplacian operator and other quantities are defined in the nomenclature.

The appropriate boundary conditions for the above stated model are as follows:

(i) On the inclined walls:(6) $$u=v=0,T=T_c,C=C_h$$(6)

(ii) On the bottom wall:(7) $$u=v=0,T=T_c+\mathrm{\Delta }T\left(x/L\right)\left(1-\left(x/L\right)\right),C=C_h$$(7)

3. Dimensional analysis

Dimensional analysis is one of the most important mathematical tools in the study of fluid mechanics. To describe several transport mechanisms in nanofluids, it is meaningful to make the conservation equations into non-dimensional form. The advantages of non-dimensionalization can be listed as follows: (i) non-dimensionalization gives freedom to analyze any system irrespective of their material properties, (ii) one can easily understand the controlling flow parameters of the system, (iii) makes a generalization of the size and shape of the geometry, and (iv) helps doing experiment to get insight of the physical problem. These aims can be achieved through the appropriate choice of scales. As a scale of distance, we choose the length of the cavity of the region under consideration measured along the x-axis. Thus, in order to reduce the dimensionless form of the governing Equations (1)–(5) with boundary conditions (6)–(7), we incorporate the following dimensionless variables:(8) $$\left.X=\frac{x}{L},Y=\frac{y}{L},U=\frac{uL}{{\mathit{\alpha }}_f},V=\frac{vL}{{\mathit{\alpha }}_f},P=\frac{p{L}^2}{{\mathit{\rho }}_f{\mathit{\alpha }}_f^2},\mathit{\theta }=\frac{T-T_c}{T_h-T_c},\mathit{\varphi }=\frac{C-C_0}{C_h-C_0}\right\}$$(8)

Introducing the relation (8) into Equations (1)–(5), the governing dimensional equations can be written in the following dimensionless form:(9) $$\frac{\mathit{\partial }U}{\mathit{\partial }X}+\frac{\mathit{\partial }V}{\mathit{\partial }Y}=0$$(9) (10) $$\frac{\mathit{\partial }\left(U^2\right)}{\mathit{\partial }X}+\frac{\mathit{\partial }\left(UV\right)}{\mathit{\partial }Y}=-\frac{\mathit{\partial }P}{\mathit{\partial }X}+Pr{\mathrm{\nabla }}^{2}U+Pr{\text{Ha}}^{\text{2}}\left(Vsin\mathit{\gamma }cos\mathit{\gamma }-U{sin}^2\mathit{\gamma }\right)$$(10) (11) $$\frac{\mathit{\partial }\left(UV\right)}{\mathit{\partial }X}+\frac{\mathit{\partial }\left(V^2\right)}{\mathit{\partial }Y}=-\frac{\mathit{\partial }P}{\mathit{\partial }Y}+Pr{\mathrm{\nabla }}^{2}V+RaPr\left(\mathit{\theta }-Nr\mathit{\varphi }\right)+Pr{\text{Ha}}^2\left(Usin\mathit{\gamma }cos\mathit{\gamma }-V{cos}^2\mathit{\gamma }\right)$$(11) (12) $$\frac{\mathit{\partial }\left(U\mathit{\theta }\right)}{\mathit{\partial }X}+\frac{\mathit{\partial }\left(V\mathit{\theta }\right)}{\mathit{\partial }Y}={\mathrm{\nabla }}^2\mathit{\theta }+Nb\left(\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }X}\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }X}+\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }Y}\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }Y}\right)+Nt\left[{\left(\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }X}\right)}^2+{\left(\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }Y}\right)}^2\right]$$(12) (13) $$\frac{\mathit{\partial }\left(U\mathit{\varphi }\right)}{\mathit{\partial }X}+\frac{\mathit{\partial }\left(V\mathit{\varphi }\right)}{\mathit{\partial }Y}=\frac{1}{Le}{\mathrm{\nabla }}^2\mathit{\varphi }+\frac{Nt}{LeNb}{\mathrm{\nabla }}^2\mathit{\theta }$$(13)

The dimensionless forms of the boundary conditions are as follows:

(i) On the inclined walls:(14) $$U=V=0,\mathit{\theta }=0,\mathit{\varphi }=1$$(14)

(ii) On the bottom wall:(15) $$U=V=0,\mathit{\theta }=X\left(1-X\right),\mathit{\varphi }=1$$(15)

The parameters introduced in the above Equations (10)–(13) are as follows: $Pr=\frac{{\mathit{\mu }}_f}{{\mathit{\rho }}_f{\mathit{\alpha }}_f}$ is the Prandtl number, $Ha=B_{0}L\sqrt{\frac{{\mathit{\sigma }}_f}{{\mathit{\mu }}_f}}$ is the Hartmann number, $Ra=\frac{g{\mathit{\beta }}_f\left(1-C_0\right)\left(T_h-T_c\right)L^3}{{\mathit{\alpha }}_f{\mathit{\upsilon }}_f}$ is the Rayleigh number, $Nr=\frac{\left({\mathit{\rho }}_p-{\mathit{\rho }}_f\right)\left(C_h-C_0\right)}{{\mathit{\rho }}_f{\mathit{\beta }}_f\left(T_h-T_c\right)\left(1-C_0\right)}$ is the buoyancy ratio parameter, $Nt=\frac{{\left(\mathit{\rho }{c}_p\right)}_p}{{\left(\mathit{\rho }{c}_p\right)}_f}\frac{D_T\left(T_h-T_c\right)}{T_c{\mathit{\alpha }}_f}$ is the thermophoresis parameter, $Nb=\frac{{\left(\mathit{\rho }{c}_p\right)}_p}{{\left(\mathit{\rho }{c}_p\right)}_f}\frac{D_B\left(C_h-C_0\right)}{{\mathit{\alpha }}_f}$ is the Brownian motion parameter, and $Le=\frac{{\mathit{\alpha }}_f}{D_B}$ is the Lewis number.

4. Evaluation of stream function and average Nusselt number

The fluid motion is displayed using the stream function ψ obtained from velocity components U and V. The relationships between stream function ψ and velocity components for two-dimensional flows are:(16) $$U=\frac{\mathit{\partial }\mathit{\psi }}{\mathit{\partial }Y}\text{and}V=-\frac{\mathit{\partial }\mathit{\psi }}{\mathit{\partial }X}$$(16)

Using the above definition of the stream function, the positive sign of ψ denotes anti-clockwise circulation whereas the clockwise circulation is represented by the negative sign.

The most important physical quantities for this model are the local Nusselt number Nu and average Nusselt number Nu_av along the heated wall. Now the local Nusselt number is defined as(17) $$Nu=\frac{L{q}_w}{k_f\left(T_h-T_c\right)},$$(17)

where the heat transfer from the bottom heated wall q_w is given by (18) $$q_w=-k_f{\left(\frac{\mathit{\partial }T}{\mathit{\partial }y}\right)}_{y=0}$$(18)

Thus, the average Nusselt number for the bottom heated wall is calculated from the following expression:(19) $$N{u}_{av}=-{\int }_0^1\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }Y}dX$$(19)

5. Thermophysical properties of ferrofluid

Better thermo-physical properties of ferrofluids are the main reason of their use in heat transfer intensification. While analyzing heat transfer performance, different ferrofluids have been investigated by many researchers and it was concluded that significant enhancement of heat transfer was evident. Among the available ferrofluid, Fe₃O₄-H₂O and Co-kerosene are being used. The thermophysical properties of pure water, kerosene, Fe₃O₄, and Co are presented in Table 1.

Table 1. Thermophysical properties of base fluids and solid nanoparticles

Physical properties	Water $\left({\text{H}}_2\text{O}\right)$	Kerosene	${\text{Fe}}_3{\text{O}}_4$	Cobalt
${\text{c}}_{\text{p}}\left[\text{J/kgK}\right]$	4,179	2,090	670	420
$\mathit{\rho }\left[{\text{kg/m}}^3\right]$	997.1	780	5,180	8,900
$\text{k}\left[\text{W/mK}\right]$	0.613	0.149	80	100
$\mathit{\mu }\left[{\text{Ns/m}}^2\right]$	0.001003	0.00164	–	–
$\mathit{\beta }\left[1/\text{K}\right]$	21 × 10^−5	99 × 10^−5	20.6 × 10^−5	1.3 × 10^−5
$\mathit{\sigma }\left[\text{W/mK}\right]$	5.5 × 10^−6	6 × 10^−10	0.112 × 10^6	16.02 × 10^6
Pr	6.8377	23.004	–	–

6. Computational procedure

The governing dimensionless Equations (9)–(13) along with the boundary conditions (14)–(15) have been solved numerically by employing the finite-element method (FEM). The FEM is such a powerful method for solving both ordinary and partial differential equations that arise in science and engineering problems. The basic idea of this method is dividing the whole domain into smaller elements of finite dimensions called finite elements. This method is such a good numerical method in modern science and engineering analysis, and it can be applied for solving integral equations including heat and mass transfer, fluid mechanics, chemical processing, electrical systems, and many other fields. The advantages of FEM are: ability to deal with the complex 2D or 3D domains, higher accuracy, and rapid convergence. The details of this method are well described by Zienkiewicz and Taylor (1991), Rahman, Alim, and Mamun (2009), Rahman, Parvin, Saidur, and Rahim (2011) and Uddin (2015). In this method, the solution domain is discretized into finite-element meshes, which are composed of non-uniform triangular elements. The six node triangular elements are used in this work for the development of the finite-element equations. All six nodes are associated with velocities, temperature as well as isoconcentration; only the corner nodes are associated with pressure. This means that a lower order polynomial is chosen for pressure and which is satisfied through the continuity equation. Then the nonlinear governing partial differential equations (i.e. conservation of mass, momentum and energy equations) are transferred into a system of integral equations by applying Galerkin weighted residual method. The integration involved in each term of these equations is performed using Gauss’s quadrature method. The nonlinear algebraic equations so obtained are modified by imposition of boundary conditions. To solve the set of the global nonlinear algebraic equations in the form of matrix, the Newton–Raphson iteration technique has been adapted through partial differential equation solver with MATLAB interface. The convergence criterion of the numerical solution along with error estimation has been set to $\left|{\mathit{\Phi }}^{m+1}-{\mathit{\Phi }}^m\right|\le {10}^{-5}$, where Φ is the general dependent variable $(U,V,\mathit{\theta },\mathit{\varphi })$ and m is the number of iteration.

6.1. Mesh generation

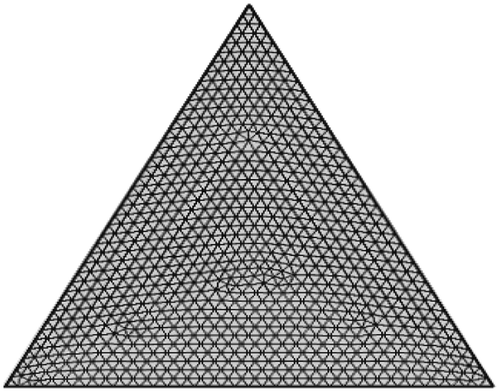
In the FEM, the mesh generation is the technique to subdivide a domain into a set of subdomains, called finite element. The discrete locations are defined by the numerical grid, at which the variables are to be calculated. It is basically a discrete representation of the geometric domain on which the problem is to be solved. Meshing the complicated geometry makes the FEM a powerful technique to solve the boundary value problems occurring in a range of engineering applications. Figure 2 displays mesh configuration of the present physical domain with triangular finite elements.

Figure 2. Mesh structure of the physical domain with triangular finite elements.

6.2. Grid sensitivity test

An extensive mesh testing procedure is conducted to guarantee a grid-independent solution for Ra = 10⁵ and Pr = 6.8377 in an equilateral triangular enclosure filled with ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid. In the present work, we examine five different non-uniform grid systems with the following number of elements within the resolution field: 661, 1,063, 1,636, 7,417, and 29,510. The numerical design is carried out for highly precise key in the average Nusselt number (Nu_av) for the aforesaid elements to develop an understanding of the grid fineness as shown in Table 2. The scale of Nu_av for 7,417 elements shows a little difference with the results obtained for the other elements. Hence a grid size of 7,417 elements is found to meet the requirements of both the grid independency study and the computational time limits.

Table 2. Grid sensitivity check for ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid at Pr = 6.8377, Ra = 10⁵, Ha = 20, Nr = 0.1, γ = 15⁰and d_p = 10 nm

Nodes	368	579	877	3,834	14,998
Elements	661	1,063	1,636	7,417	29,510
Nuav	0.93329	0.94424	0.95234	0.96945	0.96947

7. Results and discussion

In this section, a numerical study has been performed through FEM to analyze the laminar natural convection heat transfer and fluid flow in an equilateral triangular enclosure filled with ferrofluid in the presence of oriented magnetic field. In the numerical simulation, ${\text{Fe}}_3{\text{O}}_4$-water and cobalt-kerosene ferrofluids have been considered. Streamlines, isotherms and isoconcentrations are presented graphically for ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid whereas the rate of heat transfer at bottom heated wall has been shown in tabular form for both ${\text{Fe}}_3{\text{O}}_4$-water and cobalt-kerosene ferrofluids for a wide range of the controlling parameters. Particular efforts have been focused on the effects of three influential factors such as the Rayleigh number, the Hartmann number, and magnetic field inclination angle on the fluid flow and heat transfer. It is obvious that if the nanoparticles are distributed uniformly in the base fluid, then more heat transfer rate is expected. But due to the Brownian motion of the nanoparticles and thermophoretic effects of nanofluids, it is assumed that there is a little bit concentration difference and it is expected that this concentration difference can be ΔC = 0.01. Thus, for ${\text{Fe}}_3{\text{O}}_4$-water nanofluid with 1% volume fraction nanoparticles of diameter $d_p=10\text{nm}$, T_c = 300 K, temperature difference ΔT = 10 K, the values of the Brownian diffusion coefficient D_B = 4.3795 × 10⁻¹¹ and thermal diffusion coefficient D_T = 4.1801 × 10⁻¹² for ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid, whereas the corresponding values for cobalt-kerosene ferrofluid are D_B = 2.6785 × 10⁻¹¹ and D_T = 9.4533 × 10⁻¹² have been calculated following Uddin et al. (2016). With these calculated results, the values of Pr = 6.8377, Nt = 7.9417 × 10⁻⁷, Nb = 2.4795 × 10⁻⁶, and Le = 3359.1 have been taken into the numerical simulation for ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid, whereas the corresponding values for cobalt-kerosene ferrofluid are Pr = 23.004, Nt = 7.9583 × 10⁻⁶, Nb = 6.7195 × 10⁻⁶ , and Le = 3,412.4. The default values of the other parameters are considered as Ha = 20, γ = π/6, Nr = 0.1, and Ra = 10⁵ unless otherwise specified.

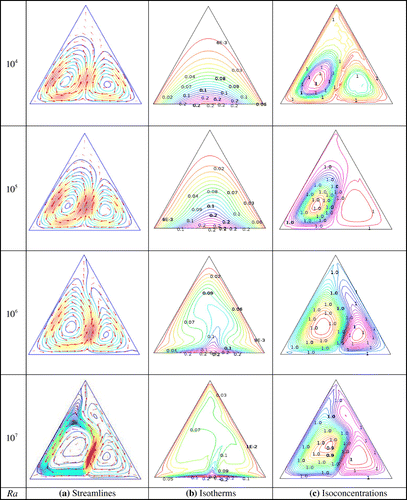
The effect of the Rayleigh number Ra $\left(Ra={10}^4-{10}^7\right)$ on the streamlines, isotherms, and isoconcentrations is shown in Figures 3(a)–(c), respectively, for ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid. From Figure 3(a), we observe that for every case of Ra, there are two oppositely rotating vortices inside the enclosure. The left vortex is much stronger than the right one due to the natural convective effect for a heated bottom wall. The hot fluid near the bottom wall of the cavity moves upwards due to the buoyancy effect while the relatively cold fluid moves downwards along the sidewalls completing a symmetric flow pattern. All values of Ra show the similar streamlines pattern. However, strength of fluid currents increases with Ra as higher Ra results in higher convective force. From Figure 3(b), the isotherms pattern indicate that at low value of Ra, convection is weaker inside the enclosure as the isotherms are seen nearly parallel to each other near the heated wall and forming parabolic shape. This pattern indicates dominance of conduction mode of heat transfer near the walls at low values of Ra. But, as the value of Ra increases, the isotherms spread near the middle of the enclosure forming a pattern like mushroom. This pattern suggests that heat energy flows into the fluid inside the enclosure from the bottom heated wall. From Figure 3(c), we see that the isoconcentration curves are almost uniformly distributed in the entire enclosure for all values of the Rayleigh number and form two loops in almost symmetric manner.

Figure 3. (a–c) Streamlines, isotherms and isoconcentrations for different values of Ra.

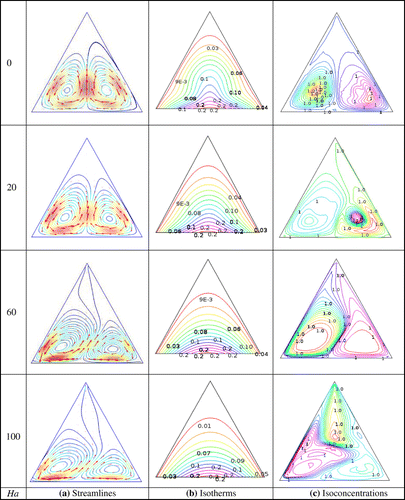
The influence of the Hartmann number Ha $\left(Ha=0-100\right)$ on the streamlines, isotherms, and isoconcentrations is shown in Figures 4(a)–(c), respectively, for ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid. From Figure 4(a), we see that when the Hartmann number Ha = 0, there formed two symmetric cells inside the cavity. Among them one is rotating in the anticlockwise direction while other is at clockwise with same strength. The phenomenon is quite obvious which reveals the general trend of natural convection. An increased Hartmann number i.e. a stronger magnetic field diminishes the flow strength within the cavity. The magnetic susceptibility due to the applied magnetic field over a moving fluid creates a Lorentz force that has the tendency to oppose the flow; as a consequence streamlines became weaken inside the cavity. Thus, when Ha is increased to 20, it is found that the vortices are no more symmetric. This occurs due to the presence of magnetic field which gives rise to the Lorentz force and tries to retard the convection. Increasing Ha further $\left(Ha=100\right)$ reduces the strength of the vortex and the eyes of the vortices are shifted to the bottom region of cavity.

Figure 4. (a–c) Streamlines, isotherms and isoconcentrations for different values of Ha.

From Figure 4(b), the effect of the Hartmann number (Ha) is more prominent which gives indication of the mode of heat transfer. As it can be observed that for Ha = 0 and Ha = 20, the isotherms pattern are like plume which is an indication of strong convection. When Ha is increased $\left(Ha=60\text{or}Ha=100\right)$, isotherms are almost parallel that is Hartmann number acts against convection inside the cavity. From Figure 4(c), we observe that in the absence of a magnetic field $\left(Ha=0\right)$, the isoconcentration curves are symmetric and almost uniformly distributed in the entire enclosure. But the isoconcentration curves become asymmetric in the presence of a magnetic field.

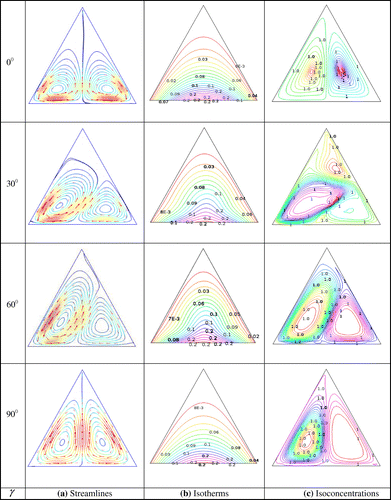
The influence of the magnetic field inclination angle $\left(\mathit{\gamma }\right)$ on streamlines, isotherms, and isoconcentrations for ${\text{Fe}}_3{\text{O}}_4-{\text{H}}_2\text{O}$ nanofluid is shown in Figures 5(a)–(c), respectively. For streamline as it can be seen from Figure 5(a) that at γ = 0 and γ = 90°, two opposing symmetric vortices are present. For γ = 30° and γ = 60°, the symmetric opposing vortices (at γ = 0°) no more exist. The left vortex becomes stronger than the right one. Again from Figure 5(b), we see that the isotherm lines are almost parallel for γ = 0 and γ = 90° which shows conduction mode of heat transfer. When the inclination angle changes to γ = 30° and γ = 60°, then both the horizontal and vertical components of the body forces due to the magnetic and buoyancy fields are present; consequently a plume pattern can be visualized which is an indication of convective heat transfer. From Figure 5(c), we observe that at γ = 0 and γ = 90°, the isoconcentration curves are symmetric and almost uniformly distributed in the entire enclosure. But the isoconcentration curves symmetry breaks down when γ = 30° and γ = 60°. It is interesting to see that the effect of magnetic field inclination angle on the pattern of isoconcentrations in equilateral triangular enclosure is almost similar to that of streamlines. This kind of outcome is very rare in other types of enclosure. This clearly indicates that the equilateral triangular shape enclosure plays very important role to obtain full-bodied flow and uniform concentration of nanoparticles.

Figure 5. (a–c) Streamlines, isotherms and isoconcentrations for different values of γ.

One of the main objective of this study is to show the effects of the governing parameters, namely the Hartmann number (Ha)and magnetic field inclination angle (γ) on the rate of heat transfer at the heated part of the enclosure for both ${\text{Fe}}_3{\text{O}}_4$-water and cobalt-kerosene ferrofluids. Table 3 has been displayed to satisfy this goal. From this table, we observe that the rate of heat transfer is decreased with the increasing values of the Hartmann number (Ha) while it increases with the increment in the magnetic field inclination angle (γ). From this Table 3, it is also observed that the heat transfer rate is higher for cobalt-kerosene ferrofluid than ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid.

Table 3. Variation of the average Nusselt number (Nu_av) for ${\text{Fe}}_3{\text{O}}_4$-water and cobalt-kerosene ferrofluids with different values of Hartmann number (Ha) and magnetic field inclination angle (γ)

Ha	γ	${\text{Fe}}_3{\text{O}}_4$-water	Cobalt-kerosene
		Nuav	Nuav
1	0	0.96448	1.45328
	30^°	0.96457	1.46345
	45^°	0.96469	1.47432
	60^°	0.96478	1.48763
	90^°	0.97546	1.49342
50	0	0.94342	1.32456
	30^°	0.94359	1.33365
	45^°	0.94368	1.34564
	60^°	0.94379	1.35432
	90^°	0.95354	1.36574
100	0	0.92426	1.24325
	30^°	0.92435	1.25675
	45^°	0.92443	1.26453
	60^°	0.92457	1.27345
	90^°	0.93452	1.28654

8. Conclusions

In this paper, the problem of steady hydromagnetic laminar natural convective flow and heat transfer of ferrofluids inside an equilateral triangular enclosure under the influence of an oriented magnetic field is studied using a two-component non-homogeneous thermal equilibrium model. The governing nonlinear partial differential equations are transformed into the dimensionless form using suitable non-dimensional quantities. The Galerkin weighted residual FEM has been used to solve the governing dimensionless equations. Comparison with previously published works is performed which gives excellent agreement. All numerical results are discussed from the physical point of view. From the numerical simulations, the following major outcomes are listed:

•	Conduction is the preliminary mode of heat transfer for lower values of the Rayleigh number.
•	Better heat transfer through convection is achieved for higher values of the Rayleigh number.
•	Equilateral triangular shape enclosure plays a very important role to obtain a full-bodied flow and uniform concentration of nanoparticles.
•	The magnetic field reduces the heat transfer rate significantly.
•	The direction of magnetic field within the enclosure determines the flow pattern of the ferrofluid.
•	The heat transfer rate is higher for cobalt-kerosene ferrofluid than ${\text{Fe}}_3{\text{O}}_4$-water ferrofluid.

Present research is carried out with a view to develop an advanced thermo-fluid for particular application. Experimental work is required for validation of the simulated findings.

Nomenclature
B0	=	magnetic field strength (Tesla)
cp	=	specific heat at constant pressure (Jkg−1K−1)
C	=	nanoparticle volume fraction
DB	=	Brownian diffusion coefficient (m2s−1)
DT	=	thermophoretic diffusion coefficient (m2s−1)
g	=	gravitational acceleration (ms−2)
H	=	height of the cavity (m)
Ha	=	Hartmann number
k	=	thermal conductivity (W m−1K−1)
K	=	wave number
L	=	length of the cavity (m)
Le	=	Lewis number
Nb	=	Brownian motion parameter
Nr	=	buoyancy ratio parameter
Nt	=	thermophoresis parameter
Nu	=	Nusselt number
p	=	dimensional pressure (Pa)
P	=	dimensionless pressure
Pr	=	Prandtl number
Ra	=	Rayleigh number
T	=	temperature (K)
u, v	=	dimensional velocity components (ms−1)
U, V	=	dimensionless velocity components
x, y	=	dimensional coordinates (m)
X, Y	=	dimensionless coordinates

Greek symbols
α	=	thermal diffusivity (m2s−1)
β	=	coefficient of thermal expansion (K−1)
γ	=	magnetic inclination angle (°)
σ	=	electric conductivity (Wm−1K−1)
θ	=	dimensionless temperature
ϕ	=	normalized nanoparticle volume fraction
ψ	=	stream function
μ	=	dynamic viscosity (kgm−1s−1)
ρ	=	density (kgm−3)
$\left(\mathit{\rho }{c}_p\right)$	=	heat capacity (JK−1m−3)

Subscripts
av	=	average
c	=	condition at cold wall
f	=	base fluid
h	=	condition at heated wall
p	=	solid nanoparticle
0	=	reference value

Additional information

Funding

M.M. Rahman is grateful to The Research Council (TRC) of Oman for funding under the Open Research [grant number ORG/SQU/CBS/14/007] and College of Science [grant number IG/SCI/DOMS/16/15].

Notes on contributors

M.M. Rahman

M.M. Rahman, PhD, is Associate Professor of Applied Mathematics at the Sultan Qaboos University, Sultanate of Oman. He received his MSc degree in 1994 from the University of Dhaka, Bangladesh, and PhD in 2003 in Applied Mathematics from the University of Glasgow, UK. His research interests include mathematical fluid mechanics, nano-fluidic phenomena, magnetohydrodynamics, heat and mass transfer, transport in porous media, and biofluid flows. He has supervised 15 PhD/MSc students. Currently, he is involved in supervising several PhD and MSc students. He has published more than 90 research papers in archived international journals and conference proceedings. He is the principal investigator of several grants funded by The Research Council of Oman and Sultan Qaboos University. He is an active member of several scholarly societies.