Closed form wave solutions of two nonlinear evolution equations

Abstract

The exploration of closed form wave solutions of nonlinear evolution equations (NLEEs) is an important research area in the field of physical sciences and engineering. In this article, we investigate closed form wave solution of two nonlinear equations, namely, the time regularized long wave equation and the (2 + 1)-dimensional nonlinear Schrodinger equation by the modified simple equation method. These equations play significant role in nonlinear sciences. The solutions are obtained in explicit form of the variables in the considered equations. The derived solutions are revealed in the form of exponential and trigonometric functions including solitary and periodic solutions. It is shown that the method is effective and an essential mathematical tool for constructing the closed form wave solutions of NLEEs in mathematical physics.

Keywords:

• modified simple equation (MSE) method
• time regularized long wave (TRLW) equation, the (2 + 1)-dimensional nonlinear Schrodinger equation
• nonlinear evolution equations (NLEEs)
• closed form wave solutions

Public Interest Statement

Nonlinear evolution equations (NLEEs) frequently arise in formulating fundamental laws of nature and a wide variety of problems naturally arising from solid-state physics, plasma physics, ocean and atmospheric waves, meteorology etc. Closed form solutions to NLEEs play a significant role in nonlinear science, especially in nonlinear physical science, since it can provide much physical information and more insight into the physical aspects of the problem. Therefore, numerous techniques have been developed by several groups of mathematicians and physicists to examine closed form solutions to NLEEs. In this article, we use the modified simple equation method to extract fresh and further general exact traveling wave solutions to the time regularized long wave equation and nonlinear telegraph equation. Thus, we obtain closed form wave solutions of these two equations among them some are new solutions. We expect that the new exact traveling wave solutions will be helpful to illuminate the connected phenomena.

1. Introduction

It is noteworthy to observe that the nonlinear evolution equations (NLEEs) are broadly used to formulate mathematical model of nonlinear wave phenomena appearing in the field of science and engineering. Therefore, the studies of the NLEEs have become a significant area of research in the recent years. In order to better understand the inner infrastructure of the phenomena described by the NLEEs, closed form solitary wave solutions play an imperative role. The closed form solutions of these equations give information about the structure of these problems and allow the researchers to design and experiments by creating appropriate conditions to determine these parameters or functions. Thus, we are motivated to search the closed form wave solutions of two important nonlinear wave equations, as for instance the time regularized long wave (TRLW) equation and the (2 + 1)-dimensional nonlinear Schrodinger equation (NLSE). The TRLW equation arises in the study of shallow water waves and the (2 + 1)-dimensional NLSE is the modeling equation of optics, heat conduction in solids. A soliton is special sort of solitary wave that retains it shape, velocity, and amplitude after colliding with another solitary wave. Soliton phenomena are observed in optical fibers, plasma physics, nuclear physics, biophysics, high-energy physics, meteorology, biology, solid-state physics, elastic media, chemical kinematics, geochemistry etc. As a result, the closed form solitary wave solutions of NLEEs have been investigated by many researchers who are interested in nonlinear phenomena. Recently significant improvements have been made for searching closed form solitary wave solutions of NLEEs and several effective and useful methods have been established and extended, such as the nonlinear transform method (Yang, Liu, & Yang, 2001), the first integration method (Taghizadeh & Mirzazadeh, 2011), the homogeneous balance method (Wang, 1995; Zayed, Zedan, & Gepreel, 2004), the simplified Hirota’s method (Wazwaz, 2014), the functional variable method (Çevikel, Bekir, Akar, & San, 2012), the Jacobi-elliptic function expansion method (Liu, Fu, Liu, & Zhao, 2001), Hirota’s bilinear transformation method (Hirota, 1973; Hirota & Satsuma, 1981), the tanh-function method (Nassar, Abdel-Razek, & Seddeek, 2011), the complex hyperbolic function method (Wang & Zhou, 2003), the Adomian decomposition method (Adomian, 1994), the Exp-function method (Akbar & Ali, 2011; Ebadi, Krishnan, Labidi, Zerrad, & Biswas, 2011), the modified Exp-function method (He, Li, & Long, 2012), the Painleve expansion method (Weiss, Tabor, & Carnevale, 1982), the variational iteration method (Helal & Seadawy, 2009; Seadawy, 2011), the Riccati equation method (Dai, Wang, & Biswas, 2014), the $exp(-\mathit{\varphi }(\mathit{\eta }))$-expansion method (Islam, Alam, Sazzad Hossain, Roshid, & Akbar, 2013; Islam, Khan, & Akbar, 2015; Khan & Akbar, 2013), the perturbation method (Antonova & Biswas, 2009; Girgis & Biswas, 2010), the extended Jacobi elliptic function method (Bhrawy, Abdelkawy, & Biswas, 2014), the Lie group symmetry method (Biswas & Kara, 2011), the (G^′/G)-expansion method (Akbar, Ali, & Zayed, 2012; Alam, Akbar, & Roshid, 2013; Taghizadeh & Foumani, 2016), the enhanced (G^′/G)-expansion method (Hossain & Akbar, 2017), the improve (G^′/G)-expansion method (Zhang, Jiang, & Zhao, 2010), the generalized Kudryashov method (Zayed & Al-Nowehy, 2016), the modified simple equation method (Akter & Akbar, 2015; Hossain & Akbar, 2017; Hossain, Akbar, & Wazwaz, 2017; Jawad, Petkovic, & Biswas, 2010; Khan & Akbar, 2013; Taghizadeh, Mirzazadeh, Paghaleh, & Vahidi, 2012), the sine-cosine function method (Jawad, Kumar, & Biswas, 2014), the extended direct algebraic method (Seadawy, 2014, 2015, 2016, 2017; Seadawy & El-Rashidy, 2013), the modified extended direct algebraic method (Seadawy, 2015, 2016), the modified extended auxiliary equation method (Seadawy, Arshad, & Lu, 2017), the solitary ansatz method (Biswas, 2008, 2009, 2010; Biswas & Milovic, 2008, 2009; Krishnan, Triki, Labidi, & Biswas, 2011; Sturdevant, Lott, & Biswas, 2009; Triki, Lepule, Love, Kara, & Biswas, 2014; Triki, Mirzazadeh, Bhrawy, Razborova, & Biswas, 2015; Xu et al., 2013), the symmetry reduction method (Abdel-Rahman, 2008) and others (Biswas, 2009; Khalique, Majid, & Biswas, 2011; Triki, Sturdevant, Hayat, Aldossary, & Biswas, 2011).

The modified simple equation (MSE) method is a recently developed straightforward, effective and rising method and getting popular day by day. The objective of this article is to execute the MSE method to construct the closed form soliton solutions to the TRLW equation and the (2 + 1)-dimensional NLSE. The rest of the article is prepared as follows: In Section 2, MSE method is delineated. In Section 3, the method is implemented to examine the NLEEs indicated above. In Section 4, results and physical explanations are discussed and in Section 5 conclusions are provided.

2. The modified simple equation MSE Method

In order to describe the MSE method, let us consider a nonlinear evolution equation in two independent variables x and t in the form:(2.1) $$\mathcal{F}\left(u,u_t,u_x,u_{tt},u_{xx},u_{xt}\dots \right)=0,$$(2.1)

where u = u(x, t) is an unknown function and $\mathcal{F}$ is a polynomial of u(x, t) and its partial derivatives wherein the highest order derivatives and nonlinear terms are involved and the subscripts are used for partial derivatives. The important steps of this method are presented in the following:

Step 1: Initiating a compound variable $\mathit{\xi }$, we combine the real variables x and t:

(2.2) $$u\left(x,y,t\right)=u\left(\mathit{\xi }\right),\mathit{\xi }=x+y\pm ct,$$(2.2)

where c is the speed of the solitary wave.

The wave transformations (2.2) allow us in reducing Equation (2.1) into an ODE for $u=u\left(\mathit{\xi }\right)$ in the form:

(2.3) $$\mathcal{R}\left(u,u^{\prime },u^{″},u^{‴}\dots \right)=0,$$(2.3)

where $\mathcal{R}$ is a polynomial in $u\left(\mathit{\xi }\right)$ and its derivatives, the prime stands for the derivative with respect to ξ.

Step 2: Assume the solution of (2.3) can be revealed of the form:

(2.4) $$u\left(\mathit{\xi }\right)=\sum _{i=0}^N{a}_i{\left(\frac{{\mathit{\psi }}^{\prime }(\mathit{\xi })}{\mathit{\psi }(\mathit{\xi })}\right)}^i$$(2.4)

where $a_i\left(i=0,1,2,3,\dots N\right)$ are arbitrary constants to be determined such that a_N ≠ 0 and ψ(ξ) is an unknown function to be evaluated later, such that ${\mathit{\psi }}^{\prime }\left(\mathit{\xi }\right)\ne 0$. The characteristic and uniqueness of this method is that, ψ(ξ) is not known function or not a solution of any predefined differential or algebraic equation, whereas in the sine-cosine method, Exp-function method, tanh-function method, (G^′/G)-expansion method, Jacobi elliptic function method etc., the solution are introduced in the form of known function. Therefore, it is not possible to speculate in advance what kind of solutions one may obtain through this method. Thus, it might be possible to achieve some fresh solution by this method.

Step 3: We determine the positive integer N arises in (2.4) by balancing the highest order of linear and nonlinear terms appearing in (2.3).

Step 4: Compute the necessary derivatives $u^{\prime },u^{″},\dots$ and insert Equation (2.4) into (2.3) and then we account the function $\mathit{\psi }(\mathit{\xi })$. The above procedure yields a polynomial in (1/ψ(ξ)). Equating the coefficients of same power of this polynomial to zero, yields a system of algebraic and differential equations that can be solved to get $a_i\left(i=0,1,2,3,\dots N\right)$, ψ(ξ) and the value of other needful parameters. This completes the determination of solutions to the Equation (2.1).

3. Formulations of the solutions

In this section, MSE method has been put to use to examine the closed form solutions directed to solitary wave solutions to the TRLW equation and the (2 + 1)-dimensional NLSE.

3.1. The TRLW equation

In this sub-section, the MSE method has been implemented to examine the closed form solutions to the TRLW equation , which is one of the alternative forms of the KdV equation (Islam et al., 2015):

(3.1) $$u_t+u_x+\mathit{\alpha }u{u}_x+u_{xtt}=0.$$(3.1)

where u, t and x denote the amplitude, time, and spatial coordinate, respectively, and α is a nonzero constant. The first term is the evolution term, and the third term is the nonlinear term, while the fourth term is the dispersion term. The third term uu_x accounts for steepening of the wave and the dispersion term represented by u_xtt spreading the wave. Nonlinearity tends to localize the wave while dispersion spreads it out. The solitons are the result of a intricate balance between dispersion and nonlinearity.

The traveling wave transformations $\mathit{\xi }=\left(x-ct\right),$ $u\left(x,t\right)=u\left(\mathit{\xi }\right)$ where c is the wave speed, converts the Equation (3.1) into an ODE of the form

(3.2) $$c^2{u}^{‴}+\mathit{\alpha }u{u}^{\prime }+(1+c)u^{\prime }=0$$(3.2)

Integrating (3.2) with respect to ξ once and the setting the constant of integration to zero, reduces to

(3.3) $$c^2{u}^{″}+\frac{\mathit{\alpha }}{2}{u}^2+(1+c)u=0.$$(3.3)

Balancing u² and u^″, yields N = 2.

Therefore, the solution of Equation (3.3) turns out to be

(3.4) $$u\left(\mathit{\xi }\right)=a_0+a_1\left(\frac{{\mathit{\psi }}^{\prime }}{\mathit{\psi }}\right)+a_2{\left(\frac{{\mathit{\psi }}^{\prime }}{\mathit{\psi }}\right)}^2$$(3.4)

where a₀, a₁ and a₂ are constants, such that a₂ ≠ 0 and ψ(ξ) is an unknown function to be calculated. Substituting (3.4) and its derivatives into (3.3) and then equating the coefficients of ψ⁰, ψ⁻¹, ψ⁻², ψ⁻³, ψ⁻⁴ to zero we achieve the successive algebraic and differential equations

(3.5) $$\frac{\mathit{\alpha }}{2}{a}_0^2+c{a}_0+a_0=0,$$(3.5)

(3.6) $$c^2{a}_1{\mathit{\psi }}^{‴}+\mathit{\alpha }{a}_0{a}_1{\mathit{\psi }}^{\prime }+c{a}_1{\mathit{\psi }}^{\prime }+a_1{\mathit{\psi }}^{\prime }=0,$$(3.6)

(3.7) $$-3c^2{a}_1{\mathit{\psi }}^{\prime }{\mathit{\psi }}^{″}+2c^2{a}_2{\mathit{\psi }}^{\prime {\mathit{\psi }}^{‴}}+2c^2{a}_2{\mathit{\psi }}^{″2}+\left(\mathit{\alpha }{a}_0{a}_2+\frac{\mathit{\alpha }}{2}{a}_1^2+a_2+c{a}_2\right){\mathit{\psi }}^{\prime 2}=0$$(3.7)

(3.8) $$-10a_2{\mathit{\psi }}^{\prime 2}{\mathit{\psi }}^{″}+\mathit{\alpha }{a}_1{a}_2{\mathit{\psi }}^{\prime 3}+2c^2{a}_1{\mathit{\psi }}^{\prime 3}=0,$$(3.8)

(3.9) $$\frac{\mathit{\alpha }}{2}{a}_2^2{\mathit{\psi }}^{\prime 4}+6c^2{a}_2{\mathit{\psi }}^{\prime 4}=0.$$(3.9)

From Equation (3.5), we obtain $a_0=0,-\frac{2\left(1+c\right)}{\mathit{\alpha }}.$

Also from Equation (3.9), we achieve $a_2=-\frac{12c^2}{\mathit{\alpha }},$ since a₂ ≠ 0.

From Equation (3.8), it can be deduced that

(3.10) $$\frac{{\mathit{\psi }}^{″}}{{\mathit{\psi }}^{\prime }}=\mathit{\lambda }$$(3.10)

where $\mathit{\lambda }=\frac{(2c^2{a}_1+\mathit{\alpha }{a}_1{a}_2)}{10c^2{a}_2}.$

Integrating (3.10) with respect to ξ, yields

(3.11) $${\mathit{\psi }}^{\prime }=c_1{\text{e}}^{\mathit{\lambda }\mathit{\xi }}$$(3.11)

And

(3.12) $$\mathit{\psi }=\frac{c_1{\text{e}}^{\mathit{\lambda }\mathit{\xi }}}{\mathit{\lambda }}+c_2$$(3.12)

where c₁ and c₂ are integral constants.

Case 1: When $a_0=0$ and $a_2=-\frac{12c^2}{\mathit{\alpha }}$, solving Equations (3.6) and (3.7) by using (3.11)–(3.12), we attain $a_1=\pm \frac{12c\sqrt{-\left(1+c\right)}}{\mathit{\alpha }}$ and c = c. Inserting the values of a₀, a₁ and a₂ in (3.4), it is derived(3.13) $$u\left(\mathit{\xi }\right)=\pm \frac{12(1+17\left(\right)c)}{\mathit{\alpha }}\left(\frac{i{c}_1{e}^{\mathit{\lambda }\mathit{\xi }}}{\left(c_1{e}^{\mathit{\lambda }\mathit{\xi }}+c_2\mathit{\lambda }\right)}-\frac{c_1^2{e}^{2\mathit{\lambda }\mathit{\xi }}}{{(c_1{e}^{\mathit{\lambda }\mathit{\xi }}+c_2\mathit{\lambda })}^2}\right)$$(3.13)

where $\mathit{\xi }=\left(x-ct\right)$ and $\mathit{\lambda }=\pm \frac{\sqrt{\left(1+c\right)}}{c}$.

Simplifying the exponential function solution (3.13), it transformed to the hyperbolic function as,

(3.14) $$u\left(\mathit{\xi }\right)=\pm \frac{12\left(1+c\right)}{\mathit{\alpha }}\left(\frac{i{c}_1\left(cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}{\left(\left(c_1+c_2\mathit{\lambda }\right)cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+\left(c_1-c_2\mathit{\lambda }\right)sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}-\frac{c_1^2{\left(cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}^2}{{\left(\left(c_1+c_2\mathit{\lambda }\right)cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+\left(c_1-c_2\mathit{\lambda }\right)sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}^2}\right)$$(3.14)

Since c₁ and $c_2$ are arbitrary constants, one might randomly choose their values, Therefore, if we choose c₁ = 1 and $c_2=1/\mathit{\lambda }$, from Equation (3.15), we obtain the following closed form soliton solution.

$$u\left(\mathit{\xi }\right)=\frac{6\left(1+c\right)}{\mathit{\alpha }}\left(1+tanh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)\left(2i+1+tanh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)$$

In (x, t) variables the above closed form wave solution can be written as follows:

(3.15) $$u\left(x,t\right)=\frac{6\left(1+c\right)}{\mathit{\alpha }}\left(1+tanh\left(\pm \frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)\right)\left(2i+1+tanh\left(\pm \frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)\right)$$(3.15)

Again if we choose c₁ = 1 and $c_2=-1/\mathit{\lambda }$, the closed form solution (3.14) turns into$$u\left(\mathit{\xi }\right)=\frac{6\left(1+c\right)}{\mathit{\alpha }}\left(1+coth\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)\left(2i+1+coth\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)$$

Therefore, the closed form wave solution of the TRLW equation in (x, t) variables as follows:

(3.16) $$u\left(x,t\right)=\frac{6\left(1+c\right)}{\mathit{\alpha }}\left(1+coth\left(\pm \frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)\right)\left(2i+1+coth\left(\frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)\right)$$(3.16)

Case 2: When $a_0=-\frac{2(1+c)}{\mathit{\alpha }}$ and $a_2=-\frac{12c^2}{\mathit{\alpha }}$, solving Equation (3.6) and (3.7), we get $a_1=\pm \frac{12c\sqrt{\left(1+c\right)}}{\mathit{\alpha }}$ and c = c. Then by setting the values of a₀, a₁ and a₂ in (3.4), we obtain

(3.17) $$u\left(\mathit{\xi }\right)=-\frac{2(1+c)}{\mathit{\alpha }}\left(1-\frac{6c_1{e}^{\mathit{\lambda }\mathit{\xi }}}{\left(c_1{e}^{\mathit{\lambda }\mathit{\xi }}+c_2\mathit{\lambda }\right)}+\frac{6c_1^2{e}^{2\mathit{\lambda }\mathit{\xi }}}{{(c_1{e}^{\mathit{\lambda }\mathit{\xi }}+c_2\mathit{\lambda })}^2}\right),$$(3.17)

where $\mathit{\xi }=\left(x-ct\right)$ and $\mathit{\lambda }=\pm \frac{\sqrt{\left(1+c\right)}}{c}$

Converting the solution into hyperbolic function by using the exponential function identity, the close form solution (3.17) becomes

(3.18) $$u\left(\mathit{\xi }\right)=-\frac{2\left(1+c\right)}{\mathit{\alpha }}\left(1-\frac{6c_1\left(cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}{\left(\left(c_1+c_2\mathit{\lambda }\right)cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+\left(c_1-c_2\mathit{\lambda }\right)sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}+\frac{6c_1^2{\left(cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}^2}{{\left(\left(c_1+c_2\mathit{\lambda }\right)cosh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)+\left(c_1-c_2\mathit{\lambda }\right)sinh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}^2}\right)$$(3.18)

Since c₁ and c₂ integral constants, setting c₁ = 1 and $c_2=1/\mathit{\lambda }$ into (3.18), provides

$$u\left(\mathit{\xi }\right)=\frac{\left(1+c\right)}{\mathit{\alpha }}\left(4+6tanh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)-3{\left(1+tanh\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}^2\right).$$

The above closed form soliton solution of the TRLW equation in (x, t) variables becomes:(3.19) $$u\left(x,t\right)=\frac{\left(1+c\right)}{\mathit{\alpha }}\left(4+6tanh\left(\pm \frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)-3{\left(1+tanh\left(\pm \frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)\right)}^2\right)$$(3.19)

Again if we set c₁ = 1 and $c_2=-1/\mathit{\lambda }$, the solution (3.18) becomes

$$u\left(\mathit{\xi }\right)=\frac{\left(1+c\right)}{\mathit{\alpha }}\left(4+6coth\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)-3{\left(1+coth\left(\frac{\mathit{\lambda }\mathit{\xi }}{2}\right)\right)}^2\right)$$

Thus, in (x, t) variables, the closed form traveling wave solution of the TRLW equation becomes:

(3.20) $$u\left(x,t\right)=\frac{\left(1+c\right)}{\mathit{\alpha }}\left(4+6coth\left(\pm \frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)-3{\left(1+coth\left(\pm \frac{\sqrt{\left(1+c\right)}}{2c}\left(x-ct\right)\right)\right)}^2\right)$$(3.20)

3.2. The nonlinear Schrodinger equation

In this sub-section, we derive the closed form solitary wave solutions of the (2 + 1)-dimensional NLSE (Jawad et al., 2014) by means of the method described in Section 2:

(3.21) $$i{q}_t+a{q}_{xx}-b{q}_{yy}+c{\left|q\right|}^{2}q=0$$(3.21)

where q = q(x, y, t) is a complex valued function, $i=\sqrt{-1}$ and $a,b$ and c are non-zero real parameters wherein a and b dissipation coefficients and c self-phase modulation. The first term represents the evolution term, the second and third terms represent the dissipation while the fourth term represents nonlinearity. The balance between these linear term and nonlinear term formulate the solitons. The mathematical model of the nonlinear Schrodinger Equation (3.21) arises as an approximate model of the evolution of a nearly monochromatic wave of small amplitude in pulse propagation along optical fibers and in gravity waves in deep water (Abdel-Rahman, 2008).

The complex transformations $q\left(x,y,t\right)=e^{i(\mathit{\alpha }x+\mathit{\beta }y+\mathit{\delta }t)}u\left(\mathit{\xi }\right),\mathit{\xi }=k(x+y-\mathit{\omega }t)$ where $\mathit{\alpha },\mathit{\beta },\mathit{\delta }$, $k$ are real constants and $\mathit{\omega }$ is velocity of the solitary wave, reduce the Equation (3.21) into an ordinary differential equation of the form:

(3.22) $$\left(a-b\right)k^2{u}^{″}-ik\left(\mathit{\omega }-2a\mathit{\alpha }+2b\mathit{\beta }\right)u^{\prime }-\left(\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2\right)u+c{u}^3=0$$(3.22)

From the above Equation (3.22), we obtain ω = 2(aα + bβ) and $u\left(\mathit{\xi }\right)$ satisfy the ODE

(3.23) $$\left(a-b\right)k^2{u}^{″}+c{u}^3-\left(\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2\right)u=0.$$(3.23)

Equation (3.23) can be written as

(3.24) $$u^{″}+{\mathit{\lambda }}_1{u}^3-{\mathit{\lambda }}_{2}u=0,$$(3.24)

where ${\mathit{\lambda }}_1=\frac{c}{\left(a-b\right)k^2}$ and ${\mathit{\lambda }}_2=\frac{\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2}{\left(a-b\right)k^2}$.

Taking homogeneous balance between the highest-order derivative term u^″ and the highest-order nonlinear term u³ yields n = 1.

Therefore, the solution of Equation (3.24) reduces to the form,

(3.25) $$u\left(\mathit{\xi }\right)=a_0+a_1\left(\frac{{\mathit{\psi }}^{\prime }}{\mathit{\psi }}\right)$$(3.25)

where a₀ and a₁ are constants, such that a₁ ≠ 0 and ψ(ξ) is an unknown function to be calculated. Substituting (3.25) and its derivatives into (3.24) and completing the similar procedure as described in subsection 3.1, we attain the following successive algebraic and differential equations,

(3.26) $${\mathit{\lambda }}_1{a}_0^3-{\mathit{\lambda }}_2{a}_0=0,$$(3.26)

(3.27) $$a_1{\mathit{\psi }}^{″\prime }+3{\mathit{\lambda }}_1{a}_0^2{a}_1{\mathit{\psi }}^{\prime }-{\mathit{\lambda }}_2{a}_1{\mathit{\psi }}^{\prime }=0,$$(3.27)

(3.28) $$-3a_1{\mathit{\psi }}^{\prime }{\mathit{\psi }}^{″}+3{\mathit{\lambda }}_1{a}_0{a}_1^2{\mathit{\psi }}^{\prime 2}=0,$$(3.28)

(3.29) $$2a_1{\mathit{\psi }}^{\prime 3}+{\mathit{\lambda }}_1{a}_1^3{\mathit{\psi }}^{\prime 3}=0.$$(3.29)

From Equations (3.26) and (3.29), we obtain $a_0=0,\pm \sqrt{\frac{{\mathit{\lambda }}_2}{{\mathit{\lambda }}_1}}$ and $a_1=\pm \sqrt{\frac{-2}{{\mathit{\lambda }}_1}},$ since $a_1\ne 0$.(3.30) $$\text{From Equation (3.28), it can be deduced that}\frac{{\mathit{\psi }}^{″}}{{\mathit{\psi }}^{\prime }}=\mathit{\theta }$$(3.30)

where $\mathit{\theta }={\mathit{\lambda }}_1{a}_0{a}_1$Integrating (3.30) with respect to ξ, yields

(3.31) $${\mathit{\psi }}^{\prime }=c_1{\text{e}}^{\mathit{\theta }\mathit{\xi }},$$(3.31)

And

(3.32) $$\mathit{\psi }=\frac{c_1{\text{e}}^{\mathit{\theta }\mathit{\xi }}}{\mathit{\theta }}+c_2,$$(3.32)

where c₁ and $c_2$ are constants of integration.

Case 1: When $a_0=\pm \sqrt{\frac{{\mathit{\lambda }}_2}{{\mathit{\lambda }}_1}}$, $a_1=\pm \sqrt{\frac{-2}{{\mathit{\lambda }}_1}}$, and ω = 2(aα − bβ), substitute these values into (3.25), it is found that

(3.33) $$u\left(\mathit{\xi }\right)=\pm \sqrt{\frac{{\mathit{\lambda }}_2}{{\mathit{\lambda }}_1}}\left(1-\frac{2c_1}{c_1+c_2\mathit{\theta }{e}^{-\mathit{\theta }\mathit{\xi }}}\right),$$(3.33)

where ξ = k(x + y - 2(aα − bβ)t) and $\mathit{\theta }=\pm \sqrt{-2{\mathit{\lambda }}_2}$.

Since c₁ and c₂ are constants of integration, one might randomly pick their values. Therefore, if we pick c₁ = 1 and c₂ = 1/θ from Equation (3.33), we attain exponential form wave solution and simplifying this exponential solution, we derive the following closed form solitary solution of the nonlinear Schrodinger equation:

(3.34) $$u\left(\mathit{\xi }\right)=\pm \sqrt{\frac{{\mathit{\lambda }}_2}{{\mathit{\lambda }}_1}}\left(tanh\left(\frac{\mathit{\theta }\mathit{\xi }}{2}\right)\right).$$(3.34)

On the other hand, if we pick c₁ = −1 and c₂ = 1/θ, from Equation (3.33), we attain the following closed form solution of the nonlinear Schrodinger equation:

(3.35) $$u\left(\mathit{\xi }\right)=\mp \sqrt{\frac{{\mathit{\lambda }}_2}{{\mathit{\lambda }}_1}}\left(coth\left(\frac{\mathit{\theta }\mathit{\xi }}{2}\right)\right)$$(3.35)

Thus, in $(x,y,t)$ variables, the general closed form traveling wave solution of the nonlinear Schrodinger equation is obtained as follows:

(3.36) $$q\left(x,y,t\right)=\mp \sqrt{\frac{\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2}{c}}\left(tanh\left(\frac{\sqrt{\frac{-2(\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2)}{\left(a-b\right)k^2}}[k\left(x+y-2\left(a\mathit{\alpha }-b\mathit{\beta }\right)t\right)]}{2}\right)\right)$$(3.36) (3.37) $$\text{and}q\left(x,y,t\right)=\mp \sqrt{\frac{\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2}{c}}\left(coth\left(\frac{\sqrt{\frac{-2(\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2)}{\left(a-b\right)k^2}}[k\left(x+y-2\left(a\mathit{\alpha }-b\mathit{\beta }\right)t\right)]}{2}\right)\right)$$(3.37)

Using hyperbolic functions identities, Equations (3.34) and (3.35) can be rewritten as

(3.38) $$q\left(x,y,t\right)=\mp \sqrt{\frac{\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2}{c}}\left(itan\left(i\frac{\sqrt{\frac{-2(\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2)}{\left(a-b\right)k^2}}[k\left(x+y-2\left(a\mathit{\alpha }-b\mathit{\beta }\right)t\right)]}{2}\right)\right)$$(3.38) (3.39) $$\text{and}q\left(x,y,t\right)=\mp \sqrt{\frac{\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2}{c}}\left(icot\left(i\frac{\sqrt{\frac{-2(\mathit{\delta }+a{\mathit{\alpha }}^2-b{\mathit{\beta }}^2)}{\left(a-b\right)k^2}}[k\left(x+y-2\left(a\mathit{\alpha }-b\mathit{\beta }\right)t\right)]}{2}\right)\right)$$(3.39)

Case 2: When a₀ = 0 and$a_1=\pm \sqrt{\frac{-2}{{\mathit{\lambda }}_1}}$, and ω = 2(aα - bβ) then substitute these values of a₀, a₁and ω in (3.25) does not satisfy one of the algebraic Equation (3.28) hence the solution must be rejected.

4. Discussion and physical explanations

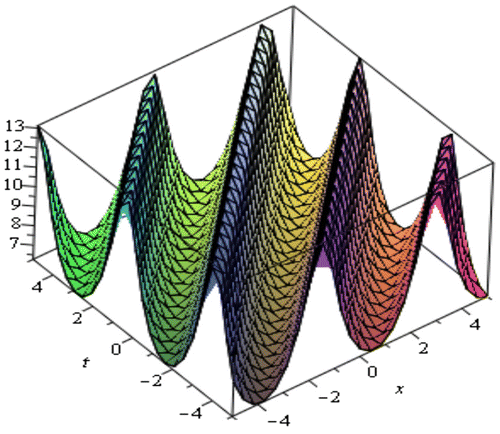
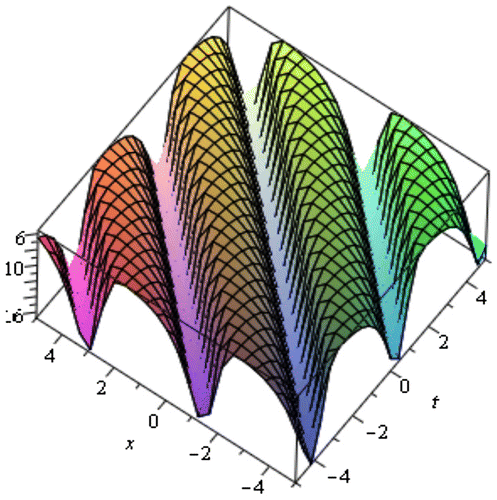
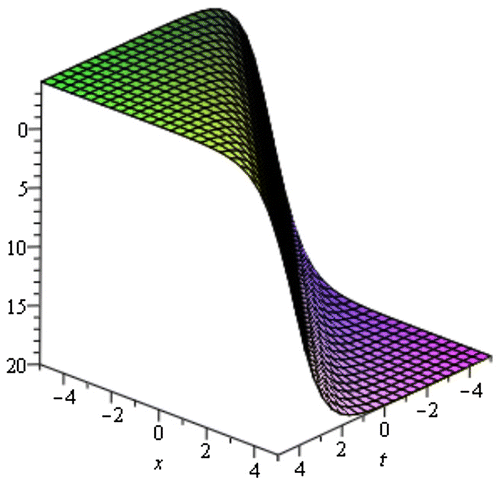
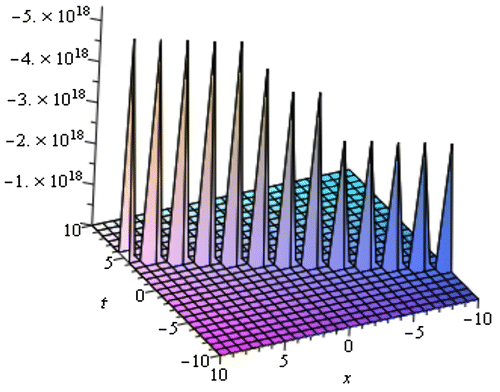
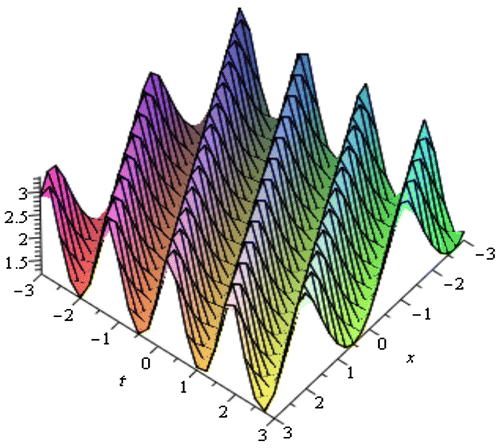
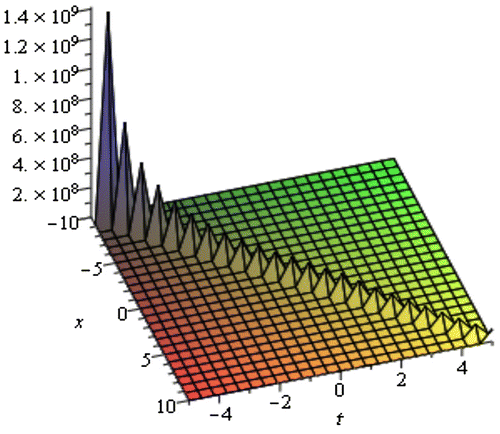
In this section, we have discussed about the obtained solution of the TRLW equation and the (2 + 1)-dimensional NLSE. Using the MSE method, we achieved the solitary wave solutions from (3.13) to (3.20) of the TRLW equation. These solutions are generally closed form traveling wave solutions which includes periodic wave solution, soliton solution, kink shape wave solution, bell shape soliton solution, and singular solution. When the center position of the solitary wave is imaginary then singular solitons can be connected to solitary waves. Since this type of solution has the nature of spike and therefore it can probably provide an explanation to the formation of Rogue waves. Kink type soliton solutions are important to transfer signal and information in optical fiber. Periodic traveling waves also play an important role in various physical phenomena, including reaction-diffusion-advection systems, impulsive systems, self-reinforcing systems, etc. Mathematical modeling of many intricate physical events, for instance physics, mathematical physics, computer science and many more phenomena resemble periodic traveling wave solutions. From the above solution, it has been detected that the solutions (3.13) and (3.14) provides periodic wave solution where the solutions (3.15) and (3.16) gives soliton solution. The solutions (3.18)–(3.19) and the solution (3.20) shows the nature of bell shape soliton and singular soliton, respectively, where (3.17) represents kink shape solution. The periodic wave solution (3.13) and (3.14) is represented by the Figures 1 and 2 for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1,c_2=2and{a}_0=0$ within the interval $-5\le x,t\le 5$. The solution (3.17) shows the shape of kink type solution in Figure 3 for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1and{c}_2=2$ within the interval $-5\le x,t\le 5$.The bell shape soliton solution (3.19) for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1and{c}_2=1/\mathit{\lambda }$ within the interval $-5\le x,t\le 5$ is corresponding to the Figure 4. 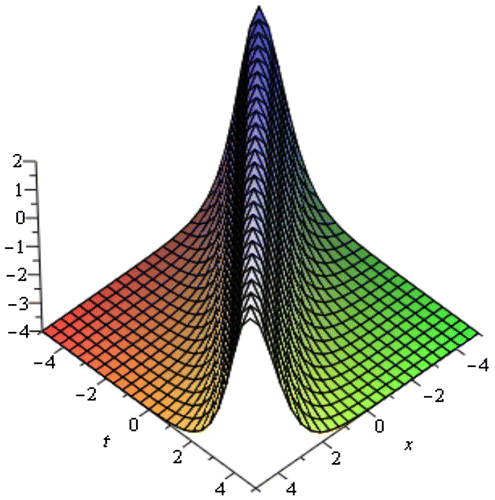The singular soliton solution (3.20) for $\mathit{\alpha }=\mathit{\omega }=1,c_1=1and{c}_2=-1/\mathit{\lambda }$ within the interval −10 ≤ x, t ≤ 10 is represented by Figure 5. From the solutions of the (2 + 1)-dimensional nonlinear Schrodinger equation, it is observed that the solutions (3.34)–(3.39) are singular periodic solutions where the solution (3.33) represents periodic wave solution. The solution (3.33) is represented in Figure 6. It shows the periodic solution with $\mathit{\alpha }=1,\mathit{\beta }=1,\mathit{\delta }=1,k=1,a=2,b=1,c_1=1and{c}_2=2$ within the interval −3 ≤ t ≤ 3. The singular periodic solution (3.39) for $\mathit{\alpha }=1,\mathit{\beta }=1,\mathit{\delta }=1,k=1,a=2,b=1andc=1$ within the interval −10 ≤ x ≤ 10 and −5 ≤ t ≤ 5 is given by Figure 7. The figures of others solutions are similar to singular periodic solution type and ignored these figures for simplicity.

Figure 1. Periodic solution u(ξ) in (3.13) for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1,c_2=2\text{and}{a}_0=0.$

Figure 2. Periodic solution u(ξ) in (3.14) for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1,c_2=2\text{and}{a}_0=0.$

Figure 3. Kink shape solution u(ξ) in (3.17) for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1\text{and}{c}_2=2$.

Figure 4. Bell shape soliton solution u(ξ) in (3.19) for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1\text{and}{c}_2=1/\mathit{\lambda }$.

Figure 5. Singular soliton solution u(ξ) in (3.20) for $\mathit{\alpha }=1,\mathit{\omega }=1,c_1=1\text{and}{c}_2=-1/\mathit{\lambda }$.

Figure 6. Periodic solution u(ξ) in (3.33) for $\mathit{\alpha }=1,\mathit{\beta }=1,\mathit{\delta }=1,k=1,a=2,b=1,c=1\text{and}{c}_2=2$.

Figure 7. Singular periodic solution u(ξ) in (3.39) for $\mathit{\alpha }=1,\mathit{\beta }=1,\mathit{\delta }=1,k=1,a=2,b=1\text{and}c=1$.

5. Conclusion

In this article, the modified simple equation method has been successfully implemented to establish the closed form solitary wave solutions of the TRLW equation and the (2 + 1)-dimensional NLSE. The solutions are verified to check the correctness by inserting them back into the original equation and found correct.Here, we achieved the value of the coefficients a₀, a₁ etc. without using any symbolic computation software such as Maple, Mathematica, etc. The used method is much simpler in comparing to other methods because this method is straightforward and its calculation procedure is very concise. Therefore, the applied method is quite efficient and practically well suited and could be more effectively used to solve various NLEEs which regularly arise in science, engineering and other technical arenas.

Funding

The authors received no direct funding for this research.

Acknowledgement

The authors wish to take this chance to express their gratitude to the anonymous referees for their valuable comments and suggestions to improve the quality of this article.

Additional information

Notes on contributors

A.K.M. Kazi Sazzad Hossain

Mr A.K.M. Kazi Sazzad Hossain is an assistant professor at the Department of Mathematics, Begum Rokeya University, Rangpur, Bangladesh. Earlier in 2012, he joined at the same Department as a lecturer. He obtained his BSc (Honors) from Mathematics and MSc from Applied Mathematics, Rajshahi University, Bangladesh. At present he is undertaking PhD at the Department of Applied Mathematics, Rajshahi University, Bangladesh. He has published four research article and submitted another five.

M. Ali Akbar

M. Ali Akbar is an associate professor at the Department of Applied Mathematics, Rajshahi University, Bangladesh. He received his PhD in Mathematics from the Department of Mathematics, Rajshahi University, Bangladesh. He is actively involved in research in the field of nonlinear differential equations and fractional calculus. He has published more than 150 research articles of which 60 articles are published in ISI (Thomson Reuter) indexed journals and other 15 articles published in Scopus indexed journals.

Md. Abul Kalam Azad

Md. Abul kalam Azad is a professor at the Department of Applied Mathematics, Rajshahi University, Bangladesh. He has published more than 50 articles in the international journals.