Are Options Trading Strategies Really Effective for Hedging in the Indian Derivatives Market?

Abstract

Hedging being a predominant financial concern, is considered as a robust method of managing investment risks. Literature evinces that the covered call strategy provides nominal returns alongside effective hedging. However, studies have not compared the hedging effectiveness of covered call, covered put, collar, and synthetic long call strategies in the equity segment. The study evaluates the hedging effectiveness of option trading strategies by applying them to the companies of the top six National Stock Exchange (NSE) sector indices for twelve years, from 2009 to 2020 under volatile and neutral market conditions. The study collects data of 18,720 option contracts and considers 3744 observations for each strategy. The panel regression analysis approach is being incorporated into the study. Hausman test results determine the appropriate model between fixed and random effects. Furthermore, the study compares the mean scores of selected strategies to identify significant differences between the groups using the Games-Howell Post Hoc Tukey Test. The study recommended covered call and covered put strategies effectively hedge the investment in both market conditions. The study’s findings help retail investors choose a better hedging strategy and employ the same in their trading, specific to the market condition. Future studies can apply and compare the effectiveness of these strategies in other emerging derivative markets.

Keywords:

• Derivatives market
• options
• options strategies
• hedging
• panel regression
• Games-Howell post hoc Tukey test

JEL Classifications:

• G11
• G12
• G32

1. Introduction

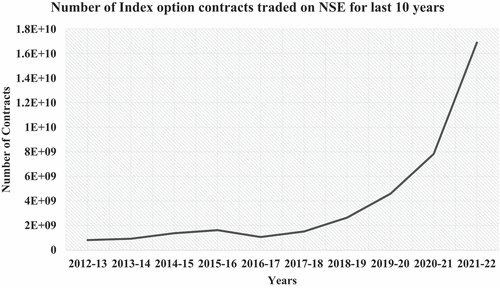
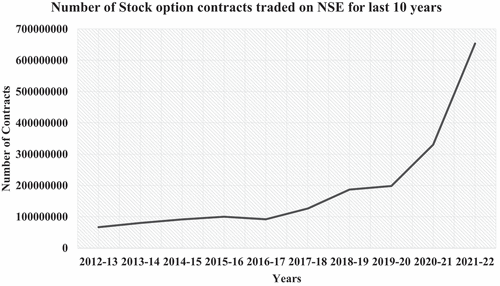
Investors always seek strategies that hedge the equity risk (Antonakakis et al., 2020) and minimize the uncertainties in their investment (Fontanills, 2005; Samuel, 2017 and Kedžo & Šego, 2021). Derivatives are one of the financial instruments used for risk management (Dewobroto et al., 2010). Though the fundamental objective of derivatives is hedging, it has also been used for speculation. Forwards, futures, options, and swaps are derivative instruments; however, options have gained prominence due to their unique features and applicability in managing the risk of any underlying financial asset (Dewobroto et al., 2010and Kedžo & Šego, 2021). These options provide the right to buy or sell but not the obligation to buy or sell any specified financial asset at a specified price and time. Options trading allows to hedge the underlying asset and minimize the risks in the investment; it has attained huge momentum in the Indian capital market in recent years in terms of the number of contracts traded and premium turnover¹ (Table 1, Figure 1 & 2). However, it is noted that individual investors incur huge losses on equity investment due to market volatility (Kumar Meher et al., 2021). Therefore, option strategies allow investors to employ suitable hedging strategies to manage the equity price risk.

Figure 1. Total number of index option contracts traded on national stock exchange from 2012–2022.

Figure 2. Total number of stock option contracts traded on national stock exchange from 2012–2022.

Table 1. Total number contracts traded and total premium turnover of index and stock options on national stock exchange from 2012 to 2022

Year	Index Options		Stock Options
	No. of Contracts	Premium Turnover(₹ crore)	No. of Contracts	Premium Turnover(₹ crore)
2012–13	820,877,149	184,383.24	66,778,193	34,288.56
2013–14	928,565,175	244,090.71	80,174,431	46,428.41
2014–15	1,378,642,863	265,315.63	91,479,209	61,732.59
2015–16	1,623,528,486	351,221.01	100,299,174	61,118.39
2016–17	1,067,244,916	350,021.53	92,106,012	95,570.09
2017–18	1,515,034,222	460,653.71	126,411,376	148,217.50
2018–19	2,652,457,487	654,099.95	186,986,542	200,010.31
2019–20	4,586,692,584	1,082,514.05	198,377,569	229,034.28
2020–21	7,824,035,680	2,629,426.05	330,394,648	579,351.62
2021–22	16,875,505,904	5,605,923.72	653,038,720	1,012,991.90

Available studies on options hedging strategies focused on the performance of covered call or buy-write strategy (Diaz & Kwon, 2016; Hoffmann & Fischer, 2012; Mugwagwa et al., 2012 and Niblock & Sinnewe, 2018) and observed superior risk-adjusted returns. Limited attention is directed to other hedging strategies, such as collar strategy (Bartonova, 2012 and Israelov & Klein, 2016) and synthetic long call strategy (Figlewski et al., 1993; Dewobroto et al., 2010; and Mohil et al., 2020). Although studies have examined the performance of options strategies, such as covered call, straddle, and strangle strategies, the comparative study on options hedging strategies on covered call, covered put, collar, and the synthetic long call is not investigated much (Dewobroto et al., 2010 and Kedžo & Šego, 2021). Additionally, limited studies have compared the options strategies in the equity segment. Hence, evaluating and comparing the effective options hedging strategies is indispensable as it helps the investors in trading and hedging the investment.

Further in the literature, studies have explored the performance of options strategies in providing risk-adjusted returns. Studies by Chen & Leung (2003), Guo et al. (2020), and Fullwood et al. (2021) found positive risk-adjusted returns using straddle strategies. However, limited studies have analyzed the performance of options strategies from the Indian perspective. Bangur (2020) Bhat (2021) and S.P. et al. (2022) studied straddle and strangle strategies and observed that short straddle and short strangle strategies provide significant positive returns. Nevertheless, these strategies are applied to take advantage of market volatility and are considered as volatility strategies.

Prior studies express that a covered call strategy can be applied as a hedging strategy (Mugwagwa et al., 2012 and Niblock & Sinnewe, 2018; however, it is also noted that strategies like the collar and synthetic long call can hedge the equity price risk. The literature evinces that the covered call strategy is a prominent hedging strategy that provides nominal returns to retail investors. Hence, this opens the opportunity to analyze further the effectiveness/validity of the other option hedging strategies like the covered put, collar, and synthetic long call. Additionally, researchers have prescribed further enquiry to examine the efficacy of hedged investment in the equity market using hedging strategies against the equity price risk. Therefore, the study’s primary objective is to evaluate the influence of equity payoff and options premiums on options strategy’s payoff and, thereby, measure the hedging effectiveness under volatile and neutral market conditions. Further, the study compares the hedging effectiveness of options strategies. In order to evaluate and compare the hedging effectiveness of selected options strategies, the study considered the data from companies of the top six National Stock Exchange (NSE) sectoral indices for a period of 12 years from 2009 to 2020 and examined a total of 18,720 option contracts. The study follows a two-stage method where in the first stage, the study evaluates the influence of equity payoffs and options premiums on the options strategy’s payoff and measures the hedging effectiveness by applying the panel regression approach (Bhaduri & Sethu Durai, 2008). In the second stage, the study compares the mean scores of selected strategies to identify significant differences in the mean returns between the strategy (Goltz & Lai, 2009 and Dewobroto et al., 2010). Thus, the study justifies the appropriate hedging strategy for the investors.

The present study contributes to the literature in the following ways. Primarily, this study attempts to evaluate the hedging effectiveness of options hedging strategies using Indian equity options data and measure the performance of options strategies in the equity segment. Further, the study compares the hedging effectiveness of options strategies against the equity price risk by applying the panel regression approach (Bhaduri & Sethu Durai, 2008; Bonga-Bonga & Umoetok, 2016; Addae-Dapaah & Abdullah, 2020; Abou Elseoud et al., 2020and Badi Baltagi, 2021). This approach identifies the options strategy that hedges equity investment effectively. Thus, the investor can make informed decisions during their investment. Secondarily, the study compares the option strategy’s returns to identify the significant difference in mean scores between the strategies. A non-parametric tool, i.e., the Games-Howell Host Hoc Tukey Test, is applied to compare the mean returns of strategies. This approach helps in identifying the significant mean differences between strategies payoff.

2. Literature review

The literature review section mainly focuses on various option strategies and hedging methods.

2.1. Option strategies

There are studies on option trading strategies, where most of the studies concentrate on covered call strategy. This strategy holds a long position in the equity stock and protects against changes in the equity price of a stock by writing a slightly Out of The Money (OTM) call option (Mugwagwa et al., 2012 and Israelov & Nielsen, 2015). Theoretically, a covered call strategy should reduce both expected return and risk. Studies by Board et al. (2000), Leggio & Lien (2002), Whaley (2002), Israelov & Nielsen (2015), O’Connell & O’Grady (2014), and Diaz & Kwon (2016) opined that covered call strategy attracts investors by enhancing realized returns not much lower to index returns with minimal risk. However, these studies focused on applying a covered call strategy to equity index options. Mugwagwa et al. (2012) and Niblock and Sinnewe (2018) studied the performance of the covered call strategy using performance measures and observed that the strategy yields nominal returns at lower risk in the Australian equity market. Further, Israelov & Nielsen (2015) opined that covered call strategy contributes to hedging effectiveness up to 64% of the market beta. Moreover, a covered put strategy is applied when the investors seek moderately bearish market by selling an OTM put option along with the short position in the equity (Kang et al., 2021). This strategy generates a maximum payoff of profit on the sale of equity plus the put option premium received for the put sold.

On the other hand, buying an ATM (At-The-Money) put option to the covered call strategy leads to constructing a collar strategy. Thus, this strategy holds a long position in the underlying security and put option, where buying a put option acts as insurance against the downside risk in the underlying asset’s price (El-Hassan et al., 2018). At the same time, the cost of the put option premium is mitigated by the premium received for the call option sold, thereby mitigating the cost of construction of the strategy. Bartonova (2012) and Israelov & Klein (2016) opined that selling a call option mitigates the cost of buying a put option in a collar strategy and covers 65% of loss risk to exhibit the best return-risk ratios. Further, Bartonova (2012) highlighted the impact of employing a zero-cost collar strategy as hedging against a drop in the exchange rate. However, a study by El-Hassan et al. (2018) debated Bartonova’s (2012) findings and observed a negative effect on hedging using collar strategy as the put option was not exercised in any situations.

A synthetic long call strategy is an alternative hedging strategy adopted to protect the unexpected price drops in the underlying asset (Figlewski et al., 1993; Dewobroto et al., 2010; and Kedžo & Šego, 2021). This strategy is also known as the protective put strategy, where an investor buys a security in the open market, and to mitigate the loss of downside price risk, an investor buys an OTM put option (Mohil et al., 2020). Dewobroto et al. (2010) compared stock hedging strategies for five years and declared that the covered call strategy is the best among other stock hedging strategies. Furthermore, Kedžo & Šego (2021) analyzed the efficiency of hedging strategies such as covered call, collar, and other trading strategies by applying the stochastic dominance method. The study results depicted that unhedged portfolios never dominated portfolios with hedging strategies.

Studies are available on the performance of straddle, strangle, and butterfly options strategies. Studies by Chen & Leung (2003), Guo et al. (2020), and Fullwood et al. (2021) analyzed the performance of straddle strategies and found significant positive returns. From the Indian perspective, Bangur (2020) developed and compared the performance of the new trading strategy with the short straddle strategy. The study found that the new trading strategy’s performance is superior to the straddle strategy’s profitability and success rate. While a study by Bhat (2021) has opined that short straddle and short strangle strategies provide significant positive returns. Basson et al. (2018) suggested adopting butterfly strategies to earn limited profit with limited risk. Though there are studies on the performance of straddle, strangle and butterfly strategies, they are considered volatility strategies and applied to take advantage of the market volatility. There are studies on options pricing and performance of options hedging strategies; however, limited studies have compared the hedging effectiveness of covered call, covered put, collar, and synthetic long call strategies (Kedžo & Šego, 2021). Hence, this study attempts to compare the hedging effectiveness of selected strategies using an appropriate hedging tool in the equity segment and measure the hedge ratio.

2.2. Measuring hedging effectiveness

Different studies have employed diverse methods for analyzing hedging effectiveness. For example, EDERINGTON (1979) estimated the hedging effectiveness of treasury bill futures contracts using the Ordinary Least Squares (OLS) method and concluded that the OLS method generates nominal portfolio variance. Further, FRANCKLE’s (1980) study highlighted the EDERINGTON’s (1979) findings by opining that the hedge ratio calculated using OLS improves the hedging effectiveness. Moreover, Bhaduri & Sethu Durai (2008) study analyzed the effectiveness of stock futures index hedging and found 93.39% hedging effectiveness on spot index prices. Further, the study opined that the OLS method provides better hedging results at a shorter time horizon. Bonga-Bonga & Umoetok’s (2016) study results concurred with Bhaduri & Sethu Durai (2008) study findings, where their study determined that the least-squares approach provides effective results in a shorter time horizon. However, the study found 95.84% hedging effectiveness using index futures. Additionally, the study added the reason behind the effectiveness of the least-squares method as it attributed to the hedge ratio estimation using the slope of the independent variables, which is interpreted as the hedge ratio.

Lien (2008), in his study, opined that determining hedge ratio using a regression model performs better, but researchers explore alternative methods to identify improved hedging effectiveness. Further adding to the prior study findings, G. Singh (2017) suggests that hedge ratio calculated using OLS provides better results than hedging ratios estimated using Vector Error Correction Model (VECM), Vector Autoregressive (VAR), Generalized Autoregressive Conditional Heteroskedasticity (GARCH), and Exponential GARCH. Luo & Wang (2018) studied currency derivatives to hedge currency risk using the least-squares method.

Bhatia et al. (2020) examined the hedging effectiveness of metals and compared their relationship with the stock market by employing Dynamic Conditional Correlation—GARCH. Addae-Dapaah & Abdullah (2020) studied the hedging effectiveness of exchange-traded funds using VECM and OLS. However, the study opined that the linear regression model is a relatively robust and simple technique. Major literature overviewed that the regression method is better for measuring hedging effectiveness. The primary purpose of this study is to determine the influence of equity payoffs on options strategy payoffs and measure the hedging effectiveness of selected options strategies. Further, the study compares the mean returns of these strategies to identify the significant differences in the mean returns and tests the below-mentioned hypotheses.

H₁: There is a difference in hedging effectiveness of a covered call, covered put, collar, and synthetic long call strategies under volatile and neutral market conditions

H₂: There is a difference between mean payoffs of a covered call, covered put, collar, and synthetic long call strategies

With the above hypotheses, the study attempted to present the panel data considered for the analysis and present the empirical analysis on hedging effectiveness and comparison of mean returns of selected strategies.

The methods section describes the data considered for the study and methods of calculating the payoffs of different strategies. Further, this paper reports the empirical analysis on the comparison of hedging performances and mean comparison of selected strategies and presents the evidence. The final section concludes the research article.

3. Research design

3.1. Data

This study considers monthly stock options data of companies that are part of the top six sectoral indices of the National Stock Exchange (NSE)² available for trading in equity derivatives from 2009 to 2020. The study collects 18,720 option contracts for applying four option strategies. The required data is downloaded from the NSE repository. This study considers a one-month stock options contract and assumes that contracts are bought on the beginning day and held until expiry. The selected option strategies are constructed for twelve years. This study classifies the market conditions as volatile market conditions and neutral market conditions based on volatility levels is determined by considering the monthly volatility spread between S&P Nifty 50 implied volatility (IV) and realized volatility (RV) indexed over the total sample period (Niblock & Sinnewe, 2018).

(1) $\mathrm{V}{\mathrm{S}}_t=\mathrm{I}{\mathrm{V}}_t-\mathrm{R}{\mathrm{V}}_t$(1)

If VS_t > 0.036, it is deemed to be high volatility or volatile market condition, and If VS_t < 0.036 is considered low volatility or neutral market condition (Niblock & Sinnewe, 2018).

3.2. Methodology

3.2.1. The method of payoffs calculation

The present study begins with calculating payoffs from selected option strategies and equities. The payoffs are calculated using the equations mentioned below:

The equity payoff is calculated as,

(2) $Payoff=\left(P_1-P_0\right)$(2)

If the stock price at expiration is more than the OTM call strike price, the payoff from the covered call strategy is calculated as,

(3) $Payoff=\left(S_{t+1}-S_t\right)+\left[\left(X_{OTM}-S_{t+1}\right)+C_{OTM}\right]\hspace{0.17em}$(3)

If the stock price at expiration is less than or equals the OTM call strike price, then the payoff from the covered call strategy is estimated as the OTM call premium.

where, $P_1$ is Price at the end of the holding period, $P_0$ is the purchase price, $S_{t+1}$ is the closing value of underlying security, $S_t$ is the value of underlying security purchased, $X_{OTM}$ is OTM call strike price and $C_{OTM}$ is OTM call premium.

If the stock price at expiration is less than the opening stock price and is less than OTM put strike price, then the payoff from the covered put strategy is assessed as,

(4) $Payoff=\left(S_t-S_{t+1}\right)+\left[\left(S_{t+1}-Y_{OTM}\right)+P_{OTM}\right]$(4)

If the stock price at expiration is more than the opening stock price and is more than OTM put strike price, then the payoff from the covered put strategy is assessed as OTM put premium.

where $Y_{OTM}$ is OTM put strike price and $P_{OTM}$ is OTM put premium.

If the stock price at expiration is more than ATM put strike price and more than the OTM call strike price, the collar strategy payoff is calculated as,

(5) $Payoff=\left(S_{t+1}-S_t\right)+\left[\left(X_{OTM}-S_{t+1}\right)+C_{OTM}\right]+\left(-P_{ATM}\right)$(5)

If the stock price at expiration is more than ATM put strike price and less than the OTM call strike price, the collar strategy payoff is calculated as,

(6) $Payoff=\left(S_{t+1}-S_t\right)+C_{OTM}-P_{ATM}$(6)

If the stock price at expiration is less than the ATM put strike price and less than the OTM call strike price, the collar strategy payoff is calculated as,

(7) $Payoff=C_{OTM}+\left(\left(X_{ATM}-S_{t+1}\right)-P_{ATM}\right)$(7)

where, ${\mathrm{X}}_{\mathrm{A}\mathrm{T}\mathrm{M}}$ is the ATM put strike price and ${\mathrm{P}}_{\mathrm{A}\mathrm{T}\mathrm{M}}$ is the ATM put option premium.

If the stock price at expiration is more than OTM put strike price and more than ${\mathrm{S}}_{\mathrm{t}}$, the synthetic long call strategy payoff is calculated as,

(8) $Payoff=\left(S_{t+1}-S_t\right)-P_{OTM}$(8)

If the stock price at expiration is less than OTM put strike price and less than ${\mathrm{S}}_{\mathrm{t}}$, the synthetic long call strategy payoff is calculated as,

(9) $Payoff=\left(X_{OTM}-S_{t+1}\right)-P_{OTM}$(9)

If the stock price at expiration is more than the OTM put strike price and less than ${\mathrm{S}}_{\mathrm{t}}$, the synthetic long call strategy payoff is calculated as, $-P_{OTM}$.

where, ${\mathrm{X}}_{\mathrm{O}\mathrm{T}\mathrm{M}}$ is the OTM put strike price and ${\mathrm{P}}_{\mathrm{O}\mathrm{T}\mathrm{M}}$ is the OTM put option premium.

3.3. The panel regression method

The study’s primary objective is to investigate the hedging effectiveness of option trading strategies. The study considers twenty-six companies (cross-sectional) for twelve years (Time series). Badi Baltagi (2021) opined that the cross-sectional observations are bound to be heterogeneous over time. However, the panel regression approach considers unobserved heterogeneity between the cross-section and provides better results with more information than the OLS approach. Hence, the study applies the panel regression method for measuring hedging effectiveness with three approaches. The Pooled Ordinary Least Squares (POLS) model is applied initially to measure the influence of independent variables on the dependent variable. Further, the Breusch - Pagan LM Test (1980) identifies heteroskedasticity in the POLS model. If heteroskedasticity is identified in the POLS model, Fixed and Random Effect Models (FEM & REM) are applied, and the appropriate model is determined between FEM and REM using the Hausman test.

The panel regression analysis examines the influence of independent variables on the dependent variable. In this study, the payoffs of a covered call, covered put, collar, and synthetic long call strategies are considered dependent variables, whereas the payoff of equity stocks, option premiums, and market conditions are considered independent variables. The option premiums considered for the study are calculated by the NSE using the Black-Scholes model.³ This model considers other variables such as underlying asset price, option strike price, risk-free interest rate, time to expiration, dividends, and volatility for calculating option premium; hence, all these variables are integrated with options premium (Black & Scholes, 1973). However, brokerage or commission fee does not affect the options premium calculation. Besides, the objective of this study is to measure the influence of equity payoff and options premiums on a strategy’s payoff. Therefore, the study does not consider other factors separately. The study introduces two dummy variables for volatile and neutral market conditions and measures the effectiveness of selected option strategies in hedging the equity position.

The mathematical equation for the panel regression model can be given as follows (Rao et al., 2021):

(10) $C_{st}={\beta }_1+{\beta }_2{\left(Equitypayoff\right)}_{it}+{\beta }_3{\left(Optionpremium\right)}_{it}+{\beta }_4{\left(Marketcondition\right)}_{it}+u_{it}$(10)

where C_st is options strategy’s payoff and u_it is error term.

3.4. Unit root tests

Econometric panel data analysis assumes the stationarity of the data. The Augmented Dickey-Fuller test (ADF) proposed by Dickey & Fuller (1979, 1981) and the Phillips-Perron unit root test (PP unit root test) (1988) that has been widely accepted to test the unit root or stationarity of the data. The stationarity of the data implies that statistical properties like means and variances should be consistent over the period. The rationality behind the stationarity of the data is that statistical properties will remain unchanged in the future.

If the data is stationary over the period, it is implied that statistical properties will remain unchanged in the future. The mathematical expression of ADF is as follows:

(11) $\mathrm{\Delta }{y}_t=a+\beta t+\gamma y_{t-1}+{\delta }_1\mathrm{\Delta }{y}_{t-1}+\dots +{\delta }_{p-1}\mathrm{\Delta }{y}_{t-p+1}+{\epsilon }_t$(11)

The mathematical expression of the Phillips-Perron unit root test (PP unit root test) is as follows:

(12) $\mathrm{y}\mathrm{t}=\mathrm{c}+\delta \mathrm{t}+\mathrm{a}\mathrm{y}\mathrm{t}-1+\mathrm{e}\left(\mathrm{t}\right)$(12)

Where y_{t =} denotes the time series to be tested, a = constant, β = coefficient on a time trend, p = lag order of the autoregressive process, ε_t = error term.

4. Data analysis and interpretations

In this section, the study has reported the results of descriptive statistics, panel regression, Kruskal-Wallis Test, and Games-Howell Post Hoc Tukey Tests. The descriptive statistics of selected option strategies and the options premiums are presented in Table 2. The highest and lowest strategy payoff observed during the study period is ₹2012.20 and ₹-513.70 for the collar strategy. The covered put strategy showed the highest average return of ₹37.53 with a deviation of ₹41.73, and the collar strategy showed the lowest average payoff of ₹28.68 with a variation of ₹90.62. These results indicated that the covered put strategy generated a superior mean payoff at a lower risk than the equity payoff, whereas the collar strategy observed a lower mean payoff at comparatively higher risk than other strategies. The Shapiro Wilcoxon test is applied to determine the normality of the data and is hypothesized as H₀: The data are normally distributed. The results showed that the p-value of the test statistics is not significant at a 5% significance level; thus, data is not normally distributed (H₁).

Table 2. Descriptive statistics

	Equity	Covered call	Covered put	Collar	Synthetic long call	OTM call premium	ATM put premium	OTM put premium
Mean	7.3309	34.1394	37.5303	28.6810	34.2374	20.4479	38.9259	27.2586
Median	3.4750	16.4500	26.0000	14.6250	10.2500	11.9250	25.9000	16.8000
Maximum	1112.45	523.0000	676.6000	2012.200	1963.250	401.9000	691.2000	649.5500
Minimum	−2035.80	0.0500	−77.9000	−513.70	−453.3000	0.0500	0.3000	0.0500
Std. Dev.	134.32	46.2954	41.7399	90.6185	97.8019	27.4730	42.2384	35.1545
Skewness	−2.0073	3.0782	3.7295	8.5979	6.3275	3.8970	4.4871	4.7817
Shapiro-Wilk	0.736	0.692	0.705	0.508	0.593	0.648	0.660	0.634
Observations	3744	3744	3744	3744	3744	3744	3744	3744

Note: The coefficients are calculated at 5 per cent significance level

4.1. Unit root test results

The ADF and PP unit root tests are applied to test unit root or stationarity in time series. It can be hypothesized as H₀: Data of selected option strategies payoff, option premiums, and equity payoffs have unit root or are not stationary. The ADF and PP unit root test statistics are significant at a 5% significance level. Hence, H₀ has been rejected, and thus, the data of payoffs of selected option strategies and selected equities do not have unit root or stationery (H₁; Table 3).

Table 3. Results of augmented Dickey-Fuller test and Phillips-Perron unit root test

	Equity	Covered call	Covered put	Collar	Synthetic long call	OTM call premium	ATM put premium	OTM put premium
ADF Fisher test statistic	658.537*	213.826*	170.044*	450.030*	449.926*	108.942*	116.362*	117.070*
PP Fisher test statistic	2081.14*	1409.47*	1251.40*	1921.42*	1989.13*	683.59*	704.17*	647.58*

Note: The coefficients are calculated at 5 per cent significance level

4.2. Hedging effectiveness of option strategies

Further, the study investigated the hedging effectiveness of the selected option strategies under neutral and volatile market conditions by applying panel regression analysis. The study applied the POLS approach, and a further cross-sectional dependence test, i.e., the Breusch-Pagan LM test, is used to determine the heteroskedasticity in the POLS results. This test can be hypothesized as H₀: The models have no cross-sectional dependence. The p-value of the Breusch-Pagan LM test is less than 0.05; hence, hypotheses are rejected at a 5% level of significance. Further, the redundant fixed effect tests are applied to examine the significant effects. The null hypothesis of this test can be written as H₀: the effects are redundant in the pooled regression model. The results reject the null hypothesis at a 5% level of significance (p < 0.05) and accept that the effects are statistically significant. Hence, FEM and REM are applied, and the Hausman test is conducted to identify the appropriate model between FEM and REM. The Durbin-Watson test results indicated the absence of autocorrelation, and the F-statistics of the F-test were found to be significant at a 5% significance level for all the models, indicating that models are a good fit.

The panel regression results of the hedging effectiveness of the covered call strategy is demonstrated in Table 4. The Hausman test results observed that the REM is more appropriate than the FEM under volatile and neutral market conditions (Chi-square statistic of 0.0000). Equity payoff and OTM call premium have a significant positive influence on covered call strategy payoff. The coefficient values of equity payoff and OTM call premium showed that a one-rupee change in the equity payoff and OTM call premium influences covered call payoff by 0.133 and 1.166 rupees, respectively. Further, the study measures the goodness-of-fit for regression models using the R² value. It tests the frequency of the interaction between the model and the dependent variable. The R² explains how much the independent variables explain the variation of a dependent variable in a regression model. In this case, the R² value for the covered call strategy is 0.6963, implying that 69.63% variation in the covered call payoff is explained by the equity payoff and OTM call premium variation. Any model having R² values of 0.75, 0.50, or 0.25 can be described as the substantial or best effective, moderate, or weak effective for hedging (J. F. Hair et al., 2011and F. F. Hair et al., 2014). The R² value of 0.6963 for the covered call strategy indicates moderate effectiveness for hedging under both market conditions.

Table 4. Covered call strategy

Variables/Panel data regression models	Volatile market condition			Neutral market condition
	POLS	Fixed	Random	POLS	Fixed	Random
Equity payoffs	0.133*	0.133*	0.133*	0.133*	0.133*	0.133*
OTM call premium	1.258*	1.144*	1.166*	1.258*	1.144*	1.166*
Volatile/Neutral	2.982*	3.007*	3.002*	−2.982*	−3.007*	−3.002*
C	6.571*	8.894*	8.443*	9.553*	11.901*	11.446*
R-squared	0.7479	0.7687	0.6963	0.7479	0.7687	0.6963
F-statistic	3700.349*	441.102*	2858.514*	3700.349*	441.102*	2858.514*
Durbin -Watson stat	1.784	1.893	1.873	1.784	1.893	1.873
Breusch-Pagan LM test (p value)	1110.403*			1110.403*
Redundant Fixed effects tests (F statistic and Chi-square statistic)	13.3463* & 322.0107*			13.3463* & 322.0107*
Hausman test		Chi-Sq (3)—0.0000 Probability value—1.0000			Chi-Sq (3)—0.0000 Probability value—1.0000

Note: The coefficients are calculated at 5 per cent significance level

Thus, the panel regression model for REM in volatile and neutral market conditions takes the following form:

(13) $Coveredcallpayof{f}_{it}=8.443+0.133Equitypayof{f}_t+1.166OTMcallpremiu{m}_t+3.002Volatil{e}_{it}$(13)

(14) $Coveredcallpayof{f}_{it}=11.446+0.133Equitypayof{f}_t+1.166OTMcallpremiu{m}_t-3.002Neutra{l}_{it}$(14)

The panel regression results of the hedging effectiveness of the covered put strategy are exhibited in Table 5. The results of the Hausman test revealed that the FEM is more appropriate than the REM in neutral market conditions (Chi-square statistic of 37.5367), whereas the REM is more efficient in volatile market conditions (Chi-square statistic of 0.0000). The equity payoffs significantly negatively influence covered put strategy payoff in volatile and neutral market conditions. It indicates that an additional increase or decrease in equity payoff by one rupee impacts the covered put strategy’s payoff by −0.076 rupees. OTM put premiums significantly positively influence the covered put strategy’s payoff. Hence, an additional change in OTM put premium by one rupee influences the strategy’s payoff by 1.069 and 1.056 rupees under volatile and neutral market conditions. The R² values have explained 87% and 90.45% variation in the covered put payoffs by the variation in equity payoff and OTM put premium under volatile and neutral market conditions. The R² values of 0.87, and 0.9045 for the covered put strategy indicate best or substantial effectiveness for hedging under volatile and neutral market conditions.

Table 5. Covered put strategy

Variables/Panel data regression models	Volatile			Neutral
	POLS	Fixed	Random	POLS	Fixed	Random
Equity payoffs	−0.076*	−0.076*	−0.076*	−0.076*	−0.076*	−0.076*
OTM put premium	1.103*	1.056*	1.069*	1.103*	1.056*	1.069*
Volatile/Neutral	0.103*	0.149	0.137	−0.103	−0.149	−0.137
C	7.991*	9.250*	8.899*	8.095*	9.399*	9.037*
R-squared	0.8982	0.9045	0.8700	0.8982	0.9045	0.8700
F-statistic	11,003.40*	1257.649*	8348.459*	11,003.40*	1257.649*	8348.459*
Durbin -Watson stat	1.795	1.874	1.853	1.795	1.874	1.853
Breusch-Pagan LM test (p value)	664.3815*			664.3815*
Redundant Fixed effects tests (F statistic and Chi-square statistic)	9.8699* & 240.7642*			9.8699* & 240.7642*
Hausman test	Chi-Sq (3)—0.0000 Probability value—1.0000			Chi-Sq (3)—37.536 Probability value—0.0000

Note: The coefficients are calculated at 5 per cent significance level

The panel regression model for the REM in volatile market conditions and FEM in neutral market conditions takes the following form:

(15) $Coveredputpayof{f}_{it}=8.899-0.076Equitypayof{f}_t+1.069OTMputpremiu{m}_t+0.137Volatil{e}_{it}$(15)

(16) $Coveredputpayof{f}_{it}=9.399-0.076Equitypayof{f}_t+1.056OTMputpremiu{m}_t-0.149Neutra{l}_{it}$(16)

The results of panel regression models for collar strategy under both market conditions are reported in Table 6. The FEM is considered as more appropriate than the REM under both market conditions (the Chi-square value of the Hausman test is 32.4213). The equity payoff and ATM put premium have a significant negative influence on collar strategy payoffs. The coefficient values indicate that an additional change in equity payoff and ATM put premium by one rupee influences the collar strategy payoffs by −0.417 rupees and −0.654 rupees, respectively, under volatile and neutral market conditions. However, OTM call premiums have a significant positive impact on the strategy’s payoff, and a one rupee increase in OTM call premium influence the strategy payoff by 1.624 rupees. The R² value of 0.5390 indicated that 53.90% variation in collar strategy’s payoff is explained by equity payoff, OTM call premium, and ATM put premium under both market conditions. This strategy showed moderate effectiveness for hedging under volatile and neutral market conditions.

Table 6. Collar strategy

Variables/Panel data regression models	Volatile			Neutral
	POLS	Fixed	Random	POLS	Fixed	Random
Equity payoffs	−0.418*	−0.417*	−0.417*	−0.418*	−0.417*	−0.417*
OTM call premium	1.737*	1.624*	1.652*	1.737*	1.624*	1.652*
ATM put premium	−0.502*	−0.654*	−0.619*	−0.502*	−0.654*	−0.619*
Volatile/Neutral	−8.496*	8.641*	8.607*	−8.496*	−8.641*	−8.607*
C	21.861*	21.538*	19.608*	21.861*	30.179*	28.216*
R-squared	0.5049	0.5390	0.5024	0.5049	0.5390	0.5024
F-statistic	953.468*	149.737*	943.926*	953.468*	149.737*	943.926*
Durbin -Watson stat	1.899	1.966	1.953	1.899	1.966	1.953
Breusch-Pagan LM test statistic	857.0233*			857.0233*
Redundant Fixed effects tests (F statistic and Chi-square statistic)	10.9705* & 266.7475*			10.9705* & 266.7475*
Hausman test	Chi-Sq (4)—32.4213 Probability value—0.0000			Chi-Sq (4)—32.4213 Probability value—0.0000

Note: The coefficients are calculated at 5 per cent significance level

The panel regression model for FEM in volatile and neutral market conditions takes the following form:

(17) $Collarpayof{f}_{it}=21.538-0.417Equitypayof{f}_t+1.624OTMcallpremiu{m}_t-0.654ATMputpremiu{m}_t+8.641Volatil{e}_{it}$(17)

(18) $Collarpayof{f}_{it}=30.179-0.417Equitypayof{f}_t+1.624OTMcallpremiu{m}_t-0.654ATMputpremiu{m}_t-8.641Neutra{l}_{it}$(18)

The results of the hedging effectiveness of the synthetic long call strategy are exhibited in Table 7. The Hausman test results reported that the REM is more appropriate under volatile market conditions (Chi-square statistic of 0.0000), and the FEM is more efficient under neutral market conditions (Chi-square statistic of 26.3199). Equity payoffs negatively influence synthetic long call strategy payoff with a coefficient value of −0.026 rupees under both market conditions. However, OTM put premiums significantly positively impact synthetic long call strategy. It can be interpreted as an additional change in OTM put premium by one rupee influences the payoffs by 0.233 rupees and 0.164 rupees under volatile and neutral market conditions. The R² values infer that the variation in equity payoffs and OTM put premiums explains 0.97% and 10.08% variations in synthetic long call payoffs in volatile and neutral market conditions. The R squared values of 0.0097 & 0.1008 indicated weak effectiveness for hedging under volatile and neutral market conditions.

Table 7. Synthetic long call strategy

Variables/Panel data regression models	Volatile			Neutral
	POLS	Fixed	Random	POLS	Fixed	Random
Equity payoffs	−0.027*	−0.026*	−0.026*	−0.027*	−0.026*	−0.026*
OTM put premium	0.491*	0.164*	0.233*	0.491*	0.164*	0.233*
Volatile/Neutral	10.487*	10.802*	10.736*	−10.487*	−10.802*	−10.736*
C	18.064*	26.877*	25.017*	28.552*	37.680*	35.753*
R-squared	0.0345	0.1008	0.0097	0.0345	0.1008	0.0097
F-statistic	44.645*	14.883*	12.238*	44.645*	14.883*	12.238*
Durbin -Watson stat	1.933	2.000	1.988	1.933	2.000	1.988
Breusch-Pagan LM test statistic	896.2576*			896.2576*
Redundant Fixed effects tests (F statistic and Chi-square statistic)	10.9553* & 266.3217*			10.9553* & 266.3217*
Hausman test	Chi-Sq (3)—0.0000 Probability value—1.0000			Chi-Sq (3)—26.3199 Probability value—0.0000

Note: The coefficients are calculated at 5 per cent significance level

The panel regression model for REM in volatile market conditions and FEM in neutral market conditions takes the following form:

(19) $SLCpayof{f}_{it}=25.017-0.026Equitypayof{f}_t+0.233OTMputpremiu{m}_t+10.736Volatil{e}_{it}$(19)

(20) $SLCpayof{f}_{it}=37.680-0.026Equitypayof{f}_t+0.164OTMputpremiu{m}_t-10.802Neutra{l}_{it}$(20)

4.3. Comparison of payoffs of selected option trading strategies

Further, the study attempted to compare the payoffs of different strategies to conclude the differences between one strategy’s payoff to another strategy’s payoff using a statistical approach. The Shapiro-Wilcoxon test results indicated that the data considered for the study is not normally distributed (Table 2); Hence, this study adopted a non-parametric method for comparison, i.e., the Kruskal-Wallis test, to find out whether the group medians are equal or not. The results indicate that there is a difference in the medians from one group to another group (Test statistic 721.584 and p =<.001; Table 8). Hence it is essential to identify the groups with significant mean/median differences. For this, the Games-Howell Post Hoc Tukey Test is applied.

Table 8. Results of Kruskal-Wallis test

Kruskal-Wallis Test
Factor	Statistic	df	p
Strategies	721.584	3	< .001***

Note: *p <.05, ** p < .01, *** p < .001

The Games-Howell Post Hoc Tukey Test results showed significant differences for covered call to covered put strategy and covered call to collar strategy at a 99% significance level (p =0.005 and 0.006, respectively). Significant differences were found for the covered put to collar strategy (p =<0.001) at a 99.9% significance level. Covered call to synthetic long call, covered put to synthetic long call, and synthetic long call to collar strategies have observed no significant mean differences between the groups. The study observed that only three groups have significant mean differences out of 6 groups (Table 9).

Table 9. Results of Games-Howell Post Hoc Test

Games-Howell Post Hoc Comparisons—Strategies
Comparison	Mean Difference	SE	t	df	p tukey
Covered call—Covered put	−3.391	1.019	−3.329	7407.088	0.005 **
Covered call—Collar	5.458	1.663	3.282	5572.247	0.006 **
Covered call—Synthetic long call	−0.098	1.768	−0.055	5340.193	1.000
Covered put—Collar	8.849	1.631	5.427	5262.842	< .001 ***
Covered put—Synthetic long call	3.293	1.738	1.895	5062.731	0.230
Collar—Synthetic long call	−5.556	2.179	−2.550	7442.854	0.053

Note: ** p < .01, *** p < .001

5. Discussions

The hedging effectiveness of the covered call, covered put, collar, and synthetic long call strategies and a comparison of their mean payoffs are discussed in this section. The hedging effectiveness of the covered call strategy found that the OTM call premiums significantly influence covered call payoff more than equity payoff under both market conditions (Table 4). Besides, the results showed that selling an OTM call option provides an absolute benefit to the investor over equity payoff (Diaz & Kwon, 2016). The investor receives a premium for the call sold, which is an additional income for the risk taken. Thus, the study findings support the findings of (Dewobroto et al., 2010; Mugwagwa et al., 2012and Niblock & Sinnewe, 2018). The results of the covered put strategy found that equity payoffs have a negative influence on covered put strategy payoff under both market conditions. However, taking a short position in equity during the construction of the strategy restricts the payoff from equity (Kang et al., 2021). Hence, equity payoffs showed a significant negative influence on the strategy’s payoff. Moreover, OTM put premiums positively influence the strategy’s payoff. The findings indicated that the premium received for selling an OTM put provides an additional income to the investor (Kang et al., 2021).

Further, the results of the collar strategy showed that OTM call premiums have a significant positive influence, and selling an OTM call provides an absolute benefit to the investors (Table 6; Bartonova, 2012). However, ATM put premiums negatively influence collar strategy payoff and reduce the absolute benefit received for call option sold (Israelov & Klein, 2016). The reduction in absolute benefit is that the ATM put option expires worthless. Hence, this finding is consistent with the findings of (El-Hassan et al., 2018). The equity payoffs significantly negatively impact the synthetic long call strategy’s payoff. As a result, any changes in the equity prices impact the strategy payoff negatively. This finding supports the findings of (Mohil et al., 2020).

Holistically, the study observed the positive impact of equity payoff on strategy’s payoff only for the covered call strategy, and the remaining strategies showed negative influence (Dewobroto et al., 2010). Moreover, the covered put strategy evidenced a higher R square value, while the synthetic long call strategy reported a lower R square value (Table 10).

Table 10. Comparison of R squared and hedge ratios

	Volatile market condition			Neutral market condition
	Model	Equity payoff h*	R^2	Model	Equity payoff h*	R^2
Covered call	Random	0.133	0.6963	Random	0.133	0.6963
Covered put	Random	−0.076	0.8700	Fixed	−0.076	0.9045
Collar	Fixed	−0.417	0.5390	Fixed	−0.417	0.5390
Synthetic long call	Random	−0.026	0.0097	Fixed	−0.026	0.1008

The second approach of our study compared the payoffs of a covered call, covered put, collar, and synthetic long call strategy. For this purpose, the study has applied the Kruskal-Wallis Test and Games-Howell Post Hoc Tukey Test. The study found significant mean differences between the covered call to covered put strategy and the covered call to collar strategy (Dewobroto et al., 2010). However, synthetic long call strategy payoffs have equal mean payoffs compared to other option hedging strategies (no significant mean differences).

6. Robustness checks

Applying robustness checks or diagnostic tests to the analysis is essential to establish that the estimated model adequately describes an economic phenomenon (BEGGS, 1988). The study applied the Breusch-Pagan LM test for verifying heteroskedasticity in the POLS model, the Hausman test for selecting an appropriate model between FEM and REM, and the Durbin-Watson test for checking autocorrelation in the regression models. The Breusch-Pagan LM test reported the presence of heteroskedasticity in the POLS model; hence, FEM and REM models are applied. The Hausman tests have identified appropriate models between FEM and REM for all the hedging strategies. Further, the Durbin-Watson test statistic reported the absence of autocorrelation in the regression models. Hence, the results are verified with the assumptions of diagnostic tests and confirmed that the results are robust.

7. Conclusion

The present paper compared the hedging effectiveness of covered call, covered put, collar, and synthetic long call strategies in the Indian derivatives market for 12 years from 2009 to 2020 under volatile and neutral market conditions. The study addressed the applicability of options strategies for hedging the equity using the panel regression approach. The study results suggest that the covered put and covered call strategies have greater hedging effectiveness than other hedging strategies. The investors can earn nominal returns by employing a covered call strategy in both market conditions. The study has evidenced the applicability of the covered put strategy in hedging the equity position. However, collar and synthetic long call strategies offer lower hedging effectiveness against the equity price risk.

Additionally, the study compared payoffs of option hedging strategies and identified mean differences between the groups are equal or not equal. The study results found that the payoff of the covered call strategy has significant mean differences with covered put and collar strategies, whereas the payoff of the synthetic long call strategy has no statistically significant mean differences with other strategies. Hence, the study establishes a benchmark to help retail investors choose a better hedging strategy and employ it in their trading, specific to the market condition.

Further, this paper provides scope for expanding research work in this area. This study does not consider brokerage or commission charges payable to the brokering firm, which directly or indirectly affects the final strategy’s payoff. Future studies can consider other variables such as brokerage or commission and taxes paid while calculating the strategy’s payoff. Further, this research has compared the hedging effectiveness of four strategies for twenty-six companies that are part of the top six sectors of NSE and are available for trading in equity derivatives from 2009 to 2020. Future studies can apply and compare the effectiveness of these strategies in other emerging derivative markets.

Disclosure statement

There are no relevant financial or non-financial competing interests to report.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Shivaprasad S P

Mr. Shivaprasad S P (first author) is a research scholar at the Department of Commerce, Manipal Academy of Higher Education, Manipal, Karnataka, India. His areas of interest include Portfolio Management, Financial Derivatives, Financial Accounting, and Taxation.

Geetha E

Dr. Geetha E (corresponding author) is presently working as an Associate Professor at the Department of Commerce, Manipal Academy of Higher Education, Manipal, Karnataka, India. Her teaching areas include Financial Accounting, Portfolio Management, Financial Management, and Business Statistics.

Raghavendra Acharya

Dr. Raghavendra Acharya (co-author) has over 20 years of teaching and research experience in India and presently working as a Professor and Associate Dean at VIT-AP School of Business, VIT-AP University, Amaravati, Andhra Pradesh. He has published papers in esteemed academic journals, and his areas of interest include Capital Market, Financial Derivatives, Portfolio Management, Financial Management, and Management Accounting.

Vidya Bai G

Dr. Vidya Bai G (co-author) is working as an Associate Professor at the Department of Commerce, Manipal Academy of Higher Education, Manipal. Her teaching and research areas include Financial analytics, Financial modelling, and Operations Research.

Rajeev Matha

Mr. Rajeev Matha (co-author) is pursuing a Ph.D. under the Dr. T.MA Pai scholarship program at the Department of Commerce, Manipal Academy of Higher Education. His area of interest includes Behavioural Finance, Econometrics, Capital Market, and Structural Equation Modelling.

Notes

1. Historical growth in FO segment in Indian capital market. https://www1.nseindia.com/products/content/derivatives/equities/historical_fo_bussinessgrowth.htm

2. Sectoral indices considered for the study are Nifty Bank Index, Nifty Auto Index, Nifty Pharma Index, Nifty IT Index, Nifty PSU Bank Index and Nifty Private Bank Index.

3. https://www1.nseindia.com/content/circulars/faop3716.htm

Appendix

Descriptive Box plots

Box plots represent the numeric data such as median, quartiles, upper and lower adjacent points, etc. Each strategy’s numeric data is described in different box plots. Figures. A1 to A4 represents the box plots of a covered call, covered put, collar, and synthetic long call strategies.

Figure A1. Covered call strategy.

Figure A2. Covered put strategy.

Figure A3. Collar strategy.

Figure A4. Synthetic long call strategy.