A Neural Network approach for integrating banks’ decision in shipping finance

Abstract

Forecasting refers to the process of predicting future trends by lying on data from the past. An error in forecasting can lead to significant business losses especially in banking industry where decisions are taken in a highly volatile and uncertain environment due to the dynamic changes in world economy. In this paper, we study both the effectuations of the exogenous factors in the tanker shipping-related financial market and the modulation of the credibility coefficient as an internal factor in shipping banks that may affect their decision to either increase or decrease loans within tanker shipping sector by adopting the artificial neural network technique. Within this context, we modeled a unique network that adjusts 88 macroeconomic indices to the real data of 89 shipping banks within a period of T = 5 years time. The main contribution of this study is the understanding of the relation between bias and either exogenous or unpredictable factors in the market as a key factor in the financing decision policy of a shipping bank for the forthcoming year T + 1.

Keywords:

• Neural network
• shipping banks
• finance
• bias

JEL Classification:

• G21
• G31
• P33

1. Introduction

Forecasting refers to the process of predicting future trends by lying on data from the past. Within this process, when forecasting is accurate, it facilitates better planning and budgeting (Mostafa et al., 2017). The forecasting error can lead to significant business losses especially in cases that it comes from a long established process rather than random effects.

This error is the sum of regular and irregular factors and its study becomes more crucial in finance industry and especially within banking industry, where relevant decisions are considered to be highly volatile and uncertain due to the dynamic changes in world economy and little information about the future (Cao et al., 2020). Banks have to take into account: i) various endogenous variables that account for the regular factors, in order to maximize their return and minimize any risk, ii) the current market variables, as well as the recent regulatory framework restrictions applied by the Basel (Sambracos & Maniati, 2013), referred as exogenous variables that account for irregular factors. To uphold competitiveness in the global world, the industry has embraced highly developed computer technologies that may approximate universal functions to a desired accuracy (Cybenko, 1989; Hornik, 1993; Huang et al., 2007).

Artificial intelligence models constitute new forecasting approaches for financial decision-makers (Sharda & Patil, 1992; Trinkle & Baldwin, 2016), while they have been proved to provide a solution over the well-established linear regression models (LRM) in case of non-linear data (Bollershev, 1986; Sambracos et al., 2020), advancing the economic modelling (Fumagalli, 2016) in a volatile, noisy environment characterized by irrelevant or partial information (Dobrescu et al., 2014; Huang et al., 2007), especially in shipping financial market (Maniati et al., 2017), where the macroeconomic environment matters a lot for shipping firm’s performance (Angelopoulos et al., 2021; Michail, 2020; Michail & Melas, 2022; Michail et al., 2021; Tsioumas et al., 2021) and hence bank’s decision to proceed or not with relevant financing. The transport sector projects require a large amount of funds, leading to different financing sources (Mostafa et al., 2017). The majority of current finance artificial intelligence approaches refer to risk and/or credit management, algorithmic trading, pattern recognition and process automation (Aziz et al., 2019; Gooijer & Hyndman, 2006).

Machine Learning (ML) techniques have been applied in several topics of financial research as well. Björkegren and Darrell (2018) applied ML techniques to predict loan repayment using mobile phone data. Apart from the ML techniques, financial time series prediction methods also refer to Deep Learning techniques (Schmidhuber, 2015), which have been mainly applied for forecasting stock price and trend in financial variables.

Credit facilities use forecasting techniques for loan appraisals (Heaton et al., 2016); while neural networks (NNs) are becoming popular in determining the revenue generation trends for repayment of the funds.

Hawley et al. (1990) applied NNs, in order to develop a new technique for financial—decision-makers dealing with environments that continuously change, such as in transport/shipping sector. This technique was then applied to lending and credit risk management decisions (Varetto, 1998). Altman et al. (1994), by analyzing industrial firms in Italy, proved that NNs can be a supplementary to the regression analysis acceptable diagnostic instrument though researchers should be careful with the structure of the NNs.

Odom and Sharda (1990), Coleman et al. (1991), Fletcher and Goss (1993), Wilson and Sharda (1994), and Inam et al. (2019) used NNs in order to forecast bankruptcy and/or business failure; Geng et al. (2015) applied artificial NNs in combination with decision trees to predict banking financial distress; Weng et al. (2018) presented an ensemble-based approach to predict the 1-day ahead stock price using various data online sources; Jessica et al. (2020) tried to develop a model based on artificial NNs to predict financial distress in the Spanish banking system by combining other financial problems with bankruptcy; Turiel and Aste (2020) tried to replicate lender acceptance and to predict default of loans and proved that they were able to predict well above 50% of defaults on loans. In all cases, NNs have shown superiority over traditional techniques for forecasting.

In principle, NNs are structured by the input, the hidden and the output layer where the last two layers are biased. Consistent with the literature and according to simulation techniques (Sambracos et al., 2020), the bias is considered as a significant factor that matches the input to the output layer after the internal process of the hidden layer. On the other hand, previous techniques such as the LRM consider the bias as error and remove it in order to present the general trend and finally provide less accurate models.

There is indeed a need for synergistic efforts between financial sector and NNs. The lasts may exhibit characteristics that on some level model the behavior or the real world. Implicitly, the real world is explained by also psychophysical aspects that arise from the human individualists (Lieder et al., 2018). Within this context, cognitive neurosciences refer to the logic-computational brain left-hemisphere that is “biased” by the innovative-enthusiastic right brain-hemisphere (Churchland, 2002) and forwarding the “decision”. Consistent with human evolution, decisions might be presumably uncontrolled and, in some sense, unpredictable because they are biased or self-controlled.

Considering a mass population of discrete units, any “decision” C is z-weighted by both the “mass” H and the “unit” R (Maniati et al., 2017) and modeled as C = z R + (1-z) H. At the extreme cases where the parameter z equals either 0 or 1, the decision follows the mass or the unit, respectively. Based on this previous study, it has been implicitly stated that when the parameter z is being modeled by hypothetical statistical distributions, it ranged between 0 and 1.

As common practice, banks are assumed to be excused from responsibility and to deal with decision-making process for loan granting or not by judging their similarity to uncontroversial and well-worn prototypes. This is assigned to values of z closed to zero.

Consequently, when banks upgrade from the simple prototypes to a multi-parametric space, they fall into a spectrum of scaled decisions that is assigned to values of z greater from zero and less than one. Finally, values of z closed to one are assigned when decision-makers have to consider and control various parameters that reflect the primary determinants of self-controlled behavior.

However, actual measurements of the parameter z showed a percentage of values outside the normal range. Such values have been biased from random effects and have neither contribution nor utility to the decision C.

Following that, a key question arises; whether we are able to predict any future bank’s decision even the knowledge of the past history and exploring any possible relationship between parameter z and bias effectuation.

In this paper, we study both the effectuations of the exogenous factors in the tanker shipping-related financial market and the modulation of the credibility coefficient as an internal factor in shipping banks that may affect their decision to either increase or decrease loans within tanker shipping sector by adopting the artificial NN technique. Within this context, we developed a unique network that adjusts 88 macroeconomic indices to the real data of 89 shipping banks within a period of 5 years time. In testing the predictive status of the developed network, we used the last year as the one to be forecasted. This approach integrated the initial classical linear regression technique (Maniati et al., 2017) and the last simulation study comparing the performance between linear regression and NN models (Sambracos et al., 2020).

The main contribution of this study is i) the relationship integrated between the parameter z and the NN bias estimation and ii) how this relationship may predict the forthcoming year. Specifically, for values of parameter z between 0 and 0.9333333 the NN bias is negligible and the prediction of the forthcoming year is matched. This result indicates that the NN simulates satisfactorily the gross market behavior. On the other hand, as the parameter 0.93333 < $z\to 1^{-}$, the NN is more (absolute) biased and the less the unit-bank decision for the forthcoming year can be predicted. Finally, for values of parameter z outside the normal range, the NN bias is totally random and no relationship was found between them. Moreover, the prediction of the forthcoming year is failed.

To this point, this is the first time that the internal factor z is combined with the bias in a NN and its output as well.

This paper is organized as follows; the next section describes the methodology applied, as well as the data set and variables used. Section 3 presents the results based on the application of NNs in bank financial decisions for increasing or decreasing loan grants portfolio for the next period. Finally, Section 4 provides some discussion and concluding remarks.

2. Methodology

Input data refer to shipping market indices and loan grants that were derived from Bloomberg, Bankscope and Clarksons databases, while all rules and restrictions were conditioned accordingly. Additionally the credibility coefficient was calculated for each bank in order to identify bank’s policy to either increase or decrease its total loans in the shipping sector towards market as a whole.

A NN was developed. For each bank, the NN was trained over the first T empirical years. The extracted optimized parameters of the architecture (weights, biases) were applied, in order to forecast the bank’s policy either to increase or decrease its total loans in the shipping sector the next year T + 1, which is the evaluation period. NN’s forecasting performance is tested by the percentage of relevant agreement compared to the credibility coefficient: whether the NN output matches the evaluated T + 1 year bank’s sign of change.

Technical analysis was forwarded with MATLAB^TM and all statistics were processed with SPSS (IBM COM, v.22).

2.1. Neural networks

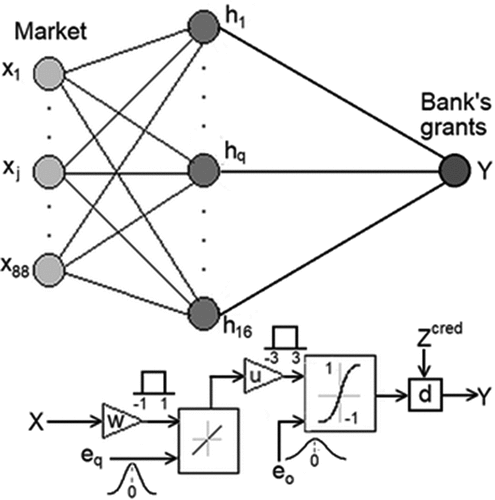
For a set of 88 index inputs over the training period ${\left\{X_{ij}\right\}}_{j=1,\dots ,88}^{i=1,\dots ,T}$, one hidden layer of 16 nodes ${\left\{h_q\right\}}_{q=1,\dots ,16}$ and 89- loan grant difference outputs over the same period, ${\left\{Y_{i,k}\right\}}_{k=1,\dots ,89}^{i=1,\dots ,T}$, we consider $w_{q,j}$ the weight projection of j- input ${\left\{X_{ij}\right\}}_{j=1,\dots ,88}^{i=1,\dots ,T}$ to q- node of the hidden layer. The number of 16 nodes was time-optimal selected according to multiple tests of 8, 32 and 64 nodes. Using 8 nodes, the network failed to match adequately the output, while using either 32 or 64 nodes made no difference with reference to the output compared to the 16 nodes’ network.

The purelin transfer function was applied between input and the hidden layer. In addition, the input to the q-node is biased by $e_q^{\left(h\right)}$ so that the lumped input is $h_q={\sum }_{j=1}^{88}{w}_{q,j}\cdot X_j+e_q^{\left(h\right)}$. The i- output is also biased by $e_i^{\left(o\right)}$ and its response is $Y_{i,k}=f\left(\sum _{q=1}^{16}{u}_{i,q}\cdot h_q+e_i^{\left(o\right)}\right)$ where $u_{i,q}$ is the weight projection of q- node to i- output. The function $f\left(t\right)=2\cdot (1+e^{-2\cdot t}{)}^{-1}-1$ is a hyperbolic tangent sigmoid tansig transfer function which assigns the value t to the point $\left(t,f\left(t\right)\right)\in \left(\mathbb{R},\left[-1,1\right]\right)$ in a non-linear way due to the data derived from shipping market and banks.

The network is being trained using a training function that updates weight and bias values according to Levenberg-Marquardt back propagation optimization process. The Levenberg-Marquardt training algorithm was considered as a valid method for finding optimal solutions over determined systems of nonlinear equations in the least-squares. Although this algorithm required more computational memory compared with other methods, it was faster for the back propagation learning process. This is performed by using the trainlm function with learning rate, goal performance and maximum number of epochs equal to 0.01, 0.001 and 1000, respectively.

Finally, the evaluated last year ${\left\{Y_k\right\}}_{k=1,\dots ,89}^{\left(est\right)}$ was estimated by the net function and compared with the actual data ${\left\{Y_{T+1,k}\right\}}_{k=1,\dots ,89}$ returning the error ${\epsilon }_k=Y_{T+1,k}-Y_k^{est}$.

All functions purelin, tansig, trainlm and net are MATLAB^TM functions.

2.2. The credibility coefficient estimate

Considering that the market consists of j = 1, …, 89 shipping banks that grant loans to the shipping sector the last i = 1, … T observed years, each bank’s credibility equals $C_j=Z_j^{cred}\cdot {\bar{R}}_j+\left(1-Z_j^{cred}\right)\cdot H$, where ${\bar{R}}_j=1/T\cdot {\sum }_T^{i=1}{R}_{ij}$ is the observed mean of loans $R_{ij}$ granted the last T-observed years and $H={\left(89\right)}^{-1}\cdot {\sum }_{j=1}^{89}{\bar{R}}_j$ is the corresponding overall mean of a shipping banks portfolio. Credibility is the difference of the total loans that will be granted from the j_th-shipping bank conditioned on a credibility coefficient $Z_j^{cred}$ that might either be explicitly calculated as $Z_j^{cred}=\left(C_j-H\right)/\left({\bar{R}}_j-H\right)$.

According to Bühlmann (1967), the coefficient $Z_{\hspace{0.17em}}^{cred}$ is in principle limited between values 0 and 1 as a percentage of the amount of credence attached to the individual experience. A zero coefficient implies that the bank grants loans based on the whole market grand average (H) while a coefficient equal to one implies that the bank grants loans by ignoring the whole market trend.

However, in the current research, the lower and upper limits of the credibility coefficient are either extended below zero or above one. For instance, when either $C_j<H<{\bar{R}}_j$ or ${\bar{R}}_j<H<C_j$ then the credibility factor $Z_j^{cred}$ is below 0, which implies bank’s aversion to its previously adopted loan grant policy in favour of the whole market grand average. On the other hand, when either $H<{\bar{R}}_j<C_j$ or $C_j<{\bar{R}}_j<H$ then the credibility factor $Z_j^{cred}$ is greater than 1, which underlines the bank’s full aggressive policy with respect to loan granting portfolio decrease or increase despite the whole market grand average.

2.3. Statistical analysis

The non-parametric Kolmogorov-Smirnov test was used for testing the null hypothesis that the projection weights of: i) either market to the hidden layer or hidden layer to the output layer and ii) either bias to hidden or output layer are uniformly or normally distributed, respectively.

Cohen’s kappa coefficient (κ) was used to measure the degree of agreement between the bank’s decision policy to either increase (p; positive) or decrease (n; negative) total loan grants and the NN output (positive or negative). There are either two ways of agreement (counts pp; positive to positive and nn: negative to negative) or disagreement (counts pn; positive to negative and np: negative to positive). Then, the κ-coefficient is defined as

$\kappa =\frac{I_o-I_e}{1-I_e}$

where $I_o=\frac{pp+nn}{pp+pn+np+nn}$ is the relative observed agreement and $I_e=\frac{pn+np}{pp+pn+np+nn}$ is the hypothetical probability of by chance agreement. In case of a complete agreement, κ-coefficient takes its maximum value of 1 and if there is no agreement then κ = 0. Negative values might be occurred and reflect a tendency of the NN to give different outputs regarding banks.

The κ-coefficient is considered to be significant at a 5% level of significance if its lower bound ${\kappa }_{\mathrm{L}\mathrm{B}}=\kappa -1.96\cdot \sqrt{\frac{I_o\cdot \left(1-I_o\right)}{\left(pp+np+pn+nn\right)\cdot \left(1-I_e\right)}}$ is greater than zero.

3. Data &empirical results

In total, we used the annual differences of 88 indices from tanker shipping market (Appendix Table A1) and of loans granted by 89 shipping banks (Appendix Table A2) over the period 2005–2009, which is characterized by high volatility for the specific shipping sector.

All differences calculated either from shipping market or shipping banks were normally distributed (Kolmogorov–Smirnov, p > 0,05) and then using their mean and standard deviation, they were normalized, according to Gauss distribution of zero mean and a standard deviation equal to one.

3.1. Credibility coefficient

In 6 and 29 banks out of 89 (6.7% and 32.6% respectively), the credibility coefficient $z^{cred}$ was found less than zero and greater than one, respectively. In the vast majority of banks (54, 60.7%), the coefficient $z^{cred}$ was limited into the normal range zero to one.

3.2. Training process

For each bank, the NN had been trained (Figure 1) to adapt with no error in the initial T periods. T was either three or four years.

Figure 1. NNs training process

The projection weights w of markets to hidden layers as well as the projection weights u of hidden layers to the single output were found to be uniformly distributed between values −1 and 1 (Kolmogorov–Smirnov Z = 0.85, p = 0.465) and from −3 to 3 (Kolmogorov–Smirnov Z = 0.74, p = 0.644), respectively. The bias weights e_q to hidden layers were found to be typical normal distributed (Kolmogorov-Smirnov Z = 0.963, p = 0.312) and the bias weights e_o to output layer were found to be normally distributed of zero mean and standard deviation 1.6 (Kolmogorov–Smirnov Z = 0.54, p = 0.824), respectively.

By applying the NN extracted from the training process to the next evaluation period T + 1, we measured the error comparing the actual with the output data.

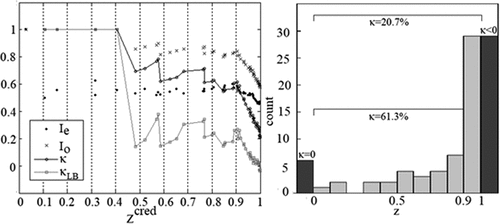
For 35 out of 89 banks (39.3%) where the z-coefficient was either less than zero or greater than one, the NN output failed to match the bank’s decision regarding the loan granted policy either increasing or decreasing loans targeted the shipping sector. In details, for six banks (6.7%) where the z-coefficient was less than zero, the NN output matched only half of them (3) and the relatively observed agreement was 50% (Io) and had no difference to the hypothetical probability of chance agreement (Ie) returning therefore a zero Cohen’s Kappa coefficient (κ). For 29 banks (32,6%) where the z-coefficient was greater than one, the NN output matched less than 1 over 3 of them by a 27.59% relative observed agreement (Io) and less than the hypothetical probability of chance agreement 50.5% (Ie), returning therefore a negative Cohen’s Kappa coefficient (κ).

On the other hand, for 54 banks (60.67%) where the coefficient $z^{cred}$ lied between zero and one (Figure 2), the NN output matched 31 bank’s decision (Ι_ο = 57.4%), i.e. significantly greater than halves (X² = 4.056, p = 0.044). This percentage is also significantly greater than the corresponding hypothetical probability of chance agreement I_e = 46.3% (Wald’s test, z = 1.651, p = 0.049) and the assigned coefficient κ = 20.7%. A detailed analysis showed that the κ-coefficient takes its maximum value for values of the coefficient $z^{cred}$ between 0 and 0.4 and then decreases gradually up to the value 0.9 of the coefficient $z^{cred}$. More specifically, for 24 banks where the coefficient $z^{cred}$ lied between zero and 0.9, the NN output matched 20 of bank’s decision (I_o = 83.7%) and with the corresponding hypothetical probability of chance agreement I_e = 57.9% it was assigned to coefficient κ = 61.3%. For values of the coefficient $z^{cred}$ between 0.9 and 1, the κ-coefficient decreases sharply and takes its minimum value of 20.7%. For all values of the coefficient 0 <$z^{cred}$<1, the κ-coefficient was found significant compared with its lower bound (κ_LB).

Figure 2. NN and z coefficient relationship

4. Conclusions

The main purpose of this study was to model a unique NN architecture for forecasting a shipping bank’s decision either to increase or decrease its loans targeted the tanker shipping sector by taking into account the exogenous factors in the relevant market. This approach integrates other approaches already applied for forecasting a similar bank’s decision, such as the linear regression technique and a simulation study comparing the performance between linear regression and NN models.

The first study revealed the disadvantages of big data analysis, which is necessary within shipping sector by default, performed by the linear regression technique. Main disadvantage issues concerned primarily the exception of possible important market variables (i.e Baltic Dirty Dry Index) due to multicollinearity effects among them and secondly, by considering a strictly linearity, all other effects were lumped into the residual errors that were ignored from further analysis.

On the other hand, the second study, that was based on all market variables with no exception and non-linear training functions, optimised the output performance in an environment characterized by both volatile and noisy information like shipping sector.

In this study, we modelled a NN architecture that was driven by all shipping market’s data. In addition, bank loan grants’ output was non-linearly functioned. This model was further used for forecasting each bank’s decision whether to increase or decrease its loans targeting the tanker shipping market.

Following the bias-error analysis, we noticed that the prediction of the aforementioned bank’s decision policy is dependent on the z-coefficient. The lower the z-coefficient, the higher the predictive performance of the NN model is. Considering the z-coefficient’s meaning, the analysis implied that it might be easier to predict a decision policy if the bank adopts a more conservative strategy. However, forecasting is heavily biased for values of z-coefficient close to one. Presumably, a self-defined policy at bank’s level based on unique characteristics might account for the noise that biases the output.

In this paper, we figured out the advantages of NNs compared with the traditional linear regression techniques for forecasting shipping bank’s decision about its financing policy either to increase or decrease shipping loans: i) it takes into account all data from the shipping market without any exception, ii) linear restrictions are not imposed, iii) it adapts perfectly to the data during the training period and iv) it returns the bias as an important factor of the model. Its main contribution is the understanding of the relation between bias and either exogenous or unpredictable factors as a key factor in the decision policy with reference to each shipping bank’s strategy compared with financial market attitude as a whole. For values of parameter z between 0 and 0.9333333, the NN bias is negligible and the prediction of the forthcoming year is matched. This result indicates that the NN simulates satisfactorily the gross market behavior. On the other hand, as the parameter 0.93333 <$z\to 1^{-}$, the NN is more biased and less the unit-bank decision for the forthcoming year can be predicted. Finally, for values of parameter z outside the normal range, the NN bias is totally random and no relationship was found between them.

To this point, this is the first time that the internal factor z is combined with the bias in a NN and its output as well for forecasting bank’s policy within a specific sector, like tanker shipping, whether to increase or decrease its loans. A future work might also use raw time series financial data from other shipping sub-sectors, as well as industries, using the same macroeconomic indices and compare the NN architecture, as well as the noise as a key factor with effect on the decision-making process.

Correction

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Marina Maniati

Marina Maniati obtained her BSc and MSc in the Maritime Studies and obtained a Phd in Shipping Finance & Bank Performance from the Department of Economics of UNIPI. As an Economist & Financial Consultant, she draws on issues of Finance & Evaluation and of shipping market to frame her analysis. She has presented her academic work in different Conferences and Journals, while she has participated in several European & National Research Projects and/or Studies.

Emeritus Sambracos

Emeritus Sambracos is a Professor emeritus of Transports Economics at the Department of Economics in the University of Piraeus. He graduated from the School of Engineers (Aristotle University) and obtained a D.E.A in the Transports Economics (University of Lyon II). In 1984, he received his PhD Diploma in the Transports Economics (University Lyon II - Ecole Nationale des Travaux Publics de l’ Etat. He has participated in many Research Studies and Projects, and he has presented his work in different Conferences and Journals.

Sokratis Sklavos

Sokratis Sklavos obtained his degree in Mathematics, his MSc in Basic Neuroscience, and his PhD in Neuroscience. He has worked as Research Assistant (Foundation for Research and Technology, Greece, 1991–1999), tutor in Neuroscience (Department of Psychology, Univ. Sheffield, UK, 2000–2004), and Assistant Professor (Medical School, Univ. Patras, Greece, 2004–2006; Laboratory of Physiology & Clinical Neurophysiology, Univ. Athens, Greece, 2005–2017). He is now Head in Research Synelixis, Athens, Greece (from 2017). He has presented his work in different conferences and journals, and he is a member in the: Hellenic Society for Mathematics, Hellenic Society for Neuroscience, American Society for Neuroscience, International Organization for Brain Research.

Appendix

Table A1. Differences of 88 indices from tanker shipping market

Input data	2006	2007	2008	2009	2010	mean	std.deviation
Baltic Dirty Dry Index	−212,67	−163,76	385,80	−928,99	377,81	−108,36	540,36
Baltic Clean Dry Index	−206,40	−138,35	181,48	−671,09	280,69	−110,73	375,00
Weighted Average Earnings All Tankers	−3021,33	−4849,21	12,166,90	−28,618,90	5567,22	−3751,06	15,494,84
Exchange Rates UK	0,02	0,16	−0,14	−0,29	−0,04	−0,06	0,17
Exchange Rates Japan	6,07	1,52	−14,21	−10,06	−2,80	−3,90	8,28
Exchange Rates Euro	0,01	0,11	0,10	−0,08	−0,07	0,02	0,09
LIBOR Interest Rates	14,982,69	−359,62	−21,846,15	−19,280,77	−5869,23	−6474,62	14,987,14
8 Year $10 m Finance based on Libor 1st yr	0,15	0,00	−0,22	−0,19	−0,06	−0,06	0,15
5 Year $10 m Finance based on Libor 1st yr	0,15	0,00	−0,22	−0,19	−0,06	−0,06	0,15
Arab Light Crude Oil Price	11,46	8,71	25,73	−35,42	15,46	5,19	23,60
Brent Crude Oil Price	10,67	7,28	26,38	−37,74	15,80	4,48	24,68
Tankers 10k + DWT Contracting	533,00	−263,00	−331,00	−275,00	138,00	−39,60	370,69
Tankers 10k + DWT Contracting	14,385,715,24	−8,626,885,14	−3,814,567,10	−8,166,177,28	4,396,696,90	−365,043,48	9,763,119,17
Tankers 10k + DWT Contracting	60,972,274,00	−44,222,210,00	8,204,994,00	−39,728,348,00	23,085,442,00	1,662,430,40	44,266,253,72
Total Tanker 10k+ DWT Deliveries	14,00	69,00	97,00	48,00	−122,00	21,20	85,60
Total Tanker 10k+ DWT Deliveries	−4,92	5,75	5,46	11,30	−6,89	2,14	7,74
Total Tanker 10k+ DWT Demolition	2,00	11,00	−10,00	64,00	75,00	28,40	38,45
Total Tanker 10k+ DWT Demolition	−1,11	0,43	0,71	4,36	4,41	1,76	2,49
Total Tanker (10k+ DWT) Fleet Development	257,00	261,00	307,00	358,00	361,00	308,80	50,29
Total Tanker (10k+ DWT) Fleet Development	23,08	19,28	21,80	19,36	29,61	22,63	4,23
Oil Tanker Average Newbuilding Prices	28,03	53,65	61,97	−175,16	−61,05	−18,51	100,25
Oil Tanker Newbuilding Prices	22,91	23,45	−5,81	−75,63	8,86	−5,24	41,14
Oil Tanker Newbuilding Price Index Yr/Yr Change	0,08	−0,01	−0,13	−0,30	0,38	0,00	0,26
Tankers 10k + DWT Orderbook	124,00	616,00	297,00	−156,00	−479,00	80,40	419,67
Tankers 10k + DWT Orderbook	1,494,954,52	15,650,293,83	5,655,662,79	−779,160,48	−10,812,236,09	2,241,902,91	9,637,608,68
Tankers 10k + DWT Orderbook	−278,023,00	63,769,554,00	14,244,465,00	13,986,816,00	−38,282,534,00	10,688,055,60	36,604,469,90
Total Tanker Sales	4,00	44,00	−111,00	−107,00	116,00	−10,80	98,23
Total Tanker Sales	−2,023,428,00	5,594,404,00	−12,288,344,00	−6,214,157,00	13,125,871,00	−361,130,80	9,958,001,49
Total Tanker Sales	1360,69	840,46	−4206,61	−5440,20	3547,39	−779,65	3853,37
Tanker Secondhand Prices Index Average	69,34	65,67	−236,53	−193,30	39,08	−51,15	150,73
Tanker Secondhand Prices Index	20,40	19,32	−69,58	−56,86	11,50	−15,05	44,34
Tanker Secondhand Prices Index % Change	0,02	−0,01	−0,38	−0,04	0,43	0,00	0,29
Other Tankers Far East Demolition Prices	−56,83	43,08	54,58	−85,83	110,24	13,05	81,75
Other Tankers Indian Sub Continent Demolition Prices	−11,67	113,75	80,00	−249,17	132,32	13,05	156,70
Bangladesh Demolition Scrap Prices—Tankers (Others)	9,00	114,83	53,58	−246,67	93,75	4,90	146,33
Total Tanker 10k+ DWT Losses	0,00	0,00	0,00	0,00	−1,00	−0,20	0,45
Total Tanker 10k+ DWT Losses	−0,02	0,00	0,01	0,08	−0,09	−0,01	0,06
AG Crude Exports	−0,77	−0,57	0,63	−2,13	0,61	−0,45	1,14
Refinery Prod. Exports	0,27	0,09	0,03	0,00	0,00	0,08	0,11
E.Med Exports	0,06	0,11	0,10	0,07	0,04	0,07	0,03
Red Sea Exports	0,00	0,00	0,00	0,00	4,46	0,89	2,00
Oil Prod. Imports, Total	0,27	−0,49	−0,27	−0,42	0,51	−0,08	0,44
Oil Prod. Imports, Japan	0,09	−0,06	−0,03	−0,06	0,06	0,00	0,07
Oil Prod. Imports, Eur-4	0,10	−0,26	0,11	0,00	0,10	0,01	0,16
Oil Prod. Imports, USA	0,08	−0,17	−0,34	−0,37	−0,20	−0,20	0,18
Crude Oil Imports, Total	−0,22	−0,59	0,05	−2,42	−1,80	−1,00	1,06
Crude Oil Imports, Japan	−0,04	−0,04	0,02	−1,05	0,07	−0,21	0,47
Crude Oil Imports, Eur-4	−0,18	−0,44	0,30	−0,68	−0,26	−0,25	0,36
Crude Oil Imports, USA	−0,01	−0,09	−0,27	−0,69	−0,84	−0,38	0,37
Oil Prod. Imports, Total	0,27	−0,49	−0,27	−0,42	−0,60	−0,30	0,34
Oil Prod. Imports, Japan	0,09	−0,06	−0,03	−0,06	0,06	0,00	0,07
Oil Prod. Imports, Eur-4	0,10	−0,26	0,11	0,00	9,09	1,81	4,07
Oil Prod. Imports, USA	0,08	−0,17	−0,34	−0,37	9,96	1,83	4,55
Crude Oil Imports, Total	−0,22	−0,59	0,05	−2,42	−2,18	−1,07	1,15
Crude Oil Imports, Japan	−0,04	−0,04	0,02	−1,05	2,19	0,21	1,19
Crude Oil Imports, Eur-4	−0,18	−0,44	0,30	−0,68	1,12	0,02	0,71
Crude Oil Imports, USA	−0,01	−0,09	−0,27	−0,69	−0,02	−0,22	0,28
NGLs/Cond. Oil Prod.	0,56	−0,09	0,06	0,33	1,16	0,40	0,49
OPEC: Crude Oil Prod.	−0,43	0,78	1,01	−2,91	−6,19	−1,55	3,03
Former S.U. Oil Prod.	−1,26	0,22	−0,09	0,02	13,09	2,40	6,00
N. Sea Oil Prod.	−0,44	−0,17	−0,18	−0,23	2,26	0,25	1,13
N. America Oil Prod.	0,14	0,03	−0,17	0,46	20,71	4,23	9,22
Global Oil Prod.	0,29	0,08	0,77	−1,09	11,70	2,35	5,27
Mid-East Oil Production	−0,43	−0,38	0,76	−2,07	0,65	−0,29	1,14
Industrial Production Europe	21,191,67	−1116,67	−37,990,91	−129,792,42	206,183,33	11,695,00	123,052,24
Industrial Production Latin America	9925,00	2433,33	−33,625,00	−78,191,67	189,858,33	18,080,00	102,177,25
Industrial Production OECD	19716,67	−11,191,67	−44,616,67	−118,175,00	224,558,33	14,058,33	128,363,00
Atlantic Region Industrial Production Growth	1,883,216,67	−624,658,33	−4,363,100,00	−11,198,433,33	17,989,825,00	737,370,00	10,831,591,35
Pacific Region Industrial Production Growth	2,664,991,67	−985,066,67	−5,660,791,67	−10,717,400,00	29,556,133,33	2,971,573,33	15,687,523,22
Industrial Production China	12,166,67	7583,33	−33,916,67	−38,666,67	87,500,00	6933,33	50,662,81
Industrial Production USA	11416,67	−22,333,33	−35,083,33	−82,250,00	136,466,67	1643,33	82,514,65
Annual GDP Germany	24,500,00	−6600,00	−12,700,00	−61,500,00	63,000,00	1340,00	46,226,00
Annual GDP UK	6800,00	−2900,00	−20,100,00	−54,700,00	61,200,00	−1940,00	42,359,69
Annual GDP USA	−3800,00	−5300,00	−17,000,00	−28,800,00	57,400,00	500,00	33,370,95
Annual GDP Japan	1100,00	3200,00	−35,500,00	−40,100,00	76,000,00	940,00	46,506,16
Annual GDP Euro Area	12,800,00	−2100,00	−21,200,00	−47,400,00	50,900,00	−1400,00	36,896,68
Annual GDP World	6000,00	1000,00	−21,600,00	−36,200,00	52,000,00	240,00	33,606,96
Annual GDP EU	12700,00	−3400,00	−24,900,00	−46,800,00	51,000,00	−2280,00	37,276,36
Annual GDP China	12,100,00	14,100,00	−34,700,00	−8100,00	17,600,00	200,00	21,934,45
Annual GDP India	6100,00	−4500,00	−29,700,00	−7300,00	37,300,00	380,00	24,410,08
Annual GDP Indonesia	−1900,00	8500,00	−3400,00	−14,600,00	10,500,00	−180,00	10,132,47
Annual GDP Korea	12,200,00	−700,00	−28,100,00	−21,000,00	48,000,00	2080,00	30,258,50
Annual GDP Malaysia	5200,00	3300,00	−15,500,00	−63,500,00	88,200,00	3540,00	54,833,87
Annual GDP Philippines	3900,00	17,400,00	−32,400,00	−29,200,00	27,100,00	−2640,00	27,018,20
Annual GDP Singapore	10,300,00	−4600,00	−68,300,00	−34,100,00	100,200,00	700,00	63,230,81
Annual GDP Taiwan	7400,00	5400,00	−52,500,00	−26,000,00	74,700,00	1800,00	47,644,67
Annual GDP Thailand	5400,00	−2200,00	−24,700,00	−47,400,00	54,800,00	−2820,00	38,256,14
Annual GDP Newly Indust. Asia	9300,00	100,00	−39,900,00	−26,900,00	75,900,00	3700,00	44,984,66

Table A2. Loans granted by 89 shipping banks

Bank	2006–05	2007–06	2008–07	2009–08	2010–09	mean	std.deviation
1	15,556,915,2	24,118,669,2	40,761,996	30,538,269,6	438,297,6	22,282,829,56	15,292,348,56
2	22,886,551,1	−8,491,609,8	47,028,126			20,474,355,9	27,838,360,07
3	24,114,000	19,912,000	14,966,000	27,509,000		21,625,250	5,418,893,699
4	−107,563,825,6	17,962,453,6	66,943,814	−35,917,576,9	12,489,248,5	−9,217,177,24	65,945,758,87
5	7,743,197,9	−36,641,530	48,089,583	43,991,072	19,049,659,9	16,446,396,46	34,135,212,59
6	16,532,256,5	−12,182,086,8	39,153,484	34,518,459,6		19,505,528,4	23,269,261,39
7	7,013,461,8	−19,270,075,3	29,444,520	35,035,552,4	−4,514,317,3	9,541,828,24	22,804,280
8	45,379,674,4	35,180,425,04	19,229,727	13,524,341,2	12,964,805,8	25,255,794,67	14,391,644,49
9	4,536,331,9	7,750,945,6	42,678,177	29,805,034,76		21,192,622,24	18,201,770,78
10	−60,152,980,9	−164,066,755,6	87,656,474	48,705,735,1		−21,964,381,8	113,523,053,8
11	−34,057,464,5	8,368,207,4	19,869,470	−93,408,377	−47,285,724,5	−29,302,777,72	45,531,676,74
12	885,262,2	−390,561,4	27,897,759	25,274,122,8		13,416,645,73	15,253,163,11
13	4,150,582,7	25,994,568,7	8,042,285,3	30,523,880,39		17,177,829,27	13,025,862,63
14	9,180,988	−25,055,703,8	22,194,713	26,780,057,5	4,244,082,5	7,468,827,38	20,377,382,74
15	23,154,243,7	6,120,755,1	11,958,873	−6,436,788,1	−18,554,379,8	3,248,540,76	16,198,220,97
16	9,390,180,5	−18,171,856,9	23,135,456	40,010,984,58	15,105,207,7	13,893,994,27	21,315,909,41
17	−17,309,859,5	36,332,964	32,570,972	19,762,272,21		17,839,087,12	24,482,640,08
18	−8,322,306,4	−4,733,903,3	42,651,805	30,542,095,95		15,034,422,89	25,426,569,16
19	6,951,697,7	−19,711,602,3	14,154,737	77,272,111,89	3,805,107,75	16,494,410,37	36,271,063,51
20	−2,108,075,61	21,185,900,33	24,377,203	21,302,161,49	−651,862,89	12,821,065,25	13,036,897,8
21	17,346,188,21	−13,315,569,9	12,333,624	21,015,692,28	11,224,976,8	9,720,982,182	13,467,413,17
22	5,174,778,78	13,649,655,63	18,266,206	8,871,656,61		11,490,574,31	5,695,577,897
23	2,673,283,87	10,579,605,29	22,346,668	13,430,220,79	2,489,682,05	10,303,891,94	8,278,986,259
24	3,480,879,85	8,630,813,63	19,496,717	10,165,073,79	1,791,876,05	8,713,072,066	6,958,463,613
25	−842,623,2	8,372,417,5	26,620,758			11,383,517,27	13,977,101,32
26	10,746,107,86	2,347,188,19	9,617,483,5	5,007,501,47	4,297,634,54	6,403,183,104	3,606,420,626
27	239,248,69	9,465,744,86	17,686,367	8,674,036,77	2,284,183,07	7,669,916,16	6,869,925,3
28	−7,415,269,2	7,426,112,6	21,935,226			7,315,356,567	14,675,561,21
29	2,184,915,18	5,969,060,84	10,810,705	5,543,804,92	1,406,152,1	5,182,927,554	3,730,691,122
30	2,421,079,91	5,460,655,59	11,469,451	2,151,947,49	−3,160,638,7	3,668,498,974	5,351,630,018
31	2,904,649,09	6,172,359,67	8,972,581,5	4,803,178,02	162,269,6	4,603,007,572	3,324,179,809
32	9,226,130,51	609,644,2	6,626,206,5	2,548,867,77	752,416,27	3,952,653,056	3,819,204,415
33	11,622,964,61	−3,248,494,35	10,977,678	−3,461,316,87	−16,804,819,6	−182,797,538	11,836,078,82
34	−4,752,407,81	5,584,750,82	12,235,034	8,902,687,91	3,018,860,06	4,997,785,006	6,460,514,166
35	1,883,743,57	−2,075,019,72	8,470,912,5	5,182,823,9	6,330,200,51	3,958,532,15	4,128,976,061
36	7,554,185,42	−13,002,877,77	4,291,851,6	27,041,099,33		6,471,064,638	16,414,250,72
37	1,618,184,56	3,893,424,98	5,939,501,3	5,440,999,34	19,728,91	3,382,367,82	2,522,784,07
38	−1,124,826,87	4,266,860,48	6,042,787,4	4,245,353,17	60,038,95	2,698,042,632	3,066,597,127
39	9,641,930,35	−18,981,809,9	15,501,064	12,283,904,94		4,611,272,308	15,910,142,46
40	−2,215,931,38	−10,658,813,12	14,405,922	13,459,651,23	12,997,974,3	5,597,760,66	11,396,119,63
41	1,090,310,61	725,011,08	13,713,679			5,176,333,487	7,395,813,634
42	1,124,194,46	5,043,538,76	3,147,289,2	1,380,807		2,673,957,365	1,817,779,046
43	−141,040,766,4	97,125,301,3	31,567,503	89,275,929,2	10,332,171,4	17,452,027,76	96,016,155,07
44	1,149,345,43	−242,989,66	5,225,487,6	1,667,524,99	2,248,750,78	2,009,623,818	2,020,540,722
45	2,643,024,4	−50,767,99	2,613,767,1	1,175,177,32	762,702,46	1,428,780,662	1,180,637,519
46	136,242,77	−3,110,935,29	4,667,640,4	9,746,810,16	−229,556,6	2,242,040,28	5,034,943,606
47	1,864,793,5	1,202,314,11	3,745,979,2			2,271,028,93	1,319,594,034
48	1,908,657,65	−2,063,397,69	3,904,510,9	3,228,503,86		1,744,568,668	2,670,514,736
49	45,040,96	2,414,523,82	2,005,235,4	1,521,360,93		1,496,540,278	1,034,235,764
50	−7,038,251,66	5,050,105,3	7,044,963,2	5,125,177,67	−6,356,951,68	765,008,568	6,863,383,766
51	1,070,949,37	−2,473,792,87	1,841,889,3	3,192,029,4	2,030,431,32	1,132,301,3	2,154,084,011
52	529,432,37	461,983,23	896,216,2	970,897,73	555,981,58	682,902,222	232,868,6925
53	−598,291,86	545,872,31	1,058,182,6	1,218,723,06	460,018,41	536,900,908	712,613,1656
54	−332,471,06	531,953,7	544,343,08	511,667,79	121,198,09	275,338,32	383,163,831
55	−665,166,45	−843,911,32	5,284,872,7			1,258,598,32	3,488,001,097
56	107,771,78	−369,275,8	774,274,93	1,179,869,75		423,160,165	688,794,9783
57	206,311,22	184,287,7	162,940,57	133,924,4	−193,328,02	98,827,174	165,494,2007
58	−2,552,502,62	−8,084,881,67	11,500,486	4,768,342	2,419,376,87	1,610,164,09	7,412,305,383
59	−268,104,52	−294,918,24	809,976,73	535,485,83	12,940,92	159,076,144	493,787,7957
60	34,637	14,809	1982	40,144	15,373	21,389	15,679,44,382
61	−19,892,1	−433,683,43	328,705,75	84,257,72	42,851,28	447,844	276,341,7612
62	−453,895,51	−193,002,87	384,018,81	392,027,44	−19,050,43	22,019,488	368,227,454
63	−34,787,083,8	−201,781,765,6	185,201,708	198,342,038,2	48,940,795,7	39,183,138,56	166,045,075,8
64	−662,307,39	−1,168,787,92	754,125,65			−358,989,8867	996,694,6776
65	−4,571,398,94	−2,121,439,03	2,314,291,1			−1,459,515,64	3,490,241,91
66	−7,599,467,17	−4,442,594,82	2,990,711,2	8,073,351,63		−244,499,7975	7,103,351,069
67	−36,637,000	−48,680,000	113,415,000	128,131,000	67,111,000	44,668,000	82,946,161,39
68	−50,083,532,9	59,756,291,5	95,812,280	2,674,525,6	−24,986,053,4	16,634,702,22	60,222,622,53
69	852,144,84	−35,376,857,82	15,540,425	22,036,031,4		762,935,7375	25,671,069,39
70	−30,015,203,6	50,893,650,5	163,701,175	−7,405,332,2	−50,704,114,1	25,294,035,18	86,191,583,05
71	−29,539,372,2	38,019,798,8	150,263,363	−4,788,795,1	−33,767,148,7	24,037,569,22	76,110,589,24
72	−37,807,911,1	57,886,050,2	198,252,513	101,059,028,8		79,847,420,25	97,970,705,01
73	43,283,406,8	−66,528,133,3	47,146,517	69,088,385,1	806,547,8	18,759,344,64	53,704,120,63
74	−11,152,989,7	56,424,609,2	62,356,789	90,352,552,9		49,495,240,35	43,054,087,62
75	8,687,854,7	43,854,647,6	122,680,001	18,134,691,6	−21,762,814,7	34,318,875,98	54,686,955,5
76	−33,027,000	40,649,000	201,706,000	131,728,000	52,535,000	78,718,200	90,218,971,84
77	−32,264,719	−9,680,404,3	99,100,676	71,498,172	12,729,121,7	28,276,569,3	55,298,877,94
78	31,774,338,1	44,206,921,7	81,611,726	108,273,651,3	−13,979,952,9	50,377,336,88	47,046,723,14
79	−2,932,608,4	81,966,468,1	54,028,922			44,354,260,53	43,268,494,34
80	37,903,916,4	8,740,182	78,378,465	59,491,713,4		46,128,569,1	29,911,902,8
81	23,207,406,5	32,319,093,7	4,776,159	115,988,193	34,297,113,7	42,117,593,18	42,912,742,5
82	168,612,045,4	107,264,363,9	89,218,322	55,322,530,6	21,581,850,2	88,399,822,5	55,563,680,2
83	289,769,826,5	32,815,974,9	137,480,569	162,434,938,6		155,625,327,3	105,597,485,4
84	110,992,529,7	−20,899,019,4	39,162,225	202,933,595,9	−22,288,668,3	61,980,132,54	95,865,707,43
85	148,329,165	103,175,667,4	77,725,072	61,249,468,9	34,191,137,4	84,934,102,16	43,415,058,26
86	808,587,1	−11,392,189,1	40,125,556	58,178,421,4	−6,577,956,5	16,228,483,86	31,030,935,57
87	235,895,648,9	89,601,625,3	77,715,643	32,700,608,3	16,215,543,8	90,425,813,92	86,837,584,27
88	39,867,681,4	37,960,245,1	22,221,139	38,091,618,4	−17,918,840,8	24,044,368,64	24,523,403,02
89	9,867,219,6	−1,823,526,2	58,514,465	36,195,380,8	18,352,047,2	24,221,117,22	23,654,917,46