Day-of-the-week effect: Petroleum and petroleum products

Abstract

This study tests for calendar anomalies in returns for petroleum and petroleum products via the futures market, specifically, the day-of-the-week (DOW) effect. The energy future contracts in this study are the WTI (West Texas Intermediate), Brent, RBOB (Reformulated Blendstock for Oxygenate Blending) Gasoline, Heating Oil, and Natural Gas. Futures provide a more liquid insight into price movements relative to spot prices, where financial market participants can engage. We ensure the most appropriate price is used by focusing on the most liquid contracts by combining the front two months of the studied commodities nearing expiration. Our research shows that the DOW effect varies across the respective energy commodities; however, for investors engaged in trading these futures, our results may help time their trade decisions.

Keywords:

• Day-of-the-week effect
• GARCH
• EGARCH
• PGARCH
• QGARCH
• TGARCH
• EMH
• calendar anomalies
• petroleum products

JEL Classification:

• G11
• G12
• G14
• L71
• Q02
• Q40

1. Introduction

The predictableness of price movements (i.e., non-random movements) within financial markets is of significant interest to financial market participants. The ability to correctly predict price movements of financial assets or the lack of randomness in asset prices within financial markets challenges the Efficient Market Hypothesis (EMH) (Fama, 1970). The EMH asserts that asset prices reflect available information making it impossible for investors to predict price movements consistently to produce abnormal profits by taking advantage of the mispricing of an asset. Finance has numerous asset pricing models to attempt to price assets efficiently. These models include the Capital Asset Pricing Model (CAPM) (Sharpe, 1964), Arbitrage Pricing Theory (APT) (Ross, 1976), and Fama and French Three-Factor Model (Fama & French, 1993), among others. However, empirical evidence in contraction to the EMH is considered an anomaly.

The extant literature provides many instances against the EMH and, thus, the documentation of many asset market anomalies. One broad anomaly receiving attention and defies the EMH is seasonal (or calendar) anomalies (Ikenberry & Lakonishok, 1989). Calendar anomalies are non-random asset price movements or returns that relate to specific calendar times, dates, and periods. Evidence of specific calendar anomalies includes the day-of-the-week (DOW), the month of the year effect (Rozeff & Kinney, 1976), and the turn of the year effect, among others (Tadepalli & Jain, 2018). In this research, we focus specifically on the DOW effect. The DOW effect shows that asset returns are not random, and certain days experience significant average returns. However, there is no systematic evidence regarding DOW effects as the presence of which day exhibits evidence against the EMH varies across assets, markets, and countries (e.g., Cross, 1973; French, 1980; Gibbons & Hess, 1981). Moreover, most calendar anomaly studies focus on equity and bond markets with little investigation into commodity markets.

Geopolitical events in recent years have brought renewed attention to and interest in energy markets, especially crude oil, petroleum products, and natural gas. These energy commodities have been and continue to be integral to domestic and international financial markets. For example, in 1973, an OPEC oil embargo led oil prices to rise significantly and quickly. These increased energy costs contributed to a global recession that led to the unemployment rate in the United States doubling within two years (Mitchell, 2010). There have been many significant price movements in energy prices throughout history and evidence of their impact on financial markets. There was another oil shock in 1979, where oil prices increased over 100%, the 1990 mini-oil shock, the 2000‘s oil crisis defined by the peak in 2008, and now the 2022 Russian—European Union Gas dispute, all demonstrating how the price of energy can play a significant role in financial markets. Major indicators of price movements in energy include the weekly reports from Baker Hughes and the Energy Information Association (EIA). These reports include rig count, monthly rig averages, total U.S. petroleum inventory, imports, and exports, allowing investors to anticipate future trends. There are many ways petroleum and petroleum products trade—spot contracts, futures contracts, and the equity of energy companies, among many others. The increased access and liquidity of commodity contracts have attracted more investor trading as they have become more acceptable as a viable asset class (Tang & Xiong, 2012). This increase in commodity futures trading is termed financialization (Huynh et al., 2020). The importance of energy (i.e., petroleum and petroleum products) motivates this study.

This paper investigates and presents the results of the DOW effect in the futures markets for petroleum and petroleum products. We study five of the most liquid energy markets, WTI, Brent, RBOB Gasoline, Heating Oil, and Natural Gas, to determine whether this is evidence of the DOW effects. Combining these petroleum and petroleum products provides an extensive review of energy markets. Furthermore, front-month futures contracts tend to see a dramatic drop in liquidity in the days leading up to expiration. To apply the results where they matter most, market participants, we use a synching method to alleviate any dramatic change in liquidity risk due to the rolling over of contracts from the front month to the following month. We explain this process in detail in Section 3.2. The sample period is from January 2002 through December 2021.

Many studies on commodities tend to focus on a particular commodity, such as the gold market (e.g., Aksoy, 2013; Ball et al., 1982; Chang & Chan-Wung, 1988; Ma, 1986). Borowski and Łukasik (2017) study metal markets and find DOW evidence in gold and copper markets. Calendar effects in agriculture markets have also received attention, focusing on commodities such as barley, corn, and soybeans (e.g., Arendas, 2017; Borowski, 2015). While broadening the focus on commodity markets, recent studies include evidence of the DOW in crude oil and natural gas (e.g., Chhabra & Gupta, 2022; Qadan et al., 2019). We extend this work by using a new method of combining futures to ensure the findings are not driven by illiquidity or model selection as we allow for asymmetric responses in the variance questions (i.e., EGARCH, PGARCH, QGARCH, and TGARCH models). The extant literature tends to estimate OLS or GARCH models. Additionally, we analyze an extensive sample period and some energy markets, such as Brent, RBOB Gasoline, and Heating Oil, that are absent in the literature.

The study’s findings exhibit evidence of the DOW effect across the five energy markets. However, the DOW effect is heterogeneous across the energy products. For example, we find a positive Friday effect in WTI, a positive Wednesday effect in Brent and Heating Oil, a negative Monday effect in RBOB and Heating Oil, and a positive effect on Monday and Tuesday, but a negative Thursday effect in Natural Gas. These findings also highlight the importance of consulting multiple models and allowing for asymmetric responses to positive and negative shocks in the variance equation. Multiple DOW effects would have been identified erroneously without asymmetrical variance modeling. Finally, the heterogeneous results across the energy markets indicate that energy commodity futures may provide diversification benefits to traditional portfolios (Bhardwaj et al., 2015; Gorton & Rouwenhorst, 2006).

The organization of this research proceeds as follows. Section 2 reviews the relevant calendar anomaly literature in financial markets. Section 3 describes the data, contract rolling method, and empirical models estimated. Section 4 presents and discusses the empirical findings. Finally, Section 5 summarizes the study.

2. Literature review

There is evidence of a plethora of various calendar anomalies in financial markets. These anomalies include intraday (e.g., Harris, 1986), day-of-the-week (DOW) (e.g., French, 1980), intramonth (e.g., Ariel, 1987), month (e.g., Haugen & Jorion, 1996), Halloween (e.g., Bouman & Jacobsen, 2002), and holiday (e.g., Lakonishok & Smidt, 1988) effects. In this research, we focus specifically on the DOW effect. The day-of-the-week effect is an anomaly where asset returns are not homogenous across the specific weekday and differ from zero. A seminal piece by Cross (1973) examines the day-of-the-week effect in U.S. markets and finds significant pricing changes on Monday relative to Friday. Cross, along with French (1980) and Gibbons and Hess (1981), shows significantly higher returns on Friday than the following Monday. These early works helped establish the DOW effect in literature. However, their focus was solely on equity markets in the United States.

Calendar anomaly research then began to expand beyond American markets. Theobald and Price (1984) and Choy and O’hanlon (1989), among others, expand the investigation of the DOW calendar anomaly into markets in the United Kingdom. They focus on measuring changes in the Financial Times Ordinary (FTO) and Financial Times Actuaries All Share (FTSA). Yan-Ki Ho and Cheung (1994) find evidence of the DOW effect in Asian markets, while Poshakwale (1996) finds a significant weekend effect in the Bombay Stock Exchange. Finally, Yalcin and Yucel (2006) document the concentration of higher returns on Friday and higher volatility on Monday in 20 emerging market economies.

Similarly, Birru (2018) and Chiah and Zhong (2019, 2021) found that speculative stocks exacerbate the Monday and Friday tendencies, which may be due to psychological factors. These papers generalized the effect in the larger markets, prompting researchers to go beyond studying major regional indices and narrow their studies into various market segments. For an extensive review of the calendar anomalies literature, please see Philpot and Peterson (2011), Rossi (2015), and Tadepalli and Jain (2018).

This research focuses on the energy market segment of financial markets. Therefore, the remainder literature review will focus on the previous literature dedicated to energy markets. For example, Sanusi and Ahmad (2016) examine oil and gas equity listed on the London Stock Exchange for calendar anomalies and find a January effect in the FTSE 100 and FTSE All Share indices. Qadan and Nama (2018) explore the impact of investor attention and sentiment on seasonal anomalies within the petroleum industry, where they used information such as daily search query data from Google Trends to determine a relationship between individuals’ emotions and the price of WTI crude oil.

The importance of WTI and Brent crude oil must be recognized as they serve as an international benchmark for crude oil prices, providing a reference point at which oil worldwide is traded at a premium or discount (Scheitrum et al., 2018). Furthermore, Ederington et al. (2019b) found that gasoline price variations are due to changes in crude oil price, not taxes, content requirements, or other factors. To explore the seasonal anomalies within the oil and gas market, researchers must go beyond the equity of energy companies and determine if the effects exist within the commodity prices that drive those stock prices. Ederington et al. (2019a) discuss factors related to petroleum product prices; these products include Heating Oil and RBOB Gasoline.

Auer (2014) analyzes Brent Crude Oil spot prices and determined a negative Monday effect. Quayyoum et al. (2020) expand on the Brent spot contracts and found a negative Monday effect consistent with Auer’s study in the WTI spot market. Qadan and Idilbi-Bayaa (2021) study DOW effects for indices of commodity implied volatility and find positive changes to volatility on Monday and negative changes to volatility on Friday. Similarly, Qadan et al. (2022) find positive turn-of-the-month effects in the forward-looking volatility for oil and gold commodities. Ye and Karali (2016) consider another factor that can affect crude oil return and volatility: current oil inventories. They find that inventory shocks created from announcements by the American Petroleum Institute (API) and EIA have an immediate inverse impact on returns and a positive impact on volatility, with the EIA inventory shocks being longer and more prominent. Li et al. (2022) also consider the impact that inventory shocks associated with the inventory announcements on Wednesdays have on WTI futures and find a Monday effect. Finally, Chhabra and Gupta (2022) examine the day-of-the-week effect of natural resource markets in India, their analysis focusing on the crude oil and natural gas future of India’s Multi Commodity Exchange (MCX).

According to the prior literature, the DOW effect is apparent in many financial markets. It has been well-studied in the equity market and appears to operate differently depending on the market. The recent oil and gas market literature has addressed some of the present seasonality, but more research is needed to extend beyond GARCH modeling. Furthermore, most of the studies have been concerned with the spot market. Most of the prior research in the futures market has yet to address the lack of liquidity associated with the front-month contract nearing expiration.

The goal of this research is to contribute to the strands of literature investigating the day-of-the-week effect in the energy market. The petroleum commodities in this research include WTI, Brent, RBOB Gasoline, Heating Oil, and Natural Gas. This broader study of the overall energy market provides deeper insight into energy markets for the presence or absence of the DOW effect. To apply this determination of abnormal returns to investors, we utilize a synching method detailed in the next section to ensure that using the most liquid contracts to calculate returns provides more appropriate returns for the analysis. Finally, relative to other studies, we extend the analysis beyond a GARCH model and allow for asymmetric modeling of the variance equation, as positive and negative shocks to assets tend not to lead to symmetrical responses.

3. Data and descriptive statistics

The energy commodities in this study are the WTI (West Texas Intermediate), Brent, RBOB Gasoline, Heating Oil, and Natural Gas. In this section, we will first describe the energy commodity and the respective futures contract, followed by the data collection process, including sample creation methods, and finish the section with a discussion of the sample’s descriptive statistics.

3.1. Commodity and contract description

The first energy commodity studied in this research is the West Texas Intermediate (WTI) futures contract that trades on the New York Mercantile Exchange (NYMEX). WTI Crude Oil futures are incredibly liquid as they are the most actively traded crude oil futures contract, with over 1 million contracts traded daily (CME Group, 2023a). The market’s depth and liquidity allow the commodity’s financialization as investors do not worry about making or taking delivery. The second major commodity is Brent Crude Oil. Brent comprises five different crude oils from the North Sea. That location serves a significant purpose because Brent Crude Oil is the primary benchmark for most (if not all) European and African crude oil prices. In addition, Brent is one of the most liquid futures available via the ICE Exchange (second behind only interest rate futures), accounting for a monthly trade volume of approximately 20 million contracts in 2022 across all various Brent contract expirations (Intercontinental Exchange, Inc. ICE, 2022), where the futures trade.

The first petroleum product future studied in this research is the New York Harbor Reformulated Blend stock for Oxygenate Blending (RBOB) Gasoline futures. RBOB Gasoline is one of the most traded and essential petroleum products, averaging approximately 60,000 contracts traded per day in 2021. The liquidity of RBOB Gasoline futures allows investors to easily trade on their views of crude oil combined with their expectations for the weather and consumer behavior (CME Group, 2023d).

This analysis’s second refined petroleum product is New York Harbor Heating Oil. Heating Oil is a heavy fuel oil derived from crude oil, also referred to as the No. 2 fuel oil. Heating Oil futures are also highly liquid contracts, with over 180 million barrels traded daily on NYMEX exchanges (CME Group, 2023c), with peak days crossing 70,000 contracts traded.

The final energy commodity is Henry Hub Natural Gas. Henry Hub Natural Gas is the benchmark for the United States as the third largest physical commodity futures contract, with approximately 400 thousand contracts across all expirations traded daily (CME Group, 2023b). We hope to provide a holistic view of the global energy market by exploring seasonality in primary energy commodities.

3.2. Data collection and sample creation

This study focuses on energy futures contract prices rather than spot prices. Investors prefer futures contracts over the spot market as futures have low costs, a high leverage effect, and dominate the contribution to price discovery in commodities (Ameur et al., 2022). Additionally, futures markets have less liquidity risk than spot markets. Liquidity risk is the risk investors face for not being able to readily transfer ownership of an asset (Keene & Peterson, 2007). Liquidity is essential in commodity futures because it allows for ease of risk transfer. This transfer contributes to lower price volatility, enhanced price efficiency, and better liquidity (Boyd et al., 2018; Kim, 2015). To investigate the day-of-the-week effect concerning the ability of investors to trade, we study the first and second-month commodity futures prices and institute a rolling mechanism to ensure the prices represent the most liquid contract. Furthermore, the sample periods represents the period to the extent of Bloomberg’s pricing and volume data. In general, a more extended sample period provides more robust results. Moreover, it may identify trends not apparent in shorter periods, which is crucial to studying the day-of-the-week effect.

WTI futures prices are from Bloomberg listed as “CL1” and “CL2” for the front-month and second-month contracts, respectively. WTI Futures contracts expire on the third business day prior to the 25th calendar day of the month preceding the delivery month. If the 25th calendar day of the month is a nonbusiness day, trading ceases on the third business day before the business day preceding the 25th calendar day. The sample data for WTI is from 1 January 2002, through 31 December 2021. In the case of the WTI futures, the expiration date and two days prior have noticeably smaller volumes. Due to this reduced liquidity, the WTI (CL1) prices on the expiration date and two days prior are replaced with CL2 prices. This results in rolling over from the front month to the second-month contract by three days. After expiration, the second-month contract (CL2) becomes the front-month contract (CL1). This rolling method allows for a calculated return that ensures the most liquid commodity contract price.

Brent futures prices from Bloomberg are “CO1” for the front-month contract and “CO2” for the following month’s contract. The sample period starts on 1 January 2002, and continues through 31 December 2021. The expiration date for Brent contracts expiring prior to January 2016 is the 15th business day before the first calendar day of the contract month or the next proceeding business day if the 15th calendar day is not a business day (ICE, 2015). After January 2016, the expiration date is the last business day of the second month preceding the relevant contract month, unless the day on which trading is due to cease would be either the business day preceding Christmas Day or the business day preceding New Year’s Day. Trading should cease on the next preceding business day. The Brent Crude Oil futures trading volume depends on these expiration dates. The four business days leading up to the expiration and the expiration date exhibit significantly lower trade volume than earlier contract days. We replace CO2 prices (second-month contracts) for the CO1 prices (near-month contracts) for four business days leading up to the expiration date and the expiration date due to the low trading volume (i.e., lack of liquidity).

The RBOB Gasoline futures prices from Bloomberg are “XB1” and “XB2” for the front month and the following month, respectively. The sample period runs from 1 January 2007, through 31 December 2021. The expiration date for RBOB futures is the last business day of the month proceeding the delivery month. As a result, the near-month contract experiences a significant reduction in trade volume for the expiration date and the two preceding days. The XB2 prices replace the prices of XB1 for the two days prior to expiration and the expiration date itself to calculate returns more accurately for liquid RBOB futures.

“HO1” and “HO2” prices from Bloomberg reflect Heating Oil futures contracts for the near month and second month, respectively. The sample period for Heating Oil is from 1 January 2002, through 31 December 2021. The expiration date for a Heating Oil future is the last business day of the month proceeding the delivery month. The significant daily trading volume decrease starts two days before expiration. The synching method of rolling from the near month to the second month described previously is used again for these dates as the HO2 prices replace the HO1 prices.

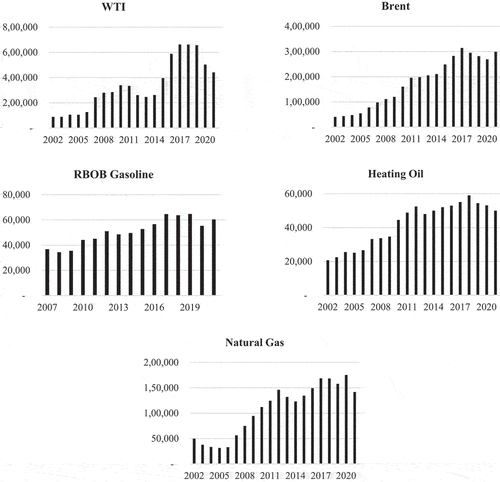
“NG1” and “NG2” are the Natural Gas futures available via Bloomberg, reflecting the front-month and following-month contracts. The sample data for Natural Gas is from 1 January 2002, through 31 December 2021. The expiration date for Natural Gas futures contracts is three business days prior to the first calendar day of the delivery month. Trading ceases on the prior business day if the expiration date is a nonbusiness day. The daily trade volume for NG1 had differing trends throughout the sample. At the beginning of the sample, from 1 January 2002, through 25 November 2002, trading volume remained approximately the same on the expiration date relative to other days. From 26 November 2002, through 25 November 2008, there was only a significant decline in trading volume on the contract’s expiration date. In the last period of the sample, from 26 November 2008, through 31 December 2021, the trend of two days prior to the expiration date decreasing in trading volume is evident in the data. The price synching method of replacing near-month contract (NG1) prices with the following month contract (NG2) prices is as follows: (1) No replacement for NG1 prices before 26 November 2002, (2) Replace NG1 prices with NG2 prices only for the expiration date from 26 November 2002, through 25 November 2008, and (3) Supplant NG1 prices with NG2 prices starting two days prior to the expiration date for the period starting 26 November 2008, and afterward. This process ensures the calculated returns reflect the most liquid contracts for Natural Gas futures. The average daily volume (ADV) of commodity futures traded using the most liquid contracts for each energy commodity is shown in Figure 1. The liquidity of all five energy commodities has improved over the sample period.

Figure 1. Traded average daily volume.

The purpose of identifying and synching contract prices is to ensure that the returns in the analysis are not subject to liquidity and contract expiration bias. Therefore, we exclude days with missing price data. For missing price data, the following return observation would be where there were two consecutive trading days of prices to calculate the return. We define the daily return for each energy futures contract as follows:

(1) $R_t=ln\left(P_t/P_{t-1}\right)$(1)

where R_t is the logarithmic return for the energy futures contract on day t, P_t is the price of the futures contract day t, and P_t-1 is the price of the futures contract on the trading day before day t.

Table 1 presents the descriptive statistics for the returns of the energy futures contracts over their respective sample period. Heating Oil futures exhibit the highest average return of 0.029 percent (or approximately 2.90 basis points). RBOB Gasoline Gas futures experience the lowest average daily return of 0.0084 percent (or approximately 0.88 basis points). Each sample contains more than 5,000 distinct daily return observations except for RBOB Gasoline. This exception is due to the sample period for RBOB starting in January 2007 due to a lack of data and trade volume prior. WTI futures experienced the most significant negative one-day return of 56.85%, which occurred on 21 April 2020. Conversely, the most significant positive daily return in the sample was for Natural Gas futures, 32.44% occurring on 24 February 2003. The standard deviation for all commodity returns ranges from 2.18% (Heating Oil) to 3.37% (Natural Gas). Given the small positive average daily returns, one can estimate that the daily returns for the energy contracts range from 4 percent to 6 percent, positively and negatively.

Table 1. Descriptive statistics

	WTI	Brent	RBOB Gasoline	Heating Oil	Natural Gas
Mean	0.000270	0.000232	0.000084	0.000290	0.000090
Median	0.001074	0.000914	0.000986	0.000671	−0.000308
Minimum	−0.568589	−0.279761	−0.385352	−0.199958	−0.323397
Maximum	0.230864	0.190774	0.261359	0.152277	0.324354
Standard Deviation	0.026979	0.022623	0.026850	0.021815	0.033713
Skewness	−2.000696	−0.581640	−0.968795	−0.268866	0.404423
Kurtosis	52.754805	13.178268	25.347924	4.977315	9.896192
Observations	5,031	5,134	3,781	5,030	5,030

Price data is from Bloomberg using the process explained in Section 3.2. Equation 1(1) $R_t=ln\left(P_t/P_{t-1}\right)$(1) provides the formula for calculating the daily return.

The skewness and kurtosis for each energy commodity are also available in Table 1. WTI returns exhibit the most extreme skewness with a value of approximately −2. This value means the probability density curve concentrates more on the higher returns. However, several negative returns extend out that probability to extremely negative returns. RBOB Gasoline futures also have a moderately high skew with a value of nearly −1. The other synched contracts are approximately symmetrical, as the skewness of Brent, Heating Oil, and Natural Gas skewness are around the −0.5 and 0.5 benchmarks for symmetricalness. WTI returns also have the greatest kurtosis, indicating leptokurtic returns, meaning the daily return data is heavy-tailed, and returns can vary greatly depending on the day. RBOB Gasoline, Natural Gas, and Brent are also leptokurtic, but to less extent than the WTI futures. Finally, Heating Oil has an excess kurtosis of close to 0, indicating the return data is mesokurtic, so the daily returns have less extreme tails.

3.3. Modeling

This research aims to determine whether day-of-the-week effects (calendar anomaly) exist within returns for energy commodity futures. To address this question, we estimate a GARCH (1,1) model and various alternative GARCH (1,1) model specifications. The mean return equation we estimate for each energy commodity to investigate for evidence of DOW effects is as follows:

(2) $R_t={\beta }_{1}M+{\beta }_{2}T+{\beta }_{3}W+{\beta }_{4}R+{\beta }_{5}F+{\beta }_6{R}_{(}t-1)+{\epsilon }_t$(2)

where R_t is the daily logarithmic return of the respective energy commodity on day t; M is a binary variable that receives the value of 1 if the return happens on a Monday, zero otherwise; T is a dummy variable that receives the value of 1 if the return occurs on a Tuesday, zero otherwise; W is a binary variable that receives the value of 1 if the return is on Wednesdays, zero otherwise; R is a dummy variable that receives the value of 1 if the return happens on a Thursday, zero otherwise; F is a binary variable that receives the value of 1 if the return is on a Friday, zero otherwise; R_t-1 is the prior day’s logarithmic return; and ${\epsilon }_t$ is the error term. If the expected return is not significantly different from zero across the days of the week, then the estimates of β₁ through β₅ should not be significant. If this is not the case, then a day-of-the-week effect exists.

Bollerslev (1986) introduced a generalized version of the autoregressive conditional heteroskedasticity (ARCH) model proposed by Engle (1982). As a result, Bollerslev’s model became known as the GARCH (generalized autoregressive conditional heteroskedasticity) model. GARCH models have become the standard method in financial time series to estimate the return volatility requiring stationarity (Bollerslev, 1986). In this paper, we estimate GARCH, EGARCH, PGARCH, QGARCH, and TGARCH for each energy contract to test for a day-of-the-week effect in the daily returns. The various models of the base GARCH model allow for positive and negative shocks of financial markets to have differential impacts in the variance equation. Adverse shocks tend to have more severe implications for volatility than positive ones due to the overall positive nature of financial markets (Ding et al., 1993; Glosten, Jagannathan, & Runkle, 1993; Nelson, 1991). The variance equation for the GARCH model (Model 1) is as follows:

(3) ${\epsilon }_t|{\psi }_{\left(t-1\right)}N\left(0,h_t\right)$(3)

(4) $h_t=\omega +\sum _{i=1}^q{\alpha }_i{{\epsilon }^2}_{t-i}+\sum _{j=1}^p{\beta }_j{h}_{t-j}$(4)

Equation 3(3) ${\epsilon }_t|{\psi }_{\left(t-1\right)}N\left(0,h_t\right)$(3) further defines ${\epsilon }_t$, where ${\epsilon }_t$ denotes a real-valued discrete-time stochastic process and ${\psi }_t$ is an information set ($\sigma$-field) of all information through time t (Bollerslev, 1986). Equation 4(4) $h_t=\omega +\sum _{i=1}^q{\alpha }_i{{\epsilon }^2}_{t-i}+\sum _{j=1}^p{\beta }_j{h}_{t-j}$(4) is the variance equation where ${\alpha }_i$ is the ARCH coefficient, ${\beta }_j$ is the GARCH coefficient, and $\omega$ represents an offset term, meaning the lowest value the variance can achieve in any period. Furthermore, $h_t$ is the conditional variance of ${\epsilon }_t$ given ${\epsilon }_{t-i}$,$h_{t-j}$ is the lagged conditional variance, and ${\epsilon }_{t-i}^2$ the lagged residual error term. Finally, q is the number of lagged residual errors in the model, and p is the number of lagged variances in the model.

The second model we estimate is an EGARCH model (Model 2), also known as the exponential GARCH model. An EGARCH model helps estimate parameters with leptokurtic returns and other stylized factors such as volatility clustering. The variance equation for the EGARCH model (Model 2) is as follows:

(5) $ln\left(h_t\right)=\omega +\sum _{i=1}^q{\alpha }_{i}g\left(z_{t-i}\right)+\sum _{j=1}^p{\beta }_{j}ln\left(h_{t-j}\right)$(5)

(6) $g\left(z_t\right)=\theta z_t+y_i\left[\left|z_t\left|-E\right|z_t\right|\right]$(6)

(7) $z_t=\frac{{\epsilon }_t}{\sqrt{h_t}}$(7)

where $h_t$, the conditional variance, is an asymmetric function of lagged disturbances ${\epsilon }_{t-i}$, and there are no nonnegative constraints on the parameters, ${\alpha }_i$ and ${\beta }_j$. Properties of EGARCH include $g\left(z_t\right)$ being linear with a slope of $\theta$ +1 if $z_t$ is positive, and a slope of $\theta$ − 1 if $z_t$ is negative. Also, when $\theta$ = 0 large innovations increase the conditional variance if $\left|z_t\left|-E\right|z_t\right|$ >0, and decrease conditional variance if $\left|z_t\left|-E\right|z_t\right|$ <0 (Nelson & Cao, 1992). Effectively, $y_i$ is a leverage variable and when $y_1=y_2=\dots =0$, then the model is asymmetric. However, when $y_i$ <0 volatility due to positive news is lower than that of bad news. Also, a negative shock to the returns would increase the uncertainty of future returns and could be accounted for when ${\alpha }_i>0$ and $\theta z_t<0$ (Palm, 1996).

The third model we estimate is a PGARCH model (Model 3), also known as a power GARCH model. A PGARCH model provides an alternative way to model the variance equation by incorporating a long memory property. The variance equation for the PGARCH model (Model 3) is as follows:

(8) $h_t={\sigma }^2$(8)

(9) ${\sigma }^{\delta }=\omega +\sum _{i=1}^q{\alpha }_i\left(\left|{\epsilon }_{t-1}\right|+{\gamma }_i{\epsilon }_{t-i}{ }^{\delta }\right)+\sum _{j=1}^p{\beta }_j{\left({\sigma }_{t-j}\right)}^{\delta }$(9)

where $\omega$ >0, ${\alpha }_i$ >0, ${\beta }_j$ >0, $\left|y_i\right|$ <1, and $\delta$ >0. Along with leptokurtic returns, the PGARCH model also captures volatility clustering and return shocks as a shock at $t-1$ impacts variance at $t.$ Furthermore, the PGARCH captures the asymmetry in return volatility through ${\gamma }_i$ When ${\gamma }_i$ is less than 0, the asymmetric effect is evident in the model (Ding, 2011).

The fourth model we estimate is a QGARCH model (Model 4), also known as a quadratic GARCH model. A QGARCH model provides an alternative way to model asymmetric effects of negative and positive shocks (Sentana, 1995). The variance equation for the QGARCH model (Model 3) is as follows:

(10) $h_t=\omega +\sum _{i=1}^q{\alpha }_i{\left({\epsilon }_{t-i}-\gamma \right)}^2+\sum _{j=1}^p{\beta }_j{h}_{t-j}$(10)

where $h_t$, the conditional variance, is now a non-linear function of the lagged variance and lagged residual errors, p and q, respectfully. α, β, γ and ω are the parameters to be estimated, where α, β, and ω are as defined as in GARCH(p,q), but the term γ models for asymmetry and the absolute value of γ must be equal to or less than 1 (Engle & Ng, 1993). When γ is positive, a negative ${\epsilon }_{t-i}$ value has a more significant impact on $h_t$ (Franses & Van Dijk, 1996). Likewise, when γ is negative, a positive lagged residual error has a more consequential impact on $h_t$.

The final model we estimate is a TGARCH model (Model 5), also known as a threshold GARCH model. A TGARCH model provides an alternative way to model the leverage effects in variance equation. The variance equation for the TGARCH model (Model 5) is as follows:

(11) $h_t=\omega +\sum _{i=1}^q\left({\alpha }_i+{\mathbb{I}}_{{\epsilon }_{t-i}}\gamma \right){\epsilon }_{t-i}^2+\sum _{j=1}^p{\beta }_j{h}_{t-j}$(11)

(12) ${\mathbb{I}}_{{\epsilon }_{t-i}}=\left\{\begin{array}{c}0if{\epsilon }_{t-i}\ge 0\\ 1if{\epsilon }_{t-i}<0\end{array}\right.$(12)

where $h_t$, the conditional variance, is an asymmetric function of the lagged squared residual errors and lagged conditional variance. $I{I}_{{\epsilon }_{t-i}}$ is an indicator function activated when the lagged residual error is less than 0, meaning $\gamma$ will then influence the overall conditional variance. Essentially, this model allows good and bad news to take on different effects on variance, where good news has an impact of $\alpha$ and bad news has an impact of $\alpha +\gamma$, demonstrating the asymmetric shocks (Glosten et al., 1993).

4. Results and discussion

Table 2 presents the results from our empirical analysis of the WTI futures. Model 1 presents evidence supporting a positive Wednesday effect of approximately 13 basis points and a positive Friday effect of approximately 16 basis points. However, the Wednesday effect dissipates when we allow for asymmetric reactions for positive and negative shocks for the variance equation (Models 2 through 5). Nevertheless, the Friday effect is still significant and ranges from 10 to 13 basis points. These results lead one to reject the null hypothesis of the absence of a DOW effect in the WTI futures market. Across all models, the lagged return is negative and significant. This positive Friday effect is consistent with the findings of Qadan et al. (2019) and Chhabra and Gupta (2022). Focusing on the Akaike information criterion (AIC) and Schwarz information criterion (SBC) of the asymmetric models (Models 2 through 5), one can conclude that the model best suited for predicting returns in the WTI futures market would be the TGARCH model (Model 5).

Table 2. WTI daily return regressions

	(1)	(2)	(3)	(4)	(5)
	GARCH (1,1)	EGARCH (1,1)	PGARCH (1,1)	QGARCH (1,1)	TGARCH (1,1)
Return Equation
Monday	−0.000070	−0.000738	−0.000715	−0.000639	−0.000522
	(0.000627)	(0.003122)	(0.000618)	(0.000621)	(0.000630)
Tuesday	0.000238	−0.000348	−0.000285	−0.000086	0.000001
	(0.000572)	(0.000574)	(0.000572)	(0.000584)	(0.000593)
Wednesday	0.001342**	0.000358	0.000419	0.000622	0.000593
	(0.000522)	(0.000641)	(0.000588)	(0.000642)	(0.000646)
Thursday	0.000679	−0.000189	−0.000155	−0.000010	0.000270
	(0.000569)	(0.000611)	(0.000609)	(0.000596)	(0.000602)
Friday	0.001550**	0.001017*	0.001041*	0.001113*	0.001349**
	(0.000601)	(0.000564)	(0.000571)	(0.000570)	(0.000567)
Return(t-1)	−0.036300**	−0.030700**	−0.032600**	−0.032500**	−0.037900**
	(0.015400)	(0.019200)	(0.013600)	(0.015500)	(0.015200)
Variance Equation
ω	0.000011***	−0.125800***	0.000325***	0.000005**	0.000011***
	(0.000002)	(0.030600)	(0.000089)	(0.000005)	(0.000003)
α	0.101600***	0.143500***	0.080100***	0.090300***	0.035400***
	(0.005000)	(0.020200)	(0.012300)	(0.007695)	(0.010500)
β	0.882200***	0.983000***	0.917000***	0.884600***	0.890000***
	(0.006577)	(0.004073)	(0.012900)	(0.000000)	(0.000000)
θ	.	−0.590600***	0.605000***	0.010500***	0.109000***
		(0.084100)	(0.079200)	(0.002102)	(0.017900)
δ	.	.	0.545000***	.	.
			(0.000000)
R^2	0.0034	0.0033	0.0034	0.0034	0.0037
Log Likelihood	12253.017	12308.750	12310.976	12293.152	12290.541
AIC	−24488.035	−24597.501	−24599.952	−24566.304	−24561.082
SBC	−24429.326	−24532.269	−24528.197	−24501.072	−24495.850

The symbols *, **, and *** denote statistical significance at the 0.10, 0.05, and 0.01 levels, respectively.

The mean equation (Equation #2) allows us to estimate the return on a specific day given the day of the week and the previous day’s return. For example, assume the return on Thursday was negative 1% (−0.01%). Model 3 (PGARCH model) would estimate a positive return for Friday of 0.001367. This estimate reflects the Friday DOW effect. A practical trading implication based upon the estimates of Models 1 through 5 would suggest that the best time to sell a WTI futures contract is as close to the close of the market on Friday, ignoring all transaction costs. A potentially more active trading strategy could be buying WTI futures after a significant price decline on Thursday and closing the position on Friday.

The result of our analysis of the DOW effect in Brent futures is in Table 3. The base model (Model 1 - GARCH model) has initial evidence of positive Wednesday (approximately 14 basis points) and Friday (approximately 11 basis points) DOW effects, similar to the results from WTI futures. However, the Friday DOW effect is absent in Models 2 through 5, which allows for asymmetric responses to positive and negative news in the volatility equation. There is marginal evidence of the positive Wednesday DOW effect in Models 4 and 5. The lagged return across all Models is significantly negative and is consistent with prior literature that lagged returns can help predict future returns.

Table 3. Brent daily return regressions

	(1)	(2)	(3)	(4)	(5)
	GARCH (1,1)	EGARCH (1,1)	PGARCH (1,1)	QGARCH (1,1)	TGARCH (1,1)
Return Equation
Monday	−0.000294	−0.000641	−0.000613	−0.000689	−0.000578
	(0.000546)	(0.000520)	(0.000523)	(0.000538)	(0.000536)
Tuesday	0.000118	−0.000538	−0.000512	−0.000210	−0.000137
	(0.000534)	(0.000519)	(0.000527)	(0.000533)	(0.000529)
Wednesday	0.001424***	0.000757	0.000786	0.000941*	0.001013**
	(0.000485)	(0.000484)	(0.000489)	(0.000491)	(0.000479)
Thursday	0.000773	0.000261	0.000275	0.000362	0.000406
	(0.000505)	(0.000501)	(0.000511)	(0.000516)	(0.000509)
Friday	0.001105*	0.000641	0.000570	0.000728	0.000833
	(0.000578)	(0.000559)	(0.00056)	(0.000572)	(0.000575)
Return(t-1)	−0.046000***	−0.045800***	−0.045700***	−0.042200***	−0.048500***
	(0.015300)	(0.014000)	(0.013900)	(0.015200)	(0.014800)
Variance Equation
ω	0.000006***	−0.1126***	0.000352**	0.000002	0.000006***
	(0.000001)	(0.013200)	(0.000148)	(0.000001)	(0.000001)
α	0.080900***	0.126800***	0.069300***	0.073200***	0.029400***
	(0.003615)	(0.007263)	(0.004139)	(0.004129)	(0.005427)
β	0.910000***	0.985100***	0.931500***	0.911300***	0.917800***
	(0.004393)	(0.001667)	(0.004057)	(0.004735)	(0.004394)
θ	.	−0.568400***	0.602100***	0.008991***	0.081300***
		(0.056100)	(0.061900)	(0.001070)	(0.007056)
δ	.	.	0.491600***	.	.
			(0.048600)
R^2	0.0048	0.0049	0.0049	0.0050	0.0050
Log Likelihood	12973.263	13027.583	13026.701	13007.741	13007.624
AIC	−25928.526	−26035.165	−26031.402	25995.481	−25995.248
SBC	−25869.635	−25969.731	−25959.424	25930.047	−25929.813

The symbols *, **, and *** denote statistical significance at the 0.10, 0.05, and 0.01 levels, respectively.

Despite modeling an asymmetric response function in the variance equation, the EGARCH and PGARCH models fail to detect a positive significant Wednesday effect. However, Models 4 (QGARCH) and 5 (TGARCH) still support the supposition of a positive Wednesday effect. The evidence in Table 3 reinforces the need for appropriate econometric modeling by allowing asymmetric reactions in the variance equations for financial time series. For example, one would have initially concluded a Friday effect in the Brent futures market, but the estimates from the rest of the models do not support that assertion. Additionally, depending on the model selection, one may not detect a DOW effect. Table 4 provides marginal evidence for a DOW effect (i.e., Wednesday) in the Brent futures market, but not unanimously across all models.

Table 4. RBOB gasoline daily return regressions

	(1)	(2)	(3)	(4)	(5)
	GARCH (1,1)	EGARCH (1,1)	PGARCH (1,1)	QGARCH (1,1)	TGARCH (1,1)
Return Equation
Monday	−0.002344***	−0.002709***	−0.002694***	−0.002644***	−0.002571***
	(0.000717)	(0.000697)	(0.000725)	(0.000737)	(0.000749)
Tuesday	0.000930	0.000495	0.000527	0.000755	0.000610
	(0.000750)	(0.000716)	(0.000738)	(0.000753)	(0.000751)
Wednesday	0.000865	−0.000180	−0.000012	0.000600	0.000337
	(0.000605)	(0.000582)	(0.000597)	(0.000607)	(0.000607)
Thursday	0.000939	0.000468	0.000497	0.000752	0.000772
	(0.000739)	(0.000706)	(0.000734)	(0.000754)	(0.000747)
Friday	0.000756	0.000489	0.000567	0.000600	0.000895
	(0.000738)	(0.000732)	(0.000760)	(0.000761)	(0.000771)
Return(t-1)	−0.010400	−0.013200	−0.011200	−0.010800	−0.009842
	(0.017100)	(0.016000)	(0.016600)	(0.017100)	(0.016400)
Variance Equation
ω	0.000013***	−0.089200***	0.000115**	0.000010***	0.000007***
	(0.000001)	(0.010700)	(0.000045)	(0.000001)	(0.000001)
α	0.087200***	0.126700***	0.062600***	0.075700***	0.001007
	(0.005139)	(0.007333)	(0.004903)	(0.004751)	(0.003044)
β	0.894000***	0.987300***	0.934000***	0.904500***	0.944700***
	(0.005805)	(0.001421)	(0.00413)	(0.005572)	(0.002996)
θ	.	−0.455900***	0.476800***	0.006015***	0.081700***
		(0.050900)	(0.058300)	(0.001172)	(0.004994)
δ	.	.	0.652700***	.	.
			−0.045800
R^2	0.0053	0.0049	0.0050	0.0054	0.0053
Log Likelihood	9020.114	9059.511	9061.117	9026.137	9053.437
AIC	−18022.228	−18099.023	−18100.235	−18032.274	−18086.874
SBC	−17966.091	−18036.648	−18031.622	−17969.899	−18024.499

The symbols *, **, and *** denote statistical significance at the 0.10, 0.05, and 0.01 levels, respectively.

The next energy market we test for the DOW effect is the RBOB Gasoline futures market. Table 4 provides the results from the empirical tests. The base model (Model 1 - GARCH model) presents evidence of a negative Monday DOW effect in the RBOB Gasoline market of a negative 23 basis points. This negative Monday effect persists across all models, and the effect size is approximately negative 27 basis points once the volatility equation allows for an asymmetric response. A unique finding for the RBOB Gasoline analysis is that while negative, none of the lagged returns are significant in predicting returns.

A negative Monday effect is prevalent in the RBOB Gasoline market. This DOW finding could be helpful when developing a potential investment strategy involving RBOB Gasoline futures. All models support a negative Monday effect at the 0.01 level. A practical approach, ignoring transaction costs, is to sell RBOB futures on a Friday and repurchase them on the Monday close. From a corporate risk management standpoint, a company needing to hedge a long gasoline position should consider selling RBOB contracts on Fridays. No matter the strategy, any entity involved in the gasoline market should be cognizant of a negative Monday effect in RBOB Gasoline futures.

The Heating Oil futures market is the second petroleum product we analyze for the DOW effect. Model 1 (GARCH model) results suggest several DOW effects in the Heating Oil market. There is the initial evidence of a negative Monday effect (approximately 14 basis points), a positive Tuesday effect (approximately 9 basis points), and a Wednesday effect (approximately 20 basis points). However, like the WTI and Brent markets, one of the DOW effects dissipates when the modeling choice allows for asymmetric responses to positive and negative shocks in the variance equation. The marginal positive Tuesday effect disappears in Models 2 through 5. Similar to our RBOB Gasoline analysis results, the lagged return is negative in all models but only significant in predicting returns in the PGARCH (Model 3) and TGARCH (Model 5) models.

Nevertheless, the negative Monday effect is still significant across Models 2 through 5, with an effect size ranging from 16 to 18 basis points. The positive Wednesday effect persists in the additional models and ranges from 15 to 17 basis points. These results lead one to reject the null hypothesis of the absence of a DOW effect in the Heating Oil futures market. The rejection of the null hypothesis suggests a negative Monday effect (consistent with Cross (1973) and French (1980)) and a positive Wednesday DOW effect. These two DOW effects are consistent with Qadan et al. (2019). However, we do not find evidence supporting the positive Thursday effect that Qadan et al. (2019) document. The evidence in Table 5 reinforces the need to allow for asymmetric reactions in the variance equations for financial time series. One could erroneously conclude that a Tuesday effect exists for Heating Oil.

Table 5. Heating oil daily return regressions

	(1)	(2)	(3)	(4)	(5)
	GARCH (1,1)	EGARCH (1,1)	PGARCH (1,1)	QGARCH (1,1)	TGARCH (1,1)
Return Equation
Monday	−0.001369**	−0.001718***	−0.001694***	−0.001812***	−0.001617***
	(0.000563)	(0.00054)	(0.00054)	(0.000548)	(0.000551)
Tuesday	0.000942*	0.000504	0.000558	0.000646	0.00075
	(0.000528)	(0.000518)	(0.000524)	(0.000537)	(0.000523)
Wednesday	0.002023***	0.001542***	0.001573***	0.001546***	0.001703***
	(0.000497)	(0.000499)	(0.000497)	(0.000504)	(0.000502)
Thursday	0.000848	0.000349	0.000338	0.000501	0.000562
	(0.000517)	(0.000523)	(0.000523)	(0.000524)	(0.00052)
Friday	−0.000054	−0.000243	−0.000224	−0.000336	−0.000186
	(0.00055)	(0.000548)	(0.000545)	(0.000558)	(0.000558)
Return(t-1)	−0.024700	−0.022400	−0.024000*	−0.021700	−0.024200*
	(0.015100)	(0.014100)	(0.013900)	(0.014800)	(0.014700)
Variance Equation
ω	0.000004***	−0.087100***	0.000267**	0.000000	0.000004***
	(0.000001)	(0.014200)	(0.000133)	(0.000001)	(0.000001)
α	0.067000***	0.126800***	0.067700***	0.064200***	0.034900***
	(0.004293)	(0.008604)	(0.004573)	(0.004601)	(0.005478)
β	0.926700***	0.988500***	0.937500***	0.928300***	0.930100***
	(0.004714)	(0.001792)	(0.004455)	(0.004917)	(0.004742)
θ	.	−0.431500***	0.449300***	0.00793500***	0.057800***
		(0.049800)	(0.053900)	(0.001057)	(0.006935)
δ	.	.	0.478500***	.	.
			(0.057000)
R^2	0.0051	0.0050	0.0050	0.0051	0.0051
Log Likelihood	12688.909	12731.205	12729.731	12714.104	12708.966
AIC	−25359.817	−25442.410	−25437.461	−25408.208	−25397.932
SBC	−25301.110	−25377.180	−25365.709	−25342.978	−25332.702

The symbols *, **, and *** denote statistical significance at the 0.10, 0.05, and 0.01 levels, respectively.

The mean equation allows us to estimate again the return on a specific day given the day of the week and the previous day’s return in the Heating Oil futures market. For example, assume the return on Friday was negative 1% (−0.01%). Then, Model 3 (PGARCH model) would predict a positive return for Monday of 0.022306. This effect lowers the predicted returns for Mondays by approximately 17 basis points. For another example, assume the return on Tuesday was negative 1% (−0.01%). Then, Model 5 (TGARCH model) would predict a positive return for Wednesday of 0.025573. An investment strategy without transaction costs considering the DOW effects (Monday and Wednesday) in the Heating Oil market could consist of buying the Monday close and closing the position at the Wednesday close. Even if not engaged in active trading, being aware of the negative Monday effect and positive Wednesday effect can help one understand when to enter long or short positions in the Heating Oil market.

We finish our investigation of the DOW effect in energy commodities by analyzing returns in the Natural Gas futures market. Table 6 presents the results from this analysis. There is the initial evidence of two DOW effects in the Natural Gas markets in Model 1 (GARCH model), a positive Monday effect (approximately 13 basis points) and a negative Thursday effect (approximately 17 basis points. Model 1 (GARCH model) results are consistent with the WTI and Brent markets findings. The lagged return is negative and significant across all models.

Table 6. Natural gas daily return regressions

	(1)	(2)	(3)	(4)	(5)
	GARCH (1,1)	EGARCH (1,1)	PGARCH (1,1)	QGARCH (1,1)	TGARCH (1,1)
Return Equation
Monday	0.001265*	0.001958***	0.001861**	0.001561**	0.001706**
	(0.000741)	(0.000735)	(0.000741)	(0.000747)	(0.00075)
Tuesday	0.001295	0.001857**	0.001695*	0.001508*	0.001620*
	(0.000879)	(0.000872)	(0.000885)	(0.000894)	(0.000892)
Wednesday	0.000862	0.001170	0.001092	0.000988	0.000946
	(0.000936)	(0.000904)	(0.000928)	(0.000953)	(0.000949)
Thursday	−0.001671**	−0.001339*	−0.001333*	−0.001432*	−0.001323*
	(0.000712)	(0.000726)	(0.000732)	(0.000736)	(0.000736)
Friday	−0.000745	−0.000720	−0.000680	−0.000607	−0.000673
	(0.000875)	(0.000923)	(0.000938)	(0.000948)	(0.000929)
Return(t-1)	−0.037400**	−0.041300***	−0.040700***	−0.037600**	−0.037700**
	(0.014600)	(0.014200)	(0.014600)	(0.014700)	(0.014800)
Variance Equation
ω	0.000014***	−0.0918***	0.000117***	0.000013***	0.000014***
	(0.000002)	(0.0176)	(0.000043)	(0.000003)	(0.000002)
α	0.095100***	0.189200***	0.097900***	0.093000***	0.107600***
	(0.005038)	(0.008502)	(0.006108)	(0.005309)	(0.005567)
β	0.898500***	0.985700***	0.913300***	0.900600***	0.902600***
	(0.005534)	(0.002578)	(0.005296)	(0.005814)	(0.005852)
θ	.	0.141900***	−0.124700***	−0.002860***	−0.034500***
		(0.023900)	(0.022700)	(0.000957)	(0.006127)
δ	.	.	0.663500***	.	.
			(0.043500)
R^2	0.0052	0.0050	0.0050	0.0051	0.0051
Log Likelihood	10444.497	12731.205	12729.731	12714.104	12708.966
AIC	−20870.995	−25442.410	−25437.461	−25408.208	−25397.932
SBC	−20812.288	−25377.180	−25365.709	−25342.978	−25332.702

The symbols *, **, and *** denote statistical significance at the 0.10, 0.05, and 0.01 levels, respectively.

A unique finding for Natural Gas futures relative to the results for all other energy commodities emerges once the variance equation allows for asymmetric responses to positive and negative shocks. Models 2 through 5 reveal a positive Tuesday effect ranging from 15 to 19 basis points when the GARCH model (Model 1) failed to detect this DOW Effect. This lack of detecting the Tuesday effect provides further evidence in support of allowing for asymmetric responses when modeling energy commodity returns, as failing to do so may lead to incorrect model interpretations. In addition, the positive Monday effect and negative Thursday effect persist across all models. These results imply that investors should be aware of trading on Mondays, Tuesdays, and Thursdays when dealing with Natural Gas futures. A weekly strategy incorporating these DOW effects involves taking a long position at the Thursday close and then closing that position at the Tuesday close. Awareness of the positive Monday and Tuesday effects and negative Thursday effect can help multiple market players understand better times to enter long or short positions in the Natural Gas market.

All research has limitations, and this study is no exception. While the findings show that some days of the week exhibit abnormal returns in petroleum and petroleum product futures, several limitations must be acknowledged. First, we only analyzed the combination of first and second-month contracts, and longer-term contracts may have differing abnormalities. Secondly, we only examined price and volume data, so factors that may influence returns, such as global politics, supply and demand changes, and macroeconomic events, should be considered in future studies. Finally, without trade and quote data, this study could not consider transaction costs, which may cut into the profitability of any strategy that uses abnormal returns to generate a profit. That acknowledged it is still essential for investors to be aware of the DOW effects in energy futures that this study found.

5. Conclusion

This research tests for the day-of-the-week effect in WTI, Brent, RBOB Gasoline, Heating Oil, and Natural Gas futures using a synching method that more accurately represents the fair daily price change of commodities within the energy futures market. The models estimated to test for DOW effects within each time series of returns are GARCH (1,1), EGARCH (1,1), PGARCH (1,1), QGARCH (1,1), and TGARCH (1,1), respectively. We find that DOW effects are present in energy futures.

All estimated models find a significantly positive Friday effect for WTI contracts. There is also a positive Wednesday effect for WTI when using a GARCH (1,1), but it becomes insignificant in the other models. This change from significant to insignificant provides evidence that failing to allow for an asymmetric effect on the variance could lead to erroneous conclusions. Brent exhibits a significant positive Wednesday effect. The results from the RBOB Gasoline estimates provide a consistent and significant negative Monday effect. The Heating Oil futures returns tend to exhibit a significant negative Monday effect and a significant positive Wednesday effect. Finally, Natural Gas futures exhibit a positive effect on Monday and Tuesday but a negative DOW effect on Thursday.

The DOW evidence across energy contracts has important Implications for numerous financial market participants. The evidence suggests that a DOW trading strategy could be more successful than a simple buy-and-hold approach; however, when transaction costs are considered, the paper profits exploited through DOW effects may be reduced or eliminated. This research also provides evidence that may explain the Monday DOW anomaly in the energy equity sector. The higher oil prices on Friday may lead to higher equity prices for energy companies the following Monday. In summary, this paper provides evidence that day-of-the-week effects exist in energy futures, accounting for the change in liquidity nearing expiration. These seasonality effects do not appear to be homogenous across petroleum commodities.

Declaration of conflicting interests

The authors declare no potential conflicts of interest concerning the research, authorship, and/or publication of this article.

Disclosure statement

No potential conflict of interest was reported by the authors.

Data availability statement

The data supporting this study’s findings are available on request from the corresponding author, SAH. The raw data is collected via a Bloomberg terminal.