Impact of banking sector competition on emerging market banks’ safety and soundness – A study on Indian Banks

Abstract

The literature is unsettled on the simultaneous existence of Competition-Stability and Competition-Fragility phenomena in the banking system. Our study has extended the debate where we have incorporated accounting-based information along with 2-SLS system equation modeling to further explore linkages between competition, systemic risk, and stability prevailing in the Indian banking system. The study revealed that for Indian banks competition and systemic risk are inversely related. Systemic risk build-up occurs during the business growth cycle, and it spillovers onto the banking system during the economic down-cycle. The article finds that while a healthy competition would support the overall stability of banks, a fierce competition exerts competitive pressure on the banking system, and hence it negatively contributes to the bank’s stability. It has supported the financial fragility hypothesis and envisages that increased capital restricts competition, and aggressive loan creation increases fragility.

Keywords:

• Bank’s competition
• stability
• systemic risk
• CoVar
• Lerner Index

JEL Classification:

• G01
• G21

1. Introduction

The Basel Committee on Banking Supervision (BCBS) has mandated member countries to disclose various accounting-based ratios for the effective governance of banks. These ratios pertain to profitability, risk management, capital structure, asset classification, income recognition, and market valuations. These accounting ratios provide information on the competitive power, risk appetite, and banks’ stability. Market share in loans and deposits, along with the competitive nature of the pricing of various products, indirectly represents bank’s competitive power in the market. Similarly, regulatory capital and its adequacy ratios, along with various profitability ratios, indicates bank’s systemic stability. It is evident that banks with higher liquidity reduce their riskiness (S. Roy et al., 2019). At the same time, loan growth, balance sheet leverage, risk leverage, and market valuation signal the formation of systemic risk within the balance sheet. However, banks thrive in a system-based interconnected environment. Given the interconnectedness of its assets and liabilities, banks trade surplus liquidity in the interbank market. Banks compete amongst themselves by devising innovative methods to finance riskier loans based on their adequacy of risk capital. Stiff competition and possibly lowering the loan screening process leads to rising non-performing assets (NPAs) impacting the solvency of individual banks. Systemic failures in banks within an interconnected system generate systemic risk, which percolates across the banking system. While in most of the non-financial sectors, competition brings in positive changes with lower prices and an increase in product quality led by innovation, in the case of banks, competition might lead to its instability. The concept of systemic risk draws attention to assets that are highly interconnected and is studied even for emerging asset classes like cryptocurrencies (Akhtaruzzaman et al., 2022).

Competition, systemic risk, and stability of a single bank though can be analysed through accounting disclosure-based ratios, its spillover to the banking system needs to be ascertained through econometric modeling. Accounting disclosure-based ratios, along with macroeconomic parameters, are the influencing factors to understand the interrelationship among competition, systemic risk, and stability. The financial system framework has changed post the global crisis. Post-crisis, financial stability has been recognised as an integral element of the macroeconomic policy framework globally. It is evident that institute-specific risk spillover resulted in the crisis. Interconnectedness among banks and financial institutions leads to the transmission of idiosyncratic risks, resulting in systemic risk, which in turn triggers an economic crisis (Betz et al., 2016). Competition effect on banks’ safety, stability, and overall financial stability has deeply intrigued academicians and policymakers alike. The subject has gained further momentum post-2007 financial crisis, with academicians and policymakers pondering over the impact of competition and marketing of riskier products with higher margins that possibly led to the widespread crisis (Acharya & Richardson, 2009; Beck et al., 2013; Carletti, 2008).

The Indian banking system is inherently competitive (Rakshit & Bardhan, 2019) in nature. The study on bank competition in India has been carried out using network techniques (Rahman & Misra, 2021). Followed by the global economic downturn, Indian banks witnessed a sharp demand recovery by the mid of 2011. However, between the years 2013–16, banks witnessed a surge in their non-performing assets owing to regular corporate defaults. This has led to the gradual accumulation of systemic risk almost to the point that even a small shock might have amplified effects on the entire banking system.

In the current study, we investigate Indian Banks’ relationship between competition, stability, and their systemic risk-taking ability by deploying their accounting-based ratios and balance sheet disclosures. We measure banking competition through the inverse of the Lerner Index, where accounting disclosures on various cost-related parameters play a decisive role in measuring bank’s market power. The accounting disclosures on book value along with market valuation and macroeconomic variables are used to estimate systemic risk using Conditional VaR (CoVaR). We use quantile regressions for computing the CoVaR values for individual banks. For measuring the bank’s stability, we apply the Z-score, where accounting disclosures on RoA and asset adjusted equity value are used to estimate the distance from insolvency (Demirgüç-Kunt & Huizinga, 2010; Houston et al., 2010). We further establish the relationship among banks’ competition, systemic risk, and stability through system equation modelling. In this article, we look to interpret the interrelationship of the aforesaid variables for a deeper understanding of the banking system at large, including its spillover effect on the overall financial stability.

This article supplements existing literature by endorsing the simultaneous existence of Competition-Stability and Competition-Fragility theories. The findings of this article confirm the validity of the financial fragility hypothesis. It empirically corroborates that stiff competition increases fragility (Diamond & Rajan, 2000, 2001). The empirical findings of this article would help the regulators to frame macro-prudential policies for achieving stability while promoting competition amongst banks. Our findings advocate that central banks must design a policy framework for identifying banks that are exerting competitive pressure and restricting the overall effectiveness of banks in general. The article advises central banks to encourage banks to build healthy credit portfolio with gradual reduction in lending rate. Central banks should put in place cautious entry norms for both national and foreign banks to maintain financial stability.

2. Literature review & objectives of the study

As per the traditional “Competition-Fragility” view, any unwarranted competition pushes the banks to the brink of failure as they bear the excessive risk of maintaining their profitability (Keeley, 1990; Marcus, 1984). Besides, as per the “Competition-Stability” theory, in a lesser competitive banking market, banks considered “too big to fail” enjoy government safety-net policy and take excessive risk in their lending patterns (Mishkin, 1999). Additionally, banks having greater market power have a tendency to lend at rising rates enforcing default at the borrowers’ end. However, it is noted that bank competition has implications for banking stability (Tan et al., 2020). Competition-Fragility opinion has been supported for the non-life insurance sector when examined in Turkey (Kasman et al., 2020).

While the Fragility theory proposes that lower competition improves stability, the “Competition-Stability” theory argues that lesser competition decreases stability. Keeley (1990) first mooted the former theory, stating that excess competition lowers margins and pushes banks towards a situation preferring higher risk. Higher risks combined with lower profits thereby cause instability of the system. On the contrary, Boyd and De Nicolo (2005) pointed out that high margins in monopolistic markets create a new problem, which they call the “risk-shifting problem.” The high margin prevails upon borrowers to compensate by getting loans for riskier projects, which results in a higher risk for banks.

As per Boyd and De Nicolo (2005), competition and stability display a positive association, prompting banks to continue lending at lower rates. There could also be a strong likelihood of a relationship between bank competition and stability that is non-linear in nature. (Martinez-Miera & Repullo, 2010). Similarly, Berger et al. (2009) documented that simultaneous stability or fragility can be induced in the sector by the co-existence of competition as well as concentration. Weak corporate governance and poor risk management practices have emerged as the prime factors responsible for the Global Financial Crisis (Huy, 2015). Therefore, it is apparent that corporate governance and risk management policy could enhance systemic risk and competition in the banking system. Abnormal fluctuations in bank stock prices lead to risk-spillover, which in turn influences systemic risk and competition (Huy, Dat, et al., 2020; Huy, Loan, et al., 2020). It is essential to have policies that consider the impact of macro factors on market risk to build an effective risk management system for sustainable growth (Huy et al., 2021).

Financial innovation is considered as one of the important factors contributing to systemic crisis (Dimsdale, 2009). During the subprime crisis, it was evident that the default of subprime mortgage markets essentially led to the crisis (Kero, 2013). On the other hand, diversification, led by competition, reduces systemic risk; thereby, in a competitive market, banks diversify their portfolios (Anginer et al., 2014), which makes them more stable, reducing systemic risk thereof. Countries, which primarily have government-owned banks, tend to have restrictive policies for competition and are prone to systemic shocks (Schaeck et al., 2009; Silva-Buston, 2019). Martinez-Miera and Repullo (2010) opined that a competitive environment prevails upon banks to sanction loans at cheaper interest rates, enabling borrowers thereby to repay loans easily; hence, banks would remain safe from default.

While prior literature suggests the existence of a negative relationship between competition and stability owing to an inverted U-shaped curve, suggesting consistency with the stability theory (Allen & Gale, 2000; Boyd & De Nicolo, 2005), recent studies by Diamond and Rajan (2000, 2001) predict that increased capital restricts competition and aggressive loan creation increases the fragility.

Interconnectedness is the fundamental feature of banks. Negative externalities in the operational environment due to market failures lead to systemic risk. Interbank lending and borrowing lead to interconnectedness in the banking industry; however, the problem is magnified when banks are exposed to similar kinds of risks in the economy resulting in distress spillover. This subject gains further relevance in economies like India where branch banking is significantly prevalent which leads to intense competition in order to expand the customer base and maximize the operational profits.

The study by Cai et al. (2018) highlights that diversification drives interconnectedness, which is highly correlated with systemic risk measures. Aggressive competition forces banks to reduce their lending rates and rating quality while sanctioning loans. Similarly, banks in many emerging markets, including India, have significant exposure to investment banking activities, which may create systemic risk.

Even though there is no denial that the competition has resulted in innovation and efficiency (Schaeck & Čihák, 2010), still literature is inconsistent to conclude that competition has indeed induced fragility. The financial crisis witnessed in 2007 has compelled us to re-examine the risk assessment practices along with the banking system’s fragility (Brunnermeier, 2009; Milne, 2009). Literature on “Competition-Stability” and “Competition-Fragility” theories provide conflicting results from different countries and data sets. Although an extensive literature has emerged (Allen & Gale, 2000; Beck, 2008; Brunnermeier, 2009; Carletti, 2008; Milne, 2009; Schaeck & Čihák, 2010), discussing this critical issue, the problem needs to have adequate coverage considering Indian banks.

The study includes the following objectives focusing on competition, systemic risk, and stability for the Indian banking system:

1. It would measure bank competition, systemic risk, and stability using accounting disclosure-based indices along with the Lerner Index, CoVaR, and the Z-score methodology.

2. It would bring out the relationship between bank competition and its impact on systemic risk and stability.

3. It would examine the interdependency among bank competition, systemic risk, and stability through instrumental variables regression.

The study period spread over more than a decade covers phases of the financial turmoil of 2008–10, high credit off-take during 2011–13, and domestic banking crisis of 2014–16.

3. Empirical methodology

3.1. Accounting-based indices of systemic risk, stability and competition

The accounting disclosures, as depicted in Table 1, are used to construct indices for systemic risk, stability, and competition through Principal Component Analysis. The indices are formulated using the equations (1)(1) $SY{S}_{i,t}=w_{1}BS{L}_{i,t}+w_{2}R{L}_{i,t}+w_{3}A{Q}_{i,t}+w_{4}I{D}_{i,t}+w_{5}A{D}_{i,t}$(1) , (2(2) $STA{B}_{i,t}=w_{1}NPA{P}_{i,t}+w_{2}SIZ{E}_{i,t}+w_{3}CRA{R}_{i,t}+w_{4}PRO{F}_{i,t}$(2) ), (3(3) $COM{P}_{i,t}=w_{1}YO{F}_{i,t}+w_{2}RE{V}_{i,t}+w_{3}SIZ{E}_{i,t}$(3) ) for systemic risk, stability, and competition, respectively, are normalized with mean zero and standard deviation one. The normalized index value above 0 is considered extremely systemic, most stable, and highly competitive. $w_i$ are weights, estimated through, principal component analysis.

Table 1. Accounting Disclosures for Indices

Index	Variables	Abbreviation	Influence	Measure	Explanations
Systemic Risk	Balance Sheet Leverage	BSL	Positive	$\frac{TatalAsset}{TotalEquity}$	The churning of equity in the creation of assets enhances systemic risk in case of significant defaults.
	Risk Leverage	RL	Positive	$\frac{NetWorth}{Risk-WieghtedAssets}$	Leveraging of Networth in the creation of Risk-Weighted Assets would add more risk to the balance sheet.
	Asset Quality	AQ	Positive	GNPA	A higher GNPA ratio decreases banks withstanding capacity to systemic events, thereby increasing systemic risk.
	Income Diversification	ID	Positive	$\frac{InterestIncome}{Non-InterestIncome}$	Systemic risk increases with rise in bank’s interest income over fee-based income.
	Asset Diversification	AD	Positive	$\frac{CorporateLoan}{RetailLoan}$	As corporate loans are much higher compared to retail loans, a default by the corporate can initiate a systemic crisis.
Stability	NPA Provision	NPAP	Positive		With the increase in provisions for NPAs, banks’ asset base becomes weak to resist economic shocks.
	Bank Size	SIZE	Positive	Ln (Total Assets)	Big-sized banks are more stable owing to their large asset base.
	Capital Adequacy	CRAR	Positive	CRAR	Capital adequate banks can withstand macroeconomic downturn, and hence more stable.
	Profitability	PROF	Positive	$\frac{Profit}{TotalAssets}$	Profitable banks are stable due to their higher profit margin.
Competition	Yield on Funds	YOF	Positive	$\frac{Profit}{AvailableFunds}$	A competitive bank would be able to charge more prices for its products.
	Total Revenue	TR	Positive		Higher revenue highlights that banks tend to have a larger market share, and hence more competitive.
	Bank Size	SIZE	Positive	Ln (Total Assets)	Large banks are more competitive due to their large asset base and presence in the market.

(1) $SY{S}_{i,t}=w_{1}BS{L}_{i,t}+w_{2}R{L}_{i,t}+w_{3}A{Q}_{i,t}+w_{4}I{D}_{i,t}+w_{5}A{D}_{i,t}$(1)

(2) $STA{B}_{i,t}=w_{1}NPA{P}_{i,t}+w_{2}SIZ{E}_{i,t}+w_{3}CRA{R}_{i,t}+w_{4}PRO{F}_{i,t}$(2)

(3) $COM{P}_{i,t}=w_{1}YO{F}_{i,t}+w_{2}RE{V}_{i,t}+w_{3}SIZ{E}_{i,t}$(3)

3.2. Assessment of competition through Lerner index

Absence or significant reduction of market power indicates a build-up of a competitive environment in the banking system. The Lerner Index, which factors individual bank’s pricing power, measures market power. The inverse of the Lerner Index is considered as the proxy for the competition (Beck et al., 2013; Demirguc-Kunt & Martínez Pería, 2010). There are several advantages to the Lerner index in measuring market power when compared to other potential alternative measures. First, Beck et al. (2013) Lerner Index measures individual bank’s pricing power. It also has the theoretical capability to capture the bank’s franchise value. It utilizes both assets and funding information, and it can predict the price on both the asset and liabilities side. Third, as the Lerner index does not recognize the long-run equilibrium, it is favoured over the H-statistic (Schaeck & Čihák, 2010). Fourth, since some banks operate across geographies, the Lerner index specializes in measuring banking competition, as there is no dependency in interpreting definitions across markets.

In equation (4)$w_t=\frac{1-\alpha }{\alpha }{r}_{k,t}{\left(\frac{Y_t}{A_t{L}_t}\right)}^{1/\alpha }$, we estimate the Lerner Index by deducting the marginal cost ($M{C}_{i,t}$) from the Average Price of Assets ($P_{i,t}$), as shown below:

(4a) $LernerInde{x}_{i,t}=\hspace{0.17em}\frac{P_{i,t}-\hspace{0.17em}M{C}_{i,t}}{P_{i,t}}$(4a)

(4b) $Competitio{n}_{i,t}=\hspace{0.17em}\frac{1}{Lerner\hspace{0.17em}Inde{x}_{i,t}}$(4b)

Where;

$M{C}_{i,t}$ = Marginal Cost for bank i at a given time t.

$P_{i,t}$ = Average price of Bank Assets for bank i at a given time t.

Imagine a producer wants to minimise costs from labour $L_t$ and capital $K_t$, which come at factor prices $w_{t\hspace{0.17em}}$and $r_t$ respectively, subject to the production technology of the Cobb-Douglas function $Y_t=A_t{L_t}^{1-\alpha }{K_t}^{\alpha }$, $A_t$ is total factor productivity and $\alpha$ the capital share of production.

The minimal cost is given as;

C ($w_{t\hspace{0.17em}}$, $r_t$, $Y_t$,$\hspace{0.17em}{A}_t)=A_t{L_t}^{1-\alpha }{K_t}^{\alpha }$

$C(w_{t,}\hspace{0.17em}{r}_{t,}{Y}_{t,}\hspace{0.17em}{A}_t$) =$\underset{L_{t,}{K}_t}{\mathrm{m}\mathrm{i}\mathrm{n}}\hspace{0.17em}{w}_t{L}_t+r_t{K}_t$, Subject to :$\hspace{0.17em}{Y}_t=A_t{L}_t^{1-\alpha }{K_t}^{\alpha }$

Solving the constraint for capital, we obtain

$K_t={\left(\frac{Y_t}{A_t{L}_t^{1-\alpha }}\right)}^{1/\alpha }$

So that

$C(w\hspace{0.17em}{r}_{t,}{Y}_{t,}\hspace{0.17em}{A}_t$) = $\underset{L_t}{min}{w}_t\hspace{0.17em}{L}_t+$ $r_{k,t}$ ${\left(\frac{Y_t}{A_t{L}_t^{1-\alpha }}\right)}^{1/\alpha }$

The first-order condition of that problem is

$w_t=\frac{1-\alpha }{\alpha }{r}_{k,t}{\left(\frac{Y_t}{A_t{L}_t}\right)}^{1/\alpha }$

$=\frac{1-\alpha }{\alpha }{r}_{k,t}{\left(\frac{K_t}{L_t}\right)}^{1/\alpha }$

So the optimal use of labour in production,

$L_t^{\ast }(w_{t,}\hspace{0.17em}{r}_{t,}{Y}_{t,}\hspace{0.17em}{A}_t$)$={\left(\frac{1-\alpha }{\alpha }\times \frac{r_t}{W_t}\right)}^{\alpha }\left(\frac{Y_t}{A_t}\right)$

$K_t^{\ast }(w_{t,}\hspace{0.17em}{r}_{t,}{Y}_{t,}\hspace{0.17em}{A}_t$)$={\left(\frac{\alpha }{1-\alpha }\times \frac{W_t}{r_t}\right)}^{1-\alpha }\left(\frac{Y_t}{A_t}\right)$

Now plugging $L_t^{\ast }$ and $K_t^{\ast }$ into initial minimization problem, we obtain

$C(w_{t,}\hspace{0.17em}{r}_{t,}{Y}_{t,}\hspace{0.17em}{A}_t$) = $\left[{\left(\frac{1-\alpha }{\alpha }\times \frac{r_t}{W_t}\right)}^{\alpha }{w}_t+{\left(\frac{\alpha }{1-\alpha }\times \frac{W_t}{r_t}\right)}^{1-\alpha }{r}_t\right]\frac{Y_t}{A_t}$

The above equation can further be simplified as

$C(w_{t,}\hspace{0.17em}{r}_{t,}{Y}_{t,}\hspace{0.17em}{A}_t$)=${\left(\frac{r_t}{\alpha }\right)}^{\alpha }{\left(\frac{W_t}{1-\alpha }\right)}^{1-\alpha }\frac{Y_t}{A_t}$

Then, the marginal cost is just the first derivative of the above equation w.r.t $Y_t$

$M{C}_t={\left(\frac{r_t}{\alpha }\right)}^{\alpha }{\left(\frac{w_t}{1-\alpha }\right)}^{1-\alpha }\left(\frac{1}{A_t}\right)$

We compute the Marginal cost using the production function against the constraint of the total cost.

$Y=\hspace{0.17em}A{K}^{\alpha }{L}^{1-\alpha }$

$Ln\hspace{0.17em}Y=Ln\hspace{0.17em}A+\alpha Ln\hspace{0.17em}K+\left(1-\alpha \right)\hspace{0.17em}Ln\hspace{0.17em}L$

$\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{t}=\mathrm{w}\mathrm{L}+rK$

The marginal cost, obtained from the above equation for each bank, is used for estimating the Lerner Index for competition. The Yield on Fund is used as price in the Lerner Index. While the Lerner Index illustrates the Market Power, the inverse of the Lerner Index measures the degree of competition. This article first estimates the cost function and optimises it to estimate the marginal cost function, which in turn, is deployed for estimation of the Lerner Index.

3.3. Estimation of banks’ systemic risk

This study assesses systemic risk using ΔCoVaR, developed by Betz et al. (2016). It computes the systemic spillover resultant due to an individual institution’s failure, using CoVaRs at a median state and a stress state in quantile regression. The stress state is at the 1% quantile, and the median state is at the 50% quantile. Assets growth $(G{A}_t^i$)for a particular bank i at time t depends on the state variables, with a one-period lag.

(5) $G{A}_t^i={\beta }_0^i+{\beta }_1^{i}S{V}_{t-1}+e_t^i$(5)

The financial system’s asset growth ($G{A}_t^i)$ is a function of a bank’s asset growth and the state variables with a one-period lag.

(6) $G{A}_t^{Sys}={\beta }_0^{Sys/i}+{\beta }_1^{Sys/i}G{A}_t^i+{\beta }_2^{Sys/i}S{V}_{t-1}+{e_t}^{Sys/i}$(6)

We predict an individual bank’s VaR using quantile regression against state variables, with a one-period lag, at 1% and 50% as in equation (7)(7) $Va{R}_{t\left(q\right)}^i={\alpha }_{0\left(q\right)}^i+{\alpha }_{1\left(q\right)}^{i}S{V}_{t-1}$(7) .

(7) $Va{R}_{t\left(q\right)}^i={\alpha }_{0\left(q\right)}^i+{\alpha }_{1\left(q\right)}^{i}S{V}_{t-1}$(7)

We use equation (5)(5) $G{A}_t^i={\beta }_0^i+{\beta }_1^{i}S{V}_{t-1}+e_t^i$(5) to predict CoVaR through quantile regression against state variables and predict VaR for individual banks obtained using equation (7)(7) $Va{R}_{t\left(q\right)}^i={\alpha }_{0\left(q\right)}^i+{\alpha }_{1\left(q\right)}^{i}S{V}_{t-1}$(7) . We estimate equation (8)(8) $CoVa{R}_{t\left(q\right)}^i={\alpha }_0^{Sys/i}+{\alpha }_1^{Sys/i}Va{R}_{t\left(q\right)}^i+{\alpha }_2^{Sys/i}S{V}_{t-1}$(8) at 1% and 50% quantiles.

(8) $CoVa{R}_{t\left(q\right)}^i={\alpha }_0^{Sys/i}+{\alpha }_1^{Sys/i}Va{R}_{t\left(q\right)}^i+{\alpha }_2^{Sys/i}S{V}_{t-1}$(8)

The difference between the predicted CoVaRs at 1% and 50% is each bank’s systemic risk.

(9) $\mathrm{\Delta }CoVa{R}_{t\left(q\right)}^i=CoVa{R}_{t\left(q\right)}^i-CoVa{R}_t^i$(9)

We consider six state variables: (1) liquidity, (2) short-term rates (91-day T-Bill Rate), (3) long-term interest rates (10-Year G-Sec Rate), (4) Nifty-50 equity index return, (5) Nifty implied volatility, and (6) credit spread. The weighted average call money rate represents liquidity.

3.4. Estimation of bank’s stability

We deploy the widely used “Z-score” as a stability indicator (Boyd & Runkle, 1993; Lepetit et al., 2008; Laeven & Levine, 2009; Čihák and Hesse, 2010) for measuring the remoteness from insolvency (A. D. Roy, 1952).

(10) $Z_{i,t}=\frac{Ro{A}_{i,t}-{\left(E/A\right)}_{i,t}}{\sigma {\left(RoA\right)}_{i,t}}$(10)

Where;

$Ro{A}_{i,t}$ = Return on Assets for bank i at a given time t.

${\left(E/A\right)}_{i,t}$ = Equity to Asset Ratio for bank i at a given time t.

$\sigma {\left(RoA\right)}_{i,t}$ = Standard Deviation of Return on Assets for bank i at a given time t.

We compute the standard deviation of RoA for a 3-year rolling window (Beck et al., 2013) enabling exclusivity in capital and profitability variations (Schaeck & Čihák, 2010). A lower insolvency probability is given by a higher Z-score.

3.5. Interactive effect among competition, systemic risk and stability

Interbank transfer of funds, consortium lending, group-exposures and interbank liquidity management are the essential features of banks In an efficient banking system, between the banks, there would be arrangement of lines of credit, liquidity support, syndicated loans, etc., which are essential for their survival and hence they are significantly interconnected. However, interconnectedness leads to systemic risk transmission from a single bank to multiple banks. Transmission of illiquidity, insolvency and losses among the interconnected banks leads to systemic upheavals. Interconnectedness and risk transfer risk, leading to multiple bank-runs, the problem is further magnified when banks are exposed to similar kinds of risks in the economy leading to distress spillover.

“Competition-Fragility” theory states that a lower competition improves stability, while the “Competition-Stability” theory argues that bank’s stability can be improved with enhanced competition. The competition-stability theory (Allen & Gale, 2000; Boyd & De Nicolo, 2005) states that in a less competitive environment, banks can exercise their monopoly power and charge more interest rates on loans to protect their value. However, with the increasing competition, the monopoly power of individual banks reduces, and loans become cheaper. When competition becomes very stiff, and interest rates on loans significantly decline, competition starts hitting the bottom-line banks, reducing their stability.

On similar lines, the Competition-Fragility theory (Boyd & De Nicolo, 2005; Keeley, 1990) articulates that banks reduce risks with rising interest rates on advances in a lower competitive environment. However, this gives rise to two major problems: firstly, higher interest rates increase the default probability of the borrower, as the borrower finds difficulty in repaying the loans. Secondly, borrowers choose high-risk projects since banks are charging high interest on loans. In a lower competitive banking system, due to higher interest rates, investors tend to take riskier projects, as riskier projects fetch higher returns, thereby increasing banks’ systemic risk. This clearly highlights that when a low-interest rate prevails in a highly competitive environment, it reduces the moral hazard problem, resulting in banking system stability.

Martinez-Miera and Repullo (2010) extended the Competition-Fragility model by introducing the “margin effects.” The MMR model is based on two opposing forces: the margin effect and the risk-shifting effect. In a reduced competitive environment, margins are high, and this causes banks to build up a buffer from the profits derived by high margins. The risk-shifting problem refers to the risk preference of borrowers based on interest rates. The MMR model shows a trade-off between both forces. While margin effect clearly stands out in markets reflecting competition, monopolistic markets display a risk-shifting problem. Therefore, the banking system stability is low in markets with high or low degrees of competition.

In a lower competitive environment, the risk-shifting problem is too large to be compensated for with buffers from high margins, while highly competitive markets suffer very little from the risk-shifting problem, but here, the margins are too low for banks to be profitable. Thus, the most stable position is a situation where the risk-shifting problem and the margin effects are relatively equal. There would certainly be some risk-shifting problems, but the buffers are sufficient to cope with it. This, in turn, results in a U-shaped and inverted U-shaped relationship of competition with riskiness and stability, respectively. In practice, it means that competition increases stability until a given point beyond which any increase in competition leads to lesser stability.

Systemic risks influence the market values of banks’ assets. A low degree of competition provides market power to a few banks to set high-interest rates on loan products; these, in turn, are monopolistic rates, which are the main drivers of the banks’ franchise value. Additionally, it may be noted that banks want to protect their franchise value, and therefore have a low-risk preference (Berger et al., 2009), whereby the resultant effect would be less risky, translating thereby to high-quality loans with high margins. However, with the increase in competition, banks’ pricing power decreases, and they prefer to sanction riskier loans to improve their margin. Thus, competition over a period of time builds up risk and threatens the systemic stability of banks.

Two hypotheses are tested hereby to ascertain the association between stability, systemic risk, and competition.

Null Hypothesis 1: Banks’ Stability and Competition have inverted “U” shaped relationship

Null Hypothesis 2: Banks’ Systemic Risk and Competition have “U” shaped relationship

Along with the non-linear quadratic regression, the article performs the Sasabuchi-Lind-Mehlum (Lind & Mehlum, 2010; Sasabuchi, 1980) SLM-test to confirm the presence of any non-linear relationship.

We measure the stability using the Z-score and regress it against the bank’s competition to obtain the relationship. Similarly, we measure the systemic risk through ∆covar method and regress the same against the bank’s competition for obtaining the relationship.

(11) $Z_{i,t}=\gamma +\beta competitio{n}_{i,t}+\alpha competitio{n}_{i,t}^2+e_{i,t}$(11)

Where;

$Z_{i,t}$ = stability of bank i at a given instance t

$Competitio{n}_{i,t}$ = Competition for bank i at time t

In order to obtain an inverted “U” shaped relationship, the Null Hypothesis is:

$\alpha$= Negative Values

$\beta$ = Positive Values

The SLM-test for U-Shaped required has the following hypothesis:

Null Hypothesis: $\beta +\alpha Competitio{n}_{max}$ ≥0

$\beta +\alpha Competitio{n}_{min}$

Rejection of null highlights a U-shaped non-linear relationship between stability and competition.

Similarly, we measure the Systemic Risk through $\mathrm{\Delta }CoVaR$ method, and regress it against bank’s competition as per the equation given below:

(12) $\mathrm{\Delta }CoVa{R}_{i,t}^q=\tau +\phi competitio{n}_{i,t}+\pi competitio{n}_{i,t}^2+\hspace{0.17em}{e}_{i,t}$(12)

Where;

$\mathrm{\Delta }CoVa{R}_{i,t}^q$ = Systemic Risk of Bank i time t

In order to obtain a “U” shaped relationship, the Null Hypothesis is:

$\pi$ = Positive Values

$\phi$ = Positive Values

The SLM-test for U-Shaped required has the following hypothesis:

$\phi +\pi competitio{n}_{max}\hspace{0.17em}$

$\phi +\pi competitio{n}_{min}\hspace{0.17em}\ge 0$

Rejection of null indicates a U-shaped non-linear relationship between systemic risk and competition.

This study further analyses the interactive effects of competition, stability, and systemic risk through system equation modeling. For examining the relationship, we control for a list of firm-specific variables. Our empirical design is in line with the previous studies of Beck et al. (2013), who controlled for bank size, profitability, risk leverage, capital adequacy, asset quality, and operating cost margin.

3.5.1. Impact of bank’s competition and stability on systemic risk

Bank’s competition and stability, along with a set of exogenous variables, influence the bank’s systemic risk, as depicted in Table 2. Banks’ competition is influenced by loan growth and the price of bank’s loan. Bank’s stability, on the other hand, depends upon leveraging of balance sheet and profit margin from such leverage. We have selected loan growth and the average price of loans as instruments whereby the instrumented variable is the bank’s competition. Similarly, the operating profit margin and balance sheet leverage are instruments for the bank’s stability is instrumented.

$\begin{array}{rl}& SystemicRis{k}_{i,t}={\beta }_0+{\beta }_{1}AssetQualit{y}_{i,t}+{\beta }_{2}RiskLeverag{e}_{i,t}+{\beta }_3{R}_0{A}_{i,t}+{\beta }_{4}OperatingCostMargi{n}_{i,t}\\ & +{\beta }_{5}CRA{R}_{i,t}+{\beta }_{6}BankSiz{e}_{i,t}+{\beta }_{7}ProvisonCoverageRati{o}_{i,t}\\ & +{\beta }_{8}Ban{k}^{\prime }sCompetitio{n}_{i,t}+{\beta }_{9}Ban{k}^{\prime }sstabilit{y}_{i,t}+{\in }_{i,t}\end{array}$

$Bank\prime s\hspace{0.17em}Competitio{n}_{i,t}=\hspace{0.17em}{\beta }_0+\hspace{0.17em}{\beta }_1\hspace{0.17em}Loan\hspace{0.17em}Growt{h}_{i,t}+\hspace{0.17em}{\beta }_2\hspace{0.17em}Average\hspace{0.17em}Pric{e}_{i,t}+{\mu }_{i,t}$

$Bank{ }^{\mathrm{\prime }}sStabilit{y}_{i,t}={\theta }_0+{\theta }_1\mathrm{O}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{M}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}{\mathrm{n}}_{i,t}+{\theta }_{2}BalanceSheetLeverag{e}_{i,t}+{\gamma }_{i,t}$

Table 2. Hypothesis for Control Variables based on Systemic Risk

Control Variables	Impact on Systemic Risk	Explanation
Bank’s Competition	Negative	Creates competitive pressure in the overall banking system.
Bank’s Stability	Negative	It reduces the default probability d hence reduces systemic risk.
Bank Size (Log of Total Assets)	Positive	Big-sized banks are systemically important banks.
Asset Quality (GNPA)	Positive	GNPA increases the systemic risk.
Risk Leverage (Networth to RWA)	Positive	Leveraging of networth in the creation of risky assets and hence a higher contribution to systemic risk.
Return on Assets	Negative	More profitable banks are less risky nature.
Operating Cost Margin	Positive	Higher operational cost reduces the profit margin and may enhance the systemic risk.
CRAR	Negative	The probability of insolvency decreases with increasing CRAR.
Provision Coverage Ratio	Negative	Higher provision for NPA reduces systemic vulnerability.

3.5.2. Impact of bank’s competition and systemic risk on bank’s stability

Bank’s competition and systemic risk, along with a set of exogenous variables, influence the bank’s stability, as depicted in Table 3. We have selected loan growth and the average price of loans as instruments, and the instrumented variable is the bank’s competition. Similarly, asset quality and risk leverage are instruments for the bank’s systemic risk, which is also instrumented.

Table 3. Hypothesis for Control Variables based on bank’s stability

Control Variables	Impact on Bank’s Stability	Explanation
Bank’s Competition	Negative	Creates competitive pressure in the overall banking system
Systemic Risk	Negative	Stability reduces the probability of default.
Bank Size	Positive	Big-sized banks are more diversified in business, and hence there is a higher contribution to profits and hence stability.
Operating Profit Margin	Positive	Higher operational profits subsequently add to ility.
Balance sheet Leverage	Positive	Leveraging of networth in the creation of more assets and hence a higher contribution to profits.
Return on Assets	Positive	More profitable banks are less risky nature.
Asset Quality (GNPA)	Positive	GNPA increases systemic risk.
Operating Cost Margin	Negative	Higher operational cost reduces the profit margin affecting bank’s stability
Risk-weighted Assets	Positive	The probability of insolvency decreases with increasing CRAR.
Provision Coverage Ratio	Positive	Higher provisions for NPA reduce the probability of default.

$\begin{array}{rl}& Ban{k}^{\prime }sStabilit{y}_{i,t}={\gamma }_{i0}+{\gamma }_1{R}_0{A}_{i,t}+{\gamma }_{2}OperatingProfitMargi{n}_{i,t}+{\gamma }_{3}BalanceSheetLeverag{e}_{i,t}\\ & +{\gamma }_{4}OperatingCostMargi{n}_{i,t}+{\gamma }_{5}CRA{R}_{i,t}+{\gamma }_{6}BankSiz{e}_{i,t}\\ & +{\gamma }_{7}ProvisonCoverageRati{o}_{i,t}+{\gamma }_{8}Ban{k}^{\prime }sSystemicRis{k}_{i,t}\\ & +{\gamma }_{9}Ban{k}^{\prime }sCompetitio{n}_{i,t}+{\mu }_{i,t}\end{array}$

$Bank{ }^{\mathrm{\prime }}s\hspace{0.17em}Systemic\hspace{0.17em}Ris{k}_{i,t}={\beta }_0+\hspace{0.17em}{\beta }_1\hspace{0.17em}Asset\hspace{0.17em}Qualit{y}_{i,t}+\hspace{0.17em}{\beta }_2\hspace{0.17em}Risk\hspace{0.17em}Leverag{e}_{i,t}+{\epsilon }_{i,t}$

$Bank{ }^{\mathrm{\prime }}s\hspace{0.17em}Competitio{n}_{i,t}={\gamma }_0+{\gamma }_1\hspace{0.17em}Loan\hspace{0.17em}Growt{h}_{i,t}+\hspace{0.17em}{\gamma }_{2\hspace{0.17em}}Average\hspace{0.17em}Pric{e}_{i,t}+k_{i,t}$

3.5.3. Impact of systemic risk and bank’s stability on bank’s competition

Bank’s stability and its systemic risk, along with a set of exogenous variables, influence its competition, as depicted in Table 4. Bank’s systemic risk is influenced by asset quality and risk leverage, while the bank’s stability, on the other hand, depends upon the operating profit margin and balance sheet leverage. We have selected balance sheet leverage and operating profit margin as instruments, whereby the instrumented variable is the bank’s stability. Similarly, asset quality and risk leverage are instruments for the bank’s systemic risk, which is also instrumented.

Table 4. Hypothesis for Control Variables based on Bank’s Competition

Control Variables	Impact on Bank’s Competition	Explanation
Systemic Risk	Negative	Increases the probability of insolvency and hence negatively impacts the bank’s competition.
Stability	Negative	Bank’s stability creates pressure on the banks to maintain a healthy balance sheet and reduces the overall competition.
Bank Size	Negative	Big-sized banks have more diversified businesses and hence exercises competitive pressure in the banking system.
Return on Assets	Positive	A more profitable banking system magnifies the competitive pressure.
Operating Cost Margin	Positive	Higher operational cost reduces the profit margin and increase the competitive pressure.
Risk-weighted Assets	Negative	More capitalised banks take higher risks and exert higher competitive pressure.
Loan Growth	Positive	Banks with higher loan growth are expected to create more competitive pressure.
Provision Coverage Ratio	Positive	Higher provisions for NPA diminishes default probability and improve the competition in the long-run.

$\begin{array}{rl}& Ban{k}^{\prime }sCompetitio{n}_{i,t}={\theta }_{i0}+{\theta }_{1}LoanGrowt{h}_{i,t}+{\theta }_{2}AveragePric{e}_{i,t}+{\theta }_{3}ValueCreatio{n}_{i,t}\\ & +{\theta }_{4}CRA{R}_{i,t}+{\theta }_{5}BankSiz{e}_{i,t}+{\theta }_{6}OperatingCostMargi{n}_{i,t}\\ & +{\theta }_{7}ProvisonCoverageRati{o}_{i,t}+{\theta }_8{R}_0{A}_{i,t}+{\theta }_{9}Ban{k}^{\prime }sSoundnessInde{x}_{i,t}\\ & +{\theta }_{10}Ban{k}^{\prime }sSystemicRis{k}_{i,t}+{\vartheta }_{i,t}\end{array}$

$Ban{k}^{\prime }s\hspace{0.17em}Soundness\hspace{0.17em}Inde{x}_{i,t}={\gamma }_0+{\gamma }_1\mathrm{B}\mathrm{a}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{S}\mathrm{h}\mathrm{e}\mathrm{e}\mathrm{t}\mathrm{L}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}{\mathrm{e}}_{i,t}+\hspace{0.17em}{\gamma }_2\mathrm{O}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{M}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}{\mathrm{n}}_{i,t}+{\mathrm{k}}_{\mathrm{i},\mathrm{t}}$

$Bank{ }^{\mathrm{\prime }}sSystemicRis{k}_{i,t}={\theta }_0+{\theta }_1\mathrm{A}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{t}\mathrm{Q}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{t}{\mathrm{y}}_{i,t}+{\theta }_2\mathrm{R}\mathrm{i}\mathrm{s}\mathrm{k}\mathrm{L}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}{\mathrm{e}}_{i,t}+{\gamma }_{\mathrm{i},\mathrm{t}}$

The article has considered 33 banks belonging to both public and private sectors across business cycles.

4. Results and analysis

4.1. Systemic risk, stability and competition: accounting disclosures indices

Table 5 depicts the correlation matrix between systemic risk, stability, and competition indices, constructed using accounting disclosures. A strong positive correlation is observed between competition and stability. A weak positive correlation between systemic risk and competition indicates that competition derives the systemic risk.

Table 5. Correlation Matrix: Indices Scores

	Systemic Risk	Stability	Competition
Systemic Risk	1
Stability	0.44	1
Competition	0.22	0.93	1

On the basis of accounting disclosures indices, the article estimated the number of banks falling above and below average categories of systemic risk, stability, and competition, as per the full sample period, business up-cycle, and down-cycle, as depicted in Table 6. During the business down-cycle, more banks are falling under the category of above-average systemic risk, and they command more market power than the average competitiveness prevalent in the industry. Similarly, a higher number of banks are stable during the down-cycle compared to the average stability index score.

Table 6. Number of Banks: Accounting Disclosures Indices

Indices	Full Sample		Up-cycle		Down-cycle
	Above Average	Below Average	Above Average	Below Average	Above Average	Below Average
Systemic Risk	16	17	11	22	18	15
Stability	17	16	13	20	19	14
Competition	18	15	15	18	19	14

Table 7 provides a comparative analysis of accounting-based disclosures indices. As per the ownership category, public sector banks are more competitive, with higher systemic risk. However, public sector banks are more stable compared to private sector banks. Public sector banks have government supports in the form of interest subsidy and ownership capital, and hence these banks enjoy customers’ confidence in the market. On the other hand, big-size banks are more competitive, more systemic risk emitter, and more stable compared to small-size banks. Big banks have a large customer base, diversified business, and more capital to sustain any kind of systemic pressure. As per the literature, the study has also found that banks are more unstable, have high systemic risk emitters, and are more competitive during economic down-cycle as significant corporate loan defaults occur during economic slow-down.

Table 7. Average Indices Scores Across Categories

Categories	Classifications	Competition	Stability	Systemic Risk
Full Sample	All banks	14.94	15.22	12.79
Ownership	Public Banks	15.34	15.94	15.53
	Private Banks	14.32	14.10	8.57
Bank Size	Big Banks	15.81	16.29	12.99
	Small Banks	14.32	14.45	12.69
Economic Cycles	Up-cycle	14.72	15.55	11.69
	Down-cycle	15.05	14.56	13.39

To confirm the findings of accounting-based disclosures indices on competition, stability, and systemic risk, the article has undertaken the following econometric modeling.

4.2. Estimation of marginal cost function and competition

The article estimated the total cost function by fitting a Cobb-Douglas production. It considered “Total Assets” as the primary output, which is regressed against Cost of Funds and Labour Cost. From the panel diagnostic tests, we inferred that the Breusch–Pagan test supports the panel Random Effect against pooled OLS, and the Hausman test justifies the consistency of panel Random Effect against panel Fixed Effect as depicted in Table 8.

Table 8. Estimation of Cobb-Douglas Production Function

	Coefficient	Std. Error	Z stat	p-value
Constant	0.3546	0.0323	10.98	<0.0001
Ln Working Funds	0.9704	0.0057	170.2	<0.0001
Ln Labour Cost	0.0126	0.0062	2.02	0.0434
Pooled OLS is adequate against fixed effects F(38, 349) = 12.6319, p-value 1.42326e-045
Pooled OLS is adequate against Random effects Breusch-Pagan test statistic: LM = 452.264, ChiSquare(1): 2.319e-100
Random effect is consistent against fixed effects. Hausman test statistic: H = 5.68047, ChiSquare (2): 0.058412

We deploy the coefficients of the Cobb-Douglas production function for computing the Marginal Cost function as per the following equation.

$M{C}_t={\left(\frac{r_t}{0.9704}\right)}^{0.9704}{\left(\frac{w_t}{1-0.9704}\right)}^{1-0.9704}\left(\frac{1}{Antilog\left(0.3545\right)}\right)$

Then, the Lerner Index is assessed for each bank over a period 2005–18 by factoring in the MC and Average Price.

The average competition estimated for all banks is 1.0164. Competition among private sector banks is less than that among public sector banks, indicating a higher market power for private banks. Similarly, big-size banks are less competitive compared to small-size banks. Competition is lower during economic up-cycle as compared to down-cycle (See Table 9).

Table 9. Estimated Market Power

Categories	Classifications	Lerner Index	Competition
Full Sample	All banks	0.9839	1.0164
Ownership	Public Banks	0.9824	1.0179
	Private Banks	0.9851	1.0151
Bank Size	Big Banks	0.9849	1.0153
	Small Banks	0.9833	1.0169
Economic Cycles	Up cycle	0.9834	1.0169
	Down cycle	0.9832	1.0171

4.3. Estimation of bank’s stability

We compute the Z-score as a proxy for measuring stability for the period 2005–18 (Demirgüç-Kunt & Huizinga, 2010; Houston et al., 2010). We use 3 years of rolling standard deviation of RoA.

Private banks are stable as and when compared against their public counterparts. Similarly, large banks are relatively less stable as compared to their smaller peers. The banking system is more stable during the economic up cycle compared to the economic down-cycle (See Table 10).

Table 10. Estimated Bank’s Stability

Categories	Classifications	Z-Score
	All Banks	−0.0806
Ownership	Public Banks	−0.1108
	Private Banks	−0.0353
Economic Cycles	Up-Cycle	0.5526
	Down-cycle	−0.3972
Bank Size	Big Size	−0.1608
	Small Size	0.0076

4.4. Estimation of bank’s systemic risk

Systemic risk is estimated using the ΔCoVaR method for the period of 2005–18. Table 11 depicts the estimated average systemic risk for all banks, both private and public, along with their economic-up and down-cycle.

Table 11. Estimated Systemic Risk

Category	Classification	Systemic Risk
	All banks	0.3407%
Ownership	Private banks	0.3417%
	Public banks	0.3399%
Business Cycle	Up-cycle	0.3354%
	Down-cycle	0.3455%

The average systemic risk estimated for all banks is 0.3407%. Systemic risk for private banks is higher, indicating that private banks are riskier to financial stability in India. Systemic risk is higher during the economic down-cycle as compared to up-cycle and is a typical example of systemic risk spillover effect (Adrian & Brunnermeier, 2011).

4.5. Competition and systemic risk

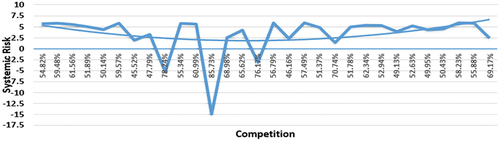
We analyse the association between the bank’s systemic risk and co through the non-linear equation depicted in Table 12. The positive “Squared term” of the competition index indicates that the relationship between competition and the bank’s systemic risk is U-shaped, as shown in Figure 1.

Figure 1. “U” shaped relationship between bank’s competition and systemic risk.

Table 12. Competition and Systemic risk

Variable	Coefficient	Std. Error	t-ratio	p-value
Constant	−0.0047	0.0003	−13.66	<0.0001
Bank’s Competition	0.0027	0.0008	3.168	0.0036
(Bank’s Competition)^2	0.0039	0.0011	3.517	0.0015

Note: Adjusted R-squared: 0.5547

Durbin-Watson:1.4944

F(2, 387):53.5386, P-value(F): 2.46e-21

H0: Bank’s Systemic Risk and Competition haS ‘U’ shaped relationship

SLM Test: 307.006–265.912$Competitio{n}_{max}\hspace{0.17em}$ ≥ 39.80103307.006–265.912$Competitio{n}_{min}\hspace{0.17em}$ ≥ 30.38702

Systemic risk achieves its minimum level with a certain threshold level of competition; beyond that, competition induces systemic risk. In a stiff competitive environment, banks generally ignore borrowers’ credit qualities and sanction high risky loans, contributing more to systemic risk.

4.6. Competition and stability

The relationship between a bank’s stability and competition is analysed through the quadratic equation as per the regression equation given in Table 13.

Table 13. Competition and Bank’s Stability

Variable	Coefficient	Std. Error	t-ratio	p-value
Constant	−82.7555	11.7084	−7.068	<0.0001
Bank’s Competition	307.066	38.1811	8.042	<0.0001
Bank’s Competition^2	−265.912	30.0155	−8.859	<0.0001

Note: Adjusted R-squared: 0.2315

Durbin-Watson: 1.9217

F(2, 387): 59.58376 P-value(F): 2.76e-23

H0: Bank’s Stability and Competition has ‘inverted U’ shaped relationship

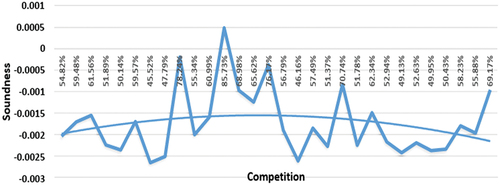
The negative “Squared term” of the competition index indicates an inverted U-shaped relationship between competition stability, as shown in Figure 2. Stability improves with competition, but beyond a certain threshold level, it declines with the competition. Results indicate that banks compromise their stability by sanctioning low-quality loans during a stiff competitive environment.

Figure 2. Inverted “U” shaped relation between bank’s competition and stability.

4.7. Interactive effects of bank’s stability, systemic risk and competition

We analyse the interrelationship among bank’s competition, systemic risk, and stability through a series of system equations through 2-SLS system regression, based on selected instruments and the associated control variables.

4.7.1. Impact of bank’s stability & systemic risk on competition

Bank’s stability and systemic risk are instrumented, and Asset Quality, Risk Leverage, Operating Profit Margin, and Balance Sheet Leverage are instrumental variables for the 2-SLS system equation on Bank’s Competition Index, as shown in Table 14. Bank’s stability provides an incentive to banks to exercise competitive pressure in the banking system, and hence it negatively contributes to bank’s competition. With the increasing systemic risk, the probability of insolvency of banks increases, and hence banks would exercise all possible competitive pressure to improve their profitability. The negative relationship between a bank’s competition and systemic risk justified the above argument. CRAR negatively contributes to bank’s competition, as more capitalised banks diversify their business, bear more risk, and exercise more competitive pressure. Loan growth indicates a surge in business activities and hence contributes positively to competition. The market-to-book value ratio indicates the aggressive nature of the bank, and hence value creation would have a negative relation with the competition.

Table 14. 2-SLS System Equation for Competition

Variables	Coefficient	Std. Error	t-ratio	p-value
Constant	2.8337	0.1915	14.8	<0.0001
Bank’s Stability	−0.0023	0.0008	−3.018	0.0027
Bank’s Systemic Risk	−58.9651	34.1537	−1.727	0.083
Loan Growth	0.0039	0.0019	1.963	0.0504
Average Price	−0.0066	0.0324	−0.202	0.8401
ROA	6.7721	1.2429	5.448	<0.0001
Operating Cost Margin	5.5184	1.0486	5.263	<0.0001
Bank Size	−0.9797	0.0669	−14.63	<0.0001
CRAR	0.5792	0.2582	2.243	0.0255
Value Creation	−0.1318	0.0411	−3.213	0.0014

Note: Adjusted R-squared: 0.7631

F(9, 380): 150.0549, P-value(F): 2.9e-119

OLS estimates are consistent

Hausman test: $X^2$(2): 16.2813 (p-value: 0.00029)

Sargan over-identification test: All instruments are valid

LM Test: 31.616, $X^2$(1):1.87e-008

The above findings are in line with the Financial Fragility hypothesis. It predicts that with increased capital there is restricted competition, while aggressive loan creation increases fragility (Diamond & Rajan, 2000, 2001). We also observe that a greater degree of liquidity creation through enhanced loan disbursements increases the liquidity risk for banks. The Hausman test rejects the OLS estimates’ consistency, and all the instruments of the 2SLS system equation are valid, which justifies its robustness.

4.7.2. Role of competition & systemic risk on stability

Bank’s competition and systemic risk are instrumented, and loan growth, average price, asset quality, and risk leverage are contributory variables for the 2SLS system equation on the bank’s stability index, as shown in Table 15.

Table 15. 2-SLS System Equation for Bank’s Stability

Variables	Coefficient	Std. Error	t-ratio	p-value
Constant	−797.04	340.80	−2.339	0.0199
Bank’s Competition	159.97	68.15	2.347	0.0199
Bank’s Systemic Risk	−23812.00	13530.20	−1.76	0.0792
Balance Sheet Leverage	−317.91	72.42	−4.39	<0.0001
Operating Profit Margin	−1507.30	711.19	−2.119	0.0347
ROA	1958.42	614.56	3.187	0.0016
Bank Size	250.48	116.33	2.153	0.0319
Provision Coverage Ratio	2.74	1.75	1.566	0.1181

Note: Adjusted R-squared: 0.3306

F(7 381): 7.0719, P-value(F): 5.99e-08

Sargan over-identification test: All instruments are valid

LM Test: 0.6272, $x^2$(2):0.7309

OLS estimates are consistent

Hausman test: $x^2$(2): 19.0623 (p-value: 7.25559e-005)

Healthy competition would enhance the stability of the balance sheet, and hence competition would improve the bank’s stability. Stiff competition would exert competitive pressure on the banking system and may negatively contribute to bank’s stability. The negative relationship between the bank’s systemic risk and the bank’s stability may be due to the increase in the probability of insolvency with rising systemic risk. Bank size positively influences a bank’s stability, as big-sized banks have a more diversified business and hence contribute more to profit. The operating profit margin of a bank is expected to positively influence its stability; however, we got an inverse relation, which could be attributed to the fact that more profit margins may attract new entrants into the system, which in turn may hamper the bank’s stability. Similarly, Balance Sheet Leverage (Networth to Total Asset) is expected to positively influence bank’s stability, as leveraging net worth in creating assets would contribute more to profit.

However, our analysis showed an inverse relationship; we thereby infer that more loans creating banks might be generating less profit. The analysis finds a positive relation between RoA and bank’s stability, which implies that more profitable banks are less risky in nature.

Hausman’s test rejects the consistency of OLS estimates, and all the instruments of the 2SLS system equation are valid, which justifies its robustness.

4.7.3. Impact of bank’s competition & stability on systemic risk

Bank’s competition and stability are instrumented; loan growth, average price, operating profit margin, and balance sheet leverage are instrumental variables for the 2SLS system equation on bank’s systemic risk index as given in Table 16.

Table 16. 2-SLS System Equation for Systemic Risk

Variables	Coefficient	Std. Error	t-ratio	p-value
Intercept	0.0062	0.0033	1.895	0.0589
Bank’s Competition	−0.0024	0.0009	−2.556	0.0110
Bank’s Stability	−0.0024	0.0008	−3.113	0.0024
ROA	0.0499	0.0169	2.954	0.0033
Asset Quality	0.0004	0.0017	0.204	0.8384
Provision Coverage Ratio	0.0002	3.75E–05	3.731	0.0002
Bank Size	−0.0031	0.0012	−2.683	0.0076
Risk Leverage	−0.0041	0.0017	−2.525	0.0120

Note: Adjusted R-squared: 0.3815

F (7, 381): 9.1815, P-value(F): 1.67e-10

Sargan over-identification test: All instruments are valid

LM Test: 0.468951 $x^2$2(1) :0.790985

OLS estimates are consistent

Hausman test: $x^2$(2): 3.6862 (p-value: 0.158323)

Competition and systemic risk have an inverse relationship, as increasing competition would exert competitive pressure in the banking system. Stiff competition may force banks to sanction risky loans, which would increase systemic risk. Bank’s stability, therefore, reduces the probability of insolvency, which would prevail upon banks to create riskier loans; hence, a bank’s stability would have a negative relation with systemic risk.

Large banks are systemically important; hence, systemic risk has a negative relation with bank size. Our analysis revealed a positive relationship between RoA and systemic risk, as more profitable banks are less risky in nature. Risk leverage, therefore, has a negative relation with systemic risk, as leveraging of net worth in the creation of risky assets may contribute to profitability more than to systemic risk. Provision Coverage Ratio has positively contributed to systemic risk, as more provision for NPA prevails upon banks to sanction further riskier loans.

Hausman’s test rejects the consistency of OLS estimates, and all the instruments of the 2SLS system equation are valid, which justifies its robustness.

5. Conclusion & policy implications

The article examined the nexus among competition, systemic risk, and stability prevailing in emerging market banks, using panel data of 33 listed Indian banks across the study period 2005–18. This article confirms the simultaneous existence of Competition-Stability and Competition-Fragility theories in an emerging market economy like India. Our findings are in accordance with the financial fragility hypothesis, predicting a restricted competition owing to increased capital, and aggressive loan creation increases fragility (Diamond & Rajan, 2000, 2001).

The accounting disclosures-based indices reveal the interrelationship among competition, systemic risk, and stability. It also reveals that during the economic down-cycle, banks are more unstable, high systemic risk emitters, and are more competitive. Systemic risk is largely influenced by profitability, asset quality, balance sheet leverage, bank size, and income diversification. Profitable banks contribute positively to systemic risk as they tend to take more risk by disbursing riskier loans.

For the given study period, our results display a significant shift in a bank’s average risk exposure supplemented by a steady increase in competition. The results highlight a significant negative relationship between competition and systemic risk. We further confirm the accounting disclosures-based indices finding through a series of econometric modeling.

Our analysis indicates the negative influence of a bank’s systemic risk on the financial stability of the economy at large. Systemic risk in the case of private banks is relatively higher than public banks, thereby indicating the susceptibility that private banks bring on to the financial stability in India. It is also observed that systemic risk invariably accumulates in the banking system during business growth cycles, resulting thereby in large-scale defaults during economic down-cycle as compared to up-cycle, which in turn is a typical example of systemic risk spillover effect (Adrian & Brunnermeier, 2011). Private banks have higher systemic risk than public banks during economic up-cycle, whereas it is reversed during the down-cycle. Public sector banks emit less systemic risk onto the system due to sovereign support during an economic up-cycle.

Systemic risk creation is more common in the case of profitable banks, as they tend to disburse risky loans for attaining higher profitability. We ascertain this pattern as we comprehend the relationship between bank’s systemic risk and competition, which is “U-shaped,” indicating the loan-disbursal behaviour of banks. In a competitive environment, these banks tend to ignore the borrower’s creditworthiness and end up sanctioning risky loans, thereby contributing to a growth in systemic risk. We observe that small-sized banks are more prone to upsurge in competition as compared to their bigger counterparts, who are successful in exerting their market power.

We conclude by stating that while the sector’s stability improves with the rise in banking competition, it gradually declines with a stiff increase in competition. Based on our findings analysing the inverted U-shaped relationship between competition and stability, we conclude that banks are actually forced to compromise the banking system stability by sanctioning low-quality loans during a stiff competitive environment. This relationship can be further established inferring on the argument that while a healthy competition would definitely support the overall stability of a bank’s balance sheet, a fierce competition would exert competitive pressure in the banking system, and hence it might negatively contribute to bank’s stability. The negative relationship between systemic risk and stability might be due to an increase in the probability of insolvency with rising systemic risk. Moreover, we observe that in the case of emerging economies like India, bank size positively influences banks’ stability, as big size banks have more diversified businesses and hence contribute more to profit. The Reserve Bank of India (RBI), regulating the Indian banking system, should monitor excessive loan creation during an economic up-cycle. Regulators should prescribe higher risk weights on corporate loans during economic up-cycle to prevent excessive loan creation. The RBI should carefully monitor banks having high NPL and implement a stringent policy of prompt corrective actions and disclosure norms. The RBI should fix a limit on each bank for interbank exposure to reduce interbank risk spillover. Banking regulators should encourage mergers of small banks to create larger banks which can bear systemic risk.

Central bankers must adopt a watchful approach to identifying banks that are exerting market power and restricting competition in the banking system. At the same time, while promoting competition, central banks should also encourage banks to build stronger credit growth with a gradual reduction in lending rate. In a stiff competitive banking system, the central bank should be vigilant so that banks should not undermine the proper screening of loan proposals. Central banks should increase the risk weight of risky loans and impose buffer provisioning norms to avoid cut-throat competitive lendings. Central banks should put in place a higher degree of entry restrictions for both national and foreign banks to maintain financial stability and discourage shadow banking activities. Interconnection among banks for liquidity support and syndicated loans leads to risk spillover and it is quite prominent during business down-cycle. Therefore, the banking system regulator should be more vigilant while controlling the same. The recent crisis further emphasizes the role of regulatory bodies as well as supervisory frameworks in monitoring product innovation and bank interlinkages as they significantly contribute to the systemic risk and stability.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Notes on contributors

Sabyasachi Mohapatra

Sabyasachi Mohapatra is Associate Professor, Finance & Accounting at Indian Institute of Management Bodh Gaya, India. Prior to joining IIM, he was a Banking and Financial Services Domain Consultant for one of the biggest global consulting majors headquartered outside of Mumbai. His teaching and research interests include Asset Pricing, Value and Growth Investing, Portfolio & Asset Management, Market Microstructure and Behavioural Finance.

Arun Kumar Misra

Arun Kumar Misra is Associate Professor, Finance & Accounting at Indian Institute of Management Sambalpur, India. He is an ex-banker with experience in Commercial Banking space comprising Risk Management, Asset-Liability Management and Basel-II implementation. His teaching and research experience includes Global Banking and Capital Markets.

Molla Ramizur Rahman

Molla Ramizur Rahman is an Assistant Professor in Finance, Accounting and Control at Amrut Mody School of Management at Ahmedabad University. He obtained a PhD from Vinod Gupta School of Management at the Indian Institute of Technology Kharagpur. His research interests include financial stability, banking, corporate finance, and capital markets.