Tunneling of hybridized pairs of electrons through a one-dimensional channel

Abstract

Recently, the electron transport through a quasi-one dimensional (quasi-1D) electron gas was investigated experimentally as a function of the confining potential. We present a physical model for quantum ballistic transport of electrons through a short conduction channel, and investigate the role played by the Coulomb interaction in modifying the energy levels of two-electron states at low temperatures as the width of the channel is increased. In this regime, the effect of the Coulomb interaction on the two-electron states has been shown to lead to four split energy levels, including two anticrossings and two crossing-level states. Due to the interplay between the anticrossing and crossing of the energy levels, the ground state for the two-electron model switches from one anticrossing state for strong confinement to a crossing state for intermediate confinement as the channel width is first increased, and then returned to its original anticrossing state. This switching behavior is related to the triplet spin degeneracy as well as the Coulomb repulsion and reflected in the ballistic conductance. Here, many-body effects can still affect electron occupations in the calculation of quantum ballistic conductance although it cannot vary the center-of-mass velocity.

Graphical Abstract

Keywords:

• Ballistic transport
• quasi 1D conductance hybrid clusters

PACS:

• 72.10.-d Theory of electronic transport
• scattering mechanisms
• 72.20.-i Conductivity phenomena in semiconductors and insulators
• 73.21.Hb Quantum wires; 73.23.Ad Ballistic transport

1. Introduction

In this paper, we review the importance of many-body effects on the ballistic electron transport in a quasi-one-dimensional (1D) electron gas with varied confinement potential. This area of research has been receiving a considerable amount of attention in recent times ever since it was discovered that for a range of electron distribution and potential strength, the ground state of a 1D quantum wire splits into two rows with a Wigner lattice beginning to form. It was also demonstrated that when a perpendicular magnetic field is applied, a double-row electron formation may change completely into a single row due to an enhanced confinement potential. Furthermore, it has been verified experimentally that weak confinement, in competition with the electron–electron interaction, causes the electron level occupation to reorder so that the ground state, conforming to the standard or common type, passes through the excited levels. The data in Ref. [1] show that the energy levels may be controlled by exploiting their separate geometric dependence on confinement and electron density. This means that in simulating the electron transport data, many-body effects must be considered.

It has been well known that electrostatic potential confinement of a two-dimensional electron gas (2DEG) used to create a quasi-1D wire [2] gives rise to quantization of the conductance [3,4] in integer multiples of which is not affected by a weak electron–electron interaction [5]. The long-range Coulomb interaction between electrons becomes relatively important at low electron densities resulting in the formation of a 1D Wigner crystal [2,6,7]. But, the role played by the Coulomb repulsion between electrons is also made greater until it overcomes the confinement potential, as the density is increased, at which point the ground state and one of the excited states are interchanged [8] which may result in hybridization and anticrossing. In Refs. [1,9], conductance measurements were reported for weakly confined quantum wires in a 2DEG and determined by the boundaries of top split-gates.

Experiment has shown that making the confinement potential less effective results in the appearance of two rows, accompanied by a sudden change in conductance G from zero to . This behavior may be attributed to the possibility that there was no coupling between these two rows so that each row contributes independently and additively. Another way to account for this is to say that their energy eigenstates become hybridized and the resulting state causes a breakdown of the single-particle picture when the Coulomb interaction becomes important. Recent investigations have confirmed that there exists a Coulomb interaction between the rows resulting in this anomalous jump in the conductance [10].

The devices used in Refs. [1] and [9] were fabricated using electron beam lithography on 300 nm deep GaAs/AlGaAs heterostructures. Typically, the sample consisted of split gates, m long and m wide, and a top gate of width m defined above the split gates, separated by a 200 nm layer of cross-linked polymethyl methacrylate. After partial illumination, the carrier density and mobility were estimated to be cm and cmVs, respectively. The two-terminal conductance, , was measured at 70 mK, using a 77 Hz voltage of V. Previously, the conductance through two laterally aligned but uncoupled parallel wires formed by surface gates have been shown to be the sum of the conductances of each individual wire, resulting in plateaus at multiples of , [11,12] indicating that hybridization of states within a wire is a many-body effect but not a single-particle one. Two side-by-side wires with very small inter-wire separation have lent support for the theory, i.e. there exists a coupling between the parallel wires [13,14]. When this coupling between wires becomes strong, the electron wave functions hybridize, forming bonding and antibonding states, which manifest as anticrossings in the 1D energy subbands. Our model calculations [15] further confirm that the minimum energy gap between the states occurs at the point of anticrossing but is not given by the energy difference between the symmetric and antisymmetric states.

In Figure 1, we present a schematic illustration of a device used in the experiments carried out in Refs. [1,9], showing a pair of split gates and a top gate which adjust the confinement potential and carrier density by choosing their voltages suitably. Figure 1 also shows typical conductance features obtained with the device used in Ref. [1] as a function of the split-gate voltage, , for fixed top-gate voltage, . The traces for strong confinement are on the left-hand side, whereas those for weak confinement are on the right. When the confinement is weak, the step may be lost and the appears as the lowest plateau [1]. But, as the confinement is reduced further, the plateau is found to be restored.

With regard to the interpretation that the carriers separate into two rows, the observed emergence of the crossing or anticrossing of energy levels needs explanation, preferably with the use of a quantum-mechanical theory. This may be verified by calculations of the kinetic, direct Coulomb, and exchange energies of electrons in wires with intermediate widths as well as for two extreme limits of very narrow and wide wires. In fact, we have recently demonstrated that these cases may be tracked down to the physical mechanism responsible for switching of the ground state as the wire width is varied from one value to another [15]. In the presence of the Coulomb interaction, two-electron states may be employed as a basis set for constructing the anticrossing-level states [1] when two electrons travel ballistically along a quasi-1D channel. The corresponding calculations have shown that the significance of the Coulomb induced level anticrossing within a quantum wire may be adjusted by varying the confinement potential with a top gate voltage [15].

Figure 1. (Color online) Schematic illustration of a device used in our experiments (left-upper corner), including a pair of split gates and a top gate.

Notes: Additionally, typical measured conductance features of the device are also shown as a function of split-gate voltage, for various fixed top-gate voltages, .

There has been related work on conductance measurements of a quasi-1D wire having a quantum dot within the channel due to the presence of an impurity, as well as imperfections in the device geometry [16]. These undesired features may result in results differing from integer multiples of for the conductance steps [17] or oscillations superimposed on the conductance trace [18]. Electron tunneling through the quantum dot in the channel as well as interference effects due to electron back-scattering from an impurity potential are believed to be responsible for these deviations in the values of the conductance plateaus of narrow quantum wires [18].

In the next section, we present a theoretical approach for calculating the conductance for a quasi-1D quantum wire at a low density of electrons. For this, we calculate the lowest energy eigenstates for a pair of interacting electrons within a confinement region. We explicitly determine the ground state of a dilute electron liquid and consequently the lowest conductance plateau. The complex two-electron tunneling [19,20] is not included in this review since it does not contribute to the formation of conductance-plateaus. Furthermore, we highlight below that there is a range of wire widths for which two-electron transport is mediated by anticrossing-level states based on the Coulomb interaction, and, therefore, it is not possible to describe the conductance by using a single-particle formalism.

2. Theoretical formulation of the problem

We will exploit the results for the eigenstates of a pair of interacting electrons within a harmonic confining potential [21,22]. In Ref. [21], a symmetric harmonic potential was introduced. According to Kohn’s theorem [22], for this potential the Coulomb interaction should only affect the relative motion of electrons but not that for the center-of-mass. It has been pointed out that as a perpendicular magnetic field is increased, the ground state will oscillate between a spin singlet and a spin triplet. Bryant [22] showed these electron correlation effects depend on the area of containment. By solving the Schrödinger equation exactly for two interacting electrons, it becomes clear how correlations may select the ground state and give rise to quasiparticles which participate in the transport.

Coherent wavefunctions of two interacting electrons may be maintained during their transport along the channel if scattering by randomly distributed impurities and defects (negligible lattice scattering at low temperatures) is very small for high-mobility short channel samples. Also, if the transmission coefficient for two injected electrons is almost perfect and the inelastic scattering between different two-electron states is nearly vanishing, we are able to use a quantum ballistic transport model for two interacting electrons then the Coulomb interaction between electrons in the channel can be fully taken into account. Ballistic transport of two-electron clusters is assumed along the channel (y) direction. However, the finite width of a conduction channel in the transverse x direction gives rise to quantization of the split cluster energy levels. Each level is assigned to have a free-electron-like kinetic energy for a ballistically moving noninteracting two-electron cluster. This leads to a hierarchy of subbands with quadratic wave-vector dependence. The cluster energy levels are given by with label p and , where is the wave vector of electrons along the channel, is the electron effective mass and the ‘subband edges’ are presented after Equation (27(27) ) in terms of the dimensionless Coulomb integrals. For a fixed linear electron density , the two-electron chemical potential within the channel may be calculated using(1)

which is expressed in terms of the temperature T of the system. Also, the chemical potentials for the left (L) and right (R) electrodes (with areal electron density ) are and , respectively, in the presence of a low biased voltage .

For quantum ballistic charge/heat transport of two interacting electrons in the channel, the charge and heat current densities are calculated from [23](2)

where is the half of the total group velocity of the two-electron state, and are the Fermi functions for noninteracting two-electron states in the left (L) and right (R) electrodes with chemical potentials and , respectively, for noninteracting two-electron states.

In formulating our theory, we start by considering two interacting electrons in an elongated quantum dot within a quantum wire. For this quantum dot, an anisotropic confinement is assumed with a shorter confining length -pagination across the channel (x direction) with a longer confining length along the channel (y direction). Here, the Hamiltonian for two interacting electrons can be written as(3)

where labels each electron, , is the confining potential for the conduction channel, is the single-electron Hamiltonian, and represents the electron–electron interaction in a medium with background dielectric constant .

The single-particle eigenstates can be determined from the Schrödinger equation , where the eigenfunctions constitute a complete orthonormal set in the single particle Hilbert space. After properly antisymmetrizing the two particle basis, including both the orbital and spin parts, we obtain(4)

where is the spinor for the spin state of an electron. Here, the basis states in Equation (4(4) ) are degenerate eigenstates of the noninteracting Hamiltonian with . We restrict ourselves in the following to the case when only the lowest two orbitals and are populated.

If we assume that two electrons stay in the same spin state with , the spinor part can be factored out, giving rise to(5)

However, if we assume that two electrons remain in opposite spin state with and , then the result becomes(6)

Consequently, the subspace of the lowest states for two independent electrons can be spanned by the following basis [24](7)

Here, the six components of these two-electron sets are orthonormal, i.e. . Moreover, using the above six states, the interacting Hamiltonian matrix can be cast into the form of(8) where is the Coulomb matrix element. Explicitly, we define the notations for the Coulomb matrix elements as(9)

Introducing the Fourier transform to the Coulomb potential, we are able to express its matrix elements using the Coulomb and exchange integrals, i.e.(10)

This gives rise to(11)

where we have employed the form factor, given by(12)

Similarly, we can obtain other nonzero matrix elements from(13)

After we diagonalize the Hamiltonian matrix in Equation (8(8) ), both the energy eigenvalues and associated eigenstates can be obtained in a straightforward way.

Now, let us consider explicitly a harmonic confining potential for electrons within the plane, i.e.(14)

with . As a result, the orbital parts of the single-particle eigenstates can be written down as(15)

We will choose two eigenstates, and , where is the one-dimensional oscillator wavefunction for . This yields(16)

as well as(17)

Here, and are the confining lengths, and then, the system dimension may be significantly larger along the y-direction compared to that in the x-direction.

We know from Equations (15(15) ) and (16(16) ) that eigenstates and have opposite parity. Consequently, we find , , and . This directly leads to . Moreover, for a harmonic potential the block part of the truncated Hamiltonian in Equation (8(8) ) becomes(18)

From this, we obtain two split energy eigenvalues for the states and , given by(19)

and the uncoupled energy level for the state , as well as the triple-degenerate energy levels for the states , , and . In Equaion (19(19) ), the energy-level coupling , and the level splitting is .

For evaluating , , , , and , we require the following Coulomb integrals:(20)

where we have used , , is the angle between the wave vector and x axis, , and . Additionally, we obtain(21)

where(22)

By combining the results for , , and , this leads to(23)

In a similar way, we find(24)

where(25)

By combining these results for and , we have(26)

The last integral is calculated as(27)

It is important to note that we have assumed a quasi-continuum energy spectrum for a traveling quasiparticle in the longitudinal direction, in contrast with split energy levels in the transverse direction. In this case, the pair of electrons forming the quasiparticle always have the lowest transverse energy plus a free electron-like kinetic energy, resulting from the longitudinal motion. However, the Coulomb interaction between a pair of electrons in this cluster will significantly modify the ‘subband edges’ () due to quantization in the transverse direction.

All quasiparticles, except the transported one, may be treated as a ‘background’ making up the total electron density and have a quasiparticle chemical potential which is determined using Equation (1(1) ). For the interacting two-electron states, by using the above derivations, their energy levels are calculated as , , , and , where that Coulomb coupling term for the two-electron anticrossing states is given by . In this notation, the single-particle energy levels for the harmonic-potential model with anisotropic harmonic frequencies and in the transverse (x) and longitudinal (y) directions, respectively, are: and , while the introduced Coulomb interaction energies are found to be , , , , and , where in terms of the channel length and the background dielectric constant , () is the single-particle level occupation factor, and is the single-electron chemical potential within the channel. At the time when a quasiparticle enters a conduction channel, it will occupy single-particle energy levels and , i.e. occupying the same one or different levels. Such a selection is determined from the subband occupation by the sea of electrons within the channel. After these two noninteracting electrons are injected into the channel, they will interact with each other through either the intrasubband or intersubband Coulomb coupling. The ballistic injection of two noninteracting electrons and the existence of a sea of electrons in the conduction channel are reflected through the inclusion of these two level occupation factors. The Coulomb integral is represented by for if we only consider interacting electron states formed from the lowest (‘0’) and first excited (‘1’) single-particle states.

The channel width and length are directly related to the frequencies and of the 2D harmonic-confining potential by and , respectively. Therefore, we get the simple relations, i.e. , , and . Furthermore, for , we find that scales as for .

In the random-phase approximation, the static dielectric function at low temperature for screening for an electron density and in the channel, may be expressed as [25](28)

where the wave vector . For the parameters chosen in our numerical calculations, we found that the effect due to static screening may be neglected. On the other hand, the static dielectric function for shielding by surface gate electrodes of the electron–electron interaction may be modeled as , for which we may take and d represents the gate insulator thickness [26]. For the parameters used in our numerical calculations, we found that shielding of the interaction between two-electron states may also be neglected.

From the calculated in Equation (2(2) ), the electrical conductance for interacting two-electrons may be expressed as [23](29)

We now present our numerical results and their relationship to recently report experimental data in Ref. [1].

3. Numerical results and experimental data

In our numerical calculations, we use the following parameters:  mK,  mV,  nm, ,  m ( is the free-electron mass). The chosen values are indicated in the figure captions. Specifically, we denote the quantum ballistic transport of two-electron states with anticrossing levels through a conduction channel as one moving through either one of two states .

For clarity, we point out that as two electrons are injected into a conduction channel, they may occupy specific single-particle subbands for their ballistic transport. The selection rule is determined by the occupation factor of the electrons already sustained within the conduction channel. During the time interval that the two injected moving electrons remain within the channel, they may interact with each other through either the intrasubband or the intersubband Coulomb coupling. We emphasize that the linear density for confined electrons within the channel may be kept constant even when the channel width is varied. However, for this to occur, the Fermi energy must automatically adjust itself to accommodate all electrons and additional subbands will be populated with reduced energy level separations. Specifically, although the Fermi energy is reduced, the number of electrons in the channel is not changed at all. Furthermore, even when the Fermi energy is reduced, the second level can still be populated due to reduced level separation at the same time so as to keep the number of electrons in the channel a constant. Clearly, enhancement of the Coulomb interaction is not solely determined by the electron density, since it also depends on how electrons are distributed. For the Coulomb effect on the two-electron states, the inclusion of a new populated two-electron state, where one electron stays in a lower-energy level while the other electron populates a higher level, will introduce a new Coulomb-interaction channel for the two-electron states.

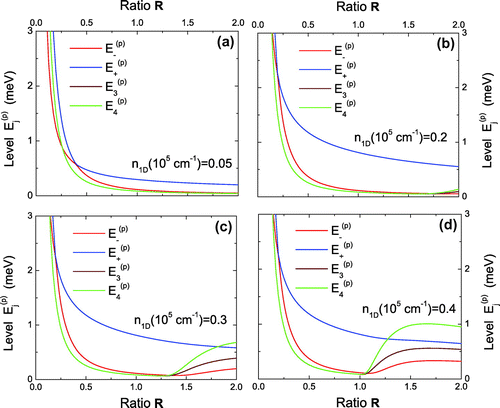
3.1. Two-electron energies within the channel

We know that as the transverse confinement becomes weaker (or the value is increased), the kinetic part of the energy levels of a two-electron state will decrease like as for fixed . On the other hand, the Coulomb interaction only scales as as per our discussion preceding Equation (28(28) ). Consequently, the significance of the Coulomb interaction is expected to increase relatively by increasing . Moreover, the level separation will be reduced by increasing , leading to occupation of the second energy level for fixed electron density. Therefore, the additional Coulomb repulsion between two electrons on different single-particle energy levels must be considered. This effect can be seen from Figure 2(b)–(d) as the upward shifting of energy levels and (as ) in the region of as  cm. At the same time, the level is pushed upward above the level due to the enhanced Coulomb interaction for . On the other hand, for the two-electron state, which is associated with two excited-state electrons, it is largely dominated by the kinetic energy part for the whole range of shown in this figure. When is further increased, the Coulomb repulsion effect pushes into the intermediate confinement regime () in Figure 2(d). Due to the combined effect of these two factors, we observe the recovery of the ground state level in Figure 2(d) for large values of and (where the Coulomb energy is dominant) from that in Figure 2(a) for small values of and (where the kinetic energy of electrons is dominant). It is interesting to see that the Coulomb interaction between electrons stands out to give rise to a pushing up of three energy levels and the recovery of the the ground level at the same time in an intermediate confinement regime () between the strong (scaling as fast drop for ) and weak (scaling as slow drop for ) confinement regimes.

Figure 2. (Color online) Plots of cluster energy levels as a function of geometry ratio with four different values of linear electron density .

Figure 3. (Color online) Plots of conductance G as a function of geometry ratio with four different values of linear electron density for both noninteracting and interacting cases.

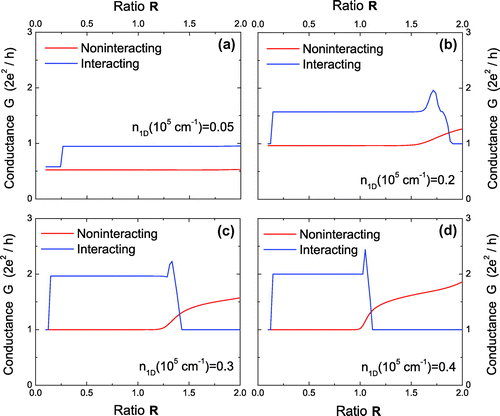
3.2. Ballistic conductance within a quasi-1D channel

The recovery of the ground-state in Figure 2 plays a significant role on both the distribution of conductance plateaus and the interplay from interaction effects, as displayed in Figure 3. We know the Coulomb coupling may be neglected for small , where the conductance plateau is found for the interacting two-electron state as shown in 3(a) with almost all values of . As increases to  cm in 3(b), the plateau shown in 3(a) disappears except for its reappearance very close to . If the value of gets even larger, as seen from Figure 3(c) and (d), the new conductance plateau occurs for an interacting two-electron state, corresponding to the population of the degenerate lowest and energy levels after their level crossing with another state. However, when further increases above one in the very-weak confinement regime, the ground-state recovery, as discussed in Figure 2(c) and (d), enforces the reoccurrence of the conductance plateau due to the Coulomb repulsion between electrons in the central region of the channel.

Figure 4. (Color online) Plots of cluster energy levels as a function of linear electron density with four different values of geometry ratio .

Note: Inset in 4(b) brings us a blow-out view for the anticrossing of energy levels and .

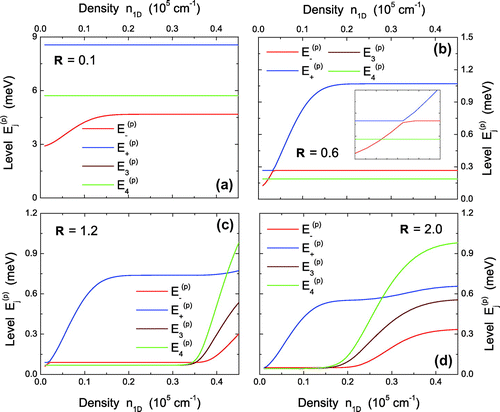
3.3. Dependence of interacting electron energy on linear density

When electrons interact with each other, their energy levels are expected to depend on the electron density , as shown in Figure 4. When the geometry ratio is small for strong confinement in Figure 4(a), only the ground state is affected by varying due primarily to in this case. As is increased to 0.6 in Figure 4(b), both the level crossing between of the anticrossing state with the degenerate state and the level anticrossing between and states occur at lower densities. As , the Coulomb interaction between electrons becomes much stronger, as presented in Figure 4(c) and (d). Therefore, both and levels are pushed up significantly at higher densities (i.e. ), leading to a recovery of the ground state to . At the same time, the state in Figure 4(c) and (d) changes from the degenerate ground state at lower to the highest-energy state at higher . Furthermore, under a transverse magnetic field, we expect that the state should decouple from the magnetic field due to total spin , while the degenerate state with total spin will be split into three by the Zeeman effect, leading to new and conductance plateaus [27].

Figure 5. (Color online) Plots of conductance G as a function of linear electron density with four different values of geometry ratio for both noninteracting and interacting cases.

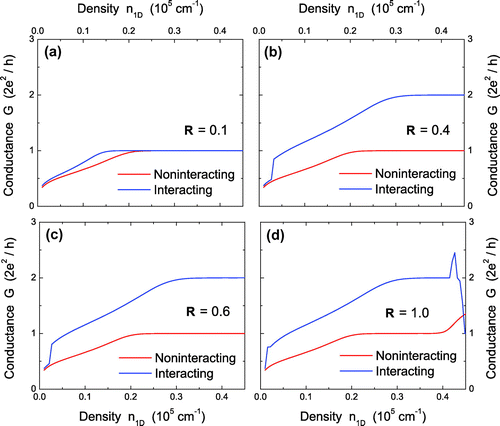
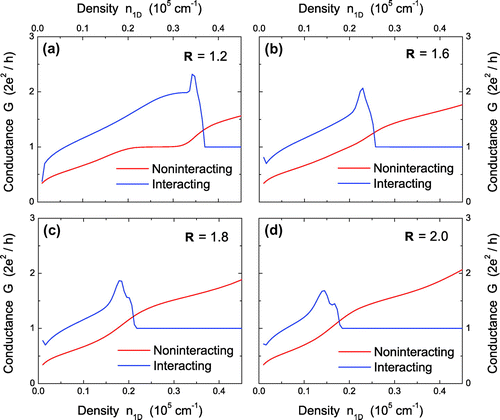
3.4. Conductance for two interacting and noninteracting electron pairs

Figure 5 presents a comparison of the conductance G for both a noninteracting and interacting two-electron state in the range of . For very strong confinement in 4(a), the Coulomb-interaction effect becomes negligible in comparison with the dominant kinetic energy of electrons and a conductance plateau remains with increasing . On the other hand, as goes up to 0.4 in 5(b) and 0.6 in 5(c) for cases with strong confinement, although G for a noninteracting two-electron state remains largely unchanged, for an interacting two-electron state, the conductance plateau in Figure 5(a) is completely destroyed by the Coulomb interaction and replaced by a new plateau. This unique feature is attributed to the result of both a level-crossing and a level anticrossing observed in Figure 4(b). However, the new conductance plateau is severely perturbed at higher densities by a sharp spike and followed by a deep dip to the lower plateau as for intermediate confinement in 5(d).

Although the dimensionless Coulomb integrals do not depend on the linear electron density , the energy levels for a two-electron cluster is proportional to the occupation factors ( and ) in addition to these Coulomb integrals. Moreover, these occupation factors are determined by the chemical potential for noninteracting electrons through the Fermi function for fixed . On the other hand, the cluster chemical potential , determined by Equation (1(1) ), controls the behavior of cluster ballistic transport in the presence of a bias voltage .

Figure 6. (Color online) Plots of conductance G as a function of linear electron density with another four different values of geometry ratio for both noninteracting and interacting cases.

3.5. Conductance for weak confinement

We present in Figure 6 the change in the conductance plateau with increasing in the weak confinement regime. When , conductance plateaus for the noninteracting two-electron state are washed out in Figure 6(b)–(d) due to very small single-particle energy level separation compared to the thermal energy . It is also evident that the incomplete conductance plateau in Figure 6(a) for the interacting two-electron state is completely destroyed in this regime. However, the recovery of the single-particle-like plateau, as displayed in Figure 5(a), is found in Figure 6. Additionally, the plateau further expands and extends to lower and lower electron densities as increases to 2.0 in Figure 6(d). This unique reoccurrence feature can be fully accounted for by the rising energy levels at higher densities due to the relatively enhanced Coulomb repulsion as shown in Figure 4(c) and (d).

As displayed in Figure 4, both and remain degenerate for all chosen values of as far as or alternatively for only small values as . The level-crossing between and the degenerate levels and is the reason behind the upward jump of the conductance from 2 to , as can be seen from Figure 5. However, the degeneracy of the and levels may be lifted by an enhanced Coulomb repulsion for as well as for large values of . Consequently, the subsequent downward dip in the conductance from 4 to is observed in Figure 6.

Figure 7. (Color online) Contour plots of conductance G as functions of both linear electron density and geometry ratio for either noninteracting (left panel) or interacting (right panel) case.

Notes: As labeled by the color bars in this figure, the color scales (from blue up to orange) are (left) and (right), respectively.

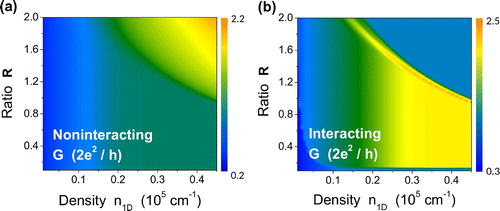
In order to acquire a complete picture of the quantum ballistic transport of interacting two-electron states passing through a quasi-1D conduction channel, we present the contour plots of electron conductance G as functions of and in Figure 7 for both noninteracting and interacting two-electron states as a direct comparison. By comparing Figure 7(a) with Figure 7(b), we find that the effect of the Coulomb coupling becomes most dominant in the upper right-hand corner of Figure 7(b) within a weak confinement regime and with a relatively high electron density at the same time. In this case, a gradually increasing conductance for noninteracting electrons is replaced by a conductance plateau. This is due to the Coulomb repulsion in interacting two-electron states. In addition, another conductance plateau shows up in the lower right-hand corner of Figure 7(b). This is separated by a spike in G from the upper right-hand corner. In this region, confinement is intermediate or strong but the electron density is high.

In our numerical results presented above, we limit the bias voltage to a very small value (0.01 mV), where G becomes essentially independent of . The increase of can induce a ‘hot-carrier’ effect and reduce the ballistic conductance with increasing temperature, as presented in Figure 8, where the conductances G for both noninteracting [in Figure 8(a)] and interacting [in Figure 8(b)] with mV are compared with each other. From Figure 7(a) and (b), we find G for noninteracting electrons has been changed qualitatively for different values of , although G for electron clusters is only modified quantitatively. We further demonstrate such a bias dependent effect on G of electron clusters in Figure 8(c), where three different values of are chosen for  cm. As can be seen from Figure 8(c), the spike in G is significantly broadened and the plateau of G on both sides of the spike is reduced simultaneously with increasing . This is similar to the hot-carrier effect with increased T.

Figure 8. (Color online) Contour plots of G as functions of both linear electron density and geometry ratio for either noninteracting (a) or interacting (b) case at  V, as well as the plot of G as a function of (c) at  cm for three different values of bias voltage .

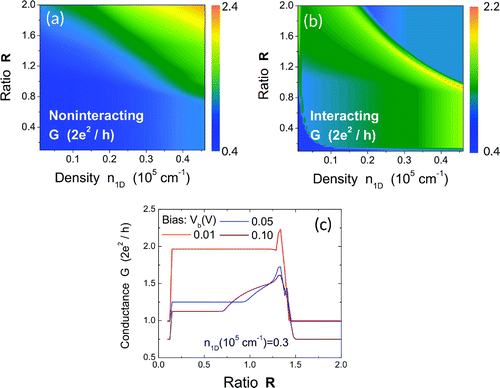
Figure 9. (Color online) Plot of measured differential conductance in (a) as functions of split gate voltage for various values of top gate voltage , and in (b) the transconductance ( plot of the data shown in (a).

Notes: The confinement in (a) is controlled by making the top gate negative so that left (right) of the plot is strong (weak) confinement, where a direct jump to (indicated by arrows) occurs when the confinement is weakened using a top gated, split-gate device. In addition, the first trace in (a) on the left is taken at  V and successive traces were plotted in steps of 90 mV until  V.

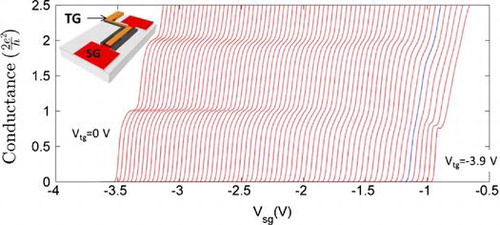
We now turn our attention to the experimental aspects which are related to the preceding theoretical results. Two-terminal differential conductance measurements were performed with an excitation voltage of V at 73 Hz using the Oxford Instruments cryofree dilution refrigerator, where the device is estimated to have an electron temperature of around 70 mK.

In order to the test the samples, a top gated, split gate device provided additional confinement to the quasi-1D electrons. This allowed us to vary the confinement from being very strong (zero top gate) to very weak (very negative top gate voltage). In the present study, as shown in Figure 9, the top gate voltage, , is varied from  V (left) to V (right) in steps of 90 mV.

Figure 9 shows a plot of the differential conductance in (a) for the device as a function of the split gate voltage for various values of the top gate voltage , as well as in (b) for the transconductance ( drawn from the data in (a). As can be seen from Figure 9(a), as the confinement is reduced, the conductance plateau is weakened. If the confinement is further reduced, the plateau disappears and is replaced by a direct jump in conductance to the (rounded) plateau at both and  V (indicated by arrows). Eventually the first plateau at is recovered on further reducing the confinement to  V (right-most red curve). In comparison with our calculated results presented in Figures 5 and 6, we find the sequence from the appearance of the conductance plateau for small values of . We have obtained results for strong confinement as well as the conductance plateau for intermediate confinement, and again the conductance plateau in the weak-confinement regime which is preceded by a double-kink structure. In addition, from Figure 9(b) we know the crossing/anticrossing of the ground state and the first excited states depends on the confinement strength. Here, when is around V, the ground state and the first excited states cross, leading to energy reversal such that previous excited state becomes the new ground state, and then, the previous ground state further moves up in the energy and anticrosses with the second excited state. This observation qualitatively agrees with the calculated results presented in Figure 2.

We would like to emphasize that the appearance/disappearance/reappearance of a conductance plateau has been qualitatively reproduced in our numerical calculations. This is displayed in Figure 3, although some nonmonotonic features in our reported results are not verified experimentally. We acknowledge that there is some nonmonotonic behavior in the results of our simulations, e.g. in Figures 3 and 6, preceding the onset of the first conductance plateau which is verified by the experimental data. However, apart from this, we do believe that we have qualitatively reproduced a significant part of the experimentally observed recurrence of the first conductance plateau with increasing channel width. This is an aim of our review, and such an observation highlights the importance of the Coulomb interaction between electrons after appreciably suppressing the electron kinetic energy contribution as the channel confinement becomes very weak.

4. Concluding remarks

The ballistic conductance for a quasi-1D channel (quantum wire) has exhibited an interesting behavior as functions of the electron density as well as confinement. We demonstrated that electron–electron interaction plays a crucial role in our calculations in the weak confinement regime. Extensive calculations were carried out in regards the effects due to confinement on the conductance and its associated dependence on the interplay between level anticrossing and crossing in quantum transport of two interacting-electron clusters. As shown in our numerical results, depending on the confinement parameter, the conductance manifests the signature of single-particle or interacting two-electron state behavior. This dependence can be observed in the deviation of the conductance from (single-particle) to (interacting crossing state) and back to (interacting anticrossing state) as a function of the width of the quantum wire. It is interesting to observe how many-body effects enter the calculation of the quantum ballistic conductance, where the center-of-mass velocity is not affected by the electron–electron interaction but the electron distribution is affected.

We conclude that the experimental observations qualitatively agree well with our theoretical calculations. Furthermore, such experimentally observed features for switching conductance plateau can be physically explained by the interchange of the ground between and the degenerate and and back to , which is reflected as an upward jump from 2 to and followed by another step jump from back to with increasing channel width. Additionally, we note that the Lüttinger-liquid behavior in a one-dimensional electronic system under the electrical-quantum limit is expected in the presence of an electron–electron interaction, where all electrons occupy the same lowest conduction subbband. However, in our system, four considered spin-dependent paired-electron states come from the combination of two electron orbital states associated with different conduction subbands. Therefore, the recovery of our system to the Lüttinger liquid should not occur here by going beyond this electrical-quantum limit. Thus, our system does not satisfy the major criteria of a Lüttinger liquid. On the other hand, in the electric-quantum limit, we do expect a full recovery of the Lüttinger-liquid behavior in our system as described by standard many-body theory. However, the effects of tunneling of hybridized pairs of electrons through a one-dimensional channel discussed in this paper will be lost completely in this limit.

Acknowledgements

We are grateful to EPSRC,(UK), for support of work at UCL.

Notes

No potential conflict of interest was reported by the authors.