Disorder effects on quantum transport and quantum phase transition in low-dimensional superconducting and topological systems

ABSTRACT

Disorder effects inevitably exist in realistic samples, manifesting in various physical properties. In this paper, we review the recent progress in understanding the disorder effects on quantum transport and quantum phase transition properties in low-dimensional superconducting and topological systems. As a consequence of the pronounced quantum fluctuation in low-dimensional systems, rare events drastically change the physical characteristics and underlying microscopic transport process in these systems, which are beyond the traditional paradigms. Associating with recent experimental observations, we emphasize the microscopic mechanism for disordered Ising superconductivity, the quantum Griffiths singularity of superconductor metal transition and the discrete scale invariance in topological materials.

GRAPHICAL ABSTRACT

KEYWORDS:

• Ising superconductivity
• quantum Griffiths singularity
• discrete scale invariant
• disorder effect
• quantum transport

1. Introduction

Recent years, the rapid developments of two-dimensional (2D) superconductor and topological materials have provided new platforms to investigate a variety of quantum phenomena [1–7]. Exploring these phenomena remains an important pursuit for both experimental and theoretical research. In the early days, the fundamental Hohenberg-Mermin-Wagner theorem points out that the long range ordered phase can not exist in finite temperature 2D system due to the thermal fluctuation [8,9]. However, the Berezinskii-Kosterlitz-Thouless (BKT) transition occurs in a realistic 2D superfluid and superconductor, which allows for the establishment of quasi-long-range correlation of the order parameter [10–12]. In recent years, with the advancements of the nanotechnology including molecular beam epitaxy, pulsed laser deposition, scanning tunneling microscopy/spectroscopy and so on, various types of atomic-scale superconducting materials have been fabricated and characterized in unprecedented progress [13–15]. Also, the prominent fluctuation and spin-orbit coupling have been proven indispensable in two-dimensional (2D) superconductors. As a consequence, 2D superconductors exhibit many exotic properties different from conventional three-dimensional (3D) system, such as the Zeeman-protected Ising superconductivity in 2D superconductors protected by spin-orbit interaction [1,16–25], the emergence phase of anomalous quantum metal [2,26], the quantum Griffiths singularity (QGS) [27] of superconductor-metal transitions (SMTs) etc. Explanations for these phenomena are beyond the scope of traditional paradigms.

Meanwhile, large emergence of topological materials have attracted considerable attention in the field of condensed matter physics [5–7]. Especially, certain topological semimetals have extremely low carrier concentrations, and are easy to reach the quantum limit under a strong magnetic field, showing anomalous transport properties [28–32]. In addition, topological Dirac or Weyl semimetals show linear dispersion around the Weyl points, and the supercritical Coulomb attraction around the charge impurity can lead to novel phenomena such as supercritical collapse behaviour [29,33]. In topological semimetals, the supercritical Coulomb attraction can lead to quasi-bound state spectra obeying discrete scale invariance, namely the binding energy is in geometric progression. Under magnetic field, novel type of quantum oscillations emerge with periodicity in ln(B), in sharp contrast to the well-known Shubnikov-de Haas oscillations. In general, the characteristics of quantum transport and quantum phase transition in topological semimetals and 2D superconductor are largely enriched by disorder effects, which can provide a platform to testing the new theoretical paradigms and to searching for possible original framework for understanding the anomalous transport features in recent experiments.

2. Disordered ising superconductivity

The research of superconductivity has always been a hot topic. In 1957, John Bardeen, Leon Cooper and Robert Schrieffer (BCS) proposed a microscopic theory of superconductivity that the attractive electron–electron interaction mediated by phonons gives rise to Cooper pairs and superconductivity can be described as a microscopic effect caused by the condensation of Cooper pairs [34]. Such a theory has many qualitative and a few quantitative points of agreement with related experiments, in particular with specific-heat data, energy gap measurements, and transition-temperature versus impurity curves [35]. To further prove the validity of BCS theory, P. W. Anderson studied the dirty superconductors with elastic scattering from impurities and demonstrated that other types of pairing except for the s-wave pairing are not compatible with the existence of dirty superconductors [36]. Meanwhile, A. A. Abrikosov and L. Gor’kov studied alloys containing paramagnetic impurities based on the quantum field theory [37], and had shown that the presence of paramagnetic impurities can diminish the s-wave pairing superconductivity. The dependence of $T_c$ on the paramagnetic impurity concentration can be derived via the Gor’kov Green function [38–40]. Moreover, apart from magnetic impurity, there exist other pair-breaking mechanisms of the conventional superconductor. Clogston and Chandrasekhar had illustrated under magnetic field the Zeeman energy exceeds the condensation energy corresponding to the so-called value of Pauli limit for the magnetic field [41–43]. Subsequently, Werthamer, Helfand and Hohenberg (WHH) generalized the Abrikosov and Gor’kov theory to include the orbital effect, the paramagnetic effect, and the spin-orbital scattering effect [44].

Nevertheless, the WHH theory mainly focus on the 3D superconductors, which is not suitable to describe low dimensional superconductors [16–20]. In layered superconductors, the reduction of dimensionality weakens the orbital effect when the magnetic field parallels the layered plane, thus the spin-orbit scattering can randomize the spin orientation and lead to enhancement of in-plane critical field $B_c$³⁵. Klemm-Luther-Beasley (KLB) had firstly proposed the microscopic theory applicable to layered superconductors in the dirty limit with strong spin-orbit scattering [45,46].

Afterward, with the advancements of film-growth techniques, various types of high-quality 2D crystalline superconducting films have been fabricated [13–15]. One striking discovery is the Ising pairing mechanism with pronounced enhancement of in-plane upper critical field $B_c$ beyond the Pauli limit, such as ion-gated $Mo{S}_2$, monolayer $NbS{e}_2$. However, this enhancement of in-plane $B_c$ can not be explained by the KLB theory, because the value of the spin-orbit scattering time estimated from the KLB theory turns out to be much shorter than that of the total scattering time obtained from transport data [16]. In $Mo{S}_2$ and $NbS{e}_2$, the atomic spin-orbital interaction (SOI) is very strong due to the heavy transition metal atoms. And inversion symmetry breaking and SOI lead to the spin polarizing perpendicular to the layer plane around the Dirac points, namely the type-I (inversion-asymmetric) Ising superconductors [1,16–23]. However, in addition to the inversion-asymmetric Ising pairing, certain 2D inversion-symmetric materials with spin splitting around the $\mathrm{\Gamma }$ point due to intrinsic SOI are very recently found capable of superconductivity [47] [see Figure 1]. Systematic models are needed to investigate the pair-breaking mechanism and in-plane $B_c$ in both the inversion-symmetric and inversion-asymmetric Ising superconductors, taking into account of the combination effects of spin-orbit interaction and impurity scattering.

Figure 1. Mechanisms for an enhanced in-plane upper critical field. (a) Type-I Ising superconductivity: pairing of electrons on opposite spin split valleys. Here only one pair of electron pockets centered on $K$ and $K{ }^{\mathrm{\prime }}$ points are highlighted. (b) Type-II Ising superconductivity: pairing of charge carriers on orbits around Γ point with their spins aligned in the out-of-plane orientation. Hole bands are illustrated as an example. The red and blue circles indicate two energetically degenerate bands with opposite spin orientations, each of which have spin split counterparts below the Fermi level (indicated by the dashed circles). Reproduced from Ref.[47]

2.1. The microscopic theory of two-dimensional Ising superconductivity

To improve agreement between theory and experiment, a general microscopic theory for 2D Ising superconductors is proposed in Ref.[48], which generalize the Ising superconductivity theory containing the intrinsic SOI, the impurity scattering, and the Rashba SOI simultaneously. This theory stem from the Gor’kov equation of transition temperature $T$ [44,49]:

(1) $ln\left(\frac{T_c}{T}\right)=k_{B}T\sum _n\left[\frac{\pi }{|\omega |}-\frac{1}{2k_{B}T}tr{S}_{\omega }\right],$(1)

where the system has translation symmetry after the impurity average and the integral kernel function $S_{\omega }(\hat{p})\equiv \frac{k_{B}T}{\mathrm{\Delta }}\int d\xi F_{\omega }(\vec{p})$ is assumed to be isotropic. $F_{\omega }(\vec{p})$ is the anomalous Green’s function in momentum space.

2.1.1. Type-I (Inversion-asymmetric) Ising superconductivity

We firstly discuss the inversion-asymmetric Ising superconductivity caused by the Zeeman-type intrinsic SOI. Taking 2D hexagonal lattice as an example [see Figure 2(a,b)], the intrinsic SOI serves as effective out-of-plane magnetic field which takes opposite value at valley $K$ and $K{ }^{\mathrm{\prime }}$, inducing the spin spiltting of energy bands, namely the Zeeman-type SOI. Around each valley, the Zeeman-type SOI can give rise to double Fermi surfaces (FSs) with almost the same radius and shape. Then the electrons at $K+k_r$ and $-K-k_r$ ($r=1,2$ labels the two FSs) with opposite out-of-plane spins form the inter-valley Cooper pairs obeying the time-reversal symmetry. When applying an in-plane magnetic field $B\hat{x}$, the Hamiltonian reads [50]:

(2) $H_I(k)=\frac{{\mathrm{\hslash }}^2{k}^2}{2m}-{\beta }_{so}{\sigma }_z{\tau }_z-{\mu }_{B}B{\sigma }_x,$(2)

Figure 2. (Colour online) (a) Brillouin zone of ultrathin Pb film (inversion-asymmetric Ising pairing), with double non-degenerate Fermi surfaces (FSs) at each valley (green dashed circles). Inter-valley Cooper pairing form between electrons with the same color and opposite momentum. (b) Valley structure of Pb film in the vicinity of $E_F$. Each valley has two electron pockets, and Zeeman-type SOI polarizes electron spin oppositely around $K$ and $K{ }^{\mathrm{\prime }}$. (c-d)Theoretical fitting of $B_c/B_p$ as a function of $T/T_c$ for 6-ML Pb film. (c) shows good agreement with the microscopic theory of Zeeman-protected superconductivity [black solid line, .Eq. (3(3) $ln\left(\frac{T_c}{T}\right)=\frac{{\mu }_B^2{B}^2}{{\widetilde{{\beta }_{SO}}}^2+{\mu }_B^2{B}^2}Re\left[\psi \left(\frac{1}{2}+\frac{i\sqrt{{\widetilde{{\beta }_{SO}}}^2+{\mu }_B^2{B}^2}}{2\pi k_{B}T}\right)-\psi \left(\frac{1}{2}\right)\right].$(3) )] and yielding an effective Zeeman-type SOI $\widetilde{{\beta }_{SO}}=3.01$ meV. (d) shows the results with a fixed effective Zeeman-type SOI and increasing effective Rashba-type SOI. The black curve presents the best fit of the experimental data with effective Zeeman-type SOI $\widetilde{{\beta }_{SO}}=3.16$ meV and effective Rashba-type SOI $\widetilde{{\alpha }_R{k}_F}=0.22$ meV. The olive line indicates a special case with only effective Rashba-type SOI ($\widetilde{{\alpha }_R{k}_F}=30$meV, $\widetilde{{\beta }_{SO}}=0$ meV), which is far below the experimental results. Reproduced from Ref. [21]

where $m$ is the effective mass, $\sigma$ and $\tau$ denote the real spin subspace and valley subspace, respectively. Then the relation between critical field $B_c$ and temperature $T$ can be solved within the WHH framework.

To be specific, if considering Zeeman-type SOI protected superconductivity with spin-independent scattering, the spin-independent scattering disorder gives a finite lifetime $\frac{\mathrm{\hslash }}{{\tau }_0}=2\pi n_{i}N(0)V^2$ with $n_i$ denoting the disorder concentration. Here, one can introduce effective Zeeman-type SOI parameter $\widetilde{{\beta }_{SO}}=\frac{{\beta }_{SO}}{1+\mathrm{\hslash }/2\pi k_B{T}_C{\tau }_0}$, and the upper critical field $B_c(T)$ for the Zeeman-type SOI protected superconductivity in the dirty limit reads [21,48]:

(3) $ln\left(\frac{T_c}{T}\right)=\frac{{\mu }_B^2{B}^2}{{\widetilde{{\beta }_{SO}}}^2+{\mu }_B^2{B}^2}Re\left[\psi \left(\frac{1}{2}+\frac{i\sqrt{{\widetilde{{\beta }_{SO}}}^2+{\mu }_B^2{B}^2}}{2\pi k_{B}T}\right)-\psi \left(\frac{1}{2}\right)\right].$(3)

If taking both the spin-independent scattering and the spin-flipping scattering into account, the characteristic time satisfies ${\tau }^{-1}={\tau }_0^{-1}+{\tau }_{SO}^{-1}$, and $\tau$, ${\tau }_0$, ${\tau }_{SO}$ denote the mean free time for total scattering, spin-independent scattering and spin-flipping scattering, respectively [21]. Besides, Rashba-type SOI tends to polarize the spin to the in-plane direction, which weakens Zeeman-protection mechanism and changes the $B_c$. The Hamiltonian including the Zeeman-type SOI and Rashba-type SOI simultaneously at the $K$ and $K{ }^{\mathrm{\prime }}$ points are [21]:

(4) $H_{\vec{p},K(K^{\mathrm{\prime }})}=\frac{p^2}{2m}-{\beta }_{SO}{\sigma }_z{\tau }_z-{\mu }_{B}B{\sigma }_x\mp {\alpha }_R\left({\sigma }_x{k}_y-{\sigma }_y{k}_x\right).$(4)

Likewise, one can define the effective Rashba SOI $\widetilde{{\alpha }_R{k}_F}\equiv \frac{{\alpha }_R{k}_F}{\sqrt{2}\left(1+\mathrm{\hslash }/2\pi k_{B}T{\tau }_0\right)}$ and effective Zeeman-type SOI parameter $\widetilde{{\beta }_{SO}}=\frac{{\beta }_{SO}}{1+\mathrm{\hslash }/2\pi k_B{T}_C{\tau }_0}$, the relationship between $T/T_c$ and $B_c$ can be given as well. This microscopic calculation is consistent with previous phenomenological formula [16] after the setting the disorder renormalized value of related parameters.

2.1.2. Type-II (inversion-symmetric) Ising superconductivity

Different from inversion-asymmetric Ising superconductors, like Figure 3(a), the energy valley locates at zero-momentum point $\mathrm{\Gamma }$ in inversion-symmetric Ising superconductors. The intrinsic SOI can split the 4-fold degenerate $P_{x,y}^{+}$ level into two doubly-degenerate levels, opening a gap at the $\mathrm{\Gamma }$ point [14,51]. The lower level crosses $E_F$ at two different Fermi wavevectors form two different-shaped FSs [14], each of which holds two states [see Figure 3(a, b)]. If the radius of the FS is small, the eigenstates of the lower energy level can be approximated by $P_{x-iy,\uparrow }^{+}$, $P_{x+iy,\downarrow }^{+}$. The SOI at valley $\mathrm{\Gamma }$ can be viewed as an out-of-plane magnetic field which takes opposite value $-B_{eff}\hat{z}$ and $B_{eff}\hat{z}$ on different orbits $P_{x+iy}^{+}$ and $P_{x-iy}^{+}$, respectively. Thus, the system has TRS at $B=0$ and electrons with opposite momenta and spins on the same FS can form s-wave Cooper pairs. These pairs with out-of-plane spin-orbit locking give rise to the large in-plane $B_c$. Based on previous study [52], the inversion-symmetric system can be represented by a four band model with basis ($P_{x+iy,\uparrow }^{+}$, $P_{x-iy,\uparrow }^{+}$, $P_{x-iy,\downarrow }^{+}$, $P_{x+iy,\downarrow }^{+}$) with external in-plane magnetic field $B\hat{x}$,

(5) $H_{II}(k)=A{k}^2+\left[\begin{array}{c}{H}_{+}(k)-{\mu }_{B}B{\sigma }_x\\ -{\mu }_{B}B{\sigma }_x{H}_{-}(k)\end{array}\right],H_{\pm }(k)=\left[\begin{array}{c}{M}_0-M_1{k}^{2}v\left(\pm k_x-i{k}_y\right)\\ v\left(\pm k_x+i{k}_y\right)-M_0+M_1{k}^2\end{array}\right].$(5)

Figure 3. Mechanisms for an enhanced in-plane upper critical field and superconducting properties of trilayer stanene. (a) Two doubly-degenerate FSs (green dashed circle) around the $\mathrm{\Gamma }$ point in the Brillouin zone of stanene (inversion-symmetric Ising). The arrows on the FSs denote spin directions along $\pm z$ direction, $k_1$ in blue and $k_2$ in orange. Each FS is doubly degenerate, consisting of two different $P_{x,y}^{+}$ orbitals and out-of-plane spin directions. The pairing happens between $P_{x-iy,\uparrow }^{+}$ and $P_{x+iy,\downarrow }^{+}$ on the same FS if $k_r$ is small. (b) 4-fold degenerate $P_{x,y}^{+}$ level of stanene splits to two doubly-degenerate levels due to SOI. The lower level forms two FSs at $k_1$ (blue) and $k_2$ (orange). (c-e) show the temperature dependence of the in-plane upper critical fields in few-layer stanene samples. Data obtained from four samples with different stanene and $PbTe$ substrate thicknesses. For example, $3-Sn/6-PbTe$ refers to a trilayer stanene grown on top of 6 layers of $PbTe$. The ratio of the in plane upper critical fields. i.e. the magnetic fields at which the sample resistance becomes $50\mathrm{\%}$ of the normal state resistance at a given temperature, to the Pauli limit field $B=1.86T_{c,0}$ are plotted as circular symbols. Solid/dashed curves are theoretical fits by .Eq. (6)(6) $ln\frac{T_c}{T_{c,0}}=-\frac{{\mu }_B^2{B}^2}{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}Re\left[\psi \left(\frac{1}{2}+\frac{i\sqrt{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}}{2\pi k_B{T}_c}\right)-\psi \left(\frac{1}{2}\right)\right],$(6) . $T_{c,0}$ is the zero-field transition temperature. ${\beta }_{SO}^{\ast }$ is the intrinsic SOC strength renormalized by disorder. $\alpha k_F$ denotes the renormalized Rashba SOC strength. Reproduced from Ref. [47]

Here ${\mu }_B$ is the effective Bohr magneton and $A$, $M_0$, $M_1$, $v$ are fitting parameters. Considering the situation of lower band $E_{-}(k)$ crossing $E_F$ at two different Fermi wave-vector and the spin-independent scattering disorder within each FS, the temperature dependence of the in-plane upper critical field read as [48]:

(6) $ln\frac{T_c}{T_{c,0}}=-\frac{{\mu }_B^2{B}^2}{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}Re\left[\psi \left(\frac{1}{2}+\frac{i\sqrt{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}}{2\pi k_B{T}_c}\right)-\psi \left(\frac{1}{2}\right)\right],$(6)

where ${\beta }_{SO}^{\ast }=\frac{\sqrt{{\left(M_0-M_1{k}_F^2\right)}^2+v^2{k}_F^2}}{1+\mathrm{\hslash }/2\pi {\tau }_0\cdot k_B{T}_{C,0}}$ is the disorder renormalized SOC strength, $k_F$, $\psi$, $\tau$ denote the Fermi momentum, the digamma function and the scattering time, respectively. Near $T_c$, this result is consistent with the result from 2D Ginzburg-Landau (GL) theory [53] and the KLB theory [45,46].

2.2. Recent experimental observations of Ising superconductivity

With the advancements of the nanotechnology including molecular beam epitaxy, pulsed laser deposition etc, various types of 2D superconducting materials have been fabricated [13–15]. The high-quality 2D superconductors give rise to many novel physical phenomena due to the prominent influence of intrinsic spin-orbit coupling and quantum fluctuations. Therefore, these systems provide an insightful platform to explore the essence of superconductivity [4,27,54–63].

2.2.1. Type-I Ising superconductors

It has been a significant discovery that ion gated $Mo{S}_2$ and $NbS{e}_2$ can be superconducting [64,65]. Unlike the bulk transition metal dichalcogenides (TMDs) that preserve inversion symmetry, monolayer $Mo{S}_2$ and $NbS{e}_2$ are inversion-asymmetric superconductors [66]. Moreover, the strong SOC in these systems give rise to Ising pairing mechanism. In addition to the aforementioned mechanism, the interface can also give rise to the type-I (inversion-asymmetric) Ising pairing. Ref[21]. has reported the observation of interface-induced Zeeman-protected superconductivity in ultrathin crystalline Pb films epitaxially grown on the striped incommensurate phase on a Si(111) substrate. The $R(B)$ curves of a 6-ML sample are measured in a pulsed parallel magnetic field up to $47$ T. The superconductivity survives under a high parallel magnetic field of $40$ T at $1.7$ K. The experimental data of $B_c/B_p$ versus $T/T_c$ can be quantitatively fitted by Eq. (3)(3) $ln\left(\frac{T_c}{T}\right)=\frac{{\mu }_B^2{B}^2}{{\widetilde{{\beta }_{SO}}}^2+{\mu }_B^2{B}^2}Re\left[\psi \left(\frac{1}{2}+\frac{i\sqrt{{\widetilde{{\beta }_{SO}}}^2+{\mu }_B^2{B}^2}}{2\pi k_{B}T}\right)-\psi \left(\frac{1}{2}\right)\right].$(3) . The fitting procedure gives effective Zeeman-type SOI $\widetilde{{\beta }_{SO}}=3.01$ meV, as shown in Figure 2(c). The enhancement of in-plane critical field can be well explained by the type-I (inversion-asymmetric) Ising superconductivity mechanism. Moreover, in order to clarify the influence of Rashba-type SOI, Figure 2(d) displays a set of theoretical curves with a fixed effective Zeeman-type SOI $\widetilde{{\beta }_{SO}}=3.16$ meV and increasing effective Rashba-type SOI $\widetilde{{\alpha }_R{k}_F}$ from 0.22 to 1.26 meV. The Rashba-type SOI bends the curves down at low temperatures and gives rise to a relatively small in-plane critical field, which deviates from the quasi-linear temperature dependence of measured data, indicating Rashba-type SOI alone cannot account for the observed large in-plane critical field.

2.2.2. Type-II Ising superconductor

Recent experiment has identified a pronounced enhancement of in-plane critical field $B_c$ at low temperature in epitaxial few layer $\alpha$-Sn(111) [14,15,47]. Distinct from the previous system, few-layer stanene has no $M_z$ mirror symmetry and is centro-symmetric in the free standing case [51]. Stanene hosts bands around $\mathrm{\Gamma }$-point instead of the $K$ and $K{ }^{\mathrm{\prime }}$ points as in type-I Ising superconductor. Thus, it needs an alternative mechanism in stanene to produce the out-of-plane spin orientations.

According to the results shown in Figure 3, the experimental data matches well with Eq. (6(6) $ln\frac{T_c}{T_{c,0}}=-\frac{{\mu }_B^2{B}^2}{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}Re\left[\psi \left(\frac{1}{2}+\frac{i\sqrt{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}}{2\pi k_B{T}_c}\right)-\psi \left(\frac{1}{2}\right)\right],$(6) ), which captures the prominent up-turn feature in the low-T regime and helps to qualitatively understand the substrate and layer-thickness dependence of $B_{c,//}$. Such pairing mechanisms behind Eq. (6(6) $ln\frac{T_c}{T_{c,0}}=-\frac{{\mu }_B^2{B}^2}{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}Re\left[\psi \left(\frac{1}{2}+\frac{i\sqrt{{\beta }_{so}^{\ast 2}+{\mu }_B^2{B}^2}}{2\pi k_B{T}_c}\right)-\psi \left(\frac{1}{2}\right)\right],$(6) ), without the participation of inversion symmetry breaking, are termed type-II (inversion-symmetric) Ising superconductivity. In fact, the upturn of $B_{c,//}$ in low-T result from frozen spin orientation at $T\to 0$. When the temperature goes up, thermal activation results in a partially polarized system, suppressing the contribution of the spin-orbit induced spin split effect on $B_{c,//}$. Figure 3 (c-e) show the temperature dependence of the in-plane upper critical fields in few-layer stanene samples. Comparing to $3Sn/12-PbTe$, the smoothening in $3-Sn/6-PbTe$ can be attributed to the variation of the spin locking strength as one moves away from the $\mathrm{\Gamma }$ point along the inverted Mexican hat band shape (inset to Figure 3(c)). Spins of the $|+>$ and $|->$ orbitals are strongly locked out-of-plane at the $\mathrm{\Gamma }$ point. This Ising-like orientation becomes however less favorable at larger momenta. Lowering the Fermi level thus suppresses the spin polarization of the outer hole band, which can be simulated by an effective Rashba term in the Hamiltonian. Taking into account this effect, the modified formula nicely describes the upper critical fields of bilayer stanene (Figure 3d). Since stronger inversion symmetry breaking attribute to the missing up-turn feature, a penta-layer stanene should experience a weaker Rashba effect, giving rise to an apparent enhancement of $B_{c,//}$ at low $T$. This indicates a broader range of inversion symmetry materials host such pairing mechanisms. Recent experiment in ultra-thin crystalline PdTe2 films also demonstrates clear feature of type-II Ising pairing with in-plane critical field more than 7 times the Pauli limit [67].

2.3. Discussion

There may be multiple types of SOI, including the Zeeman type SOI and the Rashba type SOI both may affect the in-plane $B_c$^16,[17], Zeeman-type SOI can cause an out-of-plane spin polarization of energy valleys; hence, it protects the superconductivity under a high in-plane magnetic field both in type-I and type-II Ising superconductor. In contrast, the Rashba-type SOI alone cannot account for the observed large in-plane critical field. Besides, the weak Rashba-type SOI tends to polarize the spin to the in-plane direction, making the Cooper pairs more susceptible to the in-plane magnetic, and destructs the upturn at very low temperature. Lastly, the combination effect large intrinsic SOI and quantum fluctuation may also dramatically influence the perpendicular critical field $B_{c,2}$, including the quantum Griffiths singularity along the anomalous phase boundary [68]. The influence of large intrinsic SOI on the quantum fluctuation needs to be considered with the second order corrections [68,69], which is beyond the WHH framework.

3. Disorder effect on superconductor metal transition: quantum griffiths singularity

The 2D superconductor not only help to explore new superconductivity characteristics, but also exhibit some properties largely deviated from the prediction of mean field theory, such as quantum Griffith singularity (QGS) associated with the superconductor-metal transition [1,27,70–80]. Before introducing this novel property, we briefly introduce the basic theoretical concepts of continuous phase transition and critical phenomena. Phase transitions occur upon variation of an external control parameter. Classical phase transitions are characterized by temperature, and the macroscopic order is destroyed by thermal fluctuations at finite temperature. In contrast, quantum phase transitions take place at $T=0$ in which the control parameter is non-thermal, such as pressure, magnetic field, or chemical composition [81]. When approaching the critical point of continuous phase transition, the characteristic length scales become divergent [82]. Upon approaching the critical point, the correlation length $\xi$ and the correlation time diverge as [83,84]:

(7) $\xi \sim r^{-v},{\xi }_{\tau }\sim {\xi }^z\sim r^{-vz},$(7)

where $r\sim \left|\left(B-B_c\right)/B_c\right|$ is dimensionless parameter and $B_c$ is the critical parameter, $v$ is the correlation length critical exponent and $z$ is dynamical critical exponent. Power-law singularities in the length scales at the critical point generically lead to power-law singularities in observables [85]. The disorder effects may dramatically change the power-law singularity into other kind of universality class, i.e. the quantum Griffiths singularity, as shown in the following subsections. Before demonstrating this anomalous case, we firstly outline the general considerations of scaling theory for continuous phase transition.

3.1. Scaling theory for continuous phase transition

The first unification of phase transitions theories was achieved by L. D. Landau [86,87]. He proposed a mean-field order parameter $m$ describing phase transition behavior at the transition point, $m=0$ represents a disordered state while $m\ne 0$ represents an ordered state. The Landau theory successfully predicts the critical behavior of phase transitions in many systems and intuitively explains the universality of them [84]. Nevertheless, it often deviates from the experimental results, because Landau theory does not take into account the spatial fluctuations or the long-range correlations of order parameters of reality system. Hence, the Landau-Ginzburg-Wilson theory is proposed, which can be attacked successfully using modern renormalization group techniques [88].

The power law behavior at critical point implied the scaling theory. Widom firstly put forward as the scaling hypothesis [89]. The system is scale invariant close to criticality. If we rescale all lengths in the system by a common factor, the physical properties become unchanged. Therefore, the free energy density can be written as [82]:

(8) $f(r,h)=b^{-d}f\left(r{b}^{1/v},h{b}^{y_h}\right),$(8)

where $r$ denotes the distance from the critical point, $h$ is dimensionless measure of external magnetic field, $d$ is the space dimensionality, $v$ and $y_h$ are two critical exponents and $b$ is an arbitrary positive number represents the scale factor. Since all thermodynamic observables can be determined from free energy density that only depends on two exponents, the various exponents are therefore connected by scaling relation [89]. Indeed, the critical exponents are determined only by the symmetries of the Hamiltonian and the spatial dimensionality of the system. The scaling theory indicates the universality of critical exponents [90], and the related concept of universality classes can be well explained within the framework of the modern renormalization group theory [91].

Scaling theory for classical phase transition can be generalized to quantum phase transition (QPT). In general, the kinetic and potential part of Hamiltonian does not commute in quantum statistical mechanics. Therefore, quantum Landau-Ginzburg-Wilson functional needs to be formulated in terms of space and time dependent fields. Then, the imaginary time variable $\tau$ acts as an additional coordinate [84]. Consider the fluctuations in the imaginary axis, ${\xi }_t\propto {\xi }^z$, if we scale length according to $L\to bL$, the imaginary time need scale like $\tau \to b^z\tau$, and temperature regarded as an energy scales like an inverse time $T\to b^{-z}T$. Consequently, the scaling form of the free energy density at a quantum critical point reads [83]:

(9) $f(r,h,T)=b^{-d-z}f\left(r{b}^{1/v},h{b}^{y_h},T{b}^z\right).$(9)

Here, $T$ is the absolute temperature, $b$ is the dimensionless parameter (i.e. the dimensionless magnetic field), and $z$ is dynamics exponent. Comparing Eq. (9)(9) $f(r,h,T)=b^{-d-z}f\left(r{b}^{1/v},h{b}^{y_h},T{b}^z\right).$(9) to Eq. (8(8) $f(r,h)=b^{-d}f\left(r{b}^{1/v},h{b}^{y_h}\right),$(8) ), one can directly find that a quantum phase transition in $d$ dimensions is equivalent to a classical transition in $d+z$ spatial dimensions [92].

3.2. Quantum Griffiths singularity

Many realistic systems contain a certain amount of quenched disorder, viz., the impurities or defects that are spatially non-uniform but not varying over the relevant experimental time scales [93]. How does quenched disorder influence phase transitions and critical points? Harris [94] derived a criterion for the stability of a given critical behavior with respect to quenched disorder. For short range correlated disorder, if space dimensionality $d$ and clean correlation length exponent $v$ fulfill the Harris criterion $dv>2$, weak disorder does not affect the critical behavior of the system, corresponding to the clean limit [74,94–96]. On the contrary, if $dv<2$, weak disorder becomes important and the critical exponent change, namely the dirty limit. Note that Harris criterion only deals with the average behavior of the disorder at large length scales. Furthermore, the spatial non-uniformity random disorder may lead to off-critical singularities at phase transitions [97–100], similarly to the features of random transverse field Ising model [101]. This kind of singularities are called the Griffiths singularities, because R. B. Griffiths firstly proved its existence in 1969 [102]. T. Vojta has provided the whole classification of disorder effect on the scaling behaviours, based on the analysis of the dimension of range regions [84]. Specifically, when Harris criterion is violated, besides the situation of phase transition destruction at strong disorder, there exist two possible critical points according to the behavior of the average disorder strength under coarse-grain [98].

(i) The disorder strength approaches a finite value under coarse-grain. It results in the divergence behavior of quantities near the critical point still obey power-law but with a different set of critical exponent (the new correlation length exponent $v{ }^{\mathrm{\prime }}$ fulfill the inequality $dv{ }^{\mathrm{\prime }}>2$), which differ from those of the clean system.

(ii) The disorder strength diverges under coarse-grain, the transition is characterized by an exotic infinite-randomness critical point. Surprisingly, the temporal correlation length ${\xi }_t$ and spatial correlation length satisfy a activated (exponential) scaling ${\xi }_t\propto {\mathrm{e}}^{{\xi }^{\psi }}$, distinctive from the relation ${\xi }_t\propto {\xi }^z$ in power law scaling. Here $\psi$ is the activated dynamical index.

The second special case is relevant to recent experiments in 2D superconductors. A typical model demonstrating the activated (exponential) scaling behaviour is the random transverse-field Ising model, as introduced in the following subsection.

3.2.1. Random transverse-field Ising model

Let us start by discussing the effects of rare strong spatial disorder fluctuations on phase transitions. Considering the example of a diluted classical ferromagnet, the dilution reduces the tendency towards magnetic long-range order and thus reduces $T_c$ from its clean bulk value $T_{c,0}$. In an infinite system, one can find arbitrarily large spatial regions that are devoid of impurities. These regions will show local magnetic order even though the bulk system is globally in the para-magnetic phase, called rare regions [84].

Long-range disorder correlations can immensely increase the rare region effects. This rare region effect was firstly well depicted in the McCoy-Wu model [103], a 2D classical Ising model with linear defects. In quantum phase transitions with quenched impurities, the systems are therefore always correlated at least in the temporal dimension. Thus, rare region effects in a quantum phase transition are expected to be stronger than in a classical one. One of the typical random quantum systems models displaying a quantum phase transition is the random transverse field Ising model, the Hamiltonian reads:

(10) $H=-\sum _{(ij)}{J}_{ij}{\sigma }_i^z{\sigma }_j^z-\sum _i{h}_i{\sigma }_i^x,$(10)

where the $J_{i,j}$ are random positive interactions, the random transverse fields $h_i$ cause the quantum fluctuations. At temperature T, such a quantum system in d-dimensions is equivalent to a $d+1$ dimensional classical Ising model with the couplings independent of the ”time” direction in which it has extent $1/T$. The behavior of the random transverse field Ising model was not fully understood until D. S. Fisher [101,104,105] applied a strong-disorder renormalization group method to the problem.

The main idea of the strong-disorder renormalization group is to take the strongest coupling $\omega =max(h_i,J_{i,j})$ in the system and coupling to the rest of the system is treated perturbatively [91]. After integrating the strongest coupling bond (or site), one can eliminate one bond (or site) and derive a new effective Hamiltonian with fewer degrees of freedom. The repeated application of this procedure establishes an exponential relationship between the length scale $L$ of the clusters and effective bonds scale with the logarithm of the energy scale

(11) $L^{\psi }\sim ln\left({\omega }_0/\omega \right),$(11)

with the exponent $\psi$, and ${\omega }_0$ represents the basic energy scale. Thus, the random transverse field Ising model displays activated dynamical scaling rather than conventional power-law scaling. The critical fixed point in the random transverse field Ising model is also called infinite randomness fixed point. This peculiar activated scaling property originates from the property that the probability for finding a large spatial region of volume $V$ decreases exponentially $\sim exp(-pV)$⁸⁴. Moreover, if a system is pushed slightly off critical with a distance $\delta$, the correlation lengths satisfies $\xi \sim |\delta {|}^{-\nu }$ with $\nu$. In the quantum Griffiths phase, the activated scaling law results in a typical energy scale $\omega$, which obeys $ln(\frac{\omega }{{\omega }_0})\sim {\xi }^{\psi }$. If the conventional scaling analysis is applied to the finite temperature regime in the quantum Griffiths phase, one can obtain a diverging effective dynamical exponent $z$ satisfying [105]:

(12) $z\sim {\delta }^{-\psi \nu },$(12)

which indicates the feature of Griffiths singularity. In other words, Griffiths phase is dominated by the rare regions in which the probability of correlation length $\xi$ proportional to $e^{-p{\xi }^d}$, ($p$ is parameter of system, $d$ denotes dimensionality). The rare regions cause the non-analytic behavior of the thermodynamic potential function before reaching the critical point, thus, break the power law scaling law of the system [19,106]. Moreover, the activated scaling analysis can be applied directly to elucidate the quantum Griffiths phase [107–109].

3.3. Observations of quantum Griffiths singularity in SMT experiments

The superconductor insulator/metal transitions, representing typical examples of quantum phase transitions (QPTs), have been observed in several quasi-2D disordered superconducting systems [110–112]. Such QPTs are expected to be realized by tuning the film thickness or the applied magnetic field in these systems. The critical magnetic field $B_c$ of superconductor insulator/metal transition is considered equal to the crossing point of sheet resistance $R_S(B)$ curves at different temperatures [74,113]. Recently, it is striking that two crossing points of $R_S(B)$ curves were observed in superconductor metal transitions (SMTs) in 2D superconductor thin films [76,114]. Moreover, finite size scaling analysis elucidates two different values of critical exponents around these crossing points. This discordance limits the feasibility of universality class, and new theoretical paradigm is needed to clarified this inconsistency. In 2015, Xing, et. al. firstly discovered the QGS in 2D superconducting Ga films grown on a 3-mm GaN(0001) substrate in an ultrahigh-vacuum molecular beam epitaxy chamber [27]. In Figure 4, the magneto-resistance $R(B)$ curve of the sample under different temperatures do not cross at one point [110,111,115], but forming a crossing line. Meanwhile, there is an upturn of $B_c$ at $T\to 0$ beyond the WHH theory. Utilizing the finite-size scaling (FSS) method for a bundle of $R_S(B)$ curves around the multiple crossing points,

(13) $\frac{R\left(B-B_{\mathrm{c}},T\right)}{R_{\mathrm{c}}}=F\left(\frac{B-B_{\mathrm{c}}}{T^{1/zv}}\right).$(13)

Figure 4. Quantum Griffiths singularity in Ga film. (a) Magneto-resistance isotherms. The magnetic field dependence of $R_S$ at various temperatures ranging from 0.025 K to 2.80 K, with the same sweep direction and the same sweep rate, exhibits an SMT region. Inset: the critical magnetic fields $B_c$(T). Crossing points of $R_S$ (B) curves at every two adjacent temperatures are denoted as black dots on the transition boundary; the red stars come from the temperature plateaus on $R_S$ (T) curves at given magnetic fields. The blue line is the fitting curve using WHH theory and the dashed blue line (below 1.00 K) are guides to the eye. (b) The activated quantum scaling behavior: exponent $zv$ as a function of magnetic field $B$. When approaching the zero-temperature limit, $zv$ rapidly increases with no sign of saturation. The magenta line shows a fitting based on the activated scaling law. (c) Sketch of the $B-T$ phase diagram of 2D SMT with quenched disorder. $B_2$ is the upper critical field and would be the QCP for a clean system. When temperature decreases to $T<T_M$, quenched disorder overtakes thermal fluctuation and gives rise to a vortex glass–like phase. Rare regions of superconducting islands emerge and result in activated scaling behavior around such an infinite-randomness QCP $B_c^{\ast }$. Reproduced from Ref.[27]

It turns out the critical exponents $zv$ exhibit a power-law divergence when $B\to B_c$ at $T\to 0$,

(14) $zv=C{\left|B_{\mathrm{c}}^{\ast }-B\right|}^{-v\psi },$(14)

which matches well with QGS feature [105]. In addition, Figure 4(c) sketch the $B-T$ phase diagram of 2D SMT with quenched disorder in Ga film. The anomalous upturn of upper critical field as $T\to 0$ appears. In the conventional theory of homogeneous type II superconductors, the Abrikosov vortex lattice forms in the region of $B_1(T)<B<B_2(T)$, characterized by a continuous phase transition at the upper critical field $B_2(T)$ [38,116]. In clean systems, thermal fluctuations give rise to phonon-like excitations of the vortex lattice. At $T>T_M$ regime, thermal fluctuations become sufficiently large, the system is expected to melt into the vortex liquid phase [117]. While at $T<T_M$, the effect of quenched disorder overtakes the thermal fluctuation effect and produces a vortex glass–like phase on length scales greater than characteristic length of disorder [118]. This vortex glass–like phase consists of spatially separated superconducting regions, where the local upper critical field exceeds the average mean-field value $B_2(T)$. In the ultralow temperature regime, these separate superconducting islands, namely, the rare regions can couple via long-range Josephson coupling and manifest global superconductivity in the system. These rare regions of superconductivity cause the peculiar upward turn of upper critical field as $T\to 0$.

Shortly after, in 2016, Shen, et.al observed the SMT driven by a perpendicular magnetic field in superconducting 2D electron gas can form at the $LaAl{O}_3/SrTi{O}_3(110)$ interface and the dynamic critical exponent approaching the quantum critical point also exhibits QGS [119]. Subsequently, QGS has been reported in a wide range of crystalline 2D superconductors, such as $NbS{e}_2$¹⁹, $ZrNCl$ and $Mo{S}_2$¹²⁰. Different from traditional superconductor Ga film with weak SOC, $NbS{e}_2$ monolayer film is Ising superconductor with strong SOC. The discovery of the QGS in the $NbS{e}_2$ thin film not only shows the universality of the QGS in the 2D superconducting system, but also shows that the QGS is not sensitive to the specific superconducting mechanism. The coexistence of Ising superconductivity and QGS at 2D limit could be an important topic in the future for further understanding 2D superconductivity [121–123].

Distinct from previous reports of QGS, in 2019, Liu, et. al. have observed the QGS associated with the anomalous phase boundary of SMT in ultra-thin crystalline Pb films at ultra-low temperatures [68]. Usually, the SMT shows monotonic phase boundary separating the regions of $dR/dT<0$ and $dR/dT>0$. However, $R_s(T)$ curves in 4-ML Pb films exhibit a remarkable re-entrant behavior at lower temperatures in Figure 5(a). When applying the magnetic field slightly large than 3.3 T, the sheet resistance firstly decreases with decreasing temperature, reaches the minimum at $T_{min}$ and then rises at a lower temperature. This re-entrant behavior, including the fact that $T_{min}$ increases with increasing magnetic field, can be quantitatively reproduced after taking the superconducting fluctuation and the influence of large SOI into account [125,126]. Also, the $R_s(B)$ curves cross each other in a relatively large transition region instead of a critical point. The measured SMT phase boundary in 4-ML Pb film is anomalous since it bends down at low temperatures $>2.44$ K as shown in Figure 5(b), which can be ascribed to superconducting fluctuation as well. The SOI leads to the changes in the Cooperon propagator by introducing spin-triplet channel in addition to the spin-singlet channel [126]. When approaching the quantum critical point along the anomalous phase boundary, large superconducting islands emerge and dominate the dynamical property of the system, the divergent behavior of $zv$ matches well with QGS behavior [97,99].

Figure 5. Anomalous quantum Griffiths singularity of SMT in Pb film. (a)$R_s(T)$ curves at various magnetic fields show SMT and re-entrant behavior. (b) The crossing points from neighboring $R_s(B)$ curves and the onset $T_c$ from $R_s(T)$ curves determine the phase boundary of SMT. The phase boundary abnormally bends down at lower temperatures. (c) Scaling analysis indicates anomalous QGS behavior in 3.5-ML Pb film. The critical exponent diverges as $z\nu \propto {\left|B-B_c^{\ast }\right|}^{-0.6}$ with temperature approaching zero and magnetic field tending to $B_c^{\ast }$. (d) Schematic of the $B-T$ phase diagram of 2D SMT with pronounced fluctuation effect. $B_2$ is the value of upper critical field with mean field theory. Under the influence of superconducting fluctuations with strong SOI, the mean field phase boundary (blue dashed line) buckles outward to the solid red line. The anomalous phase boundary exists in the regime $\left[B_c^{\ast },B_c^{\mathrm{\prime }}\right]$. When approaching the real infinite-randomness quantum critical point $B_c^{\ast }$ along this anomalous phase boundary, the system exhibits anomalous QGS behavior. Reproduced from Ref.[124]

The QGS phase can be directly verified by the activated scaling analysis [108,109]. In practical analysis, certain irrelevant scaling variables influence the crossing point [127], and needs to be considered. The activated scaling with irrelevant corrections reads: $R=\mathrm{F}(\frac{B-B_c}{B_c}\cdot ln{\frac{T_0}{T}}^{\frac{1}{\psi }},u\cdot ln{\frac{T_0}{T}}^{-y})$. Here $\nu$ and $\psi$ are critical exponent and $-y$ is related to the irrelevant parameter. Both the relevant and irrelevant parameters are associated with the activated scaling form with effective length scale $ln\frac{T_0}{T}$. The irrelevant parameter also changes the phase boundary of the system: $\frac{B_c-B\left(T\right)}{B_c}\propto u\cdot {\left(ln\frac{T_0}{T}\right)}^{-\frac{1}{\nu \psi }-y}$. The influence of irrelevant parameter is pronounced in related experiments, but the irrelevant parameter is ignored in the previous theoretical consideration. The activated scaling analysis with irrelevant critical exponents is utilized for analyzing recent SMT experiments in 2D superconducting thin films [108,109].

3.4. Discussion

In the previous subsection, we mainly mention the disorder effect on SMT, which is associated with the pair-breaking of cooper pairs and the corresponding critical resistance is much smaller than the resistance quantum $R_Q=\frac{h}{4e^2}$. On the other hand, there exist a large class of QPT with critical resistance near $R_Q$, namely the SIT. The disorder and dissipation effects may dramatically change the quantum critical behaviour in SIT, and give rise to the anomalous metal phase in recent experiments. This very fascinating field is beyond the scope of this review article.

4. Discrete scale invariance in topological semimetals with charge impurity

Topological materials are hot topic comparable to superconductor in exploring novel quantum phenomena. The related studies can not only deepen our understanding of quantum behaviours in solids, but also provide possible applications for future information technology [7,128]. Recently, the discrete scale invariance (DSI) behavior in Dirac materials has attracted attention in related subfields of physics [28,129–132]. Especially, a new magneto-resistance oscillation beyond the quantum limit [28,30,133] has been found in several high-quality topological materials. Different from the previously known periodic quantum oscillations (Shubnikov–de Haas oscillations in $1/B$ periodic [134,135], Aharonov-Bohm and Altshuler-Aronov-Spivak effects induced quantum oscillations in B periodic [136]), this novel oscillation is $ln(B)$ periodic which manifests the appearance of DSI in solid-state system [28,30,133]. Such a peculiar DSI feature is considered to be universal in Dirac materials with Coulomb attraction [28,29], which may be closely related to the quasi-bound states formed by massless Dirac fermions and the long-pursue atomic-collapse phenomenon [28,131,137]. Thus, it is desirable to explore the underlying mechanisms of this novel phenomenon.

4.1. Heuristic analysis for DSI in topological semimetal with charge impurity

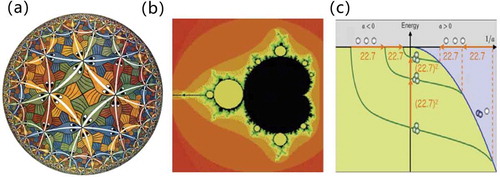
Scale invariance is a prominent ingredient in the area of phase transitions. It means a field $\varphi (x)$ has the property that $\varphi (vx)=v^d\varphi (x)$, where $v$ is a continuous parameter and $d$ is the scaling dimension. When considering the quantization effect, the continuous scale invariance will be spontaneously broken down to the DSI, where $v$ takes on discrete values [138]. Its applicability to bound-state problems in quantum mechanics was exploited by Vitaly Efimov, who found the $1/r^2$ potential suited to Schrödinger equation and confirmed the DSI energy spectrum could occur in 3-body problem in the limit of resonant scattering [139,140] [see Figure 6]. Analogy to Efimov 3-body problem, topological semimetals hold Weyl equation that the energy and momentum satisfy $E\propto k$ and DSI is also expected to achieve with $1/r$ potential [141].

Figure 6. System with discrete-scale invariance (a) M. C. Escher’s painting: Circle LimitIII represents a famous fractal structure: Poincarë disk model. (b) Mandelbrot set (c) Efimov 3-body states

Considering the Weyl fermions with Coulomb attraction near the Weyl point, the Hamiltonian read [29]:

(15) $\mathrm{\hslash }{v}_F\left[\begin{array}{c}-i{\mathrm{\partial }}_z-i{\mathrm{\partial }}_x-{\mathrm{\partial }}_y\\ -i{\mathrm{\partial }}_x+{\mathrm{\partial }}_{y}i{\mathrm{\partial }}_z\end{array}\right]\psi =[E-V(r)]\psi ,$(15)

with potential $V=\mathrm{\hslash }{v}_F\frac{\alpha }{r}$. Here $\alpha \equiv \frac{Z{e}^2}{\in \mathrm{\hslash }{v}_F}$ denotes fine structure constant, $v_F$ is the fermion velocity, $Ze$ is the charge on the impurity and $\in$ is the dielectric constant. At $B=0$, then Eq. (15)(15) $\mathrm{\hslash }{v}_F\left[\begin{array}{c}-i{\mathrm{\partial }}_z-i{\mathrm{\partial }}_x-{\mathrm{\partial }}_y\\ -i{\mathrm{\partial }}_x+{\mathrm{\partial }}_{y}i{\mathrm{\partial }}_z\end{array}\right]\psi =[E-V(r)]\psi ,$(15) can be solved analytically [142,143]. In the case of attractive potential $\alpha <\kappa$ ($\kappa$ is a dimensionless quantum numbers of angular momentum), the energy levels of quasi-bound states exhibit DSI [129,130,144,145],

(16) $E_{n+1}/E_n=e^{-\frac{\pi }{\sqrt{{\kappa }^2-{\alpha }^2}}}.$(16)

At $B\ne 0$, the magnetic field introduces a new characteristic length $l_B=\sqrt{\mathrm{\hslash }c/eB}$ that breaks the DSI at large $r>l_B$. The problem with the finite magnetic field is no longer exactly solvable but can be deal with based on Wentzel-Kramers Brillouin (WKB) approximation [29]. In this quasi-classical picture, the energy change occurs when $l_B=\frac{\mathrm{\hslash }{v}_F\gamma }{|E|}$ with $\gamma =\sqrt{{\kappa }^2-{\alpha }^2}$. And since $E$ satisfy Eq. (16(16) $E_{n+1}/E_n=e^{-\frac{\pi }{\sqrt{{\kappa }^2-{\alpha }^2}}}.$(16) ), the characteristic values of $B$ meet $B_{n+1}/B_n=e^{-2\frac{\pi }{\gamma }}$. As shown in Figure 7, with the magnetic field increasing, the binding energy of resonances states cross the Fermi energy at discrete values of the magnetic field which constitute a geometric series. This indicates the $ln(B)$ periodic transport property [29].

Figure 7. The DSI properties of quasi-bound states. (a) Without magnetic field, quasi-bound states form around the charge center. The Klein tunneling with electron-hole excitation gives rise to finite widths to the quasi-bound state spectra. Due to the small FS, screening is relatively weak. (b) The local density of states (LDOS) at certain location as a function of the dimensionless energy showing the broad quasi-bound states. The exact analytical solutions (solid line) and the WKB-type solutions (dashed line) are shown. (c) With a magnetic field, the potential changes in the large $r$ region, and the quasi-bound states move to the Fermi level at certain field values $B_n$. (d) The evolution of the quasi-energy spectrum versus the dimensionless inverse magnetic length $l_B$. Only the real part of five quasi-energies are shown. The broad quasi-bound states evolve into sharp resonances in the presence of the magnetic field, and approach the Fermi energy at certain sharp values of the magnetic field strength $B_n$ that form a geometric series. Reproduced from Ref.[29]

4.2. Influence of screening effect, finite mass and Zeeman effect on the DSI

Above studies neglect the influence of screening effect, finite mass and Zeeman effect on DSI which are exist in realistic system. We generally discuss the influence of these effects on the DSI. Considering screening effects, the impurity potential is $V=\mathrm{\hslash }{v}_F\frac{\alpha }{r}{e}^{-r/\xi }$ within Thomas Fermi approximation, where the screening length $\xi$ obeys the relation ${\xi }^{-2}=4\pi e^2\frac{dn}{d\mu }$, with $n,\mu$ and $g$ denoting the carrier density, the chemical potential, and the degeneracy, respectively. The results point out the introduction of the length parameter $\xi$ in $V$ causes the breaking of DSI and when $\xi \to \mathrm{\infty }$, DSI is restored. Moreover, the finite mass term also introduce a new length scale and it may break the DSI down. Solving the radial equation with mass term $m_0=M{v}_F/\mathrm{\hslash }$, the spectrum still satisfies Eq. (16)(16) $E_{n+1}/E_n=e^{-\frac{\pi }{\sqrt{{\kappa }^2-{\alpha }^2}}}.$(16) . The detailed results illustrate the DSI quasi-bound states are robust against a small finite mass gap at the Weyl point. Lastly, the Zeeman effect needs to be considered at large magnetic fields. Take the previous analysis in $ZrT{e}_5$ as an example [146], the Zeeman spin splitting can influence the lowest Landau level [29]. When magnetic field is applied perpendicularly on the layered $ZrT{e}_5$ sample. The Zeeman field gives rise to a spin-polarized conduction band and valence band. The influence of the Zeeman energy can be represented by the effective Fermi energy $E_F=\sqrt{E_{F0}^2+{\left(\tilde{g}{\mu }_{B}B\right)}^2}$. When magnetic field is applied parallel on the layered $ZrT{e}_5$. The Zeeman field only shifts the wave vector parallel to the magnetic field and the Zeeman effect does not influence the Fermi energy in this case.

4.3. Ln(B) periodic oscillation

The $ln(B)$ periodic transport property of system can be captured by the T-matrix approximation for the Kubo formula [29]. According to the classical treatment of Bastin et al. [29,147], the formula for the transverse magneto-conductivity ${\sigma }_{xx}$ at zero temperature is [29]:

(17) ${\sigma }_{xx}=\frac{4e^2{\mathrm{\ell }}_B^2}{\mathrm{\hslash }}\left[n_s+\sum _n\frac{n_{C}U(B){\mathrm{\Gamma }}^2(B)}{{\left[E_F-E_n(B)\right]}^2+{\mathrm{\Gamma }}^2(B)}\right],$(17)

where $U(B)=\frac{t^2}{8\pi \mathrm{\hslash }v{\mathrm{\ell }}_{\ast }^{-1}\mathrm{\Gamma }(B)}$. $n_s$ is the density of short-range scatterers, $n_C$ is the density of Coulomb scatterers, $E_n$ are the quasi-bound state energies as calculated and shown above, and $\mathrm{\Gamma }(B)$ is the width determined by overlap with the lowest Landau level. $l^{\ast }$ is the effective length along the magnetic field, $t$ is the coupling strength between the bound states with the lowest Landau level states.

The above microscopic formula can be further simplified into an empirical form by parameterization which is more suitable for fitting the experimental data [29]:

(18) ${\sigma }_{xx}=\frac{4e^2{\mathrm{\ell }}_B^2}{\mathrm{\hslash }}\left[n_s+\sum _n\frac{n_{C}U(B){\eta }^2}{{sin}^2\left(\frac{\gamma }{2}ln\frac{B_n}{B_0}\right)+{\eta }^2}\right],$(18)

with fitting parameters $\eta$ denoting an effective broadening factor and $B_0$ denoting a characteristic magnetic field. The longitudinal magneto-conductivity can be obtained by relation ${\rho }_{xx}\approx \frac{{\sigma }_{xx}}{{\sigma }_{xy}^2}$. The conductivity in Eq. (18)(18) ${\sigma }_{xx}=\frac{4e^2{\mathrm{\ell }}_B^2}{\mathrm{\hslash }}\left[n_s+\sum _n\frac{n_{C}U(B){\eta }^2}{{sin}^2\left(\frac{\gamma }{2}ln\frac{B_n}{B_0}\right)+{\eta }^2}\right],$(18) contains two terms. The first term is short-range impurity scattering, giving linear-B magneto-resistance(MR), regarded as background. The second term is resonant scattering between mobile carrier and the quasi-bound state, which leads to $ln(B)$ periodic MR oscillations.

This new type of log-periodic MR oscillations was observed beyond the quantum limit in ultra-quantum topological materials $ZrT{e}_5$. Figure 8(a) shows the extract oscillations in different $ZrT{e}_5$ samples (s6, s7, and s9) [28]. Using formula Eq. (18)(18) ${\sigma }_{xx}=\frac{4e^2{\mathrm{\ell }}_B^2}{\mathrm{\hslash }}\left[n_s+\sum _n\frac{n_{C}U(B){\eta }^2}{{sin}^2\left(\frac{\gamma }{2}ln\frac{B_n}{B_0}\right)+{\eta }^2}\right],$(18) can quantitatively fit these $ln(B)$ periodic oscillations (black curves). To better presentation, the magnetic fields ($B_n$) corresponding to MR peaks/dips were extracted, and the dependence of $ln(B_n)$ on $n$ are plotted in Figure 8(b). Here, the MR peaks and dips were indexed by integers $(n)$ and half-integers $(n-0.5)$. The well-defined linear behavior for the $ln(B_n)$ vs $n$ curve indicates the clearest feature of DSI. This feature can be understood vividly like Figure 8(c). $ZrT{e}_5$ are high-quality single crystals with no signature of real-space fractal or strong disorder-induced multi fractal properties. Therefore, the observed DSI is very likely a notable aspect of the quasi-bound states with geometrical scaling. Owing to the ultra-low carrier density in $ZrT{e}_5$ samples, the absence of screening effect can give rise to the Coulomb attraction, and the small Fermi velocity further guarantees the supercritical collapse condition, which in combination, result in the two-body quasi-bound states with DSI.

Figure 8. DSI in ultra-quantum $ZrT{e}_5$. (a) Index plot for the log-periodic oscillations. (b) Quantitative fitting (black curves) of the log-periodic oscillations in $ZrT{e}_5$. arb.u, arbitrary units. (c) Schematic of the two-body quasi-bound states composed of a Dirac-type massless hole and charged center via Coulomb attraction. Reproduced from Ref.[28]

Such peculiar work also inspires people to explore the log-periodic quantum oscillations and the DSI in other physical observables and topological materials. Ref[30]. reported the logB-periodic quantum oscillations in both the longitudinal MR $({\rho }_{xx})$ and the Hall resistance $({\rho }_{yx})$ of $HfT{e}_5$ crystals, which identify the $ln(B)$ phenomenon in the total transport coefficients as a general quantum effect. Recently, in the small gap semiconductor tellurium with a relatively small carrier density and unique band topology [148] found similar logB-periodic longitudinal MR and the Hall resistance oscillations to those observed in $HfT{e}_5$. The small gap does not change the DSI feature in this system, which is consistent with previous theoretical analysis [33]. Moreover, the MR quantum oscillations $TaAs$¹³³ is considered as a possible candidate for logB-periodic oscillation, revealing the universality of DSI property in Dirac/Weyl materials with supercritical Coulomb attraction.

4.4. Outlook

Dirac materials provide new platforms to explore the ultra-relativistic quantum phenomenon due to their massless spectrum. The effective speed of light in these Dirac materials are far less than the speed of light in nature, and thus the effective fine-structure constant can be greater than 1, providing an ideal platform to investigate the supercritical phenomena under tunable electric field and magnetic field [129,131]. Furthermore, the novel DSI of quasi bound states in massless Dirac particles manifests as a remarkable feature that is distinctive from the previous prediction of supercritical atomic collapse in massive Dirac particles. Both advantages may stimulate further investigations of relativistic quantum phenomena by transport measurement, spectral measurement etc. under extremely high magnetic field and ultra-low temperature in condensed matter systems.

5. Conclusions and outlook

This review mainly involves three peculiar features in low-dimensional superconducting and topological materials enriched by disorder effects, (i) 2D disordered Ising superconductivity mechanism in inversion-symmetric or asymmetric system; (ii) quantum Griffths singularity induced by quenched disorder in superconductor-metal transition; (iii) discrete scale invariance of quasi-bound states in topological materials. These anomalous features are beyond the traditional paradigms, provide clues for underlying microscopic processes, and reveal the profound characteristics of disordered quantum systems. Many important issues remain unsolved. For example, the mechanism for exotic anomalous metal phase associated with the superconductor-insulator transition is still under debate. Moreover, the systematic renormalization group treatment of supercritcal collapse for massless Dirac particles under magnetic field remains to be carried out. Future theoretical and experimental endeavors in these directions can largely enrich our knowledge of this exotic quantum garden, which may generate fruitful quantum technology.

Acknowledgements

We thank Jian Wang, Qi-Kun Xue, Robert Joynt, Ding Zhang, Jie Xiong, Faxian Xiu, Xi Lin, Ziqiang Wang, Xu-cun Ma, Yi Liu, Huichao Wang, Hongchao Liu, Chao Yang and Ce Huang for continuous collaboration of related works in this review. This work is financially supported by the National Basic Research Program of China (Grants No. 2017YFA0303301, No. 2017YFA0304600, and No. 2019YFA0308403) and the National Natural Science Foundation of China (Grants No. 11534001, No. 11674028, No. 11822407, and No. 11921005).

* Haiwen Liu: [email protected]

^† X. C. Xie: [email protected]

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the National Natural Science Foundation of China [11534001,11674028,11822407,11921005]; National Basic Research Program of China [2017YFA0303301,2017YFA0304600,2019YFA0308403].