Information in electrodeposited dendrites

ABSTRACT

Dendrites are structures that develop with a continuously branching tree-like form. Such patterns are found in many aspects of the natural world, which indicates the universality of their topology. This review presents an examination of dendritic structures, addressing their stochasticity and fractal character, and exploring their information content or more specifically their ability to provide a very large number of unique patterns that may be used as a novel form of item identification. A brief summary of fractals and their dimensionality is presented and applied to the well-known diffusion limited aggregate (DLA) dendritic construct. Dendrites formed by electrochemical ‘self-assembly’ are explored and examples given of their formation under different conditions. Stochastic variations in the self-similar Y-shaped symbol that underlies these fractals can carry information, leading to significant entropy, even though the structural entropy of the overall pattern is relatively small.

KEYWORDS:

• Dendrites
• fractals
• fractal dimension
• entropy
• information

Introduction

A dendrite, from the Greek word dendron, meaning ‘tree’, is a structure that develops with a continuously branching tree-like form. This review presents an examination of dendritic structures, addressing their fractal topology and exploring their information content, or more specifically their ability to provide a very large number of unique patterns that may be used as a novel form of identification in track-and-trace schemes. Advanced information management approaches, such as blockchain [1], are already being employed in supply chains to monitor the movement of goods [2] and push back the rising tide of counterfeit and tainted items [3], but there is often a weakness in the chain of trust caused by the lack of an incorruptible physical identifier or ‘trust mark’ that securely links individual products to the database [4]. We believe that electrochemically grown dendrites are highly suitable for this application as not only are they unique in every instance of formation and therefore may act as artificial fingerprints for every item to which they are attached, but they also have attributes, including a unique micro- to nano-scale topography, which make their exact replication extremely difficult, so they are much more secure than mere barcodes. Their geometric character is also quite unusual, a consequence of growth processes that have both stochastic and rule-based aspects which result in the formation of random minutiae in an otherwise recognizable overall structure; this structural predictability has potential utility in error correction schemes, just as a damaged fingerprint can still yield sufficient information to connect it to its owner since we know the rules that govern its loops and whorls. We are currently researching the use of ‘dendritic identifiers’ in the food supply chain with support from the US Department of Agriculture [5] to reduce the likelihood of public health and financial catastrophes caused by outbreaks of foodborne illness [6,7] and thwart the economic damage of counterfeit or adulterated foods and additives [8,9]. Although our current focus is on food and agricultural product protection, this technology may also be applied to other supply chains, where counterfeit goods are destroying brand integrity and weakening market trust by providing inferior performance and reliability.

The attributes of dendrites described above suggest that electrochemically grown structures are a type of physical unclonable function (PUF) [10]. The key characteristics of a PUF are (1) they are relatively simple to evaluate but their fine detail is extremely difficult to predict, (2) they are simple to make but practically impossible to duplicate even if the exact manufacturing process is known, and (3) in the presence of noise, the function remains distinct and therefore the information it represents is well preserved. There are a number of PUF technologies in development for the secure tagging of items, including those based on the natural variations that are present in products and materials, for example, parametric deviations in ICs [10], speckle patterns due to disorder [11], or surface wrinkles [12]. Random variations introduced by materials or processes suffer from the problem that these may be largely out of the control of the user and hence will not supply a well-understood and reliable basis for large-scale identifier generation and error-free evaluation.

This review starts with an introduction to dendrites in nature and presents a primer on fractals and their dimensionality, and then transitions to a well-known dendritic construct, the diffusion limited aggregate (DLA) and its properties. The section following describes dendrites formed by electrochemical means and gives examples of these grown under different conditions. The next three sections focus on information in fractal patterns and connect this to natural (irregular) dendrites. The overarching purpose of the paper is to show that dendrites formed by electrochemical ‘self-assembly’ do indeed have sufficient entropy to be used in tagging applications that require a vast number of unique patterns to be produced naturally without the need for human intercession.

Dendrites and fractals

In mathematical terms, a dendrite is merely a system of non-crossing line segments which connect a set of points in a way that the total length of the construct is as short as possible [13]. Dendritic patterns are common in nature at vastly different scales; given their geometric frugality, they are essentially natural solutions to optimization problems involving the transport of mass, energy, or information [14,15]. These include the networks of blood vessels [16], bronchial tubes [17], and neurons in the human body [18,19], electrical breakdown pathways in dielectrics [20], and, of course, the structures responsible for the harvesting of energy and supply of nutrients in plants and fungi [21]. Examples of naturally occurring non-biological (and therefore not influenced by genetic factors) dendritic patterns, ranging from several millimetres to several kilometres in scale, are shown in Figure 1. The branching mineral deposits in Figure 1(a) are a result of diffusion-reaction mechanisms between constituent species within a crack in the hosting rock structure [22], whereas the form of the electrical discharge pattern in Figure 1(b) comes from the dielectric breakdown of the air under high electric field [20], and the desert drainage pattern is a result of the soil eroding properties of water as it flows downhill [23].

Figure 1. Examples of non-biological dendritic patterns in nature; (a) mineral deposits on a rock in the author’s garden in Arizona, (b) lightning over the River Forth in Scotland [24], (c) desert drainage channels in northern Egypt [25]

Despite their drastically different formation methods, dendritic patterns in nature still share an obvious similarity of form, hinting at the universality that underpins their creation [26]. Complex patterns often emerge from processes that are significantly out of equilibrium [27], but the influence of thermal fluctuations in otherwise well-behaved fields is of great import in dendritic pattern formation. Many diverse physical processes involving balanced flows across nominally smooth interfaces are well represented by the Laplace equation, including steady state heat flow, incompressible fluid flow, and particle diffusion. Laplacian instabilities, in which small statistical irregularities on an otherwise smooth interface between regions are amplified to produce significant extensions, often and perhaps surprisingly result in ramified patterns [28,29]. In the world of materials processing, Laplacian instabilities lead to an astonishing range of branching patterns from disparate physical processes, including the Mullins–Sekerka instability [30] which results in solid tree-like protrusions at the surface of a solidifying metal. These exotic structures emerge from the molten surface because heat is conducted away faster at the tip of the protrusion due to the high temperature gradient there, resulting in rapid solidification. The Saffman–Taylor instability [31] is seen when a less viscous fluid (e.g. air) is forced into a more viscous medium (e.g. oil) and is another beautiful example of the formation of ramified patterns due to Laplacian instability. In this case, the interface between the air bubble and the oil moves more quickly where the pressure gradient is highest, with steeper gradients occurring at random bulges in the interface, leading to a positive feedback effect and ‘viscous fingering’. The sides of the air bubble fingers suffer the same fate due to statistical bulges and develop their own branches or forks. Laplacian instabilities have been modelled using a variety of algorithms, including the Hastings–Levitov iterative conformal mapping [32], the dielectric breakdown model [19], and diffusion limited aggregation [33]. Diffusion limited aggregation will be discussed more extensively later in this review due to its connection with electrochemically formed dendrites. In all cases, the position and orientation of such branching is influenced by arbitrary processes, such as thermal fluctuations or the randomized movement or placement of the particles that make up a structure or its hosting environment so that the resulting form is a stochastic tree. In some specific cases, crystal anisotropy promotes growth along preferred branching angles and positions, as in snowflakes (which are not quite as symmetric or as unique as common folklore would suggest [14]) or in ‘fern’-like metal electrodeposits as shown in Figure 2.

Figure 2. Electron micrograph of a ‘fern’-like silver electrodeposit grown in 0.03 M silver nitrate solution on silver agglomerate-coated glass at 3 V (the size bar is 5 µm)

Dendritic patterns appear, at least superficially, to share the property of self-similarity at different magnifications; zooming-in on a section of the pattern reveals a shape that looks somewhat like the form of the entire object or one of its major components. Such self-similarity suggests that dendrites are fractals, and a great deal of work has been done on this topic in the last several decades. Several methods have been employed to quantify the self-similarity that is at the heart of ‘fractality’, including geometric and probabilistic aspects based on Renyi dimensions [34,35]. In globally self-similar fractals, the dimensions of capacity, information, and correlation all coincide [36–38], and it is appropriate to use a single fractal dimension D to describe the pattern. In the simplest terms, the fractal (or Hausdorff-Besicovitch) dimension D is given by

(1) $D=logN/logS$(1)

where N is the number of elements that make up the pattern, and S is the scale to which the individual elements compare to the full object [37]. Clearly, as the number of elements in the pattern increases, or the scale factor decreases (meaning that the individual elements become smaller), D increases. So D is both a measure of how a pattern fills the space in which it resides (a pattern with D close to 2 fills a two-dimensional space more fully than a pattern with D closer to 1), and it is also an indication of a fractal’s information density as we will investigate later in this paper.

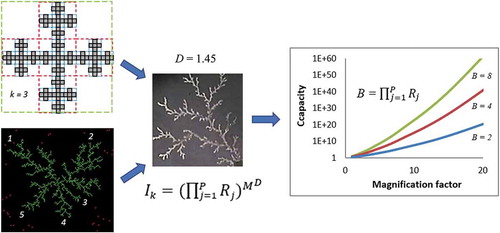
A structure that illustrates the nature of fractal objects is the Vicsek fractal (also called the box fractal), which is representative of a simple deterministic dendritic pattern in that it contains constantly branching, albeit highly regular, structures [39]. A demonstration of the development of the first, second, and third generations or k-prefractals (denoted k = 1, 2, and 3, respectively) of the Vicsek fractal is given in Figure 3.

Figure 3. First (k = 1), second (k = 2), and third (k = 3) generations or k-prefractals of the Vicsek fractal

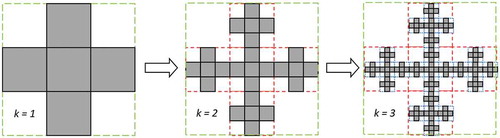
The first generation comprises five elements (N = 5) arranged in the shape of a cross, each with edges that are one third the size of the edges of the enveloping square, that is, the scale factor S = 3. This defines the basic shape that will be used to form the full pattern. The second generation replaces each of the squares in the first generation with smaller crosses that have the same form as the first generation shape; now N = 25 and S = 9. The third generation replaces each of the squares of the second generation with crosses so that N = 125 and S = 27, and so on. Using eqn.1(1) $D=logN/logS$(1) for the first, second, and third generation patterns, D ≈ 1.465 in all cases, that is, the fractal dimension remains constant regardless of generation k. If we have a fractal that can be resolved to the kth generation, by eqn. 1(1) $D=logN/logS$(1) the number of elements we can observe N_k will be given by

(2) $N_k={S_k}^D$(2)

where S_k is the scale factor at generation k. This power law-governed increase in the number of ‘building blocks’ with the decrease in their size is one of the most interesting aspects of fractal patterns and is a common aspect of all naturally occurring dendritic patterns.

Before we leave our discussion of fractals and the definition/determination of their dimensionality, we should also contemplate the concept of similarity dimension [40–43], which has its origins in the analysis of natural dendritic fractals, such as river networks [44,45]. In this method, for a self-similar structure, the ratio of the number of branching points, r_N, and the ratio of branch lengths, r_L, between successive generations (or successive ‘orders’ of river basin tributaries) are both constant, regardless of which successive generations/orders are considered. This scaling law (or power law) relationship is very common in nature [14,44] and seems to be universal in systems in which side branches emerge due to the presence of randomly placed elements and ‘Laplacian amplification’. The similarity dimension is defined the ratio log(r_N)/log(1/r_L), which is equivalent (or at least very close to) to the fractal dimension D (note that 1/r_L is equivalent to S in this representation, due to the commonly accepted definition of 1/r_L). For example, in the Vicsek fractal of Figure 3, at k = 2 the number of side branches not including the tips is 8 with length 1/3 (assuming a 1 × 1 envelope), and at k = 3 the number of side branches is 40 with length 1/27, which leads to r_N = 5 and r_L = 1/3. The similarity dimension is therefore log 5/log 3 ≈ 1.465, which is the same as the calculated fractal dimension we saw earlier.

Diffusion limited aggregates

The earliest fractal growth models of dendrites were based on the diffusion-limited aggregate (DLA) approach of Witten and Sander [33,46]. In the DLA model, random walker particles (e.g. by Brownian motion or diffusion) are immobilized as soon as they collide with an initial seed and then with the deposit that forms on this. Growth proceeds so far from equilibrium conditions that the result is an irregular stochastic structure. It is clear from this treatment that the random walk process that supplies the entropy in the growth process leads to the random placing of the minutiae in the dendrites; the Laplacian instability then ensures the final stochastic tree topology. The analyses by Witten and Sander [46] also show how the fractal-like nature of the dendrites arises from the growth process. Any trunk or stem that nucleates and grows outward from the starting point (the ‘seed’) can in turn have branches grow from its sides at random positions due to small irregularities along its length that are more likely to be struck by the arrival of new wandering particles and thereby grow faster than the rest of the surface. The larger branch area captures even more particles and positive feedback keeps it growing, especially at its exposed tip. As growth progresses and the trunks get longer, the likelihood of branches forming increases. The major branches are subject to the same outward growth along their lengths and so minor branches will form with time and as these increase in length, we will see more and more ‘twigs’ forming along their lengths, and so on. Growth proceeds outwards and with greater speed as the new deposits extend to capture more free particles and the branches of the core clusters therefore grow faster than the interior regions. In addition, since the outer branches form a ‘canopy’ that essentially blocks the ingress of further particles from the periphery into the particle-depleted interior, the inner regions are never fully filled, and the global form of the pattern has considerable internal space.

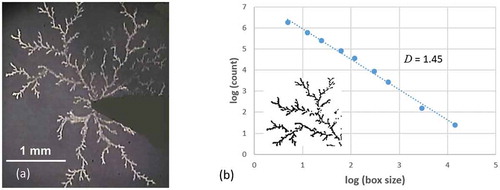
Three DLA patterns are shown in Figure 4, from a simulation produced using Netlogo in which all unattached (red) particles are launched from the periphery of the field and are allowed to move with equal probability in any direction on each hop (a 360° ‘wiggle angle’ in the parlance of the program) until they strike an immobile (green) particle and become attached themselves [47]. Clearly, these stochastic shapes do not possess the regularity of the Vicsek pattern, and so defining the fractal dimension, or, for that matter, their fractality in general, is a considerable challenge. The work of Argoul et al. [36], in which both numerical (simulated) and experimental (grown) aggregates were subjected to a sophisticated wavelet analysis, demonstrated unambiguously that such patterns are indeed globally self-similar fractals. This is an extremely important finding as it not only provides confirmation that diffusion-limited aggregates are true fractals but also that electrochemically formed patterns are sufficiently similar as to be in the same universality class. This is useful as it is relatively easy to produce physical dendrites via electrochemical processes as discussed later in this paper. Returning to the issue of fractal dimension in these globally self-similar but complex irregular structures, one can obtain an estimate of D via a variety of techniques, including ‘radius of gyration’ [36,46] and ‘box counting’ methods [48]. The latter is generally the simplest and functions by providing a scale S and then placing the minimum number N of squares of edge 1/S that are required to cover as much of the pattern as possible. D is then calculated as log N/log S. Since the scale of the fractal is unknown ahead of time, various scales/box sizes are chosen and the number of boxes that contain the pattern are counted, then log(count) is plotted against log(box size) so that the magnitude of the slope is the fractal dimension.

Figure 4. Three examples of simulated DLA patterns using Netlogo [41]

It should be stressed that even though stochastic processes dictate the formation of these DLA patterns, their final form is still very much ‘rule based’. They display the general rules of dendritic structures, which include non-crossing line segments, no closed structures, and no retrograde branch growth since the particles are fed from the periphery and therefore the branches tend to grow/point outward. An emergent feature related to this is that the patterns exhibit favored angles between branches, specifically a ~ 36° screening angle between branches of successive generations and a corresponding characteristic ~72° angular separation between major features/trunks in radial dendrites, leading to a roughly five-fold (360°/72°) symmetry [36,49,50]; an example of this is the five major trunks extending from the pattern origin (seed) marked 1 to 5 in Figure 4(a,b). However, Figure 4(c), which was produced under exactly the same conditions as the other two patterns, exhibits a ~ 90° angle between major trunks, leading to a shape that has approximately four-fold symmetry. This is a reminder to us that there are stochastic forces at work in the formation of these patterns, which leads to ranges in parameters, rather than specific values, although angles at the smaller end of the range tend to dominate. Perhaps not surprisingly, we see the same effect in nature, where the branching angles seen in natural dendritic structures, such as blood vessels and trees also tend to range from around 70° to 90° [14]. Another point worth noting is that DLA structures have a common fractal dimension in the order of 1.6 to 1.7 [35,51], but radial structures with n-fold symmetry can appear to exhibit a lower D unless the analysis is restricted to the main branches [52], especially if n becomes less than five, which can lead to ‘statistically exaggerated’ gaps between trunks as shown in Figure 4(c).

Electrochemical dendrites

Forming dendrites via electrochemical processes has a number of practical advantages, including the relative simplicity of the required apparatus – essentially a power supply, two electrodes, and an electrolyte – and the inherent ability to control the outcome of the deposition process by adjusting the deposition parameters. For an electrolyte containing a single metal ion species M ^z+, such as silver (Ag⁺), copper (Cu⁺⁺), or zinc (Zn⁺⁺), plus an anode of the same metal and an electron-supplying cathode, the basic reduction-oxidation (redox) half reactions are

M → M ^z+ + ze⁻(anode),

M ^z+ + ze⁻ → M(cathode).

The required overpotential for this reaction for the above metals is quite small, typically in the order of a few hundred mV. The oxidation of the metal at the anode maintains the concentration of ions necessary for the formation of the electrodeposit by reduction at the cathode and subsequently on the electrodeposited metal, which is an extension of the electron-supplying cathode. Many examples of electrochemical dendrite growth use an electrode geometry that encourages the radial, n-fold symmetric patterns of DLA growth. In such cases, the ‘seed’ is a central point cathode which supplies electrons to reduce and immobilize the ions as electrodeposited atoms. The point cathode is surrounded by a coaxial oxidizable anode that acts as a source of ions from the outer boundary of the growth area via oxidation of the electrode metal.

Building on the random walker DLA approach of Witten and Sander, Brady and Ball created an early model for dendritic electrodeposit formation [53], assuming that non-equilibrium electrochemical growth has the same general features as the DLA model, which include random diffusion of ions and their eventual attachment to the growing electrodeposit. This is true as long as the applied voltage is not too high so that the drift component is still relatively small and thermal fluctuations dominate. In such cases, it has been noted that branched electrodeposits tend to have a fractal dimension that is very similar to the patterns produced via the DLA process [35]. As mentioned previously, this fractal similarity was confirmed by Argoul et al. [36]. The most obvious difference between particle-based DLA and electrochemical forming methods arises from the fact that the wandering particles in the case of electrochemistry are ions but these lead to fundamental building blocks in the dendrite that are tens of millions of times larger. The electrodeposition process typically starts with the nucleation of the new metal atom phase with a structure that generally follows a Volmer–Weber island growth, leading to three-dimensional adatom clusters [54]. If the deposition is slow (attained via low applied voltage/low Faradaic current), it is possible to produce a relatively smooth, uniform metal coating on the cathode from these clusters, which is the basis of electroplating. If the process is driven far from equilibrium, the clusters still form but instead of becoming a continuous film, their arrangement is now chaotic, leading to an irregular and branching nanoscale structure typified by the image in Figure 5. The silver crystallites are in the order of 50 to 100 nm in size, corresponding to around 10 million to 50 million atoms in each crystal. This granularity appears to be a common aspect of silver dendrite growth in general and of course limits the scale to which the self-similarity can extend due to the relatively featureless facets of the crystals.

Figure 5. High resolution electron micrograph of a silver electrodeposit grown in ultra-pure water on a glass substrate with evaporated silver electrodes, showing its granular structure (the size bar is 1 µm)

In practice, the growth rules and the corresponding morphology of the electrodeposit depend on the magnitude of the applied voltage and the concentration and diffusivity of the ions in the electrolyte, so the dendrites may not look anything like the DLA patterns of Witten and Sander [46]. Indeed, we may use different deposition conditions to create various ‘species’ of dendrite, with different growth rules that lead to a difference in general structure. For liquid electrolytes, in which the ion diffusivity is relatively high, a bias above 6–8 V in a high concentration electrolyte (e.g. >0.1 M) tends to lead to patterns that are less ramified and therefore have a lower fractal dimension, whereas lower bias results in densely branched structures with high fractal dimension, trends that appear in the studies of Sawada et al. [55]. This is expected as thermal fluctuations will dominate in the lower bias case, leading to more (random) branching along the length of each feature. The nature of the local electric field, ℰ, in the high bias case will favor growth at the tips of the electrodeposits, while the rest of the structure has lower growth due to Faraday screening, leading to a structure that is more one-dimensional or ‘stringy’ in form. Models of electrical breakdown have shown that a fractal dimension close to that of a DLA (e.g. close to 1.7) is only likely when growth is proportional to the electric field but when a nonlinear relationship exists, D may be considerably smaller [20]. Such nonlinearities exist in ionic systems, as ion current density and therefore ion flux into the dendrite growth increases as sinh(ℰ) due to barrier lowering in the electrolyte [56]. In addition, as the conducting electrodeposit front moves toward the anode, the distance between each tip and anode decreases, resulting in an increase in the electric field and a corresponding increase in growth rate due to the increase in Faradaic current [56]. This will favor whichever branch is closest to the anode so that a ‘winner takes all’ situation can arise, resulting in a single branch that ultimately connects the cathode to the anode, even when many branches initially emanate from the cathode.

For solid and gel electrolytes, in which the ion mobility is orders of magnitude lower than in most liquid electrolytes, other effects can influence the morphology of the electrodeposits, including the nature of the electrolyte itself [57]. As branches form in the electrodeposits on these materials, the resupply of ions is hindered by the low ion diffusivity, and side branch lengths tend to be quite short on average. The growth is still clearly ramified but the density and fractal dimension of the pattern are relatively low, as is demonstrated in Figure 6, which gives three examples of Ag electrodeposits grown under the same conditions, 40 V for 1000 s on a 60 nm thick Ag-doped Ge₃Se₇ solid electrolyte that has been deposited on an oxidized silicon wafer. The tungsten needle cathode was applied during growth at the points indicated by the arrows and the circular silver anode is just beyond the edge of the field in each case. These patterns are just over a cm in diameter and contain a great deal of fine detail, as illustrated in the enlarged image in the right part of the figure. The fractal dimension of this pattern is about 1.3, as determined by a box counting method using the Fiji program [58], which is considerably less than the 1.6 to 1.7 value of a typical DLA pattern. Similar solid electrolyte-based electrodeposits were the subjects of one of our early studies of the use of dendrites as identifiers, using a unique graph matching approach [59]. Despite the much lower fractal dimension, the n-fold symmetry of DLA patterns in Figure 4 is again evident in these electrodeposits, with n being 5 and occasionally closer to 4, just as in the case of our simulated DLAs.

Figure 6. Examples of silver electrodeposits grown on a solid electrolyte film. The arrows indicate the position of the cathode (and the point of initiation) during growth

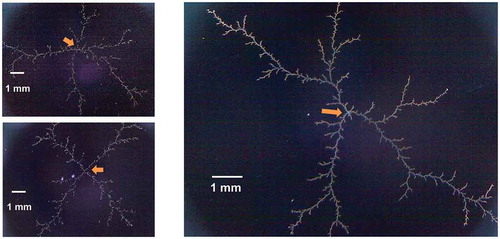
Although the growth of dendrites in liquid electrolytes is relatively easy to achieve (and is therefore the bane of the battery world, where metal dendrites are a nuisance), the electrodeposits are likely to extend into the liquid medium to form fully three-dimensional structures. These tend to overlap and detach all too readily when the liquid is removed, which makes their characterization and potential use as identifiers more difficult. To produce planar dendritic electrodeposits with liquid electrolytes, such as silver nitrate solution, we employ materials that hold the aqueous electrolyte within the substrate itself or in a thin layer on the substrate surface. An example of this approach is given in Figure 7, in which the substrate material is Teslin® [60], a synthetic microporous material comprising a single-layer polyolefin/silica matrix that is normally used for high durability/high security print applications. The strong polyolefin web holds the silica in place and this arrangement retains the liquid electrolyte during the growth of the electrodeposits. In the patterns featured in Figure 7, the central circular cathode (1.5 mm diameter) and annular coaxial anode (20 mm inner diameter) were screen printed using silver ink. The ink-patterned substrates were soaked after curing in 0.05 M silver nitrate (AgNO₃) solution until saturated. Spring-loaded probes were then pushed onto the printed electrodes and 10 V was applied for 25 seconds in each case to produce the patterns shown. These are clearly more dense than those shown in Figure 6 and have a box counting fractal dimension that is slightly in excess of 1.6, which is closer to that reported for DLA patterns. The major difference between these patterns and the simulated DLAs of Figure 4 and the electrodeposits of Figure 5 is that since the initial seed was a relatively large circular electrode and not a point, multiple well-spaced independent nucleation sites appeared along its circumference, leading to about 20 trunks in each case (although some were cut off by adjacent growth and therefore remained short). The result of this increased nucleation and trunk count is that there is still n-fold symmetry present in the trunk arrangement, but n is considerably larger than five in this ‘species’ of dendrite. This is similar to the growth between parallel ‘strip geometry’ electrodes [61], in which the total number of individual trees with their own distinct trunks is only limited by the width of the electrode.

Figure 7. Examples of silver dendrites around 15 mm in diameter grown at 10 V for 25s on a synthetic paper substrate with screen printed Ag ink electrodes soaked in 0.05 M silver nitrate solution

The two-dimensional or planar dendritic form of electrodeposits is evident from the images in this paper, but the growth process is actually three dimensional, even when the electrolyte is fully on or in the substrate. The process behind this is quite simple: as the metal deposits on the cathode and moves laterally outward, supplied at its tip by ions from the substrate’s electrolyte, electrodeposition also occurs at the base of the electrodeposit along its length. So, as growth proceeds, the basal deposition pushes the earlier-deposited material upwards and away from the substrate while continuously widening the electrodeposit at the interface. This leads to a three-dimensional form with a generally triangular cross-section, but with microscale faceting; essentially, the surface electrodeposits look like microscopic mountain ranges. An example of this is given in Figure 8(a), which is a high-resolution electron micrograph of a silver dendrite grown on an Ag-Ge-Se solid electrolyte, similar to those in Figure 6. These features are in the order of 1 µm high at their peaks, which means that they are still substantially two-dimensional since the vertical to lateral dimension ratio is in the order of 10⁻⁴. This attribute of electrochemical dendrites is extremely useful in the context of their use as secure identifiers as the topography can be detected using a variety of optical methods, including light scattering, polarization, and holography techniques, as well as high-resolution microscopy. The image in Figure 8(b) is a silver dendrite grown on an Ag-Ge-Se solid electrolyte taken using a linearly polarizing microscope, which highlights the subtle relief of the structure. It would be very difficult to replicate such fine features, making these patterns virtually unclonable.

Figure 8. (a) Electron micrograph of a silver dendrite grown on an Ag-Ge-Se solid electrolyte, showing the microscale topography of this electrodeposited structure. The size bar is 1 µm. (b) Polarizing microscope image of silver dendrite grown on an Ag-Ge-Se solid electrolyte. The field is about 2 mm across

Information in fractal structures

An obvious question that arises when considering the use of dendritic patterns as unique identifiers is how many different variations can there be of the same general pattern? This question can be answered by considering the entropy or information content of the patterns. One would expect that given the high entropy of the formation processes, the patterns would also exhibit considerable entropy. The most appropriate way to initiate an analysis of information in patterns is to consider the Shannon entropy H, which is essentially the number of binary digits or bits per symbol,

(3) $H=-\sum _i{p}_{i}lo{g}_2{p}_i$(3)

where p_i is the probability of the ith possible value of the symbol [62]. But the fundamental question becomes, what are the information carrying ‘symbols’ in the case of fractals and dendrites and what constitutes their ‘values’? The geometric elements contained within a fractal pattern, such as individual branches or groups of elements, including the self-similar units that make up the fractal, could readily be the symbols. But there is only information content if these symbols are modified in a way that allows subsequent unambiguous determination of several states. The processes that cause the modifications to the elements could be deliberate, for example, we may alter each unit to encode a particular number that we specify ahead of time, or they could be random, for example, caused by the influence of some stochastic process that sets these configurations during the formation of the pattern. The latter approach is what nature provides and is particularly interesting in the context of mass-produced identifiers as a stochastic self-assembly process would automatically generate unique patterns, thereby avoiding the cost of programming the features, which could be substantial when micro- or nano-scale elements are involved.

To illustrate this using the Vicsek pattern of Figure 3, we can consider encoding information via the alteration of some parameters associated with each of the smallest side branches, for example, their positions along the carrying branch, their angles with this branch, and their lengths. The number of these side branches in each generation, E_k, is determined by a scaling or power law,

(4) $E_k=2\left(5^{k-1}-5^{k-2}\right),fork>1.$(4)

This function rises by a factor of 5 in each successive generation; there are only eight side branches for the second generation, but this number rises to 40 and 200 for the third and fourth generations, respectively. If parametric alterations are introduced to provide several distinct or readable geometric states for each side branch, then the pattern can represent information. For example, if the measured parameter associated with each branch can fall into one of B ranges, each with an equal probability p_i = 1/B, the number of possible configurations or information capacity I_k of the pattern would be

(5) $I_k=B^{E_k}.$(5)

In the case of binary encoding (B = 2, H = 1 bit/symbol), the information capacity of the Vicsek patterns at the second, third, and fourth generations is 256, 1.10 × 10¹², and 1.61 × 10⁶⁰ respectively. This latter number is more than enough to label every atom on Earth with a unique pattern, and the huge growth in information capacity with generation is a characteristic of ‘power tower’ functions. Coding information in the side branches of the Vicsek fractal is not the only option at our disposal. For example, if we include all branches, including those from which the side branches emanate, the number of these is given by

(6) $Q_k=2(5^{k-1}+1),$(6)

which is obviously larger than E_k [41]. Note that this is equivalent to the number of terminations in the pattern. Considering the second, third, and fourth generations as before, Q_k is 10, 52, and 252 for these, respectively. Assuming that some geometrical aspect of these features, such as the positions of the apices, can be unambiguously read as one of B values, the information capacity in this case is

(7) $I_k=B^{Q_k},$(7)

which leads to binary and quaternary (B = 4, H = 2 bits/symbol) capacities at the fourth generation of 7.24 × 10⁷⁵ and 5.24 × 10¹⁵¹ respectively.

The fractal nature of natural dendrites

To determine what the information capacity of a dendritic fractal pattern is, we may start by considering the Mandelbrot-Vicsek self-similar fractal tree [63], which is constructed by recursively replacing each line segment by a half-scale version of the Y-shaped bifurcation from the previous generation, is shown in Figure 9. Since the self-similar unit has three elements (N = 3) and the scaling factor S = 2, the fractal dimension D = log 3/log 2 = 1.585. Alternatively, considering the similarity dimension approach with the k = 1 overall length equal to 1 and each line segment equal to 1/2, at k = 2 the number of side branches (not including continuations of the branches from which they emerge) is 3 with length 1/4, and at k = 3 the number of side branches is 9 with length 1/8, which leads to r_N = 3 and r_L = 1/2. The similarity dimension is log 3/log 2 = 1.585, which is the same as the fractal dimension. So, the number of side branches increases by a factor of 3 for each generation and the power law governing this is simply

(8) $E_k=3^{k-1}.$(8)

Figure 9. First (k = 1), second (k = 2), and third (k = 3) generations of the Mandelbrot-Vicsek fractal tree

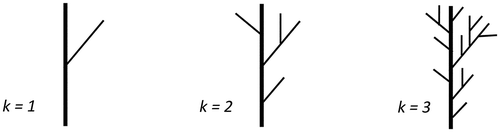
The number of branches including the leading tips of the trunks in this pattern Q_k is given by [41]

(9) $Q_k=1/2(3^k+1),$(9)

resulting in Q_k = 5, 14, and 41 for the second, third, and fourth generations, respectively. By eqn. 7(7) $I_k=B^{Q_k},$(7) , this would lead to binary and quaternary information capacity at the fourth generation of 2.20 × 10¹² and 4.84 × 10²⁴ respectively. These are considerably smaller than the capacities of the modified Vicsek fractal, but our stochastic tree might only be a single element in a radial dendrite. Assuming five-fold symmetry, that is, the radial pattern has five of such trees/trunks, the total number of branches would rise by a factor of 5 and information capacity would increase to 5.14 × 10⁶¹ and 2.64 × 10¹²³ for binary and quaternary coding schemes, respectively.

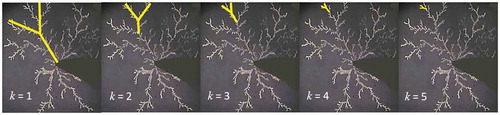
The fractal tree is often used in the literature to represent dendrites due to its true fractal nature and suitable topology, but its deterministic form clearly does not fully exemplify the patterns that we see in electrochemical dendrites. To generate a more ‘natural’ dendritic shape, we can consider a somewhat different approach. The image in Figure 10(a) is a micrograph of a silver dendrite at the termination of its growth [64]; the dark object in the lower right quadrant is the tungsten point cathode which contacts an Ag-Ge-Se solid electrolyte in the center of the pattern (the coaxial circular silver anode is just beyond the field of view). Figure 10(b) shows the result of a box counting analysis performed using Fiji software [58] on the top-left quadrant of the image, which indicates that the fractal dimension of the binary form of the image D = 1.45 (the inset in Figure 10(b) is the binary version of the image of Figure 10(a) which helps to facilitate the box counting analysis). Note that this dendrite, at around 4 mm in diameter, is much smaller than the dendrites in Figure 6 and was grown at lower voltage (5 V) so the pattern is denser, and its D is larger. The dendritic fractal of Figure 10 clearly does not contain identical repeating units as in the Mandelbrot-Vicsek fractal tree, but there are forms within the pattern which do appear to be somewhat self-similar as a result of the rule-based growth. As shown in Figure 11, the most obvious self-similar unit that we can apply to this pattern is again a Y-shaped bifurcation with approximately equal line segment lengths, but, in this case, the arms split symmetrically from the trunk with an angle between them of approximately 70º, which is consistent with the five-fold pattern symmetry discussed earlier. For this shape, we may say that N = 3 and S = 2, leading to a calculated D of 1.585, just as in the Mandelbrot-Vicsek fractal tree. This is larger than the structure dimension obtained by box counting (~1.45), but the fitting of this Y-shaped self-similar unit is only an approximation in our attempt to assign more order on this irregular dendritic shape so that we may assess how many generations can be resolved. There is also the possibility that the box counting method has over-estimated the fractal dimension by over-estimating the coverage of the pattern [35,65]. The most dominant bifurcation in the dendrite has trunk and branches that are each approximately 1 mm long; this represents the first generation (the k = 1 image in Figure 11) of the fractal. With a scaling factor S = 2, we would expect the k^th generation of this shape to be a factor of 2^k−1 times smaller than that of the first generation. Seeking a second generation bifurcation that is approximately half the size of the first generation unit leads to the bifurcation highlighted in the k = 2 image. Similarly, the third generation bifurcation is approximately half this size again (k = 3 image), and so on until we reach the limit of resolution at k = 5. In this smallest resolvable bifurcation, the trunk and branches are all around 1/16 mm or approximately 60 µm in length. Interestingly, the entire structure does indeed appear to consist of concatenations of a large number of these fifth generation elements (the smallest Y-shaped bifurcation in the k = 5 image of Figure 11). Unlike deterministic fractals, there is less predictability in how these units are placed, and this leads to the very unique construction of each dendrite. Another aspect of natural dendrites that is very clear from Figure 11 is the general lack of mirror symmetry in their branching. This is expected as any bifurcation will tend to have a dominant arm, due to the statistical distribution of growth rates between them. The arm that grows faster will ‘starve’ the other of growth material (ions, in the above case) and this will significantly stunt its growth.

Figure 10. (a) Micrograph of a silver dendrite. (b) Box counting analysis of the major branch in the top left quadrant of the dendrite showing D = 1.45 (inset is the binary version of the dendrite image used in the analysis)

Figure 11. Self-similar elements in a silver dendrite, showing nearly equal length bifurcations (yellow Y-shaped features) denoting five generations (k = 1 to 5) of the irregular fractal

Information in dendritic fractals

We contend that the smallest resolvable self-similar units that make up a fractal dendrite should be used as the symbols which represent information in the pattern. The advantage of this approach over the use of, say, individual branches is that the self-similar units have a distinct shape, for example, a Y-shaped bifurcation with a limited range of geometrical features (segment lengths and branch angles), so it would be relatively easy to distinguish them in the presence of random pattern noise. This robustness via predictability of form carries into the entire pattern and has utility in applications that may be complicated by visual noise.

Assuming that the physical nature of the pattern allows a large number of generations to be present, the number of self-similar units that can be used to represent information will depend on the magnification employed to view the image in order to determine the geometrically encoded state; the higher the magnification, the more ‘information units’ that can be resolved and read in the fractal pattern. For every generation of the fractal k, the number of information units U_k is given by

(10) $U_k={N_1}^k/N_1={N_1}^{k-1}.$(10)

N₁, the number of elements in the first generation pattern, is related to the initial scale S₁ by

(11) $N_1={S_1}^D,$(11)

so that

(12) $U_k={S_1}^{D(k-1)}.$(12)

In terms of scale, k can be written as log S_k/log S₁, where S_k is the scale at generation k, which leads to

(13) $U_k={S_1}^{D((log{S}_k/log{S}_1)-1)},$(13)

which can be rewritten as

(14) $log{U}_k=D\left(log{S}_k/S_1\right).$(14)

If we define the magnification factor M which allows us to resolve the elements within the self-similar information units at generation k as the scale ratio

(15) $M=S_k/S_1={S_1}^{k-1},$(15)

we obtain the simple relationship between the number of readable information units U_k and the magnification factor M and fractal dimension D,

(16) $U_k=M^D.$(16)

If we can resolve B individual states in each unit, the information capacity I_k of the structure is

(17) $I_k=B^{U_k}=B^{M^D}.$(17)

This double exponential function is interesting due to the large growth rate it represents. Double exponential functions obviously grow much faster than single exponentials and they also grow faster than factorials, which makes them of significant interest in fields where large random numbers must be generated, including in the field of cryptography for large unique keys and ciphers.

Generalizing, we note that the radix or coding base B can be represented by

(18) $B=R^P,$(18)

where R is the number of readable states and P is the number of parameters measured, such as branch lengths or angles, or the position of branching node with respect to a reference, assuming that each parameter has the same number of readable states and each state has an equal (and reasonable) probability p_i of existing. For a single parameter measured to give two states, P = 1 and R = 2, so that B = 2, H = 1 bit/symbol, giving us binary coding. For two parameters with two states, P = 2 and R = 2, or one parameter with four states, P = 1 and R = 4, B = 4, H = 2 bits/symbol in both cases, giving us quaternary coding; for P = 2 and R = 4 (or vice-versa), we get B = 16, H = 4 bits/symbol (hexadecimal), and so on. Combining this with our expression for information capacity gives

(19) $I_k={(R^P{)}^M}^D$(19)

Note that if there was only a single readable state in each self-similar unit, R = 1 and I_k = 1, that is, there is only a single configuration for the pattern, which would be the case for a deterministic fractal, such as the unaltered Vicsek pattern (by eqn. 3(3) $H=-\sum _i{p}_{i}lo{g}_2{p}_i$(3) , the Shannon entropy H = 0). In the case where the readable states are >1 and are not the same for each measured parameter in the information unit (but still have equal probability), the equation for the coding base B can be generalized as

(20) $B=R_1\times R_2\times R_3\times \dots \times R_P=\prod _{j=1}^P{R}_j$(20)

where R_j is the number of readable states for parameter j. This leads to a more general expression for information capacity,

(21) $I_k={\left(\prod _{j=1}^P{R}_j\right)}^{M^D}={\left(\prod _{j=1}^P{R}_j\right)}^{U_k}$(21)

This assumes that the information base is the same for each information unit, a reasonable assumption since these are self-similar and therefore contain elements that will yield similar readable states and parameters. Taking the fractal dimension of our natural dendrite D = 1.45, at the resolution limit (k = 5) the magnification factor M = 16, and this leads to U_k = 55.7, which is actually quite close to what we see if we count all the branching nodes in the major branch of the dendrite highlighted by the first generation bifurcation in the k = 1 image of Figure 11. Exploring eqn. 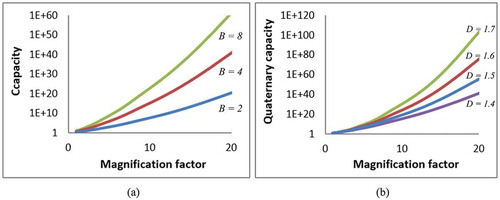21(21) $I_k={\left(\prod _{j=1}^P{R}_j\right)}^{M^D}={\left(\prod _{j=1}^P{R}_j\right)}^{U_k}$(21) with the above parameters and taking the simplest reading case of P = 1 and R = 2 gives I_k = 5.85 × 10¹⁶, the number of unique versions of this pattern under these conditions. Figure 12 gives examples of how I_k varies with magnification factor, which is an attribute of the reading apparatus, for coding base of 2, 4, and 8 (Figure 12(a)), and fractal dimension 1.4, 1.5, 1.6, and 1.7 for quaternary coding (Figure 12(b)). Clearly, even moderate combinations of P, R, D, and M can lead to a sufficient number of pattern variations to uniquely tag every item grown, mined, or manufactured on Earth, considering that the total number of atoms on the planet is in the order of 10⁵⁰.

Figure 12. (a) Information capacity for D = 1.45 and B = 2, 4, and 8. (b) Quaternary capacity (B = 4) for dendrites with D = 1.4, 1.5, 1.6, and 1.7

Concluding remarks

Dendritic patterns are remarkable, both in terms of their universal character, which leads to their extensive appearance in the natural world, and their inherently high information content. Electrochemical dendrites are in the same universality class as diffusion limited aggregates, both being fractals, but the general form of their structure, including their fractal dimension, can be controlled by formation conditions. Factors that influence morphology include material choice (including electrolyte and molarity), electrode geometry, and voltage. Given their topological characteristics, it is no surprise that metallic dendrites have found applications in a variety of fields, including in solar cells [64,66], batteries and supercapacitors [67,68], electroreduction [69], and even fractal antennas [70].

Considering their application as unique identifiers, the fractal quality of dendrites leads to a new way of looking at these structures as a collection of self-similar (but not identical) symbols with Shannon entropy that arises from their geometric ranges. The deliberate coding of a myriad of variations would be challenging at scale but nature supplies us with stochastic pattern deviations as part of the self-assembly process. In addition, the electrochemical formation of centimeter-scale patterns leads to readability by cell phone technology, and the subtle topography adds a degree of unclonability, paving the way for their use as secure physical identifiers in supply chains. It should be noted that attaining the maximum Shannon entropy from the pattern relies on a selection of states that leads to equal probability for each state. For example, if we select two parametric ranges of a geometrical feature p₁ = 0.25 and p₂ = 0.75, by eqn. 3(3) $H=-\sum _i{p}_{i}lo{g}_2{p}_i$(3) , H = 0.811 bits/symbol (vs. 1 bit/symbol for p₁ = p₂ = 0.5), reducing the overall harvestable entropy of the pattern. But the growth rules of a pattern that are enforced by formation conditions could be used to ensure that the parametric ranges are chosen to be equiprobable for any particular ‘species’ of dendrite.

The geometric form of the dendrite could also lead to a natural error detection scheme, in that pattern corruption would be easily recognized as a deviation from the rule-based multi-scale branching arrangement. Specific growth rules lead to patterns that are at the same time different but recognizable. One way to think about this property is to return to nature – real trees within the same species are different from each other but are recognizable as being an oak or a maple due to the growth rules that are particular to the species. Or, as Phillip Ball stated, ‘the branching patterns of trees are a fingerprint of their species’ [14]. Taking this thought in a purely mathematical direction, previous studies [41] have noted that by using the ‘Maximum Entropy Principle’ [71], fractal constructs such as the DLA pattern actually have a very small amount of structural information. This is not to say that the pattern contains little information in general, but instead speaks to the predictability of the overall rule-based form – again, each pattern is recognizable via the limited set of rules which dictate its growth. This rule-based predictability of general form provides an advantage when dendrites are used as identifiers, in that we can potentially tell where errors in the pattern have occurred when the global or local rules have been violated, and this could have utility in error correction. It must be noted that the use of known (zero entropy) functions to provide structure in arbitrary data for error correction is actually very common, for example, the Reed–Solomon approach in QR code applications [72].

Finally, although electrochemical formation has many advantages and will likely be scalable to allow mass-manufacturing, for example, via roll-to-roll processing, other dendrite creation techniques are possible and will produce patterns that may be analyzed in the same way as electrochemical dendrites. In particular, the unusual properties of antimony on surfaces, including the fast diffusion of Sb clusters [73] and their subsequent assembly into a variety of extended forms [74], has been exploited by various researchers to make dendritic antimony ‘islands’ at the microscale, merely by evaporating and ‘soft landing’ Sb onto a suitable substrate, typically graphite [75–78]. The aggregate morphologies depend on the deposition conditions, including the deposition flux. Interestingly, it has been noted that the initial morphology is governed by Volmer–Weber type growth, which leads to 60 nm clusters that ultimately make up dendritic islands [76]. This is similar to what is typically observed for electrochemical formation of dendrites in a liquid electrolyte (see Figure 5), although, in this case, the process is likely driven by a supercooling effect, perhaps not-unlike the Mullins–Sekerka instability mentioned earlier in this review. Branching metallic clusters have also been created by depositing other metals onto graphite, including platinum [79] and silver [80]. We have experimented with photochemical methods that lead to vast numbers of micro-scale dendrites in a ‘one pot’ process [81]. These approaches do not lend themselves to producing individual tags that can be read by cell phone but the micro-dendrites could be used as taggant agents in goods and materials, much like coded nanostructures [82]. Finally, there is also the possibility of using the Saffman–Taylor instability, also described earlier, to make large-scale coarse dendrites in a ‘lifted Hele-Shaw cell apparatus’, in which a viscous fluid is pressed between two plates that are separated at one edge to allow the influx of air which results in a ramified viscous fingering effect [83].

Acknowledgments

This work is currently supported by the USDA National Institute of Food and Agriculture (NIFA), under Grant 2020-67017-33078, Secure Traceability in the Food Supply Chain Using Cell Phone Readable Dendritic Identifiers. The use of facilities within the ASU NanoFab supported in part by NSF program ECCS-1542160 is also acknowledged. The author thanks Smitha Swain and Ninad Chamele of Arizona State University for the images presented in Figures 2, 6, 7, and 8.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the National Institute of Food and Agriculture [2020-67017-33078]; NSF NNCI [NNCI-ECCS-1542160].