Quantum transport in topological nodal-line semimetals

ABSTRACT

Topological nodal-line semimetals offer an attractive research platform for exploring a variety of novel phenomena, which have attracted great research interest in the past decade. There are three unique features of the nodal-line semimetals: (i) band crossing along the closed loop that carries $\pi$ Berry phase, (ii) torus-shaped Fermi surface as the Fermi energy deviates from the nodal loop, and (iii) drumhead-like surface states induced by the band topology, which comprise the main scenarios for most of its electronic properties. Here, we review recent progress on the quantum transport theory of nodal-line semimetals. We show that the properties (i) and (ii) result in a fascinating interplay between the effective dimensionality of electron diffusion and the band topology, which may give rise to 3D weak localization or 2D weak anti-localization effect that can be probed by the magnetoconductivity induced by a weak magnetic field. Moreover, (i) and (ii) can also be revealed by the pattern of the Shubnikov–de Hass oscillation in a strong magnetic field. For the massive nodal-line semimetals with spin-orbit coupling, we show that the magnetic field can induce a topological Lifshitz transition of the Fermi torus from genus 1 to 0. Interestingly, the Lifshitz transition is in good coincidence with the sign reversal of the magnetoresistivity. Compared to the conventional Fermi sphere, the Fermi torus possesses multiple reflection channels, which may give rise to novel scattering processes such as anomalous Andreev reflection at the interface between the semimetal and a superconductor. Besides the bulk states, the drumhead surface states also possess interesting properties. It is shown that the spin polarization of the surface states can induce resonant spin-flipped reflection, which can be detected through both spin and charge transport measurements. We also briefly review the recent experimental progress on the transport properties of nodal-line semimetals and compare the results with the theoretical predictions.

Graphical Abstract

KEYWORDS:

• Nodal-line semimetals
• magnetoresistivity
• weak (anti-)localization
• Lifshitz transition
• Andreev reflection

I. Introduction

In the past two decades, the topological phase of matter has become the frontier of condensed matter physics [1–3]. In stark contrast to the conventional Landau paradigm of phase transition in terms of symmetry breaking, different topological phases are characterized by the topological properties of the Bloch bands. According to their gapped and gapless nature, the topological phases can be roughly divided into insulating and semimetal phases, respectively [1–5]. A variety of topological semimetals have been theoretically predicted and experimentally confirmed, involving Weyl [6,7], Dirac [8], and nodal-line semimetals [9], etc., which correspond to different types of band crossing and the associated band topologies [5–15]. Specifically, the adjacent bands meet linearly at isolated points in the Brillouin zone for the Weyl and Dirac semimetals while intersect along closed loops for the nodal-line semimetals. Interestingly, the one-dimensional nodal loops can be arranged into various configurations, which yield different topological phases and rich physical effects [16–18]. Exotic surface states generally emerge at the open boundaries of topological semimetals due to the bulk-boundary correspondence. For example, the helicoid surface states in the Weyl and Dirac semimetals result in disconnected surface Fermi arcs, which connect the projections of the bulk nodal points in the surface Brillouin zone [7,8]. For the nodal-line semimetals, the so-called drumhead-like surface states (DSS) are induced by the $\pi$ Berry phase carried by the nodal loop, which occupy the area enclosed by the nodal loop projected onto the surface Brillouin zone [19,20]. A common feature of topological semimetals is that both bulk and surface states can participate in various physical processes, making it an attractive research platform for exploring their sole and combined effects. This differs from the situation of topological insulators, in which only the topological surface states are usually of interest because the bulk bands stay far away from the Fermi energy. Various material candidates have been theoretically proposed or experimentally confirmed as nodal-line semimetals, such as HgCr${ }_2$Se${ }_4$ [21], graphene networks [22], Cu${ }_3$ (Pd/Zn)N [23,24], SrIrO${ }_3$ [25,26], TiTaSe${ }_2$ [27], Ca${ }_3$P${ }_2$ [19,28], CaTe [29], compressed black phosphorus [30], CaAg(P/As) [31], CaP${ }_3$ family [32], PdS monolayer [33], Zintl compounds [34], Ba$M{X}_3$ ($M$ = V,Nb, and Ta,$X$ = S,Se) [35], rare earth monopnictides [36], alkaline-earth compounds [37–39], other carbon-based materials [40], and metallic rutile oxides $X{O}_2$,($X$ = Ir,Os,Rd) [41], PbTaSe${ }_2$ [42], ZrXY(X = Si,Ge,Y = S,Se,Te) [17,43–48], and PtSn${ }_4$ [49]. The experimental approaches widely used for probing the electronic properties of topological materials involve the angle-resolved photoemission spectroscopy (ARPES), scanning tunneling microscopy (STM) and transport measurements. The ARPES directly probes the band structures of the bulk and surface states. The information of the Fermi surface can also be revealed by the STM through the quasiparticle interference process. Compared with ARPES and STM, transport measurements possess their own advantages. First, by elaborate design and fabrication of electronic devices and proper field manipulations, the message of the bulk and surface states can be selectively extracted; second, the transport techniques are especially pertinent to potential applications of topological materials in functional electronic devices. Great advances have been made in the transport studies on both Weyl/Dirac and nodal-line semimetals. A special review for the former has been given in Ref [50], while that for the latter is still absent.

In this paper, we give a concise review of the recent progress in quantum transport theories of nodal-line semimetals. The rest of this paper is organized as follows. In Section II, we introduce the main properties of nodal-line semimetals, which include the specific band topology, surface states and the peculiar torus-shaped Fermi surface. Several novel effects stemming from these properties are introduced in the following sections, which involve the weak (anti-)localization effect in Section III, quantum oscillation in Section IV, topological Lifshitz transition of the Fermi surface in Section V, anomalous Andreev reflection in Section VI, and the resonant spin-flipped reflection in Section VII. In Section VIII, we also review the recent experimental progress and compare it with theories. Finally, we draw our conclusion and give an outlook in Section IX.

II. Main properties of nodal-line semimetals

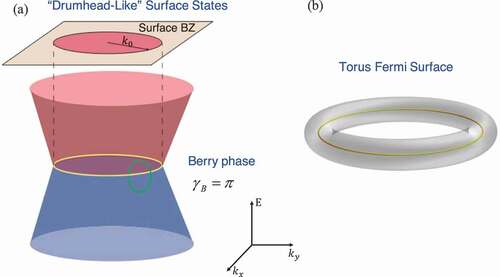
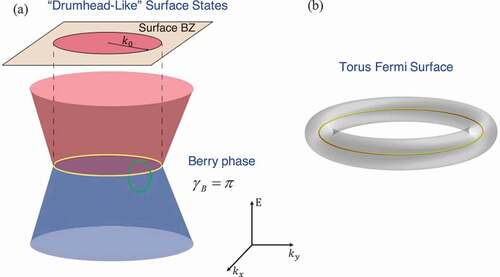
The terminology of nodal-line semimetal indicates a particular type of band crossing along one-dimensional lines or loops [9]. For most of the candidates, the Hamiltonian of the system can be linearized around the nodal-line in the reciprocal space. One can understand each point of the nodal-line as a single Dirac cone in the plane locally perpendicular to the nodal-line. Therefore, the nodal-line semimetal can be understood as a collection of two-dimensional massless Dirac Fermion along the line. As a result, the band topology can be interpreted by the Berry phase carried by the nodal-line as shown in Figure 1), which is similar to that of the Dirac cone in graphene and surface states of the topological insulator. Besides the similarity to the two-dimensional Dirac fermion, the three-dimensional nodal-line semimetal possesses its own features, such as the drumhead-like surface states and the torus-shaped Fermi surface when doped. For real materials, there may exist one or more nodal-lines. In most of cases, several isolated nodal-lines/loops can be analyzed separately so that the effective model with a single nodal-line is sufficient to capture the main physics therein.

Figure 1. (a) Sketch of the band structure of the nodal-line semimetal and the drumhead-like surface states in the surface Brillouin zone. (b) Torus-shaped Fermi surface.

To be specific, we adopt the following Hamiltonian to describe the nodal-line semimetal as [9]

(1) $H(\mathit{k})=\mathrm{\hslash }v{k}_z{\sigma }_x+\mathrm{\hslash }\lambda (k^2-k_0^2){\sigma }_z,$(1)

where $\lambda$ is the model parameter, $v$ is the velocity along the $z$-direction, $k^2=k_x^2+k_y^2+k_z^2$ is the total momentum squared and the Pauli matrices ${\sigma }_{x,z}$ operate in the spin or pseudo-spin space that will be specified if necessary. The Hamiltonian (1) yields the eigenvalues $E_{\pm }=\pm \mathrm{\hslash }\sqrt{v^2{k}_z^2+{\lambda }^2{(k_0^2-k^2)}^2}$ and the corresponding eigenstates $\left|u_{\pm }(\mathit{k})\right.⟩=(\mathrm{\hslash }v{k}_z/\sqrt{{\mathrm{\hslash }}^2{v}^2{k}_z^2+{\gamma }^2},$ $\gamma /\sqrt{{\mathrm{\hslash }}^2{v}^2{k}_z^2+{\gamma }^2})$, with $\gamma =E_{\pm }-\mathrm{\hslash }\lambda (k_0^2-k^2)$. The band degeneracy occurs as $k_x^2+k_y^2=k_0^2$ and $k_z=0$, which defines a nodal loop in the momentum space, see Figure 1). As the Fermi energy $E_F$ deviates from zero that usually occurs for real materials, the nodal loop grows into a torus-shaped Fermi surface; see Figure 1). For $E_F\ll \mathrm{\hslash }\lambda k_0^2$, it is convenient to linearize and parameterize the Hamiltonian (1) into

(2) $\mathcal{H}(\delta \mathit{k})=\mathrm{\hslash }{v}_0\kappa (cos\phi {\sigma }_z+sin\phi {\sigma }_x),$(2)

through the substitution $k_x=(k_0+\kappa cos\phi )cos\theta ,k_y=(k_0+\kappa cos\phi )$ $sin\theta ,k_z=\kappa /\alpha$, in which $v_0=2\lambda k_0$ and $\alpha =v/v_0$ is the ratio between the velocities along the $z$ direction and in the $x$-$y$ plane. The small radius $\kappa$, the toroidal angle $\theta$ and the poloidal angle $\phi$ are labeled in Figure 2). The small momentum $\delta \mathit{k}=\kappa (cos\phi ,sin\phi /\alpha )$ is defined in a local poloidal plane in momentum space denoted by the toroidal angle $\theta$.

Figure 2. (a) Torus-shaped Fermi surface, with major radius $k_0$, minor radius $\kappa$, toroidal angle $\theta$, and poloidal angle $\phi$. (b) The impurity potentials results in 3D and 2D diffusion behaviors, respectively. (c) A coherent backscattering process from wave vector $k$ to $-k$ around the toroidal direction, which is a 3D diffusion behavior. (d) Backscattering from wave vector $\delta k$ to $-\delta k$ around poloidal direction, which is a 2D diffusion behavior [54].

To understand the band topology, let us consider the transverse wavevector ${\mathit{k}}_{||}=(k_x,k_y)$ as a parameter, and then the Hamiltonian (1) describes an effective 1D system in the $z$-direction. If ${\mathit{k}}_{||}$ lies inside the nodal loop, i.e. $|{\mathit{k}}_{||}|<k_0$, the effective 1D system is insulating with an energy gap $\mathrm{\Delta }({\mathit{k}}_{||})=\mathrm{\hslash }v{k_0}^{\prime }$ opening around $k_z={k_0}^{\prime }=\sqrt{k_0^2-|k_{||}{|}^2}$. One can verify that a nontrivial Berry phase can be obtained as ${\gamma }_B=i{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d{k}_z\left.⟨u_{-}(\mathit{k})\right|{\mathrm{\partial }}_{k_z}|u_{-}(\mathit{k})⟩=\pi$ [19,20]. Otherwise, the effective gap is opened at $k_z=0$ and one has ${\gamma }_B=0$ for $|{\mathit{k}}_{||}|>k_0$. This result together with the fact that the Berry curvature vanishes anywhere away from the nodal loop indicates that the $\pi$-Berry phase is exactly carried by the nodal-line and the wave function will pick up the Berry phase along any closed path linked with the nodal-line. In the presence of chiral symmetry, such nontrivial topological winding results in zero-energy surface states encircled by the projection of the nodal loop onto the surface Brillouin zone [51,52], dubbed DSS [22]; see Figure 1). The above features of nodal-line semimetal can give rise to several unique transport properties that will be introduced in the following sections.

III. Weak localization and anti-localization effects in nodal-line semimetals

An electronic system subject to weak disorder and at sufficiently low temperatures resides in the quantum diffusive regime, in which the mean free path is much less than the phase coherence length. The quantum interference effect results in additional quantum corrections to the conductivity [53]. It has been known that the quantum correction to the electronic conductivity exhibits a universal dependence on the dimensionality and band topology of the system. The nontrivial properties of nodal-line semimetal enrich the conventional results of quantum diffusion [54]. First, the torus-shaped Fermi surface brings additional backscattering channels compared with the conventional Fermi sphere, which strongly modifies the quantum diffusion behavior; see Figure 2. Specifically, the effective dimension of diffusion will be two and three for the long-range (LR) and short-range (SR) disordered potentials, respectively. Second, whether the electron can feel the $\pi$-Berry phase carried by the nodal line is determined by its diffusion dimension, thus exhibiting a fascinating interplay between the diffusion dimensionality and the band topology.

We start with the Hamiltonian (1) and (2) and make the substitutions ${\sigma }_z\to {\sigma }_x,{\sigma }_x\to {\sigma }_y$ for a convenient gauge choice, which yield

(3) $\begin{array}{cc}H{ }^{\mathrm{\prime }}(\mathit{k})& =\mathrm{\hslash }v{k}_z{\sigma }_y+\mathrm{\hslash }\lambda (k^2-k_0^2){\sigma }_x,\\ {\mathcal{H}}^{\prime }(\delta \mathit{k})& =\mathrm{\hslash }{v}_0\kappa (cos\phi {\sigma }_x+sin\phi {\sigma }_y).\end{array}$(3)

The Fermi energy $E_F$ is assumed to intersect the conduction band that is the only band concerned below. For ${\mathcal{H}}^{\prime }$, the dispersion of the conduction band is ${ϵ}_k=\mathrm{\hslash }{v}_0\kappa \text{]}$ and the corresponding wave function is ${\psi }_{\mathit{k}}(\mathit{r})=[1,e^{i\phi }{]}^{\mathrm{T}}{e}^{i\mathit{k}\cdot \mathit{r}}/\sqrt{2V}$, with $V$ the volume of the system. The density of states at the Fermi energy is ${\rho }_0=\mathcal{K}{E}_F/(\alpha h^2{v}_0^2)$, proportional to the circumference $\mathcal{K}=2\pi k_0$ of the nodal loop.

The Hamiltonian $H{ }^{\mathrm{\prime }}(\mathit{k})$ and ${\mathcal{H}}^{\prime }$ satisfy two types of anti-unitary symmetries as

(4) $\begin{array}{cc}{\mathcal{T}}_{1}H{ }^{\mathrm{\prime }}(\mathit{k}){\mathcal{T}}_1^{-1}& =H{ }^{\mathrm{\prime }}(-\mathit{k}),\\ {\mathcal{T}}_2{\mathcal{H}}^{\prime }(\delta \mathit{k}){\mathcal{T}}_2^{-1}& ={\mathcal{H}}^{\prime }(-\delta \mathit{k}),\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(4)

where ${\mathcal{T}}_1=K$ and ${\mathcal{T}}_2=i{\sigma }_{y}K$ with $K$ being the complex conjugation. Here, ${\mathcal{T}}_1$ is a spinless time-reversal symmetry, while ${\mathcal{T}}_2$ is a local antiunitary symmetry involving a spin/pseudospin inversion. The second equation of Equation (4)(4) $\begin{array}{cc}{\mathcal{T}}_{1}H{ }^{\mathrm{\prime }}(\mathit{k}){\mathcal{T}}_1^{-1}& =H{ }^{\mathrm{\prime }}(-\mathit{k}),\\ {\mathcal{T}}_2{\mathcal{H}}^{\prime }(\delta \mathit{k}){\mathcal{T}}_2^{-1}& ={\mathcal{H}}^{\prime }(-\delta \mathit{k}),\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(4) can be regarded as the spinful time-reversal symmetry for the 2D subsystem in the plane labeled by $\theta$ [see Figure 2)]. According to the symmetry classification, ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ correspond to the orthogonal and symplectic classes, respectively [55,56]. As a result, they will lead to weak localization (WL) and weak anti-localization (WAL), respectively, depending on which physical process in Figure 2 dominates the backscattering.

There are two backscattering channels for the torus-shaped Fermi surface; see Figure 2. Which type of backscattering dominates the WL or WAL effects is determined by details of the disorder potential and size of the nodal loop. In this section, we consider two limiting cases of the disorder potentials with either SR or LR type relative to the size of the nodal loop. The SR limit is also referred to as the so-called white-noise disorder, which causes constant scattering strength in the reciprocal space so that the backscattering is dominated by the interference along the toroidal direction [see Figure 2)]. Such an interference loop does not encircle the nodal-line so that electrons can not feel the $\pi$ Berry phase. The LR disorder may exist due to unconventional screening effects [57]. In this case, the backscattering is dominated by the interference along the poloidal direction locally in the reciprocal space. The interference loop encircles the nodal line [see Figure 2)] so that the $\pi$ Berry phase plays an important role in the quantum diffusion.

The interference effect is manifested as the quantum correction to the conductivity, which can be obtained by calculating the Feynman diagrams in Figure 3). Three leading-order diagrams are involved in the calculation, namely, the bare Hikami box [56] and two dressed Hikami boxes [58,59]. The latter two jointly contribute −1/2 to the correction of the former for both the SR and LR limits, the same as that in graphene [58]. The overall quantum correction to the zero-temperature conductivity in the $z$-direction in both the SR and LR limits is given by

Figure 3. Relevant Feynman diagrams. (a) Three leading-order diagrams of the quantum interference corrections to the conductivity, with one bare Hikami box and two dressed Hikami boxes. The arrowed solid line represents Green functions and the arrowed dashed line represents impurity scattering. (b) Ladder diagram vertex correction to the velocity. (c) The Cooperon correction [54].

(5) $\begin{array}{cc}{\sigma }_z^S& =-\frac{s{\eta }_z^2\alpha e^2}{2{\pi }^{2}h}(\frac{1}{{\mathrm{\ell }}_e}-\frac{1}{{\mathrm{\ell }}_{\varphi }}),\\ {\sigma }_z^L& =\frac{s{\eta }_z^2\mathcal{K}\alpha e^2}{2(2\pi {)}^{2}h}ln({\mathrm{\ell }}_{\varphi }/{\mathrm{\ell }}_e),\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(5)

where ${\mathrm{\ell }}_e=v_0{\tau }_e$ is the mean free path and ${\mathrm{\ell }}_{\varphi }$ is the phase coherence length. In the SR limit, a 3D scaling is obtained for the quantum correction of the conductivity and the overall minus sign means the WL effect [53]. In contrast, the LR correction is positive that exhibits a WAL behavior with a 2D scaling law. The prefactor $\mathcal{K}$ in ${\sigma }_z^L$ ensures the unit of a 3D conductivity and also indicates an enhancement of the WAL effect contributed by a large number of 2D diffusion planes; see Figure 2). Because of the different dimensionality of diffusion, ${\sigma }_z^S$ will saturate as ${\mathrm{\ell }}_{\varphi }\to \mathrm{\infty }$ while ${\sigma }_z^L$ always increases as $ln({\mathrm{\ell }}_{\varphi }/{\mathrm{\ell }}_e)$.

The quantum correction to the conductivity can be suppressed by a magnetic field-induced dephasing effect [60]. It allows the probe of WL and WAL corrections using magnetoconductivity measurements. The magnetoconductivities of the nodal-line semimetal for the two types of disorder are defined by the difference between the conductivity with and without a magnetic field, i.e. $\delta {\sigma }_z^{S,L}(B)\equiv {\sigma }_z^{S,L}(B)-{\sigma }_z^{S,L}(0)$, with

(6a) $\begin{array}{c}{\sigma }_z^S(B)=-\frac{s{\eta }_z^2\alpha e^2}{{(2\pi )}^{2}h}\left[\begin{array}{c}\mathrm{\Psi }\left({\mathrm{\ell }}_B^2/{\mathrm{\ell }}_e^2+\frac{1}{2}\right)/{\mathrm{\ell }}_e-\mathrm{\Psi }\left({\mathrm{\ell }}_B^2/{\mathrm{\ell }}_{\varphi }^2+\frac{1}{2}\right)/{\mathrm{\ell }}_{\varphi }-{\int }_{1/{\mathrm{\ell }}_{\varphi }}^{1/{\mathrm{\ell }}_e}dx\\ -\mathrm{\Psi }\left({\mathrm{\ell }}_B^2{x}^2+\frac{1}{2}\right)\end{array}\right]\\ \hspace{0.17em}\end{array},$(6a)

(6b) ${\sigma }_z^L(B)=\frac{s{\eta }_z^2\mathcal{K}\alpha e^2}{16{\pi }^{2}h}{\int }_0^{2\pi }\frac{d\theta }{2\pi }\left[\begin{array}{c}\mathrm{\Psi }\left(\frac{{\mathrm{\ell }}_B^2}{{\mathrm{\ell }}_e^2\alpha |sin\theta |}+\frac{1}{2}\right)\\ -\mathrm{\Psi }\left(\frac{{\mathrm{\ell }}_B^2}{{\mathrm{\ell }}_{\varphi }^2\alpha |sin\theta |}+\frac{1}{2}\right)\end{array}\right]$(6b)

The numerical results are shown in Figure 4. Specifically, in the SR regime, the WL effect leads to a positive magnetoconductivity [Figure 4)]; In the LR regime, a negative magnetoconductivity corresponds to the WAL effect [Figure 4)]. Moreover, the magnetoconductivities exhibit different $B$-dependence for the two regimes. Specifically, $\delta {\sigma }_z^S(B)\propto \sqrt{B}$ in the SR regime while $\delta {\sigma }_z^L(B)\propto -lnB$ in the LR regime; see Figure 4. It is notable that $\delta {\sigma }_z^L(B)$ in the SR regime is three orders larger than $\delta {\sigma }_z^S(B)$. This is because the system is composed of a large number of 2D planes of diffusion in the SR regime, as discussed above.

Figure 4. The magnetoconductivity $\delta {\sigma }_z(B)$ in the (a) SR limit and (b) LR limit for different phase coherence lengths ${\mathrm{\ell }}_{\varphi }$, which are represent by the different color [54].

From the discussion, one can see that quantum diffusion in the nodal-line semimetal can lead to intriguing phenomena such as the 3D magnetoconductivity with a 2D scaling law and an extraordinarily large value. Relevant effects have been reported in a variety of nodal-line semimetals [61,62], which may be attributed to the scenario discussed in this section; see section VIII.

VI. Quantum oscillations in nodal-line semimetals

The shape of the Fermi surface as well as the geometry phase encoded in the wave functions can be probed through the quantum oscillation method [63,64], or specifically, Shubnikov-de Haas oscillation of resistivity that will be discussed here. The shape and size of the Fermi surface and the Berry phase information can be extracted through the periodicity and phase shift of the oscillation pattern, respectively [65]. The coexistence of the torus-shaped Fermi surface and the $\pi$ Berry flux in nodal-line semimetal indicates that the fascinating interplay between the two may lead to interesting results in the quantum oscillation measurements [66–68]. A series of experiments have reported the results of quantum oscillations of the resistivity $\rho$ [69–91] in nodal-line semimetals subjected to a strong magnetic field. Several theories have been developed on this problem and we will review the results in Ref [66]. here.

The main results of the Shubnikov-de Haas oscillation of resistivity are reflected by the Lifshitz-Kosevich formula [64] as

(7) $\rho \sim cos[2\pi (F/B+\varphi )],$(7)

where $F$ is the oscillation frequency, $\varphi$ is the phase shift and $B$ is the magnetic field. The information of the Fermi surface and the geometric phase is revealed by $F$ and $\varphi$. In experiments, both $F$ and $\varphi$ can be extracted from the Landau fan diagram. Specifically, the condition for the $n$ th peak of the resistivity is $n=F/B+\varphi$. Therefore, $F$ is the slope of the linear function and the intercept on the $n$ axis corresponds to the phase shift $\varphi$.

According to the Onsager relation [92] $F=(\mathrm{\hslash }/2\pi e)A$, the oscillation frequency $F$ is proportional to the extremal cross-section area $A$ of the Fermi surface perpendicular to the magnetic field. By changing the directions of the external magnetic field, the frequency $F$ varies and the shape and size of the Fermi surface can then be extracted. For nodal-line semimetal with light doping, the Fermi surface possesses a torus shape that is highly anisotropic, which is in stark contrast to the spherical Fermi surface for conventional electrons and Weyl fermions. For a magnetic field normal to the nodal-line plane, the extremal cross sections are determined by $\mathrm{\partial }A/\mathrm{\partial }{k}_z{|}_{E_F}=0$, which yields two extremal cross sections labeled by $\alpha$ and $\beta$ lying in the $k_z=0$ plane; see Figure 5). The energy dispersions are $E_{\pm }=\pm \sqrt{{\mathrm{\hslash }}^2{\lambda }^2{(k^2-k_0^2)}^2+{\mathrm{\hslash }}^2{v}^2{k}_z^2}$ for electron (+) and hole ($-$), respectively. By combining the dispersion and Onsager relation, the high and low frequencies are found to be $F_{\alpha }=(\mathrm{\hslash }\lambda k_0^2+E_F)/2\lambda e$ for the outer circle and $F_{\beta }=(\mathrm{\hslash }\lambda k_0^2-E_F)/2\lambda e$ for the inner circle, respectively [66]. For the magnetic field in the plane of the nodal-line, the extremal cross sections labeled by $\gamma$ and $\delta$ can be obtained similarly; see Figure 5.

Figure 5. (a) The maximum ($\alpha$) and minumum ($\beta$) cross sections in the nodal-line plane of the torus Fermi surface. (b) The maximum ($\gamma$) and minimum ($\delta$) cross sections out of the nodal-line plane of the torus Fermi surface [66].

The phase shift for each frequency component of the quantum oscillation satisfies the relation as

(8) $\varphi =-1/2+{\varphi }_B/2\pi +{\varphi }_{3D}$(8)

where ${\varphi }_B$ is the Berry phase [93,94] and ${\varphi }_{3D}=\mp 1/8$ is a correction pertinent to three-dimensional systems. The rule for the “$\mp$” sign is as follows: for a maximum cross section, ${\varphi }_{3D}=-1/8$ for electrons and $1/8$ for holes; for a minimum cross section, the opposite sign should be taken. For a conventional Fermi sphere, there is only a maximum cross section so that ${\varphi }_{3D}=-1/8$ for electrons and $1/8$ for holes. The situation becomes more complex for the nodal-line semimetal with a torus-shaped Fermi surface [66]. The Fermi torus possesses both maximum and minimum cross sections; see Figure 5) for the magnetic field normal to the nodal-line plane and Figure 5) for the in-plane magnetic field. Moreover, the Berry phase is determined by the fact whether the contours encircle the nodal line or not. For the out-of-plane magnetic field, the contours denoted by $\alpha$ and $\beta$ do not encircle the nodal line and thus ${\varphi }_B=0$ for both cross sections. For the in-plane magnetic field, it is easy to see ${\varphi }_B=0$ for the contour $\gamma$ while ${\varphi }_B=\pi$ for $\delta$.

Combining the arguments above, one can obtain the overall phase shift for various cross sections as summarized in Table 1. For example, as the magnetic field is normal to the nodal-line plane, the cross sections are $\alpha$ and $\beta$ and ${\varphi }_B=0$ for both. The phase shift for the maximum cross section $\alpha$ is calculated as $\varphi =-1/2+0-1/8=-5/8$ for electrons and $\varphi =-1/2+0+1/8=-3/8\leftrightarrow 5/8$ for holes. The phase shift for the minimum cross section $\beta$ is calculated as $\varphi =-1/2+0+1/8=-3/8\leftrightarrow 5/8$ for electrons and $\varphi =-1/2+0-1/8=-5/8$ for holes. The phase shift for the cross sections $\gamma$ and $\delta$ can be obtained in a similar way.

Table 1. The phase shift $\phi$ of nodal-line semimetals in Figure 5 [66]

Cross section	Berry phase	Min./Max	Electron	Hole
α	0	Max.	-1/2+0-1/8=-5/8	+5/8
β	0	Min.	-1/2+0+1/8=-3/8↔5/8	-5/8
γ	0	Max.	-1/2+0-1/8=-5/8	+5/8
δ	π	Min.	-1/2+π/2π+1/8=1/8	-1/8

Although the theory is based on the minimal model (1) of the nodal-line semimetal, the scenario for the phase shift should hold generally, which can be compared with experimental results of real materials with different configurations of nodal loops, such as Cu ${ }_3$ PdN and ZrSiS; see the discussion in section VIII.

V. Magnetic field induced Lifshitz transition

Transport measurements are a direct manifestation of the properties of the Fermi surface. Therefore, modulation of the Fermi surface by pressure, doping or external fields can be well reflected by the transport signatures. Interestingly, apart from continuous deformations, the Fermi surface can also undergo abrupt changes in its topology, the so-called topological Lifshitz transition [95]. Such a transition may lead to the discontinuity of physical quantities. The torus-shaped Fermi surface of the nodal-line semimetal possesses genus one and thus provides an ideal platform to investigate its Lifshitz transition. Moreover, the interplay between the topology of the Fermi surface and that of the wave functions may yield unique physical effects.

It is convenient to change the Fermi surface by an external field. For this purpose, we consider a massive nodal-line semimetal with finite spin-orbit coupling which exists in many material candidates. We revise the linearized Hamiltonian ${\mathcal{H}}^{\prime }(\delta \mathit{k})$ in Equation (3)(3) $\begin{array}{cc}H{ }^{\mathrm{\prime }}(\mathit{k})& =\mathrm{\hslash }v{k}_z{\sigma }_y+\mathrm{\hslash }\lambda (k^2-k_0^2){\sigma }_x,\\ {\mathcal{H}}^{\prime }(\delta \mathit{k})& =\mathrm{\hslash }{v}_0\kappa (cos\phi {\sigma }_x+sin\phi {\sigma }_y).\end{array}$(3) by involving a mass term induced by the spin-orbit coupling, which yields [96]

(9) ${\mathcal{H}}_{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}={\mathcal{H}}^{\prime }+\mathrm{\Delta }{\tau }_z{\sigma }_z$(9)

with the sign of the mass term depending on the spin ${\tau }_z$ while ${\sigma }_z$ is the pseudo-spin. The energy spectra become ${\epsilon }_k^{\pm }\left(\kappa \right)=\pm \sqrt{{\left(\mathrm{\hslash }{v}_0\kappa \right)}^2+{\mathrm{\Delta }}^2}\hspace{0.17em}$ in which a gap $2\mathrm{\Delta }$ is opened along the nodal loop. The gap induces a finite spreading of the Berry curvature in the reciprocal space that introduces the self-rotation and thus a finite orbit magnetic moment (OMM) of the wave packet. Then the coupling between the OMM and a magnetic field can be implemented [94,98]. We focus on the regime that the Zeeman coupling between the magnetic field and the electronic spin is weak so that the main results do not rely on the spin or equivalently, the sign of the mass. We set ${\tau }_z=1$ henceforth.

Without loss of generality, we consider a positive Fermi energy, such that only the conduction band contributes to the transport and the wave function is found to be $|u_{\mathit{k}}⟩=(\kappa e^{-i\phi }/\sqrt{{\kappa }^2+{\gamma }^2},\gamma /\sqrt{{\kappa }^2+{\gamma }^2})$ with $\gamma =\sqrt{m^2+{\kappa }^2}-m$ and $m=\mathrm{\Delta }/(\mathrm{\hslash }{v}_0)$. The Berry curvature defined by ${\mathbf{\Omega }}_{\mathit{k}}=i⟨{\mathrm{\nabla }}_{\mathit{k}}{u}_{\mathit{k}}|\times |{\mathrm{\nabla }}_{\mathit{k}}{u}_{\mathit{k}}⟩$ has only a nonzero value along the toroidal direction in the parametric coordinates as ${\mathbf{\Omega }}_{\mathbf{k}}=-m/2({\kappa }^2+m^2{)}^{\frac{3}{2}}{\hat{\mathit{e}}}_{\theta }$ which reduces to a Berry flux density as $m\to 0$. In the present two-band system, the OMM is related to the Berry curvature by ${\mathcal{M}}_{\mathbf{k}}=\frac{e}{2\mathrm{\hslash }}{\mathbf{\Omega }}_k\left({\epsilon }_{\kappa }^{+}-{\epsilon }_{\kappa }^{-}\right)\hspace{0.17em}$, which is also a vector field along the toroidal direction. One can infer that when an external magnetic field is imposed, only its components in the $x$-$y$ plane couple to the OMM. We consider a magnetic field $\mathit{B}=B\hat{\mathit{x}}$ in the $x$-direction, which gives rise to the coupling energy as

(10) $\delta {\text{isin}}_k(\kappa ,\theta )=-{\mathcal{M}}_{\mathit{k}}\cdot B=-(me{v}_{0}B)sin\theta /[2({\kappa }^2+m^2)].\text{]}$(10)

The whole energy of the conduction band becomes $\widetilde{ϵ}k(\kappa ,\theta )={ϵ}_k^{+}(\kappa )+\delta k(\kappa ,\theta )$, which now depends on the toroidal angle $\theta$. A direct consequence of this anisotropy is a deformation of the Fermi torus, as shown in Figure 6. We will demonstrate in the following that such a deformation plays a pivotal role in the magnetotransport.

Figure 6. (a) Schematic diagram of the torus-shaped Fermi surface in nodal-line semimetal, the major radius is $k_0$, minor radius is $\kappa$, the toroidal angle and poloidal angle are $\theta$,$\varphi$, respectively. (b) Finite berry curvature distribution in the poloidal cross section. (c-e) The deformation process of the Fermi surface induced by the increasing external magnetic field [97].

In the weak field limit $B\ll {ϵ}_F^2/(\mathrm{\hslash }e{v}_0^2)\text{]}$ the impact of Landau level can be neglected. By using the semiclassical Boltzmann formalism, the longitudinal conductivity can be obtained as [97,99]

(11) ${\sigma }^{\mu }=-\int \frac{d^3\mathit{k}}{{(2\pi )}^3}\frac{e^2\tau }{D_{\mathit{k}}}{\left({\stackrel{\sim }{v}}_{\mathit{k}}^{\mu }+\frac{e}{\mathrm{\hslash }}{B}^{\mu }\stackrel{\sim }{\mathit{v}}.{\mathrm{\Omega }}_k\right)}^2\frac{\mathrm{\partial }f}{\mathrm{\partial }\stackrel{\sim }{\in }}$(11)

Analytical results can be obtained in the ${\kappa }_F\gg m$ regime as ${\sigma }_0^x={\sigma }_0^y={\sigma }_0^z/2{\alpha }^2=e^2{k}_0{ }_{ϵ}\tau /8\pi \alpha {\mathrm{\hslash }}^2\text{]}$ and $\delta {\sigma }^x=\delta {\sigma }^y/3=\delta {\sigma }^z/4{\alpha }^2=-(3\alpha e^4{v}_0^6{\mathrm{\hslash }}^2{k}_0\tau B^2{m}^2)$ $/(32{ϵ}_F^5)\text{]}$, where ${\kappa }_F$ is the Fermi vector, ${\sigma }_0$ is the Drude conductivity and $\delta \sigma$ is the additional magnetic conductivity induced by the OMM. Different from the situation of Weyl semimetal [100] or topological insulator [99], the magnetoconductivity in the massive nodal-line semimetal cannot be induced by the pure Berry curvature effect without taking into account the OMM effect [97]. That is to say, the magnetoconductivity is exactly caused by the deformation of the Fermi torus [see Figure 6] due to the coupling between the OMM and the magnetic field.

As the coupling between the OMM and the magnetic field becomes stronger, which can be achieved by increasing either $B$ or the ration $m/\kappa$, the deformation of the Fermi torus becomes more severe. Surprisingly, the magnetoresistivity (MR) does not obey a monotonic dependence on $B$; see Figure 7, which first goes up to its maximum and then drops rapidly as B increases. As B increases further, the MR can even change its sign. The sign reversal of MR induced by the Berry curvature has not been found in other systems [99,100], which indicates a possible new scenario in the massive nodal-line semimetal. The unique response of MR with respect to $B$ in nodal-line semimetals is deeply rooted in the fact that the torus-shaped Fermi surface can undergo a topological Lifshitz transition from genus one to zero; see Figure 6, which has no counterpart in a conventional Fermi sphere. The topological Lifshitz transition provides us with a possible explanation of the sign reversal of MR in massive nodal-line semimetal, which is proved to be correct.

Figure 7. (a) MR as a function of the external magnetic field with and without sign reversal. (b) Correspondence between MR’s sign reversal point and the critical magnetic field $B^{\ast }$ (open circles) [97].

In the limit ${\kappa }_F\ll m$, the Lifshitz transition can be induced by a small magnetic field. The numerical results show that the sign reversal points of MR are in good coincidence with those of the Lifshitz transition (open circles); See Figure 7. Such correspondence can also be analytical proved by expanding the energy as ${ϵ}_F=\mathrm{\hslash }{v}_0(m+\eta )\text{]}$ given that $\eta \ll m$. The critical field of Lifshitz transition can be obtained as $B^{\ast }=2\mathrm{\hslash }m\eta /e$. By expanding Equation (11)(11) ${\sigma }^{\mu }=-\int \frac{d^3\mathit{k}}{{(2\pi )}^3}\frac{e^2\tau }{D_{\mathit{k}}}{\left({\stackrel{\sim }{v}}_{\mathit{k}}^{\mu }+\frac{e}{\mathrm{\hslash }}{B}^{\mu }\stackrel{\sim }{\mathit{v}}.{\mathrm{\Omega }}_k\right)}^2\frac{\mathrm{\partial }f}{\mathrm{\partial }\stackrel{\sim }{\in }}$(11) to the linear order of $\eta$, we obtain $\sigma (B^{\ast })=\sigma (0)$, which means that the correspondence holds strictly in this regime [97].

VI. Anomalous Andreev reflection

One important feature of the torus-shaped Fermi surface is the existence of one additional backscattering channel compared with the conventional Fermi sphere, which has nontrivial effects on the quantum diffusion as discussed in Section III. In the ballistic regime, the torus-shaped Fermi surface can be revealed by the reflection process. Given that the current due to normal reflection compensates with the injected current, it is beneficial to search for other types of reflection processes. Andreev reflection (AR) is referred to as the electron-to-hole reflection at the interface between a metal and a superconductor, by which a pair of electrons penetrate into the superconductor and form a Cooper pair. Therefore, the AR process gives rise to a measurable current.

There exist two types of AR previously. The conventional retro-AR (RAR) indicates that all velocity components of the reflected hole are inverted so that the reflected hole retraces the path of the incident electron; see Figure 8). The specular AR (SAR) occurs if the incident electron and the reflected hole are from the conduction and valence bands, respectively [102]. During SAR only the velocity perpendicular to the interface is inverted; see Figure 8, which resembles the normal reflection apart from the electron-hole conversion. The most promising candidates for the implementation of SAR are the massless Dirac Fermion in graphene and topological semimetals [102–104], in which no energy gap needs to be overcome during the SAR progress.

Figure 8. Three types of AR, (a) RAR, (b) SAR, (d) AAR. (c) torus-shaped Fermi surface [101].

According to the sign inversion of the velocities during the AR processes, it can be inferred that the RAR and SAR constitute a complete set of AR in two dimensions, in which only two velocity components exist. Interestingly, in three dimensions, the types of AR can be further enriched. A novel type of AR dubbed ‘anomalous-trajectory Andreev reflection’ (AAR) was proposed in Ref [101]., in which only one of the two lateral velocities is inverted; see Figure 8). Three types of AR processes are compared by their sign inversion during the AR in Table 2. Note that the type of AR is determined by the band structure of the normal metal or semimetal rather than that of the superconductor, because AR takes place on the normal side of the junction. As a result, it is sufficient to obtain the AAR by adopting a conventional superconductor.

Table 2. Different features in the RAR, SAR, and AAR [101]

	$v_x$	$v_y$	$v_z$
RAR	$-$	$-$	$-$
SAR	$-$	$+$	$+$
AAR	$-$	$-\left(+\right)$	$+\left(-\right)$

Consider a nodal-line semimetal-superconductor junction oriented along $x$-direction with the toroidal circle of the Fermi torus perpendicular to the interface of the junction as shown in Figure 8. A spin-degenerate nodal-line semimetal lies in the $x<0$ region and a conventional $s$-wave superconductor occupies the $x>0$ region. To study the problem of electron-hole scattering, it is convenient to write the Hamiltonian in the Nambu space. The Hamiltonian of the whole junction can be expressed as

(12) $H=H_{NL}\Theta (-x)+H_S\Theta (x)+U\delta (x)\tilde{\tau }z{H}_{NL}38;=(H^{\prime }-\mu )\otimes \tilde{\tau }z,H_S={ϵ}_k{\sigma }_0\otimes \tilde{\tau }z+\Delta {\sigma }_0\otimes \tilde{\tau }x,$(12)

where $\mathrm{\Theta }(x)$ is the unit step function and ${\tilde{\tau }}_{x,z}$ are the Pauli matrices in the Nambu space, ${\mathcal{H}}_{NL}$ and ${\mathcal{H}}_S$ correspond to the nodal-line semimetal and the conventional $s$-wave superconductor, respectively, $H{ }^{\mathrm{\prime }}(\mathit{k})$ captures a spin-degenerate nodal-line semimetal and $\mu$ is its chemical potential, and $U\delta (x){\tilde{\tau }}_z$ is a $\delta$-function interface barrier at $x=0$. The normal state energy of the superconductor is ${\epsilon }_{\mathit{k}}={\mathrm{\hslash }}^2{\mathit{k}}^2/(2m)-{\mu }_S$ (measured from the chemical potential ${\mu }_S$) with $\mathrm{\Delta }$ the pair potential that is diagonal in the pseudo-spin space and $m$ the effective mass. For a nodal-line semimetal with slight doping such that $\mu \ll \mathrm{\hslash }\lambda k_0^2$, the Fermi surface possesses a torus shape. Unlike previous sections where only the conduction band is considered, in this section, both conduction and valence bands will be involved in the discussion. The excitation energies for the electron and hole in the nodal-line semimetal are $E_e=\pm \mathrm{\hslash }{v}_0\kappa -\mu$ and $E_h=\mp \mathrm{\hslash }{v}_0\kappa +\mu$, with “$\pm$”(“$\mp$”) corresponding to the conduction and valence band, respectively.

The nontrivial effect of the torus-shaped Fermi surface on AR is the doubling of reflection channels. By involving both reflection waves and solving the scattering problem at the interface, one can obtain the probabilities for various processes [101]. The types of the AR depend on the magnitude of the chemical potential of the nodal-line semimetal. Specifically, in the limit $E,\mathrm{\Delta }\ll \mu$, the electron and AR hole belong to the same band, and two types of AR are the RAR and AAR (with inversion of $v_x$ and $v_z$); for $E,\mathrm{\Delta }\gg \mu$, the electron and AR hole reside in different bands, and the AR types become the SAR and AAR (with inversion of $v_x$ and $v_y$). One can see that AAR occurs in both regimes.

For a transparent interface with $U=0$, the AR amplitudes in the limit of $E,\mathrm{\Delta }\ll \mu$ can be obtained as

(13) $\begin{array}{cc}{r}_R& =\frac{2\chi [2\chi cos\beta {cos}^2\phi +isin\beta ({cos}^2\phi +{\chi }^2)]}{{[isin\beta ({cos}^2\phi +{\chi }^2)+2\chi cos\beta ]}^2-4{\chi }^2{sin}^2\phi }\\ r_A^{xz}& =\frac{-2\chi e^{i\phi }sin\beta sin\phi ({cos}^2\phi -{\chi }^2)}{{[isin\beta ({cos}^2\phi +{\chi }^2)+2\chi cos\beta ]}^2-4{\chi }^2{sin}^2\phi }\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(13)

where $r_R$ and $r_A^{xy}$ correspond to the RAR and AAR, respectively, $\chi =v_x^e/v_x^F$ with $v_x^e$ as the $x$-direction velocity of electron in the nodal-line semimetal and $v_x^F=\sqrt{2m{\mu }_S-{\mathrm{\hslash }}^2(k_y^2+k_z^2)}/m$ as that in the superconductor. In this limit, the RAR process dominates the electron transport for $E<\mathrm{\Delta }$. For $E=\mathrm{\Delta }$ and thus $\beta =0$, $r_R=1$ and $r_A^{xy}=0$, meaning that perfect RAR takes place for all incident angles $(\theta ,\phi )$.

For the opposite limit $E,\mathrm{\Delta }\gg \mu$, the AR amplitudes reduce to

(14) $r_S=0,r_A^{xy}=\frac{2\chi e^{i\phi }cos\phi }{isin\beta ({cos}^2\phi +{\chi }^2)+2\chi cos\beta }$(14)

where $r_S$ and $r_A^{xy}$ correspond to the SAR and AAR processes, respectively. In this case, one can see that the AAR dominates the electron transport with the inversion of $v_x$ and $v_y$.

In order to probe the AAR, one should focus on the inter-band AR regime, such that the AAR dominates the transport. The feature of the AAR is its unique reflection trajectory as shown in Figure 8). It was then proposed to use the nonlocal scanning tunneling spectroscopy (STM) to extract such a trajectory of the reflected hole. The AAR can be manifested as a spatially resolved ridge structure of the nonlocal conductance as shown in Figure 9, which is in stark contrast to the peak structure of the RAR [101].

Figure 9. (a)The two-terminal setup for detecting the AAR. (b) Nonlocal conductance in RAR regime. (c) (d) Nonlocal conductance in AAR regime with different interface barrier [101].

VIII. Surface states induced resonant spin-flipped reflection

The manifestation of the bulk-boundary correspondence principle in nodal-line semimetals is the existence of drumhead-like surface states (DSS) [22], as we described in section II. Although the spectra of the DSS can be probed by the ARPES measurements, it is impossible to extract its spatial distribution in this way. On the other hand, it is hopeful to reveal the spatial distribution of the DSS through transport measurements by fabricating electrodes directly coupled to the surface. No matter whether the full energy spectra are gapped or gapless, the surface states are always composed of bound states in the corresponding transverse channels labeled by the lateral momenta ${\mathit{k}}_{||}$. For topological semimetal phases, only the transverse channels that coincide with the nodal points or nodal-lines are gapless, while the other channels are still gapped. Specifically, the DSS in nodal-line semimetals are a set of bound states shown in Figure 1) and Figure 10 enclosed by the projection of the nodal loop. According to quantum mechanics, the formation of a bound state indicates a relevant resonance effect. For the nodal-line semimetals with spin-orbit coupling, the spin-polarized DSS correspond to the resonant spin-flipped reflection at the interface between a normal metal and a nodal-line semimetal [105].

Figure 10. (a) A junction between normal metal and nodal-line semimetal, The drumhead-like surface state at the boundary are encircled by the projection of the bulk nodal loop onto the surface Brillouin zone. The inset show trivial (dashed line) and nontrivial (solid line) band dispersion. (b) Probability of spin-flipped reflection [101].

Consider the heterojunction in Figure 10) in the $z$-direction that is composed of a normal metal with spin degeneracy and a nodal-line semimetal with spin-orbit coupling. In the $z<0$ region, the normal metal is described by the Hamiltonian $H_{NM}=C|\mathit{k}{|}^2-{\mu }_0$, where $C$ is a mass-dependent parameter and ${\mu }_0$ is the chemical potential that relates to the Fermi wavevector through $|{\mathit{k}}_F|=\sqrt{{\mu }_0/C}$. In the $z>0$ region, the nodal-line semimetal is described by Hamiltonian (1), with the Pauli matrices being the real spin here. The $\delta$-function barrier $U\delta (z)$ is imposed at the interface. Solving the scattering problem at the interface for a given ${\mathit{k}}_{||}$ inside the nodal loop yields the spin-flipped reflection amplitude as

(15) $r_f=-\frac{4}{{(\eta +1/\eta +iZ{ }^{\mathrm{\prime }})}^2{\mathrm{{\rm Y}}}_1+{(\eta -1/\eta +iZ{ }^{\mathrm{\prime }})}^2/{\mathrm{{\rm Y}}}_1}$(15)

where $\eta =\sqrt{v_{NM}/v_{SM}}$ is the square root of the ratio of perpendicular velocities in the normal metal and nodal-line semimetal, with $v_{NM}=2C|{\mathit{k}}_F|cos\theta$ and $v_{SM}=2\mathrm{\hslash }\lambda k{{ }^{\mathrm{\prime }}}_0$, respectively, $\theta$ is the electron’s incident angle (relative to the $z$-axis), $Z{ }^{\mathrm{\prime }}=2U/\sqrt{v_{NM}{v}_{SM}}$ is a dimensionless interface barriar height, and ${\mathrm{{\rm Y}}}_1=[E+\mathrm{\hslash }\lambda (k_1^2-{k{{ }^{\mathrm{\prime }}}_0}^2)]/(k_1\mathrm{\hslash }v)$ with $k_1=\sqrt{{{k{ }^{\mathrm{\prime }}}_0}^2-({\mathrm{\hslash }}^2{v}^2-\sqrt{4E^2{\mathrm{\hslash }}^2{\lambda }^2+{\mathrm{\hslash }}^4{v}^4-4{\mathrm{\hslash }}^4{v}^2{\lambda }^2{{k{ }^{\mathrm{\prime }}}_0}^2})/(2{\mathrm{\hslash }}^2{\lambda }^2)}$.

In the tunneling limit $Z{ }^{\mathrm{\prime }}\gg 1$, the probability of the spin-flipped reflection $R_f=|r_f{|}^2$ exhibits a sharp resonant peak around zero energy; see Figure 10). This can be understood by expanding Equation (15)(15) $r_f=-\frac{4}{{(\eta +1/\eta +iZ{ }^{\mathrm{\prime }})}^2{\mathrm{{\rm Y}}}_1+{(\eta -1/\eta +iZ{ }^{\mathrm{\prime }})}^2/{\mathrm{{\rm Y}}}_1}$(15) to a series of Feynman paths constructed by multiple reflection processes [105]. It can be shown that the condition of resonant spin-flipped reflection is equivalent to the Bohr–Sommerfeld quantization condition for the surface bound states, meaning that such a resonance is exactly induced by the DSS and thus provides a direct evidence for its detection.

Two transport schemes were proposed to detect such an effect [105]; see Figure 11) and (d). For the spin transport scheme in Figure 11), spin-polarized electrons are injected from a ferromagnetic lead into the normal metal and then get reflected along with spin-flipping at the interface with the nodal-line semimetal. It generates a nearly pure spin current (zero charge current) around the resonance energy as shown in Figure 11, which can be measured by the spin Hall voltage $V_{SH}$ [106] taking advantage of the inverse spin Hall effect [107,108]. For the charge transport scheme in Figure 11), the charge current flowing between two anti-parallel magnetic terminals directly reveals the resonant spin-flipped reflection, which can be manifested as the resonant peak in the differential conductance; see Figure 11).

Figure 11. (a) Setup for detecting DSS with spin transport. (b) The spin (thick lines) and charge (thin lines) with different interface barrier heights. (c) Effect of finite dispersion of DSS on the spin conductance, where the interface barrier $Z=10$. (d) Setup for detecting DSS with charge transport. (e) Charge conductance with different interface barrier heights. (f) Effect of finite dispersion of DSS on the charge conductance, where the interface barrier $Z=10$ [105].

The spin-flipped reflection is induced by all the bound states that comprise the DSS so that any dispersion of the DSS will result in a broadening of the resonant peak; see Figure 11) and (f). Moreover, the interface disorder has similar effect on the resonant peak [105]. Therefore, in order to observe a sharp resonant peak, nodal-line semimetals with flat DSS are favorable. Nevertheless, even the DSS possess finite dispersion, the spin current will still be strongly enhanced by the resonant spin-flipped reflection, which may lead to interesting application in spintronics.

Finally, the resonant spin-flipped reflection does not rely on the exact form of the Hamiltonian (1), which differs from that of most materials. The key point for such a scenario is the spin polarization of the DSS. It was shown that the effective model of HgCr${ }_2$Se${ }_4$ that gives rise to spiral spin texture of the DSS will yield the same results as well [105]. For the nodal-line semimetals with negligible spin-orbit coupling, the DSS may undergo a Stoner ferromagnetic instability [109,110]. As a result, the DSS split into two bands with opposite spin polarization. Whether such spin-polarized DSS will induce resonant spin-flipped reflection remains to be explored.

VIII. Transport experiments

ARPES measurements provide an effective way to obtain the band structures of new materials. This method combined with the first principle’s calculation has become a powerful tool to detect nodal-line semimetals [42–48,111–123]. Different from topological insulators in which the surface-state spectra are well separated from the bulk ones [1,2], the bulk states in topological semimetals always coexist with the surface states, making the latter difficult to identify. Apart from the band structures, other information such as the geometric phase encoded in the wave functions cannot be extracted by ARPES either.

Transport measurements provide another powerful tool for the investigation of the physical properties of topological materials. Although the current flowing through the sample cannot tell the detailed band structures, it can provide other important information of electronic properties, such as the spatial distribution of the surface states, the geometric phase of the wave function, and the topology of the Fermi surface as discussed in previous sections. The transport measurements have two advantages: first, various field manipulation schemes can be applied in transport experiments; second, some transport signatures such as the scaling of MR stemming from WL or WAL effects and the geometric phase involved in the pattern of quantum oscillation are universal and thus do not rely on the details of the sample.

The MR in a weak magnetic field is dominated by the WL/WAL effects or the Berry curvature effect. Several experiments have reported the MR results that are consistent with the WAL theory of nodal-line semimetal [54] as introduced in section III. Zhou et al [61] reported that the MR of $\mathrm{M}{\mathrm{g}}_3\mathrm{B}{\mathrm{i}}_2$ films can be well fitted by the MR formula defined by Equation (6b), which is dedicated for the WAL in nodal-line semimetals in the presence of LR disorder potential [54]. The magnetotransport experiment in the nodal-line semimetal YbCdGe shows that the magnetoconductivity due to WAL effect is five orders larger than that for 2D systems [124], which is also consistent with the theoretical predictions. Similar results with large negative MR was also reported in nodal-line semimetal SrAs${ }_3$ [125]. The Berry curvature effect on the low-field magnetotransport in the nodal-line semimetals remains to be explored. To have a notable effect, the Fermi energy and the strength of the spin-orbit coupling should be comparable. This stems from the fact that only the electrons at the Fermi surface contribute to the longitudinal conductance. For many nodal-line semimetals, the spin-orbit coupling is small compared with the Fermi energy and so the Berry curvature effect on the MR is negligible.

As the magnetic field increases, the system enters the quantum regime in which Landau levels dominate the physics. The MR in the stong-field limit exhibits quantum oscillation, known as Shubnikov–de Hass oscillation. By analyzing the oscillation pattern one can extract the shape of the Fermi surface as well as the Berry phase therein, as discussed in section IV. A series of experiments of quantum oscillation on nodal-line semimetals have been performed [69,70,84–91]. Several works have reported the large unsaturated magnetoresistance [84,85,87–89] as well as an unusual butterfly-shaped titanic angular magnetoresistance [85,87,88]; see for example, Figure 12, which reveals the high anisotropy of the nodal-line semimetal. Moreover, Ali et al. [85] showed that the oscillation may or may not exhibit a nontrivial $\pi$ Berry phase as the magnetic field is set to different directions. Such directional dependence of the geometric phase is consistent with the theory in Ref [66], as discussed in section IV. Similar results were also reported in Ref [87]. Other experiments on HfSiS [70], $\mathrm{S}\mathrm{r}\mathrm{A}{\mathrm{r}}_3$ [125], $\mathrm{Z}\mathrm{r}{\mathrm{P}}_2$ [126] all observed nontrivial Berry phase extracted from the oscillation patterns. The nodal lines can have rich configurations, which explains the high anisotropy of the physical results. Meanwhile, the Berry phase is a robust effect that is not sensitive to the modulation of the nodal lines, which is the reason why it can be observed in various materials.

Figure 12. MR measurements of ZrSiS. (a) The curves of MR in different temperatures. (b) The MR curves with different measurement angles. (c) The MR data in the log-log frame. (d) The MR’s angular dependence, forming a butterfly shape [87].

IX. Summary and outlook

We have reviewed a variety of interesting transport properties of the nodal-line semimetal. These transport phenomena are induced by the unique features of the nodal-line semimetal, which are the $\pi$ Berry phase carried by the nodal line, the torus-shaped Fermi surface for slightly doped samples and the existence of the DSS. Transport experiments on the WL/WAL effects and quantum oscillation have shown consistency with the theoretical predictions. Among all the transport properties, the results of the WL/WAL effect and quantum oscillations are quite universal, which do not rely on high-quality samples. Actually, the WL/WAL effect resides in the quantum diffusive regime and the scaling of the resultant MR can reveal both the effective dimension of electron diffusion and the Berry phase of the wave function. Quantum oscillation can be achieved as long as the magnetic length is much smaller than the mean free path. Meanwhile, other effects such as the AAR and the spin-flipped reflection do require samples and devices of high quality. These two effects arise only when the system is in the ballistic regime. Otherwise, the conservation of the transverse momentum breaks down and the AAR turns into diffuse reflection and the specific trajectory disappears. Similarly, the signal of the resonant spin-flipped reflection will be strongly suppressed by the disorder in the bulk.

Apart from the quality of samples, the transport signatures rely on the intrinsic properties of the nodal-line semimetals as well. For theoretical studies, a minimal model as Equation (1)(1) $H(\mathit{k})=\mathrm{\hslash }v{k}_z{\sigma }_x+\mathrm{\hslash }\lambda (k^2-k_0^2){\sigma }_z,$(1) is favorable. However, only a few real materials can be captured by such an effective model [9]. In reality, the nodal line may have various configurations, such as closed loops with deformation and open nodal lines [127–130]. There may also exist finite dispersion along the nodal lines, which makes the Fermi surface deviate from the standard torus shape [131]. The natural question is whether the theoretical results obtained from the minimal model are applicable or not. We give some remarks on this point below.

Complex configurations of the nodal line and finite dispersions along the nodal line can easily break the ${\mathcal{T}}_1$ symmetry in Equation (4)(4) $\begin{array}{cc}{\mathcal{T}}_{1}H{ }^{\mathrm{\prime }}(\mathit{k}){\mathcal{T}}_1^{-1}& =H{ }^{\mathrm{\prime }}(-\mathit{k}),\\ {\mathcal{T}}_2{\mathcal{H}}^{\prime }(\delta \mathit{k}){\mathcal{T}}_2^{-1}& ={\mathcal{H}}^{\prime }(-\delta \mathit{k}),\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(4) . As a result, the WL effect cannot be achieved even when the disorder potential is of the SR type. At the same time, the local ${\mathcal{T}}_2$ symmetry, as well as the WAL effect may persist apart from some modifications of the MR formula (6b) by taking into account the different Fermi surfaces for various 2D subsystems. Different configurations of the nodal lines will also change the quantitative results of the quantum oscillations given that the latter is a direct manifestation of the Fermi surface. In principle, the Berry phase can still be extracted from the oscillation patterns by noting that the variation of the Fermi surface only changes the periodicity of the oscillation, i.e. the $F$ factor in Equation (7). However, the complex Fermi surface will make the analysis of the oscillation patterns quite challenging, especially for the Fermi surfaces with nodes, in which the phase factor ${\varphi }_{3D}$ in Equation (8)(8) $\varphi =-1/2+{\varphi }_B/2\pi +{\varphi }_{3D}$(8) may change alternately along the nodal lines from electron to hole. The nodes of Fermi surfaces may also induce magnetic breakdown for certain magnetic orbits that intersect with the nodes, which needs further exploration. The Berry curvature effect on the magnetotransport of the massive nodal-line semimetals should still exist. However, the coincidence between the Lifshitz transition and the sign reversal of the MR will probably fail.

The change of the nodal lines and accordingly, the torus-shaped Fermi surface will directly affect the AAR effect. The unique trajectory of the AAR in Figure 8) is a direct result of the Fermi torus. As it deforms, the group velocities of the quasiparticles will change dramatically as well. Therefore, in order to implement the AAR, nodal-line semimetals with torus-shaped Fermi surface such as CaTX (T = Ag,Cd; X = As,Ge) [132] and CaAgAs [133,134] are favorable. On the contrary, the resonant spin-flipped reflection induced by the DSS does not rely on the configurations of the nodal lines. Such an effect is directly related to the DSS itself. As long as the spin polarization is established for the DSS, the resonant spin-flipped reflection should be achieved.

Apart from the conventional nodal-line semimetals, the so-called type-II nodal-line semimetals have been proposed recently [135–139]. Similar to the type-II Weyl semimetal [140], the bands of the type-II nodal-line semimetal are tilted as well. The change of the density of states at the nodal line indicates that the transport properties of the type-II nodal-line semimetal should be quite different from the conventional nodal-line semimetals. Very recently, another type of nodal-line semimetal with linked nodal loops [17,18] has been reported [141,142]. The results and scenarios reviewed here may not be applicable to this case because one cannot analyze different nodal loops separately anymore. The nodal links encircle with each other which is topologically distinct from the isolated nodal loops. The transport properties of the nodal-link semimetals such as WL/WAL effect and quantum oscillation are interesting open questions for further study.

Acknowledgment

We thank O. Zilberberg, J. L. Lado, H. Z. Lu, G. Blatter and D. Y. Xing for collaboration in related topics and helpful discussions.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the National Natural Science Foundation of China [No.12074172] (W.C.) and [No. 11804130] (W.L.).