Ultrafast dynamics of electrons and phonons: from the two-temperature model to the time-dependent Boltzmann equation

ABSTRACT

The advent of pump-probe spectroscopy techniques paved the way to the exploration of ultrafast dynamics of electrons and phonons in crystalline solids. Following photo-absorption of a pump pulse and the initial electronic thermalization, the dynamics of electronic and vibrational degrees of freedom is dominated by electron-phonon and phonon-phonon scattering processes. The two-temperature model (TTM) and its generalizations provide valuable tools to describe these phenomena and the ensuing coupled dynamics of electrons and phonons. While more sophisticated theoretical approaches are nowadays available, the conceptual and computational simplicity of the TTM makes it the method of choice to model thermalization processes in pump-probe spectroscopy, and it keeps being widely applied in both experimental and theoretical studies. In the domain of ab-initio methods, the time-dependent Boltzmann equation (TDBE) ameliorates many of the shortcomings of the TTM and enables a realistic and parameter-free description of ultrafast phenomena with full momentum resolution. After a pedagogical introduction to the TTM and TDBE, in this manuscript we review their application to the description of ultrafast process in solid-state physics and materials science as well as their theoretical foundation.

GRAPHICAL ABSTRACT

KEYWORDS:

• Ab-initio methods
• ultrafast dynamics
• electron-phonon coupling
• carrier thermalization
• two-temperature model
• time-dependent boltzmann equation

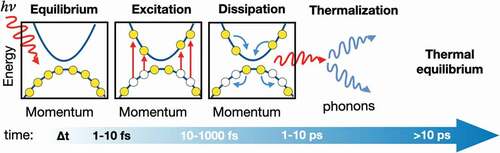
1. Introduction

Electron-phonon coupling is one of the fundamental interaction mechanisms in solids [1]. It determines the temperature dependence of the electron band structure [2,3] and of the fundamental gap [4], it influences the band effective masses [5] and charge transport [6–8], it underpins the absorption of light in indirect band-gap materials [9,10], plasmon damping [11–13], Kohn anomalies [14–20], the formation of quasiparticles, as e.g. Fröhlich [21–23] and Holstein [24,25] polarons, and it underlies several exotic states of matter, such as superconducting [26–30] and charge-density-wave [31–33] phases. Phonon-assisted scattering processes further govern the ultrafast dynamics of electrons and phonons and determine the time scale for the thermalization of electronic and vibrational degrees of freedom [34,35]. For example, a photo-excited electron distribution loses its energy by undergoing phonon-assisted scattering processes which entail the emission and absorption of phonons.

Pump-probe experiments provide a versatile tool to directly probe these phenomena [36,37]. Time- and angle-resolved photoemission spectroscopy, for example, enables to directly probe the dynamics of photoexcited electrons and holes with energy and momentum resolution [38,39]. Additionally, pump-probe scattering techniques as, e.g. ultrafast electron diffuse scattering, complement optical and photoemission measurements by providing direct insight into the dynamics of the crystalline lattice and electron-phonon scattering processes with time and momentum resolution, and they are suitable to attain a detailed understanding of the energy flow between hot electrons and the crystalline lattice [40–42].

The two-temperature model (TTM) [43–46] describes the dynamics of electrons and phonons as the thermalization involving two coupled thermal reservoirs. This idea provides perhaps the simplest and most intuitive description of the thermalization of electronic and vibrational degrees of freedom in systems out of equilibrium and it has seen wide application to the description of ultrafast processes in solids [40,47–71]. The TTM has been employed to examine the fingerprints of ultrafast dynamics in several experimental techniques including photoemission spectroscopy [72–81], Raman scattering [82,83], ultrafast electron diffuse scattering [40,63,84,85], and pump-probe optical techniques [48,77,86–101]. It has further been extended to account for the emergence of coherent phonons [102,103], ultrafast dynamics in warm-dense matter [60,98,104–107], thermalization via electron-plasmon channel [108], spin dynamics [109], magnon scattering with lattice degrees of freedom [110–115], and thermalization of magnetic-nematic order [116]. An effort has also been made in upgrading the TTM to account for the nascent non-equilibrium electron distribution, while retaining the numerical simplicity of the model [51,90,117,118]. While the application of the TTM to ultrafast electron dynamics in metals and laser ablation has been reviewed in Refs. [119] and [120], respectively, we here focus on its application to the dynamics of electrons and phonons in presence of electron-phonon coupling in the context of first-principles simulations. Furthermore, the non-thermal lattice model (NLM), also referred to as N-temperature or multi-temperature model, extends the TTM to account for anisotropies in electron-phonon interaction [40,62,121–123]. In this framework, the lattice is treated as a set of N distinct thermal reservoirs coupled to the electrons. At variance with the TTM, this generalization enables to account for the establishment of hot phonons or, more generally, a non-thermal state of the lattice, characterized by the enhanced population of the phonon modes which actively take part in the hot-carrier relaxation [76,78,82,124–127].

A rigorous description of electron-phonon coupling and its influence on the dynamics inevitably requires to account for phase-space constraints in the phonon-assisted scattering processes as well as for the anisotropies of the electron-phonon coupling. A suitable approach to attain this requirement is the time-dependent Boltzmann equation (TDBE). Ultrafast dynamics simulations based on the TDBE formalism have been widely employed to describe non-equilibrium processes involving electrons and phonons in condensed matter. The TDBE has been applied to investigate the thermalization of electrons and phonons following photoirradiation in metals [49,54,128–134], semiconductors [135–138], and two-dimensional [139–144] and layered [145] materials, and it has further been extended to investigate the ultrafast magnetization dynamics in photo-excited ferromagnets [146,147]. In comparison to simplified models – as, e.g. the TTM and NLM – a major advantage of the TDBE approach consists of enabling the investigation of the coupled non-equilibrium dynamics of electrons and phonon populations with a full momentum resolution. This aspect is particularly important to capture the anisotropic population of the electronic and vibrational states in reciprocal space which may be established out of equilibrium. For example, the absorption of circularly polarized light in transition metal dichalcogenide monolayers is governed by valley-selective circular dichroism [148–150]: carriers are photoexcited in either the K or $\bar{\mathrm{K}}$ valleys in the Brillouin zone depending on the light helicity, leading to an anisotropic electronic distribution which cannot be captured via a density-of-state approximation [151]. Similarly, highly anisotropic phonon populations in reciprocal space can be established upon the preferential emission of strongly-coupled phonons [143,144], leading to the characteristic spectral signatures in ultrafast diffuse scattering techniques [85,145,152–154].

This manuscript aims at introducing the fundamentals of effective-temperature model approaches and of the time-dependent Boltzmann equation in the context of non-equilibrium dynamics of coupled electrons and phonons. In particular, in Section 2 we introduce the TTM and in Section 2.1 its generalization to several temperature reservoirs, i.e. to the NLM. In Section 3, we introduce the TDBE and discuss its theoretical foundation (Section 3.1) as well as its relation to the TTM. In Section 4, after a concise overview of the experimental signatures of non-equilibrium processes in graphene (Section 4.1) we proceed to discuss the theoretical description of the ultrafast carrier and lattice dynamics based on the NLM (Section 4.2) and the TDBE (Section 4.3) approaches. In Section 5 we discuss the limitation of the TDBE formalism. Summary and outlook are presented in Section 6.

2. The two-temperature model

The underlying ideas of the TTM [43–46] are most easily illustrated by considering the thermalization dynamics of two systems $S_1$ and $S_2$. Quantum mechanics is not required at this point; $S_1$, $S_2$, and their interactions can be assumed to be governed by the laws of thermodynamics. If $S_1$ and $S_2$ are initially at thermal equilibrium at the temperatures $T_1$ and $T_2$, respectively, in the absence of interactions (Figure 1(a)) the temperature of each subsystem will remain unaltered in the course of time (Figure 1(b)). If heat can be exchanged (Figure 1(c)), on the other hand, one can expect that for a sufficiently small temperature difference $T_2-T_1$ the energy transferred from $S_1$ to $S_2$ (from $S_2$ to $S_1$) during the interval $\mathrm{\Delta }t$ will be linear in $T_2-T_1$ ($T_1-T_2$), leading to [43]:

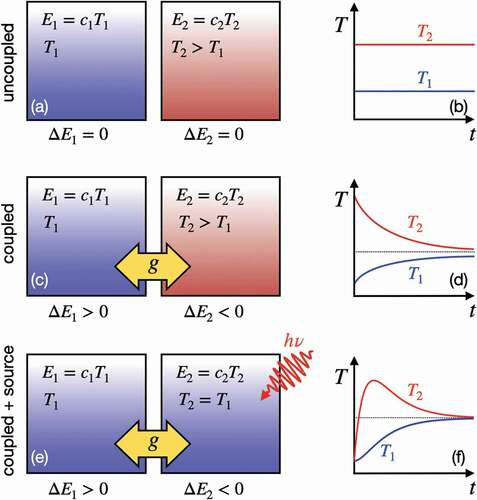
Figure 1. Schematic representation of two thermal reservoirs at temperatures $T_1$ and $T_2>T_1$ and energies $E_1=C_1{T}_1$ and $E_2=C_2{T}_2$ – where $C_1$ and $C_2$ denote the heat capacities – in absence of interactions (a), in presence of mutual interactions characterized by a coupling constant $g$ (c), and in presence of an external field (e). (b), (d), and (f): Time dependence of the temperature for the systems in (a), (c), and (e), respectively, as obtained from the solution of the TTM.

(1) $\frac{\mathrm{\Delta }{E}_1}{\mathrm{\Delta }t}=g_1(T_2-T_1),$(1)

(2) $\frac{\mathrm{\Delta }{E}_2}{\mathrm{\Delta }t}=g_2(T_1-T_2).$(2)

Here, the energy of $S_1$ is given by $E_1=c_1{T}_1$, where $c_1$ is the specific heat, and similarly for $S_2$. $g_1$ and $g_2$ are proportionality constants with units of $\left[\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}\times {(\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\times \mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e})}^{-1}\right]$. Energy conservation throughout the thermalization dynamics requires $\mathrm{\Delta }{E}_1=-\mathrm{\Delta }{E}_2$, which in turn promptly leads to condition $g_1=g_2=g$. In the limit of infinitesimal time interval, the thermalization dynamics of $S_1$ and $S_2$ can thus be formulated by the coupled first-order differential equations:

(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3)

(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4)

Equations (3(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) )(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) and (4(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) ) are the central equations of the two-temperature model. If the temperature dependence of $c_1$ and $c_2$ is neglected, Eqs. (3)(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) and (4(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) ) admit analytical solutions in the form of decaying exponentials (see Appendix). A detailed discussion of the analytical solution of the TTM can be found in Ref [59]. The resulting time dependence of the temperatures $T_1$ and $T_2$ is illustrated in Figure 1(d). In short, the presence of a coupling constant $g$ tends to restore a regime of thermal equilibrium where $T_2=T_1$. More generally, owing to the non-trivial temperature dependence of the specific heat, the TTM must be solved numerically via time-stepping algorithms (e.g. the Euler or Runge-Kutta algorithms).

The TTM is often modified to introduce a time-dependent source (driving) term coupled to $S_1$ or $S_2$ [52,155]. This scenario is clearly reminiscent of pump-probe experiments whereby either electrons or lattice are driven out of equilibrium through the coupling to ultrashort pulses. Figure 1(e) schematically depict such a scenario, whereby one of the two thermal baths, initially at thermal equilibrium with $T_1=T_2$, is coupled to a light source which drives the system out of equilibrium. If a coupling in the form $S(t)=\alpha e^{-\frac{|t|}{\tau }}\theta (t)$ is added to Eq. (4)(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) , i.e. a laser pulse with the amplitude of $\alpha$ that lasts for time period of $\tau$ and starts at $t=0$, the model still admits analytic solution (Appendix), leading to the trend illustrated in Figure 1(f). For a more detailed discussion on the time-dependent source term and its different functional forms we refer the reader to the Refs. [51,62,120]. Besides the source term, we additionally note that the form of the TTM equations, i.e. Eqs. (3)(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) and (4(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) ), is often extended to include the electron and lattice thermal conductivities [45,120,156–158] in order to capture the space-dependent diffusion and heat flow, which are important for understanding material melting and ultrafast laser ablation [120]. The initial increase of $T_2$ reflects the rise in temperature of $S_2$ induced by the interaction with a source, whereas at a later stage, the thermalization follows a similar trend to that of Figure 1(d).

The TTM can be straightforwardly employed to model the dynamics of electrons and phonons in presence of electron-phonon interactions via the following steps [46,52]: one of the subsystems ($S_1$) is identified with lattice, whereas the other ($S_2$) with the electrons. The temperatures $T_1$ and $T_2$ are identified with the effective temperatures of the lattice ($T_{\mathrm{p}\mathrm{h}}$) and electrons ($T_{\mathrm{e}\mathrm{l}}$) and the source term $S(t)$ is employed to model the coupling to an external light source. $c_1$ and $c_2$ are replaced by the phonon ($C_{\mathrm{p}\mathrm{h}}$) and electron ($C_{\mathrm{e}\mathrm{l}}$) heat capacities, which can be expressed as [52]:

(5) $C_{\mathrm{e}\mathrm{l}}(T)={\int }_{\mathrm{\infty }}^{\mathrm{\infty }}d\epsilon D_{\mathrm{e}\mathrm{l}}(\epsilon )\epsilon \frac{\mathrm{\partial }f(\mu ,\epsilon ,T_{\mathrm{e}\mathrm{l}})}{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}},$(5)

(6) $C_{\mathrm{p}\mathrm{h}}(T)={\int }_0^{\mathrm{\infty }}d(\mathrm{\hslash }\omega )D_{\mathrm{p}\mathrm{h}}(\omega )\mathrm{\hslash }\omega \frac{\mathrm{\partial }n(\omega ,T_{\mathrm{p}\mathrm{h}})}{\mathrm{\partial }{T}_{\mathrm{p}\mathrm{h}}},$(6)

where $D_{\mathrm{e}\mathrm{l}}$ and $D_{\mathrm{p}\mathrm{h}}$ are the electron and phonon density of states. Similarly, the coupling constant $g$ can be expressed as [1,52]:

(7) $g=\frac{\pi k_B}{\mathrm{\hslash }{D}_{\mathrm{e}\mathrm{l}}({\epsilon }_F)}\lambda ⟨{\omega }^2⟩{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d\epsilon D_{\mathrm{e}\mathrm{l}}^2(\epsilon )\left(-\frac{\mathrm{\partial }f(\mu ,\epsilon ,T_{\mathrm{e}\mathrm{l}})}{\mathrm{\partial }\epsilon }\right),$(7)

where the thermalization rate of electron-lattice system is governed by the electron-phonon coupling strength and second moment of the phonon spectrum, which are related to the Eliashberg function ${\alpha }^{2}F(\mathrm{\Omega })$ as $\lambda ⟨{\omega }^2⟩=2\int d\mathrm{\Omega }\mathrm{\Omega }{\alpha }^{2}F(\mathrm{\Omega })$. The equations of the TTM, i.e. Eqs. (3)(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) and (4(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) ), can thus be expressed as:

(8) $\frac{\mathrm{\partial }{T}_{\mathrm{p}\mathrm{h}}}{\mathrm{\partial }t}=\frac{g}{C_{\mathrm{p}\mathrm{h}}}(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}}),$(8)

(9) $\frac{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}}{\mathrm{\partial }t}=\frac{g}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}-T_{\mathrm{e}\mathrm{l}})+S(t).$(9)

The theoretical foundation of the TTM, and its relation to the TDBE is discussed in Section 3.2. While the electron and phonon heat capacities $C_{\mathrm{e}\mathrm{l}}$ and $C_{\mathrm{p}\mathrm{h}}$ can be immediately obtained from calculations based on density-functional theory and density-functional perturbation theory [159], respectively, the parameters $g$ can be estimated from first-principles calculations of the Eliashberg function via well-established simulation packages [160]. This procedure enables the solution of the TTM entirely ab initio, without resorting to free parameters [52,57,64,70,81]. Alternatively, $g$ can be deduced from experimental data, e.g. by fitting Eq. (9)(9) $\frac{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}}{\mathrm{\partial }t}=\frac{g}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}-T_{\mathrm{e}\mathrm{l}})+S(t).$(9) to pump-probe photoemission measurements (see, e.g. Section 4) [78].

As discussed in Section 3.2, the application of the TTM to the non-equilibrium dynamics of electrons and phonons in solids can be justified through its formal derivation from the time-dependent Boltzmann equation [46](46) $\frac{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}}{\mathrm{\partial }t}=\frac{g}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}-T_{\mathrm{e}\mathrm{l}})+S(t),$(46) . The description of ultrafast processes via Eqs. (3)(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) and (4(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) ), however, entails two main approximations: (i) at each time steps throughout the dynamics, electrons are assumed to populate electronic bands according to a Fermi-Dirac function at the effective temperature $T_{\mathrm{e}\mathrm{l}}$; (ii) the lattice is assumed to be at thermal equilibrium throughout the dynamics, i.e. all bosonic occupations are described by the Bose-Einstein statistics at the effective temperature $T_{\mathrm{p}\mathrm{h}}$. These approximations limit the domain of applicability of the TTM. Because of the approximation (i), the TTM is unsuitable to describe the early stages of the electron dynamics ($t<100$ fs), which can be characterized by non-thermal electronic excitation (i.e. which cannot be described by a Fermi-Dirac function), the anisotropic excitation of electron-hole pairs in the Brillouin zone, and electron-electron scatterings. The domain of application of the TTM is thus restricted to metals, semimetals, and doped semiconductors with short electron thermalization times, since, on the other hand, electronic excitations in gapped systems (e.g. semiconductors) are inherently linked to a regime of non-thermal electronic excitation that cannot be properly modeled via a Fermi-Dirac function. Additionally, the approximation (ii) makes the TTM unsuitable to describe the non-equilibrium dynamics of the lattice. The TTM is sometimes extended to model non-thermal electronic excitation in semiconductors by defining separately electron and hole thermal baths [161], i.e. electron and hole temperatures [162], or by dividing the electronic bath into a majority of thermal and a small portion of non-thermal carriers [51,90,117,118]. However, in these extensions, the issue of thermalized lattice bath (ii) is still present. In the following, we discuss how this limitation can be overcome by extending the TTM to account for anisotropic coupling to different phonon modes.

2.1. The non-thermal lattice model

Ultrafast diffuse-scattering experiments and first-principles calculations provide strong evidence that non-thermal regimes of the lattice – i.e. vibrational states characterized by bosonic occupations which deviate significantly from the Bose-Einstein statistics – can be established upon photo-excitation in both semiconducting and metallic layered compounds, such as, black phosphorus [145], MoS₂ [144,163, graphite [85], graphene [143], and TiS₂ [152]. Even for simple metals such as Al, the anisotropic coupling between electrons and acoustic phonons can trigger the emergence of non-equilibrium vibrational states persisting for several picoseconds [40]. Generally, whenever the electron-phonon interaction is dominated by one or several strongly-coupled modes, these lattice vibrations may provide a preferential decay channel for the relaxation of photo-excited electrons and holes [81]. As mentioned in the introduction, such a scenario can lead to the formation of hot phonons, i.e. a non-thermal state of the lattice [76,78,82,126,127]. Because of the assumption that the lattice can be described by a Bose-Einstein distribution at temperature $T_{\mathrm{p}\mathrm{h}}$, the TTM is unsuitable to describe these phenomena [40,85,145]

To enable the description of hot phonons and non-thermal states of the lattice, a generalization of the TTM to account for anisotropies in the coupling with different subsets of lattice vibrations – referred to as non-thermal lattice model (NLM) [40,62,122,123] or three-temperature model [81,82], depending on the level of approximation – has recently been proposed. In short, while in the TTM the electrons are coupled to the lattice via a single coupling constant $g$ (Figure 2(a)), in the NLM the lattice is partitioned into phonon groups characterized by distinct coupling constants $g_{\mu }$ (Figure 2(b)). Phonons characterized by higher coupling play a primary role in the electronic relaxation, and therefore exhibit a larger effective temperature on short timescales, whereas on longer timescales thermal equilibrium is restored by phonon-phonon coupling. This behaviour is schematically illustrated in Figure 2(c) for aluminum, where only three acoustic phonons are present.

Figure 2. (a) Schematic illustration of the TTM and (b) NLM. At variance with the TTM, the NLM accounts for coupling with different subsets of phonon modes, as well as phonon-phonon interactions. (c) Time-dependence of the electronic (blue) and vibrational temperatures of the longitudinal (LA) and transverse acoustic phonons (TA₁ and TA₂) of aluminum. Reproduced from Ref [40].

In general, by partitioning the $N_{\mathrm{p}\mathrm{h}}$ normal modes of the lattice into $N_g$ groups, where $1<N_g\le N_{\mathrm{p}\mathrm{h}}$ (for $N_g=1$, the TTM is recovered), the total energy can be expressed as $E_{\mathrm{p}\mathrm{h}}={\sum }_{\mu =1}^{N_{\mathrm{g}}}{E}_{\mathrm{p}\mathrm{h}}^{\mu }$. The rate of change of the energy of the $\mu$-th phonon group can be expressed as ${\mathrm{\partial }}_t{E}_{\mathrm{p}\mathrm{h}}^{\mu }=C_{\mathrm{p}\mathrm{h}}^{\mu }{\mathrm{\partial }}_t{T}_{\mathrm{p}\mathrm{h}}^{\mu }$, where $C_{\mathrm{p}\mathrm{h}}^{\mu }$ is the specific heat of the $\mu$-th phonon group, which is obtained by replacing the group density of states in Eq. (6)(6) $C_{\mathrm{p}\mathrm{h}}(T)={\int }_0^{\mathrm{\infty }}d(\mathrm{\hslash }\omega )D_{\mathrm{p}\mathrm{h}}(\omega )\mathrm{\hslash }\omega \frac{\mathrm{\partial }n(\omega ,T_{\mathrm{p}\mathrm{h}})}{\mathrm{\partial }{T}_{\mathrm{p}\mathrm{h}}},$(6) . The NLM can thus be formulated as a set of coupled first-order differential equations which relates the electronic temperature $T_{\mathrm{e}\mathrm{l}}$ to the temperatures $T_{\mathrm{p}\mathrm{h}}^{\mu }$ of the $N_g$ phonon groups:

(10) $\frac{\mathrm{\partial }{T}_{\mathrm{p}\mathrm{h}}^{\mu }}{\mathrm{\partial }t}=\frac{g_{\mu }}{C_{\mathrm{p}\mathrm{h}}^{\mu }}(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}}^{\mu })+\sum _{\mu { }^{\mathrm{\prime }}}\frac{T_{\mathrm{p}\mathrm{h}}^{\mu { }^{\mathrm{\prime }}}-T_{\mathrm{p}\mathrm{h}}^{\mu }}{{\tau }_{\mu \mu { }^{\mathrm{\prime }}}},$(10)

(11) $\frac{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}}{\mathrm{\partial }t}=\sum _{\mu }^{N_g}\frac{g_{\mu }}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}^{\mu }-T_{\mathrm{e}\mathrm{l}})+S(t).$(11)

Here, the coupling constant $g_{\mu }$ is defined as in Eq. (7)(7) $g=\frac{\pi k_B}{\mathrm{\hslash }{D}_{\mathrm{e}\mathrm{l}}({\epsilon }_F)}\lambda ⟨{\omega }^2⟩{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d\epsilon D_{\mathrm{e}\mathrm{l}}^2(\epsilon )\left(-\frac{\mathrm{\partial }f(\mu ,\epsilon ,T_{\mathrm{e}\mathrm{l}})}{\mathrm{\partial }\epsilon }\right),$(7) by restricting the sum of all phonons in the $\mu$-th group, ${\tau }_{\mu \mu { }^{\mathrm{\prime }}}$ denotes the time constant for the decay of the $\mu$-th subgroup due to phonon-phonon interaction with phonons in the $\mu { }^{\mathrm{\prime }}$-th group, and it can be obtained from first-principles via calculations of the phonon-phonon scattering matrix elements [62].

As illustrated in Figure 2(c) for Al [40], at variance with TTM, the NLM enables to account for the establishment of a non-thermal regime in the lattice. In particular, following photo-excitation of the electrons, energy is transferred to each phonon group $\mu$ proportionally to the coupling constant $g_{\mu }$, thus, leading to a discrepancy among the vibrational temperatures $T_{\mathrm{p}\mathrm{h}}^{\mu }$. On longer timescales, the onset of phonon-phonon scattering (via the second term in Eq. (10(10) $\frac{\mathrm{\partial }{T}_{\mathrm{p}\mathrm{h}}^{\mu }}{\mathrm{\partial }t}=\frac{g_{\mu }}{C_{\mathrm{p}\mathrm{h}}^{\mu }}(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}}^{\mu })+\sum _{\mu { }^{\mathrm{\prime }}}\frac{T_{\mathrm{p}\mathrm{h}}^{\mu { }^{\mathrm{\prime }}}-T_{\mathrm{p}\mathrm{h}}^{\mu }}{{\tau }_{\mu \mu { }^{\mathrm{\prime }}}},$(10) )), drives the lattice back to a thermalized regime, where all vibrational temperatures coincide.

With the exception of elemental metals, where the identification of different phonon groups is straightforward due to the reduced vibrational degrees of freedoms (see, e.g. Figure 2), in compounds with several atoms in the unit cell the definition of phonon groups is to some extent arbitrary, and it represents a shortcoming of the NLM. In some limiting cases (e.g. cuprates, graphene, and MgB₂ [76,81,82]), it is possible to distinguish strongly and weakly coupled modes and, correspondingly, phonons can be grouped according to their coupling strength. The arbitrariness in the definition of phonon groups can be lifted by resorting to a first-principles description of the ultrafast dynamics of electrons and phonons based on the time-dependent Boltzmann equation(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) .

3. The time-dependent Boltzmann equation

The time-dependent Boltzmann equation (TDBE) constitutes an optimal compromise between accuracy and efficiency to investigate the ultrafast dynamics of coupled electron-phonon systems. In the TDBE, the dynamics of electronic and vibrational excitations are described by changes of the electron and phonon distribution functions $f_{n\mathbf{k}}(t)$ and $n_{\mathbf{q}\nu }(t)$, respectively, whereas electron and phonon energies are left unchanged throughout the dynamics. At thermal equilibrium, $f_{n\mathbf{k}}$ and $n_{\mathbf{q}\nu }$ are time independent and they coincide with the Fermi-Dirac and the Bose-Einstein occupations $f_{n\mathbf{k}}^0$ and $n_{\mathbf{q}\nu }^0$:

(12) $f_{n\mathbf{k}}^0(T)={\left[e^{({\epsilon }_{n\mathbf{k}}-{\epsilon }_{\mathrm{F}})/k_{\mathrm{B}}T}+1\right]}^{-1},$(12)

(13) $n_{\mathbf{q}\nu }^0(T)={\left[e^{\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }/k_{\mathrm{B}}T}-1\right]}^{-1}.$(13)

Here, ${\epsilon }_{\mathrm{F}}$ is the Fermi energy, ${\epsilon }_{n\mathbf{k}}$ is the single-particle energy of a Bloch electron, and $\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }$ the phonon energy. This case is exemplified by the left panel of Figure 3, where the Fermi-Dirac occupations are superimposed to the band structure of monolayer MoS${ }_2$, with yellow (blue) denoting fully occupied (empty) states with $f_{n\mathbf{k}}=1$ ($f_{n\mathbf{k}}=0$). In this framework, a regime of non-equilibrium requires either $f_{n\mathbf{k}}$ or $n_{\mathbf{q}\nu }$ (or both) to differ from the equilibrium Fermi-Dirac and the Bose-Einstein occupations, as illustrated in the right panel of Figure 3. The non-equilibrium distributions change over time, and their dynamics is determined by the TDBE:

Figure 3. Electron distribution function $f_{n\mathbf{k}}$ superimposed to the band structure of monolayer MoS₂. Energies are relative to the Fermi level. At equilibrium (left), bands are occupied according to the Fermi-Dirac statistics (Eq. (12)(12) $f_{n\mathbf{k}}^0(T)={\left[e^{({\epsilon }_{n\mathbf{k}}-{\epsilon }_{\mathrm{F}})/k_{\mathrm{B}}T}+1\right]}^{-1},$(12) ). Adapted from Ref [144].

(14) ${\mathrm{\partial }}_t{f}_{n\mathbf{k}}(t)={\mathrm{\Gamma }}_{n\mathbf{k}}(t)$(14)

(15) ${\mathrm{\partial }}_t{n}_{\mathbf{q}\nu }(t)={\mathrm{\Gamma }}_{\mathbf{q}\nu }(t),$(15)

where ${\mathrm{\partial }}_t=\mathrm{\partial }/\mathrm{\partial }t$ and ${\mathrm{\Gamma }}_{n\mathbf{k}}$ and ${\mathrm{\Gamma }}_{\mathbf{q}\nu }$ denote the collision integrals for electrons and phonons. The numerical solution of Eqs. (14)(14) ${\mathrm{\partial }}_t{f}_{n\mathbf{k}}(t)={\mathrm{\Gamma }}_{n\mathbf{k}}(t)$(14) and (15(15) ${\mathrm{\partial }}_t{n}_{\mathbf{q}\nu }(t)={\mathrm{\Gamma }}_{\mathbf{q}\nu }(t),$(15) ) requires the development of suitable approximations for the evaluation of the collision integrals. In short, ${\mathrm{\Gamma }}_{n\mathbf{k}}$ and ${\mathrm{\Gamma }}_{\mathbf{q}\nu }$ account for the several scattering mechanisms which may lead to changes of the distributions functions as, e.g. electron-electron, electron-phonon, phonon-phonon, and impurity scattering as well as the coupling to external fields. The recent development of electronic structure codes for the study of electron-phonon and phonon-phonon coupling has enabled to estimate the contribution of these scattering processes to collision integrals, enabling the investigation of the coupled dynamics of electrons and phonons entirely from first principles [35,61,134,143,144].

3.1. First-principles expressions for the collision integrals

In the following, we outline the derivation of the collision integral due to the electron-phonon and phonon-phonon interactions from Fermi’s golden rule. A similar treatment can be generalized to other contributions to the collision integral as, e.g. electron-electron and impurity scattering or coupling to external fields. The Hamiltonian for an anharmonic crystal in presence of electron-phonon and phonon-phonon interactions can be expressed as:

(16) $\hat{H}={\hat{H}}_{\mathrm{e}}+{\hat{H}}_{\mathrm{p}}+{\hat{H}}_{\mathrm{e}\mathrm{p}}+{\hat{H}}_{\mathrm{p}\mathrm{p}}.$(16)

Here ${\hat{H}}_{\mathrm{e}}={\sum }_{n\mathbf{k}}{\epsilon }_{n\mathbf{k}}{\hat{c}}_{n\mathbf{k}}^{†}{\hat{c}}_{n\mathbf{k}}$ is the electronic Hamiltonian, where ${\hat{c}}_{n\mathbf{k}}^{†}$ and ${\hat{c}}_{n\mathbf{k}}$ are fermionic creation and annihilation operators, respectively. ${\hat{H}}_{\mathrm{p}}={\sum }_{\mathbf{q}\nu }\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }[{\hat{a}}_{\mathbf{q}\nu }{\hat{a}}_{\mathbf{q}\nu }^{†}+1/2]$ is the Hamiltonian of the lattice in the harmonic approximation. ${\hat{a}}_{\mathbf{q}\nu }^{†}$ and ${\hat{a}}_{\mathbf{q}\nu }$ are phonon creation and annihilation operators. The eigenstates of ${\hat{H}}_{\mathrm{p}}$ can be expressed as $|{\chi }_s⟩={\prod }_{\mathbf{q}\nu }|n_{\mathbf{q}\nu }^s⟩$, where $|n_{\mathbf{q}\nu }^s⟩$ are the eigenstates of the number operator ${\hat{N}}_{\mathbf{q}\nu }={\hat{a}}_{\mathbf{q}\nu }^{†}{\hat{a}}_{\mathbf{q}\nu }$ with eigenvalue $n_{\mathbf{q}\nu }^s$. The quantity $n_{\mathbf{q}\nu }^s$ is the occupation number of the bosonic mode characterized by quantum numbers $\nu$ and $\mathbf{q}$. The superscript $s$-th indicates that the occupations are relative to the $s$-th eigenstate $|{\chi }_s⟩$ of the harmonic Hamiltonian. With this notation, the energy of the harmonic lattice can be expressed as $E_s=⟨{\chi }_s|{\hat{H}}_{\mathrm{p}}|{\chi }_s⟩={\sum }_{\mathbf{q}\nu }\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }[n_{\mathbf{q}\nu }^s+1/2]$.

The third term in Eq. (16)(16) $\hat{H}={\hat{H}}_{\mathrm{e}}+{\hat{H}}_{\mathrm{p}}+{\hat{H}}_{\mathrm{e}\mathrm{p}}+{\hat{H}}_{\mathrm{p}\mathrm{p}}.$(16) is the electron-phonon coupling Hamiltonian:

(17) ${\hat{H}}_{\mathrm{e}\mathrm{p}}=N_p^{-\frac{1}{2}}\sum _{\genfrac{}{}{0ex}{}{nm\nu }{\mathbf{k}\mathbf{q}}}{g}_{mn}^{\nu }(\mathbf{k}\mathbf{,}\mathbf{q}){\hat{c}}_{m\mathbf{k}+\mathbf{q}}^{†}{\hat{c}}_{n\mathbf{k}}[{\hat{a}}_{\mathbf{q}\nu }+{\hat{a}}_{-\mathbf{q}\nu }^{†}],$(17)

where $N_p$ is the number of unit cells in the Born–von Kármán (BvK) supercell [1]. The electron-phonon coupling matrix elements $g_{mn}^{\nu }(\mathbf{k}\mathbf{,}\mathbf{q})$ can be derived from first principles within the framework of density-functional perturbation theory and they are defined as $g_{mn}^{\nu }(\mathbf{k}\mathbf{,}\mathbf{q})=⟨{\psi }_{m\mathbf{k}\mathbf{+}\mathbf{q}}|{\mathrm{\Delta }}_{\mathbf{q}\nu }{\hat{v}}^{\mathrm{K}\mathrm{S}}|{\psi }_{n\mathbf{k}}⟩$, where ${\mathrm{\Delta }}_{\mathbf{q}\nu }{\hat{v}}^{\mathrm{K}\mathrm{S}}$ is the linear change of the Kohn-Sham potential $v^{\mathrm{K}\mathrm{S}}$ due to a phonon perturbation, and $|{\psi }_{n\mathbf{k}}⟩$ are single-particular orbitals, solutions of the single-particle Kohn-Sham equations [1(1) $\frac{\mathrm{\Delta }{E}_1}{\mathrm{\Delta }t}=g_1(T_2-T_1),$(1) ,159].

Finally, the last term in Eq. (16)(16) $\hat{H}={\hat{H}}_{\mathrm{e}}+{\hat{H}}_{\mathrm{p}}+{\hat{H}}_{\mathrm{e}\mathrm{p}}+{\hat{H}}_{\mathrm{p}\mathrm{p}}.$(16) is the phonon-phonon coupling Hamiltonian, which arises from anharmonicities of the lattice and it can be expressed as [164]:

(18) ${\hat{H}}_{\mathrm{p}\mathrm{p}}=\frac{1}{3!}\sum _{\mathbf{q}{\mathbf{q}}^{\prime }{\mathbf{q}}^{{ }^{\prime \prime }}}\sum _{\nu {\nu }^{\prime }{\nu }^{{ }^{\prime \prime }}}{\mathrm{\Psi }}_{\genfrac{}{}{0ex}{}{\nu {\nu }^{\prime }{\nu }^{{ }^{\prime \prime }}}{\mathbf{q}{\mathbf{q}}^{\prime }{\mathbf{q}}^{{ }^{\prime \prime }}}}[{\hat{a}}_{\mathbf{q}\nu }+{\hat{a}}_{-\mathbf{q}\nu }^{†}][{\hat{a}}_{{\mathbf{q}}^{\prime }{\nu }^{\prime }}+{\hat{a}}_{-{\mathbf{q}}^{\prime }{\nu }^{\prime }}^{†}][{\hat{a}}_{{\mathbf{q}}^{{ }^{\prime \prime }}{\nu }^{{ }^{\prime \prime }}}+{\hat{a}}_{-{\mathbf{q}}^{{ }^{\prime \prime }}{\nu }^{{ }^{\prime \prime }}}^{†}].$(18)

${\mathrm{\Psi }}_{\genfrac{}{}{0ex}{}{\nu {\nu }^{\prime }{\nu }^{{ }^{\prime \prime }}}{\mathbf{q}{\mathbf{q}}^{\prime }{\mathbf{q}}^{{ }^{\prime \prime }}}}$ denotes the phonon-phonon scattering matrix elements, which is related to the probability amplitude of three-phonon scattering processes.

The derivation of the collision integrals for the Hamiltonian in Eq. (16)(16) $\hat{H}={\hat{H}}_{\mathrm{e}}+{\hat{H}}_{\mathrm{p}}+{\hat{H}}_{\mathrm{e}\mathrm{p}}+{\hat{H}}_{\mathrm{p}\mathrm{p}}.$(16) begins with the observation that electron-phonon and phonon-phonon interactions in solids are typically weak and, thus, the terms ${\hat{H}}_{\mathrm{e}\mathrm{p}}$ and ${\hat{H}}_{\mathrm{p}\mathrm{p}}$ in the Hamiltonian in Eq. (16)(16) $\hat{H}={\hat{H}}_{\mathrm{e}}+{\hat{H}}_{\mathrm{p}}+{\hat{H}}_{\mathrm{e}\mathrm{p}}+{\hat{H}}_{\mathrm{p}\mathrm{p}}.$(16) can be treated as perturbations. Correspondingly, the rate ${\mathrm{\Gamma }}_{i\to f}$ of transitions from an initial state $|i⟩$ to a final state $|f⟩$ can be obtained via Fermi’s golden rule:

(19) ${\mathrm{\Gamma }}_{i\to f}=\frac{2\pi }{\mathrm{\hslash }}|⟨f|\hat{V}|i⟩{|}^2\delta (E_f^{\mathrm{t}\mathrm{o}\mathrm{t}}-E_i^{\mathrm{t}\mathrm{o}\mathrm{t}}),$(19)

where $E_i^{\mathrm{t}\mathrm{o}\mathrm{t}}$ and $E_f^{\mathrm{t}\mathrm{o}\mathrm{t}}$ are the total energies of the initial and final states, respectively, and $\hat{V}$ is an arbitrary perturbation. To proceed further, we focus on the electron-phonon interaction and we consider initial and final states in the form of a Born-Oppenheimer ansatz as $|i⟩=|{\mathrm{\Psi }}_i⟩|{\chi }_i⟩$, where $|{\chi }_i⟩$ and $|{\mathrm{\Psi }}_i⟩$ are eigenstates of the harmonic Hamiltonian ${\hat{H}}_{\mathrm{p}}$ and of the electronic Hamiltonian ${\hat{H}}_{\mathrm{e}}$, respectively. The matrix elements of the electron-phonon coupling Hamiltonian can be expressed as:

(20) $⟨f|{\hat{H}}_{\mathrm{e}\mathrm{p}}|i⟩=N_p^{-\frac{1}{2}}\sum _{nm\nu }\sum _{\mathbf{k}\mathbf{q}}{g}_{mn}^{\nu }(\mathbf{k}\mathbf{,}\mathbf{q})⟨{\mathrm{\Psi }}_f|{\hat{c}}_{m\mathbf{k}+\mathbf{q}}^{†}{\hat{c}}_{n\mathbf{k}}|{\mathrm{\Psi }}_i⟩⟨{\chi }_f|{\hat{a}}_{\mathbf{q}\nu }+{\hat{a}}_{-\mathbf{q}\nu }^{†}|{\chi }_i⟩.$(20)

The matrix elements of fermionic operators in Eq. (20)(20) $⟨f|{\hat{H}}_{\mathrm{e}\mathrm{p}}|i⟩=N_p^{-\frac{1}{2}}\sum _{nm\nu }\sum _{\mathbf{k}\mathbf{q}}{g}_{mn}^{\nu }(\mathbf{k}\mathbf{,}\mathbf{q})⟨{\mathrm{\Psi }}_f|{\hat{c}}_{m\mathbf{k}+\mathbf{q}}^{†}{\hat{c}}_{n\mathbf{k}}|{\mathrm{\Psi }}_i⟩⟨{\chi }_f|{\hat{a}}_{\mathbf{q}\nu }+{\hat{a}}_{-\mathbf{q}\nu }^{†}|{\chi }_i⟩.$(20) differs from zero only if $|{\mathrm{\Psi }}_i⟩$ and $|{\mathrm{\Psi }}_f⟩$ differ in the occupation of the $n\mathbf{k}$ and $m\mathbf{k}+\mathbf{q}$ states. In such case, it yields:

(21) $⟨{\mathrm{\Psi }}_f|{\hat{c}}_{m\mathbf{k}+\mathbf{q}}^{†}{\hat{c}}_{n\mathbf{k}}|{\mathrm{\Psi }}_i⟩=[f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}}){]}^{\frac{1}{2}}.$(21)

Similarly, from elementary considerations on the action of bosonic operators on the vibrational eigenstates $|{\chi }_s⟩$, one can deduce that the matrix element $⟨{\chi }_f|{\hat{a}}_{\mathbf{q}\nu }|{\chi }_i⟩=\sqrt{n_{\mathbf{q}\nu }}$ (and similarly, $⟨{\chi }_f|{\hat{a}}_{-\mathbf{q}\nu }^{†}|{\chi }_i⟩=\sqrt{n_{-\mathbf{q}\nu }+1}$) if the state $|{\chi }_f⟩$ differs from $|{\chi }_i⟩$ only in the occupation of the phonon $\mathbf{q}\nu$ ($-\mathbf{q}\nu$) such that $n_{\mathbf{q}\nu }^f=n_{\mathbf{q}\nu }^i-1$ (and $n_{\mathbf{q}\nu }^f=n_{\mathbf{q}\nu }^i+1$), and it vanishes otherwise. The total rate (number of events per unit time) for the absorption of a phonon with quantum numbers $\mathbf{q}\nu$ can be directly derived from Eq. (19)(19) ${\mathrm{\Gamma }}_{i\to f}=\frac{2\pi }{\mathrm{\hslash }}|⟨f|\hat{V}|i⟩{|}^2\delta (E_f^{\mathrm{t}\mathrm{o}\mathrm{t}}-E_i^{\mathrm{t}\mathrm{o}\mathrm{t}}),$(19) making use of Eqs. (20)(20) $⟨f|{\hat{H}}_{\mathrm{e}\mathrm{p}}|i⟩=N_p^{-\frac{1}{2}}\sum _{nm\nu }\sum _{\mathbf{k}\mathbf{q}}{g}_{mn}^{\nu }(\mathbf{k}\mathbf{,}\mathbf{q})⟨{\mathrm{\Psi }}_f|{\hat{c}}_{m\mathbf{k}+\mathbf{q}}^{†}{\hat{c}}_{n\mathbf{k}}|{\mathrm{\Psi }}_i⟩⟨{\chi }_f|{\hat{a}}_{\mathbf{q}\nu }+{\hat{a}}_{-\mathbf{q}\nu }^{†}|{\chi }_i⟩.$(20) and (21(21) $⟨{\mathrm{\Psi }}_f|{\hat{c}}_{m\mathbf{k}+\mathbf{q}}^{†}{\hat{c}}_{n\mathbf{k}}|{\mathrm{\Psi }}_i⟩=[f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}}){]}^{\frac{1}{2}}.$(21) ) and summing over all initial and final electronic states:

(22) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{a}\mathrm{b}\mathrm{s}}=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }-{\epsilon }_{m\mathbf{k}+\mathbf{q}})n_{\mathbf{q}\nu }.$(22)

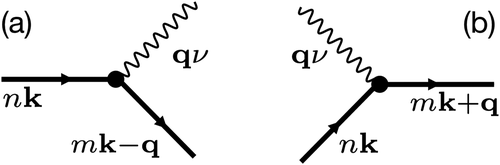
The energy difference between the initial and final states has been expressed as $E_i^{\mathrm{t}\mathrm{o}\mathrm{t}}-E_f^{\mathrm{t}\mathrm{o}\mathrm{t}}={\epsilon }_{n\mathbf{k}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }-{\epsilon }_{m\mathbf{k}+\mathbf{q}}$. The diagrammatic representation of a phonon absorption process of this kind is reported in Figure 4(b). The same procedure can be repeated by considering phonon emission processes (Figure 4(a)), yielding:

(23) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{e}\mathrm{m}}=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }-{\epsilon }_{m\mathbf{k}+\mathbf{q}})(n_{\mathbf{q}\nu }+1).$(23)

Figure 4. Diagrammatic representation of (a) phonon-emission and (b) phonon-absorption processes. Wavy lines represent non-interacting phonon propagator, whereas straight lines denote non-interacting single-particle propagators. In both diagrams, time increases from left to right.

The total rate of change in the phonon occupation $n_{\mathbf{q}\nu }$ due to the electron-phonon interactions ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}$ can thus be defined as the difference between the rates of phonon emission (${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{e}\mathrm{m}}$) and absorption (${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{a}\mathrm{b}\mathrm{s}}$) processes:

(24) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}(t)=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})$(24)

$\times [\delta ({\epsilon }_{n\mathbf{k}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }-{\epsilon }_{m\mathbf{k}+\mathbf{q}})(n_{\mathbf{q}\nu }+1)-\delta ({\epsilon }_{n\mathbf{k}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }-{\epsilon }_{m\mathbf{k}+\mathbf{q}})n_{\mathbf{q}\nu }].$

Equation (24)(24) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}(t)=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})$(24) is the phonon collision integral due to the electron-phonon interaction. Its time dependence arises from the changes of the electron and phonon distribution functions ($f_{n\mathbf{k}}$ and $n_{\mathbf{q}\nu }$) over time. In conditions of thermal equilibrium between electrons and the lattice, as for instance in an ideal situation in which electron and phonon occupations are described by Fermi-Dirac and Bose-Einstein statistics at a given temperature, the rates ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{a}\mathrm{b}\mathrm{s}}$ and ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{e}\mathrm{m}}$ are equal and opposite in sign, indicating that the total change in the phonon number $n_{\mathbf{q}\nu }$ vanishes, since the emission and absorption of phonons are perfectly compensated.

Following similar steps, the electronic collision integral due to the electron-phonon interaction can be derived as:

(25) $\begin{array}{rl}& {\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}(t)=\frac{2\pi }{\mathrm{\hslash }{N}_p}\sum _{m\nu \mathbf{q}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2\\ & \times \{(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & +(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\}.\end{array}$(25)

Each term in this expression is directly related to phonon-assisted electronic transitions involving states in the vicinity of the Fermi surface, as depicted in Figure 5. In particular, the first and second terms in Eq. (25)(25) $\begin{array}{rl}& {\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}(t)=\frac{2\pi }{\mathrm{\hslash }{N}_p}\sum _{m\nu \mathbf{q}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2\\ & \times \{(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & +(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\}.\end{array}$(25) arise from processes in which an electron scatters from $m\mathbf{k}+\mathbf{q}$ in to $n\mathbf{k}$ via the emission and absorption of a phonon, respectively. The third and fourth terms arise from the scattering from $n\mathbf{k}$ into $m\mathbf{k}+\mathbf{q}$ due to phonon-emission and absorption processes. In analogy to Eq. (24(24) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}(t)=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})$(24) ), at thermal equilibrium, scattering processes in and out of $n\mathbf{k}$ balance each other, leading to ${\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}=0$. Note that the rate ${\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}$ of electron population relaxation defined with Eq. (25)(25) $\begin{array}{rl}& {\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}(t)=\frac{2\pi }{\mathrm{\hslash }{N}_p}\sum _{m\nu \mathbf{q}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2\\ & \times \{(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & +(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\}.\end{array}$(25) and the corresponding lifetime ${\tau }_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}=\mathrm{\hslash }/{\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}$ should not be confused with the quasiparticle decay rate and lifetime as obtained from the imaginary part of the electron self-energy [165]. It is the former and not the latter that is usually extracted from pump-probe measurements (e.g. tr-ARPES).

Figure 5. Schematic representation of the four phonon-assisted scattering processes included in the electron collision integral due to the electron-phonon interaction (Eq. (25)(25) $\begin{array}{rl}& {\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}(t)=\frac{2\pi }{\mathrm{\hslash }{N}_p}\sum _{m\nu \mathbf{q}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2\\ & \times \{(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & +(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\}.\end{array}$(25) ). Adapted from Ref [8].

The derivation of the scattering rate due to the phonon-phonon scattering involves the tedious (but otherwise straightforward) evaluation of several matrix elements of bosonic operators. The result can be recast in the form:

${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{p}}(t)=\frac{2\pi }{\mathrm{\hslash }}\sum _{\nu { }^{\mathrm{\prime }}\nu { }^{\mathrm{\prime }}{ }^{\mathrm{\prime }}}\int \frac{d{\mathbf{q}}^{\prime }}{{\mathrm{\Omega }}_{\mathrm{B}Z}}{\left|{\mathrm{\Psi }}_{\mathbf{q}{\mathbf{q}{ }^{\mathrm{\prime }}}^{\prime }{\mathbf{q}}^{{ }^{\prime \prime }}}^{\nu {\nu }^{\prime }\nu { }^{\mathrm{\prime }}{ }^{\mathrm{\prime }}}\right|}^2$

$\begin{array}{rl}& \times [[(n_{\mathbf{q}\nu }+1)(n_{{\mathbf{q}}^{\mathrm{\prime }}{v}^{\mathrm{\prime }}}+1)n_{{\mathbf{q}}^{\mathrm{\prime }\mathrm{\prime }}{v}^{\mathrm{\prime }\mathrm{\prime }}}\\ & -n_{\mathbf{q}\nu }{n}_{{\mathbf{q}}^{\mathrm{\prime }}{v}^{\mathrm{\prime }}}(n_{{\mathbf{q}}^{\mathrm{\prime }\mathrm{\prime }}{v}^{\mathrm{\prime }\mathrm{\prime }}}+1)]\delta \left({\omega }_{\mathbf{q}\nu }+{\omega }_{{\mathbf{q}}^{\mathrm{\prime }}{v}^{\mathrm{\prime }}}-{\omega }_{{\mathbf{q}}^{\mathrm{\prime }\mathrm{\prime }}{v}^{\mathrm{\prime }\mathrm{\prime }}}\right){\delta }_{{ }_{\mathbf{q}{\mathbf{q}}^{\mathrm{\prime }}-{\mathbf{q}}^{\mathrm{\prime }\mathrm{\prime }}}}^{\mathbf{G}}+\end{array}$

(26) $\frac{1}{2}[\left(n_{q\nu }+1\right)nq\nu \prime nq\nu \prime \prime -n_{q\nu }(nq\nu \prime +1(nq\nu \prime \prime +1)\delta ({\omega }_{q\nu }-\omega q\nu \prime -\omega q\nu \prime \prime \delta q-q-qG]$(26)

where the modified Kronecker’s ${\delta }_{\mathbf{q}}^{\mathbf{G}}$ equals unity if $\mathbf{q}=0$ or $\mathbf{q}=\mathbf{G}$, where $\mathbf{G}$ is a reciprocal-lattice vector, and it is zero otherwise. Equation (26)(26) $\frac{1}{2}[\left(n_{q\nu }+1\right)nq\nu \prime nq\nu \prime \prime -n_{q\nu }(nq\nu \prime +1(nq\nu \prime \prime +1)\delta ({\omega }_{q\nu }-\omega q\nu \prime -\omega q\nu \prime \prime \delta q-q-qG]$(26) vanishes identically if the lattice is at thermal equilibrium.

Combining Eqs. (25)(25) $\begin{array}{rl}& {\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}(t)=\frac{2\pi }{\mathrm{\hslash }{N}_p}\sum _{m\nu \mathbf{q}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2\\ & \times \{(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & +(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\}.\end{array}$(25) -(26(26) $\frac{1}{2}[\left(n_{q\nu }+1\right)nq\nu \prime nq\nu \prime \prime -n_{q\nu }(nq\nu \prime +1(nq\nu \prime \prime +1)\delta ({\omega }_{q\nu }-\omega q\nu \prime -\omega q\nu \prime \prime \delta q-q-qG]$(26) ), the time-dependent Boltzmann equation can be rewritten as:

(27) ${\mathrm{\partial }}_t{f}_{n\mathbf{k}}(t)={\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}[f_{n\mathbf{k}}(t),n_{\mathbf{q}\nu }(t)],$(27)

(28) ${\mathrm{\partial }}_t{n}_{\mathbf{q}\nu }(t)={\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}[f_{n\mathbf{k}}(t),n_{\mathbf{q}\nu }(t)]+{\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{p}}[n_{\mathbf{q}\nu }(t)].$(28)

A numerical procedure to solve Eqs. (27)(27) ${\mathrm{\partial }}_t{f}_{n\mathbf{k}}(t)={\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}[f_{n\mathbf{k}}(t),n_{\mathbf{q}\nu }(t)],$(27) and (28(28) ${\mathrm{\partial }}_t{n}_{\mathbf{q}\nu }(t)={\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}[f_{n\mathbf{k}}(t),n_{\mathbf{q}\nu }(t)]+{\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{p}}[n_{\mathbf{q}\nu }(t)].$(28) ) consists in: (i) defining an initial electronic (or vibrational) excited state characterized by electronic (vibrational) occupations which differs from the equilibrium ones (as e.g. in Figure 3); (ii) solve the differential equation using iterative methods (as, e.g. the Euler of Runge-Kutta methods); (iii) update the collision integrals via Eqs. (25)(25) $\begin{array}{rl}& {\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}(t)=\frac{2\pi }{\mathrm{\hslash }{N}_p}\sum _{m\nu \mathbf{q}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2\\ & \times \{(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & +(1-f_{n\mathbf{k}})f_{m\mathbf{k}+\mathbf{q}}\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })(1+n_{\mathbf{q}\nu })\\ & -f_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})\delta ({\epsilon }_{n\mathbf{k}}-{\epsilon }_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu })n_{\mathbf{q}\nu }\}.\end{array}$(25) -(26(26) $\frac{1}{2}[\left(n_{q\nu }+1\right)nq\nu \prime nq\nu \prime \prime -n_{q\nu }(nq\nu \prime +1(nq\nu \prime \prime +1)\delta ({\omega }_{q\nu }-\omega q\nu \prime -\omega q\nu \prime \prime \delta q-q-qG]$(26) ) at each time step.

Besides the aforesaid microscopic scattering process, electron-electron interaction plays a major role in thermalization of electron-lattice system, especially in the 10-fs timescale. The corresponding collision integral ${\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{e}}[f_{n\mathbf{k}}(t)]$ enters Eq. (27)(27) ${\mathrm{\partial }}_t{f}_{n\mathbf{k}}(t)={\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}[f_{n\mathbf{k}}(t),n_{\mathbf{q}\nu }(t)],$(27) and it is usually defined in terms of electron scatterings $\{\mathbf{k},{\mathbf{k}}^{\prime }\}\to \{\mathbf{k}+\mathbf{q},{\mathbf{k}}^{\prime }-\mathbf{q}\}$ (and vice versa) mediated by the statically screened Coulomb interaction. For a detailed description of electron-electron scattering processes we refer the reader to Refs. [123,132,134,166]. Note that the electron-plasmon scatterings, as a part of the dynamical electron-electron interaction, is as well considered to be essential in the early stage of electron thermalization process [128,167,168], however, these dynamical effects are rarely taken into account when studying hot carrier thermalization.

In addition, we note that the TDBE (as well as TTM) simulate the relaxation dynamics of carrier population following the pump-induced laser excitations within pump-probe scheme, while assuming that the probe laser does not affect the excited electrons. This approximation is equivalent to assume that the act of measurement does not induce further significant scattering channels for electrons [169], i.e. the probe is not an active, but rather a passive part of measured electron scattering dynamics. With these assumptions the effects arising from the overlap of pump and probe at zero delay [170] are neglected, as well as additional nonlinear effects induced by probe, such as multiple plasmon excitations [171].

3.2. Relation between the TTM and the time-dependent Boltzmann equation

As demonstrated by Allen [46], the thermalization dynamics of electrons and phonons in presence of the electron-phonon interaction can be recast in the form of a TTM, as formulated via Eq. (3)(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) and (4(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) ), starting entirely from first principles. In short, by expressing the coupling parameter $g$ in terms of the Eliashberg function ${\alpha }^{2}F$, all free parameters of the models are fixed. A detailed derivation of this scheme can be found, for instance, in Refs. [62,123].

In the following, we report an alternative derivation of the TTM with scope of emphasizing the link with the phonon lifetime, as obtained from phonon self-energy due to the electron-phonon interaction. We begin by considering the total energy of a set of non-interacting electrons ($E_{\mathrm{e}\mathrm{l}}$) and phonons ($E_{\mathrm{p}\mathrm{h}}$):

(29) $E_{\mathrm{e}\mathrm{l}}(t)=N_p^{-1}\sum _n\sum _{\mathbf{k}}{\epsilon }_{n\mathbf{k}}{f}_{n\mathbf{k}}(t),$(29)

(30) $E_{\mathrm{p}\mathrm{h}}(t)=N_p^{-1}\sum _{\nu }\sum _{\mathbf{q}}\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }\left[n_{\mathbf{q}\nu }(t)+\frac{1}{2}\right].$(30)

The rate of change of the energies can be expressed as:

(31) $C_{\mathrm{e}\mathrm{l}}{\mathrm{\partial }}_t{T}_{\mathrm{e}\mathrm{l}}=N_p^{-1}\sum _n\sum _{\mathbf{k}}{\epsilon }_{n\mathbf{k}}{\mathrm{\partial }}_t{f}_{n\mathbf{k}}.$(31)

(32) $C_{\mathrm{p}\mathrm{h}}{\mathrm{\partial }}_t{T}_{\mathrm{p}\mathrm{h}}=N_p^{-1}\sum _{\nu }\sum _{\mathbf{q}}\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }{\mathrm{\partial }}_t{n}_{\mathbf{q}\nu },$(32)

where ${\mathrm{\partial }}_t=\mathrm{\partial }/\mathrm{\partial }t$, the left-hand side has been rewritten making use of the chain rule ${\mathrm{\partial }}_{t}E=\frac{\mathrm{\partial }E}{\mathrm{\partial }T}\frac{\mathrm{\partial }T}{\mathrm{\partial }t}$, and the heat capacity $C_{\mathrm{e}\mathrm{l}(\mathrm{p}\mathrm{h})}=\mathrm{\partial }{E}_{\mathrm{e}\mathrm{l}(\mathrm{p}\mathrm{h})}/\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}(\mathrm{p}\mathrm{h})}$ has been introduced. Equations (31)(31) $C_{\mathrm{e}\mathrm{l}}{\mathrm{\partial }}_t{T}_{\mathrm{e}\mathrm{l}}=N_p^{-1}\sum _n\sum _{\mathbf{k}}{\epsilon }_{n\mathbf{k}}{\mathrm{\partial }}_t{f}_{n\mathbf{k}}.$(31) and (32(32) $C_{\mathrm{p}\mathrm{h}}{\mathrm{\partial }}_t{T}_{\mathrm{p}\mathrm{h}}=N_p^{-1}\sum _{\nu }\sum _{\mathbf{q}}\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }{\mathrm{\partial }}_t{n}_{\mathbf{q}\nu },$(32) ) rely on the assumption that electron energies ${\epsilon }_{n\mathbf{k}}$ and phonon frequencies ${\omega }_{\mathbf{q}\nu }$ do not depend on time. The time derivative of the fermionic and bosonic distribution functions entering Eqs. (31)(31) $C_{\mathrm{e}\mathrm{l}}{\mathrm{\partial }}_t{T}_{\mathrm{e}\mathrm{l}}=N_p^{-1}\sum _n\sum _{\mathbf{k}}{\epsilon }_{n\mathbf{k}}{\mathrm{\partial }}_t{f}_{n\mathbf{k}}.$(31) and (32(32) $C_{\mathrm{p}\mathrm{h}}{\mathrm{\partial }}_t{T}_{\mathrm{p}\mathrm{h}}=N_p^{-1}\sum _{\nu }\sum _{\mathbf{q}}\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }{\mathrm{\partial }}_t{n}_{\mathbf{q}\nu },$(32) ) can be obtained via the time-dependent Boltzmann equation.

A central assumption of the non-thermal lattice model is that, at each time $t$, the electronic occupation $f_{n\mathbf{k}}$ can be approximated by a Fermi-Dirac function at temperature $T_{\mathrm{e}\mathrm{l}}$:

(33) $f_{n\mathbf{k}}\simeq \{exp[({\epsilon }_{n\mathbf{k}}-\mu )/k_{\mathrm{B}}{T}_{\mathrm{e}\mathrm{l}}]+1{\}}^{-1}.$(33)

Similarly, it is assumed that the lattice remains at thermal equilibrium throughout the dynamics, that is, all vibrational modes are at the same temperature $T_{\mathrm{p}\mathrm{h}}$ (a condition that may be violated in the non-equilibrium dynamics of the lattice following photo-excitation [144]). Under these assumptions, the arguments of the collision integrals can be simplified. For instance, the argument of Eq. (24)(24) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}(t)=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})$(24) can be rewritten as [62]:

(34) $\begin{array}{rl}& [\left(1-f_{n\mathbf{k}}\right)f_{m\mathbf{k}+\mathbf{q}}\left(n_{\mathbf{q}\nu }+1\right)-f_{n\mathbf{k}}\left(1-f_{m\mathbf{k}+\mathbf{q}}\right)n_{\mathbf{q}\nu }]\\ & =(f_{m\mathbf{k}+\mathbf{q}}-f_{n\mathbf{k}})[n_{\mathrm{B}\mathrm{E}}({\omega }_{\mathbf{q}\nu },T_{\mathbf{q}\nu })-n_{\mathrm{B}\mathrm{E}}({\omega }_{\mathbf{q}\nu },T_{\mathrm{e}\mathrm{l}})],\end{array}$(34)

where we introduced the Bose-Einstein function:

(35) $n_{\mathrm{B}\mathrm{E}}(\omega ,T)=[exp(\mathrm{\hslash }\omega /k_{\mathrm{B}}T)-1{]}^{-1}.$(35)

Additionally, we set ${\epsilon }_{m\mathbf{k}+\mathbf{q}}-{\epsilon }_{n\mathbf{k}}=\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }$ because of the Dirac-$\delta$ in Eq. (24(24) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}(t)=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})$(24) ), and we used $n_{\mathbf{q}\nu }=n_{\mathrm{B}\mathrm{E}}({\omega }_{\mathbf{q}\nu },T_{\mathrm{p}\mathrm{h}})$. A Taylor expansion of $n_{\mathrm{B}\mathrm{E}}$ to first order yields:

$n_{\mathrm{B}\mathrm{E}}({\omega }_{\mathbf{q}\nu },T_{\mathrm{p}\mathrm{h}})-n_{\mathrm{B}\mathrm{E}}({\omega }_{\mathbf{q}\nu },T_{\mathrm{e}\mathrm{l}})\simeq (T_{\mathrm{p}\mathrm{h}}-T_{\mathrm{e}\mathrm{l}}){\left.\frac{\mathrm{\partial }{n}_{\mathrm{B}\mathrm{E}({\omega }_{\mathbf{q}\nu },T)}}{\mathrm{\partial }T}\right|}_{T=T_{\mathrm{p}\mathrm{h}}}=(T_{\mathrm{p}\mathrm{h}}-T_{\mathrm{e}\mathrm{l}})\frac{c_{\mathbf{q}\nu }}{\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }}.$

In the last equality, we introduced the specific heat of a single harmonic oscillator $c_{\mathbf{q}\nu }=\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }\mathrm{\partial }{n}_{\mathbf{q}\nu }/\mathrm{\partial }T$.

Making use of Eq. (34(34) $\begin{array}{rl}& [\left(1-f_{n\mathbf{k}}\right)f_{m\mathbf{k}+\mathbf{q}}\left(n_{\mathbf{q}\nu }+1\right)-f_{n\mathbf{k}}\left(1-f_{m\mathbf{k}+\mathbf{q}}\right)n_{\mathbf{q}\nu }]\\ & =(f_{m\mathbf{k}+\mathbf{q}}-f_{n\mathbf{k}})[n_{\mathrm{B}\mathrm{E}}({\omega }_{\mathbf{q}\nu },T_{\mathbf{q}\nu })-n_{\mathrm{B}\mathrm{E}}({\omega }_{\mathbf{q}\nu },T_{\mathrm{e}\mathrm{l}})],\end{array}$(34) ), the integrand within the phonon-electron collision integral in Eq. (24)(24) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}(t)=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn}^{\nu }(\mathbf{k},\mathbf{q}){|}^2{f}_{n\mathbf{k}}(1-f_{m\mathbf{k}+\mathbf{q}})$(24) can be rewritten as:

(36) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}=\frac{c_{\mathbf{q}\nu }}{\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }}\frac{(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}})}{{\tau }_{\mathbf{q}\nu }}.$(36)

Where we introduced the phonon lifetime due to the electron-phonon interaction [1]:

(37) ${\tau }_{\mathbf{q}\nu }^{-1}=\frac{4\pi }{\mathrm{\hslash }{N}_p}\sum _{mn\mathbf{k}}|g_{mn\nu }(\mathbf{k},\mathbf{q}){|}^2(f_{n\mathbf{k}}-f_{m\mathbf{k}\mathbf{+}\mathbf{q}})\delta \left({\epsilon }_{m\mathbf{k}\mathbf{+}\mathbf{q}}-{\epsilon }_{n\mathbf{k}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }\right).$(37)

Via the identity ${\tau }_{\mathbf{q}\nu }^{-1}=-2\mathrm{I}\mathrm{m}{\mathrm{\Pi }}_{\mathbf{q}\nu }$, Eq. (36)(36) ${\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}=\frac{c_{\mathbf{q}\nu }}{\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }}\frac{(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}})}{{\tau }_{\mathbf{q}\nu }}.$(36) further establishes a simple relation between the phonon self-energy due to the electron-phonon interaction ${\mathrm{\Pi }}_{\mathbf{q}\nu }$ and the corresponding collision integral. The limit of validity of this identity are defined by the assumptions made thus far. Combining (37) with Eq. (32)(32) $C_{\mathrm{p}\mathrm{h}}{\mathrm{\partial }}_t{T}_{\mathrm{p}\mathrm{h}}=N_p^{-1}\sum _{\nu }\sum _{\mathbf{q}}\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }{\mathrm{\partial }}_t{n}_{\mathbf{q}\nu },$(32) :

(38) $C_{\mathrm{p}\mathrm{h}}{\mathrm{\partial }}_t{T}_{\mathrm{p}\mathrm{h}}=N_p^{-1}\sum _{\nu }\sum _{\mathbf{q}}{c}_{\mathbf{q}\nu }\frac{(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}})}{{\tau }_{\mathbf{q}\nu }}.$(38)

A similar identity can be derived by applying the same procedure for the electronic term. After introducing the effective electron-phonon coupling constant $g$:

(39) $g=N_p^{-1}\sum _{\nu }\sum _{\mathbf{q}}\frac{c_{\mathbf{q}\nu }}{{\tau }_{\mathbf{q}\nu }},$(39)

the equations of the TTM, Eqs. (3)(3) $\frac{\mathrm{\partial }{T}_1}{\mathrm{\partial }t}=\frac{g}{c_1}(T_2-T_1),$(3) and (4(4) $\frac{\mathrm{\partial }{T}_2}{\mathrm{\partial }t}=\frac{g}{c_2}(T_1-T_2).$(4) ) are recovered.

4. Ultrafast carrier dynamics in graphene

Graphene constitutes a paradigmatic example to introduce the hot-carrier dynamics revealed by pump-probe experiments in 2D materials. Ultrafast phenomena in graphene have been extensively investigated experimentally to explore its suitability for optoelectronic applications and light harvesting. Additionally, a recent discovery of the light-induced Hall effect has revealed a novel route to trigger a non trivial topological behaviour using light pulses [172–174]. The first ultrafast experimental studies resorted to optical techniques [124,161,162,175–183]. Subsequently, time- and angle-resolved photoemission spectroscopy (tr-ARPES [184]) enabled to directly monitor the non-equilibrium dynamics of photo-excited carriers with momentum resolution [39,78–80,125,185–197]. These experimental endeavours have been accompanied by a vast number of theoretical work exploring hot-carrier dynamics in graphene [81,122,131,166,167,170,198–204]. The utilized theoretical approaches vary from simple TTM [81,122], which were proven to be helpful in understanding graphene carrier dynamics above 100 fs [78], to more sophisticated, but numerically demanding methods [81,131,166,167,170,198–204], including full [166,200] or relaxation-time-approximation [201] versions of the TDBE, Bloch equations [167,198,199], time-dependent-density-functional theory methods [170,203,204], and non-equilibrium Green’s functions [205]. The latter body of work provided more insights into the nascent carrier dynamics, with photo-induced non-equilibrium electron distribution, such as Auger (electron-electron) processes [166], creation of non-thermal electronic excitation [131], plasmon emission [167], dynamical screening [200], as well as non-equilibrium electron-phonon scatterings [204]. Despite over a decade of extensive research, ultrafast hot carrier dynamics in graphene is still actively explored [70,81,97,170,193,196,203,205–207].

4.1. Experimental signature of hot-carrier dynamics in graphene

The ultrafast dynamics of Dirac carriers in pump-probe experiments is usually approximated as a four-step process consisting of (i) photo-excitation, (ii) formation of a quasi-equilibrium state, (iii) full electron thermalization, and (iv) energy transfer to the lattice (acoustic phonons). In the step (i), the interaction with a pump pulse drives the system into an electronic excited state, with carriers photo-excited above the Fermi level. With this a non-equilibrium electron distribution is created. The step (ii) involves electron-electron scatterings, impact ionization, and Auger processes (timescale of $\sim 10$ fs) [166,208], which promote photo-excited electrons and holes towards the Fermi level. Some experiments indicate that under suitable conditions a regime of the so called ‘population inversion’ can be established, i.e. when a certain portion of photo-excited electrons occupy the lowest conduction states, while the highest valence states are depopulated [79,180,209]. In general, this population state could be achieved in semiconductors and semimetals (such as graphene) when the electrons (holes) are photo-excited above the energy band gap, and subsequently thermalized in the lowest conduction (highest valence) states, with relaxation rates much higher than the electron-hole recombination rate. Interestingly, some theoretical works suggested that strong scatterings between non-equilibrium electrons and phonon are active already at this stage [132,204]. Even more, this early electron-phonon scattering process might be responsible for majority of energy flow, leaving a small portion of excess energy for the later scatterings between equilibrium electrons and phonons [132]. In step (iii), Auger recombination [179,210], scatterings with optical phonons [78,124], as well as plasmon emission [167,168] bring the electrons to a thermalized regime ($\sim 100$ fs), where the electronic distribution function is described by a high-temperature Fermi-Dirac function. Finally, in step (iv), the photo-excited electrons and holes dissipate their energy via phonon-assisted scattering processes, mostly via the acoustic modes ($\sim 1-10$ ps). Supercollisions [78] and the formation of hot phonons [211] have been proposed as underlying physical processes to explain the energy transfer to the lattice [124,212]. Further experimental investigations on the parent compound graphite corroborated the hot-phonon picture [39,213]. Overall, these studies revealed a complex non-equilibrium dynamics characterized by the coexistence of several scattering mechanisms which are challenging to decipher based on purely experimental investigations.

Exemplary tr-ARPES experiments on hole-doped graphene are illustrated in Figure 6 [79]. As a result of substrate-induced hole-doping, the Fermi energy is located 0.2 eV below the Dirac point (Figure 6(a)). Figures 6(b-d) illustrate several snapshots of the tr-ARPES spectral function in the vicinity of the Dirac point. Before excitation (Figure 6(b)), the spectral intensity reflects occupied electronic states at equilibrium, with broadening arising from finite temperature and experimental resolution. Owing to the optical selection rules governing the coupling with linearly-polarized light, the spectral intensity is dominated by contributions arising from the left sub-band [214]. The change in spectral intensity for $t=30$ fs (Figure 6(c)) reflects the excitation of carriers above the Fermi level, whereas measurements at longer time delays (Figure 6(d)) indicates the recovery of an equilibrium regime.

Figure 6. (a) Schematic representation of the thermalization dynamics of electrons and holes following photo-excitation in the vicinity of the Dirac cone of graphene. Time and angle-resolved photoemission spectral function of doped graphene before photo-excitation (b), and at time delays $t=30$ fs (c), and $t=1$ ps (d). Momentum integrated spectral function (e) and, superimposed as a continuous line, the Fermi-Dirac function at the effective electronic temperature $T_e$. (f) Time-dependent effective electronic temperature derived by the fitting procedure illustrated in (e). Adapted from Ref [79].

Tr-ARPES measurements can be analysed to extract the effective electronic temperatures $T_{\mathrm{e}\mathrm{l}}$ and its time dependence [73,74,78,79,125,215–217], thus, establishing a direct link with the TTM and NLM discussed in Sections 2 and 2.1. For a given time delay, $T_{\mathrm{e}\mathrm{l}}$ can be determined by fitting the normalized momentum-integrated photoemission intensity with a Fermi-Dirac function. This procedure is illustrated in Figure 6(e) where the fit Fermi-Dirac function (continuous line) is superimposed to the measured energy distribution curves (dots). The time dependence of $T_{\mathrm{e}\mathrm{l}}$, shown in Figure 6(f), is obtained by repeating this procedure for several measured time delays. The photo-excitations of the electrons by the pump pulse manifests itself through the initial increase of electronic temperature, whereas the subsequent cooling reflects the thermalization dynamics due electron-phonon scattering processes, following a trend that closely resembles the one reported for the light-driven TTM illustrated Figure 1(f).

4.2. Theoretical modelling of carrier thermalization in graphene

First-principles calculations of the electron-phonon interaction can be combined with the time-propagation algorithms discussed in Sections 2–3 to investigate the origin of the hot-carrier dynamics and its fingerprints in spectroscopy. The band structure and phonon dispersion of hole-doped graphene is illustrated in Figure 7(a,b), respectively [70], whereas the phonon density of state ($F$) and the Eliashberg function (${\alpha }^{2}F$) are shown in the right panel of Figure 7(b). The Eliashberg function reflects the weighted and integrated phonon density of states, to which individual phonons contribute according to their electron-phonon coupling strength [218]. The sharp peaks in ${\alpha }^{2}F$ at 160 and 190 meV indicate that the electron-phonon coupling arises primarily from longitudinal optical (LO or $E_{2g}$) phonons at $\mathrm{\Gamma }$ and transverse optical (TO or ${A_1}^{\prime }$) modes at K (green dots in Figure 7(b)), whereas remaining phonons couple relatively weakly to the electrons. This finding suggests that only few phonons are likely to provide a preferential decay channel for the relaxation of excited carriers, leading to the emergence of hot phonons – namely, phonons characterized by a higher vibrational temperature. The pronounced anisotropy of the electron-phonon interaction in graphene can be explicitly accounted for by formulating a NLM (i.e. a three-temperature model) which discriminates between strongly- (sc) and weakly-coupled (wc) phonons [81], and by determining the model parameters from first-principles calculations [159,160,219]. The effective electronic temperature $T_{\mathrm{e}\mathrm{l}}$ and the vibrational temperatures ($T_{\mathrm{w}\mathrm{c}}$ and $T_{\mathrm{s}\mathrm{c}}$) obtained from the solution of the NLM (Eqs. (10)(10) $\frac{\mathrm{\partial }{T}_{\mathrm{p}\mathrm{h}}^{\mu }}{\mathrm{\partial }t}=\frac{g_{\mu }}{C_{\mathrm{p}\mathrm{h}}^{\mu }}(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}}^{\mu })+\sum _{\mu { }^{\mathrm{\prime }}}\frac{T_{\mathrm{p}\mathrm{h}}^{\mu { }^{\mathrm{\prime }}}-T_{\mathrm{p}\mathrm{h}}^{\mu }}{{\tau }_{\mu \mu { }^{\mathrm{\prime }}}},$(10) and (11(11) $\frac{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}}{\mathrm{\partial }t}=\sum _{\mu }^{N_g}\frac{g_{\mu }}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}^{\mu }-T_{\mathrm{e}\mathrm{l}})+S(t).$(11) )) are illustrated in Figures 7 (c,d) for different excitation conditions [81]. The electronic temperature follows the characteristic trend expected for photoexcited electrons and it is in good agreement with the experimental values extracted from tr-ARPES. The preferential excitation of strongly-coupled modes upon carrier relaxation leads to a pronounced rise of $T_{\mathrm{s}\mathrm{c}}$, whereas the vibrational temperatures of weakly-coupled modes $T_{\mathrm{w}\mathrm{c}}$ is smaller.

Figure 7. (a) DFT Band structure of graphene in the vicinity of the Dirac cone along the M-K high-symmetry path in the Brillouin zone. (b) Left: Phonon dispersion of graphene obtained from DFPT. Right: Phonon density of states ($F$) and Eliashberg function (${\alpha }^{2}F$) of graphene. The peaks at 0.16 and 0.19 eV reflect the strong coupling to transverse optical (TO) and longitudinal optical (LO) phonons in the vicinity of the K and $\mathrm{\Gamma }$ points, respectively [green dots in panel (b)]. (c-d) Pump-probe photoemission measurements of the effective electronic temperature $T_{\mathrm{e}\mathrm{l}}$ of graphene (dots) for photo-excitation fluences $F=8\mathrm{J}/{\mathrm{m}}^2$ (c) and (d) $F=3.46\mathrm{J}/{\mathrm{m}}^2$ from Refs. [78,79]. Simulations based on the NLM (more precisely, three-temperature model) with first-principles parameters are reported as continuous lines. Panels (a-b) and (c-d) are adapted from Ref. [70] and Ref. [81], respectively.

By post-processing the effective temperatures $T_{\mathrm{e}\mathrm{l}}$, $T_{\mathrm{w}\mathrm{c}}$, and $T_{\mathrm{s}\mathrm{c}}$, one can define a simple procedure to estimate the transient changes of many-body interactions and their signatures in photoemission. The self-energy due to electron-phonon interaction can be modified to account for changes of the electronic and vibrational distribution functions as:

(40) ${\mathrm{\Sigma }}_{n\mathbf{k}}(\omega ,\mathrm{\Delta }t)=\frac{1}{N_p}\sum _{m\nu \mathbf{q}}|g_{mn\nu }(\mathbf{k},\mathbf{q}){|}^2$(40)

$\times \left[\frac{n_{\mathbf{q}\nu }(\mathrm{\Delta }t)+f_{m\mathbf{k}+\mathbf{q}}(\mathrm{\Delta }t)}{\mathrm{\hslash }\omega -{\tilde{\epsilon }}_{m\mathbf{k}+\mathbf{q}}+\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }}+\frac{n_{\mathbf{q}\nu }(\mathrm{\Delta }t)+1-f_{m\mathbf{k}+\mathbf{q}}(\mathrm{\Delta }t)}{\mathrm{\hslash }\omega -{\tilde{\epsilon }}_{m\mathbf{k}+\mathbf{q}}-\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }}\right]$

The time dependence arise from the dependence of the electron and phonon distribution functions on the effective temperatures, given by $f_{n\mathbf{k}}=[e^{{\epsilon }_{n\mathbf{k}}/k_{\mathrm{B}}{T}_{\mathrm{e}\mathrm{l}}}+1{]}^{-1}$ and $n_{\nu \mathbf{q}}=[e^{{\omega }_{\nu \mathbf{q}}/k_{\mathrm{B}}{T}_{\nu }}-1{]}^{-1}$, respectively, where $T_{\nu }=T_{\mathrm{s}\mathrm{c}}$ ($T_{\nu }=T_{\mathrm{w}\mathrm{c}}$) for the strongly (weakly) coupled modes. The tr-ARPES spectral function can be directly derived from Eq. (40)(40) ${\mathrm{\Sigma }}_{n\mathbf{k}}(\omega ,\mathrm{\Delta }t)=\frac{1}{N_p}\sum _{m\nu \mathbf{q}}|g_{mn\nu }(\mathbf{k},\mathbf{q}){|}^2$(40) via $A_{\mathbf{k}}(\omega ,\mathrm{\Delta }t)={\pi }^{-1}{\sum }_n\mathrm{I}\mathrm{m}[\mathrm{\hslash }\omega -{\epsilon }_{n\mathbf{k}}-{\mathrm{\Sigma }}_{n\mathbf{k}}(\omega ,\mathrm{\Delta }t){]}^{-1}$. The spectral function of graphene obtained from this procedure is illustrated in Figure 8, and it reproduces the main spectral signatures of photoexcitations revealed by experiments as well as the characteristic time scales of photoexcitations.

Figure 8. (a) DFT Band structure of graphene in the vicinity of the Dirac cone. The dashed line denotes the Fermi energy ${\epsilon }_{\mathrm{F}}=-0.2$ eV, corresponding to a carrier concentration $8\times {10}^{12}$ cm ${ }^{-2}$. The inset illustrates the hexagonal Brillouin zone. First-principles calculations of the time- and angle-resolved spectral function obtained by considering electronic and vibrational occupations derived from the solution of the TTM before excitation (b), and at time delays $\mathrm{\Delta }t=0$ (c), $\mathrm{\Delta }t=0.5$ ps (d), and $\mathrm{\Delta }t=2.5$ ps (e). Reproduced from Ref [81].

Other time-dependent physical features of ultrafast hot carrier cooling visible in pump-probe spectroscopy can be theoretically captured in a similar fashion, i.e. by benefiting from the time dependence of electron and phonon temperatures. For instance, time dynamics of electron excitations (e.g. plasmons and screened interband transitions) immediately after the laser excitation can be simulated via optical conductivity $\sigma (\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})$ or dielectric function $\epsilon (\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})$ [90,126]. The spectral function of electron excitations (or the so-called electron energy loss function) is defined as [70,220]

(41) $-\mathrm{I}\mathrm{m}\left[\frac{1}{\epsilon (\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})}\right]=-\mathrm{I}\mathrm{m}\left[\frac{{\omega }^2}{{\omega }^2-{\mathrm{\Omega }}^2(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})+i\mathrm{\Gamma }(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})}\right]$(41)

where ${\mathrm{\Omega }}^2(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})=v(\mathbf{q})q^2\mathrm{R}\mathrm{e}{\pi }_{\alpha \alpha }(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})$ and $\mathrm{\Gamma }(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})=-v(\mathbf{q})q^2\mathrm{I}\mathrm{m}{\pi }_{\alpha \alpha }(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})$, define the energy and corresponding damping (e.g. Landau damping and electron-phonon channel) of electronic excitations as a function of time delay (via time dependence of $T_{\mathrm{e}\mathrm{l}}$ and $T_{\mathrm{p}\mathrm{h}}$). $v(\mathbf{q})$ is the Coulomb interaction and ${\pi }_{\alpha \alpha }$ is the current-current response function (photon self-energy) for the polarization direction $\alpha$. Useful optical quantities such as optical absorption $\sigma (\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})=i{\pi }_{\alpha \alpha }(\mathbf{q}=0,\omega )/\omega$ or photoconductivity $\mathrm{\Delta }\sigma (\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})=\sigma (\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})-\sigma (\omega ;T_{\mathrm{e}\mathrm{l}}=T_{\mathrm{p}\mathrm{h}}=T_0)$ can also be simulated in the same way. The combination of Eq. (41)(41) $-\mathrm{I}\mathrm{m}\left[\frac{1}{\epsilon (\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})}\right]=-\mathrm{I}\mathrm{m}\left[\frac{{\omega }^2}{{\omega }^2-{\mathrm{\Omega }}^2(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})+i\mathrm{\Gamma }(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})}\right]$(41) and the TTM equations was recently utilized in order to track ultrafast dynamics of Dirac plasmon in graphene, including energy loss of plasmon in non-equilibrium regime [70]. It was concluded that although steady state plasmon is mostly damped due to scatterings with acoustic phonons, the non-equilibrium Dirac plasmon dissipates most of its energy to intrinsic strongly coupled optical phonons. The same approach was also applied to study laser-induced band renormalization close to van Hove singularity point of graphene band structure [221,222], where it was concluded that electron-phonon coupling plays a significant role in photo-induced band modifications in graphene [97].

Note that the approach of incorporating time dependence into Eqs. (40)(40) ${\mathrm{\Sigma }}_{n\mathbf{k}}(\omega ,\mathrm{\Delta }t)=\frac{1}{N_p}\sum _{m\nu \mathbf{q}}|g_{mn\nu }(\mathbf{k},\mathbf{q}){|}^2$(40) and (41(41) $-\mathrm{I}\mathrm{m}\left[\frac{1}{\epsilon (\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})}\right]=-\mathrm{I}\mathrm{m}\left[\frac{{\omega }^2}{{\omega }^2-{\mathrm{\Omega }}^2(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})+i\mathrm{\Gamma }(\mathbf{q},\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})}\right]$(41) ) via the TTM results is actually general and can be applied to any spectral function or self-energy defined in terms of electron and phonon distribution functions. For instance, this approach was exploited to monitor hot-phonon dynamics in conventional superconductor MgB${ }_2$ via phonon spectral function $B(\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})$ and many-body phonon self-energy $\mathrm{\Pi }(\omega ;T_{\mathrm{e}\mathrm{l}},T_{\mathrm{p}\mathrm{h}})$ of strongly-coupled $E_{2g}$ mode [82]. All in all, this way of modelling ultrafast carrier and lattice thermalization can provide many microscopic insights of spectroscopic quantities in time domain, and was proven to have a well-balanced ratio between accuracy and numerical cost.

4.3. Non-equilibrium lattice dynamics from the time-dependent Boltzmann equation

To illustrate the application of the TDBE formalism to the ultrafast electron-phonon dynamics of 2D materials and its suitability for the description of these phenomena, we report in Figure 9 ultrafast dynamics simulations for graphene obtained from the numerical solutions of Eqs. (27)(27) ${\mathrm{\partial }}_t{f}_{n\mathbf{k}}(t)={\mathrm{\Gamma }}_{n\mathbf{k}}^{\mathrm{e}\mathrm{p}}[f_{n\mathbf{k}}(t),n_{\mathbf{q}\nu }(t)],$(27) and (28(28) ${\mathrm{\partial }}_t{n}_{\mathbf{q}\nu }(t)={\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{e}}[f_{n\mathbf{k}}(t),n_{\mathbf{q}\nu }(t)]+{\mathrm{\Gamma }}_{\mathbf{q}\nu }^{\mathrm{p}\mathrm{p}}[n_{\mathbf{q}\nu }(t)].$(28) ) and reproduced from Ref [143]. In panels (a)-(c), the electron ($f_{n\mathbf{k}}$) and hole (1-$f_{n\mathbf{k}}$) distribution functions are superimposed to the band dispersion of graphene for energies above and below the Fermi level (dashed) for several time delays. The initial ($t=0$) distribution of electrons and holes loses its excess energy via emitting phonon in the vicinity of the $\mathrm{\Gamma }$ and K high symmetry points and relaxes back to Fermi level within few picoseconds. The non-equilibrium phonon population is illustrated in Figures 9(d-f), where the point size is proportional to the phonon occupation $n_{\mathbf{q}\nu }(t)$. The phonon population at 300 fs (Figure 9 (e)) is characterized by an enhancement of the number LO and TO phonons at $\mathrm{\Gamma }$ and K, indicating that these modes constitute the primary decay path for excited electrons for the initial phases of the relaxation. These findings are compatible with the Eliashberg function shown in Figure 7(b). On longer time scales, the phonon-phonon scattering leads to the thermalization of lattice and a redistribution to the excess energy of these modes to low-energy modes Figure 9(g).

Figure 9. Population of excited electrons and holes for an initial electronic excitation (a) superimposed to the band structure of graphene, and at subsequent time steps throughout the non-equilibrium dynamics as obtained from the solution of the time-dependent Boltzmann equation (b-c). The left panels denote the density of states of electrons and holes. (d-f) Time-dependent phonon distribution functions $n_{\mathbf{q}\nu }(t)$ superimposed to the phonon dispersion for several snapshot, with the point size being proportional to $n_{\mathbf{q}\nu }(t)$. (g) Energy resolved phonon population $n_{\mathbf{q}\nu }(t)$ as a function of time. Reproduced from Ref [143].

More generally, phonon-emission processes are constrained by energy and momentum conservation laws, which reduce the phase-space available for phonon-assisted electronic transitions. For example, graphene carriers in the vicinity of the Fermi level at K can scatter to states within the same Dirac cone at K, leading to the emission of phonons with $\mathbf{q}\simeq \mathrm{\Gamma }$, alternatively they can scatter to the second Dirac cone at $-$ K, emitting phonons with crystal momentum around K or -K. Transitions to other region of the BZ are forbidden as they violate conservation laws. This stringent momentum selectivity confines the emitted phonons to narrow regions in reciprocal space, leading to the emergence of hot spots in the BZ, i.e. regions characterized by an enhanced vibrational temperature. Figure 10(a) illustrates the BZ and high-symmetry points of monolayer MoS${ }_2$, reproduced from Ref [223]. The superimposed color coding denotes the effective vibrational temperature obtained by inverting the Bose-Einstein distribution as $T_{\mathbf{q}\nu }(t)=\mathrm{\hslash }{\omega }_{\mathbf{q}\nu }\{k_{\mathrm{B}}ln[1+n_{\mathbf{q}\nu }(t)]{\}}^{-1},$ and averaging over all mode indices $\nu$ via ${\tilde{T}}_{\mathbf{q}}=N_{\mathrm{p}\mathrm{h}}^{-1}{\sum }_{\nu }{T}_{\mathbf{q}\nu }$ – with $N_{\mathrm{p}\mathrm{h}}=9$ being the number of phonons of monolayer MoS${ }_2$. Here, the phonon distribution function $n_{\mathbf{q}\nu }(t)$ is obtained from the solution of the coupled TDBE for electrons and lattice. The preferential emission of phonons around $\mathrm{\Gamma }$, K, and -$\bar{\mathrm{K}}$ is reflected by the enhanced vibrational temperature at these high-symmetry points for the initial phases of hot-carrier relaxation. Phonon hot-spots in the BZ can persist for several picoseconds, until the onset of phonon-phonon scattering processes restores a regime of thermal equilibrium.

Figure 10. (a) Hexagonal Brillouin zone and high-symmetry points (dots) of monolayer MoS${ }_2$. The color coding reflects the effective vibrational temperature of the lattice for an initial ($t=0$) state of thermal equilibrium at $T=100$ K (see color bar). (b-e) Enhancement of the phonon temperature in the vicinity of the Γ and K high-symmetry points due to momentum-selective phonon emission throughout the relaxation of a photo-excited electronic distribution. Reproduced from Ref [223].

5. Beyond the time-dependent Boltzmann formalism

The TDBE formalism constitutes a powerful and computationally affordable scheme to explore ultrafast processes in presence of electron-phonon interactions, yet several non-equilibrium phenomena extend beyond its domain of applicability. These include, for instance, correlation effects on the electron dynamics [224–227], coherence and dephasing of electronic and vibrational excitations [228,229], dynamics in highly-anharmonic crystals (structural phase transitions) [230–232], topological Floquet states [233–235], and the transient formation of quasiparticle states [236]. While a comprehensive overview of these phenomena and of the related theoretical approaches would be lengthy and beyond the scope of this review, below we limit ourselves to discuss some of the limitations of the TDBE for a selection of such examples.

5.1. Coherent electron dynamics

In addition to incoherent electron dynamics – as exemplified by the transient changes of the electron population $f_{n\mathbf{k}}$ – the dynamics of photoexcited carriers can display coherent time-dependent features which are not captured by the TDBE [229,237]. Coherent electronic excitations manifest themselves as periodic oscillations of the electronic polarization at the frequency of the driving field and they can be observed via several experimental techniques [238,239]. Coulomb scattering limits the coherence time and, thus, coherent electronic excitations are only observed at the initial stages of the dynamics for time delays typically shorter than 100 fs. The density-matrix formalism [240] and non-equilibrium Green’s functions (NEGF) are suitable frameworks for the description of electron coherence, as discuss in several recent theoretical works [205,229,241–249]. The solution of the Kadanoff-Baym equations (KBE), for example, enables to gain information on both coherent and incoherent electron dynamics via diagonal and off-diagonal elements of density matrix, respectively, and it is further suitable to capture non-Markovian effects [250]. Several recent theoretical studies have focused on making the KBE approach numerically accessible [205,229,251], and in particular the $G1-G2$ approach has allowed to achieve linear scaling in the time-propagation of NEGF [251].These advancements have recently enabled the extension of the KBE approach within the $GW$ approximation to the domain of ab-initio calculations, providing microscopic insight into correlated and coherent hot-carrier dynamics in grephene [205].

5.2. Coherent lattice dynamics

The excitation of coherent phonons via ultrashort infrared (IR) or UV pulses has been widely investigated as a route to achieve light-assisted control of structural degrees of freedom [94,240,252–260]. Coherent phonons – displacive in-phase excitations of the nuclei away from their equilibrium position – can be excited by either IR absorption, impulsive stimulated Raman scattering (ISRS) [254,261,262], or ionic Raman scattering [263,264]. The lattice dynamics triggered by either of these mechanisms is characterized by an incoherent component, which arises from the enhanced population of IR- or Raman-active modes upon absorption or scattering of light [265]. Additionally, a coherent dynamics can arise upon photo-excitation with short pulses (namely, with a pulse duration shorter than the phonon period) leading to the formation of coherent phonons [253]. As mentioned, the TDBE formalism provides a suitable approach to describe the incoherent lattice dynamics triggered by light pulses. The enhanced population of IR- and/or Raman-active modes established upon absorption or scattering of light can be approximated via a bosonic distribution function, in the spirit of Section 3.1, and its time dependence can be inferred from the solution of the TDBE with an appropriate choice for the collision integrals [265]. Phonon coherence, conversely, entails a precise phase relation between photoexcited phonons which is not captured by Fermi golden rule and the TDBE. Theoretical approaches to the coherent lattice dynamics can be formulated classically by explicitly solving the classical equation motion of the lattice in presence of an external field. This can be accomplished via classical [266] or ab-initio [121,267,268] molecular dynamics (MD), where the classical equations of motion are solved in real time on the DFT potential energy surface (PES). The MD approach has also been combined with the real-time time-dependent density functional theory (i.e. rt-TDDFT-MD) in order to study coupling between coherent optical phonons and photo-induced electron excitations [204,232,269,270]. Additionally, phenomenological models based on the driven quantum harmonic oscillator have widely employed to describe coherent lattice dynamics in solids [230,262,271–276]. A fully quantum approach to coherent phonons requires the time-propagation of the bosonic operators of the lattice in presence of an external field and it can be formulated within the density-matrix formalism. The theoretical foundation of this approach are reviewed in Ref [240].

5.3. Lattice dynamics of highly anharmonic crystals: light-induced phase transitions

At high-fluence conditions, the coherent lattice dynamics triggered by light pulses can act as a precursor for driving matter across phase transitions [277–279] or into metastable states inaccessible in equilibrium conditions [276]. The perturbative treatment of third-order anharmonic effects and phonon-phonon interactions in the TDBE constitutes a clear shortcoming which limits its application to the investigation of these phenomena. A theoretical description of ultrafast lattice dynamics in concomitance with structural distortion requires (i) to explicitly account for third- and fourth-order anharmonic terms in the expansion of the potential energy surface in a non-perturbative fashion and (ii) to account for the external driving field. Methods based on ab-initio Ehrenfest dynamics (MD) are the most suitable routes to seamlessly integrate the influence of anharmonic effects [280], external driving fields [281], and electron-phonon interactions [282,283]. Ehrenfest dynamics simulations in presence of a driving field, for example, have recently been conducted for pentacene crystals to reveal the coupling between coherent structural distortions and optical excitations [280]. Owing to the high computational cost of Ehrenfest dynamics for solids, the long timescales (10–100 ps) required to properly model lattice thermalization still remain prohibitive. Additionally, the momentum resolution of phonon-phonon scattering processes is defined by the supercell size adopted in the simulation, limiting the predictive power for the lattice thermalization following photo-excitation. An overview of ab-initio approaches for anharmonic calculations of the PES can be found in [284] and references therein.

Alternatively, a normal-coordinate representation can be formulated via the quantum-harmonic oscillator approach adopted in Ref [271]. and subsequent works [230,262,272–276] These approaches, however, have thus far been limited to structural distortions arising from the excitation of $\mathrm{\Gamma }$ phonons and anharmonic effects have been included in a parametrized fashion only for a selection of strongly coupled phonons. To extend the predictive power of ab-initio methods to the domain of light-induced phase transitions, it would be desirable to combine a reciprocal-space formulation of the structural dynamics (e.g. in normal coordinates) with an atomistic description of the anharmonic PES.

6. Summary and outlook

In this manuscript we have reviewed the two-temperature model, the time-dependent Boltzmann equation and their application to the study of the coupled ultrafast dynamics of electrons and phonons in solids. The two-temperature and the non-thermal lattice models recast the thermalization dynamics of electrons and phonons into a set of coupled first-order differential equations, which is formally equivalent to the ones governing the temperature evolution of coupled thermal baths. While on the one hand these approximations are sufficient to capture the characteristic timescales and dynamics of the electron thermalization with the lattice revealed by pump-probe experiments, on the other hand, the non-equilibrium electron, vibrational and structural dynamics are poorly described, restricting the domain of applicability of these approaches. The time-dependent Boltzmann equation overcomes several of these limitations while retaining an affordable computational cost. The main advantage of this approach is two-fold: (i) it provides a description of ultrafast electron and phonon dynamics with full momentum resolution (ii) it accounts for phase-space constraints in phonon-assisted electronic transitions. These points are important prerequisites to capture the non-equilibrium phonon dynamics as revealed, e.g. by ultrafast diffuse scattering experiments [40,41,85,145,152,285]. A particularly appealing feature of the time-dependent Boltzmann equation is the possibility to make the collision integrals fully parameter-free by determining electron-phonon and phonon-phonon coupling matrix elements via available first-principles electronic-structure codes [138,160,286].

Fostered by the relentless advances in the experimental characterization of ultrafast phenomena, first-principles approaches for ultrafast dynamics in presence of electron-phonon interactions constitute a rapidly evolving research field and novel challenges are continuously being unveiled. Addressing these challenges requires to simultaneously advance theoretical models and devise computationally affordable simulation frameworks for ab-initio calculations of realistic materials. We envision that ab-initio methods will play an increasingly important role in the prediction and interpretation of novel ultrafast phenomena, providing endless opportunities to consolidate synergies between theoretical and experimental ultrafast science.

Acknowledgments

This project has been funded by the Deutsche Forschungsgemeinschaft (DFG) – Projektnummer 443988403. D.N. acknowledges financial support from the Croatian Science Foundation (Grant no. UIP-2019-04-6869) and from the European Regional Development Fund for the “Center of Excellence for Advanced Materials and Sensing Devices” (Grant No. KK.01.1.1.01.0001). Discussions with Mariana Rossi and Branko Gumhalter are gratefully acknowledged.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Deutsche Forschungsgemeinschaft [Projektnummer 443988403]; Croatian Science Foundation [Grant no. UIP-2019-04-6869]; European Regional Development Fund [Grant No. KK.01.1.1.01.0001].

Appendix A.

Analytical solution of the TTM

Below we report the analytical solution of the TTM for the limiting case of temperature-independent heat capacities. The TTM equations in absence of external driving field are reported below:

(42) $\frac{\mathrm{\partial }{T}_{\mathrm{p}\mathrm{h}}}{\mathrm{\partial }t}=\frac{g}{C_{\mathrm{p}\mathrm{h}}}(T_{\mathrm{e}\mathrm{l}}-T_{\mathrm{p}\mathrm{h}}),$(42)

(43) $\frac{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}}{\mathrm{\partial }t}=\frac{g}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}-T_{\mathrm{e}\mathrm{l}}).$(43)

The TTM thus forms a set of two coupled first-order differential equation, which can be solved analytically via standard techniques. Its solution is:

(44) $T_{\mathrm{e}\mathrm{l}}(t)=a_1{e}^{-\gamma t}+a_2,$(44)

(45) $T_{\mathrm{p}\mathrm{h}}(t)=-\frac{C_{\mathrm{e}\mathrm{l}}{a}_1}{C_{\mathrm{p}\mathrm{h}}}{e}^{-\gamma t}+a_2,$(45)

where we introduced the constants $a_1=(T_{\mathrm{e}\mathrm{l}}^0-T_{\mathrm{p}\mathrm{h}}^0)C_{\mathrm{p}\mathrm{h}}/(C_{\mathrm{p}\mathrm{h}}+C_{\mathrm{e}\mathrm{l}})$, $a_2=T_{\mathrm{e}\mathrm{l}}^0-c_1$, and $\gamma =g/(1/C_{\mathrm{e}\mathrm{l}}+1/C_{\mathrm{p}\mathrm{h}})$. The solution is easily verified by substitution.

By introducing a source term coupled to the electronic temperature, the TTM gets modified as follows:

(46) $\frac{\mathrm{\partial }{T}_{\mathrm{e}\mathrm{l}}}{\mathrm{\partial }t}=\frac{g}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}-T_{\mathrm{e}\mathrm{l}})+S(t),$(46)

where $S(t)$ describes the interaction with a light pulse, and the second equation remains unchanged. Analytic solution of the TTM is still possible for a simple time dependence of $S(t)$. For example, by considering $S(t)=\alpha e^{-\frac{t}{\tau }}\theta (t)$, the solution can be written as:

(47) $T_{\mathrm{e}\mathrm{l}}(t)=-\tau b_1{e}^{-\frac{t}{\tau }}-b_2{\gamma }^{-1}{e}^{-\gamma t}+b_3,$(47)

(48) $T_{\mathrm{p}\mathrm{h}}(t)=T_{\mathrm{e}\mathrm{l}}(t)+\frac{C_{\mathrm{e}\mathrm{l}}}{g}\left[(b_1-\alpha )e^{-\frac{t}{\tau }}+b_2{e}^{-\gamma t}\right],$(48)

with the constants:

(49) $b_1=\alpha \left(\frac{g\tau }{C_{\mathrm{p}\mathrm{h}}}-1\right)(\gamma \tau -1{)}^{-1},$(49)

(50) $b_2=\frac{g}{C_{\mathrm{e}\mathrm{l}}}(T_{\mathrm{p}\mathrm{h}}^0-T_{\mathrm{e}\mathrm{l}}^0)+\alpha -b_1,$(50)

(51) $b_3=T_{\mathrm{e}\mathrm{l}}^0+\frac{b_2}{\gamma }+b_1\tau .$(51)