Revised inverse problem algorithm-based prediction of coronary artery stenosis readings from the clinical data of patients with coronary heart diseases

Abstract

Aim: Coronary artery stenosis readings were predicted in this study on the basis of clinical data for patients with coronary heart diseases using the inverse problem algorithm.

Method: Five factors, including age, BSA (body surface area), MAP (mean artery pressure), sugar AC (ante cibum), and LDL-C (low-density Lipoprotein-Cholesterol) were incorporated into a nonlinear first-order regression fit analysis to develop a prediction equation with sixteen terms derived via a revised inverse problem algorithm implemented through the STATISTICA default regression fit. The clinical data acquired from ninety-three coronary heart disease patients were first normalized to the same domain range of [-1 to +1], and then processed by the above algorithm to find the compromised solution of predicted coronary artery stenosis reading. The actual reading was obtained by weighting the stenosis of three major cardiac artery branches, namely, the left anterior descending artery (LAD) (wi 0.3), left circumflex artery (LCA) (wi 0.3), and right coronary artery (RCA) (wi 0.4).

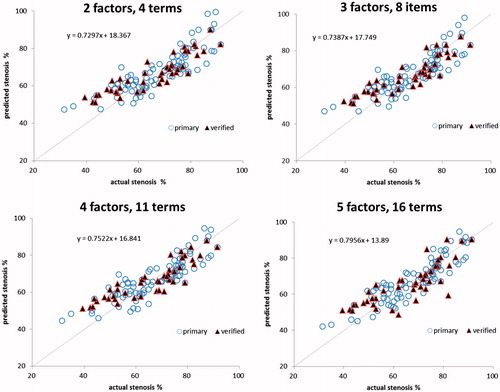
Result: The derived regression fit possessed the final loss function value Φ = 3.589 and correlation coefficient r2 = 0.892 with variance of 79.55%. Accordingly, forty-five patients with similar syndromes were analyzed to verify the prediction, which exhibited a high coincidence. The LDL-C factor was dominant for the prediction of the largest coefficient in the derived equation, whereas the age factor exhibited a minor contribution to the regression fit. The attempts to reduce the number of influence factors to 4, 3 or 2 for the model simplification yielded the results, whose low linearity and high loss function values reflected their inappropriate setting.

Conclusion: The algorithm proved to be an effective technique for prediction of the potential diagnosis in the medical field.

Keywords:

• Coronary artery stenosis
• inverse problem algorithm
• normalize
• low-density lipoprotein-cholesterol

Introduction

Coronary artery stenosis readings were predicted in this study on the basis of clinical data for patients with coronary heart diseases using the inverse problem algorithm. Globally, the coronary artery disease (CAD) causes the highest mortality [1], while in Taiwan the mortality of heart disease is ranked the second highest after carcinoma. Nevertheless, most of heart diseases are classified as CAD [2]. A proper prediction system would be very instrumental for reducing the potential risk for CAD patients, but vast data arrays available in the health care system lack comprehensive interpretation yet. Numerous researchers have tried to apply various approaches for predicting the above risk based on the patient clinical data. Hachesu et al. predicted the length of stay in hospital for 4948 cardiac patients based on 36 input factors and reached an overall accuracy of 96.4% [3]. Dangare and Apte used fifteen factors to refine the heart disease prediction system that originally included thirteen factors by adding the smoking and obesity factors. They used the neutral network analysis coupled with the decision tree and naïve Bayes classification to attain the prediction accuracy of 100, 99.62, and 90.74%, respectively [4]. Shouman et al. summarized the similar studies from 2003 to 2010 and reported the diagnosis accuracy according to different data mining techniques or heart disease datasets [5]. However, few of them can propose an efficient technique to quantify the contribution from specific factor and still to fulfill clinical verification from medical viewpoint. Among the executable techniques used in the data mining, the inverse problem algorithm is the most lucrative for the potential risk prediction based on bountiful medical information. The quantified index derived on the basis of this algorithm is shown to provide a reliable proof for the clinical research [6,7]. The accuracy of prediction can be effectively improved, provided the input factors are well manipulated and normalized in building up the dataset.

In this study, a revised technique was established to quantitatively predict the coronary artery stenosis readings for heart disease patients according to five clinical factors using the inverse problem algorithm. The factors included age, BSA (body surface area), MAP (mean artery pressure), Sugar AC (ante cibum), and LDL-C (low-density Lipoprotein-Cholesterol). The five factors were normalized in this revised algorithm to eliminate the different dimensions, then the algorithm configuration was established via a computational program run with STATISTICA [8]. The algorithm compiled the data on ninety-three patients, which exhibited a potential coronary heart disease within the past three years (2012-2014), and computed a nonlinear first-order regression fit with sixteen terms, in order to obtain a compromised solution. Furthermore, the coefficient of each term also implied the dominance of the specific factor. The prediction was then verified using the data of another group of forty-five patients with similar clinical syndromes, attaining a high accuracy.

Materials and methods

Revised inverse problem algorithm

Assuming a first-order linear correlation equation to have the form of y=βx+a, then y-a=y^*=βx, where y is the expected value, β is the sensitivity of x to y, and a is a constant or the interception for the regressed line to y-axis. Similarly, if the expected value, y, is correlated to a multiple group of factors, M, then the correlation equation can be expressed as follows (1) (2) set ∅ is the standard loss function, (3) (4) (5) (6) where V is the coefficient matrix and V^T is the transpose matrix of the correlation coefficient. In order to derive an extreme value in the compromised process, the first-order derivative of the standard loss function, Φ, must be zero in Eq. (4)(4) , so that the factor matrix, M, can be obtained by deriving the inverse matrix of (V^T·V), according to [9]. The computational analysis is implemented via the STATISTICA default program.

Five factors of clinical data

Five factor readings were included in the revised inverse problem algorithm, defined as (1) A: age, (2) B: BSA (body surface area), (3) C: MAP (mean artery pressure), (4) D: sugar AC (Sugar Ante Cibum), (5) E: LDL-C (low-density Lipoprotein-Cholesterol) and (6) F: predicted coronary artery stenosis reading, i.e., the expectation value. The respective mathematical expression is as follows: (7)

As follows from Eq. (7)(7) , the algorithm configuration was defined to correlate the predicted coronary artery stenosis reading (F) with the other five factors (A–E), according to either individual factors (a1–a5) or the cross-interactions between two factors (a6–a15), resulting in a total of sixteen terms. The matrix of coefficients, V[15 × 15], can be used to derive the compromised solution according to Eqs. (2–6), whereas the factor terms, M[15 × 1], need to be normalized to the same domain range from approximately −1 to +1, prior to the program execution. This is required for the algorithm configuration to unify the dominating contributions of the dataset.

The factor reading X* after the normalized conversion takes the following form: (8) where X, X_max, and X_min are the original unconverted, maximum, and minimum readings of a specific factor (A-E), respectively. For example, the maximum and minimum readings for BSA equaled 2.40 and 1.39 [m²], respectively; thus, the BSA of cases Nos. 20 and 35 were converted from their original values, (1.53 and 2.17), to normalized ones (-0.572 and 0.586), respectively, according to Eq. (8)(8) . The main goal of the normalization process was to create a unified scale ranging from −1.00 to +1.00, so that every specific BSA reading, as well as the readings of other factors, after normalization would fall within that range.

Table 1 displays the readings of the five factors and actual coronary artery stenosis reading before (original) and after the normalization process [cf. Eq. (8)(8) ] for the 93 coronary heart disease patients with the diagnosis made in the Taichung Armed Forces General Hospital, Taiwan from 2012 to 2014. The survey was approved by the permission No. 2-105-05-007 of the Institutional Review Board (IRB) of the Tri-Service General Hospital. The BSA ( [m²]) [10] was included in the correlation analysis, since human metabolic mechanisms are known to be strongly correlated with BSA. Large BSA and BMI values are interpreted as high fluid and solute turnover rates in human patients [11]. The MAP is defined as the average pressure in the patient arteries during one cardiac cycle, which is considered to be a better indicator of perfusion to vital organs than the systolic blood pressure. The MAP was calculated as (SBP +2•DBP)/3, whereas SBP and DBP implied systolic and diastolic blood pressures, respectively [12]. Nevertheless, age, sugar AC and LDL-C were essential factors in predicting the coronary heart disease, as reported by numerous researchers [1–5]. As shown in Table 1, the readings in each normalized column vary between −1.00 and +1.00 and thereby provide equal contributions to the computational algorithm.

Table 1. The readings of the five factors and actual coronary artery stenosis reading before (original) and after the normalization process [cf. Eq. (8)] for the 93 coronary heart disease patients with the diagnosis made in the Taichung Armed Forces General Hospital, Taiwan from 2012 to 2014. The last column shows the predicted coronary artery stenosis reading.

	Original						Normalized						Predicted
Case	AGE	BSA	Mean Artery	Sugar ac	LDL-C	Stenosis	AGE	BSA	Mean Artery	Sugar ac	LDL-C	Stenosis	Stenosis
No	Years	[m^2]	Pressure mmHg	mg/dL	mg/dl	%	Years	[m^2]	Pressure mmHg	mg/dL	mg/dl	%	%
1	79	1.58	101	181.63	106.03	63	0.571	−0.483	−0.010	−0.252	−0.342	0.033	65
2	72	1.61	101	112.80	93.53	59	0.321	−0.432	−0.003	−0.656	−0.462	−0.083	63
3	74	1.73	109	92.12	64.19	44	0.393	−0.207	0.147	−0.777	−0.745	−0.583	54
4	58	1.80	127	81.89	72.09	55	−0.179	−0.091	0.505	−0.837	−0.669	−0.217	55
5	53	2.11	127	124.59	117.29	76	−0.357	0.472	0.498	−0.587	−0.233	0.467	77
6	71	1.69	120	146.45	68.71	62	0.286	−0.282	0.355	−0.459	−0.702	0.000	58
7	82	1.70	102	112.16	71.90	58	0.679	−0.274	0.010	−0.660	−0.671	−0.133	57
8	66	1.31	136	182.92	95.62	79	0.107	−0.974	0.681	−0.245	−0.442	0.583	67
9	77	1.68	94	99.77	51.24	54	0.500	−0.311	−0.140	−0.732	−0.870	−0.267	51
10	56	1.55	119	104.58	58.24	59	−0.250	−0.536	0.349	−0.704	−0.803	−0.083	53
11	78	1.89	99	147.03	124.67	86	0.536	0.072	−0.055	−0.455	−0.162	0.817	77
12	70	1.80	124	192.55	146.14	92	0.250	−0.079	0.440	−0.188	0.046	1.000	90
13	55	1.98	115	326.64	49.50	58	−0.286	0.242	0.264	0.598	−0.887	−0.117	54
14	77	1.43	90	91.77	115.93	70	0.500	−0.755	−0.231	−0.779	−0.246	0.283	68
15	77	1.68	112	122.67	141.03	89	0.500	−0.300	0.199	−0.598	−0.004	0.917	80
16	40	1.82	103	106.95	61.56	61	−0.821	−0.048	0.023	−0.690	−0.771	−0.027	52
17	36	2.01	108	384.78	192.55	89	−0.964	0.295	0.121	0.939	0.493	0.917	92
18	82	1.85	90	96.56	117.53	75	0.679	0.000	−0.225	−0.751	−0.231	0.450	73
19	67	2.01	90	94.57	123.49	77	0.143	0.295	−0.225	−0.763	−0.173	0.517	76
20	70	1.53	99	84.87	108.12	65	0.250	−0.572	−0.049	−0.820	−0.321	0.100	67
21	74	1.53	95	98.56	223.18	87	0.393	−0.581	−0.121	−0.740	0.789	0.833	95
22	65	1.78	101	114.25	120.73	65	0.071	−0.127	−0.016	−0.648	−0.200	0.117	72
23	42	1.56	87	106.99	134.65	74	−0.750	−0.519	−0.283	−0.690	−0.065	0.400	68
24	70	1.71	96	288.90	61.09	52	0.250	−0.246	−0.114	0.377	−0.775	−0.327	47
25	65	1.90	120	213.39	79.18	63	0.071	0.102	0.368	−0.066	−0.601	0.050	65
26	76	1.62	107	98.70	144.05	88	0.464	−0.423	0.107	−0.739	0.025	0.883	79
27	71	1.60	96	93.44	191.81	88	0.286	−0.445	−0.107	−0.770	0.486	0.867	90
28	82	1.62	111	146.78	82.51	50	0.679	−0.407	0.179	−0.457	−0.569	−0.400	62
29	85	1.67	101	102.58	100.15	73	0.786	−0.318	−0.003	−0.716	−0.398	0.383	66
30	59	1.58	142	93.64	133.07	78	−0.143	−0.491	0.785	−0.768	−0.081	0.550	77
31	54	1.84	101	95.74	120.60	75	−0.321	−0.008	−0.010	−0.756	−0.201	0.450	72
32	49	2.06	135	90.62	93.59	57	−0.500	0.381	0.661	−0.786	−0.462	−0.150	63
33	50	1.64	105	200.37	51.03	43	−0.464	−0.373	0.075	−0.142	−0.872	−0.617	46
34	82	1.97	72	125.27	95.67	55	0.679	0.231	−0.583	−0.583	−0.442	−0.217	64
35	57	2.17	86	88.04	114.57	79	−0.214	0.586	−0.303	−0.801	−0.259	0.583	73
36	55	1.91	104	104.80	103.93	76	−0.286	0.112	0.042	−0.703	−0.362	0.483	67
37	60	1.47	145	131.45	131.64	85	−0.107	−0.687	0.857	−0.547	−0.094	0.783	78
38	76	1.61	123	102.27	114.08	68	0.464	−0.438	0.427	−0.718	−0.264	0.217	71
39	76	1.71	120	152.22	142.03	79	0.464	−0.246	0.355	−0.425	0.006	0.583	84
40	72	1.70	102	298.45	186.52	88	0.321	−0.270	0.016	0.433	0.435	0.883	89
41	91	1.58	103	181.43	92.69	57	1.000	−0.481	0.036	−0.253	−0.470	−0.150	65
42	77	1.39	131	217.57	68.64	53	0.500	−0.831	0.583	−0.041	−0.703	−0.283	63
43	55	1.75	96	90.66	146.35	78	−0.286	−0.173	−0.114	−0.786	0.048	0.550	79
44	55	1.80	112	183.83	39.52	46	−0.286	−0.086	0.205	−0.239	−0.984	−0.533	45
45	81	1.69	88	135.46	81.22	63	0.643	−0.295	−0.264	−0.523	−0.581	0.053	58
46	86	1.50	101	77.01	97.37	63	0.821	−0.641	−0.003	−0.866	−0.425	0.050	65
47	52	2.04	98	275.21	80.99	60	−0.393	0.345	−0.068	0.297	−0.583	−0.047	56
48	62	1.76	120	177.54	76.11	63	−0.036	−0.162	0.362	−0.276	−0.630	0.033	60
49	76	1.69	95	102.17	165.61	76	0.464	−0.295	−0.127	−0.718	0.233	0.483	85
50	57	1.72	86	97.16	176.79	81	−0.214	−0.227	−0.296	−0.748	0.341	0.650	85
51	41	2.01	102	138.19	82.66	56	−0.786	0.306	0.016	−0.507	−0.567	−0.183	58
52	82	1.44	84	115.58	64.79	65	0.679	−0.747	−0.342	−0.640	−0.740	0.117	55
53	70	1.93	102	100.19	99.26	56	0.250	0.145	0.016	−0.730	−0.407	−0.183	66
54	71	1.99	115	102.18	108.78	76	0.286	0.263	0.257	−0.718	−0.315	0.467	71
55	64	1.73	75	101.18	98.77	65	0.036	−0.217	−0.511	−0.724	−0.412	0.117	63
56	68	1.62	115	134.55	140.63	77	0.179	−0.419	0.257	−0.528	−0.008	0.517	78
57	77	1.40	81	172.84	133.23	72	0.500	−0.818	−0.394	−0.304	−0.079	0.350	61
58	61	1.77	110	141.58	83.86	56	−0.071	−0.150	0.173	−0.487	−0.556	−0.183	60
59	65	1.75	117	128.04	144.03	81	0.071	−0.183	0.303	−0.567	0.025	0.650	82
60	68	1.53	96	87.44	118.15	71	0.179	−0.582	−0.114	−0.805	−0.225	0.317	69
61	61	1.78	123	143.91	73.85	51	−0.071	−0.124	0.420	−0.474	−0.652	−0.350	59
62	67	1.65	113	175.14	177.77	83	0.143	−0.365	0.231	−0.290	0.351	0.717	89
63	81	1.77	101	213.85	94.49	67	0.643	−0.150	−0.003	−0.063	−0.453	0.167	66
64	35	2.40	97	143.11	68.85	60	−1.000	1.000	−0.081	−0.478	−0.701	−0.050	53
65	80	1.65	114	101.36	112.07	76	0.607	−0.351	0.251	−0.723	−0.283	0.483	71
66	69	1.49	116	151.61	105.41	74	0.214	−0.660	0.283	−0.428	−0.348	0.417	66
67	58	1.70	105	92.76	134.04	78	−0.179	−0.265	0.062	−0.774	−0.071	0.550	75
68	66	1.61	108	124.83	132.31	73	0.107	−0.429	0.127	−0.585	−0.088	0.383	74
69	71	1.99	115	102.18	108.78	66	0.286	0.263	0.257	−0.718	−0.315	0.133	71
70	68	1.62	115	134.55	140.63	77	0.179	−0.419	0.257	−0.528	−0.008	0.517	78
71	57	2.17	86	88.04	94.57	59	−0.214	0.586	−0.303	−0.801	−0.452	−0.083	65
72	66	1.50	144	54.16	103.04	54	0.107	−0.632	0.831	−1.000	−0.370	−0.267	65
73	85	1.30	110	159.15	82.16	58	0.786	−1.000	0.173	−0.384	−0.572	−0.117	61
74	59	1.72	91	98.05	121.01	74	−0.143	−0.241	−0.212	−0.743	−0.197	0.417	70
75	51	1.99	101	114.81	138.71	75	−0.429	0.260	−0.003	−0.644	−0.026	0.450	80
76	78	1.73	50	110.42	137.80	70	0.536	−0.213	−1.000	−0.670	−0.035	0.283	71
77	44	1.83	99	159.52	37.82	32	−0.679	−0.036	−0.055	−0.382	−1.000	−1.000	42
78	64	1.75	69	149.09	42.16	35	0.036	−0.174	−0.642	−0.443	−0.958	−0.883	43
79	80	1.90	108	72.37	82.91	66	0.607	0.100	0.121	−0.893	−0.565	0.150	59
80	81	1.48	93	101.24	82.77	62	0.643	−0.673	−0.166	−0.724	−0.566	0.000	60
81	76	1.78	108	125.4	122.79	77	0.464	−0.125	0.121	−0.582	−0.180	0.500	75
82	53	1.75	153	108.98	118.53	78	−0.357	−0.183	1.000	−0.678	−0.221	0.533	75
83	38	1.63	69	124.35	96.07	52	−0.893	−0.391	−0.629	−0.588	−0.438	−0.317	56
84	48	1.84	56	88.52	138.34	77	−0.536	−0.010	−0.883	−0.798	−0.030	0.517	74
85	55	1.58	135	109.02	158.68	81	−0.286	−0.491	0.655	−0.678	0.167	0.633	84
86	80	1.62	69	101.31	93.51	52	0.607	−0.417	−0.635	−0.723	−0.463	−0.317	62
87	55	1.83	129	95.17	106.40	77	−0.286	−0.024	0.531	−0.759	−0.338	0.500	69
88	65	1.86	81	395.13	245.03	90	0.071	0.026	−0.394	1.000	1.000	0.933	88
89	84	1.72	101	91.1	100.80	72	0.750	−0.226	−0.003	−0.783	−0.392	0.350	67
90	76	1.89	97	126.45	123.03	78	0.464	0.072	−0.094	−0.576	−0.178	0.550	75
91	83	1.91	106	104.68	110.25	83	0.714	0.110	0.094	−0.704	−0.301	0.700	72
92	57	2.04	105	122.13	109.01	74	−0.214	0.345	0.068	−0.601	−0.313	0.417	71
93	45	1.89	120	152.17	57.49	43	−0.643	0.086	0.355	−0.425	−0.810	−0.617	51

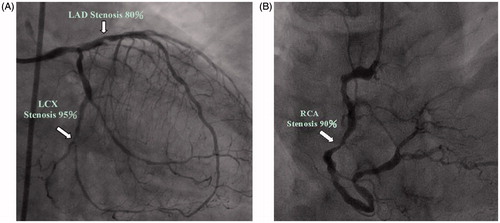
Figure 1 depicts a typical sample of coronary heart disease patient (case no. 17 in Table 1) who got the cardiac diagnosis in the Cardiac Catheterization Laboratory. The three major arteries are: the right coronary artery (RCA) and two major branches of the left coronary artery, i.e., the left anterior descending artery (LAD) and left circumflex artery (LCA). The coronary artery stenosis reading is defined as the sum of 30% of LAD, 30% of LCA, and 40% of RCA. Thus, the reading is 89% (0.3 × (80%+95%) + 0.4 × 90% = 89%), which corresponds to the converted value of 0.917 after normalization by the computational algorithm.

Figure 1. A typical sample of coronary heart disease patient (case no. 17 in Table 1) who got the cardiac diagnosis in the Cardiac Catheterization Laboratory. The three major arteries are: the right coronary artery (RCA) and two major branches of the left coronary artery, i.e., the left anterior descending artery (LAD) and left circumflex artery (LCA).

STATISTICA program

In this study, the revised inverse problem algorithm was implemented via the STATISTICA program [8]. The correlations of the factors [cf. Eq. (7)(7) ] were determined and defined as nonlinear models, nonlinear estimations, and user-specified regressions with customized loss functions, in order to perform the numerical analysis using the normalized data of 93 patients. The actual coronary artery stenosis readings were the expectation values of the computational results. Therefore, 1488 individual data points [(15 + 1) × 93 = 1488] were included in the algorithm, in order to optimize the compromised solution array [93 × 1= 93] of the coronary artery stenosis readings. In addition, sixteen items, including one constant, were used in the algorithm to identify any correlation of the factors. The loss function was defined as the total deviation between the predicted and actual coronary artery stenosis readings for all 93 patients.

Results

Table 2 shows the derived coefficients of all sixteen terms from the STATISTICA computation analysis. The ranks of the normalized coefficients are also listed for reference. The final loss function (Φ) and correlation coefficient (r²) were 3.589 and 0.89191, respectively with the variance of 79.55%. As is seen from Table 2, LDL-C is the most dominant factor, in view of its high-contribution coefficient of 1.17. Prior to input, all factors were normalized to the range [−1.0 to +1.0] via the computational algorithm (cf., Eq. (8)(8) ), so that the derived coefficients could be interpreted as adjustable amplitudes of the respective factors, in order to manipulate the STATISTICA compromised solution. Accordingly, MAP and BSA were the secondary dominant factors, whereas age factor barely contributed to the prediction. The negative coefficient, −0.085, for Sugar AC factor confirmed the well-known medical indication that low Sugar AC can suppress the coronary artery stenosis. The ability of this revised algorithm to analyze not just factors, but their possible cross-interaction as well, has significantly accelerated the convergence of STATISTICA computational analysis and made it possible to reached a high coincidence with r² = 0.89191.

Table 2. The derived coefficients of all sixteen terms from the STATISTICA computation analysis. The ranks of the normalized coefficients are also listed for reference.

			After Normalized
Clinical data	Factor	Coefficient	Value	Rank
Age	A	a1	0.335	8
BSA	B	a2	0.675	4
MAP	C	a3	0.843	3
Sugar ac	D	a4	−0.085	12
LDL-C	E	a5	1.170	1
Age × BSA	A × B	a6	−0.021	15
Age × MAP	A × C	a7	0.014	16
Age × Sugar ac	A × D	a8	0.307	10
Age × LDL-C	A × E	a9	0.144	11
BSA × MAP	B × C	a10	−0.076	13
BSA × Sugar ac	B × D	a11	0.441	7
BSA × LDL-C	B × E	a12	0.639	5
MAP × Sugar ac	C × D	a13	0.878	2
MAP × LDL-C	C × E	a14	0.329	9
Sugar ac × LDL-C	D × E	a15	−0.041	14
Constant		a16	0.560	6

The last column of the Table 1 shows the predicted coronary artery stenosis readings. The data were calculated using the revised inverse problem algorithm [cf. Eqs. 2–6]. The predicted data coincided well with the actual readings [Table 1, column 7] indicating that the algorithm exhibited neither systematic errors in the primary definition, nor any runtime errors during the analyzing process.

Discussion

Clinical verification

The second group of data was obtained from 45 patients with similar symptoms, in order to verify the derived algorithm. The age, BSA, MAP, Sugar AC and LDL-C t-test results indicated the absence of any significant differences between the two groups. The age, BSA, MAP, Sugar AC and LDL-C two tailed p-value were equal to 0.67, 0.99, 0.38, 0.79 and 0.54, respectively. Table 3 displays the data of 45 coronary heart disease patients used for verification. As shown in Table 3, some of the readings, including MAP or LDL-C, become mostly negative after normalization. This can be attributed to the fact that the acquired data are close to the minimum readings of those specific factors in the original group [cf. Table 1]. The predicted coronary artery stenosis readings and their relative discrepancies (%) from the actual ones are listed in the last two columns of Table 3. The average discrepancy between the predicted and actual reading is 10.5 ± 7.9%.

Table 3. The data of 45 coronary heart disease patients used for verification. The predicted coronary artery stenosis reading and its relative discrepancy (%) from the actual reading are listed in the last two columns. The average and standard deviation of the discrepancies between predicted and actual reading is 10.5 ± 7.9%.

	Original						Normalized						Predicted
Case	AGE	BSA	Average Blood Pressure	Sugar ac	LDL-C	Stenosis	AGE	BSA	Average Blood Pressure	Sugar ac	LDL-C	Stenosis	Stenosis	[(A-B)/A] 100%
No	Years	[m^2]	mmHg	mg/dL	mg/dl	%	Years	[m^2]	mmHg	mg/dL	mg/dl	%	%
1	84	1.52	90	92.90	122.20	71	0.750	−0.605	−0.225	−0.773	−0.186	0.317	70	0.72
2	65	1.79	107	120.28	58.87	53	0.071	−0.105	0.107	−0.612	−0.797	−0.283	52	2.14
3	61	1.82	93	208.49	108.52	73	−0.071	−0.041	−0.173	−0.095	−0.318	0.383	63	13.87
4	54	1.97	99	236.85	121.76	73	−0.321	0.222	−0.042	0.072	−0.190	0.383	71	2.47
5	64	1.61	95	119.68	93.49	50	0.036	−0.434	−0.127	−0.616	−0.463	−0.383	61	−22.56
6	60	1.47	91	97.13	94.11	56	−0.107	−0.687	−0.205	−0.748	−0.457	−0.183	62	−10.65
7	52	2.07	93	106.55	69.46	52	−0.393	0.413	−0.166	−0.693	−0.695	−0.317	54	−4.16
8	49	2.13	113	125.35	138.88	74	−0.500	0.510	0.231	−0.582	−0.025	0.400	85	−15.48
9	58	1.73	106	102.86	117.33	73	−0.179	−0.217	0.094	−0.714	−0.233	0.367	70	2.95
10	71	1.61	109	121.33	110.52	72	0.286	−0.440	0.147	−0.606	−0.298	0.350	68	5.03
11	71	1.60	107	120.00	51.83	43	0.286	−0.443	0.114	−0.614	−0.865	−0.633	51	−20.71
12	34	1.95	60	158.38	81.30	62	−1.036	0.180	−0.805	−0.389	−0.580	0.017	49	21.68
13	52	1.87	148	115.36	58.12	40	−0.393	0.035	0.915	−0.641	−0.804	−0.733	51	−28.87
14	70	1.59	123	112.51	95.90	69	0.250	−0.469	0.427	−0.658	−0.439	0.233	65	4.54
15	57	1.70	74	87.15	96.84	71	−0.214	−0.261	−0.544	−0.806	−0.430	0.317	64	9.69
16	54	1.84	111	87.98	72.37	50	−0.321	−0.008	0.179	−0.802	−0.667	−0.400	56	−13.00
17	79	1.75	117	88.35	75.94	53	0.571	−0.175	0.296	−0.799	−0.632	−0.283	58	−8.68
18	52	1.92	83	236.20	168.35	78	−0.393	0.126	−0.362	0.068	0.260	0.540	75	2.99
19	68	1.68	100	128.47	65.18	45	0.179	−0.306	−0.036	−0.564	−0.736	−0.550	54	−20.00
20	76	1.75	91	93.63	98.01	53	0.464	−0.170	−0.212	−0.768	−0.419	−0.283	65	−22.81
21	80	1.58	85	88.49	90.57	68	0.607	−0.482	−0.322	−0.799	−0.491	0.217	63	7.66
22	82	1.99	80	139.39	94.96	62	0.679	0.252	−0.420	−0.500	−0.448	0.017	64	−3.22
23	77	1.61	91	227.92	72.23	60	0.500	−0.426	−0.212	0.019	−0.668	−0.067	51	14.22
24	52	1.61	86	257.40	167.05	82	−0.393	−0.440	−0.296	0.192	0.247	0.683	59	27.81
25	79	1.58	101	81.63	106.03	63	0.571	−0.483	−0.010	−0.839	−0.342	0.033	67	−8.00
26	72	1.61	84	112.80	113.53	69	0.321	−0.432	−0.342	−0.656	−0.269	0.250	66	3.86
27	74	1.73	109	92.12	64.19	44	0.393	−0.207	0.147	−0.777	−0.745	−0.583	54	−22.61
28	58	1.80	127	81.89	72.09	48	−0.179	−0.091	0.505	−0.837	−0.669	−0.450	55	−14.69
29	71	1.69	120	146.45	68.71	52	0.286	−0.282	0.355	−0.459	−0.702	−0.333	58	−11.83
30	66	1.31	136	182.92	95.62	79	0.107	−0.974	0.681	−0.245	−0.442	0.583	67	15.11
31	77	1.68	94	99.77	51.24	44	0.500	−0.311	−0.140	−0.732	−0.870	−0.600	51	−16.88
32	70	1.80	124	192.55	146.14	82	0.250	−0.079	0.440	−0.188	0.046	0.667	90	−10.83
33	77	1.68	112	122.67	141.03	79	0.500	−0.300	0.199	−0.598	−0.004	0.583	80	−1.84
34	36	2.01	108	384.78	92.55	69	−0.964	0.295	0.121	0.939	−0.472	0.250	56	18.34
35	82	1.85	90	96.56	117.53	75	0.679	0.000	−0.225	−0.751	−0.231	0.450	73	3.23
36	67	2.01	90	94.57	123.49	77	0.143	0.295	−0.225	−0.763	−0.173	0.517	76	1.70
37	70	1.53	99	84.87	108.12	75	0.250	−0.572	−0.049	−0.820	−0.321	0.433	67	9.78
38	42	1.56	87	106.99	134.65	64	−0.750	−0.519	−0.283	−0.690	−0.065	0.067	68	−6.64
39	57	1.72	109	110.73	135.39	83	−0.214	−0.231	0.147	−0.668	−0.058	0.700	76	8.07
40	76	1.62	107	98.7	144.05	78	0.464	−0.423	0.107	−0.739	0.025	0.550	79	−1.20
41	71	1.60	96	93.44	191.81	88	0.286	−0.445	−0.107	−0.770	0.486	0.867	90	−2.32
42	70	1.80	124	192.55	146.14	92	0.250	−0.079	0.440	−0.188	0.046	1.000	90	1.28
43	77	1.68	112	122.67	141.03	85	0.500	−0.300	0.199	−0.598	−0.004	0.783	80	5.35
44	36	2.01	108	384.78	92.55	69	−0.964	0.295	0.121	0.939	−0.472	0.250	56	18.34
45	82	1.85	90	96.56	117.53	75	0.679	0.000	−0.225	−0.751	−0.231	0.450	73	3.23

Manipulating the dominant factors

The five assigned factors can be expanded into sixteen terms of nonlinear first-order regression equation fit (cf. Eq. (7)(7) ) for predicting the coronary artery stenosis readings and nearly reach the analytical limit in the STATISTICA program. The analytical threshold of computational frame structure was also referred by other researchers [12]. If the same number of coefficient terms is kept, but the “sugar AC” factor is replaced by “smoking” factor (defined as cigarette pack/day × smoking year), the results will be changed yielding the final loss function value Φ = 4.0917 and correlation coefficient r²=0.87571 with the variance of 76.685%. Apparently, the inappropriate factor mining might result in the incorrect prediction. The number of factors used in the revised algorithm can be reduced, in order to simplify the analysis. The five factors are regrouped to three cases as: (1) four factors, such as age, BSA, MAP, and LDL-C to form the eleven-terms’ correlated equation, (2) three factors, such as BSA, MAP, and LDL-C to form the seven-terms’ equation, and (3) two factors, MAP and LDL-C, to form the four-terms’ equation. The above three equations are reduced to (9) (10) (11)

In contrast, the final loss function value (Φ), correlation coefficient (r²), and variance are depicted via four factors as: 4.3493, 0.86728, 75.218%; three factors: 4.5834, 0.85954, 73.881%; and two factors: 4.7434, 0.85424, 72.973%, respectively. Minimizing the number of adopted factors deteriorates the prediction accuracy and increases the loss function, which should ideally approach zero in the computational analysis [cf. Eqs. (3(3) ,4(4) )]. Figure 2 illustrates the four plots linking the actual and predicted coronary artery stenosis readings for the original and verification groups, according to different numbers of factors and expanded terms. The regression lines of the actual and predicted coronary artery stenosis readings of five factors and sixteen terms imply a high degree of agreement, which is specified by the derived correlation coefficient r². A perfect straight line corresponds to r² =1.00 whereas that obtained in this study is also quite high (r² = 0.876). A linear dependence between the predicted and actual readings can be represented by the predicted-to-actual reading ratio and interpreted by the linear regression fit, as is shown in Figure 2. A perfect linearity has the ratio of 1.0 implying a perfect fit between the actual and predicted readings. In this study, this ratio was reduced from 0.7956 to 0.7522, 0.7387, and 0.7297, when the number of influencing factors was reduced from 5 to 4, 3, and 2, respectively. Therefore, five factors with sixteen terms of a nonlinear first-order equation provide a compromised option satisfying either the maximal analytical ability of the preset STATISTICA program or a highly accurate prediction of the coronary artery stenosis readings.

Figure 2. The four plots linking the actual and predicted coronary artery stenosis readings for the original and verification groups, according to different numbers of factors and expanded terms.

Conclusion

Prediction of coronary artery stenosis readings on the basis of clinical data of coronary heart diseases patients was performed using the revised inverse problem algorithm, and the respective nonlinear first-order regression fit was conducted. Five factors, such as age, BSA, MAP, Sugar AC, and LDL-C, were assigned to derive correlation between the actual and predicted coronary artery stenosis readings with sixteen terms/coefficients. The dataset was constructed for the original 93 coronary heart disease patients and then verified by another group of 45 patients with similar syndromes. The final loss function value (Φ) and correlation coefficient (r²) value were 3.589 and 0.892, respectively with the variance of 79.55%. This can be interpreted as an excellent fit between the actual and predicted readings. The algorithm proved to be an effective technique for prediction of the potential diagnosis in the medical field.

Acknowledgements

The authors would like to thank the Ministry of Science and Technology, contract No. 103-2221-E-166-003-MY3 and the Taichung Armed Forces General Hospital, Contract No. 103A06 for financially supporting this research.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The authors would like to thank the Ministry of Science and Technology, contract No. 103-2221-E-166-003-MY3 and the Taichung Armed Forces General Hospital, Contract No. 103A06 for financially supporting this research.