Optimal two-class-based storage in a live-cube compact storage system

ABSTRACT

Live-cube compact storage systems realize high storage space utilization and high throughput, due to full automation and independent movements of unit loads in three-dimensional space. Applying an optimal two-class-based storage policy where high-turnover products are stored at locations closer to the Input/Output point significantly reduces the response time. Live-cube systems are used in various sectors, such as warehouses and distribution centers, parking systems, and container yards. The system stores unit loads, such as pallets, cars, or containers, multi-deep at multiple levels of storage grids. Each unit load is located on its own shuttle. Shuttles move unit loads at each level in the x and y directions, with a lift taking care of the movement in the z-direction. Movement of a requested unit load to the lift location is comparable to solving a Sam Loyd's puzzle game where 15 numbered tiles move in a 4 × 4 grid. However, with multiple empty locations, a virtual aisle can be created to shorten the retrieval time for a requested unit load. In this article, we optimize the dimensions and zone boundary of a two-class live-cube compact storage system leading to a minimum response time. We propose a mixed-integer nonlinear model that consists of 36 sub-cases, each representing a specific configuration and first zone boundary. Properties of the optimal system are used to simplify the model without losing any optimality. The overall optimal solutions are then obtained by solving the remaining sub-cases. Although the solution procedure is tedious, we eventually obtain two sets of closed-form expressions for the optimal system dimensions and first zone boundary for any desired system size. In addition, we propose an algorithm to obtain the optimal first zone boundary for situations where the optimal system dimensions cannot be achieved. To test the effectiveness of optimal system dimensions and first zone boundary on the performance of a two-class-based live-cube system, we perform a sensitivity analysis by varying the ABC curve, system size, first zone size, and shape factor. The results show that for most cases an optimal two-class-based storage outperforms random storage, with up to 45% shorter expected retrieval time.

KEYWORDS:

• Logistics
• material handling
• live-cube compact storage system
• optimal two-class-based storage

1. Introduction

Warehouses form vital nodes in any supply chain, decoupling supply from demand. Unfortunately, land for warehouses has become increasingly scarce in many parts of Europe, Asia, and the United States, particularly in areas with major customer concentrations. Traditional storage systems, not only low-bay warehouses but also Automated Storage and Retrieval (AS/R) systems, occupy a considerable amount of space, as they require transport aisles between any two racks. These aisles may consume about 35% of all storage space and contribute to high building costs (Gue, 2006). Shortage of land has driven many companies to search for more compact storage systems.

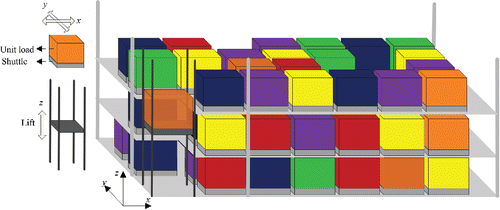
To solve this shortage of land problem, so-called live-cube compact storage systems have recently been introduced. A growing number of implementations can be found in automated parking systems, warehousing and cross-docking, container handling, and pharmacy automation (see, for example, Automotion Parking Systems (2013), Eweco (2013), EZ-Indus (2013), Hyundai Elevator (2013), OTDH (2013), Swisslog (2013), and Wöhr (2013)). The main components of a live-cube compact storage system are multiple levels of storage grids, shuttles, a lift, and an Input/Output (I/O)-point. These shuttles can move in the x and y directions. Each unit load is stored on its own shuttle and holds only one product type. The shuttles move unit loads into the empty locations to maneuver the desired unit load to the lift location at the same storage level. A lift takes care of movements across different levels in the z-direction. We assume that the I/O point is located at the lower-left corner of the system. The lift waits at the I/O point when idle. Figure 1 shows^{Figure 2}a live-cube compact storage system.

Figure 1. A live-cube compact storage system with a lift.

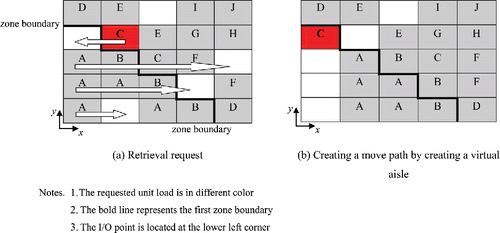
In storage systems, retrieval requests are often more critical than storage jobs, as they are directly linked to customer orders (Bartholdi and Hackman, 2014). In live-cube storage systems, the interfering unit loads on the move path of a requested unit load can slow down the retrieval process. In practice, however, utilizations of not more than 90% are common in systems containing 1000 unit loads or more. This implies that there are sufficient empty locations at each level to create a virtual aisle for any desired unit load. By creating a virtual aisle, the requested unit load can freely move to the lift location without interfering with other unit loads. A sufficient condition to create such a virtual aisle is that the number of empty locations on a level equals at least the maximum of the number of rows and the number of columns (Zaerpour et al., 2017). Figure 2 represents the top view of a five by five, single-level live-cube system. The I/O point is located at the lower-left corner. Figure 2(a) shows a situation where a unit load needs to be moved out of a live-cube system. In this case, a virtual aisle can be created by simultaneously moving some interfering unit loads (Fig. 2(b)). The desired unit load can then be moved to the I/O point without any interference. Thus, the retrieval time of any load at location (x, y), T(x, y) can then be approximated by x + y (i.e., T(x, y) = x + y), where x and y are the travel times to the I/O point in the x and y directions, respectively. For a multi-level live-cube system, the retrieval time of any load at location (x, y, z) can be approximated by max{x + y, z} + z (i.e., T(x, y, z) = max{x + y, z} + z), where z is the travel time of the lift to level z.

Figure 2. A virtual aisle in a live-cube system.

A virtual aisle can significantly reduce the response time of a live-cube system compared with (for instance) a system with one empty location (in the case where only one empty location is available Gue and Kim (2007) show that T(x, y) = 4x + 2y − 8 (if x > y)).

Although random storage has been widely used in practice, it has been shown that two-class-based storage can significantly reduce the response time of a storage system (Hausman et al., 1976; Eynan and Rosenblatt, 1994; Kouvelis and Papanicolaou, 1995; Ruben and Jacobs, 1999; Park, 2006; Yu and de Koster, 2009). Two-class-based storage can simply be implemented in practice by classifying unit loads into high-turnover and low-turnover classes. The high-turnover unit loads are assigned to the first zone containing a set of locations closer to the I/O point. Designing a two-class-based live-cube system with optimal first zone boundary and optimal system dimensions can further reduce the system's response time (Hausman et al., 1976; Yu and de Koster, 2009). In addition, questions on the effectiveness of an optimal first zone boundary and optimal system dimensions for varying skewness of the ABC curve, system size, first zone size, and shape factor need to answered. For instance, how does the skewness of the ABC curve impact the performance of a two-class-based live-cube system with optimal first zone boundary and optimal dimensions? How does the size of a live-cube system influence the performance of an optimal two-class-based live-cube system? Can an existing live-cube system (i.e., with given dimensions) still benefit by optimizing its first zone boundary?

In this article, we study a live-cube compact storage system where virtual aisles can be created for any requested load. We optimize the system dimensions and the first zone boundary of a two-class system minimizing the response time. Our contributions are as follows:

1.	We obtain the optimal boundaries of a two-class live-cube system leading to minimum response times.
2.	We extend our model to obtain the optimal first zone boundary of a two-class-based live-cube system with given dimensions and for a live-cube system under building dimension constraints.
3.	We investigate the impact of varying skewness of the ABC curve, system size, first zone size, and shape factor on the performance of an optimal two-class-based live-cube system.
4.	We consider situations where constraints are imposed on system dimension and propose the steps to optimize the first zone boundary.

To optimize the boundaries, we propose a mixed-integer nonlinear model. The objective is to minimize the expected retrieval time of an arbitrary unit load. To derive a closed-form formula for the objective function, the system needs to be decomposed in 36 complementary sub-cases based on the system configuration and first zone boundary. Each sub-case corresponds to a different objective function (Zaerpour et al., 2012). This results in a mathematical model with many constraints and also nonlinearity in both objective function and constraints. In addition, the annual demand of inventoried unit loads (i.e., the skewness of the ABC curve) affects the optimal solution. Although the model is complex, it can still be solved optimally. We first show that some sub-cases do not include the optimal solution. This reduces the solution space without losing any optimality. The remaining sub-cases can then be solved individually to obtain the optimal solution of the model. Eventually, two sets of closed-form solutions for the optimal dimensions and first zone boundary can be obtained for any desired ABC curve. The results show that an optimal two-class live-cube system can reduce the response time up to 45% compared with a random storage policy. Moreover, for a system with given dimensions, we propose a simple algorithm to obtain the optimal first zone boundary leading to a minimum response time. We also investigate the effectiveness of optimal system dimensions and first zone boundary on the performance of a two-class live-cube system using a sensitivity analysis.

Optimizing zone boundaries for class-based storage in traditional automated two-dimensional (2D) storage systems (e.g., AS/R systems) has been extensively studied in the literature. Hausman et al. (1976) derive a travel time formula for a 2D AS/R system with class-based storage, which has been used by many researchers (Park and Webster, 1989; Rosenblatt and Eynan, 1989; Eynan and Rosenblatt, 1994; Kouvelis and Papanicolaou, 1995; van den Berg, 1996; Thonemann and Brandeau, 1998; Ruben and Jacobs, 1999; Park, 2006). Researchers have used different methods to obtain the optimal zone boundaries for class-based storage policies. Hausman et al. (1976) use a grid search method to minimize the S/R one-way travel time in a Square-In-Time (SIT) 2D system. Rosenblatt and Eynan (1989) propose a solution method to determine the optimal boundaries for any desired number of zones in a 2D system. They show that a relatively small number of zones can lead to similar savings as full-turnover storage. Eynan and Rosenblatt (1994) determine the optimal zone boundaries for a Non-Square-In-Time (NSIT) system. Park (2006) determines optimal zone boundaries for a 2D SIT system numerically. He also determines the mean and variance of the travel times for AS/R systems for the two-class NSIT case. Recently, Yu et al. (2015) determined optimal zone boundaries and showed that an optimal (small) number of zones exist, if space requirements are taken into account.

Stadtler (1996), Sari et al. (2005), Gue and Kim (2007), De Koster et al. (2008), Yu and de Koster (2009), and Zaerpour et al. (2015b) study compact storage systems using different depth handling systems. Stadtler (1996) and Zaerpour et al. (2015b) study unit-load storage assignment in a satellite-based compact storage system. Sari et al. (2005) study unit-load storage assignment and De Koster et al. (2008) study the optimal design of a conveyor-based compact storage system. Yu and de Koster (2009) study optimal two-class-based storage in a conveyor-based compact storage system. They formulate a mixed-integer nonlinear model and develop a decomposition algorithm and one-dimensional search to solve the model, leading to optimal zone boundaries. Gue and Kim (2007) study a single-level live-cube storage system, which they call a puzzle-based storage system, at an operational decision level. For systems with a single and multiple empty locations, they develop a method to maneuver unit loads to the I/O point yielding short retrieval times. Zaerpour et al. (2017) study a multi-level live-cube compact storage system considering a random storage policy at a design decision level. They decompose the live-cube system into four complementary sub-cases based on system dimensions and propose a mixed-integer nonlinear mathematical model for determining the optimal system dimensions by minimizing the expected retrieval time. Zaerpour et al. (2012) study the performance of a two-class live-cube compact storage system. They derive closed-form formulas of the expected retrieval time of a live-cube system with any configuration and zone boundary. The formulas, obtained based on a continuous space assumption, appear to evaluate the performance of the discrete systems with a high precision. This article builds on that work.

In two-class-based storage, it is necessary to obtain the optimal dimensions of the system, as well as the optimal first zone boundary. Adding the first zone boundary variable increases the complexity of the problem significantly, leading to 36 sub-cases that have to be distinguished (compared with four sub-cases in the random storage problem studied in Zaerpour et al. (2017)). However, solving such a complex problem is still worthwhile, as up to a 45% reduction in response time can be achieved by using optimal two-class storage instead of optimal random storage.

The remainder of this article is organized as follows. Section 2 proposes the mathematical models and obtains the optimal zone boundaries for a live-cube system. Section 3 extends the proposed model in two directions. Section 4 discusses the results of our sensitivity analysis based on a real case. Section 5 concludes the article and proposes avenues for future research.

2. General model and optimization

In this section, we propose the mathematical models for a multi-level live-cube system under a two-class-based storage policy. The closed-form travel time formulas, each corresponding to a specific configuration (36 sub-cases in total), are obtained from Zaerpour et al. (2012). These formulas are used in the objective function of the model. The main notations are as follows:

Objective:

E[T]	The expected retrieval time of a two-class-based live-cube system
E[Tji]	The expected travel time of an arbitrary load in zone j (j = 1, 2) for sub-case I ( i ∈ {A1, …, P3})

Decision variables:

l	System length in time (i.e., shuttle travel time from/to the I/O point to/from the farthest location in the x-direction in an empty lane, l > 0)
w	System width or depth in time (i.e., shuttle travel time from/to the I/O point to/from the farthest location in the y-direction in an empty lane, w > 0)
h	System height in time (i.e., lift travel time from/to the I/O point to/from the farthest level in the z-direction, h > 0)
b	First zone boundary in time (b ≥ 0)
yi	yi = 1, if sub-case i ( i ∈ {A1, …, P3}) is considered, otherwise, yi = 0

Parameters:

s	Skewness of the ABC curve, 0 < s ≤ 1
V	System volume in cubic time, V > 0

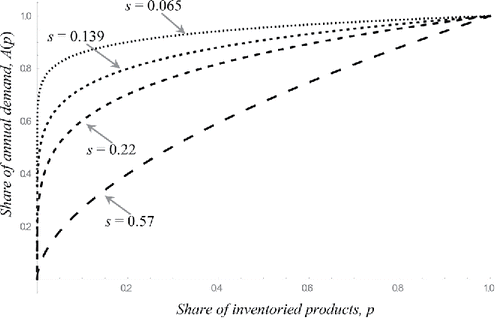
We assume a continuous space. This assumption is commonly used in the literature (see, for example, Hausman et al. (1976), Bozer and White (1984), Rosenblatt and Eynan (1989), and Yu and de Koster (2009)) and leads to an accurate approximation if the number of loads per level and the number of levels is sufficiently large. For the sake of convenience, and without loss of generality, we suppose that the length of the system is not less than the width of the system; i.e., l ⩾ w (see also Bozer and White (1984), Eynan and Rosenblatt (1994), and Yu and de Koster (2009)). The system volume (V) is constant. E[T^j_i] represents the expected travel time of zone j (j = 1, 2) and sub-case i ( i ∈ {A1, …, P3}). The conditions of all 36 sub-cases (A1, …, P3) are illustrated in Appendix A. The ABC curve function is represented by A(p) = p^s (0 < s ≤ 1) where p is the fraction of inventoried products, which are ranked in descending order based on their annual demand. A smaller skewness parameter (s) means a more skewed curve (Hausman et al., 1976). For instance, s = 0.065 represents the ABC curve 20–90%, in which 20% of highest turnover products denote the 90% of annual demand. Figure 3 illustrates some instances of different ABC curves. Section 2.1 gives the mathematical model for a two-class-based live-cube system and solves it optimally.

Figure 3. Instances of ABC curves with different values for the skewness parameter.

2.1. Optimization of a two-class-based live-cube system

To optimize the boundaries of a two-class-based storage system in a multi-level system, a Model MLS (multi-level system) can be built:

Model MLS (1) subject to: (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (111) (112) (113) (114) (115) (116) (117) (118) (119) (120) (121) (122) (123) (124) (125) (126) (127) (128) (129) (130) (131) (132) (133) (134) (135) (136) (137) (138) (139) (140) (141) (142) (143) (144) (145) (146) (147) (148) (149) (150)

Decision variables: b ≥ 0, l > 0, w > 0, h > 0 and y_i ∈ {0, 1} for i ∈ {A1, …, P3}, where V_i is a function that gives the volume of the first zone of sub-case i (i ∈ {A1, …, P3}) retrieved from Zaerpour et al. (2012) and V is the given volume of the system. G₁ represents the size of the first zone divided by the size of the system. y_i = 1 if sub-case i is considered; otherwise, y_i = 0. Equation (1(1) ) minimizes the expected retrieval time, E[T]. In Equation (1(1) ), if case i is considered (i.e., y_i = 1), G^{2s/(s + 1)}₁E[T_i¹] and (1 − G^{2s/(s + 1)}₁)E[T_i²] represent the weighted expected retrieval times of the first and second zones, respectively (Yu and de Koster, 2009; Zaerpour et al., 2012). Constraint (2(2) ) makes sure that the given system size is achieved. Constraint (3(3) ) ensures that the length of the system is at least equal to the width of the system. As the sub-cases are complementary, Constraint (4(4) ) makes sure that only one sub-case is considered. Constraint (5(5) ) relates any value of boundary b to its corresponding value of G₁ (G₁ is the relative size of the first zone). Constraints (6(6) ) to (150(150) ) are used to distinguish 36 different sub-cases. For example, the conditions of sub-case A1 are b ≤ 2h, b ≤ w, and h ≤ w. Therefore, Constraints (6(6) ) to (8(8) ) make sure that if sub-case A1 is considered these conditions are met. In order to obtain the optimal solutions of Model MLS we first give the following theorems.

Lemma 1.

In a given system, if there are two candidate shapes of the system that have the same zone volume and height, the system with a shape closer to square at each storage level has the shorter expected retrieval time.

Proof.

See the online supplement 1.

Theorem 1.

The optimal system configuration is square for a two-class live-cube system at every level; i.e., (151)

Proof.

Assuming d = l/w, since ∂E[T]/∂d > 0, ∀d ⩾ 1, the minimum value of expected retrieval time occurs at d = 1 (i.e., l = w).

Corollary 1.

Sub-cases A2, B2, C2, D2, E2, F2, L2, M2, N2, P2 (i.e., with condition w ⩽ h < l) and sub-cases B1, B3, B4, D3, D4, E3, E4, F3, F4, J1, L1, M1 (i.e., with condition w ⩽ b < l) do not include the optimal solution of the Model MLS and their corresponding constraints can be relaxed in the model.

Thus, y*_i = 0 ∀i ∈ {A2, B2, C2, D2, E2, F2, L2, M2, N2, P2, B1, B3, B4, D3, D4, E3, E4, F3, F4, J1, L1, M1}.

Proof.

From Theorem 1, l^* = w^* and so the constraints corresponding to the sub-cases that do not meet this condition can be relaxed. ▪

Theorem 2.

Within each case, the sub-case with condition h ⩽ w leads to shorter E[T] compared to sub-cases with conditionsl < h ⩽ l + w and l + w < h.

Proof.

In order to prove this, it suffices to compare the optimal solutions of sub-cases with condition l < h ⩽ l + w and l + w < h with the optimal solution of sub-case with condition h ⩽ w in each case. For the detailed proof see the online supplement 2.

Based on Theorem 2, facility managers are advised to design a two-class-based live-cube system such that the system height (in time units) is at most equal to the system width (in time units).

Corollary 2.

Sub-cases A3, A4, C3, C4, and P3 do not include the optimal solution of the Model MLS and their corresponding constraints can be relaxed in the model.

Therefore, y*_i = 0  ∀i ∈ {A3, A4, C3, C4, P3}.

Proof.

From Theorem 2, constraints representing sub-cases with conditions l < h ⩽ l + w and l + w < h can be relaxed as they do not include the overall optimal solution. ▪

Theorem 3.

Sub-case C3 compared with sub-case G3and sub-case C4 compared with sub-cases G4 and H4 lead to shorter E[T].

Proof.

See the online supplement 3.

Corollary 3.

Sub-cases G3, G4, and H4 do not include the optimal solution of the Model MLS and their corresponding constraints can be relaxed in the model.

Therefore, y*_i = 0, ∀i ∈ {G3, G4, H4}.

Proof.

From Theorem 3, constraints corresponding to the cases G3, G4, and H4 can be relaxed as they do not include the overall optimal solution. ▪

Thus, the total 36 sub-cases can be reduced to six sub-cases (see Fig. 4). Based on Theorem 1, since l* = w*, these six sub-cases are simplified by replacing w with l. The conditions of each sub-case can be derived from the shape of the first zone (e.g., see sub-case A1 in Fig. 4).

Figure 4. Sub-cases to be optimized individually. R₁ represents the first zone closer to I/O point and R₂ represents the second zone.

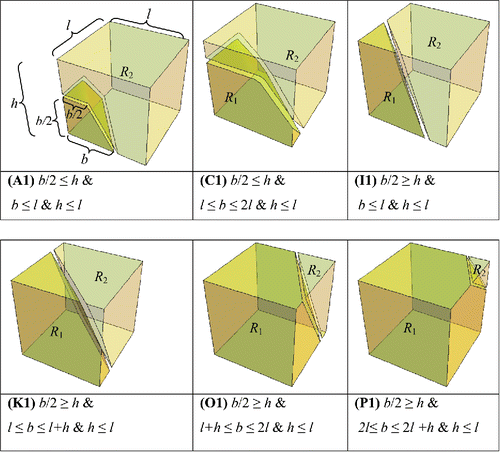
In order to solve Model MLS, we first solve each of the six remaining sub-cases individually and obtain the optimal solution in each sub-case. Next, by comparing the optimal solutions obtained from the six sub-cases the overall optimal solution of Model MLS can be found. To simplify the calculations, the volume of the system is normalized to one (V = 1).

2.2. Optimizing the dimensions in each of the six sub-cases individually

The optimization process is explained for sub-cases A1 and C1. For the rest we refer to the online supplement 4.

Sub-case A1. b/2 ≤ h & b ≤ l & h ≤ l

The objective function in this case is (obtained from Zaerpour et al. (2012)) (152)

Based on Theorem 1, in an optimal solution, w^* = l^*. In addition, the volume of the system is normalized to one and so hl² = 1. Moreover, based on the volume formula of the shape of the first zone in sub-case A1, G₁ = 7b³/48. Therefore, the objective function can be simplified to a function of two-variables (b, l), shown in Equation (153(153) ): (153)

In order to obtain the optimal value of length of the system (l^*), we solve the following equation: (154)

Although E[T_A1] is a function of two variables l and b, solving Equation (154(154) ) leads to a single optimal value for l. Comparing the one critical point obtained by solving Equation (154(154) ) with any other feasible point shows that the critical point is an absolute minimum. The following equation gives the optimal values of l and w: (155)

Consequently, from hl² = 1, we obtain the optimal value of h, which satisfies the condition 0 < h ≤ l: (156)

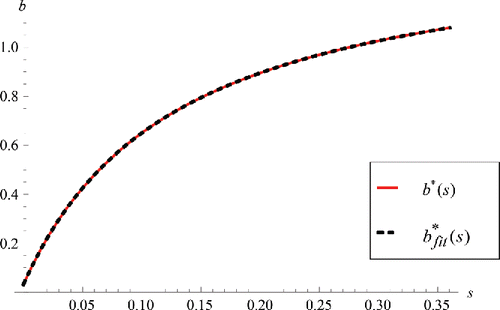
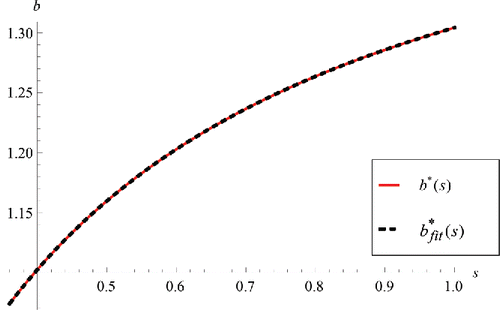
In order to obtain the optimal boundary, b^*, the following equation should be solved for l^* and any given s: (157) b^* can be obtained analytically for any given value of s. Since b^* is the only critical point, comparing the value of the objective function at b^* with any other feasible solution proves that b^* is the absolute minimum. However, a closed-form formula for the optimal boundary (b^*(s)) cannot be obtained analytically. To solve this problem, we obtain the optimal boundary as a function of s by fitting the function b*_fit(s) = a ArcTan[c s + d] + e to optimal values of boundary b for 1000 different values of s. The fit function minimizes the sum of squared residuals. Equation (158(158) ) gives the closed-form formula of the optimal boundary as a function of s: (158)

It appears that b is an increasing function of s, while according to the condition of sub-case A1, b ≤ l. Therefore, s is bounded: s ⩽ s′ (s′ is the maximum value for s where the condition b ≤ l of sub-case A1 can still be met). s′ can be obtained by solving the following equation: (159)

Figure 5 shows the plotted optimal values of b for 1000 different s values (b*(s)) and the corresponding fitted function (b*_fit(s)) for s ≤ s′.

Figure 5. Fitted function b*_fit(s) versus optimal values b^*(s) for s ≤ s′ in sub-case A1.

For s > s′, optimizing the dimensions in sub-case A1 is explained in online supplement 5. However, it turns out that the overall optimal solution of Model MLS for s > s′ is obtained from sub-case C1.

Sub-case C1. b/2 ≤ h & l ≤ b ≤ 2l & h ≤ l

The objective function in this case is (160)

From Theorem 1 we know that in an optimal solution, w^* = l^*. In addition, the volume of the system is normalized to one and so hl² = 1. Moreover, based on the volume formula of the shape of the first zone in this sub-case, we have

Therefore, the objective function can be simplified to a function of two variables (b, l), shown in Equation (161(161) ): (161)

In order to obtain the optimal value of length of the system (l^*), we solve the following equation: (162)

Although Equation (162(162) ) is a function of two variables l and b, solving dE[T_C1]/dl = 0 leads to the optimal length l^* given by Equation (155(155) ). Consequently, the optimal value of height h^* can be obtained by using Equation (156(156) ). The optimal dimensions satisfy the condition of sub-case C1 that is 0 < h ≤ l. The analysis of sub-cases A1 and C1 show that the optimal dimensions of a two-class-based live-cube system are the same for both sub-cases. In addition, results show that the optimal system dimensions are independent of the ABC curve considered (i.e., skewness parameter s).

In order to obtain the optimal boundary b, the following equation should be solved for l^* and any given s: (163)

It^{Table 1Figure 7}appears, for s ≤ s′, that the overall optimal solution of Model MLS is obtained from sub-case A1. Therefore, it suffices to consider the solution of sub-case C1 for s > s′.

For s > s′, solving Equation (163(163) ) leads to b^*. Since b^* is the only critical point, comparing the objective value at b^* with any other feasible solution shows that b^* is the absolute minimum. However, a closed-form formula for the optimal boundary (b^*(s)) cannot be obtained analytically. Thus, we obtain the optimal boundary as a function of s by fitting the function b*_fit(s) = a ArcTan[c s + d] + e to optimal values of boundary b for 1000 different s. Equation (164(164) ) gives the optimal boundary for any given skewness parameter, s > s′: (164)

Figure 6 shows the plotted optimal values of b for 1000 different s values (b*(s)) and the corresponding fitted function (b*_fit(s)) for s > s′.

Figure 6. Fitted function b*_fit(s) versus optimal values b^*(s) for s > s′ in sub-case C1.

The optimal solutions of the remaining four sub-cases can be obtained similarly (see Appendix B for the optimal solution of each sub-case). By comparing the optimal solutions of the six sub-cases, it turns out that sub-cases A1 and C1 include the overall optimal solution.

Table 1 gives the optimal solution of Model MLS (l^*, w^*, h^*, b^*, in time units) for different values of s and system volume V (in cubic time). Table 1 shows that the skewness of the ABC curve has no impact on the optimal dimensions of a two-class-based live-cube system. This makes the system very robust to changes in demand patterns of products. The system can optimally be used for different customer demand ABC curves. However, the optimal zone boundary is affected by the skewness of the ABC curve leading to different zone shapes and zone sizes.

Table 1. The optimal dimensions and zone boundary (in time units) for any s and V.

Subcase	Skewness parameter (s)	Optimal length (l^*), width (w^*), and height (h^*)	Estimated optimal boundary () b*fit(s) = (a ArcTan[c s + d] + e)V^1/3
A1. b/2 ≤ h & b ≤ l & h ≤ l	s ≤ 0.354 907
C1. b/2 ≤ h & l ≤ b ≤ 2l & h ≤ l	s > 0.354 907

By using the formulas from Table 1 and for some selected skewness parameters s and for a normalized system volume (V = 1), we obtain the optimal dimensions of the system (l^*, w^*, h^*), the optimal first zone boundary (b^*), the optimal relative size of the first zone (0% < G₁* ⩽ 100%), and the optimal expected retrieval time (). Table 2 presents the results.

Table 2. The optimal solutions for some selected skewness parameters (ABC curve).

s	ABC curve	Sub-case	l^*(= w^*) (s)	h^* (s)	b^* (s)	G1^*(%)	(s)
0.065	20–90%	A1	1.069 37	0.874 46	0.517	2.0	0.830
0.139	20–80%	A1	1.069 37	0.874 46	0.773	6.7	1.072
0.22	20–70%	A1	1.069 37	0.874 46	0.925	11.6	1.206
0.32	20–60%	A1	1.069 37	0.874 46	1.040	16.4	1.304
0.43	20–50%	C1	1.069 37	0.874 46	1.122	20.6	1.374
0.57	20–40%	C1	1.069 37	0.874 46	1.191	24.6	1.433
0.75	20–30%	C1	1.069 37	0.874 46	1.251	28.3	1.485
1	20–20%	/	1.069 37	0.874 46	/	/	1.531

“/”: for b^* is any value between 0 and 3.0132 (max{l^* + w^*, h^*} + h^*); “/” for G₁^* is any value between 0% and 100%.

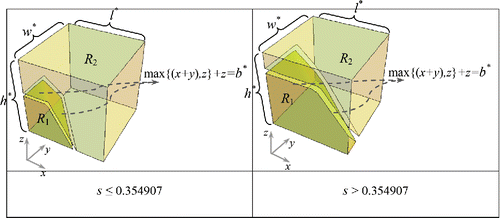
In addition, Figure 7 illustrates the optimal dimensions (in time units) and the surface representing the optimal first zone boundary (in time units) for different values of skewness parameter s. As Figure 7 shows, the optimal shape of the first and second zones differs for s ≤ 0.354 907 and s > 0.354 907. All locations (x, y, z) that satisfy the condition max{(x + y), z} + z = b^* form the surface representing the optimal first zone boundary.

Figure 7. Optimal dimensions and first zone boundary in time units for different values of s.

3. Extensions where constraints are imposed on system dimensions

The optimal dimensions of a live-cube system obtained in Section 2 can be realized in a greenfield project. In a brownfield project, however, constraints such as building dimensions exist. In this section, we extend our problem in two directions. First, we consider a situation where a new live-cube system of a desired size needs to be installed in a warehouse with fixed building dimensions. The system dimensions and zone boundary that minimize the expected retrieval time can still be obtained (Section 3.1). Second, we consider an existing live-cube system with fixed dimensions. The expected retrieval time of such a system can still be minimized by optimizing the boundary of the first zone (Section 3.2).

Illustrative example: To further explain the steps in this section, we use an illustrative example. A live-cube parking system needs to be designed given the following constraints:

Constraint 1:	The length of the system should be at least four times larger than the width (in meters).
Constraint 2:	The system height should be nine tiers.

Table 3 gives the input parameters.

Table 3. Parameters describing storage system and storage policy derived from Hyundai Elevator (2013).

Fixed parameters	Data
Dimensions of a standard vehicle (mm)	Height = 1550, length = 5160, width = 2100^*
Dimensions of a location (mm)	Height = 2945, length = 6400, width = 3200
Shuttle speed in the x-direction (vx) (m/min)	100
Shuttle speed in the y-direction (vy) (m/min)	50
Lift speed (vz) (m/min)	90
Varying parameters	Base example data	Range for scenarios
Dimensions of system (s) ^**	Height = 15.70, length = 19.20, width = 19.20
Dimensions of system (m)	Height = 26.50, length = 38.40, width = 19.20
ABC curve (percentage)	20–80%	[20–20%, 20–90%]
First zone size (percentage of system size)	6.70%^***	[20%, 100%]
System size (no. of slots)^****	324	[96, 8748]
Length/width (no. of tiers)	1	[0.25, 4]

^* Length and width denote the size in the x- and y-directions, respectively.

^** Optimal dimensions of the system for the given system size.

^*** Optimal first zone size for the base example.

^**** Size of the system including empty slots = Length × Width × Height = 6 × 6 × 9 = 324 (in number of tiers).

3.1. Designing a new live-cube system within an existing warehouse building

A live-cube system can be installed in an existing warehouse. In this case, the building dimensions might prevent the realization of the live-cube system with optimal dimensions. The system dimensions and the first zone boundary that minimize the expected retrieval time can still be obtained using the following steps:

Step 1.	Calculate the optimal system dimensions using Table 1.
Step 2.	Transform the optimal system dimensions from time units to distance units (e.g., from seconds to meters).
Step 3.	Identify the number of system dimensions that are constrained by the building dimensions. • If the number of constrained system dimensions equals zero, building constraints are not limiting and the optimal live-cube system can be realized. • If the number of constrained system dimensions is one or more, these constraints can be used to obtain the feasible sub-cases within 36 sub-cases. We then follow a similar optimization process as that in Section 2. Note: Based on Lemma 1, determine the dimensions such that the system length and width at each level are closest to SIT. The optimal first zone boundary can be found by following the steps in Section 3.2.

Steps for the illustrative example:

Step 1:	The optimal dimensions of the systems and optimal first zone boundary can be obtained using Table 1 (h* = 15.70 s, l* = 19.20 s, w* = 19.20 s, b* = 13.86 s).
Step 2:	Based on the speed of the shuttles and lift, the optimal system dimensions in time units (s) can be transformed to the distance unit (m) (H* = 26.50 m, L* = 38.40 m, W* = 19.20 m).
Step 3:	The optimal system height satisfies Constraint (2(2) ) as at least nine tiers can be achieved (# height tiers = H*/location height = 26.50/2.945 = 9). However, the optimal length and width violate Constraint (!) (L*/W* = 38.4/19.20 = 2≱4). Thus, according to Lemma 1, the system dimensions that minimize the expected retrieval time, achieve the desired system size (324 locations), and satisfy Constraints (1) and (2) equal h* = 15.70 s, l* = 30.72 s, w* = 11.52 s. The optimal first zone boundary can be found using the steps in Section 3.2.

3.2. Optimizing the first zone boundary of an existing live-cube system

The response time of an existing live-cube system with a fixed configuration can still be minimized by optimizing the first zone boundary. In this section, we propose an algorithm to find the optimal first zone boundary for a live-cube system with fixed system dimensions.

Step 1.	Using Appendix C find a set of sub-cases whose conditions can be met given the system dimensions.
Step 2.	For each sub-case, replace the values of l, w, h, and s in the corresponding closed-form formula of E[T(l, w, h, b)] yielding a one-variable objective function (E[T(b)]). For instance, if sub-case A1 is considered, replace the values of l, w, h, and s in the corresponding closed-form formula of E[TA1].
Step 3.	For each sub-case, solve d E[T]/d b = 0. Among all sub-cases where the obtained b satisfies the condition of the sub-case, the one with the minimum E[T] gives the optimal boundary (b*). Note: For a new live-cube system (discussed in Section 3.1), use the building dimension constraints to simplify E[T(l, w, h, b)] to E[T(l, b)]) and follow the same procedure as explained above.

Steps for the illustrative example:

With the system dimensions obtained in Section 3.1(h^* = 15.70 s, l^* = 30.72 s, w^* = 11.52 s), we follow the next steps to obtain the optimal first zone boundary.

Step 1:	Using Appendix C (Table A3) and given the system dimensions, these conditions are satisfied (w ⩽ h ⩽ l, l + w ⩾ 2h, 2w ⩽ l ⩽ 2h). Thus, the following sub-cases need to be considered: A2 (b ≤ w), B2 (w ≤ b ≤ 2w), D2 (2w ≤ b ≤ l), E2 (l ≤ b ≤ 2h), M2 (2h ≤ b ≤ l + w), N2 (l + w ≤ b ≤ l + h), P2 (l + h ≤ b ≤ l + w + h).
Step 2:	For each sub-case (e.g., A2), replace the values of l*, w*, h*, and s (s = 0.139 for 20–80% ABC curve) in the corresponding closed-form formula of E[T] (e.g., E[TA2]).
Step 3:	For each sub-case, solve d E[T]/d b = 0. The results for the expected retrieval time (E[T]) and the first zone boundary (b) of each sub-case are as follows: A2 (E[T] = 20.40, b = 11.52), B2 (20.14, 14.59), D2 (21.50, 23.04), E2 (24.20, 30.72), M2 (24.48, 31.40), N2 (27.81, 42.24), P2 (28.70, 46.42). Among all sub-cases, sub-case B2 results in minimum E[T] (E[T] = 20.14) and so b* = 14.59.

4. The effectiveness of the optimal dimensions and zone boundary

In this section, we present numerical results to investigate the effectiveness of optimal dimensions and optimal first zone boundary. For different ABC curves, system size, first zone size, and shape factor, the results of an optimal two-class-based storage policy are compared with the results of an optimal random storage policy and a “cuboid” two-class-based storage policy of the same dimensions and first zone size (a cuboid two-class-based storage policy is a straightforward, practical implementation of a two-class policy with a rectangular-cube-shaped first zone). In a cuboid two-class-based live-cube system, the first zone dimension ratios are equal to the system dimension ratios; i.e., l₁/w₁ = l/w, l₁/h₁ = l/h. The results for optimal random storage and cuboid two-class storage are obtained from Zaerpour et al. (2017) and Zaerpour et al. (2012), respectively. In addition, for each instance, we evaluate the accuracy of the closed-form formulas obtained based on a continuous system assumption by using a real discrete live-cube system. For the discrete system in each instance, we calculate the expected retrieval time by considering the probability of requesting each product, the probability of retrieving the requested product from each storage location, and the travel distance from each storage location to the I/O point.

For the base example, we consider a medium-sized live-cube system with optimal system dimensions and optimal first zone size and with a moderate ABC curve as described in Table 3. First, we present the results for the base example. Then, we perform a sensitivity analysis to investigate the effect of optimizing system dimensions and first zone size on the performance of a two-class-based live-cube system for different sources of variation in the input parameters. In each instance, we vary one of the parameters of the base example while the other parameters are fixed.

Table 4 shows the results for the base case. In succeeding tables, we vary the ABC curve (Table 5), system size (Table 6), first zone size (Table 7), and shape factor of the system in number of tiers (Table 8). In Table 6, for all instances the system dimensions and the first zone size are optimal. To make a fair comparison in Table 8, when varying the shape factor, the system height and system size are fixed and the optimal first zone boundary is obtained using Section 3.

Table 4. The optimal expected retrieval time for the base case.

ABC curve	Sub-case	Optimal first zone size (%)	Optimal boundary (b) (s)	E[TO] (s) ^*	E[TD] (s)	GapD (%)^**	E[TC] (s)	GapC (%)	E[TR] (s)	GapR (%)
20–80%	A1	6.70	13.86	19.22	18.55	3.51	19.61	2.03	27.48	30.05

^* E[T_x] is the expected retrieval time for method x (in seconds), where x = O (Optimal two-class-based), D (Discrete live-cube system), C (two-class-based system with Cuboid first zone), R (a system with Random storage).

^** Gap_x=((|E[T_x] − E[T_O]|)/E[T_O]) × 100%, represents the gap between the expected retrieval time of the optimal two-class-based live-cube system and the expected retrieval time of method x. For Gap_C, the first zone size and system dimensions of the cuboid two-class-based system are the same as the optimal two-class-based live-cube system.

Table 5. Results of sensitivity analysis when varying skewness parameter.

ABC curve	Sub-case	Optimal boundary (b) (s)	Optimal first zone size (%)	E[TO] (s)	E[TD] (s)	GapD (%)	E[TC] (s)	GapC (%)	E[TR] (s)	GapR (%)
20–90%	A1	9.33	2.0	14.94	14.25	4.62	15.52	3.88	27.48	45.63
20–70%	A1	16.65	11.6	21.68	21.05	2.92	22.01	1.52	27.48	21.11
20–50%	C1	20.14	20.6	24.67	24.47	0.80	24.92	1.01	27.48	10.23
20–30%	C1	22.44	28.3	26.64	26.78	0.53	26.75	0.41	27.48	3.06
20–20%	/	/	/	27.48	27.34	0.51	27.48	0.00	27.48	0.00

“/” means any sub-case, any value for b or any first zone size.

Table 6. Results of sensitivity analysis when varying system size.^*

System size (No. of slots)^**	Relative size change to base case (%)	Sub-case	Optimal boundary (b) (s)	Optimal first zone size (%)	E[TO] (s)	GapO (%)^***	E[TD] (s)	GapD (%)	E[TC] (s)	GapC (%)	E[TR] (s)	GapR (%)
96 (4 × 4 × 6)^****	−70.37^*****	A1	9.24	6.70	12.81	−33.35	12.19	4.84	13.07	2.03	18.31	30.05
768 (8 × 8 × 12)	137.04	A1	18.48	6.70	25.63	33.35	24.97	2.57	26.15	2.03	36.64	30.05
1500 (10 × 10 × 15)	362.96	A1	23.11	6.70	32.05	66.73	32.72	2.10	32.70	2.03	45.81	30.05
2592 (12 × 12 × 18)	700.00	A1	27.73	6.70	38.45	100.05	39.18	1.90	39.23	2.03	54.97	30.05
8748 (18 × 18 × 27)	2600.00	A1	41.59	6.70	57.68	200.10	58.62	1.63	58.85	2.03	82.46	30.05

^* For each instance, the dimensions and first zone boundary are optimal.

^** Including empty slots.

^*** Gap_O=((E[T_O] − E[T_base case])/E[T_base case]) × 100%, represents the gap between E[T] of base case (19.22 s) and E[T] of each instance.

^**** Length × Width × Height in number of tiers.

^***** ((96–324)/324) × 100%.

Table 7. Results of sensitivity analysis when varying the first zone size.

First zone size (%)	Sub-case	Boundary (b) (s)	E[T1st zone] (s)	Gap1st zone (%)^*	E[TD] (s)	GapD (%)	E[TC] (s)	GapC (%)	E[TR] (s)	GapR (%)
20	C1	19.94	20.04	4.09	19.20	4.19	20.70	3.29	27.48	27.07
40	C1	25.41	21.76	11.67	21.09	3.08	22.86	5.06	27.48	20.82
60	C1	29.83	23.48	18.14	22.86	2.62	24.44	4.09	27.48	14.56
80	O1	34.98	25.22	23.79	25.14	0.32	26.03	3.21	27.48	8.22
100	/	/	27.48	30.06	27.41	0.25	27.48	0.00	27.48	0.00

^* Gap_1st zone = ((E[T_1st zone] − E[T_base case])/E[T_base case]) × 100%, represents the gap between E[T] of base case (19.22 s) and E[T] of each instance.

Table 8. Results of sensitivity analysis when varying the shape factor (length/width in number of tiers).^*

Shape factor (L/W)	Sub-case	Optimal boundary (b) (s)	Optimal first zone size (%)	E[TO] (s)	E[TD] (s)	GapD (%)	E[TC] (s)	GapC (%)	E[TR] (s)	GapR (%)
4.00 (12/3)	D2	15.69	9.38	21.98	21.14	3.82	23.99	9.14	33.27	33.93
2.25 (9/4)	B2	14.59	8.07	20.14	19.45	3.43	21.05	4.52	29.42	31.54
1.00 (6/6)	A1	13.86	6.70	19.22	18.55	3.51	19.61	2.03	27.48	30.05
0.44 (4/9)	B2	14.59	8.07	20.14	19.45	3.43	21.05	4.52	29.42	31.54
0.25 (3/12)	D2	15.69	9.38	21.98	21.14	3.82	23.99	9.14	33.27	33.93

^* The system size (in number of slots) and height (in number of tiers) are fixed for all instances.

The results in Tables 4 to 8 show that an optimal two-class-based storage can significantly reduce the expected retrieval time of a live-cube system compared with optimal random storage (up to 45%). This reduction is less significant compared with a cuboid two-class-based storage (up to 10%). Note that an optimal two-class-based storage policy, as an alternative to other storage policies (e.g., optimal random storage), needs no system configuration adjustment. It only suffices to re-program the software that controls the live-cube system such that the system is virtually divided into two zones (first and second zones) by the locations with travel time b to the I/O point. Depending on the turnover of the products, the system will then assign an incoming load to either first or second zone. In addition, we make the following observations:

Observation 1 (varying skewness of the ABC curve): By increasing the skewness of the ABC curve (i.e., decreasing s), the gaps between the optimal two-class-based storage and the optimal random and cuboid two-class-based storage increase (see Gap_R and Gap_C in Table 5). For instance, for the 20–70% curve, Gap_R = 21.11%, whereas for the 20–30% curve, Gap_R = 3.06%. This is expected, as for an increasing skewness parameter, the beneficial effect of class-based storage disappears. The results are consistent with ones from Zaerpour et al. (2012). The results show that a skewed ABC curve (20–90%) reduces the expected retrieval time up to 45% compared with random storage for both optimal and non-optimal two-class-based system. However, this saving decreases more rapidly by decreasing the skewness of the ABC curve (i.e., increasing s) for an optimal two-class-based live-cube system. In addition, a skewed ABC curve (e.g., 20–90%) can result in a larger time saving for a non-optimal two-class-based live-cube system. Furthermore, with increasing skewness parameter, the optimal first zone boundary and the optimal first zone size increase. However, the optimal dimensions do not change for different ABC curves. This makes it possible to optimally use different ABC curves without any need for system configuration correction. The optimal solution for the random storage policy is a special case of optimal two-class-based storage where ABC curve is 20–20%.

Observation 2 (varying system size): By increasing the system size, the gaps between the optimal two-class-based storage and the optimal random and cuboid two-class-based storage do not change (for all instances in Table 6, Gap_R = 30.05% and Gap_C = 2.03%). This is because for each instance in Table 6, the system dimensions and first zone boundary are optimal (Zaerpour et al. (2012) do not discuss such an insight, as they do not consider optimal two-class-based live-cube system). Thus, facility managers can equally benefit for large- and small-sized systems by implementing an optimal two-class-based storage. A more-skewed ABC curve and a larger shape factor might increase these gaps further (see Observations 3 and 4). In addition, as the system size grows, the expected retrieval time of an optimal two-class-based system increases less rapidly (see Relative size change to base case (%) and Gap_O in Table 6). For instance, for the case where the system size grows by 2600% compared with the base case, the expected retrieval time only increases by 200% (Gap_O = 200%). Thus, facility managers can largely benefit from system size expansion without a significant sacrifice of system performance.

Observation 3 (varying first zone size): By increasing the first zone size, the gap between the expected retrieval time of the optimal two-class-based storage of the base case and two-class-based storage with the given first zone size increases (see Gap_{1st zone} in Table 7). This is because as the first zone size increases, the closest locations to the I/O point will more likely be occupied by low-turnover products. In addition, by increasing the first zone size, the gap between the optimal two-class-based storage and optimal random storage decreases as two-class-based storage gradually converts to random storage (see Gap_R in Table 7). Furthermore, as the first zone size increases, unlike Gap_R, the gap between the optimal two-class-based storage and cuboid two-class-based storage first increases and then decreases (see Gap_C in Table 7). This is because for a very small first zone size, optimizing the shape of the first zone is unimportant, as few locations will be affected. By increasing the first zone size further, larger reductions in retrieval time can be achieved by optimizing the first zone shape. When the first zone size becomes larger, both storage policies (two-class-based and cuboid two-class-based) gradually transform into random storage. The same pattern can be observed in Zaerpour et al. (2012), although the savings in their case are larger. In conclusion, facility managers are advised to optimize the size of the first zone of a two-class-based live-cube system that has given dimensions, in order to further improve the performance of their systems. In addition, facility managers are advised to implement the optimal two-class-based storage instead of random storage and cuboid two-class-based storage as further improvements can always be achieved with no additional investment.

Observation 4 (varying shape factor): Table 8 shows that as the length and width of a live-cube system (in number of tiers) differ more from each other (i.e., from L/W = 1 to 4 or 0.25), optimal two-class-based storage becomes more favorable compared with optimal random storage and cuboid two-class-based storage (this is consistent with Zaerpour et al. (2012)). This is because the drastic situations where frequently demanded products are assigned to far locations to the I/O point can be avoided. Therefore, in situations where constraints are imposed on system dimensions, facility managers are encouraged to optimize the system's first zone size and shape compared with no-constraint situations. Section 3 explains the procedure to optimize live-cube system dimensions and the first zone boundary in situations where there exist building constraints on system dimensions.

Observation 5 (accuracy of continuous approximation): Tables 4 to 8 show that the results obtained by using a continuous approximation are very close to those for real discrete systems, even in extreme cases such as a small system size, a very steep ABC curve, and a small first zone size (for all instances, Gap_D < 5% in Tables 4 to 8). In addition, by decreasing the skewness of the ABC curve, the gap between the results of the continuous approximation and the real discrete system decreases (see Gap_D in Table 5). By increasing the system size, Gap_D decreases as the relative system size to storage location size increases (see Gap_D in Table 6). Furthermore, by increasing the first zone size, the gap between the results of the continuous approximation and the real discrete system decreases (see Gap_D in Table 7).

5. Conclusions

We study a two-class live-cube compact storage system. We propose a mixed-integer nonlinear mathematical model to optimize the first zone boundary and system dimensions minimizing the response time. Due to the complexity of the model, we use some properties of the optimal solution to simplify the mathematical model. The optimal dimensions of a live-cube system and the optimal first zone boundary can be obtained analytically for any ABC curve. In addition, we optimize the system dimensions and first zone boundary in warehouses with fixed building dimensions. We also minimize the response time of a two-class-based live-cube system with fixed dimensions by optimizing the first zone boundary. The results show that in a live-cube compact storage system, an optimal two-class-based storage policy can significantly reduce the response time, compared with a random storage policy. For example, for a 20–90% ABC curve, a 45% reduction in response time can be obtained. Moreover, the optimal dimensions of a two-class-based live-cube system do not depend on the skewness of the ABC curve. Therefore, if the demand pattern changes, no system configuration modification is needed. Furthermore, the results of our sensitivity analysis show that by increasing the skewness of the ABC curve and system shape factor, the two-class-based storage policy becomes more favorable compared with random storage and cuboid two-class-based storage. However, varying the system size does not appear to have any impact on the performance of two-class-based storage. Thus, facility managers can equally benefit from an optimal two-class-based storage policy for both small- and large-sized systems. The results of the sensitivity analysis also show that the continuous space assumption can approximate real discrete systems with a high accuracy.

Several research questions regarding the live-cube compact storage system remain open. It is possible to extend a two-class-based storage to an n-class-based storage policy. However, due to the shuttle and lift operation of the system, analysis of an n-class-based system appears to be extremely difficult. It is also interesting to study the impact of optimally sequencing a group of retrievals on the makespan in a two-class live-cube system. We know from AS/RS literature that savings of 20–70% can be achieved compared with first-come first-served sequencing (Han et al., 1987; Yu and de Koster, 2012). As shuttles can simultaneously move unit loads on different levels to the lift, improvements might even be larger for live-cube compact storage systems. Although we have studied two-class-based storage in live-cube compact storage systems with lifts, results for other live-cube compact storage systems with different vertical movement mechanisms may also prove worthwhile to investigate.

Funding

This research is supported by the National Science Foundation of China (NSFC) with grant numbers 71520107002 and 71225002.

Additional information

Notes on contributors

Nima Zaerpour

Nima Zaerpour is an Assistant Professor of Operations and Supply Chain Management at the College of Business Administration, California State University San Marcos, California. He received his Ph.D. in operations management from Rotterdam School of Management, Erasmus University, The Netherlands in 2013. Prior to joining California State University, he was an Assistant Professor at VU University Amsterdam. In 2012, he was a visiting scholar at the School of Industrial and Systems Engineering at Georgia Tech. In 2011, he was a visiting scholar at the School of Management, University of Science and Technology of China. His research has been published in several journals including Production and Operations Management, Transportation Science, IIE Transactions, and International Journal of Production Research. His research interests are facility logistics management, distribution logistics management, supply chain management, and terminal operations management, in particular studying recent innovations in these areas. He serves as a reviewer for journals such as Operations Research, Production and Operations Management, Transportation Science, IIE Transactions, Interfaces, IJPE, IJPR, Omega, and OR Spectrum. He has developed warehousing decision support software and has served as consultant for supply chain and logistics companies.

Yugang Yu

Yugang Yu is a Professor of Logistics and Operations Management at the University of Science and Technology of China, PR China (USTC). He obtained his Ph.D. in Management Science and Engineering from the School of Management, USTC, in 2003. His current research interests are in warehousing, supply chain management and data-driven research in operations managment, and application of operations research. He has published more than 60 papers in academic journals, including Productions and Operations Management, Transportation Science, IIE Transactions, International Journal of Production Research, European Journal of Operational Research, Annals of Operations Research, IEEE Transactions on Automation Science and Engineering, and International Journal of Production Economics. His papers have been cited more than 1500 times, and he is one of the most cited researchers in China. His research results have also been patented several times in China. He received a career development project from the Netherlands Organization for Scientific Research, a distinguished research scholar grant from the National Science Foundation of China, and Yangtze Scholar Distinguished Professorship from China Ministry of Education.

René B.M. de Koster

René B. M. de Koster is a Professor of Logistics and Operations Management at Rotterdam School of Management, Erasmus University. His research interests are warehousing, terminal, and behavioral operations. He is an author/editor of eight books and over 150 papers in books and journals. He is guest lecturer at universities in Belgium, China, and South Africa. He is/was in the editorial boards of Operations Research, Journal of Operations Management, Transportation Science (SI editor), and other journals. He is a member of several international research advisory boards (including the European Logistics Association and BVL www.bvl.de). He is chairman of Stichting Logistica and founder of the Material Handling Forum (www.rsm.nl/mhf). His research has received several awards (IIE Transactions 2009, 2016; Journal of Operations Management finalist 2007; Academy of Management best paper finalist 2013).

Appendices

Appendix A. Conditions of 36 sub-cases: {A1, …,P3}

The conditions of 36 sub-cases are given in Table A1. Sixteen different cases (A, …,P) need to be distinguished corresponding to different shapes of the first and second zones illustrated in Zaerpour et al. (2012). However, it is still necessary to decompose each case into at most four sub-cases based on system configurations: configuration 1: h ⩽ w, configuration 2: w ⩽ h ⩽ l, configuration 3: l ⩽ h ⩽ l + w, and configuration 4: l + w ⩽ h. Thus, 36 sub-cases can be obtained in total, each corresponding to a specific closed-form formula for E[T]. Table A1 gives all 36 sub-cases. For instance, for the sub-case A1, the conditions of the case A (b/2 ≤ h and b ≤ w) and the configuration 1 (h ⩽ w) should be considered.

Table A1. The 36 sub-cases, each corresponding to a specific E[T] formula.

	Configuration
Case	1(h ⩽ w)	2 (w ⩽ h ⩽ l)	3 (l ⩽ h ⩽ l + w)	4 (l + w ⩽ h)
A (b/2 ≤ h and b ≤ w)	A1	A2	A3	A4
B (b/2 ≤ h and w ≤ b ≤ 2w and b ≤ 1)	B1	B2	B3	B4
C (b/2 ≤ h and l ≤ b ≤ 2w)	C1	C2	C3	C4
D (b/2 ≤ h 2 and w ≤ b ≤ l)	—	D2	D3	D4
E (b/2 ≤ h 2 and w ≤ b and l ≤ b ≤ l + w)	—	E2	E3	E4
F (b/2 ≤ h and l + w ≤ b ≤ 2l)	—	F2	F3	F4
G (b/2 ≤ h 2 and l ≤ b ≤ 2(l + w))	—	—	G3	G4
H (b/2 ≤ h 2 and (l + w) ≤ b ≤ 2h)	—	—	—	H4
I (b/2 ≥ h and b ≤ w)	I1	—	—	—
J (b/2 ≥ h and w ≤ b ≤ w + h and b ≤ l)	J1	—	—	—
K (b/2 ≥ h and l ≤ b ≤ w + h)	K1	—	—	—
L (b/2 ≥ h and w + h ≤ b ≤ l)	L1	L2	—	—
M (b/2 ≥ h and w + h≤ b and l ≤ b ≤ min{l + w,  l + h})	M1	M2	—	—
N (b/2 ≥ h and l + w ≤ b ≤ l + h)	—	N2	—	—
O (b/2 ≥ h and l + h ≤ b ≤ l + w)	O1	—	—	—
P (b/2 ≥ h and max{l + h,  l + w}≤ b≤ + w + h)	P1	P2	P3	—

Appendix B. Optimal solutions of four sub-cases I1, K1, O1, P1

The optimal solutions of the four sub-cases I1, K1, O1, and P1 are given in Table A2.

Table A2. Optimal solutions of sub-cases I1, K1, O1, P1.

Subcases (conditions)	s	Optimal length (l^*)	Optimal boundary (b^*)
I1. b/2 ≥ h and b ≤ l and h ≤ l	s > 0.275732	(0.5(67 986.3 ArcTan[663 825.0s + 50 017.7] − 106 791.0))^− 1/2	67 986.3 ArcTan[663 825.0s + 50 017.7] − 106 791.0
	s ≤ 0.275732	1.259 92	1.259 92
K1.1. 2h ≤ b ≤ l + h and h ≤ l	s > 0.275732	(0.5(39 587.7 ArcTan[18 516.9s + 22 176.5] − 62 181.4))^− 1/2	39 587.7 ArcTan[18 516.9s + 22 176.5] − 62 181.4
	s ≤ 0.275732	1.259 92	1.259 92
K1.2. l ≤ b ≤ l + h and h ≤ l	s > 0.663535	1.259 92	1.259 92
	s ≤ 0.663535	1.259 92	19.2377 ArcTan[63.4077s + 19.408] − 28.6456
O1. b/2 ≥ h and l + h ≤ b ≤ 2l and h ≤ l	0 < s ≤ 1	0.833 ArcTan[ − 10.333s − 2.965] + 2.315
P1. 2l ≤ b ≤ 2l + h and h ≤ l	s > 0.278079	1	2
	s ≤ 0.278079	3932.9 ArcTan[32 245.0s + 17 556.2] − 6176.6	2(3932.9 ArcTan[32 245.0s + 17 556.2] − 6176.6)

Appendix C. Set of possible sub-cases for any given system configuration

The set of sub-cases to be considered for any given configuration is given in Table A3.

Table A3. Set of possible sub-cases for any given system configuration: (a) configuration 1; (b) configuration 2; (c) configuration 3; and (d) configuration 4.

Config. 1	Sub-config.	Sub-config.	Boundary	Sub-case	Config. 2	Sub-config.	Sub-config.	Boundary	Sub-case
h ≤ w	w ≤ 2h	l ≤ 2h	b ≤ w	A1	w ≤ h ≤ l	l + w ≥ 2h	l ≤ 2w	b ≤ w	A2
			w ≤ b ≤ l	B1				w ≤ b ≤ l	B2
			l ≤ b ≤ 2h	C1				l ≤ b ≤ 2w	C2
			2h ≤ b ≤ w + h	K1				2w ≤ b ≤ 2h	E2
			w + h ≤ b ≤ l + h	M1				2h ≤ b ≤ l + w	M2
			l + h ≤ b ≤ l + w	O1				l + w ≤ b ≤ l + h	N2
			l + w ≤ b ≤ l + w + h	P1				l + h ≤ b ≤ l + w + h	P2
		2h ≤ l ≤ w + h	b ≤ w	A1			2w ≤ l ≤ 2h	b ≤ w	A2
			w ≤ b ≤ 2h	B1				w ≤ b ≤ 2w	B2
			2h ≤ b ≤ l	J1				2w ≤ b ≤ l	D2
			l ≤ b ≤ w + h	K1				l ≤ b ≤ 2h	E2
			w + h ≤ b ≤ l + h	M1				2h ≤ b ≤ l + w	M2
			l + h ≤ b ≤ l + w	O1				l + w ≤ b ≤ l + h	N2
			l + w ≤ b ≤ l + w + h	P1				l + h ≤ b ≤ l + w + h	P2
		w + h ≤ l	b ≤ w	A1			2h ≤ l	b ≤ w	A2
			w ≤ b ≤ 2h	B1				w ≤ b ≤ 2w	B2
			2h ≤ b ≤ w + h	J1				2w ≤ b ≤ 2h	D2
			w + h ≤ b ≤ l	L1				2h ≤ b ≤ l	L2
			l ≤ b ≤ l + h	M1				l ≤ b ≤ l + w	M2
			l + h ≤ b ≤ l + w	O1				l + w ≤ b ≤ l + h	N2
			l + w ≤ b ≤ l + w + h	P1				l + h ≤ b ≤ l + w + h	P2
	w ≥ 2h	2h ≤ l ≤ w + h	b ≤ 2h	A1		l + w ≤ 2h	l ≤ 2w	b ≤ w	A2
			2h ≤ b ≤ w	I1				w ≤ b ≤ l	B2
			w ≤ b ≤ l	J1				l ≤ b ≤ 2w	C2
			l ≤ b ≤ w + h	K1				2w ≤ b ≤ l + w	E2
			w + h ≤ b ≤ l + h	M1				l + w ≤ b ≤ 2h	F2
			l + h ≤ b ≤ l + w	O1				2h ≤ b ≤ l + h	N2
			l + w ≤ b ≤ l + w + h	P1				l + h ≤ b ≤ l + w + h	P2
		w + h ≤ l	b ≤ 2h	A1			2w ≤ l	b ≤ w	A2
			2h ≤ b ≤ w	I1				w ≤ b ≤ 2w	B2
			w ≤ b ≤ w + h	J1				2w ≤ b ≤ l	D2
			w + h ≤ b ≤ l	L1				l ≤ b ≤ l + w	E2
			l ≤ b ≤ l + h	M1				l + w ≤ b ≤ 2h	F2
			l + h ≤ b ≤ l + w	O1				2h ≤ b ≤ l + h	N2
			1 + w ≤ b ≤ l + w + h	P1				l + h ≤ b ≤ l + w + h	P2
(a)					(b)
Config. 3		Sub-config	Boundary	Sub-case	Config. 4		Sub-config	Boundary	Sub-case
l ≤ h ≤ l + w		l ≤ 2w	b ≤ w	A3	l + w ≤ h		l ≤ 2w	b ≤ w	A4
			w ≤ b ≤ l	B3				w ≤ b ≤ l	B4
			l ≤ b ≤ 2w	C3				l ≤ b ≤ 2w	C4
			2w ≤ b ≤ l + w	E3				2w ≤ b ≤ l + w	E4
			l + w ≤ b ≤ 2l	F3				l + w ≤ b ≤ 2l	F4
			2l ≤ b ≤ 2h	G3				2l ≤ b ≤ 2(l + w)	G4
			2h ≤ b ≤ l + w + h	P3				2(l + w) ≤ b ≤ 2h	H4
		l ≥ 2w	b ≤ w	A3			l ≥ 2w	b ≤ w	A4
			w ≤ b ≤ 2w	B3				w ≤ b ≤ 2w	B4
			2w ≤ b ≤ l	D3				2w ≤ b ≤ l	D4
			l ≤ b ≤ l + w	E3				l ≤ b ≤ l + w	E4
			l + w ≤ b ≤ 2l	F3				l + w ≤ b ≤ 2l	F4
			2l ≤ b ≤ 2h	G3				2l ≤ b ≤ 2(l + w)	G4
			2h ≤ b ≤ l + w + h	P3				2(l + w) ≤ b ≤ 2h	H4
(c)					(d)