Semiparametric fractional imputation using empirical likelihood in survey sampling

ABSTRACT

The empirical likelihood method is a powerful tool for incorporating moment conditions in statistical inference. We propose a novel application of the empirical likelihood for handling item non-response in survey sampling. The proposed method takes the form of fractional imputation but it does not require parametric model assumptions. Instead, only the first moment condition based on a regression model is assumed and the empirical likelihood method is applied to the observed residuals to get the fractional weights. The resulting semiparametric fractional imputation provides -consistent estimates for various parameters. Variance estimation is implemented using a jackknife method. Two limited simulation studies are presented to compare several imputation estimators.

KEYWORDS:

• Item non-response
• missing data
• quantile estimation
• robust estimation

1. Introduction

Missing data are frequently encountered in many areas, such as survey sampling, epidemiology and other fields. Simply ignoring missing values can potentially lead to biased estimation (Kim & Shao, 2013; Little & Rubin, 2002). Two statistical approaches for handling missing data have been used in practice: propensity score weighting and imputation. Propensity score weighting is used mainly to correct for unit non-response, while imputation is mainly used to handle item non-response. Haziza (2009) provides a comprehensive overview of the imputation methods in survey sampling.

Multiple imputation (MI), proposed by Rubin (1987), is a popular approach of imputation for general-purpose estimation due to its practical simplicity. However, the Rubin's variance estimator may be biased under certain situation (Fay, 1992; Kim, Brick, Fuller, & Kalton, 2006; Wang & Robins, 1998; Yang & Kim, 2016) and its validity requires the congeniality condition of Meng (1994), which may not hold for general-purpose estimation.

Fractional imputation (FI), first proposed by Kalton and Kish (1984), provides an alternative method for handling item non-response. Fay (1996), Kim and Fuller (2004), Fuller and Kim (2005), and Durrant and Skinner (2006) discussed fractional hot deck imputation. Kim (2011) and Kim and Yang (2014) discussed a fully parametric approach to FI. The parametric fractional imputation (PFI) provides a powerful tool for handling missing data for various situations. However, it relies on a strong parametric model assumption and making such an assumption is not usually preferred in survey sampling. Balanced random imputation of Chauvet, Deville, and Haziza (2011) is also an attractive imputation technique, but it still requires parametric model assumptions for multipurpose estimation.

The empirical likelihood (EL) method, considered by Owen (2001) and Qin and Lawless (1994), is a useful tool for semiparametric inference in statistics. It involves a likelihood-based inference without making a parametric distributional assumption about the observed data. Qin (1993) addressed the missing survey data problem by using a biased sampling argument of Vardi (1985). Wang and Rao (2002) brought regression-type imputation approaches to EL inference. Wang and Chen (2009) used a nonparametric regression imputation approach to handle missing data in the EL inference. Müller (2009) considered a novel application of EL method to handle missing data under a regression model assumption. In Müller (2009), the moment condition of the error term in the regression model is used to construct a fully imputed estimator.

In this paper, motivated by the fully imputed estimator of Müller (2009), we propose a semiparametric fractional imputation (SFI) method using EL that can be used to handle item non-response in survey sampling. Because the proposed SFI uses only moment conditions in the semiparametric regression model, it is more robust than the PFI method or parametric MI method. By using regression model assumptions, the proposed SFI method is more efficient than the nonparametric regression imputation method of Wang and Chen (2009). The proposed method takes the form of FI, so the actual implementation is very attractive in practice. The proposed SFI method can be used to estimate various parameters, including non-smooth parameters such as population quantiles.

The paper is organised as follows. The basic set-up is introduced and the proposed method is presented in Section 2. The asymptotic properties of the SFI estimators are presented in Section 3. Extensions to non-smooth statistics as well as random imputations are covered in Section 4. In Section 5, variance estimation is discussed. Some numerical results are given in Section 6. Some concluding remarks are made in Section 7.

2. Basic set-up

Consider a finite population where x_i is the vector of auxiliary variables that are always observed and y_i is the study variable that is subject to missingness. We assume (x_i, y_i) are realisations from a regression model (1) where is assumed to be known with unknown parameter and ε satisfies E(ε|X) = 0. No parametric distributional assumption on X is made.

Let δ_i be the response indicator such that δ_i = 1 if y_i is observed and δ_i = 0 otherwise. We assume missing at random (MAR) in the sense that (2) Even though we observe δ_i only in the sample, we can conceptually assume that δ_i's are defined throughout the population. Such extended definition of δ_i has been adopted in Fay (1992), Shao and Steel (1999), and Kim, Navarro, and Fuller (2006).

Given the finite population, suppose that sample A of size n is selected from the finite population by a probability sampling mechanism. Let π_i, i = 1, 2, … , N, be the first-order inclusion probability of unit i in the population. We are interested in estimating η₀, defined as a solution to the estimating equation E{U(η; x, y)} = 0 where U(η; x, y) is a known function with parameter η. To avoid unnecessary details, we assume that the solution to E{U(η; x, y)} = 0 is unique and the dimensions of η and U(η; x, y) are r. Thus, the parameter η is just-identified. Under complete response, a consistent estimator of η₀ is obtained by solving for η. If some of y_i are missing, under the MAR assumption, a consistent estimator of η₀ can be obtained by solving the following expected estimating equation: (3) for η. The conditional expectation in Equation (3(3) ) is with respect to f(y∣x), which is unknown as we only assume Equation (1(1) ).

In FI, our goal is to approximate the conditional expectation in Equation (3(3) ) by the weighted mean of the fractionally imputed estimating functions. That is, we wish to achieve (4) as closely as possible for some (w*_ij, y_i*^(j)) satisfying ∑^m_{j = 1}w_ij* = 1, where w*_ij's are desired fractional weights and y*^(j)_i's are m imputed values for subject i. Kim (2011) and Kim and Yang (2014) developed a FI satisfying Equation (4(4) ) using a parametric model assumption on f(y∣x).

In our proposed method, we use the EL approach to achieve the approximation in Equation (4(4) ). To explain the idea, assume for now that the true parameter in Equation (1(1) ) is known. In this case, are available among δ_i = 1. Because E(ε∣x) = 0 holds, we can compute where f_ε(ε∣x) is the (unknown) conditional density of ε given x. To apply the EL method, we assume that the conditional distribution of ε given x can be approximated by (5) such that w_i ≥ 0 with ∑δ_iw_i = 1, where w_i is the point mass assigned to the observed ε_i by assuming that the support of ε_i is equal to the set of observed ε_i. Using the approximation in Equation (5(5) ), we can obtain which can be written in the FI form in Equation (4(4) ). To determine w_j uniquely, we can use the idea of pseudo EL method of Wu and Rao (2006) to maximise (6) subject to (7) In practice, we do not know , and hence, we do not observe . We can use a -consistent estimator of to obtain and apply the above EL method to the observed residuals. In general, one can use (8) to obtain a -consistent estimator of where is an arbitrary function that enables the above equation to have a solution. If the variance function for a known function q, then one can choose where This choice is motivated by the quasi likelihood method for generalised linear models (McCullagh & Nelder, 1989, Ch. 9). The solution to Equation (8(8) ) can be called complete-case (CC) method. The CC estimator is not efficient in general, but it is efficient for estimating under MAR. Thus, the resulting SFI estimator can be constructed as follows:

Step 1	Obtain a -consistent estimator of and compute among the respondents.
Step 2	Find that maximises Equation (6(6) ) subject to (9) The solution can be written as (10) where is obtained by solving the second constraint of Equation (9(9) ).
Step 3	Use in Step 2 to approximate where and
Step 4	The SFI estimator of η is computed by solving (11) for η.

Instead of Equation (11(11) ), one can also consider a fully imputed estimating equation based on which was considered by Müller (2009) under the independently and identically distributed set-up. The fully imputed estimating equation may lead to a more efficient estimator of η (Matloff, 1981) but such over-imputation does not appeal to survey practice since we usually do not want to replace the true values of respondents with some imputed values. In the following section, we present the asymptotic properties of under complex survey designs.

3. Asymptotic properties

To discuss the asymptotic properties of the proposed SFI estimator of η, we first assume a sequence of finite populations and samples with finite fourth moments as in (Fuller, 2009, Ch.1). The following theorem presents the asymptotic normality of the proposed SFI estimator. The sketched proof of Theorem 3.1 is provided in Appendix 1.

Theorem 3.1:

Under the regularity conditions (C1)–(C13) in Appendix 1, the SFI estimator defined in Equation (11(11) ) is a -consistent estimator of η₀, that is where B = [E{∂U(η; x, y)/∂η}]^{− 1},Σ_u2 = V(N^{− 1}∑_{i ∈ A}π^{− 1}_iζ_i), and (12) and with σ² = E(ε²), and l(ε) = −∂log f_ε(ε∣x)/∂ε.

Remark 3.1:

In Equation (12(12) ), ζ_i can be written as the sum of four terms. The first two terms is the conditional expectation of U(η; x, y), the third term is the additional term due to approximating f(y∣x) by the EL method and the fourth term is the additional term due to estimating .

According to Theorem 3.1, a consistent variance estimator of can be written as (13) where with and (14) where and is a plug-in estimator of ζ_i in Equation (12(12) ). One can use with When nN⁻¹ = o(1), the second term of Equation (14(14) ) is of smaller order and can be safely ignored.

4. Extensions

In this section, we discuss two extensions of the proposed method. In Section 4.1, our proposed method is extended to handle non-smooth statistics including distribution functions and percentiles. In Section 4.2, an extension to stochastic imputation is discussed.

4.1. Inference for non-smooth statistics

Suppose that we are interested in estimating parameter η₀, the solution of E{U(η; x, y)} = 0 with non-smooth function U(η; x, y), where the non-smoothness can be with respect to either η or y. For generality, we assume that the non-smoothness is with respect to both η and y. Wang and Opsomer (2011) discussed asymptotic results for non-differentiable survey estimators. Define Let and where Denote as the solution of estimating equation To discuss asymptotic properties, we replace regularity conditions (C7)–(C10) in Appendix 1 with the regularity conditions (C14)–(C17) in Appendix 2. The following theorem presents the asymptotic expansion of under this scenario and the sketched proof is presented in Appendix 2.

Theorem 4.1:

Under regularity conditions (C1)–(C3) and (C11)–(C17) in Appendix 1 and Appendix 2, has the following asymptotic expansion: where where and evaluated at and other terms are the same as those in Theorem 3.1.

By Theorem 4.1, we can obtain where B = [E{∂U(η; x, y)/∂η}]^{− 1} and Σ_u2 = V{N^{− 1}∑_{i ∈ A}π^{− 1}_iζ_2i}. If we are interested in estimating the cumulative density function of y, which is Pr(y < t), then we can choose U(η; x, y) = I(y < t) − η and where Therefore, we have A consistent estimator of D^* can be written as with where K_x and K_y are kernel functions for x and y with bandwidth h_x and h_y. Thus, a consistent variance estimator of here can be obtained similarly to Equation (13(13) ).

If the parameter of interest is the τth percentile of Y, given by η = F^{− 1}_Y(τ), the SFI estimator of η can be obtained by solving the estimating Equation (11(11) ) with U(η; x, y) = I(y < η) − τ. Since E{I(Y < η)} = F_Y(η), it can be shown that has the asymptotic expansion in Theorem 4.1 with where f_y is the density function for y. A consistent estimator of ∂E{U(η₀; x, y)}/∂η can be written as and a consistent estimator of D^* can be written as with

4.2. Stochastic imputation

In the multi-purpose surveys, stochastic imputation is often preferred to deterministic imputation since it can preserve distributional relationship better. In stochastic imputation, imputed values are generated from a stochastic imputation mechanism and with additional variability due to the imputation. For simplicity, we only consider the case where U(η; x, y*^(j)_i) is a smooth function of η and The results can be naturally extended to non-smooth statistics. The stochastic imputation estimator can be obtained by solving the following estimating equation: where y*^(s)_i are randomly selected from with the selection probability , where w*_ij are the fractional weights in Equation (11(11) ). Since where the conditional expectation is with respect to the stochastic imputation mechanism, we have Thus, using an argument similar to Theorem 3.1, we can obtain

(15) where . Therefore, a consistent variance estimator can be written as where (16) and can be obtained similarly to Equation (13(13) ) and The second term of Equation (16(16) ) estimates the additional variance due to stochastic imputation. If m is large, the second term is negligible.

5. Replication variance estimation

Estimating the variance of the estimator can be done through the linearisation formulas presented in Section 3 for smooth statistics and the formulas in Section 4 for non-smooth statistics. However, it requires tedious algebra to compute all the terms. In this section, we consider an alternative approach using replication methods. Shao and Tu (1995) considered the theoretical aspects of replication methods such as Jackknife and Bootstrap. Wolter (2007) gives a comprehensive overview of replication variance estimation methods in survey sampling.

Suppose we are interested in estimating T = ∑^N_{i = 1}y_i. Define the design weight as d_i = π^{− 1}_i. The design unbiased estimator of T is and the consistent replication variance estimator of is given by where L is the number of replicates, c_k is the replication factor associated with the kth replication and with d^(k)_i being the kth replicate of d_i. For example, c_k = (L − 1)/L for deleting one group jackknife method. For details of corresponding c_k with different variance estimation approaches, see Wolter (2007).

To obtain replication variance estimator of our proposed SFI estimator, we apply the same SFI method to each of the replicates. In the first step, we obtain the kth replicate of by solving In the second step, the replicated EL weights are computed by maximising subject to constraints with . In the final step, the replicated SFI estimator is computed using the replicated EL weights. For smooth statistics, the kth replicate of , denoted by , is obtained by the solution to the following estimating equation where . The final replication variance estimator of is given by For non-smooth statistics, our estimator is similar to that of Wang and Opsomer (2011). Define where and are defined in Section 4.1, is defined in Equation (11(11) ) with design weight replaced by replication weight d^(k)_i and fractional weights replaced by replication fractional weights w*^(k)_ij. Then the replication variance estimator can be written as with defined in Section 4.1.

6. Simulation studies

In this section, we conduct two limited simulation studies. The first one is generated from an artificial data-set and the second one is based on the real data treated as a finite population.

6.1. Simulation one

We repeatedly generate B = 2000 finite populations of (x_i, y_i, δ_i) of size N = 10, 000 from a super-population model with x_i ∼ exp (1) and E(ε_i∣x_i) = 0. Two error distributions are considered: (E1) ε_i ∼ N(0, 1) and (E2) ε ∼ {χ²(2) − 2}/2. Given (x, y), the response indicator δ has a Bernoulli distribution with The overall response rate is about 50%. Given each finite population (x, y, δ), we draw a sample by using a Poisson sampling design with the first-order inclusion probability π_i = nz_i/∑^N_{i = 1}z_i, where n = 200 and z_i = max {0.5y_i + 2, 1} + u_i, with u_i ∼ χ²(1) and χ²(1) corresponding to the chi-squared distribution with degrees of freedom equal to one. In this simulation, we are interested in estimating three parameters:

(1)	θ1 = N− 1∑Ni = 1yi, the population mean of y.
(2)	θ2 = N− 1∑Ni = 1I(yi < 1), the proportion of y less than 1.
(3)	θ3 = F−1(0.5), the population median of y.

From each sample, we compute the following four estimators:

(1)	The CC estimator based on the complete cases only. The CC estimator is the solution to ∑i ∈ Aδiπ− 1iU(η; xi, yi) = 0, where U(η; x, y) is the corresponding estimating equation for each parameter.
(2)	Full sample estimator based on the original sampling without missing data andpseudo EL method (FULL). Specifically, we maximise l = ∑i ∈ Aπ− 1ilog (ωi), subject to the following constraints: where and is obtained by solving the following estimating equation: The full sample estimator serves as a benchmark for comparison.
(3)	The PFI estimator of Kim (2011) assuming yi∣xi ∼ N(β0 + β1xi, σ2) with imputation size M = 100.
(4)	The nonparametric fractional imputation (NFI) estimator that uses the following nonparametric fractional weights: for each unit i ∈ A with δi = 0 and j ∈ A with δj = 1. We use the reference bandwidth with and A Gaussian kernel density function Kx(t) = (2π)−1/2exp ( − t2/2) has also been used.
(5)	The stochastic regression imputation (SRI) estimator assuming the following model: yi = β0 + β1xi + εi with E(εi) = 0 and V(εi) = σ2.
(6)	The proposed SFI estimator

From the Monte Carlo sample of size B = 2000, Monte Carlo bias, standard error and root mean squared error (RMSE) are computed for each point estimator. The results are presented in Table 1. Under (E1) and (E2), the CC estimators perform worst since the response mechanism is not missing completely at random (MCAR). Unless the response mechanism is MCAR, the CC estimator is biased. The FULL estimators always perform best since they assume no missing values and use moment condition (1(1) ). Under distribution (E1), the SFI and PFI estimators have similar performances. Among the three imputation estimators, the NFI and SFI estimators perform worst in terms of RMSE for all scenarios since they used less information.

Table 1. The Monte Carlo bias (× 10⁻²), standard error (SE) (× 10⁻²) and root mean squared error (RMSE) (× 10⁻²) for four different methods with two error distributions in Simulation one.

		(E1)			(E2)
Par	Method	Bias	SE	RMSE	Bias	SE	RMSE
E(y)	CC	18.6	13.0	22.7	20.0	19.8	28.1
	FULL	0.1	5.9	5.9	0.3	9.0	9.0
	PFI	−0.1	7.8	7.8	0.7	12.0	12.0
	NFI	0.7	12.9	12.9	2.9	21.3	21.5
	SRI	−0.2	13.9	13.9	1.7	23.3	23.3
	SFI	−0.2	6.9	6.9	0.3	12.4	12.4
Pr(y < 1)	CC	−6.3	5.3	8.2	−3.5	4.8	5.9
	FULL	0.0	3.0	3.0	0.0	2.6	2.6
	PFI	0.2	3.1	3.1	−5.4	3.1	6.2
	NFI	−0.1	5.1	5.1	−0.5	4.9	4.9
	SRI	0.2	5.0	5.0	−0.4	5.0	5.0
	SFI	0.1	3.2	3.2	0.1	3.3	3.3
Quantile	CC	15.0	13.9	20.4	21.9	22.8	31.6
	FULL	0.1	7.8	7.8	0.2	13.2	13.2
	PFI	−0.3	8.5	8.5	30.0	14.5	33.3
	NFI	−0.8	14.9	14.9	2.7	25.3	25.4
	SRI	−1.0	15.7	15.7	2.4	25.4	25.5
	SFI	−0.5	9.1	9.1	0.2	17.0	17.0

Under model (E2), the SFI estimator shows negligible bias for all parameters, but the PFI estimator has non-negligible bias for estimating proportion and quantile which is due to the misspecification of the error distribution. The NFI and SRI estimators are not as efficient as the SFI estimator in terms of bias and variance. The SFI estimator outperforms PFI, NFI and SRI estimators in terms of RMSE. The overall results indicate the robustness of SFI. For variance estimation, we computed the relative bias based on the Taylor linearisation and replication methods, respectively. All the relative bias are below 7%. In addition, we calculate the Monte Carlo coverage rate for the 95% confidence intervals. Under model (E1), the coverage rates are 94.8%, 93.4% and 95.0% for estimating mean, proportion and quantile, respectively, by using Taylor method, and 94.9%, 93.6% and 95.1% by using replication method. The results under model (E2) are similar and the coverage rates are close to the nominal rate.

6.2. Simulation two

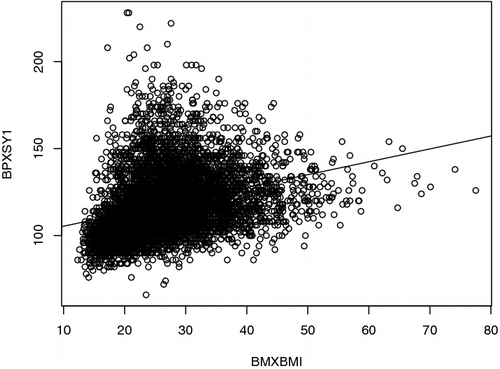
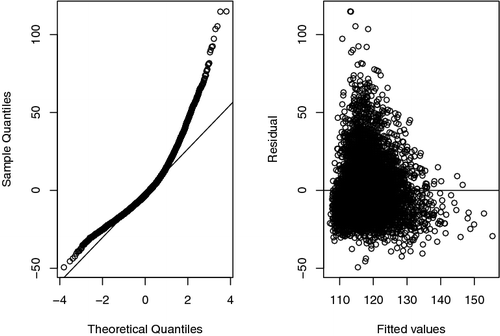
In the second simulation study, we use 2013–2014 U.S. National Health Examination and Nutrition Survey (NHANES) data as a pseudo finite population. Suppose the study variable is systolic blood pressure (BPXSY1) and the covariate variable is body mass index (BMXBMI). Keeping only the cases where both BPXSY1 and BMXBMI are greater than zero, the pseudo finite population eventually contains 7104 cases. The scatter plot of BPXSY1 versus BMXBMI is presented in Figure 1. We assume that BPXSY1 is roughly linear with respect to BMXBMI. After performing linear regression of BPXSY1 versus BMXBMI, the QQ plot of residuals and residuals vs. fitted values plot are presented in Figure 2. The residual plots suggest deviation from normality. The p value from Anderson–Darling test for normality is less than 2.2 × 10⁻¹⁶. We first generate response indicators δ_i, i = 1, 2, .… , 7104 from the following logistic regression model: The response rate is around 60%. Then given the population of (BPXSY1_i, BMXBMI_i, δ_i), B = 2000 Monte Carlo samples are generated by simple random sampling with sample size n = 200. Assume that the parameters of interest are

Figure 1. Scatter plot of BPXSY1 vs. BMXBMI.

Figure 2. QQ stands for quantile quantile plot (left panel) and residual vs. fitted value plot (right panel).

(Mean).	Finite population mean of BPXSY1, which is θm = 118.056.
(Prop1).	Finite population proportion one of BPXSY1:
(Prop2).	Finite population proportion two of BPXSY1:
(Prop3).	Finite population proportion three of BPXSY1:

We consider the same PFI, NFI, SRI and SFI estimators as discussed in Simulation one. The Monte Carlo bias, standard error and RMSE are presented in Table 2. For the population mean, PFI and SFI perform similarly and the NFI estimator has slightly larger bias and standard error. SRI has comparable bias as PFI and SFI, but it has larger SE, as expected. For population proportions, the PFI estimator has substantially larger bias than NFI, SRI and SFI which may be due to the misspecification of error distributions. The NFI and SRI estimators have larger standard errors than PFI and SFI estimators since the nonparametric methods are not as efficient as parametric or semiparametric methods and stochastic imputation will produce larger variance. Overall, SFI estimator performs the best in terms of both bias and variance.

Table 2. The Monte Carlo bias (× 10⁻²), standard error (SE) (× 10⁻²) and root mean squared error (RMSE) (× 10⁻²) for four different methods and four parameters.

Par	Method	Bias	SE	RMSE
Mean	COM	−2.9	124.8	124.9
	PFI	−2.3	153.2	153.2
	NFI	−5.0	153.5	153.6
	SRI	1.4	169.7	169.7
	SFI	−2.2	153.3	153.3
Prop1	COM	0.0	0.2	0.2
	PFI	0.5	0.3	0.6
	NFI	0.0	0.3	0.3
	SRI	0.1	0.3	0.3
	SFI	0.0	0.2	0.2
Prop2	COM	0.0	3.4	3.4
	PFI	−2.2	3.8	4.4
	NFI	−0.5	4.2	4.3
	SRI	0.5	4.2	4.3
	SFI	0.2	3.9	3.9
Prop3	COM	0.0	1.2	1.2
	PFI	0.7	1.1	1.3
	NFI	0.2	1.4	1.4
	SRI	−0.3	1.6	1.6
	SFI	0.1	1.4	1.4

7. Conclusions

Regression imputation is often used to handle item non-response in survey sampling. Unlike the usual regression imputation, the proposed SFI offers valid inference for a wide set of parameters such as population proportions and quantiles. Besides, only the first moment assumption is needed to obtain a consistent SFI estimator of the parameter, which leads to robust parameter estimation. The proposed SFI method shows good performances in the limited simulation studies.

The proposed method has several possible future research topics. First, instead of assuming ignorable response mechanism, we can consider an extension to non-ignorable non-response (Kim & Yu, 2011) using an exponential tilting response model. Also, extension of the SFI for handling multivariate missing data will be an important future research topic.

Acknowledgments

We thank an anonymous referee and the editor for very constructive comments. The first author wishes to acknowledge the partial funding provided by National Institutes of Health, National Institute of General Medical Sciences (Grant 1 U54GM104938), Oklahoma Shared Clinical and Translational Resources; Alterations and Renovations; Oversight and Management Core and IDeA-CTR to the University of Oklahoma Health Sciences Center. The research of the second author is partially supported by a grant from NSF in the US (MMS-1324922).

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

National Institutes of Health; National Institute of General Medical Sciences [grant number 1 U54GM104938]; Oklahoma Shared Clinical and Translational Resources; Alterations and Renovations; Oversight and Management Core and IDeA-CTR; NSF [grant number MMS-1324922].

Appendices

Appendix 1. Proof of Theorem 3.1

We first assume the following regularity conditions:

(C1)	The finite population is a random sample from the semiparametric regression model in Equation (1(1) ). The regression function in Equation (1(1) ) has a continuous first derivative in the neighbourhood of the true value and and are bounded in this neighbourhood.
(C2)	Function in the estimating function in Equation (8(8) ) has continuous first derivative in the neighbourhood of the true value , and and are bounded by some integrable function G1(x) in the neighbourhood.
(C3)	The model error term in Equation (1(1) ) satisfies E(ε2) < ∞ and max {||εi||: i ∈ A} = op(n1/2).
(C4)	Let assume converges to in probability uniformly in the neighbourhood of the true value For every a > 0,
(C5)	converges to continuous nonsingular derivative in probability uniformly in the neighbourhood of the true value
(C6)	as n, N → ∞, where denotes the design model variance, the variance under the joint distribution of the super-population model and the sampling mechanism.
(C7)	Function U(η; x, y) has continuous partial derivatives ∂U(η; x, y)/∂η and ∂U(η; x, y)/∂y in the neighbourhood of the true value η0 and ||U(η; x, y)||2, ||∂U(η; x, y)/∂η|| and ||∂U(η; x, y)/∂y|| are bounded by some integrable function G2(x, y) in the neighbourhood.
(C8)	Let and U(η) = E{U(η; xi, yi)}, then converges to U(η) in probability uniformly in the neighbourhood of the true value η0. For every a > 0,
(C9)	converges to continuous nonsingular derivative ∂U(η)/∂η in probability uniformly in the neighbourhood of the true value η0.
(C10)	as n, N → ∞, where denotes the design model variance.
(C11)	The first-order inclusion probabilities satisfy KL ≤ Nn−1πi ≤ KU for all i, where KL and KU are positive constants.
(C12)	max i, j|πijπ− 1iπ− 1j − 1| = o(1) for any i, j = 1, 2, … , N and i ≠ j, where πij are the second-order inclusion probability of unit i and unit j in the population.
(C13)	The response probability satisfies Equation (2(2) ) and for i = 1, 2, … , N for some fixed a > 0.

Conditions (C1)–(C2) are the model assumptions about the finite population. Condition (C3) is used to control the asymptotic order of in Equation (10(10) ). Chen and Sitter (1999, Appendix 2) argued that (C3) holds for common unequal probability sampling designs. Conditions (C4) and (C8) ensure the consistency of and , respectively. Conditions (C5), (C6), (C9) and (C10) are the regularity conditions that ensure asymptotic normality of and . Van der Vaart (1998, Ch. 5) used similar regularity conditions. Specifically, Conditions (C6) and (C10) have been used in many existing literature such as Wu and Rao (2006), Wang and Opsomer (2011), among others. Hajek (1960, 1964) established the asymptotic normality condition under simple random sampling and rejective sampling with unequal selection probabilities. Vís̆ek (1979) established the asymptotic normality for the Horvitz–Thompson estimator under Rao-Sampford sampling designs. Condition (C7) controls the smoothness and asymptotic behaviour of estimating function U(η; x, y). Conditions (C11) and (C12) are the standard assumptions for the sampling designs. Similar conditions have been used in Isaki and Fuller (1982) and Wang and Opsomer (2011). Condition (C13) controls the behaviour of the individual response probability. According to assumption (C3) and by using similar techniques as Wu and Rao (2006), we can show that Assumption (C4) and Taylor linearisation can establish Therefore, (A1) We know that is the solution of the following estimating equation: In addition, we have (A2) and (A3) Based on Equations (A2(A2) ) and (A3(A3) ), by using Taylor linearisation, we have (A4) According to Equations (A1(A1) )–(A4(A4) ) and after some algebra, it can be shown that (A5) where σ² is the variance for the residuals. With condition (C6), it can be shown that In addition, we have (A6) (A7) and (A8) where and with Define then by using Taylor linearisation, with E(S) = E{(1 − δ)U(η₀; x, y)} and According to the Hoeffding decomposition, Therefore, (A9) According to Taylor linearisation, we have (A10) By Equations (A1(A1) ), (A5(A5) )–(A10(A10) ), after some algebra, we can show that where ζ_i is defined in Equation (12(12) ) of Theorem 3.1.

Appendix 2. Proof of Theorem 4.1

We replace regularity conditions (C7)–(C10) in Appendix 1 with the following regularity conditions:

(C14)	converges to in probability uniformly in the neighbourhood of the true value θ0. For every a > 0,
(C15)	There exists a measurable function L(δ, x, y) with E{L2(δ, x, y)} < ∞ and for every θ1 and θ2 in the neighbourhood of the true value θ0,
(C16)	Assume that and has continuous and invertible first derivatives with respect to θ and the corresponding first derivatives are bounded by some integrable function in the neighbourhood of the true value θ0.
(C17)	as n, N → ∞, where denotes the design model variance.

Similar to Conditions (C4) and (C8), Condition (C14) ensures the consistency of proposed estimator. Conditions (C15) and (C16) are required to derive asymptotic expansion of proposed estimator. See Van der Vaart (1998, Ch. 5) for more details of those conditions. Similar to Conditions (C6) and (C10), Condition (C17) is used to derive the central limit theory.

The proof of the consistency of and is similar to the relevant proof in Theorem 3.1. According to the regularity conditions (C10)–(C12) and by using similar techniques as that of Theorem 19.26 of Van der Vaart (1998), we can show that (B1) In addition, we have (B2) and (B3) where D^* is defined in Theorem 4.1. According to Equations (A1(A1) ), (A5(A5) ), (A6(A6) ), (A9(A9) ), (B1(B1) )–(B3(B3) ), we have where ζ_i is defined in Theorem 4.1.