Robust dynamic risk prediction with longitudinal studies

ABSTRACT

Providing accurate and dynamic age-specific risk prediction is a crucial step in precision medicine. In this manuscript, we introduce an approach for estimating the τ-year age-specific absolute risk directly via a flexible varying coefficient model. The approach facilitates the utilisation of predictors varying over an individual's lifetime. By using a nonparametric inverse probability weighted kernel estimating equation, the age-specific effects of risk factors are estimated without requiring the specification of the functional form. The approach allows borrowing information across individuals of similar ages, and therefore provides a practical solution for situations where the longitudinal information is only measured sparsely. We evaluate the performance of the proposed estimation and inference procedures with numerical studies, and make comparisons with existing methods in the literature. We illustrate the performance of our proposed approach by developing a dynamic prediction model using data from the Framingham Study.

Keywords:

• Inverse probability weighting
• longitudinal markers
• nonparametric smoothing
• predictive accuracy
• risk prediction
• survival analysis

1. Introduction

Accurate and individualised risk prediction is a key component of precision medicine. For example in colorectal cancer, risk calculator can help tailoring individual's screening regimen and making decisions on specific ages for screening initialisation and surveillance. Factors pertaining to specific ages, such as family history and nutrition intake are important to be incorporated in the outcome prediction. For cardiovascular disease (CVD), the Framingham risk score (FRS) (Wolf, D’Agostino, Belanger, & Kannel, 1991) has been developed separately for men and women based on risk factors such as total cholesterol, HDL, systolic blood pressure and smoking status. Patients with 10-year FRS below 10% are considered to be at lower risk for vascular events during the next decade, whereas patients with scores between 10% and 20% are at moderate risk and those larger than 20% are at higher risk. Various intervention strategies can be implemented based on such risk stratification (Mosca et al., 2004). In these clinical settings, the analytical goal is to provide patients with an estimate of the likelihood of developing a disease within the next τ-years given the subject is disease free at age a and his/her risk profile updated by age a, i.e., the age-specific absolute τ-year residual life risk.

Currently available prediction models are often limited in predicting such age-specific absolute residual life risk. For example, the FRS model includes age as a standard risk factor with linear effects. However, it is well recognised that the relationship between age and CVD risk may change in magnitude through complex interactions with other risk factors (Ridker, Buring, Rifai, & Cook, 2007). Naturally, a risk equation should be a more stochastic function of age (Lloyd-Jones, 2010). Such simplistic models, failing to capture the complex age varying effects, may lead to poor risk estimates and prediction models with low discriminatory power. To be clinically useful with sufficiently adequate prediction accuracy, an ideal prediction model should take into account an individual's most up to date health information and reflect the fact that risk factors may have differential effects on the τ-year residual life risk over various stages of an individual's life span.

Constructing a model that accurately captures how risks change dynamically over lifetime, while of great importance, is challenging for several reasons. Often important risk factors change over time. However, collecting such time-varying information for a large prospective cohort can be a major undertaking. Most cohort studies only collect age-specific information intermittently, sometimes irregularly. Characterising changes over time with limited measures at discrete-time points requires much deliberation. Furthermore, the importance of risk factors on disease outcome may change during an individual's lifetime. For example, body mass index may have substantially different effects on future CVD risks depending on the age. Characterising age-varying effects with a powerful yet flexible statistical model can be challenging. Similar challenges arise when assessing the prediction performance of an age-specific prediction model since the accuracy may also vary with age.

A popular approach in the risk prediction literature is to decompose the absolute risk into two components: the age-dependent disease risk for a baseline risk profile, which can be estimated from a prospective cohort study or external disease incidence data, and the relative risk of developing disease for a particular risk factor profile compared to the baseline (Gail et al., 1989; Liu, Zheng, Prentice, & Hsu, 2014). While such an approach can accommodate differential effects of risk factors at different ages by adding interaction terms of age and the other covariates in the regression model, it does not incorporate time-varying covariates collected over time. To incorporate repeated measurements, joint modelling (JM) of both the covariate process Z(·) and a survival outcome T have been developed in recent years (Tsiatis, DeGruttola, & Wulfsohn, 1995; Wang & Taylor, 2001; Ye, Lin, & Taylor, 2008). Parameter estimation typically involves specifying the covariate process Z(·) and then linking Z(·) to T via a proportional hazard (PH) model with time-varying covariates. In addition to requiring strong modelling assumptions about Z(·) and T, these joint modelling (JM) methods have a limitation of being computationally infeasible when many time-varying covariates are under consideration. Semi-parametric methods have been proposed to directly make prediction of τ-year residual life risk given covariate information at a landmark time t₀ (Parast, Cheng, & Cai, 2012; Zheng & Heagerty, 2005). However, no existing methods allow for incorporating age-specific effects nonparametrically with sparsely measured time-varying covariates. Furthermore, procedures for nonparametrically evaluating such age-specific prediction models with longitudinal markers and censored event times are not yet available.

In this paper, we propose to directly model the age-specific absolute risk function via a flexible varying-coefficient model and estimate the covariate effects as functions of age via inverse probability weighted (IPW) kernel estimating equations. The procedure allows the estimation of age-specific risks flexibly with the longitudinally collected risk factor information on the same patient, while borrowing strength across individuals of similar ages at different study time points. It also handles irregularly measured serial covariates and censoring easily. Our proposed model, by allowing the effects of risk factors to change over age and the target residual life span τ, is more realistic and could potentially lead to improved predictive performance. To quantify the performance of the age-specific models of τ-year residual life risk, it would be desirable to consider measures of prediction performance specific to age and prediction time since the prediction accuracy of such models is likely to vary over both dimensions. A wide range of performance measures has been considered to quantify the time-specific prediction accuracy of τ-year absolute risk models constructed with baseline markers (Gerds, Cai, & Schumacher, 2008; Uno, Cai, Tian, & Wei, 2007; Zheng, Cai, & Feng, 2006). In the longitudinal setting, Zheng and Heagerty (2004) considered a model-based approach for estimating the accuracy in the absence of censoring. To guard against potential model mis-specification and incorporate censored outcomes, we propose an IPW kernel estimator to calculate model performance parameters that quantify the accuracy of the proposed prediction models in predicting τ-year residual life at age a. No existing methods provide nonparametric estimates of such prediction performance with longitudinal markers and censored outcomes.

The remainder of this manuscript is organised as follows. In Section 2; we describe the proposed model and estimation framework. Then, we present simulation results comparing our approach to other popular methods in Section 3. We apply the proposed method to the Framingham Heart Study in Section 4, assessing the age-specific effects of routinely used cardiovascular risk factors on the 10-year residual CVD risk and quantifying the performances of the prediction models. We conclude with a brief discussion in Section 5.

2. Methods

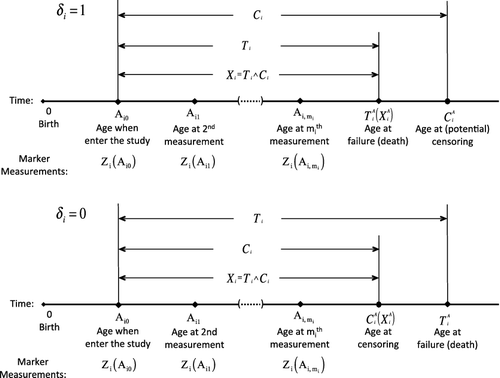
Let T_i be the time to event onset since a baseline time such as study entry. Due to censoring, one can only observe X_i = min {T_i, C_i} and δ_i = I(T_i ≤ C_i), where C_i is the censoring time and I(·) is the indicator function. To facilitate the calculation of age-specific risks, we also record age at the occurrence of the event and censoring. Let A_i0 be the age at which subject i enters the study and then is the age at which the event occurs, and is the age at which might be censored. Let . In addition to the event time information, risk markers are ascertained repeatedly during the follow-up. For the ith subject, let denote a vector of p risk factors measured at age a, let {A_ik, k = 0, ..., m_i} be the ages at which these risk factors are collected and Z_ij = Z_i(A_ij), where m_i is the total number of measurement times. We assume that Z_i(a) is potentially observable among those with , the values of Z_i(A_ij) are not dependent on the study measurement time A_ij − A_i0 given age A_ij. In addition, C_i is assumed independent of T_i , Z_i(·), entry age A_i0, and the underlying study measurement times, with support not shorter than that of A_ij − A_i0 + τ. Figure 1 provides a graphical illustration of the data structure.

Figure 1. Data structure.

2.1. Modelling, estimation and inference

We are interested in estimating the risk of experiencing the event in the next τ-years for subjects who are at age a and event-free, based on the risk factor measured at age a, Z(a). Thus, the goal is to estimate the conditional risk function: To approximate π_{τ, a}(z), we propose a flexible varying coefficient model: (1) where g(·) is a known smooth probability distribution function, such as g(x) = exp (x)/{1 + exp (x)} (which is used in Section 4), represents transformed risk factors for some known function and U(a) includes 1 as the first component, such as a log transformed risk factor (used in Section 4), is an unknown smooth function representing the covariate effects on the τ-year residual life risk at age a. Model (1(1) ) allows the effects of risk factors Z(a) to vary over both age and the residual life span τ. This flexibility is attractive when the risk factors have different effects on long-term versus short-term risks and when certain risk factor profiles have more detrimental effects for younger subjects than for older subjects.

To estimate for any given age a in the presence of censoring, we propose to obtain as the solution to the IPW kernel smoothed estimating equation, , where (2) where U_ij = U_i(A_ij), with being the Kaplan–Meier estimator for the survival function of the censoring time G(c) = P(C_i > c) of C_i, and K_h(s) = K(s/h)/h is a symmetric standard kernel function K(·) with a finite support and with h the smoothing parameter. Note that under the independent censoring assumption, .

Following similar arguments as given in Cai, Tian, Uno, Solomon, and Wei (2010) and Parast et al. (2012), one may show that converges in probability to a deterministic vector as n → ∞ regardless of whether (1(1) ) is correctly specified or not. In addition, one may also show that for h = O_p(n^−v) with v ∈ (1/5, 1/2), converges in distribution to a zero-mean normal random vector for any given a. However, it is difficult to directly estimate the asymptotic variance of . To construct confidence interval (CI) for in practice, we suggest using a perturbation resampling (sometimes referred to as wild bootstrap) method (Park & Wei, 2003; Tian, Zucker, & Wei, 2005; Wu, 1986) to approximate the distribution of the proposed estimator. Compared to the standard bootstrap, perturbation resampling tends to be more stable especially in the survival setting since all observations take positive weights and contribute to the estimation. Let , b = 1,… , B, be B sets of independent positive random variables from a known distribution with mean and variance equal to one. Then, one may obtain perturbed estimates of , , as the solution to the equation: where and is the weighted Kaplan–Meier estimator of G(·) with each subject's contribution to the estimator weighted by V^(b)_i. The asymptotic variance of , , can be estimated by the empirical variance of . The 100(1 − α)% simultaneous confidence bands for can be obtained as , where ζ_α is the 100(1 − α)th percentile of . To justify the resampling method, we may first show that where is some deterministic function and . Thus for any fixed a and h = O_p(n^−v) with v ∈ (1/5, 1/2), is asymptotically normal. Furthermore, following similar arguments as given in Tian et al. (2005), we may show that with proper normalisation, converges to an extreme value distribution. In addition, where is with respect to probability space generated by both the observed data and . Then, we may show that conditional on the data, converges in distribution to thesame limiting unconditional distribution of .

2.2. Accuracy measure estimation

With estimated as , one can then use to estimate the τ-year survival probability for event-free subjects with risk factor profile Z(a) at age a. To assess the accuracy of the limiting risk model in predicting the τ-year residual survival status for different age groups, we extend commonly used time-dependent accuracy parameters, such as true positive rate (TPR), false positive rate (FPR) and area under the receiver operating characteristic curve (AUC), to also incorporate the age dimension. Since the proposed model evaluation method is not limited to a specific prediction model, we next describe these accuracy parameters for a genetic τ-year residual life risk function, Π_{τ, A}(Z), derived based on an age A and the risk factor Z(·) collected up to age A. For the proposed model, .

2.2.1. Time and age-specific prediction accuracy

When a specific age group a is of interest, we summarise the prediction performance of risk model Π_{τ, A}(Z) using time and age-specific TPR and FPR functions, respectively, defined as We may summarise the overall predictiveness of the model for a given a and τ using where i and i′ index two independent individuals. Similar to the estimation of , these parameters can be estimated using an IPW kernel smoothing approach. For example, TPR_{τ, a}(c) can be estimated as (3) and AUC_{τ, a} can be estimated as (4)

where is the estimated risk function plugging in estimated model parameters. For the proposed varying coefficient model, and

using similar arguments as those for the consistency of , one may show that is a consistent estimator of AUC_{τ, a}. Furthermore, converges in distribution to a normal random variable. The CI for AUC_{τ, a} can be constructed by perturbed estimates. Specifically, for b = 1, ..., B, the bth perturbed estimate of can be obtained as (5) where is the perturbed counterpart of obtained similar to using weights .

2.2.2. Time-specific prediction accuracy including age as a predictor

When interest lies in evaluating the accuracy of the prediction model treating age as a risk factor, an overall summary that is not conditional on age would be preferred. That is, incorporating age as a predictor, one may seek to assess the accuracy in predicting τ-year residual life of the risk estimate Π_{τ, A}(Z), constructed using Z(·) information collected up to a random age A among those with . For such settings, one may consider where is the distribution of the age at measurement. The overall performance of the risk model Π_{τ, A}(Z) for predicting τ-year residual life can be summarised by where i and i′ index two independent subjects. Plug-in estimates may be constructed for these parameters with an estimated . For example, in the simple case when only a single measurement is taken at baseline, then AUC_τ may be estimated as (6) Given the longitudinal data structure, we may also be interested in estimating these accuracy parameters when the age at measurement A follows the marginal distribution of the observed measurement ages in the study. In which case,

and .

The accuracy measure AUC_τ in this case can be estimated as Standard error (SE) and CIs can be constructed similarly to those given above for .

2.3. Selection of smoothing parameter

It is known that the choice of the smoothing parameter h is critical as in any nonparametric estimation problem. We employ a K-fold cross validation to select the smoothing parameter. Specifically, the study subjects are divided into K folds of approximately equal sizes. The optimal bandwidth h_opt minimises the weighted mean squared prediction error: where is the set of subjects that are in fold k and is the estimate of using data excluding those from fold k. To obtain an estimator whose variance dominates bias, we follow the common practice to undersmooth (Cai et al., 2010; Neumann & Polzehl, 1998; Tian et al., 2005) using the final bandwidth , where n₁ is the number of observed events by τ years.

3. Simulations

In this section, we report results from simulation studies that examine the finite-sample performance of the proposed methods and compare our methods with existing methods. Although the proposed methods are catered for survival data with longitudinally measured risk factors, it can be applied to traditional survival data with one single measurement of the risk factor at baseline to flexibly capture the age effect. For the single measurement setting, we compare the proposed procedure to the standard PH model which includes age as a covariate. In the longitudinal setting, we will compare the proposed methods to the commonly used joint modelling (JM) approach. For both settings, we considered n = 2000 and 5000, let K(·) be the Gaussian kernel, and B = 1000 for perturbations. For each configuration, results are summarised based on 1000 simulated data-sets.

3.1. Simulations with a single measurement

For this setting, we simulate A_i0 from Uniform (15, 75) and two independent baseline covariates Z_i1(A_i0) and Z_i2(A_i0) from and respectively. The survival time from entry, T_i, is generated from log (T_i) = 2.5 + β₁(A_i0)Z_i1(A_i0) + β₂(A_i0)Z_i2(A_i0) + 0.5 ε, where β₁(a) = a²/7500, β₂(a) = {(a − 45)² − 100}/2000 and ε follows a standard logistic distribution. The censoring time C_i is generated from where , resulting in about 80% of censoring. For illustration, we choose τ to be 5 years. Throughout, we choose g(·) to be the logistic link function. Using the proposed bandwidth selection procedure with fivefold cross-validation, h is about 6.4 and 5.4 for n = 2000 and 5000, respectively. We obtain the estimates of and AUC_{τ, a} for ages from 20 to 70. Throughout the simulation studies, we let U_ij = Z_ij = Z_i(A_ij).

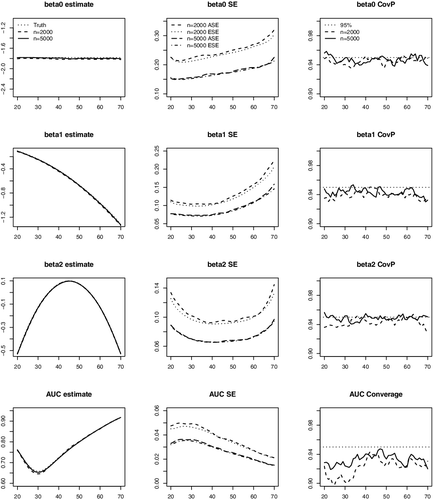
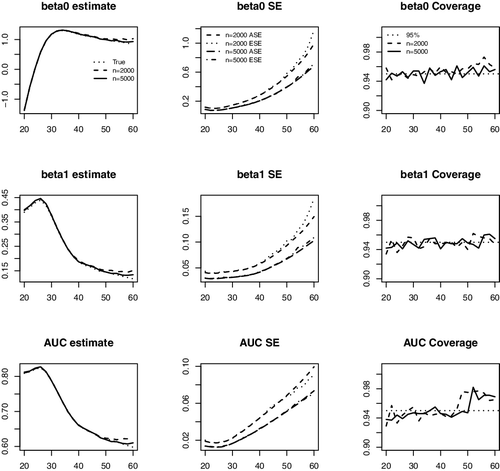
In Figure 2, we present the average of the point estimates, the average of the SE estimates compared with the empirical SEs and the coverage probabilities (CovPs) of the 95% CIs for and AUC_{τ, a} across a range of a. The results suggest that the proposed estimators produce negligible biases, and the estimated SEs are close to the empirical SEs. The empirical CovPs of the 95% CIs are close to their nominal level for coefficients. For AUC, the CovPs of the CIs are close to the nominal level but slightly below 95% for younger ages when n = 2000, possibly due to the fact the curvature of the AUC function is high in that range leading to a slight bias. The results are much improved when n increases to 5000.

Figure 2. Average of estimates, average of the standard error estimates (ASE), empirical standard errors (ESE) and empirical coverage probabilities (CovP) of the 95% CI. One measurement at baseline. Each entry is based on 1000 simulated samples.The x-axis in all the plots is age.

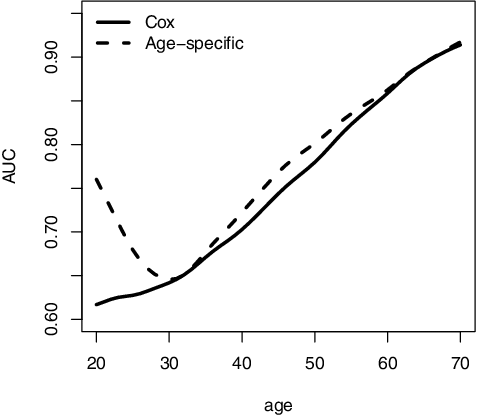
For comparison, we obtain an alternative τ-year risk estimate, , from fitting a cox model including A_i0 and as covariates, where is the estimated baseline cumulative hazard function at τ, , and are the estimated log-hazard ratio for . For both of the risk estimates from our proposed method and the cox model, we evaluate their age-specific prediction performance as well as the overall prediction performance based on AUC_τ. As shown in Figure 3, the age-specific AUC, AUC_{τ, a}, of our proposed approach was generally higher than those from the cox model. The overall AUC, AUC_τ, was about 0.817 for the proposed model and 0.77 for the cox model. The average difference between the two overall AUC_τ's was 0.047 (SE = 0.007). These results highlight the improved prediction performance for using the proposed age-specific model.

Figure 3. Age-specific AUCs for the proposed method (age-specific) and cox model (Cox). Values are averaged over 1000 repetitions with sample size n = 5000.

3.2. Simulations with longitudinal measurements

We also conducted simulation studies to examine the performance of the proposed procedures in longitudinal settings. To simulate the age at the occurrence of event and longitudinal measurements of a risk factor Z(a), we generate two random effects α₀, α₁ from N(0, 1). The age of event is obtained from where ε is generated from an uniform distribution over (0, 1) and Φ(·) is the cumulative distribution function of a standard normal distribution. We simulate age of entry to the study A₀ from Uniform (10, 70). Among the subjects who survive by the entry to the study, i.e., , we randomly sample n subjects as our cohort. For the ith subject in this cohort, the survival time since entry is , and C_i is generated from a Uniform (10, 40), which leads to about 25% of censoring. The risk factor is measured at the entry age A_i0 and ages A_ij = A_i0 + Δ_ij after entering the study until event or censored, whichever comes first, where Δ_ij is generated from a N(4, 1) distribution. And the observed marker value at age A_ij is Z_i(A_ij) = α_0i + α_1ilog (A_ij) + e_i(A_ij) where e_i(A_ij) ∼ N(0, 1.5²). We choose τ to be 10 years. The selected smoothing parameter h is around 5.0 and 1.3 for n = 2000 and 5000, respectively, using fivefold cross-validation scheme described in Section 2.3. We obtain and AUC_{τ, a} estimates for ages from 20 to 60.

The average of the point estimates, average of the SE estimators, the empirical SEs and the coverage probabilities of the 95% CIs for the and AUC_{τ, a} at a series of ages are shown in Figure 4. The proposed procedures yield estimators with negligible biases. The estimated SEs obtained through perturbation resampling are close to the empirical SEs.

Figure 4. Average of estimates, average of the standard error estimates (ASE), empirical standard errors (ESE) and empirical coverage probabilities of the 95% CI. Longitudinal measurements. Each entry is based on 1000 simulated samples. The x-axis in all the plots is age.

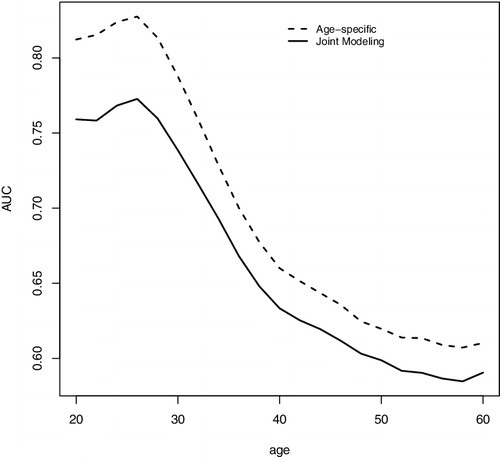
For comparison, we also fit the data with a JM approach (Rizopoulos, 2010; Tsiatis & Davidian, 2004) for longitudinal and survival data. In particular, we follow the setup in Rizopoulos (2010) to specify a linear mixed effects model with random intercept and slope for the longitudinal measurements Z_ij and a PH model relating the hazard function to the random slope, in which the log baseline hazard is approximated using B-splines. With the parameter estimates from the joint model, for subject i with measurement at A_ij, one can use a Monte Carlo approach to predict τ-year residual life risk given that the person has survived A_ij and we let denote the resulting estimate of the risk function. We can estimate its corresponding AUC_{τ, a} as discussed in Section 2.2. We present the average of the estimated AUC_{τ, a} for the two modelling approaches at n = 5000 in Figure 5. The results suggest that the proposed approach improved prediction accuracy over a wide range of ages compared to the JM approach.

Figure 5. Age-specific AUC for the proposed method (age-specific) and JM with longitudinal measurements. Values are averaged over 1000 repetitions with sample size n = 5000.

4. Application

In this section, we apply the proposed methods to the Framingham Heart Study to develop and evaluate age-specific CVD or death risk prediction models. The original goal of the study was to identify the common factors that contribute to CVD by following its development over a long period of time in a large group of participants who had not yet developed CVD. Started in 1948 with 5209 adult subjects, the study is now on its third generation of participants. Information on a wide spectrum of risk factors and disease outcomes is collected on each of the many follow-up visits during participants’ lifetime. The data-set consists of 3982 subjects (2108 females and 1874 males) with complete information on the risk factors at least one measurement time. Several traditional Framingham risk factors were collected on these subjects on each of their visits, including age, diastolic blood pressure, cholesterol, high-density lipoprotein (HDL), diabetes and smoking. In addition, an inflammation marker, C-reactive protein (CRP), was also measured at various visits. The median number of measurement times is 3. We use both Framingham risk factors and CRP to estimate age-specific 10-year risk of CVD or death for females and males separately. Thus, we only include visits where all these risk factors are measured based on the study design. The outcome of interest is time to the onset of first major CVD event or death. Such a composite outcome avoids the issues of having to account for the competing risks from other causes of death. Nevertheless, we note that our calculation of the probability of experiencing CVD or death within 10-years in this data-set can be regarded approximately as 10-year CVD risk since majority of the observed events are CVD events, especially at younger age. In the study, there are 54 subjects who had CVD prior to death within 10 years. The cumulative incidence rate for CVD prior to death within 10 year is estimated to be about 1.4%. The median follow-up time was 32 years and the entry ages range from 5 to 70 with a median of 35.

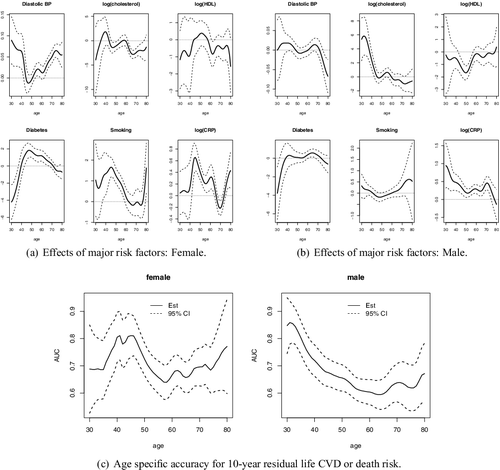
We fit the proposed age-specific 10-year risk model (1(1) ) with a logistic link. Predictors include original scale of diastolic blood pressure, diabetes, smoking, the log scale of cholesterol, HDL and CRP. We use a Gaussian kernel for K(·), with the smoothing parameter h selected as 5.2 for males and 3.8 for females using the fivefold cross-validation scheme described in Section 2.3. In Figure 6(a,b), we demonstrate how the effects of major risk factors may vary by age for women and men, respectively. For men, blood pressure does not show any significant association with risk of outcome for all the ages, whereas for women, higher blood pressure significantly increases the risk, especially for younger ages and older ages. For men, as expected, high cholesterol increases risk, and our analysis further reveals that for men, the effects decrease with ages. In other words, having high cholesterol for a younger man exposes them to higher risk compared with older men. For women, diabetes status also shows an age-varying pattern: the effect increases with age initially, reaches a peak at 50 and goes down afterward. Smoking shows significant effect at age 45 for women, but the effect diminishes as age increases. However, for men, neither diabetes status nor smoking shows significant association with the risk at almost all ages. HDL shows no significant association with outcome for women, but is inversely associated with the risk between age 40 and 60 and no significant association at other ages for men. Finally, CRP also exhibits different age-varying effects between women and men. For men, the effect of CRP is monotonically decreasing as age increases while for women, higher CRP increases risk before 60 years old and peaks at around 45 years old. In Figure 6(c), we show the age-specific AUC of the proposed age-specific risk scores for men and women. For women, the AUC_{10, a} does not vary substantially over age a with values fluctuating around 0.7. On the contrary, for men, AUC_{10, a} is substantially higher for younger ages with value as high as 0.9 and decreases to 0.6 at older ages. Thus, the age-specific risk model is highly accurate in predicting 10-year risk of CVD or death for younger males but only moderately accurate for middle aged or older males.

Figure 6. Data analysis: Framingham Heart Study. The panels (a) and (b) show the point and interval estimates of the age-specific effects of the major risk factors for male and female, respectively. The panel (c) shows the point and interval estimates of the age-specific AUC for male and female, respectively.

5. Discussion

When subjects are monitored over time for a clinical condition, it is highly desirable to dynamically recalculate risk estimates according to the updated risk factor information. Age is an important risk factor for many diseases such as CVD and the effects of other predictors on the disease risk may vary over age. Current risk prediction models used in clinical practice such as the FRS often incorporate age as an additive risk factor, which may limit the model prediction performance. Our proposed method estimates the age-specific absolute risk directly via a flexible varying-coefficient model that allows the predictor effects to vary over age and allows for easy incorporation of longitudinally collected risk factor information. We also provide procedures for nonparametrically assessing the prediction performance of such age-specific models, extending existing time-specific accuracy parameters to also incorporate the additional age domain.

Unlike the cox model with time-varying covariates, our proposed model can easily provide age-specific absolute risk estimates without having to specify the full longitudinal marker processes. Compared to the JM approach, our method has the major advantage of allowing for non-linear effects and non-trivial number of time-varying continuous or discrete risk markers. Additionally, our kernel-based procedure allows borrowing information across individuals of similar ages therefore provides a practical solution for situations where the longitudinal information is only measured sparsely and irregularly.

Our method allows for internal covariates in that it aims to make prediction for the residual life among event-free subjects at age a, although it does require the availability of the marker information at age a for those with . When the outcome is a non-terminal event that is subject to death as a competing risk, then one may easily modify the proposed procedures to instead make prediction of the disease risk for those who are still alive and have not yet developed the disease at age a. The age-specific accuracy parameters can also be modified to accommodate competing risks similar to those considered in Blanche, Dartigues, and Jacqmin-Gadda (2013).

The proposed method employs a working model that requires the specification of g and ψ, both of which could potentially impact the model prediction performance. In general, the prediction performance is less sensitive to the choice of g due to the robustness properties such as the logistic likelihood as noted in Li and Duan (1989) and Eguchi and Copas (2002). One may choose appropriate ψ based on existing literature on the functional form of known risk factors or exploratory analyses. On the other hand, regardless of the choice of ψ or g, the fitted model may be mis-specified yet our proposed method could derive a risk model with good prediction performance. The flexible varying coefficient model is expected to perform well under mis-specification and the proposed inference procedures are always valid regardless of the potential mis-specification in the fitted model. In addition, while the proposed simple IPW method has the advantage of enabling robustness in inference under model mis-specification, it may come at a cost in efficiency loss. If there are auxiliary variables available at baseline, efficiency augmentation methods leveraging such information warrant further research.

Acknowledgments

The Framingham Heart Study and the Framingham SHARe project are conducted and supported by the National Heart, Lung, and Blood Institute (NHLBI) in collaboration with Boston University. The Framingham SHARe data used for the analyses described in this manuscript were obtained through dbGaP (access number: phs000007.v3.p2). This manuscript was not prepared in collaboration with investigators of the Framingham Heart Study and does not necessarily reflect the opinions or views of the Framingham Heart Study, Boston University, or the NHLBI.

The work is supported by grants from Natural Sciences and Engineering Research Council of Canada, U01-CA86368, P01-CA053996, R01-GM085047, U54-HG007963, and R01-HL089778 from the National Institutes of Health.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The work is supported by grants from Natural Sciences and Engineering Research Council of Canada [grant number U01-CA86368], [grant number P01-CA053996], [grant number R01-GM085047], [grant number U54-HG007963], [grant number R01-HL089778] from the National Institutes of Health.

Notes on contributors

Qian M. Zhou

Qian M. Zhou holds a Ph.D. in statistics from the University of Waterloo. She is now an assistant professor of Statistics in the Department of Mathematics and Statistics at Mississippi State University. Her research interests focus on developing advanced statistical methods in survival analysis, longitudinal data analysis, risk prediction, and model diagnosis.

Wei Dai

Wei Dai holds a Ph.D. in biostatistics from Harvard University. She is now working at Citigroup.

Yingye Zheng

Yingye Zheng holds a Ph.D. in biostatistics from the University of Washington. She is now a Full Member of Public Health Science Division in the Department of Biostatistics at the Fred Hutchison Cancer Research Center. Her research interests have been in the developing novel statistical tools for medical decision making in the field of disease screening, diagnosis, prognosis and outcome prediction.

Tianxi Cai

Tianxi Cai holds a Sc.D. in biostatistics from Harvard University. She is now a professor of Biostatistics in the Department of Biostatistics at Harvard School of Public Health. Her research interests are mainly in the area of biomarker evaluation; model selection and validation; prediction methods; personalized medicine in disease diagnosis, prognosis and treatment; statistical inference with high dimensional data; and survival analysis.