A time-spectral method for initial-value problems using a novel spatial subdomain scheme

Abstract

We analyse a novel subdomain scheme for time-spectral solution of initial-value partial differential equations. In numerical modelling spectral methods are commonplace for spatially dependent systems, whereas finite difference schemes are typically applied for the temporal domain. The Generalized Weighted Residual Method (GWRM) is a fully spectral method that spectrally decomposes all specified domains, including the temporal domain, using multivariate Chebyshev polynomials. The Common Boundary-Condition method (CBC) here proposed is a spatial subdomain scheme for the GWRM. It solves the physical equations independently from the global connection of subdomains in order to reduce the total number of modes. Thus, it is a condensation procedure in the spatial domain that allows for a simultaneous global temporal solution. It is here evaluated against the finite difference methods of Crank-Nicolson and Lax-Wendroff for two example linear PDEs. The CBC-GWRM is also applied to the linearised ideal magnetohydrodynamic (MHD) equations for a screw pinch equilibrium. The growth rate of the most unstable mode was efficiently computed with an error $<0.1\mathrm{\%}$.

Keywords:

• time
• spectral
• weighted residual methods
• MHD
• Chebyshev
• subdomain
• PDE
• initial
• boundary

PUBLIC INTEREST STATEMENT

A new subdomain scheme for a recently developed time-spectral method (GWRM) is presented and compared with the original global subdomain scheme of the GWRM as well as with two finite difference methods, namely those of Crank-Nicolson and Lax-Wendroff. The new subdomain scheme, named the Common-Boundary-Condition (CBC) scheme, seeks to separate the computations of the physical equations of each subdomain and those involving internal and external boundary conditions. This is done in order to decrease the total number of modes that need to be solved globally. Furthermore, time-parallelization of the physical equations of each subdomain is shown to be possible. We believe the results are of significance in numerical modelling due to the large matrix systems often associated with spectral methods. The CBC-scheme is presented as a potential remedy.

1. Introduction

In the field of fusion plasma physics it is often necessary to solve complex sets of linear PDEs. A particular example is the sub-discipline devoted to the analysis of linearised magnetohydrodynamic equilibria and the evolution of unstable modes (Bateman, Schneider, & Grossmann, 1974; Cao & Cai, 2018; Furth, Killeen, & Rosenbluth, 1963; Glasser, Greene, & Johnson, 1976; Scheffel, 2011; Strauss, 1976; Yang et al., 2018). The analysis consists of linearising the governing magnetohydrodynamic equations, assuming an equilibrium, introducing a perturbation, and then calculating the mode growth rate. The existence of multiple time scales requires many time steps to resolve. It would be beneficial to average over small scale dynamics efficiently in order to obtain the dominant unstable mode.

The efforts of increasing the efficiency and accuracy of time dependent numerical schemes are long standing. A natural step to take is classically provided by the method of lines (Heath, 2005; Schiesser, 1991). For a more recent application to controllability analysis, see for example (Respondek, 2010). Here a finite difference approximation is often used for the spatial domain, whereas an ODE models the continuous temporal dependence along each fixed line (or surface) in the spatial domain. The spatial discretization can also be done by a finite element or spectral approach, in which case the time-dependent coefficients of the approximate solution expansion in spatial basis functions are found from solving a set of ODEs. The systems of ODEs associated with these methods are often stiff, thus there is motivation for exploring different approaches for solving the PDEs. Authors such as (Morchoisne, 1979), (Peyret & Taylor, 1983), (Tal-Ezer, 1986, 1989), and (Bar-Yoseph, Moses, Zrahia, & Yarin, 1995), to name a few, have pioneered the concept of time-spectral methods. A number of pseudo-spectral methods with polynomial basis functions such as Fourier, Legendre, and Chebyshev polynomials, with their respective advantages have been analyzed by the various authors. In the works by (Dutt, 1990) and (Maerschalck & Gerritsma, 2005) a space-time Chebyshev collocation method was implemented to solve initial value problems in a least-squared sense.

Following this trajectory we see that space-time spectral methods have seen multiple variations and a host of interesting applications. In the articles of (Fakhar-Izadi & Dehghan, 2014, 2018) a space-time method was applied to partial integro-differential equations on irregular domains. The basis functions used were Legendre polynomials in both space and time. It was shown that the space-time spectral method exhibited exponential convergence and high accuracy results. These results were not only found for the smooth solutions, but also for non-smooth solutions.

Another venue of space-time spectral methods can be seen in the field of fractional derivatives. In (Hanert & Piret, 2014) a Chebyshev pseudospectral method was developed and implemented on anomalous transport models, specifically relying on fractional-order derivatives in order to describe transport properties more effectively. In the article both space and time terms were represented by Chebyshev polynomials. The conclusion was that pseudospectral methods, due to being global methods (convergence and accuracy aside), are more apt to handle fractional differential equations because here the global behaviour is necessarily included.

Most, if not all, spectral methods mentioned have in one way or another sought to discretize the spatial and temporal domains at the nodes of the basis functions. This is done in order to approximate integrals with some form of Gaussian quadrature. The consequence being that one needs to transform back and forth between physical and spectral space multiple times. The time-spectral method proposed here, with its many similarities with other spectral methods, is distinguished in that it seeks to limit all computations to the spectral space.

The time-spectral method GWRM (Generalized Weighted Residual Method) proposed in (Scheffel, 2012) is a fully spectral method that spectrally decomposes all domains including spatial, temporal, and parameter domains. Multivariate Chebyshev polynomials are used to represent all domains in a solution ansatz. The GWRM executes all computations in spectral space, that is no collocation points are used. The only spatial points that are taken into consideration are the points where the spatial subdomains overlap. The spatial subdomains overlap in order to maintain two-point contact. It has been shown (Scheffel & Mirza, 2012) that for a system of PDEs with spatial derivatives of order $S$, employing $v$ variables (equations), the minimum number of interboundary contact points need to be at least $P=S/v$ in order to transfer external boundary value information properly across the spatial domain. Taking the 1D Burger equation as an example, where $S=2$ and $v=1$, $P$ should be at least 2. This subdomain method ensures spectral accuracy in the entire domain. Unfortunately, the resulting global matrix equations associated with solving the algebraic equations may become excessively large (Boyd, 2000; Canuto, Hussaini, Quarteroni, & Tang, 2006; Kopriva, 2009).

There are several popular methods for dealing with this issue. One such method is to use parallel algorithms that solve for large sparse matrices (Mittal & Al-Kurdi, 2002; Spagnoli, Humphrey, Price, & Kelmelis, 2011), and another is to create independent spatial domains that can be solved locally with boundary-solvers that connect the subdomains (Canuto et al., 2006; Giraldo & Restelli, 2007; Kopriva, 2009; Peraire & Persson, 2010; Scheffel & Mirza, 2012). The idea of reducing the global degrees of freedom was first implemented with the static condensation method (Guyan, 1964), and thereafter has seen many variations that make the algorithm more general and dynamic (Qu, 2004).

This brings us to the current spatial subdomain scheme, termed the Common Boundary-Condition (CBC) Method. For each iteration towards the solution this method solves the physical equations locally and separately, that is in each subdomain, but the boundary and patching conditions that connect the subdomains are solved globally. By calculating the relationship between the local physical equations (secondary degrees of freedom) and the external boundary conditions (primary degrees of freedom), the overall degrees of freedom can be substantially reduced. Combined with the time-spectral method, the CBC subdomain scheme takes into account the temporal modes, and adjusts the boundary and patching conditions throughout the entire temporal domain.

The paper is organized as follows. Section 2 briefly summarizes the time-spectral GWRM. The new spatial subdomain scheme that has been implemented is also laid out. Next follows a solution of test problems in section 3. The test problems include the linearised 1D Burger equation, a forced wave equation and a case relating to the linearised ideal MHD equations. Section 4 contains a discussion, including some observations, possible objections, and resolutions. The paper closes with a conclusion.

3. Method

We will here present a brief review of the GWRM. For a full and detailed presentation the reader is directed to (Scheffel, 2012).

3.1. Weighted residual formulation

We wish to solve a set of partial differential equations,

(1) $\frac{\mathrm{\partial }\mathit{u}}{\mathrm{\partial }t}=D\mathit{u}+f.$(1)

where $D$ is an arbitrary linear or non-linear operator and $f(t,\mathbf{x};\mathbf{p})$ is a known forcing term. The solution to equation (1) is approximated with multivariate Chebyshev expansion series in time, space, and parameter space. For a single spatial dimension and one parameter we have

(2) $u(t,x;p)\approx \mathrm{U}(\tau ,\xi ;P)=\sum _{k=0}^{K\mathrm{\prime }}\sum _{l=0}^{L\mathrm{\prime }}\sum _{m=0}^{M\mathrm{\prime }}{a}_{klm}{T}_k(\tau )T_l(\xi )T_m(P).$(2)

Here ($\prime$) denotes that the first term in each summation is divided by two. Since Chebyshev polynomials are defined in the range $[-1,1]$, a change of variables is performed; $\sigma =(z-A_z)/B_z$, $A_z=(z_1+z_0)/2$, and $B_z=(z_1-z_0)/2$. Here $\sigma$ signifies either of the transformed variables, thus $\tau$, $\xi$, or $P$, and $z$ is the physical variable, with indices 0 and 1 denoting domain limits.

A weighted residual formulation is obtained by substituting (2) into (1), multiplying the residual with weight functions, and integrating over the entire domain;

(3) ${\int }_{p_0}^{p_1}{\int }_{x_0}^{x_1}{\int }_{t_0}^{t_1}R{T}_q(\tau )T_r(\xi )T_s(P){\mathrm{w}}_t{\mathrm{w}}_x{\mathrm{w}}_{p}dtdxdp=0.$(3)

The residual has the form

(4) $R=u(t,x;p)-[u(t_0,x;p)+{\int }_{t_0}^t(Du+f)d{t}^{\prime }],$(4)

with the weight function

(5) ${\mathrm{w}}_z=(1-{\sigma }^2{)}^{-1/2}.$(5)

Equation (1) hereby is transformed into the following set of algebraic equations for the coefficients of the solution ansatz (2):

(6) $a_{qrs}=2{\delta }_{q0}{b}_{rs}+A_{qrs}+F_{qrs}$(6)

Here $b_{rs}$ are the coefficients of the Chebyshev polynomial approximation of the initial condition. The linear/non-linear operator term $A_{qrs}$ and the force term $F_{qrs}$ are functions of $a_{qrs}$. Boundary equations take the place of the highermost spatial modes of $a_{qrs}$ after inserting Eq. (2) into the given external boundary conditions; internal boundary conditions are produced by coupling the spatial subdomains. In the GWRM equation (6) plus boundary condition equations are solved with a semi-implicit root solver (SIR) (Scheffel & Håkansson, 2009). This may entail solving a global matrix equation for all the $(K+1)(L+1)(M+1)$ coefficients. The number of numerical operations, and the CPU time, would then scale as $((K+1)(L+1)(M+1){)}^3$ and the memory requirements as $((K+1)(L+1)(M+1){)}^2$. From a viewpoint of efficiency, these scalings become problematic for advanced problems.

3.2. Subdomain scheme

Subdomains, both in space and time, have the potential to remedy the efficiency problem. Concentrating here on the spatial dimension, it may be noted that a mere division of the spatial domain into subdomains does not have a radical influence on efficiency. Clearly, the possibility to adjust the subdomain length according to the physical terrain would optimize the solution procedure, but essentially the same global number of coefficient equations would need to be solved simultaneously. The Common Boundary-Condition method (CBC-GWRM) described in the following does, however, reduce the number of simultaneous global equations to be solved. 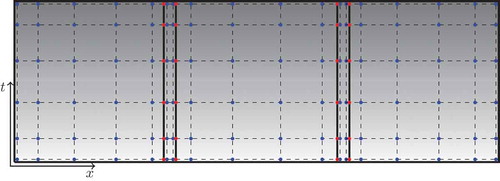The entire computational domain $D=\left\{(t,x):[0,T],[0,L]\right\}$ is discretized into $s$ overlapping spatial elements, see Figure 1. For example $s=3$ would give a discretized domain $\mathrm{\Omega }=\left\{{\mathrm{\Omega }}_1=[0,x_1+\epsilon ],{\mathrm{\Omega }}_2=[x_1-\epsilon ,x_2+\epsilon ],{\mathrm{\Omega }}_3=[x_2-\epsilon ,L]\right\}$, where $\epsilon$ is a small overlapping distance. This procedure allows us to use only a few Chebyshev modes in our ansatz for each subdomain. By overlapping the subdomains, point-wise and gradient continuity is ensured.

Figure 1. GWRM subdomains with overlapping region, distance exaggerated (red dots), Chebyshev roots ${\mathit{x}}_{\mathit{k}}\mathbf{=}\mathbf{cos}\mathbf{(}\mathbf{(}\mathbf{2}\mathit{k}\mathbf{-}\mathbf{1}\mathbf{)}\mathit{\pi }/\mathbf{2}\mathit{K}\mathbf{)}\mathbf{,}\mathit{k}\mathbf{=}\mathbf{1}\mathbf{\dots }\mathit{K}$ (blue dots), and the subdomain boundaries (solid black lines).

The system of equations we wish to solve now include $N_s$ spatial subdomains, $N_e$ number of physical equations, $K$ temporal modes, and $L$ spatial modes (we here let $M=0$). This results in $N=N_s{N}_e(K+1)(L+1)$ equations to be solved for the coefficients of the ansatz (2). A question arises: can the global amount of equations be reduced in some way?

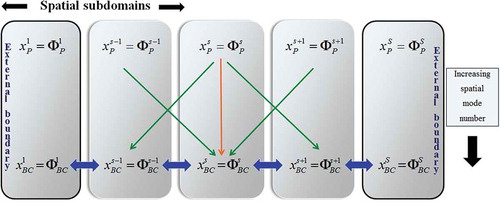
Equations (6) can be written in fixed point form formally as ${\mathbf{x}}^s={\mathbf{\Phi }}^s$, where $s$ refers to the respective subdomain; for details see (Scheffel, 2012). We now note that only the subset ${\mathbf{x}}_{BC}^s={\mathbf{\Phi }}_{BC}^s$ representing the boundary equations need to be solved globally. The reason for this is that the physics equations (6) in each individual subdomain ${\mathbf{x}}_P^s={\mathbf{\Phi }}_P^s$, representing the systems of PDEs, are only dependent on ${\mathbf{x}}_{BC}^s$. These “private” equations can be solved locally in each spatial subdomain in each iteration level. This process can be fully parallellized. Furthermore, we have the dependence ${\mathbf{x}}_{BC}^s={\mathbf{\Phi }}_{BC}^s(s-1,s,s+1)$, depicted graphically in Figure 2. Thus the internal boundary condition equations only contain Chebyshev coefficients (variables) of the immediately neighbouring spatial subdomains.

Figure 2. CBC subdomain schematic with algebraic equations indicated. The private variables (index “p”) are explicitly dependent on the boundary variables (index “BC”) of the given subdomain and implicitly on those of the neighbouring subdomains.

A numerical example may be elucidating. Let us assume that a system of five PDEs, representing second order in space, is solved in 1D. Employing $K=9$ and 10 spatial subdomains with $L=9$, a total of 5000 global equations result for the Chebyshev coefficients of Eq. (2). The CBC-GWRM algorithm reduces these to 1000. For 2D and 3D problems the reduction is even more profound.

The set of private equations ${\mathbf{x}}_P^s={\mathbf{\Phi }}_P^s$ is efficiently solved in parallel. Both these and the global equations ${\mathbf{x}}_{BC}^s={\mathbf{\Phi }}_{BC}^s$ are solved by SIR (2009). SIR solves the algebraic set of equations by iterating the following equation,

(7) ${\mathbf{x}}_{BC}^{i+1}=[\mathbf{I}+({\mathbf{R}}^i-\mathbf{I})({\mathbf{J}}_{BC}^i{)}^{-1}]({\mathbf{x}}_{BC}^i-{\mathit{\phi }}_{BC}^i)+{\mathit{\phi }}_{BC}^i\equiv {\mathbf{\Phi }}_{BC}^i({\mathbf{x}}_{BC}^i),$(7)

where $\mathit{\phi }$ denotes the right hand side of Eq. (6) plus the boundary equations. The matrix R with elements $R_{mn}=\mathrm{\partial }{\mathrm{\Phi }}_m/\mathrm{\partial }{x}_n$ controls convergence in SIR and I is the identity matrix. It should be noted that Eq. (7) is a formal representation; for efficiency matrix inversion is generally avoided and a matrix equation is solved instead. Thus the Jacobian ${\mathbf{J}}_{BC}^i$ needs to be computed,

(8) $J_{BCpq}=\frac{\mathrm{\partial }{({\mathbf{x}}_{BC}-{\mathit{\phi }}_{BC})}_p}{\mathrm{\partial }{x}_{BCq}}={\delta }_{pq}-T_{pq},$(8)

where ${\delta }_{pq}$ is the Kronecker delta and $T_{pq}$ includes the explicit and implicit derivatives;

(9) $T_{pq}=\frac{\mathrm{\partial }{\phi }_{BCp}}{\mathrm{\partial }{x}_{BCq}}+\sum _{\nu =s-1}^{\nu =s+1}\sum _{i=1}^{N_e{N}_p}\frac{\mathrm{\partial }{\phi }_{BCp}}{\mathrm{\partial }{x}_{Pi}^{\nu }}\frac{\mathrm{\partial }{x}_{Pi}^{\nu }}{\mathrm{\partial }{x}_{BCq}^{\nu }}.$(9)

The indices $p$ and $q$ refer to common BC variables and the index $i$ refers to the $N_p$ private variables. The first term is the explicit derivative. The second term shows that the common BC variables are indirectly dependent on the private variables in the neighbouring subdomains, hence the implicit derivatives. The index $\nu$ is introduced in the sum to neglect subdomains that are not directly influencing the current common BC variables.

The $\mathrm{\partial }{x}_P/\mathrm{\partial }{x}_{BC}$ coefficients in the sum require some attention. The first step is to create a vector of all private equations $f_i=z_i-{\phi }_i(z)$, $i=1\dots N_e{N}_p$, where $z$ and $\phi (z)$ only contain the private variables and equations from $x$ and $\phi (x)$. Since the private $z$ variables possess an implicit dependence on the common BC variables, the partial derivatives can be computed and saved in the matrix $F_{ij}=\mathrm{\partial }{f}_i/\mathrm{\partial }{z}_j$, $i=1\dots N_e{N}_p$ and $j=1\dots N_e{N}_{BC}$. The implicit derivatives in $F_{ij}$ are evaluated with current private values from the current scheme iteration and the $\mathrm{\partial }{x}_{Pi}/\mathrm{\partial }{x}_{BCj}$ variables are obtained by solving the linear algebraic system of equations $F_{ij}$.

An alternative method for obtaining the $\mathrm{\Delta }=\mathrm{\partial }{x}_P/\mathrm{\partial }{x}_{BC}$ coefficients in Eq. (9) is to approximate the derivative numerically with forward difference $\mathrm{\partial }{x}_P/\mathrm{\partial }{x}_{BC}\approx [x_P(x_{BC}+ϵ)-x_P(x_{BC})]/ϵ$. The set of private equations numbering $(L-1)(K+1)$ have to be solved for every BC variable, that is $2N_s{N}_e(K+1)$ times. The amount of operations can be further reduced since the calculated Jacobian from the regular solution $x_P(x_{BC})$ can be used for the perturbed solution $x_P(x_{BC}+ϵ)$ as well.

Another interesting development, with regards to the $\mathrm{\Delta }$ coefficients in (9), is that if the set of ODEs or PDEs are linear, then the $\mathrm{\Delta }$ coefficients are equal in all subdomains $s$ between $1<s<N_s$. Also, if the boundary conditions are the same on both sides of the computational domain, then only the first and second subdomain, for corresponding $\mathrm{\Delta }$ coefficients, need be solved.

A work flow of the Common Boundary Condition subdomain scheme, employing the latter numerical scheme for the Jacobian, applied to the 1D case, omitting physical parameter dependence, is given in the box below.

Table

CBC—subdomain scheme (1D, $M=0$) Comment: Define the bounded computational domain $D=\left\{(t,x):[t_0,t_1],[x_0,x_1]\right\}$. Then discretize the spatial domain into overlapping subdomains $N_s$. The $N_e$ partial differential equations, with initial conditions, are then spectrally decomposed. Assume here 2 external boundary conditions, so that $L-1$ spatial modes of Eq. (6) are computed. Precompute: Total set of equations $x_j={\phi }_j(\mathbf{x}),j=\mathrm{1..}N$, corresponding to equation (6), where $N=N_e{N}_s(K+1)(L+1)$ is the total number of equations to solve. Create set of private equations ${\mathbf{x}}_P^s={\phi }_P^s({\mathbf{x}}_P^s,{\mathbf{x}}_{BC}^s)$ numbering $N_P=N_e{N}_s(K+1)(L-1)$, and common BC equations ${\mathbf{x}}_{BC}={\phi }_{BC}({\mathbf{x}}_{BC})$ numbering $N_{BC}=2N_e{N}_s(K+1)$ by extracting the appropriate indices from the global set of equations. Step 1: Initial common boundary condition values ${\mathbf{X}}_{BC}^s$ are substituted into ${\mathbf{x}}_P^s={\phi }_P^s({\mathbf{x}}_P^s,{\mathbf{X}}_{BC}^s)$, so that only private variables are unknown. Call on SIR to solve private equations. Step 2: Compute $\mathrm{\partial }{x}_P/\mathrm{\partial }{x}_{BC}=[x_P(x_{BC}+ϵ)-x_P(x_{BC})]/ϵ$ by solving ${\mathbf{x}}_P^s={\phi }_P^s({\mathbf{x}}_P^s,{\mathbf{X}}_{BC}^s)$, for every BC variable $X_{BC}=X_{BC}+\epsilon$, i.e. $2N_s{N}_e(K+1)$ times. Here $\epsilon$ is the finite difference length. Step 3: Compute the BC Jacobian Eqs. (8)-(9) $J_{BCpq}={\delta }_{pq}-\frac{\mathrm{\partial }{\phi }_{BCp}}{\mathrm{\partial }{x}_{BCq}}-\sum _{\nu =s-1}^{\nu =s+1}\sum _{i=1}^{N_e{N}_p}\frac{\mathrm{\partial }{\phi }_{BCp}}{\mathrm{\partial }{x}_{Pi}^{\nu }}\frac{\mathrm{\partial }{x}_{Pi}^{\nu }}{\mathrm{\partial }{x}_{BCq}^{\nu }}.$ Step 4: Compute Eq. (7), ${\mathbf{x}}_{BC}^{i+1}={\mathbf{\Phi }}_{BC}^i({\mathbf{x}}_{BC}^i)$, which includes ${\mathbf{J}}_{BC}$ from step 3) and ${\phi }_{BC}({\mathbf{x}}_{BC})$ with private variables from step 1). This here is a linear system, hence it only requires a single SIR iteration to calculate the new common BC values ${\mathbf{x}}_{BC}^{i+1}$. Step 5: Repeat step 1), i.e. compute also ${\mathbf{x}}_P^s={\phi }_P^s({\mathbf{x}}_P^s,{\mathbf{X}}_{BC}^s)$, where ${\mathbf{X}}_{BC}={\mathbf{x}}_{BC}^{i+1}$ from step 4). Final: Update Chebyshev coefficients $a_{kl}$ in Eq. (2) using solution vector x.

4. Test problems

We have chosen to solve the linearised Burger equation, a forced linear wave equation, and a problem modelled with the linearised ideal MHD equations. Non-linear problems will be addressed in a forthcoming paper. All CBC-GWRM simulations are carried out on one global temporal interval, that is we here omit the use of time intervals. Also, since the following equations are linear with no-flow boundary conditions, the implicit derivatives are only calculated for the first and second subdomains.

4.1. Linearised 1D burger equation

The performance of the CBC-GWRM with regards to accuracy is here compared to that of the explicit Lax-Wendroff method, the implicit Crank-Nicolson method, and the “standard” GWRM with a global spatial subdomain scheme. The purpose of employing the Crank-Nicolson and Lax-Wendroff methods is to include two well known implicit and explicit finite difference methods that require little justification. The performance of other, more or less sophisticated, finite difference methods can easily be compared to these methods.

The parameters that determine the accuracy and efficiency of the GWRM are the order of temporal Chebyshev modes $K$, spatial Chebyshev modes $L$, and the number of spatial subdomains $N_s$. Similarly, the grid values determine the performance of the FD methods, namely $M$ temporal steps and $N$ spatial steps. The CPU time and memory consumption of all the methods are documented throughout.

The linearised 1D Burger equation is stated as follows:

(10) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}+b\frac{\mathrm{\partial }u}{\mathrm{\partial }x}=\kappa \frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}.$(10)

where $\kappa$ and b are constants. The initial condition and boundary conditions chosen here are

(11) $u(0,x)=\mathrm{s}\mathrm{i}\mathrm{n}(\pi x)e^{bx/2\kappa },$(11)

(12) $u(t,0)=u(t,1)=0.$(12)

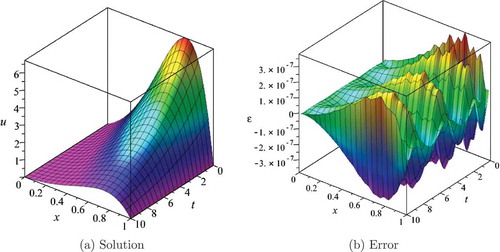
This enables an exact solution that can be used for accurate benchmarking (see Figure 3(a-b) for an example),

(13) $u(t,x)=\mathrm{s}\mathrm{i}\mathrm{n}(\pi x)e^{bx/2\kappa -(b^2/4\kappa +\kappa {\pi }^2)t}$(13)

Figure 3. CBC-GWRM solution and error with $\mathit{\kappa }\mathbf{=}\mathbf{0.01}$ and $\mathit{b}\mathbf{=}\mathbf{0.06}$; $\mathit{K}\mathbf{=}\mathbf{7}$, $\mathit{L}\mathbf{=}\mathbf{6}$ and ${\mathit{N}}_{\mathit{s}}\mathbf{=}\mathbf{7}$.

The CPU time and memory consumption of the CBC-GWRM have been compared with two finite difference methods; the explicit Lax-Wendroff and the implicit Crank-Nicolson methods. For a minimum accuracy of $\epsilon \sim {10}^{-3}$ the CBC-GWRM features a CPU runtime of $0.16s$ and a memory consumption of $20\mathrm{M}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{b}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s}$ (MB), using a Maple implementation on a desktop PC. This was achieved with the parameters $N_s=2$, $K=4$, and $L=5$. The Lax-Wendroff method with $M=340$ time steps and $N=45$ spatial steps featured a runtime of $0.94s$ and memory $54\mathrm{M}\mathrm{B}$. The Crank-Nicolson method required $0.09s$ and $20\mathrm{M}\mathrm{B}$ with parameters $M=60$ and $N=80$. Thus we see that for moderate accuracies the C-N method is approximately two times faster than CBC-GWRM and 10 times faster than L-W, all methods requiring comparable memory consumption.

However, when the accuracy is increased to $\epsilon \sim {10}^{-5}$, the CBC-GWRM with $N_s=3$, $K=6$, and $L=6$ features a CPU time of $0.50s$ and memory of $22\mathrm{M}\mathrm{B}$. The C-N method gave a CPU time of $0.77s$ and memory of $43\mathrm{M}\mathrm{B}$ for $M=120$ and $N=400$, whilst the L-W method was unable to reach a comparable accuracy. Thus the CBC-GWRM is here faster and more memory efficient for higher accuracies than both FD-methods. With the same parameters and accuracy $\epsilon \sim {10}^{-5}$ the standard GWRM (without the CBC-scheme) achieves a CPU time $t=0.27s$ and memory $23\mathrm{M}\mathrm{B}$. We show in Discussion, however, that the CPU time of the GWRM using the CBC scheme is strongly advantageous when a large number of spatial subdomains is employed.

The three methods have been analysed with optimal parameters so as to obtain the best accuracy for a given computational time. The data is displayed in Figure 4, thus showing how all three methods scale in this regard. A simple curve-fit of the data shows that the L-W method scales as ${\epsilon }_{LW}\sim t_{CPU}^{-0.6}$, and the C-N method scales slightly better at ${\epsilon }_{CN}\sim t_{CPU}^{-0.9}$. The spectral convergence properties of the CBC-GWRM allows a much stronger scaling than the FD methods; ${\epsilon }_{GWRM}\sim t_{CPU}^{-3.5}$. It is also found that the CPU time scales linearly as $t_{CPU}\sim N_s^{1.1}$ with regards to the number of subdomains used, see Figure 11(a), in Discussion. This feature of the CBC-GWRM becomes advantageous when modelling physical systems that require high local spatial accuracy.

Figure 4. Error plot vs CPU time [s].

Figure 5. Temporal plot for interval $\mathbf{[}\mathbf{0}\mathbf{,}\mathbf{80}\mathbf{]}$ at $\mathbf{x}\mathbf{=}\mathbf{0.2}$ showing how the CBC-GWRM (blue line) resolves the slower time scale of the exact solution (red line). The parameters used are ${\mathit{N}}_{\mathit{s}}=\mathbf{4}$, $\mathit{K}\mathbf{=}\mathbf{14}$, and $\mathit{L}\mathbf{=}\mathbf{5}$.

Figure 6. Comparison between the standard (global) GWRM and the CBC-scheme with analytical derivatives for the wave equation. (a) The subdomain scaling and (b) memory consumption is plotted for parameters $\mathit{A}\mathbf{=}\mathbf{10}$, $\mathit{n}\mathbf{=}\mathbf{3}$, $\mathit{T}\mathbf{=}\mathbf{30}$, $\mathit{\alpha }\mathbf{=}\mathbf{2}\mathit{\pi }/\mathit{T}$, $\mathit{\beta }\mathbf{=}\mathbf{3}\mathit{\pi }$ and $\mathit{c}\mathbf{=}\mathbf{1}$ with time interval $\mathit{t}\mathbf{\in }\mathbf{[}\mathbf{0}\mathbf{,}\mathbf{30}\mathbf{]}$.

Figure 7. Perturbed screw-pinch, CBC-GWRM $\mathit{K}\mathbf{=}\mathbf{7}$, $\mathit{L}\mathbf{=}\mathbf{5}$ and ${\mathit{N}}_{\mathit{s}}\mathbf{=}\mathbf{3}$.

Figure 8. Eigenfunction $\mathit{\xi }\mathbf{(}\mathit{r}\mathbf{)}$ of perturbation $\mathit{m}\mathbf{=}\mathbf{1}$, $\mathit{k}\mathbf{=}\mathbf{5}$. CBC-GWRM (line) mode growth rate ${\mathit{\omega }}_{\mathit{C}\mathit{B}\mathit{C}}\mathbf{=}\mathbf{0.839}$, $\mathit{K}\mathbf{=}\mathbf{7}$, $\mathit{L}\mathbf{=}\mathbf{5}$ and ${\mathit{N}}_{\mathit{s}}\mathbf{=}\mathbf{3}$; Bateman ${\mathit{\omega }}_{\mathit{B}}\mathbf{=}\mathbf{0.840}$ (point-line).

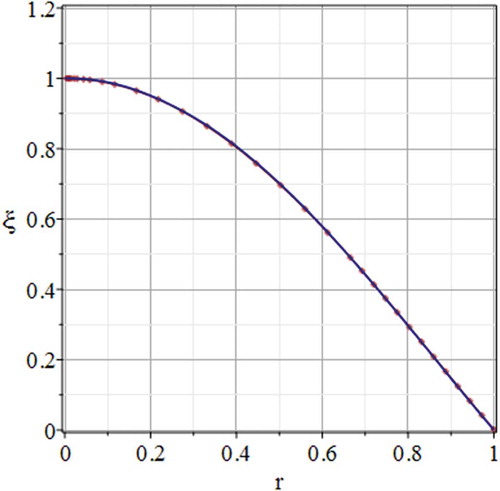
Figure 9. Total CPU time [s] vs number of subdomains for solving all corresponding algebraic equations (see Eq. (6)) for 1D linearised Burger computation; CBC-GWRM (blue) and standard GWRM (red), with the same parameters $\mathit{K}\mathbf{=}\mathbf{5}$ and $\mathit{L}\mathbf{=}\mathbf{5}$.

Figure 10. CPU time [s] with increasing subdomains for a 1D linearised Burger computation; GWRM parameters $\mathit{K}\mathbf{=}\mathbf{5}$ and $\mathit{L}\mathbf{=}\mathbf{5}$.

Figure 11. (a) CPU time [s] and (b) Memory consumption [MB] with increasing subdomains for 1D linearised Burger computation; CBC-GWRM (blue), Reduced CBC-GWRM (purple), standard GWRM (red), and an approximated parallelized time that follows Amdahl’s law for Reduced CBC-GWRM (green). All methods use parameters $\mathit{K}\mathbf{=}\mathbf{5}$ and $\mathit{L}\mathbf{=}\mathbf{5}$.

4.2. Forced wave equation

The forced wave equation in this next example is a second order hyperbolic differential equation that features two time scales. This equation is used to test efficiency, in the sense that in some cases accuracy at small scales may be ignored in favour of efficiently resolving large scale dynamics. The wave equation has the form

(14) $\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{t}^2}=c^2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+f(t,x).$(14)

It is here worth noting that the GWRM can solve the wave equation in its single equation form (14). However, in order to accurately compare with the finite difference methods the wave equation is posed as two, first order in time, partial differential equations:

$\frac{\mathrm{\partial }v}{\mathrm{\partial }t}=c^2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+f(t,x),$

$\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=v.$

The initial and boundary conditions are

$u(0,x)=\mathrm{s}\mathrm{i}\mathrm{n}(\pi x),$

$v(0,x)=\alpha A\mathrm{s}\mathrm{i}\mathrm{n}(\beta x),$

$u(t,0)=u(t,1)=0,$

$v(t,0)=v(t,1)=0.$

Here $A$, $n$, $\alpha$, $\beta$ and $c$ are free parameters. The forcing term chosen is

$f(t,x)=A(c^2{\beta }^2-{\alpha }^2)\mathrm{s}\mathrm{i}\mathrm{n}(\alpha t)\mathrm{s}\mathrm{i}\mathrm{n}(\beta x).$

This leads to the exact solution

(15) $u(t,x)=\mathrm{c}\mathrm{o}\mathrm{s}(nc\pi t)\mathrm{s}\mathrm{i}\mathrm{n}(n\pi x)+A\mathrm{s}\mathrm{i}\mathrm{n}(\alpha t)\mathrm{s}\mathrm{i}\mathrm{n}(\beta x).$(15)

We set the free parameters to to $A=10$, $n=3$, $T=80$, $\alpha =6\pi /T$, $\beta =3\pi$ and $c=1$. For the time interval $t\in [0,80]$ the CBC-GWRM requires a high number of temporal Chebyshev modes $K\ge 12$ to achieve a reasonable average (within 92% percent of the second, slowly evolving part of the solution (15)) of the fast time scale dynamics. The solution at $x=0.2$ can be seen in Figure 5.

Since it is inefficient to solve for more than one wavelength with high order temporal modes, a more efficient approach would be to solve the wave equation with parameters $A=10$, $n=3$, $T=30$, $\alpha =2\pi /T$, $\beta =3\pi$ and $c=1$ in a time interval $t\in [0,30]$. This allows a temporal mode $K=5$ to accurately average the fast time scale (within 95% percent of the slow manifold). The CBC-GWRM with parameters $K=5$, $L=5$, and $N_s=4$ achieves a CPU time of $0.69s$, which is comparable to the standard GWRM subdomain scheme with the same parameters, requiring $0.83s$. In Figure 6(a-b) the standard GWRM and the CBC-scheme, employing analytical derivatives, shows the memory consumption and CPU time with increasing subdomains.

Turning to the finite difference methods, the L-W method is able to accurately resolve the slow time scale with parameters $M=1200$ and $N=40$ in $1.5s$. The L-W method initially follows the fast time scale until the solution advances further away from the initial condition, in which case it transforms to the slow time scale.

The parameters used for the C-N solution is $M=50$ and $N=50$, which gives a run time of $1.4s$. The C-N method fails to average correctly as it is slightly out of phase. Explicit methods, unlike implicit methods, are conditionally stable because they must obey the CFL condition $\gamma \mathrm{\Delta }t/\mathrm{\Delta }x\le 1$, where $\gamma$ is the wave speed, $\mathrm{\Delta }t$ is the temporal step length, and $\mathrm{\Delta }x$ is the spatial step length. However, since the forced wave equation is a hyperbolic equation, the FD methods need to resolve the phase of the wave in order to be accurate. Furthermore, the phase can only be resolved by following the strong stability criterion, in which case the implicit method shows no favourable performance over explicit schemes (Appadu, 2013).

To conclude, in this example the CBC-scheme is approximately $2.1$ times faster than the finite difference methods when one wavelength is simulated with a $K=5$ temporal Chebyshev mode. Similar, and even higher, accuracy and efficiency levels can be attained using lower order temporal modes and multiple time intervals rather than high order temporal modes with few time intervals (Scheffel, Lindvall, Yik, & Time-Spectral, 2018). The memory consumption of the CBC-GWRM is also superior compared to the GWRM global subdomain scheme. This can be seen in Figure 6(b); a curve fit of the data reveals that the memory consumption of the CBC-scheme scales linearly, whilst the global GWRM scheme memory scaling is quadratic. These are substantial increases in performance which allows the CBC-GWRM to be highly competitive when solving physical systems with high degrees of freedom.

4.3. Ideal MHD

The ideal MHD equations are useful to investigate whether the CBC-GWRM is capable of accurately modelling complex physical systems. The ideal MHD model is a set of coupled partial differential equations that describe the dynamics of a perfectly conductive fluid or plasma. The equations may be stated as

(16) $\frac{\mathrm{\partial }\rho }{\mathrm{\partial }t}+\mathrm{\nabla }\cdot (\rho \mathbf{v})=0,$(16)

(17) $\rho \left(\frac{\mathrm{\partial }}{\mathrm{\partial }t}+\mathbf{v}\cdot \mathrm{\nabla }\right)\mathbf{v}+\mathrm{\nabla }p-\mathbf{J}\times \mathbf{B}=\mathbf{0},$(17)

(18) $\frac{\mathrm{\partial }p}{\mathrm{\partial }t}+\mathrm{\nabla }\cdot (p\mathbf{v})+(\mathrm{\Gamma }-1)p\mathrm{\nabla }\cdot \mathbf{v}=0,$(18)

(19) $\frac{\mathrm{\partial }\mathbf{B}}{\mathrm{\partial }t}+\mathrm{\nabla }\times \mathbf{E}=\mathbf{0}$(19)

(20) $\mathrm{\nabla }\times \mathbf{B}-{\mu }_0\mathbf{J}=\mathbf{0},$(20)

(21) $\mathbf{E}+\mathbf{v}\times \mathbf{B}=\mathbf{0}.$(21)

The first three equations model the fluid; the continuity Eq. (16) models the conservation of mass density $\rho$; the equation of motion (17) solves for the fluid velocity $v$; and the energy equation (18) models the adiabatic evolution of the pressure profile $p$;

(22) $\left(\frac{\mathrm{\partial }}{\mathrm{\partial }t}+\mathbf{v}\cdot \mathrm{\nabla }\right)\left(\frac{p}{{\rho }^{\mathrm{\Gamma }}}\right)=0,$(22)

where $\mathrm{\Gamma }=5/3$ is the ratio of specific heats. The second set of equations involves the electromagnetic equations that describe the evolution of the magnetic field B, electric field E, and the current density J; Faraday’s law (19), Ampere’s law (20), where ${\mu }_0$ is the permeability in vacuum, and Ohm’s law (21).

The goal here is to model ideal MHD instabilities that occur in a magnetically confined cylindrical plasma with coordinates $(r,\theta ,z)$. The CBC-GWRM is applied to the ideal MHD equations when linearized about an equilibrium, which consequently consist of 14 (7 real and 7 imaginary) coupled partial differential equations. A perturbation $\propto \mathrm{e}\mathrm{x}\mathrm{p}[i(m\theta +kz)]$ is introduced, where $m$ and $k$ are the azimuthal and axial mode numbers, respectively.

The inner boundary conditions need to be handled with some care to avoid singularities at $r=0$ (Lundin, 2006). The outer boundary $r=1$ condition is that of a perfectly conducting wall, hence the radial components are set to zero at the wall.

The equilibrium chosen is a simple screw-pinch equilibrium (in normalized variables),

$B_r=0,B_t=r,B_z=0.05,$

$p_0=1-r^2,J_t=0,J_z=2.$

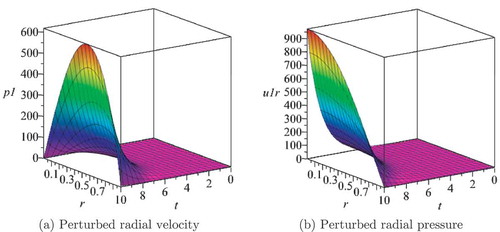
The equilibrium was then perturbed using $m=1$ and $k=5$. The time evolution of the perturbed radial velocity and pressure is shown in Figure 7(a-b). Initially the perturbed variables are dominated by a host of different waves, which is why the simulation has to advance far enough for the dominating unstable mode to become distinguishable.

The growth rate obtained from the CBC-GWRM is compared to that of a shooting code developed in (Bateman, 1978), see Figure 8. The CBC-GWRM calculates a growth rate ${\omega }_{CBC}=0.839$ whilst the shooting code obtains a growth rate ${\omega }_B=0.840$. For higher accuracy it is advisable to use multiple time intervals with fewer temporal modes. This application of the CBC-GWRM to the linearized ideal MHD equations shows the advantage of using a Chebyshev spectral ansatz because of its ability to average over small scale dynamics. The initial waves that propagate are of no interest, and are averaged out, leaving the dominating unstable mode.

5. Discussion

The CBC-GWRM has several favourable properties; 1) rapid spectral convergence and high accuracy in both time and space, 2) real-valued Chebyshev polynomials having the useful mini-max property, 3) sparse matrix methods for solving the coefficient equations, 4) reduced global coefficient matrix equations where only the internal and external boundary condition equations need be solved, and 5) parallellized solution of the subdomain private equations. The first three points are common properties of time-spectral methods, while this work is focused on points 4) and 5). Regarding 4), in the example problems of this paper the number of operations is reduced by a factor $\sim (2/L{)}^3$ and the memory usage by $\sim (2/L{)}^2$ since only the internal and external boundary condition equations are solved globally. The “2” comes from the fact that only the two highest spatial Chebyshev modes are allocated for the two boundary conditions employed.

We can find a scaling law estimate for the efficiency of the CBC-GWRM. The number of private equations for one physical equation in each subdomain of, for example the Burger equation is $(L-1)(K+1)$. In order to produce the partial derivatives of equation (9), the private set of equations need to be solved twice for each common boundary condition and temporal mode. The total number of operations is then $2N_s(K+1)(L-1{)}^3(K+1{)}^3$ when a single PDE is solved. The number of global common boundary condition equations are $2N_s(K+1)$. The CPU time of the standard GWRM scheme with sparse band matrix algorithms scales approximately as $N_s^{1.4}$; the same procedures are used to solve the condensed common boundary condition matrix. Thus the ratio of the total number of operations for the CBC-GWRM and the standard GWRM is

(23) $\frac{2N_s{(L-1)}^3{(K+1)}^4+N_s^{1.4}{2}^3{(K+1)}^3}{N_s^{1.4}{(L+1)}^3{(K+1)}^3}=\frac{2(K+1)}{N_s^{0.4}}{\left(\frac{L-1}{L+1}\right)}^3+\frac{2^3}{{(L+1)}^3}.$(23)

From Eq. (23) it can be seen that the CBC-GWRM is more efficient than the standard GWRM when $N_s$ is large. For example; $L=5$ and $K=5$ gives the criterion that $N_s\stackrel{>;}{\sim \phantom{{ }_x}}27$ for the CBC-GWRM to be more efficient. This is an important result since many fluid dynamics applications suggest $N_s>100$. The scaling law Eq. (23) only takes into account the amount of operations it takes to solve the total amount of algebraic equations (6) for both the CBC-GWRM and the standard GWRM, that is excluding all overhead operations, such as calculating the Jacobian matrices etcetera; see Figure 9 for actual CPU times consistent with the scaling argument in Eq. (23).

The effect of the first term in Eq. (23), representing private domain computations, can be reduced substantially by employing parallellization. Thus, the limiting dependence $(2/(L+1){)}^3$ can be approached. The estimation of the parallelizable time was made from the speed-up gains ascertained from Amdahl’s Law (Amdahl, 1967). Amdahl’s law is formulated as $S=1/[(1-p)+p/s]$, where S is the speed-up gain, s is the proportion of the code that can be computed in parallel, and p is the unoptimized computation time. Here s has been calculated by the CPU times corresponding to the proportion of the code that can be parallelized. In Figure 10 the CBC-GWRM, with overhead operations, shows that the CPU times are still comparable to the standard GWRM. There are, however, further means to improve efficiency.

For linear PDEs with constant coefficients it has been found that due to the constant implicit derivatives, the implicit variable dependencies $\mathrm{\partial }{x}_P/\mathrm{\partial }{x}_{BC}$ in Eq. (9) need not be solved for in more than three subdomains, which includes the first, second and last subdomain. If the two boundary conditions are the same then the minimum amount of subdomains that need to be solved are two, i.e. the first and second subdomain. Thus, the minimum amount of operations required to solve the private equations corresponding to a linear PDE with no-flow, or equal-flow, boundary conditions is $4(K+1)(L-1{)}^3(K+1{)}^3$. This gives a more favourable scaling law than (23):

(24) $\frac{4{(L-1)}^3{(K+1)}^4+N_s^{1.4}{2}^3{(K+1)}^3}{N_s^{1.4}{(L+1)}^3{(K+1)}^3}=\frac{4(K+1)}{N_s^{1.4}}{\left(\frac{L-1}{L+1}\right)}^3+\frac{2^3}{{(L+1)}^3}.$(24)

Figure 11(a) shows how the CPU time, including overhead operations, for the linearised Burger equation, scales with the number of subdomains $N_s\in [10,100]$ for the reduced CBC-GWRM, the standard GWRM with all equations solved globally, and the reduced CBC-GWRM adjusted for approximate parallelizable speedup gains. Here reduced refers to the reduction in implicit derivative calculations discussed above. The standard GWRM and reduced CBC-GWRM show comparable CPU times when few subdomains are used. However, the advantage of the CBC scheme, in both CPU times and memory consumption (see Figure 11(b)), is evident when more subdomains are used. The substantial reduction of the memory consumption that can be attained with the CBC-GWRM is of considerable importance for many applications, such as when employing more degrees of freedom in the physical domain.

The avenue of parallelizable subdomains grows even more advantageous when studying the ideal MHD equations. For the ideal MHD case approximately 95% of the code can be parallelized, which according to Almdahl’s Law gives a speedup $>12$ if more than 32 processors are used and it saturates at $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{p}=20$ for cores numbering 2048 and higher (Amdahl, 1967).

To close, it has been widely held that time-spectral methods are not as efficient as their finite difference counterparts. While spectral methods do feature higher accuracies, the idea of lacking efficiency has now been challenged by such methods as the GWRM and the spectral deferred correction method. The spectral deferred correction method still, most commonly, relies on implicit and explicit finite difference methods to create a crude initial approximation, which is then corrected. This is achieved by using spectral integration in-between the finite time steps which is included to correct the crude approximation. This makes the spectral deferred correction method a high order method, requiring longer computation times (Gustafsson & Hemmingsson, 2002; Gustafsson & Kress, 2001; Speck et al., 2015).

6. Conclusion

The CBC-GWRM solves a set of initial-value ordinary or partial differential equations in the temporal and spatial domains with a time-spectral weighted residual method, using a novel algorithm for increasing efficiency and reducing memory consumption. This allows the method to obtain high accuracy and to efficiently average over small scale dynamics, as seen in the modelling of the linearised Burger and forced wave equations. Before this work the “standard” GWRM solved all subdomains simultaneously from the global set of algebraic equations. Our goal was to break down the problem into smaller pieces for enhancing efficiency. The CBC-method provides a solution to this problem.

For the 1D linearised Burger equation the CBC-GWRM was compared to finite difference methods. At low accuracy the implicit finite difference scheme outperformed both the explicit and the time-spectral methods. The maximum error, however, of the CBC-GWRM solution scales as ${\epsilon }_{GWRM}\sim t_{CPU}^{-3.47}$, compared to ${\epsilon }_{LW}\sim t_{CPU}^{-0.6}$ and ${\epsilon }_{CN}\sim t_{CPU}^{-0.9}$. This allows CBC-GWRM to be 30% faster than Crank-Nicolson for accuracies $\epsilon \sim {10}^{-5}$. The CBC-GWRM CPU time also approaches a scaling of $\sim N_s^{1.1}$, with increasing number of subdomains, which is an improvement from the standard GWRM $N_s^{1.4}$ scaling.

An optimal scaling law for the total amount of operations of linear PDEs was found (see Eq. (23)). With the technique of only calculating the implicit derivatives in the first and second subdomain, applied to solution of the 1D linearised Burger equation, it was found for the CBC-GWRM that with $N_s=50$ there was a $\sim 53$% and $\sim 33$% reduction in CPU time and memory consumption, respectively. Thus the CBC-GWRM outperforms the standard GWRM (global subdomain scheme) in both CPU times and memory consumption.

The linearized ideal MHD equations were solved within $0.1$% error for the instability growth in a screw-pinch, in agreement with previous simulations (Scheffel, 2011). This accuracy was reached using a single time interval, making the CBC-GWRM highly competitive when solving for slow unstable mode growth rates. This shows that the CBC-GWRM is capable of solving complex physical systems that are relevant for fusion plasma physics, whilst efficiently resolving the temporal domain. The CBC-GWRM is also shown to substantially reduce memory requirements as compared to the earlier “standard” GWRM.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Kristoffer Lindvall

Kristoffer Lindvall is a Ph.D. student in the Fusion Plasma Physics department at KTH Royal Institute of Technology, Stockholm, Sweden. He received his Master of Science (M.Sc.) degree from Luleå University of Technology of Sweden in Aerospace Engineering. He specialises in numerical methods and their applications in fusion plasma physics.