An extension of Rayleigh distribution and applications

Abstract

In this article, we have derived a new distribution named as Rayleigh–Rayleigh distribution (RRD) motivated by the transformed transformer technique by Alzaatreh, Lee, and Famoye (2013). The statistical properties of RRD, comprising of explicit expressions for quantile function, moments, moment generating function, mean deviation, skewness, kurtosis, reliability measures, measures of uncertainty, distributions of order statistics and L moments have been derived. Parameter estimation is carried out using method of maximum-likelihood estimation and Fisher information matrix is derived. The flexibility of the new distribution is assessed by applying it to four real data sets. The comparative behavior of RRD with Rayleigh distribution, Generalized Rayleigh distribution, Exponentiated Rayleigh distribution, Weibull Rayleigh distribution and Alpha Power Rayleigh distribution provided the evidence that it outperforms the other competing distributions.

Keywords:

• Fisher information matrix
• moment generating function
• ORDER STATISTICS
• maximum-likelihood estimation

PUBLIC INTEREST STATEMENT

One of the basic tools of statistics is to modeling the real-life phenomenon in the form of statistical distributions. Adding parameters in the existing distribution and combining two or more existing distributions are two common techniques used for the generalization of a distribution. These generalized distributions accommodate the changing circumstances and complexities of real life. In this study, we have extended the Rayleigh distribution by adding the parameter of the other Rayleigh distribution. The resultant distribution contained two parameters and is called Rayleigh–Rayleigh distribution (RRD). Simulation study revealed that estimators of the parameters are asymptotically unbiased and efficient. The application of RRD to four real data sets exhibited the more flexibility of RRD as compared to some other life time distributions. It is hoped that the proposed distribution will attract the attention of the researcher in the fields of life sciences, physical sciences and social sciences.

1. Introduction

Uncertainties and risks are two main realities of real-life phenomena. Probability theory is used to handle these uncertainties and modeling of these real-life phenomena. Due to variation, complexities and diversities in real life, a large number of statistical distributions are derived. Still there are many important problems where the real-life data do not follow any standard probability distributions. This leads to the extensions and development of generalized statistical distributions.

In literature numerous generalized distributions have been developed with common feature of having more parameters. Induction of parameters in existing distribution improves the goodness of fit of the distribution under study and tail properties of a distribution increases.

Rayleigh distribution (RD) introduced by Lord Rayleigh in 1880 plays a crucial role in modelling and analyzing life time data such as project effort loadings modelling, life testing experiments, reliability analysis, communication theory, physical sciences, engineering, medical imaging science, applied statistics and clinical studies. Let the random variable X has RD with scale parameter, $\beta$i.e. X$\text{~}$RD (x;$\beta )$. Then the probability density function (PDF) and the cumulative density function (CDF) of RD are defined as

(1) $\psi \left(x;\beta \right)=\frac{x}{{\beta }^2}{e}^{-\frac{x^2}{2{\beta }^2}},x>0;\beta >0$(1)

(2) $\mathrm{\Psi }\left(x;\beta \right)=1-e^{-\frac{x^2}{2{\beta }^2}},x>0;\beta >0$(2)

Due to the importance of Raleigh distribution in a variety of fields, a wide range of extensions of Raleigh Distribution has been established. Kundu and Raqab (2005) proposed the generalized RD and its unknown parameters are estimated by using different estimation methods. Abd Elfattah, Hassan, and Ziedan (2006) studied the estimation of unknown parameter of RD in the presence of different censoring sampling schemes. Voda (2007) proposed the new generalization of RD by using conservability approach. In this technique the PDF of generalized distribution can be obtained as$-g\left(y\right)=\frac{yf\left(y\right)}{E\left(y\right)}$, where $f\left(y\right)$ and $E\left(y\right)$ are PDF and finite mean of positive continuous random variable. Dey (2009) derived the Bayes estimators for the parameter of RD by using square error and LINEX loss functions. Merovci (2013) developed the transmuted RD by using quadratic rank transmutation technique. Merovci (2014) proposed the transmuted generalized RD and describe its mathematical properties. Merovci and Elbatal (2015) studied the Weibull RD. Mahmoud and Ghazal (2017) deliberated the parameters estimation of exponentiated Rayleigh based on type II censored data.

In this article we have derived the generalization of the RD named as Rayleigh–Rayleigh distribution (RRD) using Transformed Transformer technique proposed by Alzaatreh, Lee, and Famoye (2013). Main motivation of this study is to generate a new distribution by adding scale parameter in the RD, so that the performance of generalized distribution becomes better than the original one.

According to Transformed Transformer method the function form of CDF of a random variable is used to transform PDF of other random variable into a new distribution. Let T be a continuous random variable with PDF and CDF $\phi \left(t\right)$ and $\mathrm{\Phi }\left(t\right)$, respectively, for$-\mathrm{\infty }\le a<t<b\le \mathrm{\infty }$. Let X is another random variable with PDF $\psi \left(x\right)$ and CDF $\mathrm{\Psi }\left(x\right)$. W [$\mathrm{\Psi }\left(x\right)$] is a functional form of CDF of the random variable X defined on the support of random variable T, it is differentiable and monotonically non- decreasing function and when $x\to -\mathrm{\infty }$ then $\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]\to a$ and when $x\to \mathrm{\infty }$ then $\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]\to b$. The PDF of random variable T is transformed into the function of random variable X through the transformer W [$\mathrm{\Psi }\left(x\right)$]. The new generalized family of distribution is called the T-X family of distribution. Let $G\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}g\left(x\right)$be the CDF and PDF of generalized family of distributions, respectively, then

$G\left(x\right)={\int }_a^{\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]}\phi \left(t\right)dt=\mathrm{\Phi }\left\{\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]\right\}$

$g\left(x\right)=\left\{\frac{d}{dx}\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]\right\}\mathrm{\varnothing }\left\{\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]\right\}$

By taking different functional forms of $\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]$, large number of generalized families of distributions can be formed. For discrete random variable X, discrete families of distributions can be derived. T-Geometric family of discrete distributions is proposed by Alzaatreh, Lee, and Famoye (2012).

Consider the support of random variable T is [0,$\mathrm{\infty }$), then the functional form of $\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]$may be defined as (-log [1-$\mathrm{\Psi }\left(x\right)$]) which satisfied all the above three conditions. The CDF of new generalized distribution is defined as

(3) $G\left(x\right)={\int }_0^{-\mathrm{l}\mathrm{o}\mathrm{g}\left[1-\mathrm{\Psi }\left(x\right)\right]}\phi \left(t\right)dt=\mathrm{\Phi }\left\{-\mathrm{l}\mathrm{o}\mathrm{g}\left[1-\mathrm{\Psi }\left(x\right)\right]\right\}$(3)

and the PDF is

(4) $g\left(x\right)=\frac{\psi \left(x\right)}{1-\mathrm{\Psi }\left(x\right)}\mathrm{\varnothing }\left\{-\mathrm{l}\mathrm{o}\mathrm{g}\left[1-\mathrm{\Psi }\left(x\right)\right]\right\}$(4)

In the literature, a large number of generalized families of distributions has been derived and studied by using Transformed-Transformer technique, e.g. T-geometric family of discrete distributions by Alzaatreh et al. (2012), T-normal family by Alzaatreh, Lee, and Famoye (2014), Logistic-X by Tahir, Cordeiro, Alzaatreh, Mansoor, and Zubair (2016), Weibull-G by Tahir et al. (2016), Gompertz-G family of distribution by Alizadeh, Cordeiro, Pinho, and Ghosh (2017), etc.

The rest of the paper is organized as follows. Section 2 presents the derivation of RRD along with shape of its PDF and CDF. Reliability analysis is studied with the shapes of survival and hazard rate function in Section 3. In Section 4, statistical properties like quantile function, moments and moment generating function, skewness and kurtosis are investigated. Section 5 present the Shannon and Re’nyi entropies. Order statistics and L-moments are derived in Section 6. Maximum-likelihood estimators and information matrix are defined in Section 7. In Section 8 simulation study is carried out to examine performance of the maximum-likelihood estimators of parameters of RRD. In Section 9, four real-life data sets are considered to examine the application of RRD in real-life phenomena and comparison of proposed distribution with parent and other existing distributions. Finally, the study is concluded in Section 10.

2. Rayleigh–Rayleigh distribution

In this Section, an RRD is derived. Let random variable T follows RD having PDF given in expression (1) with scale parameter${\sigma }^2$. The functional form of $\mathrm{W}\left[\mathrm{\Psi }\left(x\right)\right]$ is defined as (–log [1–$\mathrm{\Psi }\left(x\right)$]) depending upon the support of Rayleigh random variate T. Then the PDF of Rayleigh-X family of distributions is given as

(5) $\mathrm{g}\left(\mathrm{x}\right)=\frac{\psi \left(\mathrm{x}\right)\left[-log\left[1-\mathrm{\Psi }\left(\mathrm{x}\right)\right]\right]}{{\sigma }^2\left[1-\mathrm{\Psi }\left(\mathrm{x}\right)\right]}\mathrm{e}-\frac{[\mathrm{l}\mathrm{o}\mathrm{g}{\left(1-\mathrm{\Psi }\left(\mathrm{x}\right)\right]}^2}{2{\sigma }^2};\mathrm{x}>,\sigma >0$(5)

and the corresponding CDF is defined as

(6) $\mathrm{G}\left(\mathrm{x}\right)=1-\mathrm{e}-\frac{log{\left(1-\mathrm{\Psi }\left(\mathrm{x}\right)\right)}^2}{2{\sigma }^2};\mathrm{x}>,\sigma >0$(6)

By taking different distributions of random variable X, a large number of Rayleigh-X distributions can be obtained such as Rayleigh–Gamma, Raleigh–Pareto, Rayleigh–Gumbel, Rayleigh-Exponential, etc. In our study, we assumed that X is another Rayleigh variate with scale parameter $\beta$ i.e. X~ RD (x;$\beta )$. By substituting the value of $\mathrm{\Psi }$(x) and $\psi \left(\mathrm{x}\right)$ define in (1) and (2) having parameter $\beta$ in expression (5) the PDF of the RRD is obtained as

(7) $\mathrm{g}\left(\mathrm{x}\right)=\frac{{\mathrm{x}}^3}{2{\beta }^4{\sigma }^2}{\mathrm{e}}^{-\frac{{\mathrm{x}}^4}{8{\beta }^4{\sigma }^2}};\mathrm{x}>0\beta >0,\sigma >0$(7)

The CDF of RRD is

(8) $\mathrm{G}\left(\mathrm{x}\right)=1-{\mathrm{e}}^{-\frac{{\mathrm{x}}^4}{8{\beta }^4{\sigma }^2}};\mathrm{x}>0\beta >0,\sigma >0$(8)

By adding a scale parameter in the base line distribution, the generalized distribution is expected to be more flexible to model complicated real-life phenomena than the original one.

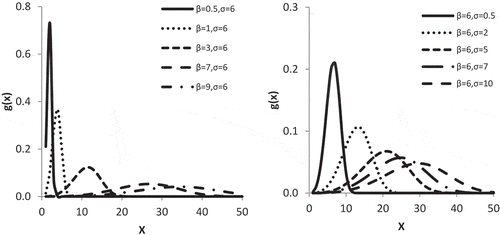
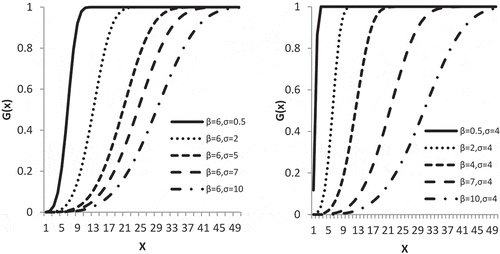
Figures 1 and 2 illustrate some of the possible shapes of the PDF and CDF of RRD for some selected values of the parameters β and σ. The PDF plots in Figure 1 reveal that the RRD is unimodel, increasing and decreasing.

Figure 1. PDF of RRD for various values of $\sigma$ and $\beta$.

Figure 2. Plots of CDF of RRD for various values of $\sigma$ and $\beta$.

3. Reliability analysis

The reliability function $S\left(x\right)$ focuses the probability of an event for a specific time without failing the event. CDF and $S\left(x\right)$ are reverse of each other. The $S\left(x\right)$ for RRD is defined as

$S\left(x\right)=e^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}$

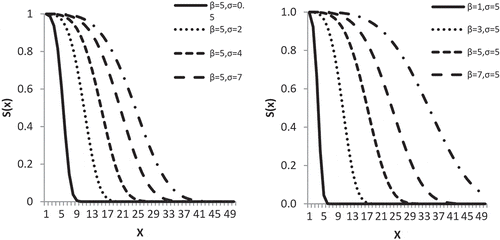
For various values of $\beta$ and$\sigma$, the reliability function is monotonically decreasing which is shown in Figure 3.

Figure 3. The survival function of RRD for various values of $\sigma$ and $\beta$.

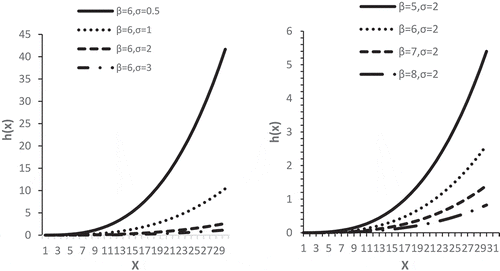
The ratio of PDF and reliability function is hazard rate function. That is another specification in reliability analysis. The hazard rate function for the NGR distribution is given as

$h\left(x\right)=\frac{g\left(x\right)}{S\left(x\right)}=\frac{x^3}{2{\beta }^4{\sigma }^2}$

The plots of hazard rate function are exponentially increasing which is shown in Figure 4.

Figure 4. The hazard functions of RRD for various values $\beta and\sigma$.

4. Statistical properties

In this section, we have derived the statistical properties of the RRD, specifically quantile function, random number generator, moments, moment generating function, skewness, kurtosis and mean deviation.

4.1. Quantile function and simulation

Here and hereafter let the random variable “X” follows RRD with parameters$\beta$and $\sigma$i.e. X$\sim$RRD (x;$\beta ,\sigma )$. The quantile function corresponding to the CDF of RRD is

$Q\left(p\right)=G^{-1}\left(p\right)={\left[8{\beta }^4{\sigma }^{2}ln\left(\frac{1}{1-p}\right)\right]}^{\frac{1}{4}},0\le \mathrm{p}\le 1$

Median, first and third quartiles of RRD can conveniently derived by substituting $p=1/2,1/4,3/4$, respectively.

The RR random variate can easily be simulated by taking U as a uniform random variate on the unit interval. By using the technique proposed by Alzaatreh et al. (2013) the random X is generated as

(9) $X={\left(8{\beta }^4{\sigma }^{2}ln\left(\frac{1}{1-U}\right)\right)}^{\frac{1}{4}}$(9)

4.2. Moments and moment generating function

Moments are necessary and important in any statistical analysis, especially in applications. It can be used to study the most important features and characteristics of the distribution e.g. central tendency, dispersion, skewness and kurtosis.

4.2.1. rth Moment

By definition the rth moment about origin of “X” is

(10) $E\left(X^r\right)={\int }_0^{+\mathrm{\infty }}{x}^{r}g\left(x\right)dxr=1,2,3,\dots ={\int }_0^{+\mathrm{\infty }}{x}^r\frac{x^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}dx=8^{\frac{r}{4}}{\beta }^r{\sigma }^{\frac{r}{2}}\mathrm{\Gamma }\left(\frac{r}{4}+1\right)$(10)

For$\mathrm{r}=1$, 2, 3 and 4, the first four non-central moments of NGR distribution are specified as

$E\left(X\right)={\mu }_1^{\prime }=\left(1.5243812\right)\beta {\sigma }^{\frac{1}{2}},$

$E\left(X^2\right)={\mu }_2^{\prime }=\left(2.5066282\right){\beta }^2\sigma$

$E\left(X^3\right)={\mu }_3^{\prime }=\left(4.3718226\right){\beta }^3{\sigma }^{\frac{3}{2}}$

$E\left(X^4\right)={\mu }_4^{\prime }=8{\beta }^4{\sigma }^2$

4.2.2. Negative moments

The negative moment generating function is defined as

$\mathrm{E}\left(X^{-r}\right)={\int }_0^{\mathrm{\infty }}{x}^{-r}g\left(x\right)$

For the random variable of RRD

(11) $\mathrm{E}\left(X^{-r}\right)={\int }_0^{\mathrm{\infty }}{x}^{-r}\frac{x^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}dx=8^{\frac{-r}{4}}{\beta }^{-r}{\sigma }^{\frac{-r}{2}}\mathrm{\Gamma }\left(1-\frac{r}{4}\right)$(11)

4.2.3. Moment generating function

The moment generating function of “X” is

(12) $E\left(e^{tX}\right)={\int }^{e^{tx}}g\left(x\right)dx={\int }_0^{+\mathrm{\infty }}{\sum }_{j=1}^{\mathrm{\infty }}{\frac{\left(tx\right)}{j!}}^j\frac{x^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}dx={\sum }_{j=0}^{\mathrm{\infty }}\frac{t^j}{j!}{8}^{\frac{j}{4}}{\beta }^j{\sigma }^{\frac{j}{2}}\mathrm{\Gamma }\left(\frac{j}{4}+1\right)$(12)

4.2.4. Characteristic function

The characteristic function of random variable X is defined as

$\mathrm{E}\left(e^{itX}\right)={\int }_0^{+\mathrm{\infty }}{\sum }_{k=1}^{\mathrm{\infty }}{\frac{\left(itx\right)}{k!}}^k\frac{x^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}dx={\sum }_{k=1}^{\mathrm{\infty }}\frac{{\left(it\right)}^k}{k!}{\int }_0^{+\mathrm{\infty }}\frac{x^{k+3}}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}dx={\sum }_{k=1}^{\mathrm{\infty }}\frac{{\left(it\right)}^k}{k!}{8}^{\frac{k}{4}}{\beta }^k{\sigma }^{\frac{k}{2}}\mathrm{\Gamma }\left(\frac{k}{4}+1\right)$

4.3. Skewness and kurtosis

The coefficient of Skewness and kurtosis of RRD is given as

$\mathrm{C}\mathrm{o}-\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{s}\mathrm{k}\mathrm{e}\mathrm{w}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}=({\beta }_1)=\frac{{\mu }_3^{2/3}}{{\mu }_2}=\frac{{\left[-0.0068229{\beta }^3{\sigma }^{\frac{3}{2}}\right]}^{2/3}}{0.18289{\beta }^2\sigma }$

$=-0.19669$

$\mathrm{C}\mathrm{o}-\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{k}\mathrm{u}\mathrm{r}\mathrm{t}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{s}=({\beta }_2)=\frac{{\mu }_4}{{\mu }_2^2}=\frac{\left[0.0919116{\beta }^4{\sigma }^2\right]}{{\left[0.1828901{\beta }^2\sigma \right]}^2}$

$=2.7478295$

Hence, RRD is platykurtic and negatively skewed distribution.

4.4. Mean deviation

The mean deviation of “X” is

$M.D=E\left(\left|x-\mu \right|\right)={\int }_0^{+\mathrm{\infty }}\left|x-\mu \right|g\left(x\right)dx=2\mu [1-e^{-\frac{{\mu }^4}{8{\beta }^4{\sigma }^2}}\left]-2\right[8^{\frac{1}{4}}\beta {\sigma }^{\frac{1}{2}}\gamma \left(\frac{5}{4},\frac{{\mu }^4}{8{\beta }^4{\sigma }^2}\right)$

5. Measure of uncertainty

Entropy measures the dynamical uncertainty of the probability distribution, unpredictability of the state or disorder of a system … …

5.1. Shannon entropy

Shannon (1948) proposed the idea of entropy. The Shannon entropy of “X” is defined as

(13) $I_s\left(x\right)=E\left(-log\left[g\left(x\right)\right]\right)=-{\int }_0^{\mathrm{\infty }}\left[logg\left(x\right)\right]g\left(x\right)dx=-log\left[\frac{{\left(8{\beta }^4{\sigma }^2\right)}^{3/4}}{2{\beta }^4{\sigma }^2}\right]+\frac{3}{4}\left(\gamma \right)+1$(13)

Where $\gamma$ is the Euler constant and its value is 0.5772.

5.2. Renyi Entropy

The generalized form of Shannon entropy is R$\text{mathop elimits^}$nyi entropy, proposed by R$\text{mathop elimits^}$nyi (1961). The R$\text{mathop elimits^}$nyi Entropy of “X”, denoted by $I_R\left(x\right)$ can be defined as

(14) $I_R\left(x\right)=\frac{1}{1-\lambda }\mathrm{l}\mathrm{o}\mathrm{g}{\int }_0^{+\mathrm{\infty }}{g}^{\lambda }\left(x\right)dx=\frac{1}{1-\lambda }log\left[1-\frac{{\left(2{\beta }^4{\sigma }^2\right)}^{\left(1-\lambda \right)}{(8{\beta }^4{\sigma }^2)}^{\frac{3}{4}\left(\lambda -1\right)}}{{\lambda }^{\left(\frac{3}{4}\lambda +\frac{1}{4}\right)}}\left(\frac{3}{4}\lambda +\frac{1}{4}\right)\right],\mathrm{f}\mathrm{o}\mathrm{r}\lambda \ge 0$(14)

6. Order statistics

For the sake of data analysis relating to quality control, reliability, hydrological and extreme values, order statistics and moments of order statistics play a starring role. In this Section, we have derived the PDFs of the kth order, maximum and minimum order statistics from the RRD.

6.1. The PDF of the smallest order statistic

Let $X_{\left(1\right)}$is the first order statistics from random sample $X_1,X_2,\dots ,X_m$from RRD. The PDF of $X_{\left(1\right)}$is defined as

$g_{1:m}\left(x\right)=m\left[\frac{x^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}\right]{\left[e^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}\right]}^{m-1};0\le x_{\left(1\right)}\le +\mathrm{\infty }$

6.2. The PDF of the largest order statistic

For the order statistics of the sample drawn from RRD, the PDF of the largest order statistics $X_{\left(m\right)}$ is given as

$g_{m:m}\left(x\right)=m\left[\frac{x^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}\right]{\left[1-e^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}\right]}^{m-1}$; $0\le x_{\left(m\right)}\le +\mathrm{\infty }$

6.3. The joint PDF of ith and jth order statistics

Let the joint pdf of the $ith$ and $jth$ order statistics is denoted by $g_{i:j:m}\left(x,y\right),$then using the standard formula this can be derived as

$g_{i:j:m}\left(x,y\right)=\frac{m!}{\left(i-1\right)!\left(j-i-1\right)!\left(m-j\right)!}[\frac{x^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}]\left[\frac{y^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{y^4}{8{\beta }^4{\sigma }^2}}\right]$

$\times {\left[1-e^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}\right]}^{i-1}{\left[e^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}-e^{-\frac{y^4}{8{\beta }^4{\sigma }^2}}\right]}^{j-i-1}{\left[e^{-\frac{x^4}{8{\beta }^4{\sigma }^2}}\right]}^{m-j}$

$;1\le i\le j\text{lem},;0\le x\le y\le +\mathrm{\infty }$

6.4. L-moments

In statistics, conventional moments have a great importance to describe the shape of a distribution but provide inadequate performance in case of extreme values due to the sensitivity to extreme observations. Moreover, the conventional moments are asymptotically inefficient for fat tails distributions. In such a situation many empirical studies shows that the L-moments, the linear combination of ordered statistics outperform the conventional moments. Like the conventional moments, the estimation process using the population L-moments and sample L-moments of a distribution can be carried out. The measures of skewness and kurtosis derived in term of L-moments are named as L-skewness and L-kurtosis, respectively.

In this study, the L-moments of X have been derived through the probability weighted moments (PWM) and this method was introduced by Hosking (1990). The PWM denoted by ${\beta }_r$ are given below

${\beta }_r=E[X{\left[G\left(x\right)\right]}^r]$; r = 0, 1, 2, 3 …

${\beta }_0=8^{\frac{1}{4}}\beta {\sigma }^{\frac{1}{2}}\mathrm{\Gamma }\left(\frac{5}{4}\right)$

${\beta }_1={\left(8{\beta }^4{\sigma }^2\right)}^{\frac{1}{4}}\mathrm{\Gamma }\left(\frac{5}{4}\right)\left[1-\frac{1}{2^{\left(\frac{5}{4}\right)}}\right]$

${\beta }_2={\left(8{\beta }^4{\sigma }^2\right)}^{\frac{1}{4}}\mathrm{\Gamma }\left(\frac{5}{4}\right)]\left[1+\frac{1}{3^{\left(\frac{5}{4}\right)}}-\frac{1}{2^{\left(\frac{1}{4}\right)}}\right]$

${\beta }_3={\left(8{\beta }^4{\sigma }^2\right)}^{\frac{1}{4}}\mathrm{\Gamma }\left(\frac{5}{4}\right)]\left[1-\frac{3}{2^{\left(\frac{5}{4}\right)}}+\frac{1}{3^{\left(\frac{1}{4}\right)}}-\frac{1}{4^{\left(\frac{5}{4}\right)}}\right]$

The rth L-Moment denoted by${\lambda }_r$ is the linear combination of PW moments. The first four L-moments of X are

${\lambda }_1={\beta }_0=8^{\frac{1}{4}}\beta {\sigma }^{\frac{1}{2}}$ $\mathrm{\Gamma }\left(\frac{5}{4}\right)$=$1.52438\beta {\sigma }^{\frac{1}{2}}$

${\lambda }_2=2{\beta }_1-{\beta }_0=2.10123\beta {\sigma }^{\frac{1}{2}}$

${\lambda }_3=6{\beta }_2-6{\beta }_1+{\beta }_0==-0.0046\beta {\sigma }^{\frac{1}{2}}$

${\lambda }_4=20{\beta }_3-30{\beta }_2+12{\beta }_1-{\beta }_0=0.02659\beta {\sigma }^{\frac{1}{2}}$

Consequently the L-Skewness of RRD is

${\tau }_3=\frac{{\lambda }_3}{{\lambda }_2}=\frac{-0.0046\beta {\sigma }^{1/2}}{2.10123\beta {\sigma }^{1/2}}=-0.00219$

and the L-Kurtosis of RRD is

${\tau }_4=\frac{{\lambda }_4}{{\lambda }_2}=\frac{\left(0.02659\right)\beta {\sigma }^{\frac{1}{2}}}{\left(2.10123\right)\beta {\sigma }^{\frac{1}{2}}}=0.01266$

7. Maximum-likelihood estimation and Fisher information matrix

Due to possessing the asymptotic properties of normality and efficiency, the maximum-likelihood estimators have greater importance in statistical inference. In this Section, maximum-likelihood estimators of the parameters of RRD have been derived. Let X_1, X_2, X_{3, …,} X_n be a random sample from X$\text{~}$RRD(x;$\beta ,\sigma )$. Then the likelihood function of the observed sample is given as

$\mathrm{L}\left(x_1,x_2,\dots ,x_n;\beta ,\sigma \right)={\prod }_{i=1}^n\left[\frac{x_i^3}{2{\beta }^4{\sigma }^2}{e}^{-\frac{x_i^4}{8{\beta }^4{\sigma }^2}}\right]$

and the corresponding log likelihood function is

(17) $l=lnL\left(x_1,x_2,\dots ,x_n;\beta ,\sigma \right)={\sum }_{i=1}^{n}ln{x}_i^3-nln2-4nln\beta -2nln\sigma -\frac{{\sum }_{i=1}^n{x}_i^4}{8{\beta }^4{\sigma }^2}$(17)

By applying the rule of maximum-likelihood estimation, expression (17) is partially differentiated with respect to $\beta$ and $\sigma$ and equating to zero, the corresponding normal equations are given as

(18) $\frac{\mathrm{\partial }l}{\mathrm{\partial }\beta }=-\frac{4n}{\beta }-\frac{{\sum }_{i=1}^n{x}_i^4}{2{\beta }^5{\sigma }^2}=0$(18)

(19) $\frac{\mathrm{\partial }l}{\mathrm{\partial }\sigma }=-\frac{2n}{\sigma }+\frac{{\sum }_{i=1}^n{x}_i^4}{4{\sigma }^3{\beta }^4}=0$(19)

The expression (18) and (19) cannot be solved analytically. R package is used to solve them numerically by using Newton–Raphson method.

To obtain the Fisher’s information matrix (FIM), the second derivatives of the log likelihood function are derived as

$\frac{{\mathrm{\partial }}^{2}l\left(\mathrm{x};\beta ,\sigma \right)}{\mathrm{\partial }{\beta }^2}=\frac{4}{{\beta }^2}-\frac{5x^4}{2{\sigma }^2{\beta }^6}$

$\frac{{\mathrm{\partial }}^{2}l\left(\mathrm{x};\beta ,\sigma \right)}{\mathrm{\partial }\beta \mathrm{\partial }\sigma }=-\frac{x^4}{{\beta }^5{\sigma }^3}$

$\frac{{\mathrm{\partial }}^{2}l\left(\mathrm{x};\beta ,\sigma \right)}{\mathrm{\partial }{\sigma }^2}=\frac{2}{{\sigma }^2}-\frac{3x^4}{4{\beta }^4{\sigma }^4}$

$\mathrm{F}\mathrm{I}\mathrm{M}=\mathrm{I}\left(\mathrm{\Delta }\right)=-E\left[\begin{array}{cc}\frac{2}{{\sigma }^2}-\frac{3x^4}{4{\beta }^4{\sigma }^4}& -\frac{x^4}{{\beta }^5{\sigma }^3}\\ -\frac{x^4}{{\beta }^5{\sigma }^3}& \frac{4}{{\beta }^2}-\frac{5x^4}{2{\sigma }^2{\beta }^6}\end{array}\right]=\left[\begin{array}{cc}\frac{4}{{\sigma }^2}& \frac{8}{\beta \sigma }\\ \frac{8}{\beta \sigma }& \frac{16}{{\beta }^2}\end{array}\right]$

As the MLE are asymptotically unbiased and normally distributed with its variance covariance matrix obtained from the inverse of FIM. Hence, the interval estimation and hypothesis testing of the model parameters can easily be applied.

8. Simulation study

In this Section, simulation study has been carried out to check the performance of the estimators. Using the R statistical package 5,000 replications of sample sizes n = 50, 100, 150, 200, 300 and 400 have been generated from RRD by using the random number generator given in expression (9). Four different combinations of values of the actual parameters are taken. The average ML estimates (MLE_AV.) of the parameters along with average bias (BIAS_AV.) and average root mean square error ($RMS{E}_{AV.})$ are reported in Tables 1–4.

Table 1. MLE’s, average bias and average root mean square error at β = 1.5, 2, 2.5, 3 and σ = 1.5

ACTUAL VALUE			$ML{E}_{AV.}$		$BIA{S}_{AV.}$		$RMS{E}_{AV.}$
n	β	σ	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$
50	1.5	1.5	1.49,596	1.49,383	−0.00404	−0.00617	0.05360	0.10,677
100			1.49,939	1.49,970	−0.00060	−0.00029	0.03682	0.07362
150			1.49,950	1.49,963	−0.00050	−0.00037	0.03098	0.06191
200			1.49,814	1.49,675	−0.00186	−0.00325	0.02643	0.05274
300			1.49,951	1.49,933	−0.00049	−0.00067	0.02154	0.04305
400			1.49,980	1.49,984	−0.00019	−0.00016	0.01879	0.03758
50	2	1.5	1.99,621	1.49,621	−0.00379	−0.00379	0.07116	0.10,647
100			1.99,790	1.49,780	−0.00209	−0.00219	0.05025	0.07526
150			1.99,936	1.49,966	−0.00065	−0.00034	0.04101	0.06147
200			1.99,879	1.49,867	−0.00120	−0.00133	0.03549	0.05318
300			1.99,983	1.50,006	−0.00017	6.25e-05	0.02903	0.04354
400			1.99,945	1.49,940	−0.00055	−0.00059	0.02446	0.03667
50	2.5	1.5	2.49,439	1.49,510	−0.00561	−0.00489	0.08726	0.10,439
100			2.49,692	1.49,724	−0.00307	−0.00276	0.06203	0.07427
150			2.49,835	1.49,864	−0.00165	−0.00136	0.05064	0.06071
200			2.49,879	1.49,901	−0.00121	−0.00099	0.04401	0.05279
300			2.49,911	1.49,925	−0.00089	−0.00075	0.03632	0.04357
400			2.49,992	1.50,010	−7.38e-05	0.00014	0.03109	0.03731
50	3	1.5	2.99,414	1.49,603	−0.00586	−0.00397	0.10,636	0.10,599
100			2.99,703	1.49,796	−0.00297	−0.00204	0.07480	0.07469
150			2.99,864	1.49,927	−0.00136	−0.00073	0.06126	0.06123
200			2.99,877	1.49,925	−0.00123	−0.00075	0.05375	0.05369
300			2.99,961	1.49,992	−0.00039	−7.77e-05	0.04325	0.04321
400			2.99,988	1.50,011	−0.00012	−0.00012	0.03755	0.03754

Table 2. MLE’s, average bias and average root mean square error σ = 1, 1.25, 1.5, 1.75 and β = 2

ACTUAL VALUES			$ML{E}_{AV.}$		$BIA{S}_{AV.}$		$RMS{E}_{AV.}$
n	β	σ	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$
50	2	1.00	1.99,552	0.99,683	−0.00447	−0.00317	0.07219	0.07191
100			1.99,691	0.99,753	−0.00309	−0.00247	0.05000	0.04990
150			1.99,912	0.99,954	−0.00088	−0.00046	0.04097	0.04092
200			1.99,857	0.99,889	−0.00143	−0.00111	0.03556	0.03553
300			1.99,919	0.99,931	−0.00081	−0.00060	0.02884	0.02882
400			1.99,940	0.99,956	−0.00051	−0.00044	0.02502	0.02500
50	2	1.25	1.99,561	1.24,611	−0.00430	−0.00381	0.07092	0.08833
100			1.99,938	1.25,002	−0.00062	1.73,145	0.05038	0.06297
150			1.99,907	1.24,936	−0.00093	−0.00063	0.04134	0.05161
200			1.99,889	1.24,900	−0.00111	−0.00099	0.03514	0.04390
300			1.99,954	1.24,969	−0.00046	−0.00031	0.02899	0.03623
400			1.99,987	1.25,004	−0.00013	3.60,225	0.02548	0.03185
50	2	1.50	1.99,568	1.49,538	−0.00431	−0.00462	0.07025	0.10,506
100			1.99,713	1.49,662	−0.00287	−0.00337	0.04978	0.07447
150			1.99,814	1.49,783	−0.00186	−0.00216	0.04077	0.06103
200			1.99,838	1.49,805	−0.00161	−0.00195	0.03547	0.05318
300			1.99,971	1.49,988	−0.00029	−0.00011	0.02907	0.04358
400			1.99,954	1.49,955	−0.00045	−0.00045	0.02466	0.03698
50	2	1.75	1.99,739	1.74,757	−0.00261	−0.00242	0.06985	0.12,205
100			1.99,705	1.74,597	−0.00294	−0.00403	0.05055	0.08823
150			1.99,906	1.74,906	−0.00094	−0.00093	0.04039	0.07067
200			1.99,925	1.74,925	−0.00074	−0.00075	0.03560	0.06225
300			2.00013	1.75,058	0.00013	0.00059	0.02839	0.04969
400			1.99,942	1.74,926	−0.00058	−0.00074	0.02510	0.04399

Table 3. MLE’s, average bias and average root mean square error for σ = 2.5, 3, 3.5, 4 and β = 1.5, 2, 2.5, 3

ACTUAL VALUES			$ML{E}_{AV.}$		$BIA{S}_{AV.}$		$RMS{E}_{AV.}$
n	β	σ	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$
50	2.5	1.5	2.49,384	1.49,439	−0.00615	−0.00561	0.08606	0.10,295
100			2.49,707	1.49,743	−0.00293	−0.00257	0.06269	0.07507
150			2.49,765	1.49,782	−0.00235	−0.00218	0.05145	0.06165
200			2.49,929	1.49,962	−0.0007	−0.00039	0.04391	0.05266
300			2.49,878	1.49,886	−0.00122	−0.00114	0.03623	0.04344
400			2.49,938	1.49,948	−0.00062	−0.00052	0.03076	0.03689
50	3	2	2.99,248	1.99,251	−0.00752	−0.00749	0.10,678	0.14,173
100			2.99,787	1.99,838	−0.00213	−0.00162	0.07409	0.09869
150			2.99,789	1.99,805	−0.00211	−0.00195	0.06208	0.08262
200			2.99,837	1.99,846	−0.00163	−0.00153	0.05348	0.07125
300			2.99,880	1.99,882	−0.00119	−0.00118	0.04282	0.05704
400			2.99,949	1.99,963	−0.00051	−0.00038	0.03732	0.04976
50	3.5	2.5	3.49,365	2.49,418	−0.00634	−0.00582	0.12,613	0.17,974
100			3.49,606	2.49,592	−0.00394	−0.00408	0.08710	0.12,425
150			3.49,645	2.49,598	−0.00354	−0.00402	0.07157	0.10,212
200			3.49,897	2.49,929	−0.00103	−0.00071	0.06151	0.08782
300			3.49,885	2.49,885	−0.00115	−0.00115	0.04955	0.07076
400			3.49,957	2.49,979	−0.00043	−0.00021	0.04467	0.06380
50	4	3	3.99,004	2.98,869	−0.00996	−0.01130	0.13,918	0.20,796
100			3.99,486	2.99,416	−0.00514	−0.00584	0.09997	0.14,972
150			3.99,693	2.99,661	−0.00308	−0.00339	0.08077	0.12,098
200			3.99,895	2.99,937	−0.00105	−0.00063	0.07110	0.10,661
300			3.99,757	2.99,696	−0.00243	−0.00304	0.05652	0.08471
400			4.00007	3.00057	7.059e-5	0.00057	0.04981	0.07471

Table 4. MLE’s, average bias and average root mean square error σ = 1.5, 2.5, 3.5, 4.5 and β = 1.5, 2.5, 3.5, 4.5

ACTUAL VALUES			$ML{E}_{AV.}$		$BIA{S}_{AV.}$		$RMS{E}_{AV.}$
n	β	σ	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$	$\hat{\beta }$	$\hat{\sigma }$
50	1.5	1.5	1.49,778	1.49,744	−0.00222	−0.00256	0.05317	0.10,602
100			1.49,869	1.49,828	−0.00131	−0.00172	0.03661	0.07313
150			1.49,983	1.50,029	−0.00017	0.00028	0.03076	0.06153
200			1.49,921	1.49,888	−0.00079	−0.00112	0.02645	0.05285
300			1.49,885	1.49,801	−0.00115	−0.00199	0.02161	0.04318
400			1.49,949	1.49,921	−0.00051	−0.00079	0.01855	0.03707
50	2.5	2.5	2.49,209	2.48,744	−0.0079	−0.01256	0.08998	0.17,919
100			2.49,696	2.49,551	−0.00303	−0.00449	0.06267	0.12,506
150			2.49,800	2.49,707	−0.00199	−0.00293	0.05171	0.10,328
200			2.49,912	2.49,904	−0.00088	−0.00096	0.04466	0.08926
300			2.49,891	2.49,835	−0.00109	−0.00165	0.03607	0.07209
400			2.49,959	2.49,955	−0.00042	−0.00045	0.03084	0.06170
50	3.5	3.5	3.49,208	3.48,849	−0.00792	−0.01150	0.12,315	0.24,559
100			3.49,689	3.49,595	−0.00311	−0.00404	0.08726	0.17,441
150			3.49,771	3.49,686	−0.00229	−0.00314	0.07119	0.14,225
200			3.49,819	3.49,746	−0.00181	−0.00254	0.06113	0.12,213
300			3.49,826	3.49,722	−0.00174	−0.00278	0.04924	0.09844
400			3.49,808	3.49,668	−0.00194	−0.00332	0.04300	0.08594
50	4.5	4.5	4.49,232	4.49,023	−0.00768	−0.00977	0.15,861	0.31,610
100			4.49,279	4.48,842	−0.00720	−0.01158	0.11,261	0.22,454
150			4.49,747	4.49,681	−0.00253	−0.00318	0.09200	0.18,380
200			4.49,888	4.49,911	−0.00112	−0.00088	0.07820	0.15,639
300			4.49,921	4.49,934	−0.00079	−0.00066	0.06451	0.12,899
400			4.49,886	4.49,839	−0.00114	−0.00161	0.05483	0.10,958

The results showing in Tables 1–4 for all the combinations of four sets of values of parameters, mentioned above, demonstrate that average bias for both the parameters appear negative which indicates that the estimators are under estimated and value of bias approaches to zero by increasing sample size. Hence, estimators of the parameters of RRD are asymptotically unbiased. These maximum-likelihood estimates remains under estimated by varying the values of both parameters. Values of average root mean square error decrease by increasing the sample size indicating that the estimators are asymptotically efficient. There is no effect on value of root mean square error by increasing or decreasing the values of parameters. Both of the evidences show that maximum-likelihood estimators of the parameters of RRD perform well and estimates are precise and accurate.

9. Real-life applications

In this Section, we have explored the comparative performance of RRD with five existing distributions: RD by Lord Rayleigh (1880); Generalized Rayleigh distribution (GRD) by Kundu and Raqab (2005); Exponentiated Rayleigh distribution (ERD) by (Mahmoud and Ghazal (2017); Weibull Rayleigh distribution (WRD) by Merovci and Elbatal (2015); Alpha Power Rayleigh distribution (APRD) by Malik and Ahmed (2017).

The comparison is carried out by taking the following four real data sets:

1. Lifetime data set of the 46 patients survival times (in years) to given treatment of chemotherapy already used by Bekker, Roux, and Mosteit (2000) and Fundi, Njenga, and Keitany (2017)

2. Data set about the strengths of 1.5 cm glass fibers that is measured at the National Physical Laboratory in England used by Smith and Naylor (1987).

3. Real-life data set about the breaking stress of carbon fibers of 50 length (GPA) already used by Cordeiro and Lemonte (Cordeiro & Lemonte, 2011), Al-Aqtash, Lee (Al-Aqtash, Lee, & Famoye, 2014) .

4. Real-life data set about the wind speed of Elanora Heights. In November 2007, average wind speeds (in meter/sec) is used by Best, Rayner, & Thas (2010).

The data sets and their sources can be seen in the respective references. Hereafter we will call the above data sets as Dataset1, Dataset 2, Dataset 3 and Dataset 4, respectively.

For the comparison of the distributions, the goodness of fit criteria used are −2lnL, Akaike information criterion (AIC) by Akaike (1974), Consistent Akaike information criterion (CAIC) by Bozdogan (1987), and Bayesian information criterion (BIC) by Schwarz (1978) and Hannan-Quinn Information Criterion (HQIC) by Hannan and Quinn (1979). AIC estimates the performance of a model while comparing with other models. CAIC provide a consistent and asymptotically unbiased estimate of order of the true model. HQIC is a consistent model selection criterion. The distribution with smaller values of −2lnL, AIC, BIC, CAIC and HQIC is considered as the best distribution. The specifications of these criteria are as follows:

$AIC=2\left(k\right)-2lnL$, $BIC=kln\left(n\right)-2lnL$,

$CAIC=\frac{2kn}{n-k-1}-2lnLHQIC=2kln\left(ln\left(n\right)\right)-2lnL$

where k = number of estimated parameters in the distribution

$\mathrm{l}\mathrm{n}\mathrm{L}$ = maximized log likelihood of the distribution under consideration

n = total number of observations

The estimated parameter of the distributions under consideration along with the values of goodness fit criteria for Dataset1, Dataset2, Dataset3 and Dataset4 are given in Table 5–8, respectively.

Table 5. ML estimates with goodness-of-fit criteria for Dataset 1

Distribution	MLE’s	−2lnL	AIC	BIC	CAIC	HQIC
RRD	0.8473 2.9049	266.3496	270.3496	274.0069	270.6287	271.7196
RD	1.275,513	370.5238	372.5238	374.3524	372.6147	373.2088
GRD	6.998e + 05 33.1500	456,357.6	456,361.6	456,365.3	456,361.9	456,363
ERD	1.250e + 06 1.343e + 03	532,170	532,174	532,177.7	532,174.3	532,175.4
WRD	1.91,841 0.05829 7.31,097	709.1966	715.1966	720.6825	715.768	717.2517
APRD	1.0010 9.9230	445.1736	449.1736	452.8309	449.4527	450.5436

Table 6. ML estimates with goodness-of-fit criteria for Dataset2

Distribution	MLE’s	−2lnL	AIC	BIC	CAIC	HQIC
RRD	64.1621 2.6587	2869.298	2873.298	2877.851	2873.5	875.111
RD	87.14,575	3,290,926	3,290,928	3,290,930	3,290,928	3,290,929
GRD	5.81e + 7 0.2490	148,217	148,221	148,225.5	148,221.2	148,222.8
ERD	2.64e + 4 4.513	9,868,740	9,868,744	9,868,749	9,868,744	9,868,746
WRD	2.64e + 4 4.5130 4.32	9,868,740	9,868,746	9,868,753	9,868,746	9,868,749
APRD	1.002 2.2e + 05	2922.032	2926.032	2930.585	2926.206	2927.845

Table 7. ML estimates with goodness-of-fit criteria for Dataset3

Distribution	MLE’s	−2lnL	AIC	BIC	CAIC	HQIC
RRD	1.728 1.152	518.501	522.501	526.8803	522.6915	524.2315
RD	698.929	1397.859	1399.859	1402.049	1399.922	1400.724
GRD	7.4e + 05 5.911	43,512.92	43,516.92	43,521.3	43,517.11	43,518.65
ERD	2.5e + 06 42.00	52,163.14	52,167.14	52,171.52	52,167.33	52,168.87
WRD	1.4273 0.5705 4.1920	9.31e + 12	9.31e + 12	9.31e + 12	9.31e + 12	9.31e + 12
APRD	1.003 292.18	1374.049	1378.049	1382.429	1378.24	1379.78

Table 8. ML estimates with goodness-of-fit criteria for Dataset4

Distribution	MLE’s	−2lnL	AIC	BIC	CAIC	HQIC
RRD	0.4397 3.9565	48.1491	52.1491	5495149	52.59354	53.04561
RD	0.8832089	69.893	71.893	73.295	72.036	72.342
GRD	1.801e + 05 4.673	1338.858	1342.858	1345.66	1343.302	1343.754
ERD	1.424e + 05 21.210	1293.930	1297.930	1300.732	1298.374	1298.827
WRD	0.34350 0.00902 96.0878	87.211	93.211	97.415	94.134	94.556
APRD	1.001 12.193	295.576	299.576	302.379	300.021	300.473

The results given in Table 5–8 show that the values of −2lnL, AIC, BIC, CAIC and HQIC are smallest for NGRD as compared to the other distributions under consideration. The above results strongly lead to recommend that our proposed distribution outperforms the RD, GRD, ERD, WRD and APRD for the selected data sets.

Hence, for given data sets RRD is chosen as the best fitted model than the competitors models.

10. Conclusion

In this study, RD is successfully generalized by adding one-scale parameter from other RD. Explicit expression of probability density and cumulative distribution function are derived. Behavior of parameters is checked by PDF and CDF plots. Comprehensive studies of the statistical properties of the new distribution have been presented. The reliability behavior of RRD is investigated by varying the values of the parameters. Order statistics, distribution of the order statistics and L-moments are also derived. The estimation of the parameters is performed through maximum-likelihood approach. Results of simulation study shows that maximum-likelihood estimators of proposed model are asymptotically unbiased and root mean square error reduces by increasing the sample size. The application of the suggested distribution to four real-life data exhibited that RRD outperformed some other existing distributions. In all the four datasets proposed RRD performs better than original RD. Hence, the induction of one or more parameter improves the performance of a distribution. It is hoped that the proposed distribution will attract the attention of researchers and practitioners in the fields of physical sciences, biological sciences, actuarial studies and social sciences.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Kahkashan Ateeq

Kahkashan Ateeq is an assistant professor in the Department of Statistics, The Women University Multan and Ph.D. scholar at Bahauddin Zakariya University Multan. Her area of interest is distribution theory and Bayesian analysis.

Tahira Bano Qasim

Dr Tahira Bano Qasim is assistant professor in the Department of Statistics, The Women University Multan. She earned her M.Sc., M.phil and Ph.D. degrees in Statistics from Bahauddin Zakariya University, Multan. Her research interests lie in the field of distribution theory and time series modeling with the issue of Conditional Heteroscedasticity. She has three publications in different journals.

Ayesha Rehman Alvi

Ayesha Rehman Alvi is an M.Phil Student at The Women University Multan. Her research interests lie in the field of Distribution Theory and Applications. Present paper is a portion of her M.Phil thesis under the supervision of Dr. Tahira Bano Qasim and Co-Supervision of Kahkashan Ateeq.